Abstract
We consider the probabilistic untyped lambda-calculus and prove a stronger form of the adequacy property for probabilistic coherence spaces (PCoh), showing how the denotation of a term statistically distributes over the denotations of its head-normal forms.
We use this result to state a precise correspondence between PCoh and a notion of probabilistic Nakajima trees, recently introduced by Leventis in order to prove a separation theorem. As a consequence, we get full abstraction for PCoh. This latter result has already been mentioned as a corollary of Clairambault and Paquet’s full abstraction theorem for probabilistic concurrent games. Our approach allows to prove the property directly, without the need of a third model.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Full abstraction for the maximal consistent sensible \(\lambda \)-theory \(\mathcal {H}^\star \) [1] is a crucial property for a model of the untyped \(\lambda \)-calculus, stating that two terms M, N have the same denotation in the model iff for every context \(C[\,]\) the head-reduction sequences of C[M] and C[N] either both terminate or both diverge. The first such result was obtained for Scott’s model \(\mathcal {D}^\infty \) by Hyland [10] and Wadsworth [15]. More recently, Manzonetto developed a general technique for achieving full abstraction for a large class of models, decomposing it into the adequacy property and a notion of well-stratification [13]. An adequacy property states that the semantics of a \(\lambda \)-term is different from the bottom element iff its head-reduction terminates. Well-stratification is more technical, basically it means that the semantics of a \(\lambda \)-term can be stratified into different levels, expressing in the model the nesting of the head-normal forms defining the interaction between a \(\lambda \)-term and a context.
Our paper reconsiders these results in the setting of the probabilistic untyped \(\lambda \)-calculus \(\varLambda ^+\). The language extends the untyped \(\lambda \)-calculus with a barycentric sum constructor allowing for terms like \(M+_pN\), with \(p\in [0,1]\), reducing to M with probability p and to N with probability \(1-p\). In recent years there has been a renewed interest in \(\varLambda ^+\) as a core language for (untyped) discrete probabilistic functional programming. In particular, Leventis proves in [12] a separation property for \(\varLambda ^+\) based on a probabilistic version of Nakajima trees, the latter describing a nesting of sub-probability distributions of infinitary \(\eta \)-long head-normal forms (see Sect. 5 and the examples in Fig. 2).
We consider the semantics of \(\varLambda ^+\) given by the probabilistic coherence space \(\mathcal {D}\) defined by Danos and Ehrhard in [5] and proved to be adequate in [6]. We show that the denotation \(\llbracket M\rrbracket \) in \(\mathcal {D}\) of a \(\varLambda ^+\) term M enjoys a kind of stratification property (Theorem 1, called here strong adequacy) and we use this property to prove that \(\llbracket M\rrbracket \) is a faithful description of the probabilistic Nakajima tree of M (Corollary 1). As a consequence of this result and the previously mentioned separation theorem, we achieve full abstraction for \(\mathcal {D}\) (Theorem 2), thus reconstructing in this setting Manzonetto’s reasoning for classical \(\lambda \)-calculus.
Very recently, and independently from this work, Clairambault and Paquet also prove full abstraction for \(\mathcal {D}\) [2]. Their proof uses a game semantics model representing in an abstract way the probabilistic Nakajima trees and a faithful functor from this game semantics to the weighted relational semantics of [11]. The latter provides a model having the same equational theory over \(\varLambda ^+\) as the probabilistic coherence space \(\mathcal {D}\), so full abstraction for \(\mathcal {D}\) follows immediately. By the way, let us emphasise that all results in our paper can be transferred as they are to the weighted relational semantics of [11]. We decided however to consider the probabilistic coherence space model in order to highlight the correspondence between the definition of \(\mathcal {D}\) (Eq. (11)) and the definition of the logical relation (Eq. (13)) which is the key ingredient in the proof of our notion of stratification.
Let us give some more intuitions on this latter notion, which has an interest in its own. The model \(\mathcal {D}\) is defined as the limit of a chain of probabilistic coherence spaces \((\mathcal {D}_\ell )_{\ell \in \mathbb {N}}\) approximating more and more the denotation of \(\varLambda ^+\) terms. The adequacy property proven in [6] states that the probability of a term M to converge to a head-normal form is given by the mass of the semantics \(\llbracket M\rrbracket \) restricted to the subspace \(\mathcal {D}_2\) [6, Theorem 22]. The natural question is then to understand which kind of operational meaning carries the rest of the mass of \(\llbracket M\rrbracket \), i.e. the points of order greater than 2. Our Theorem 1 answers this question, showing that the semantics \(\llbracket M\rrbracket \) distributes over the semantics of its head-normal forms according to the operational semantics of \(\varLambda ^+\). By iterating this reasoning one gets a stratification of \(\llbracket M\rrbracket \) into a nesting of (\(\eta \)-expanded) head-normal forms which is the key ingredient linking \(\llbracket M\rrbracket \) and the probabilistic Nakajima trees (Corollary 1).
The fact that our proof of full abstraction is based on the notion of strong adequacy makes very plausible that the proof can be adapted to a more general class of models than only probabilistic coherence spaces and weighted semantics. In particular, we would like to stress that we did not use the property of analyticity of term denotations, which is instead at the core of the proof of full abstraction for probabilistic PCF-like languages [7, 8].
Notational convention. We write \(\mathbb {N}\) for the set of natural numbers and \(\mathbb {R}_{\ge 0}\) for the set of non-negative real numbers. Given any set X we write \(\mathcal {M}_{\text {f}}\!\left( X\right) \) for the set of finite multisets of  an element \(m \in \mathcal {M}_{\text {f}}\!\left( X\right) \) is a function \(X \rightarrow \mathbb {N}\) such that the support of m \(\text {Supp}\left( m\right) = \{x \in X \mathrel {|}m(x) > 0\}\) is finite. We write \([x_1,\dots ,x_n]\) for the multiset m such that \(m(x) = \textit{number of indices i}\,\textit{s.t.}\,x=x_i\), so [] is the empty multiset and \(\uplus \) the disjoint union. The Kronecker delta over a set X is defined for \(x,y \in X\) by: \(\delta _{x,y} = 1\) if \(x=y\), and \(\delta _{x,y} =0\) otherwise.
an element \(m \in \mathcal {M}_{\text {f}}\!\left( X\right) \) is a function \(X \rightarrow \mathbb {N}\) such that the support of m \(\text {Supp}\left( m\right) = \{x \in X \mathrel {|}m(x) > 0\}\) is finite. We write \([x_1,\dots ,x_n]\) for the multiset m such that \(m(x) = \textit{number of indices i}\,\textit{s.t.}\,x=x_i\), so [] is the empty multiset and \(\uplus \) the disjoint union. The Kronecker delta over a set X is defined for \(x,y \in X\) by: \(\delta _{x,y} = 1\) if \(x=y\), and \(\delta _{x,y} =0\) otherwise.
2 The Probabilistic Language \(\varLambda ^+\)
We recall the call-by-name untyped probabilistic \(\lambda \)-calculus, following [6]. The set \(\varLambda ^+\) of terms over a set \(\mathcal {V}\) of variables is defined inductively by:
where x ranges over \(\mathcal {V}\) and p ranges over [0, 1]. Note that we consider probabilities over the whole interval [0, 1] but our proofs still hold if we restrict them to rational numbers. We use the \(\lambda \)-calculus terminology and notations as in [1]: terms are considered modulo \(\alpha \)-equivalence, i.e. variable renaming; we write \({{\,\mathrm{FV}\,}}(M)\) for the set of free variables of a term M. For any finite list of variables \(\varGamma = x_1,\dots ,x_n\) we write \(\varLambda ^+_\varGamma \) for the set of terms \(M \in \varLambda ^+\) such that \({{\,\mathrm{FV}\,}}(M) \subseteq \{x_1,\dots ,x_n\}\). Given two terms \(M,N \in \varLambda ^+\) and \(x \in \mathcal {V}\) we write \(M\{N/x\}\) for the term obtained by substituting N for the free occurrences of x in M, subject to the usual proviso of renaming bound variables of M to avoid capture of free variables in N.
Example 1
Some terms useful in giving examples: the duplicator \(\mathbf {\delta } = \lambda x.xx\), the Turing fixed point combinator \(\mathbf \Theta = (\lambda xy.y(xxy))(\lambda xy.y(xxy))\) and \(\mathbf \varOmega = \mathbf \delta \mathbf \delta \).
A context C[ ] is a term containing a single occurrence of a distinguished variable denoted [ ] and called hole. A head-context is of the form \(E[~]=\lambda x_1\dots x_n.[~]M_1 \dots M_k\), for \(n,k\ge 0\) and \(M_i\in \varLambda ^+\). Given \(M\in \varLambda ^+\), we write C[M] for the term obtained by replacing M for the hole in C[ ] possibly with capture of free variables. The operational semantics is given by a Markov chain over \(\varLambda ^+\), mixing together the standard head-reduction of untyped \(\lambda \)-calculus with the probabilistic choice \(+_p\). Precisely, this system is given by the transition matrix \(\mathrm {Red}\) in Eq. (2). It is well known that any \(\varLambda ^+\)-term M can be uniquely decomposed into E[R] for E[ ] a head-context and R either a \(\beta \)-redex, or a \(+_p\)-redex (for some \(p\in [0,1]\)) or a variable in \(\mathcal {V}\). This gives the following cases:
This matrix is stochastic, i.e. for any term M, \(\sum _N \mathrm {Red}_{M,N}=1\). A head-normal form is a term of the form E[y], with \(y\in \mathcal {V}\) called its head-variable. We write \(\mathrm {HNF}\) for the set of all head-normal forms. Following [5, 6], we consider the head-normal forms as absorbing states of the process. Hence the n-th power \(\mathrm {Red}^n\) of the matrix \(\mathrm {Red}\) describes the process of performing exactly n steps: \(\mathrm {Red}^n_{M,N}\) is the probability that after n process steps M will reach state N.
Example 2
Let \(L=(x+_py)\), we have \(\mathrm {Red}_{\delta L,LL} = 1\), and \(\mathrm {Red}^n_{\delta L, xL}=p\), \(\mathrm {Red}^n_{\delta L, yL}=1-p\) for all \(n\ge 2\). In fact both xL and yL are head-normal forms, so absorbing states. The term \(\mathbf \varOmega \) \(\beta \)-reduces to itself, so \(\mathrm {Red}^n_{\varOmega ,\varOmega } = 1\) for any n, giving an example of absorbing state which is not a head-normal form.
The Turing fixed point combinator needs two \(\beta \)-steps to unfold its argument, so, for any term M, \(\mathrm {Red}^{2}_{\mathbf \Theta M,M(\mathbf \Theta M)}=1\). In the case M is a probabilistic function like \(M=\lambda f.(f+_p y)\), we get \(\mathrm {Red}^{4n}_{\mathbf \Theta M,\mathbf \Theta M}=p^n\) and \(\mathrm {Red}^{4n}_{\mathbf \Theta M,y}=1-p^n\), for any n. In the case \(M=\lambda f.(yf+_p y)\), we get: \(\mathrm {Red}^{4(n+1)}_{\mathbf \Theta M,y^n(\mathbf \Theta M)}=p^{n+1}\) and \(\mathrm {Red}^{4(n+1)}_{\mathbf \Theta M,y^n(y)}=(1-p)p^n\), where \(y^n(...)\) denotes the n-fold application \(y(\dots y(...))\).
Notice that for \(h\in \mathrm {HNF}\) and \(M\in \varLambda ^+\), the sequence \(\left( \mathrm {Red}^n_{M,h}\right) _{n \in \mathbb {N}}\) is monotone increasing and bounded by 1, so it converges. We define its limit by:
This quantity gives the total probability of M to reduce to the head-normal form h in any number (possibly infinitely many) of finite reduction sequences.
Example 3
Recall the terms in Example 2. We have \(\mathrm {Red}^\infty _{\delta L,xL} = p\) and \(\mathrm {Red}^\infty _{\delta L,yL} = 1-p\). For any \(h \in \mathrm {HNF}\) and \(n \in \mathbb {N}\) we have \(\mathrm {Red}^n_{\mathbf \varOmega ,h}=0\) so \(\mathrm {Red}^\infty _{\mathbf \varOmega ,h}=0\). The quantity \(\mathrm {Red}^\infty _{\mathbf \Theta (\lambda f.(f+_p y)),y}\) is the first example of limit, being equal to 1 whereas \(\mathrm {Red}^n_{\mathbf \Theta (\lambda f.(f+_p y)),y}<1\) for all \(n \in \mathbb {N}\). Operationally this means that the term \(\mathbf \Theta (\lambda f.(f+_p y))\) reduces to y with probability 1 but the length of these reductions is not bounded. Finally, \(\mathrm {Red}^\infty _{\mathbf \Theta (\lambda f.(yf+_p y)),y^n(y)}=(1-p)p^n\), this means that \(\mathbf \Theta (\lambda f.(yf+_p y))\) converges with probability 1 but it can reach infinitely many different head-normal forms.
Given \(M,N\in \varLambda ^+\), we say that M is contextually equivalent to N if, and only if, \(\forall C[~], \sum _{h\in \mathrm {HNF}}\mathrm {Red}^{\infty }_{C[M],h}=\sum _{h\in \mathrm {HNF}}\mathrm {Red}^{\infty }_{C[N],h}\).
An important property in the following is extensionality, meaning invariance under \(\eta \)-equivalence. The \(\eta \) -equivalence is the smallest congruence such that, for any \(M\in \varLambda ^+\) and \(x\notin {{\,\mathrm{FV}\,}}(M)\) we have \(M =_\eta \lambda x.Mx\). Notice that the contextual equivalence is extensional (see [1] for the classical \(\lambda \)-calculus).
3 Probabilistic Coherence Spaces
Girard introduced probabilistic coherence spaces (PCS) as a “quantitative refinement” of coherence spaces [9]. Danos and Ehrhard considered then the category  of linear and Scott-continuous functions between PCS as a model of linear logic and the cartesian closed category
of linear and Scott-continuous functions between PCS as a model of linear logic and the cartesian closed category  of entire functions between PCS as the Kleisli category associated with the comonad of
of entire functions between PCS as the Kleisli category associated with the comonad of  modelling the exponential modality [5]. They proved also that
modelling the exponential modality [5]. They proved also that  provides an adequate model of probabilistic PCF and the reflexive object \(\mathcal {D}\) which is our object of study.
provides an adequate model of probabilistic PCF and the reflexive object \(\mathcal {D}\) which is our object of study.
The two categories  and
and  have been then studied in various papers. In particular,
have been then studied in various papers. In particular,  is proved to be fully abstract for the call-by-name probabilistic PCF [7]. This result has been also extended to richer languages, e.g. call-by-push-value probabilistic PCF [8]. The untyped model \(\mathcal {D}\) is proven adequate for \(\varLambda ^+\) [6]. This paper is the continuation of the latter result, showing full abstraction for \(\mathcal {D}\) as a consequence of a stronger form of adequacy.
is proved to be fully abstract for the call-by-name probabilistic PCF [7]. This result has been also extended to richer languages, e.g. call-by-push-value probabilistic PCF [8]. The untyped model \(\mathcal {D}\) is proven adequate for \(\varLambda ^+\) [6]. This paper is the continuation of the latter result, showing full abstraction for \(\mathcal {D}\) as a consequence of a stronger form of adequacy.
We briefly recall here the cartesian closed category  and the reflexive object \(\mathcal {D}\). Because of space we omit to consider the linear logic model
and the reflexive object \(\mathcal {D}\). Because of space we omit to consider the linear logic model  , from which
, from which  is derived. We refer the reader to [5, 6] for more details.
is derived. We refer the reader to [5, 6] for more details.
Probabilistic coherence spaces and entire functions. A probabilistic coherence space, or PCS for short, is a pair  where
where  is a countable set called the web of \({\mathcal {X}}\) and \(\mathrm {P}\!\left( \mathcal {X}\right) \) is a subset of the semi-module
is a countable set called the web of \({\mathcal {X}}\) and \(\mathrm {P}\!\left( \mathcal {X}\right) \) is a subset of the semi-module  such that the following three conditions hold: (i) closedness: \(\mathrm {P}\!\left( \mathcal {X}\right) ^{\perp \perp }=\mathrm {P}\!\left( \mathcal {X}\right) \), where, given a set
such that the following three conditions hold: (i) closedness: \(\mathrm {P}\!\left( \mathcal {X}\right) ^{\perp \perp }=\mathrm {P}\!\left( \mathcal {X}\right) \), where, given a set  , the dual of P is defined as
, the dual of P is defined as  ; (ii) boundedness:
; (ii) boundedness:  , \(\exists \mu >0\), \(\forall x\in \mathrm {P}\!\left( \mathcal {X}\right) \), \(x_a\le \mu \); (iii) completeness:
, \(\exists \mu >0\), \(\forall x\in \mathrm {P}\!\left( \mathcal {X}\right) \), \(x_a\le \mu \); (iii) completeness:  , \(\exists x\in \mathrm {P}\!\left( {\mathcal {X}}\right) \), \(x _a>0\).
, \(\exists x\in \mathrm {P}\!\left( {\mathcal {X}}\right) \), \(x _a>0\).
Given \(x,y\in \mathrm {P}\!\left( \mathcal {X}\right) \), we write \(x\le y\) for the order defined pointwise, i.e. for every  , \(x_a\le y_a\). The closedness condition is equivalent to require that \(\mathrm {P}\!\left( \mathcal {X}\right) \) is convex and Scott-closed, as stated below.
, \(x_a\le y_a\). The closedness condition is equivalent to require that \(\mathrm {P}\!\left( \mathcal {X}\right) \) is convex and Scott-closed, as stated below.
Proposition 1
(e.g. [4]). Given an index set I and a subset \(P\subset (\mathbb {R}_{\ge 0})^I\) which is bounded and complete, we have \(P=P^{\perp \perp }\) iff the following two conditions hold: (i) P is convex, i.e. for every \(x,y\in P\) and \(\lambda \in [0,1]\), \(\lambda x + (1-\lambda )y \in P\); (ii) P is Scott-closed, i.e. for every \(x\le y\in P\), \(x\in P\) and for every increasing chain \(\{x_i\}_{i\in \mathbb {N}}\subseteq P\), \(\sup _ix_i\in P\).
A data-type is denoted by a PCS \(\mathcal {X}\) and its data by vectors in \(\mathrm {P}\!\left( \mathcal {X}\right) \): convexity allows for probabilistic superposition and Scott-closedness for recursion.
Example 4
A simple example of PCS is  with
with  a singleton set and \(\mathrm {P}\!\left( \mathcal {U}\right) =[0,1]\). Notice \(\mathrm {P}\!\left( \mathcal {U}\right) ^{\perp }=\mathrm {P}\!\left( \mathcal {U}\right) \). This PCS gives the flat interpretation of the unit type in a typed language. The boolean type is denoted by the two dimensional PCS \(\mathcal {B}\,{:}{:}{=}\,(\{\mathtt t, \mathtt f\}, \{(\rho _{\mathtt t},\rho _\mathtt f)\;\mid \,\rho _{\mathtt t}+\rho _{\mathtt f}\le 1\})\). Notice that \(\mathrm {P}\!\left( \mathcal {B}\right) \) can be seen as the set of the probabilistic sub-distributions of the boolean values.
a singleton set and \(\mathrm {P}\!\left( \mathcal {U}\right) =[0,1]\). Notice \(\mathrm {P}\!\left( \mathcal {U}\right) ^{\perp }=\mathrm {P}\!\left( \mathcal {U}\right) \). This PCS gives the flat interpretation of the unit type in a typed language. The boolean type is denoted by the two dimensional PCS \(\mathcal {B}\,{:}{:}{=}\,(\{\mathtt t, \mathtt f\}, \{(\rho _{\mathtt t},\rho _\mathtt f)\;\mid \,\rho _{\mathtt t}+\rho _{\mathtt f}\le 1\})\). Notice that \(\mathrm {P}\!\left( \mathcal {B}\right) \) can be seen as the set of the probabilistic sub-distributions of the boolean values.
As soon as one consider functional types, the intuitive notion of (discrete) sub-probabilistic distribution is lost. In particular, the reflexive object \(\mathcal {D}\) defined below is an example of an infinite dimensional PCS where scalars arbitrarily big may appear in \(\mathrm {P}\!\left( \mathcal {D}\right) \). One can think of PCS’s as a generalisation of the notion of discrete sub-probabilistic distributions allowing a cartesian closed category.
An entire function from \(\mathcal {X}\) to \(\mathcal {Y}\) is a matrix  such that for any \(x\in \mathrm {P}\!\left( \mathcal {X}\right) \), the image f(x) under f belongs to \(\mathrm {P}\!\left( \mathcal {Y}\right) \), where f(x) is
such that for any \(x\in \mathrm {P}\!\left( \mathcal {X}\right) \), the image f(x) under f belongs to \(\mathrm {P}\!\left( \mathcal {Y}\right) \), where f(x) is

Notice that the condition \(f(x)\in \mathrm {P}\!\left( \mathcal {Y}\right) \) requires that the possibly infinite sum in the previous equation must converge. Recently, Crubillé proves that the entire maps can be characterised independently from their matrix representation as the absolutely monotonic and Scott-continuous maps between PCS’s, see [3].
The cartesian closed category. The Kleisli category  has PCS’s as objects and entire maps as morphisms. Given
has PCS’s as objects and entire maps as morphisms. Given  and
and  , the composition \(g\circ f\) is the usual functional composition, whose matrix can be explicitly given by, for
, the composition \(g\circ f\) is the usual functional composition, whose matrix can be explicitly given by, for  :
:

The boundedness condition over \(\mathcal {Z}\) and the completeness condition over \(\mathcal {X}\) ensure that the possibly infinite sum over  in Eq. (5) converges. The identity is the matrix \(\text {id}_{m,a}^{\mathcal {X}}=\delta _{[a],a}\), where \(\delta \) is the Kronecker delta.
in Eq. (5) converges. The identity is the matrix \(\text {id}_{m,a}^{\mathcal {X}}=\delta _{[a],a}\), where \(\delta \) is the Kronecker delta.
The cartesian product of any countable family \((\mathcal {X}_i)_{i\in I}\) of PCS’s is:

where \(\pi _i(x)\) is the vector in  denoting the i-th component of x, i.e. \(\pi _i(x)_a\,{:}{:}{=}\,x_{(i,a)}\). This means that \(\mathrm {P}\!\left( \prod _{i\in I}\mathcal {X}_i\right) \) can be seen as the set-theoretical product \(\prod _{i\in I}\mathrm {P}\!\left( \mathcal {X}_i\right) \), by mapping \(x\in \mathrm {P}\!\left( \prod _{i\in I}\mathcal {X}_i\right) \) to the sequence \((\pi _i(x))_{i\in I}\). The j-th projection
denoting the i-th component of x, i.e. \(\pi _i(x)_a\,{:}{:}{=}\,x_{(i,a)}\). This means that \(\mathrm {P}\!\left( \prod _{i\in I}\mathcal {X}_i\right) \) can be seen as the set-theoretical product \(\prod _{i\in I}\mathrm {P}\!\left( \mathcal {X}_i\right) \), by mapping \(x\in \mathrm {P}\!\left( \prod _{i\in I}\mathcal {X}_i\right) \) to the sequence \((\pi _i(x))_{i\in I}\). The j-th projection  is defined by \(\mathrm {pr}^j_{m,b}\,{:}{:}{=}\,\delta _{m,[(j,b)]}\). If all components of a product are equal to a PCS \(\mathcal {X}\) we can use the exponential notation \(\mathcal {X}^I\). Binary products can be written as \(\mathcal {X}\times \mathcal {Y}\). In the following, we will often denote the finite multisets in
is defined by \(\mathrm {pr}^j_{m,b}\,{:}{:}{=}\,\delta _{m,[(j,b)]}\). If all components of a product are equal to a PCS \(\mathcal {X}\) we can use the exponential notation \(\mathcal {X}^I\). Binary products can be written as \(\mathcal {X}\times \mathcal {Y}\). In the following, we will often denote the finite multisets in  as I-families of finite multisets almost everywhere empty, using the set-theoretical isomorphism:Footnote 1
as I-families of finite multisets almost everywhere empty, using the set-theoretical isomorphism:Footnote 1

For example, the multi-set  will be denoted as the pair \(([a,a'],[b])\), or the multiset
will be denoted as the pair \(([a,a'],[b])\), or the multiset  as the almost everywhere empty sequence \(([],[],[a],[],[a',a''],[],\dots )\).
as the almost everywhere empty sequence \(([],[],[a],[],[a',a''],[],\dots )\).
The object of morphisms from \(\mathcal {X}\) to \(\mathcal {Y}\) is  itself, i.e.:
itself, i.e.:

The proof that \(\mathrm {P}\!\left( \mathcal {X}\Rightarrow \mathcal {Y}\right) \) so defined enjoys the closedness, completeness and boundedness conditions of the definition of a PCS is not trivial and it is argued by the fact that  is the Kleisli category associated with the exponential comonad of the linear logic model
is the Kleisli category associated with the exponential comonad of the linear logic model  mentioned in the introduction.
mentioned in the introduction.
The evaluation  and the curryfication
and the curryfication  of a morphism
of a morphism  are:
are:
The reflexive object \(\mathcal {D}\). We set \(\mathcal {X}\subseteq \mathcal {Y}\) whenever  and
and  , where
, where  is the vector in
is the vector in  obtained by restricting
obtained by restricting  to the indexes in
to the indexes in  . This defines a complete order over PCS’s. The model \(\mathcal {D}\) of \(\varLambda ^+\) is then given by the least fix-point of the Scott-continuous functor \(\mathcal {X}\mapsto \mathcal {X}^\mathbb {N}\Rightarrow \mathcal {U}\) (where \(\mathcal {U}\) is the one-dimensional PCS defined in Example 4). We do not detail here its definition, but we give explicitly the chain \(\mathcal {D}_0=(\emptyset ,\mathbf 0)\), \(\mathcal {D}_{\ell +1}=\mathcal {D}_\ell ^\mathbb {N}\Rightarrow \mathcal {U}\) whose (co)limit is the least fix-point \(\mathcal {D}\) of \(\mathcal {X}\mapsto \mathcal {X}^\mathbb {N}\Rightarrow \mathcal {U}\) by the Knaster-Tarski theorem. We refer to [5, Sect. 2] for details.
. This defines a complete order over PCS’s. The model \(\mathcal {D}\) of \(\varLambda ^+\) is then given by the least fix-point of the Scott-continuous functor \(\mathcal {X}\mapsto \mathcal {X}^\mathbb {N}\Rightarrow \mathcal {U}\) (where \(\mathcal {U}\) is the one-dimensional PCS defined in Example 4). We do not detail here its definition, but we give explicitly the chain \(\mathcal {D}_0=(\emptyset ,\mathbf 0)\), \(\mathcal {D}_{\ell +1}=\mathcal {D}_\ell ^\mathbb {N}\Rightarrow \mathcal {U}\) whose (co)limit is the least fix-point \(\mathcal {D}\) of \(\mathcal {X}\mapsto \mathcal {X}^\mathbb {N}\Rightarrow \mathcal {U}\) by the Knaster-Tarski theorem. We refer to [5, Sect. 2] for details.
The webs of these spaces are given by:

where  denotes the set of infinite sequences of multisets of
denotes the set of infinite sequences of multisets of  that are almost everywhere empty (notice we are using the isomorphism mentioned in Eq. (7)). The set
that are almost everywhere empty (notice we are using the isomorphism mentioned in Eq. (7)). The set  is the singleton containing the infinite sequence ([],[],[]...) of empty multisets, which we denote by \(\star \). Given a multiset
is the singleton containing the infinite sequence ([],[],[]...) of empty multisets, which we denote by \(\star \). Given a multiset  and a sequence
and a sequence  , we denote by \(m\,{:}{:}\,d\) the element of
, we denote by \(m\,{:}{:}\,d\) the element of  having at first position m and then all the multisets of d shifted by one position. Notice that any element of
having at first position m and then all the multisets of d shifted by one position. Notice that any element of  can be written as \({m_1}\,{:}{:}\,{\dots {m_n}\,{:}{:}\,{\star }}\) for an n sufficiently large and
can be written as \({m_1}\,{:}{:}\,{\dots {m_n}\,{:}{:}\,{\star }}\) for an n sufficiently large and  . In particular, \({[]}\,{:}{:}\,\star =\star \).Footnote 2
. In particular, \({[]}\,{:}{:}\,\star =\star \).Footnote 2
The sets of vectors \(\mathrm {P}\!\left( \mathcal {D}_\ell \right) \) and \(\mathrm {P}\!\left( \mathcal {D}\right) \) completing the definition of a PCS are:

The above definition of \(\mathrm {P}\!\left( \mathcal {D}_{\ell +1}\right) \) is actually equivalent to the standard one inferred from the definition of the countable product \(\mathcal {D}^{\mathbb {N}}\), which would require to apply v to a countable family \((u_i)_{i\in \mathbb {N}}\) of vectors in \(\mathrm {P}\!\left( \mathcal {D}_\ell \right) \). The two definitions are equivalent because of the continuity of the scalar multiplication and the sum.
It happens that any solution of  gives also a solution (although not minimal) to
gives also a solution (although not minimal) to  and hence a reflexive object of
and hence a reflexive object of  . The isomorphism pair
. The isomorphism pair  and
and  is given by, for any
is given by, for any  ,
,  , and
, and  ,
,
It is easy to check that \(\mathop {{\mathtt {app}}\circ {{\mathtt {\lambda }}}}=\text {id}^{\mathcal {D}\Rightarrow \mathcal {D}}\) and \(\mathop {{\mathtt {\lambda }}\circ {{\mathtt {app}}}}=\text {id}^{\mathcal {D}}\), so \((\mathcal {D}, \mathtt {\lambda }, \mathtt {app})\) yields an extensional model of untyped \(\lambda \)-calculus, i.e. \(\llbracket M\rrbracket =\llbracket N\rrbracket \) whenever \(M=_\eta N\).
Interpretation of the Terms of \(\varLambda ^+\). Given a term M and a list \(\varGamma \) of pairwise different variables containing \({{\,\mathrm{FV}\,}}(M)\), the interpretation of M is a morphism  , i.e. a matrix in
, i.e. a matrix in  . The definition of \(\llbracket M\rrbracket ^\varGamma \) is the standard one determined by the cartesian closed structure of
. The definition of \(\llbracket M\rrbracket ^\varGamma \) is the standard one determined by the cartesian closed structure of  and the reflexive object \((\mathcal {D}, \mathtt {\lambda }, \mathtt {app})\): \({\llbracket x\rrbracket ^\varGamma }\) is the x-th projection of the product \(\mathcal {D}^\varGamma \), \(\llbracket \lambda x.M\rrbracket ^\varGamma =\mathop {{\mathtt {\lambda }}\circ {{\mathrm {Cur}\left( {\llbracket M\rrbracket ^{x,\varGamma }}\right) }}}\) and \({\llbracket MN\rrbracket ^\varGamma }= \mathop {{\mathrm {Ev}}\circ {{\langle \mathop {{\mathtt {app}}\circ {{\llbracket M\rrbracket ^\varGamma }}}, \llbracket N\rrbracket ^\varGamma \rangle }}} \), where \(\langle \; ,\; \rangle \) is the cartesian product of two morphisms. Figure 1 makes explicit the coefficients of the matrix \(\llbracket M\rrbracket ^{\varGamma }\) by structural induction on M. The only non-standard operation is the barycentric sum \(\llbracket M+_pN\rrbracket \) which is still a morphism of
and the reflexive object \((\mathcal {D}, \mathtt {\lambda }, \mathtt {app})\): \({\llbracket x\rrbracket ^\varGamma }\) is the x-th projection of the product \(\mathcal {D}^\varGamma \), \(\llbracket \lambda x.M\rrbracket ^\varGamma =\mathop {{\mathtt {\lambda }}\circ {{\mathrm {Cur}\left( {\llbracket M\rrbracket ^{x,\varGamma }}\right) }}}\) and \({\llbracket MN\rrbracket ^\varGamma }= \mathop {{\mathrm {Ev}}\circ {{\langle \mathop {{\mathtt {app}}\circ {{\llbracket M\rrbracket ^\varGamma }}}, \llbracket N\rrbracket ^\varGamma \rangle }}} \), where \(\langle \; ,\; \rangle \) is the cartesian product of two morphisms. Figure 1 makes explicit the coefficients of the matrix \(\llbracket M\rrbracket ^{\varGamma }\) by structural induction on M. The only non-standard operation is the barycentric sum \(\llbracket M+_pN\rrbracket \) which is still a morphism of  by the convexity of \(\mathrm {P}\!\left( \mathcal {D}^\varGamma \Rightarrow \mathcal {D}\right) \) (Proposition 1).
by the convexity of \(\mathrm {P}\!\left( \mathcal {D}^\varGamma \Rightarrow \mathcal {D}\right) \) (Proposition 1).
Explicit definition of the denotation of a term in \(\varLambda ^+_\varGamma \) as a matrix in \(\mathrm {P}\!\left( \mathcal {D}^\varGamma \Rightarrow \mathcal {D}\right) \). Recall Eq. (5) for the notation \((\llbracket N\rrbracket ^\varGamma )^{\varvec{m}_2,m}\).
Proposition 2
(Soundness, [5, 6]). For every term \(M\in \varLambda ^+\) and sequence \(\varGamma \supseteq {{\,\mathrm{FV}\,}}(M)\): \(\llbracket M\rrbracket ^\varGamma =\sum _{N\in \varLambda ^+}\mathrm {Red}_{M,N}\llbracket N\rrbracket ^\varGamma .\)
4 Strong Adequacy
In this section we state and prove Theorem 1, enhancing the  adequacy property given in [6]. This latter explains the computational meaning of the mass of \(\llbracket M\rrbracket \) restricted to \(\mathcal {D}_2\subseteq \mathcal {D}\), while our generalisation considers the whole \(\llbracket M\rrbracket \), showing that it encodes the way the operational semantics dispatches the mass into the denotation of the head-normal forms. As in [6], the proof of Theorem 1 adapts a method introduced by Pitts [14], consisting in building a recursively specified relation of formal approximation \(\lhd \) (Proposition 3) which satisfies the same recursive equation as \(\mathcal {D}\). However, our generalisation requires a subtler definition of \(\lhd \) with respect to [6]. In particular, we must consider open terms in order to prove Lemma 7.
adequacy property given in [6]. This latter explains the computational meaning of the mass of \(\llbracket M\rrbracket \) restricted to \(\mathcal {D}_2\subseteq \mathcal {D}\), while our generalisation considers the whole \(\llbracket M\rrbracket \), showing that it encodes the way the operational semantics dispatches the mass into the denotation of the head-normal forms. As in [6], the proof of Theorem 1 adapts a method introduced by Pitts [14], consisting in building a recursively specified relation of formal approximation \(\lhd \) (Proposition 3) which satisfies the same recursive equation as \(\mathcal {D}\). However, our generalisation requires a subtler definition of \(\lhd \) with respect to [6]. In particular, we must consider open terms in order to prove Lemma 7.
The approximation relation. Let us introduce some convenient notation, extending the definition of \(\lambda \)-abstraction and application to general morphisms.
Definition 1
Given  , let \(\varLambda (v)\) be the vector
, let \(\varLambda (v)\) be the vector  . Given
. Given  let \({v}\mathop {@}{u}\) be the vector
let \({v}\mathop {@}{u}\) be the vector  . Finally, given a finite sequence
. Finally, given a finite sequence  , for \(n\in \mathbb {N}\), we denote by \({v}\mathop {@}{u_1\dots u_n}\) the vector \({({v}\mathop {@}{u_1})}\mathop {@}{ \dots u_n}\).
, for \(n\in \mathbb {N}\), we denote by \({v}\mathop {@}{u_1\dots u_n}\) the vector \({({v}\mathop {@}{u_1})}\mathop {@}{ \dots u_n}\).
Lemma 1
The map \(v\mapsto \varLambda (v)\) is linear, i.e. for any vectors \(v, v'\) and scalars \(p,p'\in [0,1]\) such that \(p+p'\le 1\), we have \(\varLambda (p v+p' v')=p \varLambda (v)+p'\varLambda (v')\), and Scott-continuous, i.e. for any countable increasing chain \((v_n)_{n\in \mathbb {N}}\), \(\varLambda (\sup _n(v_n))=\sup _n(\varLambda (v_n))\). The map \((v,u_1,\dots ,u_n)\mapsto {v}\mathop {@}{u_1\dots u_n}\) is Scott-continuous on all of its arguments but linear only on its first argument v.
Proof
Scott-continuity is because the scalar multiplication and the sum are Scott-continuous. The linearity is because the matrices \(\mathtt {app}\), \(\mathtt {\lambda }\) are associated with linear maps (namely, they have non-zero coefficients only on singleton multisets, see (12)) as well as the left-most component of \(\mathrm {Ev}\), see (9). \(\square \)
For any \(\varGamma \subseteq \varDelta \) there exists the projection \(\mathrm {pr}: \mathrm {P}\!\left( \mathcal {D}\right) ^\varDelta \rightarrow \mathrm {P}\!\left( \mathcal {D}\right) ^\varGamma \). Then, given a matrix \(v \in \mathrm {P}\!\left( \mathcal {D}^{\varGamma } \Rightarrow \mathcal {D}\right) \) we denote by \(v\!\!\uparrow ^{\varDelta } \in \mathrm {P}\!\left( \mathcal {D}^{\varDelta } \Rightarrow \mathcal {D}\right) \) the matrix corresponding to the pre-composition of the morphism associated with v with \(\mathrm {pr}\). This can be explicitly defined by, for  ,
,  , \(\left( v\!\!\uparrow ^{\varDelta }\right) _{\varvec{m},d}=v_{(\varvec{m}_x)_{x \in \varGamma },d}\) if \(\forall y \in \varDelta \setminus \varGamma , \varvec{m}_y = [ ]\), and \(\left( v\!\!\uparrow ^{\varDelta }\right) _{\varvec{m},d}=0\) otherwise.
, \(\left( v\!\!\uparrow ^{\varDelta }\right) _{\varvec{m},d}=v_{(\varvec{m}_x)_{x \in \varGamma },d}\) if \(\forall y \in \varDelta \setminus \varGamma , \varvec{m}_y = [ ]\), and \(\left( v\!\!\uparrow ^{\varDelta }\right) _{\varvec{m},d}=0\) otherwise.
We define an operation \(\phi \) acting on the relations \(R\subseteq \bigcup _{\varGamma } \left( \mathrm {P}\!\left( \mathcal {D}^{\varGamma } \Rightarrow \mathcal {D}\right) \times \varLambda ^+_{\varGamma }\right) \). Each component \(\phi ^\varGamma (R) \subseteq \left( \mathrm {P}\!\left( \mathcal {D}^{\varGamma } \Rightarrow \mathcal {D}\right) \right) \times \varLambda ^+_\varGamma \) is given by:
The above definition is similar to Eq. (11), giving \(\mathcal {D}_{\ell +1}\) from \(\mathcal {D}_{\ell }\). In the following we look for a fixed-point of \(\phi \) (Proposition 3). Its quest is not simple because \(\phi \) is not monotone. We derive then from \(\phi \) a monotone operator \(\psi \) on a larger space, and we compute its fixed-point by using Tarski’s Theorem (Lemma 3).
Given \((R^+,R^-) \in \mathcal {P}\left( \bigcup _{\varGamma } \left( \mathrm {P}\!\left( \mathcal {D}^{\varGamma } \Rightarrow \mathcal {D}\right) \times \varLambda ^+_{\varGamma }\right) \right) ^2\), we define \(\psi (R^+,R^-) = (\phi (R^-),\phi (R^+))\). Given two such pairs \((R^+_1,R^-_1), (R^+_2,R^-_2)\), we define \((R^+_1,R^-_1) \sqsubseteq (R^+_2,R^-_2)\) iff \(R_1^+ \subseteq R_2^+\) and \(R_1^- \supseteq R_2^-\).
Lemma 2
The relation \(\sqsubseteq \) is an order relation giving a complete lattice on \(\mathcal {P}\left( \bigcup _{\varGamma } \left( \mathrm {P}\!\left( \mathcal {D}^{\varGamma } \Rightarrow \mathcal {D}\right) \times \varLambda ^+_{\varGamma }\right) \right) ^2\).
Thanks to the previous lemma, we set \((\lhd ^+,\lhd -)\) as the glb of the set \(\{(R^+,R^-) \mathrel {|}\psi (R^+,R^-) \sqsubseteq (R^+,R^-)\}\) of the pre-fixed points of \(\psi \).
Lemma 3
\(\psi (\lhd ^+,\lhd ^-)=(\lhd ^+,\lhd ^-)\), so \(\lhd ^+=\phi (\lhd ^-)\) and \(\lhd ^-=\phi (\lhd ^+)\).
Proof
One can check that \(\psi \) is monotone increasing wrt \(\sqsubseteq \), so the result follows from Tarski’s Theorem on fixed points. \(\square \)
Lemma 4
For any \(R \subseteq \bigcup _{\varGamma } \left( \mathrm {P}\!\left( \mathcal {D}^{\varGamma } \Rightarrow \mathcal {D}\right) \times \varLambda ^+_{\varGamma }\right) \) and \(M \in \varLambda ^+_\varGamma \), the set \(\{v \in \mathrm {P}\!\left( \mathcal {D}^{\varGamma } \Rightarrow \mathcal {D}\right) \mathrel {|}(v,M) \in \phi ^\varGamma (R)\}\) contains 0, is downward closed and chain closed.
Proof
Consequence of the fact that the application \({v}\mathop {@}{u_1\dots u_n}\) and the lifting \(v\!\!\uparrow ^{\varDelta }\) are Scott-continuous (Lemma 1). Also, \(v\!\!\uparrow ^{\varDelta }\) is linear as well as \({v}\mathop {@}{u_1\dots u_n}\) on its left argument v (always Lemma 1), so \({0\!\!\uparrow ^{\varDelta }}\mathop {@}{u_1 \dots u_n} = 0\). \(\square \)
Proposition 3
We have \(\lhd ^+ = \lhd ^-\). From now on we denote it simply by \(\lhd \). We note \(\lhd ^\varGamma \) its component on \(\left( \mathrm {P}\!\left( \mathcal {D}^{\varGamma } \Rightarrow \mathcal {D}\right) \right) \times \varLambda ^+_\varGamma \).
Proof
First \((\lhd ^-,\lhd ^+)\) is a (pre-)fixed point of \(\psi \) so \((\lhd ^+,\lhd ^-) \sqsubseteq (\lhd ^-,\lhd ^+)\), i.e. \(\lhd ^+ \subseteq \lhd ^-\). To prove the converse, we reason by induction on  . For \(v \in \mathrm {P}\!\left( \mathcal {D}^{\varGamma } \Rightarrow \mathcal {D}\right) \) and \(\ell \in \mathbb N\), we note \(v_{|\ell }\) its restriction to
. For \(v \in \mathrm {P}\!\left( \mathcal {D}^{\varGamma } \Rightarrow \mathcal {D}\right) \) and \(\ell \in \mathbb N\), we note \(v_{|\ell }\) its restriction to  , i.e.: \((v_{|\ell })_{\varvec{m},d}=v_{\varvec{m}, d}\) if
, i.e.: \((v_{|\ell })_{\varvec{m},d}=v_{\varvec{m}, d}\) if  , and \((v_{|\ell })_{\varvec{m},d}=0\) otherwise. Notice that \(v_{|\ell }\) is a morphism \( \mathrm {P}\!\left( \mathcal {D}^{\varGamma } \Rightarrow \mathcal {D}\right) \), since \(v_{|\ell }\le v\in \mathrm {P}\!\left( \mathcal {D}^\varGamma \Rightarrow \mathcal {D}\right) \). We prove by induction on \(\ell \) that:
, and \((v_{|\ell })_{\varvec{m},d}=0\) otherwise. Notice that \(v_{|\ell }\) is a morphism \( \mathrm {P}\!\left( \mathcal {D}^{\varGamma } \Rightarrow \mathcal {D}\right) \), since \(v_{|\ell }\le v\in \mathrm {P}\!\left( \mathcal {D}^\varGamma \Rightarrow \mathcal {D}\right) \). We prove by induction on \(\ell \) that:
For \(\ell = 0\) we have \(v_{|0} = 0\) so by Lemma 4 \((v_{|0},M) \in \lhd ^+= \phi (\lhd ^-)\). At level \(\ell +1\) we want to prove \((v_{|\ell +1},M) \in \lhd ^+ = \phi (\lhd ^-)\). Let \(\varDelta \supseteq \varGamma \), \(u_1,\dots ,u_n \in \mathrm {P}\!\left( \mathcal {D}^{\varDelta } \Rightarrow \mathcal {D}\right) \), \(N_1,\dots ,N_n \in \varLambda ^+_\varDelta \) such that for all \(i \le n\), \((u_i,N_i) \in \lhd ^-\). By induction hypothesis we have \(((u_i)_{|\ell },N_i) \in \lhd ^+\) for all \(i \le n\). Besides by hypothesis \((v,M) \in \lhd ^-=\phi (\lhd ^+)\) and we have \(v_{|\ell +1} \le v\) so Lemma 4 gives \((v_{|\ell +1},M) \in \phi (\lhd ^+)\). Hence \({v_{|\ell +1}\!\!\uparrow ^{\varDelta }}\mathop {@}{(u_1)_{|\ell }\dots (u_n)_{|\ell }} \le \sum _{h \in \mathrm {HNF}_\varDelta } \mathrm {Red}^\infty _{M N_1 \dots N_n,h} \llbracket h\rrbracket ^\varDelta \). We conclude by observing that \({v_{|\ell +1}\!\!\uparrow ^{\varDelta }}\mathop {@}{(u_1)_{|\ell }\dots (u_n)_{|\ell }} = {v_{|\ell +1}\!\!\uparrow ^{\varDelta }}\mathop {@}{u_1 \dots u_n}\).
Now if \((v,M) \in \lhd ^-\) then for all \(\ell \in \mathbb {N}\), \((v_{|\ell },M) \in \lhd ^+\), but we have \(v = \sup _{\ell \in \mathbb {N}} v_{|\ell }\) so Lemma 4 gives \((v,M) \in \lhd ^+\). \(\square \)
The key lemma. Lemma 9 is the so-called key-lemma for the relation \(\lhd \). The reasoning is standard, except for the proof of Lemma 8 allowing strong adequacy.
Lemma 5
For \(M \in \varLambda ^+_{x,\varGamma }, N \in \varLambda ^+_\varGamma \), \((v,(\lambda x.M)N)\! \in \! \lhd ^\varGamma \) iff \((v,M\{N/x\})\! \in \! \lhd ^\varGamma \).
Proof
Observe that for all \(n\in \mathbb {N}\), \(N_1,\dots ,N_n\in \varLambda ^+\) and \(h \in \mathrm {HNF}\) we have \(\mathrm {Red}^\infty _{(\lambda x.M)NN_1\dots N_n,h} = \mathrm {Red}^\infty _{M\{N/x\}N_1\dots N_n,h}\). \(\square \)
Lemma 6
Let (v, M) and (r, L) in \(\lhd ^\varGamma \), then \((pv + (1-p)r,M +_p L) \in \lhd ^\varGamma \).
Proof
Simply observe that for all \(h \in \mathrm {HNF}\) and \(N_1,\dots ,N_n \in \varLambda ^+\) we have \(\mathrm {Red}^\infty _{(M +_p L)N_1\dots N_n,h} = p\mathrm {Red}^\infty _{MN_1\dots N_n,h} + (1-p)\mathrm {Red}^\infty _{LN_1\dots N_n,h}\). \(\square \)
Lemma 7
For all \(x \in \varGamma \), \((\mathrm {pr}^\varGamma _x,x) \in \lhd ^\varGamma \).
Proof
Given any \(\varDelta \supseteq \varGamma \), \(n \in \mathbb {N}\) and \((u_1,N_1),\dots ,(u_n,N_n) \in \lhd ^\varDelta \), we have:
Besides for all \(i \le n\), as \((u_i,N_i) \in \lhd ^\varDelta \) we have \(u_i \le \sum _{h \in \mathrm {HNF}_\varDelta } \mathrm {Red}^\infty _{N_i,h} \llbracket h\rrbracket ^\varDelta \le \llbracket N_i\rrbracket ^\varDelta \). The latter inequality is because Proposition 2 implies that for all \(k\in \mathbb N\), \(\sum _{h \in \mathrm {HNF}_\varDelta } \mathrm {Red}^k_{N_i,h}\llbracket h\rrbracket \le \llbracket N_i\rrbracket \). The application \({}\mathop {@}{}\) being increasing in both its arguments we have \({\mathrm {pr}^\varGamma _x\!\!\uparrow ^{\varDelta }}\mathop {@}{u_1 \dots u_n} \le {\mathrm {pr}^\varDelta _x}\mathop {@}{\llbracket N_1\rrbracket ^\varDelta \dots \llbracket N_n\rrbracket ^\varDelta }\). \(\square \)
Lemma 8
Let \((v,M) \in \left( \mathrm {P}\!\left( \mathcal {D}^{\varGamma } \Rightarrow \mathcal {D}\right) \right) \times \varLambda ^+_\varGamma \), we have \((v,M) \in \lhd ^\varGamma \) iff for all \((r,L) \in \lhd ^\varDelta \) with \(\varDelta \supseteq \varGamma \), \(({v\!\!\uparrow ^{\varDelta }}\mathop {@}{r},M L) \in \lhd ^\varDelta \).
Proof
If \((v,M) \in \lhd ^\varGamma = \phi ^\varGamma (\lhd )\) and \((r,L) \in \lhd ^\varDelta \) then using the definition of \(\phi \) it is easy to check that \(({v\!\!\uparrow ^{\varDelta }}\mathop {@}{r},M L) \in \lhd ^\varDelta \). Conversely if for all \((r,L) \in \lhd ^\varDelta \) we have \(({v\!\!\uparrow ^{\varDelta }}\mathop {@}{r},M L) \in \lhd ^\varDelta \) and we want to prove that \((v,M) \in \phi ^\varGamma (\lhd )\) then the conditions of Eq. (13) trivially holds whenever \(n \ge 1\), so we need to consider only the case for \(n=0\).
Suppose that for all \((r,L) \in \lhd ^\varDelta \), \(({v\!\!\uparrow ^{\varDelta }}\mathop {@}{r},M L) \in \lhd ^\varDelta \), let us prove that \(v \le \sum _{h \in \mathrm {HNF}_\varGamma } \mathrm {Red}^\infty _{M,h} \llbracket h\rrbracket ^\varGamma \). Let x be a fresh variable, according to Lemma 7 we have \((\mathrm {pr}_x^{x,\varGamma },x) \in \lhd ^{x,\varGamma }\) so \({v\!\!\uparrow ^{x,\varGamma }}\mathop {@}{\mathrm {pr}_x^{x,\varGamma }} \le \sum _{h \in \mathrm {HNF}_{x,\varGamma }} \mathrm {Red}^\infty _{M x,h} \llbracket h\rrbracket ^{x,\varGamma }\). Then:
One can check that for \(h \in \mathrm {HNF}_{x,\varGamma }\), \(\mathrm {Red}^\infty _{M x,h} = \sum _{h_0 \in \mathrm {HNF}_{\varGamma }} \mathrm {Red}^\infty _{M,h_0} \mathrm {Red}^\infty _{h_0 x,h}\) (recall that x is not free in M). If \(h_0\) is a head-normal form \(y P_1 \dots P_m\) then \(\mathrm {Red}^\infty _{h_0 x,h} \ne 0\) only if \(h = y P_1\dots P_m x\) with \(x\notin {{\,\mathrm{FV}\,}}(y P_1\dots P_m)\) (and \(\mathrm {Red}^\infty _{h_0 x,h} = 1\)). If \(h_0 = \lambda x_0.h'\) then \(\mathrm {Red}^\infty _{h_0 x,h} \ne 0\) only if \(h = h'\{x/x_0\}\) (and \(\mathrm {Red}^\infty _{h_0 x,h} = 1\)). In the first case we have \(\llbracket \lambda x.h\rrbracket ^\varGamma = \llbracket \lambda x.(h_0 x)\rrbracket ^\varGamma = \llbracket h_0\rrbracket ^\varGamma \). In the second case we have \(\lambda x.h = h_0\) modulo \(\alpha \)-equivalence and \(\llbracket \lambda x.h\rrbracket ^\varGamma = \llbracket h_0\rrbracket ^\varGamma \). Therefore: \(v \le \sum _{h_0 \in \mathrm {HNF}_\varGamma } \mathrm {Red}^\infty _{M,h_0} \llbracket h_0\rrbracket ^\varGamma \). \(\square \)
Lemma 9
(Key Lemma). For all \(M \in \varLambda ^+_\varGamma \) with \(\varGamma = \{y_1,\dots ,y_n\}\), for all \(\varDelta \supseteq \varGamma \), for all \(u_1\),...,\(u_n\) in \( \mathrm {P}\!\left( \mathcal {D}^{\varDelta } \Rightarrow \mathcal {D}\right) \) and \(N_1\),...,\(N_n\) in \(\varLambda ^+_\varDelta \) with \((u_i,N_i) \in \lhd ^\varDelta \),
Proof
The proof is by induction on M. The abstraction uses Lemmas 5 and 8, the application uses Lemma 8 and the barycentric sum Lemma 6. \(\square \)
Theorem 1
(Strong adequacy). For all \(M \in \varLambda ^+_\varGamma \) we have:
Proof
The invariance of the interpretation by reduction (Proposition 2) gives that for all \(n \in \mathbb {N}\), \(\llbracket M\rrbracket ^\varGamma = \sum _{N \in \varLambda ^+_\varGamma } \mathrm {Red}^n_{M,N} \llbracket N\rrbracket ^\varGamma \ge \sum _{h \in \mathrm {HNF}_\varGamma } \mathrm {Red}^n \llbracket h\rrbracket ^\varGamma \). When \(n \rightarrow \infty \) we get \(\llbracket M\rrbracket ^\varGamma \ge \sum _{h \in \mathrm {HNF}_\varGamma } \mathrm {Red}^\infty _{M,h} \llbracket h\rrbracket ^\varGamma \).
Conversely using Lemma 9 with \(\varDelta = \varGamma \) and \((u_i,N_i) = (\pi ^\varGamma _{y_i},y_i)\), which is in \(\lhd ^\varGamma \) thanks to Lemma 7, we get \((\llbracket M\rrbracket ^\varGamma ,M) \in \lhd ^\varGamma \). The definition of \(\lhd = \phi (\lhd )\) with \(\varDelta = \varGamma \) and \(n = 0\) gives \(\llbracket M\rrbracket ^\varGamma \le \sum _{h \in \mathrm {HNF}_\varGamma } \mathrm {Red}^\infty _{M,h} \llbracket h\rrbracket ^\varGamma \). \(\square \)
5 Nakajima Trees and Full Abstraction
We apply our strong adequacy to infer full abstraction (Theorem 2). As mentioned in the Introduction, the bridge linking syntax and semantics is given by the notion of probabilistic Nakajima tree defined by Leventis [12] (here Definitions 2 and 3) in order to prove a separation theorem for \(\varLambda ^+\). Lemma 11 shows that the equality of Nakajima trees implies the denotational equality. The proof of this lemma uses the strong adequacy property.
Definition 2
The set \(\mathcal {PT}^\eta _\ell \) of Nakajima trees with depth at most \(\ell \in \mathbb {N}\) is the set of subprobability distributions over value Nakajima trees \(\mathcal {VT}^\eta _\ell \). These sets are defined by mutual recursion as follows:
The notation \(\bot \) represents the empty function (i.e. the distribution with empty support), encoding undefinedness and allowing directed sets of approximants.
Value Nakajima trees represent infinitary \(\eta \)-long head-normal forms: up to \(\eta \)-equivalence every head-normal form \(h = \lambda x_1 \dots x_n.y\,M_1\,\dots \,M_m\) is equal to \(\lambda x_1 \dots x_{n+k}.y\,M_1\,\dots \,M_m\,x_{n+1}\,\dots \,x_{n+k}\) for any \(k \in \mathbb {N}\) and \(x_{n+1}\),...,\(x_{n+k}\) fresh, and value Nakajima trees are infinitary variants of such \(\eta \)-expansions.
Definition 3
By mutual recursion we associate value trees \( VT ^\eta \) with head-normal forms and general trees \( PT ^\eta \) with general \(\varLambda ^+\) terms:
where the \(x_i\)s are pairwise distinct variables and, for \(i>m\), the \(x_i\)’s are fresh;
Remark 1
In [12], following the definition of deterministic Nakajima trees in [1], the value tree \( VT ^\eta _{\ell +1}(\lambda x_1 \dots x_n.y\,M_1\,\dots \,M_m)\) includes explicitly the difference \(n-m\). This yields a heavier but somewhat more convenient definition, as then Lemma 10 also holds for \(\ell =1\). In this paper we chose to use the lighter definition. This choice does not influence the Nakajima tree equality by Lemma 10.
Example 5
Figure 2(a) depicts some examples of value Nakajima trees associated with the head-normal form \(\lambda x_1.y(\mathbf \varOmega x_1)x_1\). Notice that these trees are equivalent to the Nakajima trees associated with \(y(\mathbf \varOmega x_1)\) as well as \(y\mathbf \varOmega \). In fact, all these terms are contextually equivalent.
Figure 2(b) shows the Nakajima tree of depth 2 associated with the term \(y(u+_qv)+_p(y'+_{p'}\mathbf \varOmega )\). Notice that the two sums \(+_p\) and \(+_{p'}\) contribute to the same subprobability distribution, whereas they are kept distinct from the sum \(+_q\) on the argument side of an application.
Figure 2(c) gives some examples of the Nakajima trees associated with the term \(\mathbf \Theta (\lambda f.(y+_{p}y(f))\), discussed also in Examples 2 and 3. Notice that the more the depth \(\ell \) increases, the more the top-level distribution’s support grows.
It is clear that the family  converges to a limit, but we do not need to make it explicit for our purposes, so we avoid defining the topology over
converges to a limit, but we do not need to make it explicit for our purposes, so we avoid defining the topology over  yielding the convergence of
yielding the convergence of  .
.
The next lemma shows that the first levels of a \( VT ^\eta \) of a head-normal form h give a lot of information about the shape of h.
Lemma 10
Given two head-normal forms \(h=\lambda x_1\dots x_n.yM_1\dots M_m\) and \(h'=\lambda x_1\dots x_{n'}.y'M_1'\dots M_{m'}'\) and any \(\ell \ge 2\), if \( VT ^\eta _{\ell }(h)= VT ^\eta _{\ell }(h')\), then \(y=y'\) and \(n-m=n'-m'\).
Proof
The fact \(y=y'\) follows immediately from the definition of \( VT ^\eta \). Concerning the second equality, one can assume \(n=n'\) by \(\eta \)-expanding one of the two terms, in fact \( VT ^\eta \) is invariant under \(\eta \)-expansion. Modulo \(\alpha \)-equivalence, we can then restrict ourselves to consider the case of \(h=\lambda x_1\dots x_n.yM_1\dots M_m\) and \(h'=\lambda x_1\dots x_n.yM_1'\dots M_{m'}'\).
Suppose, by the sake of contradiction, that \(m>m'\). Then we should have \( PT ^\eta _{\ell -1}(M_{m'+1})= PT ^\eta _{\ell -1}(x_{n+1})\), where \(x_{n+1}\) is a fresh variable, in particular \(x_{n+1}\notin {{\,\mathrm{FV}\,}}(M_{m'+1})\). Since \(\ell -1>0\), we have that \( PT ^\eta _{\ell -1}(x_{n+1})(t)=1\) only if t is equal to \(\lambda z_1z_2\dots . x_{n+1} PT ^\eta _{\ell -2}(z_1) PT ^\eta _{\ell -2}(z_2)\dots \), otherwise \( PT ^\eta _{\ell -1}(x_{n+1})(t)=0\). So, \( PT ^\eta _{\ell -1}(M_{m'+1})= PT ^\eta _{\ell -1}(x_{n+1})\) implies that \(\mathrm {Red}^{\infty }_{M_{m'+1},h}>0\) for some h having \(x_{n+1}\) as free variable, which is impossible since \(x_{n+1}\notin {{\,\mathrm{FV}\,}}(M_{m'+1})\). \(\square \)
Thanks to the strong adequacy property we can prove that for \(M \in \varLambda _\varGamma ^+\) each coefficient of \(\llbracket M\rrbracket ^\varGamma \) is entirely defined by \( PT ^\eta _\ell (M)\) for \(\ell \) large enough. To do so we define the following size on  ,
,  and
and  :
:
-
\(\#(\star ) = 0\) for the base element,
-
\(\#(m\,{:}{:}\,d) = \#(m) + \#(d)\) for
 and
and 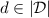 ,
, -
\(\#([d_1,\dots ,d_n]) = n + \sum _{i=1}^n \#(d_i)\) for
 ,
, -
\(\#(\varvec{m},d) = \#(d) + \sum _{x \in \varGamma }(\#(\varvec{m}_x))\) for
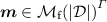 and
and  .
.
Lemma 11
Given \(\ell \in \mathbb {N}\) and \(M, N \in \varLambda _\varGamma ^+\), if \( PT ^\eta _{\ell }(M)= PT ^\eta _{\ell }(N)\) then for any  with \(\#(\varvec{m},d)<\ell \), we have \(\llbracket M\rrbracket ^\varGamma _{\varvec{m},d}=\llbracket N\rrbracket ^\varGamma _{\varvec{m},d}\).
with \(\#(\varvec{m},d)<\ell \), we have \(\llbracket M\rrbracket ^\varGamma _{\varvec{m},d}=\llbracket N\rrbracket ^\varGamma _{\varvec{m},d}\).
Proof
We do induction on \(\ell \). If \(\ell \le 1\), then \(\#(\varvec{m},d) = 0\) implies \(d=\star \) and for every \(x\in \varGamma \), \(\varvec{m}_x=[\,]\). In this case we remark that both \(\llbracket M\rrbracket ^\varGamma _{\varvec{m},d}, \llbracket N\rrbracket ^\varGamma _{\varvec{m},d}\) are null. This in fact can be easily checked by inspecting the rules of Fig. 1, computing the matrix denoting a term by structural induction over the term.
Otherwise, by Theorem 1, we have: \(\llbracket M\rrbracket ^\varGamma _{\varvec{m},d} =\sum _{h \in \mathrm {HNF}_\varGamma } \mathrm {Red}^\infty _{M,h} \llbracket h\rrbracket ^\varGamma _{\varvec{m},d}\). This last sum can be refactored as \(\sum _{t\in VT ^\eta _{\ell }}\sum _{h\in ( VT ^\eta _{\ell })^{-1}(t)}\mathrm {Red}^\infty _{M,h} \llbracket h\rrbracket ^\varGamma _{\varvec{m},d}\). A similar reasoning for N gives \(\llbracket N\rrbracket ^\varGamma _{\varvec{m},d}=\sum _{t\in VT ^\eta _{\ell }}\sum _{h\in ( VT ^\eta _{\ell })^{-1}(t)}\mathrm {Red}^\infty _{N,h} \llbracket h\rrbracket ^\varGamma _{\varvec{m},d}\).
Let us fix a \(t\in VT ^\eta _{\ell }\) and  with \(\#(\varvec{m},d)<\ell \). Let us prove that:
with \(\#(\varvec{m},d)<\ell \). Let us prove that:
-
 for any \(h,h' \in ( VT ^\eta _{\ell })^{-1}(t)\), we have \(\llbracket h\rrbracket ^\varGamma _{\varvec{m},d}=\llbracket h'\rrbracket ^\varGamma _{\varvec{m},d}\).
for any \(h,h' \in ( VT ^\eta _{\ell })^{-1}(t)\), we have \(\llbracket h\rrbracket ^\varGamma _{\varvec{m},d}=\llbracket h'\rrbracket ^\varGamma _{\varvec{m},d}\).
Notice that \(\square \) implies \(\llbracket M\rrbracket ^\varGamma _{\varvec{m},d}=\llbracket N\rrbracket ^\varGamma _{\varvec{m},d}\), since the hypothesis \( PT ^\eta _{\ell }(M)= PT ^\eta _{\ell }(N)\) gives \(\sum _{h\in ( VT ^\eta _{\ell })^{-1}(t)}\mathrm {Red}^\infty _{M,h}=\sum _{h\in ( VT ^\eta _{\ell })^{-1}(t)}\mathrm {Red}^\infty _{N,h}\), for any \(t\in VT ^\eta _{\ell }\).
Let then \(h = \lambda x_1\dots x_n.yM_1\dots M_k\) and \(h' = \lambda x_1\dots x_{n'}.y'M'_1\dots M'_{k'}\). Since \(\ell \ge 2\), \( VT ^\eta _{\ell }(h)= VT ^\eta _{\ell }(h')\) implies by Lemma 10 that \(y=y'\) and \(n-k=n'-k'\). Since \(\mathcal {D}\) is extensional (see Sect. 3), by \(\eta \)-expanding one of the two terms, we can suppose \(n=n'\) and, then, \(k=k'\). Besides if \(n > 0\) let us write \(d = m\ {:}{:}\ d'\), we have \(\llbracket h\rrbracket ^\varGamma _{\varvec{m},d} = \llbracket \lambda x_2\dots x_n.yM_1\dots M_k\rrbracket ^{x_1,\varGamma }_{(m,\varvec{m}),d'}\) with \(\#((m,\varvec{m}),d') = \#(\varvec{m},d)\), and similarly for \(\llbracket h'\rrbracket ^\varGamma _{\varvec{m},d}\). So, we can reduce to consider the case: \(h=yM_1\dots M_k\) and \(h'=yM'_1\dots M'_{k}\). If \(k=0\) the claim \(\square \) is trivial, otherwise by unfolding the applications of h using the applicative case in Fig. 1, we have that:

and the same for \(h'\), replacing each \(M_i\) with \(M_i'\). Notice that \(\llbracket y\rrbracket ^\varGamma _{\varvec{m}_0,m_1{:}{:}\cdots {:}{:}m_k{:}{:}d} \ne 0\) implies \((\varvec{m}_0)_y = [m_1\, {:}{:}\, \cdots \, {:}{:}\, m_k\, {:}{:}\, d] \), hence \(\#(m_i)<\#(\varvec{m}_0)\) for any \(i \le k\), thus \(\#(\varvec{m}_i,m_i)<\#(\varvec{m}_i) + \#(\varvec{m}_0) \le \#(\varvec{m}) \le \#(\varvec{m},d)<\ell \) and \(\#(\varvec{m}_i,m_i)<\ell -1\). Moreover, the hypothesis \( VT ^\eta _{\ell }(h)= VT ^\eta _{\ell }(h')\), implies \( PT ^\eta _{\ell -1}(M_i)= PT ^\eta _{\ell -1}(M_i')\) for any \(i\le k\), so we conclude by induction hypothesis on each term in the sums appearing in \((\llbracket M_i\rrbracket ^\varGamma )^{\varvec{m}_i,m_i}\) and \((\llbracket M_i'\rrbracket ^\varGamma )^{\varvec{m}_i,m_i}\). \(\square \)
Corollary 1
Let \(M, N \!\in \! \varLambda _\varGamma ^+\), \(\forall \ell \!\in \!\mathbb N, PT ^\eta _{\ell }(M)\!=\! PT ^\eta _{\ell }(N)\) implies \(\llbracket M\rrbracket ^\varGamma \!=\!\llbracket N\rrbracket ^\varGamma \).
Theorem 2
For any two terms \(M,N \in \lambda ^+_\varGamma \), the following are equivalent:
-
1.
M and N are contextually equivalent;
-
2.
M and N have the same Nakajima trees;
-
3.
M and N have the same interpretation in \(\mathcal {D}\).
Proof
(1) to (2) is given by [12, Theorem 10.1]. From (2) and Corollary 1, we get (3). Finally, (3) implies (1) by the adequacy of probabilistic coherence spaces, proven in [6, Corollary 25]. \(\square \)
Notes
- 1.
In fact, this isomorphism corresponds, for I finite, to the fundamental exponential isomorphism
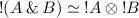 of linear logic.
of linear logic. - 2.
The elements of
 can be seen as intersection types generated from the constant \(\star \), the \(\mathop {{}{:}{:}{}}\) operation being the arrow and multisets non-idempotent intersections.
can be seen as intersection types generated from the constant \(\star \), the \(\mathop {{}{:}{:}{}}\) operation being the arrow and multisets non-idempotent intersections.
References
Barendregt, H.: The Lambda-Calculus: Its Syntax and Semantics. Studies in Logic and the Foundations of Mathematics, vol. 103. North-Holland, Amsterdam (1984)
Clairambault, P., Paquet, H.: Fully abstract models of the probabilistic lambda-calculus. In: Ghica, D.R., Jung, A. (eds.) 27th EACSL Annual Conference on Computer Science Logic, CSL 2018, 4–7 September 2018, LIPIcs, Birmingham, UK, vol. 119, pp. 16:1–16:17. Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik (2018). https://doi.org/10.4230/LIPIcs.CSL.2018.16
Crubillé, R.: Probabilistic stable functions on discrete cones are power series. In: Dawar, A., Grädel, E. (eds.) Proceedings of the 33rd Annual ACM/IEEE Symposium on Logic in Computer Science, LICS 2018, Oxford, UK, 09–12 July 2018, pp. 275–284. ACM (2018). https://doi.org/10.1145/3209108.3209198, http://doi.acm.org/10.1145/3209108.3209198
Crubillé, R., Ehrhard, T., Pagani, M., Tasson, C.: The free exponential modality of probabilistic coherence spaces. In: Esparza, J., Murawski, A.S. (eds.) FoSSaCS 2017. LNCS, vol. 10203, pp. 20–35. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54458-7_2
Danos, V., Ehrhard, T.: Probabilistic coherence spaces as a model of higher-order probabilistic computation. Inf. Comput. 209(6), 966–991 (2011)
Ehrhard, T., Pagani, M., Tasson, C.: The computational meaning of probabilistic coherence spaces. In: Grohe, M. (ed.) Proceedings of the 26th Annual IEEE Symposium on Logic in Computer Science (LICS 2011), pp. 87–96. IEEE Computer Society Press (2011)
Ehrhard, T., Pagani, M., Tasson, C.: Probabilistic coherence spaces are fully abstract for probabilistic PCF. In: Sewell, P. (ed.) The 41th Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2014, San Diego, USA. ACM (2014)
Ehrhard, T., Tasson, C.: Probabilistic call by push value (2016). http://arxiv.org/abs/1607.04690
Girard, J.Y.: Between logic and quantic: a tract. In: Ehrhard, T., Girard, J.Y., Ruet, P., Scott, P. (eds.) Linear Logic in Computer Science. London Mathematical Society Lecture Note Series, vol. 316. CUP, Cambridge (2004)
Hyland, M.: A syntactic characterization of the equality in some models for the lambda calculus. J. London Math. Soc. 12, 361–370 (1976)
Laird, J., Manzonetto, G., McCusker, G., Pagani, M.: Weighted relational models of typed lambda-calculi. In: 28th Annual ACM/IEEE Symposium on Logic in Computer Science, LICS 2013, New Orleans, LA, USA, 25–28 June 2013. IEEE Computer Society, June 2013
Leventis, T.: Probabilistic Böhm trees and probabilistic separation. In: Proceedings of the 33rd Annual ACM/IEEE Symposium on Logic in Computer Science, LICS 2018, Oxford, UK, 09–12 July 2018, pp. 649–658 (2018). https://doi.org/10.1145/3209108.3209126
Manzonetto, G.: A general class of models of \(\cal{H}^*\). In: Královič, R., Niwiński, D. (eds.) MFCS 2009. LNCS, vol. 5734, pp. 574–586. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03816-7_49
Pitts, A.M.: Computational adequacy via ‘mixed’ inductive definitions. In: Brookes, S., Main, M., Melton, A., Mislove, M., Schmidt, D. (eds.) MFPS 1993. LNCS, vol. 802, pp. 72–82. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-58027-1_3
Wadsworth, C.P.: The relation between computational and denotational properties for scott’s \(D_\infty \)-models of the lambda-calculus. SIAM J. Comput. 5, 488–521 (1976)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Leventis, T., Pagani, M. (2019). Strong Adequacy and Untyped Full-Abstraction for Probabilistic Coherence Spaces. In: Bojańczyk, M., Simpson, A. (eds) Foundations of Software Science and Computation Structures. FoSSaCS 2019. Lecture Notes in Computer Science(), vol 11425. Springer, Cham. https://doi.org/10.1007/978-3-030-17127-8_21
Download citation
DOI: https://doi.org/10.1007/978-3-030-17127-8_21
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17126-1
Online ISBN: 978-3-030-17127-8
eBook Packages: Computer ScienceComputer Science (R0)







 and
and 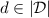 ,
, ,
,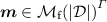 and
and  .
. for any
for any 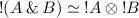 of linear logic.
of linear logic. can be seen as intersection types generated from the constant
can be seen as intersection types generated from the constant 