Abstract
Background
This paper studies soliton perturbation in optical metamaterials, with anticubic nonlinearity.
Methods
Two integration approaches, namely, the extended trial equation method (ETEM) and the improved G’/Gexpansion method (IGEM) are presented.
Results
Bright, dark and singular soliton solutions are retrieved. The existence criteria of these solitons in metamaterials are also demonstrated. All solutions have been verified back into its corresponding equation with the aid of maple package program.
Conclusions
Finally, we believe that the executed method is robust and efficient than other methods and the obtained solutions in this paper can help us to understand the variation of solitary waves in optical metamaterials.
Similar content being viewed by others
Background
The nonlinear dynamics that describes the propagation of pulses in optical metamaterials (MMs) is given by the nonlinear Schrödinger equation (NLSE). In the presence of parabolic law nonlinearity, with an additional anti-cubic nonlinear term and perturbation terms that include inter-modal dispersion (IMD), self-steepening (SS) as well as nonlinear dispersion (ND), the governing equation reads [1, 2]
In Eq. (1), the unknown or dependent variable q(x,t) represents the wave profile, while x and t are the spatial and temporal variables respectively. The first and second terms are the linear temporal evolution term and group velocity dispersion (GVD), while third term introduces the anti-cubic nonlinear term, fourth and fifth terms account for the parabolic law nonlinearity, and sixth, seventh and eighth terms represent the IMD, SS and ND respectively. Finally, the last three terms with θ k for k=1,2,3 appear in the context of metamaterials [3, 4].
The study of solitons in optical metameterials is trending as a hotspot in the field of optical materials. There has been a significant amount of results that are reported in this field. However, there is still a long way to go. There are many unanswered questions than answers. This paper will quell the thirst partially. In the past, solitons in optical metamaterials have been studied with various forms of non-Kerr laws of nonlinearity where several integration schemes have been implemented [5–24]. Interested reader also read herein references [25–41]. This paper is going to revisit the study of solitons in optical metamaterials for a specific form of nonlinear medium. This is of anti-cubic (AC) type. There are three forms of integration algorithms that will be applied to extract soliton solutions to metamaterials with AC nonlinearity. These schemes will retrieve bright, dark and singular soliton solutions that will be very important in the study of optical materials. These solitons will appear with constraint conditions that are otherwise referred to as existence criteria of the soliton Parameters [42–44]. The governing model that describes the propagation of optical solitons and optical soliton complexes (soliton molecules) is the nonlinear Schrdinger’s equation (NLSE) that comes with various forms of nonlinearity. A new form of nonlinearity was proposed during 2011, which is called quadratic-cubic (QC) [25]. Thus far, NLSE with QC nonlinearity has been studied, without prerturbation terms, by the aid of some integration algorithms, including the application of semi-inverse variational principle (SVP) [26, 31]. Optical Fiber is new medium, in which information is transmitted through a glass or plastic fiber, in the form of light. The field of applied science and engineering concerned with the design and application of optical fibers is known as fiber optics. Optical fibers are widely used in fiber optics, which permits transmission over longer distances and at higher bandwidth than other forms of communication. Optical fibers may be connected to each other or can be terminated at the end by means of connectors or splicing techniques [27].
All electromagnetic phenomena result from interactions between waves and materials. Metamaterials are engineered materials that are not found naturally. Due to unique properties of these materials, those materials are attracted for scientists especially physicists and electronic engineers. In the last decade, single-negative metamaterials with negative electrical permittivity produced artificially are important in optical frequencies. Optical metamaterials have important properties for light management. In 1968, the Russian physicist Victor Veselago is proposed the existence of electromagnetic materials called metamaterials with negative permittivity and permeability. Moreover, the advent of all-dielectric optical metamaterials provides a new route to developing novel optical metamaterials with both low absorption loss and isotropic optical properties.
Intermodal dispersion (also called modal dispersion) is the phenomenon that the group velocity of light propagating in a multimode fiber (or other waveguide) depends not only on the optical frequency (chromatic dispersion) but also on the propagation mode involved. The strength of intermodal dispersion can be quantified as the differential mode delay (DMD). It depends strongly on the refractive index profile of the fiber in and around the fiber core. For example, for a step-index profile the higher-order modes have lower group velocities, and this can lead to differential group delays of the order of 10 ps/m = 10 ns/km. It is then hardly possible to realize data rates of multiple Gbit/s in an fiber-optic link with a kilometer length. In systems for optical fiber communications based on multimode fibers, intermodal dispersion can severely limit the achievable data transmission rate (bit rate). In order to avoid strong signal distortion, it is usually necessary to keep the pulses long enough to maintain a reasonable temporal overlap of components from different modes, and this unavoidably sets a limit on the data rate. The natural way of eliminating intermodal dispersion is to use fiber links based on single-mode fibers, but intermodal dispersion can also be minimized by using multimode fibers with a parabolic refractive index profile, where intermodal dispersion is minimized. In case of graded index fiber, critical angle condition is satisfied at different distances from the axis of the core for different modes as refractive index is decreasing from the axis up to core cladding interface. The wave which is internally reflected near axis travel less distance but will also have low velocity due to higher refractive index. On the other hand, wave reflected near the interface will travel more distance but with higher velocity due to smaller refractive index. Hence, the time to reach the other end will be same for these waves which means no intermodal dispersion.
After a quick introduction to the model, the integration techniques will be applied and the details are enumerated in the subsequent sections.
In order to solve Eq. (1), the starting hypothesis is [3, 4]
where
and the phase component ϕ is given by
In (2) and (3), u(x,t) represents the amplitude portion of the soliton, and k and v are inverse width and velocity of soliton. From (4), κ is the frequency of the soliton, ω is the wave number of the soliton and finally θ is the phase constant. Inserting (2) into (1) and then decomposing into real and imaginary parts yield a pair of relations. Imaginary part gives
and
while real part leads to
To acquire an analytic solution, the transformations θ1 =0 and θ2=−θ3 are applied in Eq. (7), and gives
where
In order to obtain closed-form solutions, we employ the transformation given by
that will reduce Eq. (8) into the ODE
Extended trial equation method [12, 21] and the generalized (G’/G)-expansion approach [22–24] will now be applied, in the subsequent sections, to Eq. (11) to retrieve bright, dark and singular soliton solutions to the NLSE with AC nonlinearity (1).
This paper is organized as follows: In “Extended trial equation method” section, the extended trial equation method and its application for Eq. (1) are investigated. “The improved G′/G-expansion method” section presented a brief discussion about improved (G’/G)-expansion method and its application for solving the aforementioned equation. Besides, the results and discussion are given in “Results and discussion” section. Finally, we draw a conclusion about executed method and the generated results in “Conclusion” section.
Methods
Extended trial equation method
Suppose that solution of Eq. (11) can be expressed by
where
where ξ0,ξ1,…,ξ θ , ζ0,ζ1,…,ζ ε and τ0,τ1,…,τ δ are constants to be determined later. The elementary form of the integral by reduction of Eq. (13), one gains
where η0 is a free constant. We can determine values of δ,θ, and ε, by balancing v4 and v′2 in Eq. (11) as follows
For case I (δ=1,θ=4, and ε=0), Eq. (11) has the solution in the form
Inserting (16) into Eq. (11), and solve (14), we find the following results:
Set I:
Substituting these results into (14), we get
Integrating (18), we acquire the following exact solutions as:
First solution:
where
Moreover, α1,α2,α3 and α4 are the roots of the polynomial equation
Putting the solutions (19)-(25) into (16) and \(u=v^{\frac {1}{2}}\), we acquire the following traveling wave solutions of Eq. (5), respectively:
Remarks 1
If the modulus l→1, then the solution (31) can be reduced to the solitary wave solution
where α3=α4, and v=−α−2aκ represents the velocity of the dark soliton.
Remarks 2
If the modulus l→0, then the solution (31) can be converted into the compacton solution
where α2=α3.
Set II:
Substituting these results into (14), we get
Integrating (35), and putting the solutions (19)-(24) into (16) and \(u=v^{\frac {1}{2}}\), we acquire the following traveling wave solutions of Eq. (1), respectively:
Remarks 3
If the modulus l→1, then the solution (41) can be reduced to the solitary wave solution
where α3=α4, and v=−α−2aκ represents the velocity of the dark soliton.
Remarks 4
If the modulus l→0, then the solution (41) can be converted into the compacton solution
where α2=α3.
For case II (δ=2,θ=6, and ε=0), Eq. (11) has the solution in the form
Inserting (44) into Eq. (11), and solve (14), we find the following results:
Set I:
Substituting these results into (14), we get
where
To integrate Eq. (46), we must discuss the following families:
Family 1
If we consider
where α1 is an arbitrary constant, then, we have
Therefore, the final solution gives
Family 2
If we consider
where α1 and α2 are arbitrary constants, then, we have
where η=k[x+(α+2aκ)t]. Therefore, the final solution gives
Family 3
If we consider
where α1 and α2 are arbitrary constants, then, we have
in which
Therefore, the final solution gives
The improved G ′/G-expansion method
To start off with the improved G′/G-expansion approach, the initial assumption of the solution structure of (11) is made:
where A i for i=−M,…,−1,0,1,…,M are constants to be determined later, such that A M ≠0, while the function Φ(ξ)=G′(ξ)/G(ξ) is the solution of the ordinary differential equation
It is well known that Eq. (57) has solutions in the forms as:
Family 1: Whenk 2 ≠0,f=k 1 −k 3 and\(s=k_{2}^{2}+4k_{4} (k_{1}\,-\,k_{3})\!>\!0\),then \(\Phi (\xi)\,=\,\frac {k_{2}}{2f}\!+\frac {\sqrt {s}}{2f}\frac {C_{1}\sinh \left (\frac {\sqrt {s}}{2k_{1}}\xi \right)+C_{2}\cosh \left (\frac {\sqrt {s}}{2k_{1}}\xi \right)} {C_{1}\cosh \left (\frac {\sqrt {s}}{2k_{1}}\xi \right)+C_{2}\sinh \left (\frac {\sqrt {s}}{2k_{1}}\xi \right)}.\)
Family 2: Whenk 2 ≠0,f=k 1 −k 3 and\(s=k_{2}^{2}+4k_{4} (k_{1}\,-\,k_{3})\!\!<\!\!0\), then \(\Phi (\xi)\,=\,\frac {k_{2}}{2f}\,+\,\frac {\sqrt {-s}}{2f}\frac {-C_{1}\sin \left (\frac {\sqrt {-s}}{2k_{1}}\xi \right)+C_{2}\cos \left (\frac {\sqrt {-s}}{2k_{1}}\xi \right)} {C_{1}\cos \left (\frac {\sqrt {-s}}{2k_{1}}\xi \right)+C_{2}\sin \left (\frac {\sqrt {-s}}{2k_{1}}\xi \right)}.\)
Family 3: Whenk 2 ≠0,f=k 1 −k 3 and\(s=k_{2}^{2}+4k_{4}(k_{1}-k_{3})=0\), then \(\Phi (\xi)=\frac {k_{2}}{2f}+\frac {C_{2}}{C_{1}+C_{2}\xi }.\)
Family 4: Whenk 2 ≠0 andf=k 1 −k 3 =0, then \(\Phi (\xi)=-\frac {k_{4}}{k_{2}}+C_{1}\exp \left (\frac {k_{2}}{k_{1}}\xi \right).\)
Here, it is important to note that C1 and C2 are the integration constants. Balancing v′2 with v4 in Eq. (11) yields M=1. The improved G′/G-expansion scheme allows us to employ the substitution
Substituting (58) along with (58) into Eq. (11) and equating all the coefficients of powers of \(\frac {G^{\prime }}{G}\) to be zero, one obtains a system of algebraic equations. Solving this system by Maple yields
Set I:
where k1,k2,k3 and A1 are arbitrary constants. Substituting the solution set (59) into (58), the solution formula of Eq. (11) can be written as below:
Consequently, one gains exact solutions to the model as follows:
Family 1:
Here, it should be emphasized that these solitons exist for b1b3<0 and \(\xi =\frac {2k_{1}A_{1}}{k_{1}-k_{3}}\sqrt {-\frac {b_{3}}{3a}} \left (x+\left (\alpha +2a\frac {3b_{2}k_{1}+4b_{3}A_{1}k_{2}-3b_{2}k_{3}}{3(k_{1}-k_{3})\beta }\right)t\right)\).
Set II:
where k1,k2,k3 and k4 are arbitrary constants. Substituting the solution set (62) into (58), the solution formula of Eq. (11) can be written as below:
Accordingly, one gains exact solutions to the model as follows:
Family 1:
Here, it should be emphasized that these solitons exist for \(s=k_{2}^{2}+4k_{4}(k_{1}-k_{3})>0\) and \(\xi =\frac {2k_{1}A_{-1}}{k_{4}}\sqrt {-\frac {b_{3}}{3a}} \left (x+\left (\alpha +2a\frac {3b_{2}k_{4}+4b_{3}A_{-1}k_{2}}{3k_{4}\beta }\right)t\right)\).
Family 2:
Here, it should be emphasized that these trigonometric traveling wave solutions will exist provided the constraint condition holds: \(s=k_{2}^{2}+4k_{4}(k_{1}-k_{3})<0\) and \(\xi =\frac {2k_{1}A_{-1}}{k_{4}}\sqrt {-\frac {b_{3}}{3a}} \left (x+\left (\alpha +2a\frac {3b_{2}k_{4}+4b_{3}A_{-1}k_{2}}{3k_{4}\beta }\right)t\right)\).
Family 3:
Also, it should be emphasized that these plane wave solutions will exist for \(s=k_{2}^{2}+4k_{4}(k_{1}-k_{3})=0\) and \(\xi =\frac {2k_{1}A_{-1}}{k_{4}}\sqrt {-\frac {b_{3}}{3a}} \left (x+\left (\alpha +2a\frac {3b_{2}k_{4}+4b_{3}A_{-1}k_{2}}{3k_{4}\beta }\right)t\right)\).
Set III:
where k1,k2,k3,k4,A0 and A−1 are arbitrary constants. Substituting the solution set (67) into (58), the solution formula of Eq. (11) can be written as below:
As a result, one acquires exact solutions to the model as follows:
Family 1:
Here, it should be emphasized that these solitons exist for \(s=k_{2}^{2}+\frac {k_{4}^{2}A_{0}^{2}}{A_{-1}^{2}}+\frac {3k_{4}^{4}b_{1}}{b_{3}A_{-1}^{2}(A_{0}k_{4}+k_{2}A_{-1})^{2}}>0\) or b1b3>0 and\(\xi =\frac {2k_{1}A_{-1}}{k_{4}}\sqrt {-\frac {b_{3}}{3a}} \left (x+\left (\alpha +2a\frac {3b_{2}k_{4}+4b_{3}A_{-1}k_{2}+8k_{4}b_{3}A_{0}}{3k_{4}\beta }\right)t\right)\).
Family 2:
It should be stated that these trigonometric traveling wave solutions will exist provided the constraint condition holds: \(s=k_{2}^{2}+\frac {k_{4}^{2}A_{0}^{2}}{A_{-1}^{2}}+\frac {3k_{4}^{4}b_{1}}{b_{3}A_{-1}^{2}(A_{0}k_{4}+k_{2}A_{-1})^{2}}<0\) or b1b3<0 and \(\xi =\frac {2k_{1}A_{-1}}{k_{4}}\sqrt {-\frac {b_{3}}{3a}} \left (x+\left (\alpha +2a\frac {3b_{2}k_{4}+4b_{3}A_{-1}k_{2}+8k_{4}b_{3}A_{0}}{3k_{4}\beta }\right)t\right)\).
Family 3:
It should be stated that these plane wave solutions will exist for \(s=k_{2}^{2}+\frac {k_{4}^{2}A_{0}^{2}}{A_{-1}^{2}}+\frac {3k_{4}^{4}b_{1}}{b_{3}A_{-1}^{2}(A_{0}k_{4}+k_{2}A_{-1})^{2}}=0\) and \(\xi =\frac {2k_{1}A_{-1}}{k_{4}}\sqrt {-\frac {b_{3}}{3a}} \left (x+\left (\alpha +2a\frac {3b_{2}k_{4}+4b_{3}A_{-1}k_{2}+8k_{4}b_{3}A_{0}}{3k_{4}\beta }\right)t\right)\).
Family 4:
It should be stated that these kink-soliton wave solutions will exist for \(b_{1}=-\frac {A_{0}^{2}b_{3}\left (k_{4}^{2}A_{0}^{2}+2A_{-1}A_{0}k_{4}k_{2}+k_{2}^{2}A_{-1}^{2}\right)}{3k_{4}^{2}}\) and \(\xi =\frac {2k_{1}A_{-1}}{k_{4}}\sqrt {-\frac {b_{3}}{3a}} \left (x+\left (\alpha +2a\frac {3b_{2}k_{4}+4b_{3}A_{-1}k_{2}+8k_{4}b_{3}A_{0}}{3k_{4}\beta }\right)t\right)\).
The special cases are as follows:
When s>0 and \(C_{1}^{2}>C_{2}^{2}\), then we deduce the following optical soliton solutions from (69) as
where \(\xi \,=\,\frac {2k_{1}A_{-1}}{k_{4}}\!\sqrt {-\frac {b_{3}}{3a}}\! \left (x\,+\,\!\left (\!\alpha \,+\,2a\frac {3b_{2}k_{4}+4b_{3}A_{-1}k_{2}+8k_{4}b_{3}A_{0}}{3k_{4}\beta } \right)\!t\right)\) and ξ0= tanh−1(C2/C1). Also, setting C1=0,C2≠0 or C2=0,C1≠0 in (69), we can obtain more solitary wave solutions which are omitted.
If, however, s<0, we obtain singular periodic waves from (70) as
where \( \xi \!\,=\,\frac {2k_{1}A_{-1}}{k_{4}}\!\sqrt {\,-\,\frac {b_{3}}{3a}} \left (\!x\,+\,\left (\!\alpha \,+\, 2a\frac {3b_{2}k_{4}+4b_{3}A_{-1}k_{2}+8k_{4}b_{3}A_{0}}{3k_{4}\beta }\!\right)\!t\right)\) and ξ0= tan−1(C1/C2). Also, setting C1=0,C2≠0 or C2=0,C1≠0 in (70), we can obtain more solitary wave solutions which are omitted.
Results and discussion
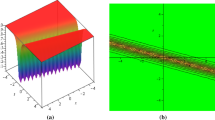
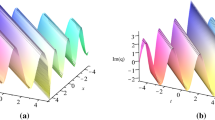
The results obtained here are rational, hyperbolic and trigonometric functions solutions and for some appropriated parameters, we gained exact solutions including bright, dark and singular soliton solutions. These solutions can help to explain the variation of solitary waves in optical metamaterials. We plot some of the solutions to have an idea on the mechanism underlying the original equation (1) by using the improved G′/G-expansion method. Specifically, we plot solutions (61), (64), (65) and (66) by using suitable values of the parameters obtained. Figures 1, 2, 3 and 4 have been plotted as the 3D plot, density plot, and contour plot of q(x,t) to illustrate the kink-soliton, soliton-soliton and singular-soliton wave solutions. By considering as special values in (61) to (74), the soliton forms can be reduced to a kind of exact solitary wave solution in the forms of the rational solution or other.
Graph of Eq. (61) by considering the parameters b1=b2=k2=c1=a=2,b3=−1,k1=c2=α=3,β=θ=1,A1=0.5 and a 3D plot, b density plot, and c contour plot
Graph of Eq. (64) by considering the parameters b1=b2=k2=c1=a=2,b3=−1,k1=c2=α=3,β=θ=1,A−1=0.5 and a 3D plot, b density plot, and c contour plot
Graph of Eq. (65) by considering the parameters b1=b2=c1=a=2,b3=−1,k3=c2=α=3,k1=k2=k4=β=θ=1,A−1=0.5 and a 3D plot, b density plot, and c contour plot
Graph of Eq. (66) by considering the parameters b2=k2=k3=c1=a=2,b3=−1,b1=c2=α=3,k1=k4=β=θ=1,A−1=1 and a 3D plot, b density plot, and c contour plot
Conclusion
This paper secured soliton solutions to optical metamaterials that maintained AC nonlinearity. The governing model was studied with a few perturbation terms all of which are Hamiltonian type. Bright, dark and singular solutions are recovered together with the required constraint conditions for their existence. As a byproduct, singular periodic solutions emerged with the reverse constraints. These periodic solutions are a byproduct of the integration methodologies. The results of this paper are extremely important and carry a lot of weightage in the optical materials community where the study of solitons in the context of metamaterials is essentially new. The results of this paper carry a lot of further research prospects in this area. Later, additional forms of nonlinear metamaterials will also be considered. These are quadratic-cubic type, log-law nonlinearity and several others. Those results are currently awaited and will be reported in the future. The merit using of the two analytical methods, namely, ETEM and IGEM is the finding of NLSE solutions including trigonometric, hyperbolic, rational function solutions where may be achieved by other methods.
References
Agarwal, GP: Nonlinear Fiber Optics. Academic Press, Agarwal (2003).
Zhou, Q, Zhu, Q, Liu, Y, Biswas, A, Bhrawy, AH, Khan, KR, Mahmood, MF, Belic, M: Solitons in optical metamaterials with parabolic law nonlinearity and spatiotemporal dispersion. J. Optoelectron. Adv. Mater. 16(1112), 1221–1225 (2014).
Biswas, A, Khan, KR, Mahmood, MF, Belic, M: Bright and dark solitons in optical metamaterials. Optik. 125, 3299–3302 (2014).
Biswas, A, Mirzazadeh, M, Savescu, M, Milovic, D, Khan, KR, Mahmood, MF, Belic, M: Singular solitons in optical metamaterials by ansatz method and simplest equation approach. J. Mod. Opt. 61, 1550–1555 (2014).
Biswas, A, Mirzazadeh, M, Eslami, M, Milovic, D, Belic, M: Solitons in optical metamaterials by functional variable method and first integral approach. Frequenz. 68, 525–530 (2014).
Krishnan, EV, Ghabshi, MA, Zhou, Q, Khan, KR, Mahmood, MF, Xu, Y, Biswas, A, Belic, M: Solitons in optical metamaterials by mapping method. J. Optoelectron. Adv. Mater. 17, 511–516 (2015).
Manafian, J: Optical soliton solutions for Schrödinger type nonlinear evolution equations by the t a n(ϕ/2)-expansion method. Optik. 127, 4222–4245 (2016).
Lan, Z-Z, Gao, Y-T, Zhao, C, Yang, J-W, Su, C-Q: Dark soliton interactions for a fifth-order nonlinear Schrödinger equation in a Heisenberg ferromagnetic spin chain. Superlattice. Microst. 100, 191–197 (2016).
Aslan, EC, Tchier, F, Inc, M: On optical solitons of the Schrödinger-Hirota equation with power law nonlinearity in optical fibers. Superlattice. Microst. 105, 48–55 (2017).
Manafian, J, Lakestani, M: Optical solitons with Biswas-Milovic equation for Kerr law nonlinearity. Eur. Phys. J. Plus. 130, 1–12 (2015).
Manafian, J: On the complex structures of the Biswas-Milovic equation for power, parabolic and dual parabolic law nonlinearities. Eur. Phys. J. Plus. 130, 1–20 (2015).
Arnous, AH, Seithuti, MZU, Moshokoa, P, Zhou, Q, Triki, H, Mirzazadeh, M, Biswas, A: Optical solitons in nonlinear directional couplers with trial function scheme. Nonlinear Dyn. 88, 1891–1915 (2017).
Ekici, M, Zhou, Q, Sonmezoglu, A, Manafian, J, Mirzazadeh, M: The analytical study of solitons to the nonlinear Schrödinger equation with resonant nonlinearity. Optik. 130, 378–382 (2017).
Taghizadeh, N, Zhou, Q, Ekici, M, Mirzazadeh, M: Soliton solutions for Davydov solitons in α-helix proteins. Superlattice. Microst. 102, 323–341 (2017).
Zhou, Q, Zhu, Q, Liu, Y, Biswas, A, Bhrawy, AH, Khan, KR, Mahmood, MF, Belic, M: Solitons in optical metamaterials with parabolic law nonlinearity and spatio-temporal dispersion. J. Optoelectron. Adv. Mater. 16(1112), 1221–1225 (2014).
Manafian, J, Lakestani, M: Dispersive dark optical soliton with Tzitzéica type nonlinear evolution equations arising in nonlinear optics. Opt. Quant. Elec. 48, 1–32 (2016).
Manafian, J: Optical soliton solutions for Schrödinger type nonlinear evolution equations by the t a n(ϕ/2)-expansion method. Optik-Int. J. Elec. Opt. 127, 4222–4245 (2016).
Manafian, J, Lakestani, M: Optical soliton solutions for the Gerdjikov-Ivanov model via t a n(ϕ/2)-expansion method. Optik. 127, 9603–9620 (2016).
Zhou, Q: Optical solitons in medium with parabolic law nonlinearity and higher order dispersion. Waves Random Complex Media. 25, 52–59 (2016).
Tchier, F, Yusuf, A, Aliyu, AI, Inc, M: Soliton solutions and conservation laws for lossy nonlinear transmission line equation. Superlattice. Microst. 107, 320–336 (2017).
Lakestani, M, Manafian, J: Analytical treatment of nonlinear conformable timefractional Boussinesq equations by three integration methods. Opt. Quant. Electron. 50(4), 1–31 (2018).
Manafian, J, Aghdaei, MF, Khalilian, M, Jeddi, RS: Application of the generalized G’/G-expansion method for nonlinear PDEs to obtaining soliton wave solution. Optik. 135, 395–406 (2017).
Sindi, CT, Manafian, J: Wave solutions for variants of the KdVBurger and the K(n,n)Burger equations by the generalized G’/G-expansion method. Math. Method Appl. Sci. (2017). https://doi.org/10.1002/mma.4309.
Sindi, CT, Manafian, J: Soliton solutions of the quantum Zakharov-Kuznetsov equation which arises in quantum magneto-plasmas. Eur. Phys. J. Plus. 132(67) (2017). https://doi.org/10.1140/epjp/i2017-11354-7.
Fujioka, J, Cortés, E, Pérez-Pascual, R, Rodriguez, RF, Espinosa, A, Malomed, BA: Chaotic solitons in the quadratic-cubic nonlinear Schrödinger equation under nonlinearity management. Chaos. 21, 033120 (2011).
Najafi, M, Arbabi, S: Dark soliton and periodic wave solutions of the Biswas-Milovic equation. Optik. 127, 2679–2682 (2016).
Ravi Teja, N, Aneesh Babu, M, Prasad, TRS, Ravi, T: Different types of dispersions in an optical fiber. Int. J. Sci. Res. Publ. 2, 1–5 (2012).
Biswas, A, Zhou, Q, Zakaullah, M, Triki, H, Moshokoa, SP, Belic, M: Optical soliton perturbation with anti-cubic nonlinearity by semi-inverse variational principle. Optk. 143, 131–134 (2017).
Biswas, A, Triki, H, Zhou, Q, Moshokoa, SP, Zakaullah, M, Belic, M: Cubic-quartic optical solitons in Kerr and power law media. Optk. 144, 357–362 (2017).
Biswas, A, Zhou, Q, Moshokoa, SP, Triki, H, Belic, M, Alqahtani, RT: Resonant 1-soliton solution in anti-cubic nonlinear medium with perturbations. Optk. 145, 14–17 (2017).
Biswas, A, Zakaullah, M, Asma, M, Zhou, Q, Moshokoa, SP, Triki, H, Belic, M: Optical solitons with quadratic-cubic nonlinearity by semi-inverse variational principle. Optk. 139, 16–19 (2017).
Bakodah, HO, Al Qarni, AA, Banaja, MA, Zhou, Q, Moshokoa, SP, Biswas, A: Bright and dark Thirring optical solitons with improved adomian decomposition method. Optk. 130, 1115–1123 (2017).
Ekici, M, Zhou, Q, Sonmezoglu, A, Manafian, J, Mirzazadeh, M: The analytical study of solitons to the nonlinear Schrödinger equation with resonant nonlinearity. Optk. 130, 378–382 (2017).
Biswas, A, Mirzazadeh, M, Eslami, M, Zhou, Q, Bhrawy, AH, Belic, M: Optical solitons in nano-fibers with spatio-temporal dispersion by trial solution method. Optk. 127(18), 7250–8257 (2016).
Zhou, Q, Biswas, A: Optical solitons in parity-time-symmetric mixed linear and nonlinear lattice with non-Kerr law nonlinearity. Superlattice. Microst. 109, 588–598 (2017).
Zhou, Q, Mirzazadeh, M, Zerrad, E, Biswas, A, Belic, M: Bright, dark, and singular solitons in optical fibers with spatio-temporal dispersion and spatially dependent coefficients. J. Mod. Opt. 63(10), 950–954 (2016).
Zhou, Q, Liu, L, Zhang, H, Wei, C, Lu, J, Yu, H, Biswas, A: Analytical study of Thirring optical solitons with parabolic law nonlinearity and spatio-temporal dispersion. Eur. Phys. J. Plus. 130(7), 138 (2015).
Zhou, Q, Zhu, Q, Liu, Y, Yu, H, Yao, P, Biswas, A: Thirring optical solitons in birefringent fibers with spatio-temporal dispersion and Kerr law nonlinearity. Laser Phys. 25(1), 015402 (2015).
Zhou, Q, Zhu, Q, Yu, H, Liu, Y, Wei, C, Yao, P, Bhrawy, AH, Biswas, A: Bright, dark and singular optical solitons in a cascaded system. Laser Phys. 25(2), 025402 (2015).
Zhou, Q, Zhong, Y, Mirzazadeh, M, Bhrawy, AH, Zerrad, E, Biswas, A: Thirring combo-solitons with cubic nonlinearity and spatio-temporal dispersion. Waves Random Complex Media. 26(2), 204–210 (2016).
Zhou, Q, Zhu, Q, Biswas, A: Optical solitons in birefringent fibers with parabolic law nonlinearity. Opt. Appl. 44(3), 399–409 (2014).
Zhou, Q, Liu, L, Zhang, H, Mirzazadeh, M, Bhrawy, AH, Zerrad, E, Moshokoa, S, Biswas, A: Dark and singular optical solitons with competing nonlocal nonlinearities. Opt. Appl. 46(1), 79–86 (2016).
Zhou, Q, Zhu, Q, Bhrawy, AH, Moraru, L, Biswas, A: Optical solitons with spatially-dependent coefficients by Lie symmetry. Optoelectron. Adv. Mater.-Rapid Commun. 8(7-8), 800–803 (2014).
Zhou, Q, Zhu, Q, Bhrawy, AH, Moraru, L, Biswas, A: Perturbation theory and optical soliton cooling with anti-cubic nonlinearity. Optik. 142, 73–76 (2017).
Funding
This work was not supported by any specific funding.
Availability of data and materials
The datasets supporting the conclusions of this article are included within the article and its additional file.
Author information
Authors and Affiliations
Contributions
All the authors made contribution to this work. JM made the numerical simulations and wrote the article. MRF and JM provided the extended trial equation method and solved the problem with it. MRF and AR made the improved G’/G-expansion method and investigated the problem by help of it. JM and AR designed the plots to equation constructed by IGEM. All the authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare they have no competing interests.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Foroutan, M., Manafian, J. & Ranjbaran, A. Solitons in optical metamaterials with anti-cubic law of nonlinearity by ETEM and IGEM. J. Eur. Opt. Soc.-Rapid Publ. 14, 16 (2018). https://doi.org/10.1186/s41476-018-0084-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s41476-018-0084-x