Fractional-order model for biocontrol of the lesser date moth in palm trees and its discretization

Abstract

In this paper, a fractional-order model of palm trees, the lesser date moth and the predator is presented. Existence conditions of the local asymptotic stability of the equilibrium points of the fractional system are analyzed. We prove that the positive equilibrium point is globally stable also. The numerical simulations come to illustrate the dynamical behaviors of the model such as bifurcation and chaos phenomenon, and the numerical simulations confirm the validity of our theoretical results.

1 Introduction

Date palm is a unisexual fruit tree native to the hot arid regions of the world, mainly grown in the Middle East and North Africa. Since ancient times this majestic plant has been recognized as the tree of life because of its integration into human settlement, well-being, and food security in hot regions of the world, where only a few plant species can flourish [1].

It is well known that approximately one third of the world food production is lost due to pests. Pesticides have a great role in destroying pests and increasing crop yield. But the excessive use of pesticides exerts harmful effects on human health. The extensive use of chemical pesticides has had many well documented adverse consequences. So, the present trend in pest control is to minimize the use of pesticides with optimum reduction in the pest population. Such a situation can be achieved when the balance between the pest and its natural enemies is least disturbed by selective use of pesticides [2].

The lesser date moth, Batrachedra amydraula (Lepidoptera: Batrachedridae), is a serious pest of date palms. Its distribution is from Bangladesh to the entire Middle East, as well as most of North America. It is one of the most important pests on date palms that may cause more than 50% loss of the crop [3].

In recent decades, the fractional calculus and fractional differential equations have attracted much attention and increasing interest due to their potential applications in science and engineering [4–17]. In this paper, we consider a fractional-order model consisting of palm trees, the lesser date moth and the predator. Sufficient conditions for the existence of the solutions of the fractional-order model are investigated. The equilibrium points and their asymptotic stability are discussed. Also, the conditions for the existence of a flip bifurcation are considered. The necessary conditions for this system to exhibit chaotic dynamics are also derived.

2 Fractional calculus

A great deal of research has been conducted on prey-predator models based on fractional-order differential equations. A property of these fractional models is their nonlocal property which is not present in integer-order differential equations. Nonlocal property means that the next state of a model depends not only upon its current state, but also upon all of its historical states as the case in epidemics. Fractional-order differential equations can be used to model phenomena which cannot be adequately modeled by integer-order differential equations [10, 13, 18–21]. There are several definitions of fractional derivatives. One of the most common definitions is the Caputo concept. This definition is often used in real applications.

Definition 1

The fractional integral of order $\beta\in{R}^{+}$ of the function $f(t)$ is defined by

$$I^{\beta}f(t)= \int_{0}^{t}\frac{ ( t-\tau ) ^{\beta -1}}{\Gamma ( \beta ) }f(\tau)\,d\tau, $$

provided the integral on the right-hand side is defined for almost every $t>0$. This occurs, for example, if $f\in L^{1}(0,+\infty)$. The fractional derivative of order $\alpha\in(n-1,n)$, $n\in N$ is defined as follows for a function f such that the n-order derivative exists and, for example, $f^{(n)}\in L^{1}(0,+\infty)$:

$$D_{t}^{\alpha}f(t)=I^{n-\alpha}f^{ ( n ) }(t),\quad\alpha>0. $$

3 Fractional-order lesser date moth model and its discretization

Following [22, 23], the model of biocontrol of the lesser date moth in palm trees can be written as a set of three coupled nonlinear ordinary differential equations as follows:

$$ \begin{gathered} \frac{dP}{d\tau} =rP\biggl(1-\frac{P}{K} \biggr)-\frac{bPL}{a+P}, \\ \frac{dL}{d\tau} =-dL+\frac{mPL}{a+P}-pLN, \\ \frac{dN}{d\tau} =-\mu N+qLN. \end{gathered} $$

(1)

The model consists of three populations. The palm tree whose population density at time t is denoted by P, the pest (lesser date moth) whose population density is denoted by L and the predator whose population density is denoted by N. In the absence of predators, the prey population density grows according to a logistic curve with carrying capacity K and with an intrinsic growth rate constant r.

The maximal growth rate of the pest is denoted by b. The half saturation a is constant, d denotes the death rate of the pests, m is the conversion rate of the pests, p is the quantity that represents decrease in the growth rate of the pests due to predator attack, q is the rate of increase in the predator population, and μ denotes the intrinsic mortality rate of the predators. Here all the parameters r, K, b, a, d, m, p, μ, and q are positive.

One can reduce the number of parameters in system (1) by using the following transformations:

$$P=K x,\qquad L=\frac{Kr}{b}y,\qquad N=\frac{r}{p}z , \qquad\tau=\frac{t}{r}, $$

then we have the following dimensionless system:

$$ \begin{gathered} \frac{dx}{dt} =x(1-x)-\frac{xy}{\beta+x}, \\ \frac{dy}{dt} =-\delta y+\frac{\gamma xy}{\beta+x}-yz, \\ \frac{dz}{dt} =-\eta z+\sigma yz, \end{gathered} $$

(2)

where

$$\beta=\frac{a}{K},\qquad\delta=\frac{d}{r},\qquad\gamma=\frac{m}{r},\qquad \eta=\frac{\mu}{r}\quad \text{and}\quad \sigma=\frac{qk}{b}. $$

Fractional-order models are more accurate than integer-order models as they allow more degrees of freedom. Fractional differential equations also serve as an excellent tool for the description of hereditary properties of various materials and processes [10, 13]. Now we introduce fractional order into the ODE model (2). The new system is described by the following set of fractional-order differential equations:

$$ \begin{gathered} D^{\alpha}x =x(1-x)-\frac{xy}{\beta+x}, \\ D^{\alpha}y =-\delta y+\frac{\gamma xy}{\beta+x}-yz, \\ D^{\alpha}z =-\eta z+\sigma yz, \end{gathered} $$

(3)

where $D^{\alpha}$ is the Caputo fractional derivative. Following [21, 24, 25], we discretize the fractional lesser date moth and predator model (3). After the discretization with piecewise constant arguments, the system is reduced to

$$ \begin{gathered} x_{n+1} =x_{n}+ \frac{h^{\alpha}}{\Gamma ( 1+\alpha ) } \biggl[ x_{n}(1-x_{n})-\frac{x_{n}y_{n}}{\beta+x_{n}} \biggr], \\ y_{n+1} =y_{n}+\frac{h^{\alpha}}{\Gamma ( 1+\alpha ) } \biggl[ -\delta y_{n}+\frac{\gamma x_{n}y_{n}}{\beta+x_{n}}-y_{n}z_{n} \biggr], \\ z_{n+1} =z_{n}+\frac{h^{\alpha}}{\Gamma ( 1+\alpha ) } [ -\eta z_{n}+ \sigma y_{n}z_{n} ] . \end{gathered} $$

(4)

Remark 1

If the fractional order $\alpha\rightarrow1$, then we have the forward Euler discretization of system (2).

In the following, we will study the dynamics of system (4).

4 Dynamical behaviors of the discretized fractional-order lesser date moth and predator model

4.1 Stability of the fixed points of the system

In this subsection, we study the asymptotic stability of the fixed points of system (4) which has the same fixed points of system (4). First, we need the following two definitions.

Definition 2

[26] (Local stability when all eigenvalues are real)

Consider the discrete, nonlinear dynamical system in (4) with a steady-state equilibrium x̄. The linearized system is given by (4). The associated Jacobian matrix has three real eigenvalues $\lambda_{i}$ ($i=1,2,3$).

Lemma 1

• (i) The steady-state equilibrium x̄ is called a stable node if $\vert \lambda_{i} \vert <1$ for all $i=1,2,3$.

• (ii) The steady-state equilibrium x̄ is called a two-dimensional saddle if one $\vert \lambda_{i} \vert >1$.

• (iii) The steady-state equilibrium x̄ is called a one-dimensional saddle if one $\vert \lambda_{i} \vert <1$.

• (iv) The steady-state equilibrium x̄ is called an unstable node if $\vert \lambda_{i} \vert >1$ for all $i=1,2,3$.

• (v) The steady-state equilibrium x̄ is called hyperbolic if one $\vert \lambda_{i} \vert =1$.

Definition 3

[26] (Local stability when complex eigenvalues)

Consider the discrete, nonlinear dynamical system in (4) with a steady-state equilibrium x̄. The linearized system is given by (4). The associated Jacobian matrix has a pair of complex eigenvalues $\lambda_{1,2}=\rho+\omega i$ and one real eigenvalue $\lambda_{3}$.

• (i) The steady-state equilibrium x̄ is called a sink if $\vert \lambda_{i} \vert <1$ for all $i=1,2,3$.

• (ii) The steady-state equilibrium x̄ is called a two-dimensional saddle if one $\vert \lambda_{3} \vert >1$.

• (iii) The steady-state equilibrium x̄ is called a one-dimensional saddle if one $\vert \lambda_{3} \vert <1$.

• (iv) The steady-state equilibrium x̄ is called a source if $\vert \lambda_{i} \vert >1$ for all $i=1,2,3$.

• (v) The steady-state equilibrium x̄ is called hyperbolic if one $\vert \lambda_{i} \vert =1$.

Now, the Jacobian matrix $J ( E_{0} )$ for system given in (4) evaluated at $E_{0}(0,0,0)$ is as follows:

$$ J ( E_{0} ) =\left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c} 1+\frac{h^{\alpha}}{\Gamma ( 1+\alpha ) } & 0 & 0 \\ 0 & 1-\frac{\delta h^{\alpha}}{\Gamma ( 1+\alpha ) } & 0 \\ 0 & 0 & 1-\frac{\eta h^{\alpha}}{\Gamma ( 1+\alpha ) }\end{array}\displaystyle \right ) . $$

(5)

Theorem 1

The trivial-equilibrium point $E_{0}$ has at least three different topological types for its all values of parameters as follows:

• (i) $E_{0}$ is a source if $h>\max \{ \sqrt[\alpha]{\frac{2\Gamma ( 1+\alpha ) }{\delta}},\sqrt[\alpha]{\frac{2\Gamma ( 1+\alpha ) }{\eta}} \}$,

• (ii) $E_{0}$ is a two-dimensional saddle if $0< h<\min \{ \sqrt [\alpha]{\frac{2\Gamma ( 1+\alpha ) }{\delta}},\sqrt[\alpha]{\frac{2\Gamma ( 1+\alpha ) }{\eta}} \}$,

• (iii) $E_{0}$ is a one-dimensional saddle if $\sqrt[\alpha]{\frac {2\Gamma ( 1+\alpha ) }{\delta}}< h<\sqrt[\alpha]{\frac{2\Gamma ( 1+\alpha ) }{\eta}}$ or $\sqrt[\alpha]{\frac{2\Gamma ( 1+\alpha ) }{\eta}}< h<\sqrt[\alpha]{\frac{2\Gamma ( 1+\alpha ) }{\delta}}$.

Proof

The eigenvalues corresponding to the equilibrium point $E_{0}$ are $\lambda_{01}=1+\frac{h^{\alpha}}{\Gamma ( 1+\alpha ) }>0$, $\lambda_{02}=1-\frac{\delta h^{\alpha}}{\Gamma ( 1+\alpha ) }$, and $\lambda_{03}=1-\frac{\eta h^{\alpha }}{\Gamma ( 1+\alpha ) }$, where $\alpha\in( 0,1 ]$ and $h, \frac{h^{\alpha}}{\Gamma ( 1+\alpha ) }>0$. Hence, applying the stability conditions using Definition 2, one can obtain the results (i)-(iii). □

The Jacobian matrix $J ( E_{1} )$ for system (4), evaluated at $E_{1}= ( 1,0,0 )$, is given by

$$ J ( E_{1} ) =\left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c} 1-\frac{h^{\alpha}}{\Gamma ( 1+\alpha ) } & \frac {-h^{\alpha}}{ ( 1+\beta ) \Gamma ( 1+\alpha ) } & 0 \\ 0 & 1+\frac{\delta ( R_{0}-1 ) h^{\alpha}}{\Gamma ( 1+\alpha ) } & 0 \\ 0 & 0 & 1-\frac{\eta h^{\alpha}}{\Gamma ( 1+\alpha ) }\end{array}\displaystyle \right ) . $$

(6)

Theorem 2

If the semi-trivial equilibrium point $E_{1}$ exists, then it has at least three different topological types for its all values of parameters.

• (i) $E_{1}$ is a source if $h>\max \{ \sqrt[\alpha]{2\Gamma ( 1+\alpha ) },\sqrt[\alpha]{\frac{2\Gamma ( 1+\alpha ) }{\mu}} \}$,

• (ii) $E_{1}$ is a two-dimensional saddle if $0< h<\min \{ \sqrt [\alpha]{2\Gamma ( 1+\alpha ) },\sqrt[\alpha]{\frac{2\Gamma ( 1+\alpha ) }{\eta}} \}$,

• (iii) $E_{1}$ is a one-dimensional saddle if $\sqrt[\alpha]{2\Gamma ( 1+\alpha ) }< h<\sqrt[\alpha]{\frac{2\Gamma ( 1+\alpha ) }{\eta}}$ or $\sqrt[\alpha]{\frac{2\Gamma ( 1+\alpha ) }{\eta}}< h<\sqrt[\alpha]{2\Gamma ( 1+\alpha ) }$.

Proof

The eigenvalues corresponding to the equilibrium point $E_{0}$ are $\lambda_{11}=1-\frac{h^{\alpha}}{\Gamma ( 1+\alpha ) }$, $\lambda_{12}=1+\frac{\delta ( R_{0}-1 ) h^{\alpha}}{\Gamma ( 1+\alpha ) }>0$, and $\lambda_{13}=1-\frac{\eta h^{\alpha}}{\Gamma ( 1+\alpha ) }$. Hence, applying the stability conditions using Definition 2, one can obtain the results (i)-(iii). □

For investigating the stability of $E_{2}= ( \frac{\beta\delta }{\gamma -\delta},\frac{\gamma ( \beta+1 ) ( R_{0}-1 ) x_{2}^{2}}{\beta\delta},0 )$, let $J ( E_{2} )$ be the Jacobian matrix for the system given in (4) evaluated at $E_{2}$, then

$$ J ( E_{2} ) =\left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c} 1-\frac{h^{\alpha}}{\Gamma ( 1+\alpha ) } [ x_{2}-\frac{ x_{2}y_{2}}{ ( \beta+x_{2} ) ^{2}} ] & \frac {-x_{2}h^{\alpha}}{ ( \beta+x_{2} ) \Gamma ( 1+\alpha ) } & 0 \\ \frac{\beta\gamma y_{2}h^{\alpha}}{ ( \beta+x_{2} ) ^{2}\Gamma ( 1+\alpha ) } & 1 & \frac{-y_{2}h^{\alpha}}{\Gamma ( 1+\alpha ) } \\ 0 & 0 & 1-\frac{h^{\alpha}}{\Gamma ( 1+\alpha ) } ( \eta -\sigma y_{2} )\end{array}\displaystyle \right ) . $$

(7)

The characteristic equation of the Jacobian matrix (7) is

$$ \bigl[ \lambda_{21}- \bigl( 1-H [ \eta-\sigma y_{2} ] \bigr) \bigr] \bigl[ \lambda^{2}-\mathit{Tr}_{2} \lambda+\mathit{Det}_{2} \bigr] =0, $$

(8)

where $H=\frac{h^{\alpha}}{\Gamma ( 1+\alpha ) }$, $\mathit{Tr}_{2}=2-B_{2}H$, $B_{2}=\frac{ ( 1+\beta ) x_{2}^{2}}{ ( \beta+x_{2} ) } [ 1-R_{0} ( 1-\beta ) ]$, $\mathit{Det}_{2}=A_{2}H^{2}-B_{2}H+1$, and $A_{2}=\frac{\beta\gamma x_{2}y_{2}}{ ( \beta+x_{2} ) ^{3}}$.

Theorem 3

If $1< R_{0}<\frac{\beta\delta\eta}{\gamma\sigma ( 1+\beta ) x_{2}^{2}}+1$, then the semi-trivial equilibrium point $E_{2}$ has at least four different topological types for its all values of parameters

• (i) $E_{2}$ is asymptotically stable (sink) if one of the following conditions holds:

  • (i.1) $\Delta\geq0$ and $0< h<\min \{ h_{1},h_{2} \}$,

  • (i.2) $\Delta<0$ and $0< h< h_{2}$;

• (ii) $E_{2}$ is unstable (source) if one of the following conditions holds:

  • (ii.1) $\Delta\geq0$ and $h>\max \{ h_{2},h_{3} \}$,

  • (ii.2) $\Delta<0$ and $h>h_{2}$;

• (iii) $E_{2}$ is a two-dimensional saddle if the following case is satisfied:

  $\Delta\geq0$ and $h<\min \{ h_{1},h_{2} \}$;

• (iv) $E_{2}$ is a one-dimensional saddle if one of the following cases is satisfied:

  • (iv.1) $\Delta\geq0$ and $h_{3}< h< h_{2}$ or $\max \{ h_{1},h_{2} \} < h< h_{3}$,

  • (iv.2) $\Delta<0$ and $0< h< h_{2}$;

• (v) $E_{2}$ is non-hyperbolic if one of the following conditions holds:

  • (v.1) $\Delta\geq0$ and $h=h_{1}$ or $h_{3}$,

  • (v.2) $\Delta<0$ and $h=h_{2}$,

where

$$\begin{aligned}& h_{1} =\sqrt[\alpha]{\frac{4\Gamma ( 1+\alpha ) }{B_{2}+\sqrt{\Delta}}},\qquad h_{3}=\sqrt[ \alpha]{\frac{4\Gamma ( 1+\alpha ) }{B_{2}-\sqrt{\Delta}}} , \\& \Delta=B_{2}^{2}-4A_{2},\qquad h_{2}=\sqrt[ \alpha]{\frac{2\Gamma ( 1+\alpha ) }{\eta-\sigma y_{2}}}. \end{aligned}$$

Proof

The eigenvalues corresponding to the equilibrium point $E_{2}$ are the roots of the characteristic equation (8), which is $\lambda_{21}=1-H [ \eta-\sigma y_{2} ]$ and $\lambda _{22,23}=\frac{1}{2} ( \mathit{Tr}_{2}\pm\sqrt{\mathit{Tr}_{2}^{2}-4\mathit{Det}_{2}} ) =1-\frac {H}{2} ( B_{2}\pm\sqrt{B_{2}^{2}-4A_{2}} )$. Hence, applying the stability conditions using Lemma 1, one can obtain the results (i)-(v). □

The fourth and fifth equilibrium points are $E_{j}= ( x_{j},y_{j},z_{j} )$, $j=3,4$, where

$$\begin{aligned}& x_{3} =\frac{1}{2} \biggl[ 1-\beta-\sqrt{ ( 1-\beta ) ^{2}-4 \biggl( \frac{\eta}{\sigma}-\beta \biggr) } \biggr] , \\& x_{4} =\frac{1}{2} \biggl[ 1-\beta+\sqrt{ ( 1-\beta ) ^{2}-4 \biggl( \frac{\eta}{\sigma}-\beta \biggr) } \biggr] , \\& y_{j} =\frac{\eta}{\sigma}, \\& z_{j} =\frac{\beta\gamma\sigma}{\eta} ( x_{j}-1 ) +\gamma -\delta. \end{aligned}$$

For the dynamical properties of the interior (positive) equilibrium point $E_{j}$ ($j=3,4$) we need to state these lemmas.

Lemma 2

[27]

Let the equation $x^{3}+bx^{2}+cx+d=0$, where $b,c,d\in R$. Let further $A=b^{2}-3c$, $B=bc-9d$, $C=c^{2}-3bd$, and $\Delta =B^{2}-4AC$. Then

• (1) The equation has three real roots if and only if $\Delta\leq0$.

• (2) The equation has one real root $x_{1}$ and a pair of conjugate complex roots if and only if $\Delta>0$. Furthermore, the conjugate complex roots $x_{2,3}$ are

  $$x_{2,3}=\frac{1}{6} \bigl[ \sqrt[3]{y_{1}}+ \sqrt[3]{y_{2}}-2b\pm\sqrt{3} i \bigl( \sqrt[3]{y_{1}}- \sqrt[3]{y_{2}} \bigr) \bigr], $$

  where

  $$y_{1,2}=bA+\frac{3}{2} \bigl( -B\pm\sqrt{B^{2}-4AC} \bigr) . $$

Lemma 3

[28–31]

Let $F(\lambda)=\lambda^{2}-\mathit{Tr}\lambda+\mathit{Det}$. Suppose that $F(1)>0$, $\lambda_{1}$ and $\lambda_{2}$ are the two roots of $F(\lambda)=0$. Then

• (i) $\vert \lambda_{1} \vert <1$ and $\vert \lambda _{2} \vert <1$ if and only if $F(-1)>0$ and $\mathit{Det}<1$,

• (ii) $\vert \lambda_{1} \vert <1$ and $\vert \lambda _{2} \vert >1$ (or $\vert \lambda_{1} \vert >1$ and $\vert \lambda_{2} \vert <1$) if and only if $F(-1)<0$,

• (iii) $\vert \lambda_{1} \vert >1$ and $\vert \lambda _{2} \vert >1$ if and only if $F(-1)>0$ and $\mathit{Det}>1$,

• (iv) $\lambda_{1}=-1$ and $\lambda_{2}\neq1$ if and only if $F(-1)=0$ and $\mathit{Tr}\neq0,2$,

• (v) $\lambda_{1}$ and $\lambda_{2}$ are complex and $\vert \lambda _{1} \vert = \vert \lambda_{2} \vert$ if and only if $\mathit{Tr}^{2}-4\mathit{Det}<0$ and $\mathit{Det}=1$.

The necessary and sufficient conditions ensuring that $\vert \lambda _{1} \vert <1$ and $\vert \lambda_{2} \vert <1$ are as follows [28]:

$$ \begin{aligned} \text{(i)}&\quad 1-\mathit{Tr} J+\det J>0, \\ \text{(ii)}&\quad 1+\mathit{Tr} J+\det J>0, \\ \text{(iii)}&\quad \det J< 1. \end{aligned} $$

(9)

If one of conditions (9) is not satisfied, then we have one of the following cases [25].

• 1. A saddle-node (often called fold bifurcation in maps), transcritical or pitchfork bifurcation if one of the eigenvalues =1 and other eigenvalues (real) ≠1. This local bifurcation leads to the stability switching between two different steady states;

• 2. A flip bifurcation if one of the eigenvalues $=-1$, other eigenvalues (real) $\neq-1$. This local bifurcation entails the birth of a period 2-cycle;

• 3. A Neimark-Sacker (secondary Hopf) bifurcation; in this case we have two conjugate eigenvalues and the modulus of each of them =1.

This local bifurcation implies the birth of an invariant curve in the phase plane. The Neimark-Sacker bifurcation is considered to be an equivalent to the Hopf bifurcation in continuous time and in fact the major instrument to prove the existence of quasi-periodic orbits for the map.

Note

You can get any local bifurcation (fold, flip and Neimark-Sacker) by taking specific parameter value such that one of the conditions of each bifurcation is satisfied.

The Jacobian matrix $J ( E_{j} )$ for system (4) evaluated at the interior equilibrium point $E_{j}$ is as follows:

$$ J ( E_{j} ) =\left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c} 1-H [ x_{j}-\frac{x_{j}y_{j}}{ ( \beta+x_{j} ) ^{2}} ] & \frac{-x_{j}H}{\beta+x_{j}} & 0 \\ \frac{\beta\gamma y_{j}H}{ ( \beta+x_{j} ) ^{2}} & 1 & -y_{j}H \\ 0 & \sigma z_{j}H & 1\end{array}\displaystyle \right ), $$

(10)

then the characteristic equation of the Jacobian matrix (10) is

$$ F(\lambda)=\lambda^{3}+b_{j}\lambda^{2}+c_{j} \lambda+d_{j}=0, $$

(11)

where

$$\begin{aligned}& b_{j}=3-\varepsilon_{j}H, \quad\varepsilon_{j}= \frac{x_{j}}{\beta +x_{j}} [ 2x_{j}+\beta-1 ] , \\& c_{j}=\psi_{j}H^{2}-2\varepsilon_{j}H+3,\quad \psi_{j}=\frac{\beta \gamma x_{j}y_{j}}{ ( \beta+x_{j} ) ^{3}}+\sigma y_{j}z_{j}, \end{aligned}$$

and

$$d_{j}=\nu_{j}H^{3}-\psi_{j}H^{2}+ \varepsilon_{j}H-1,\quad\nu _{j}=\sigma\varepsilon_{j}y_{j}z_{j}. $$

By some computation, we have

$$\begin{aligned}& A =b_{j}^{2}-3c_{j}= \bigl( \varepsilon_{j}^{2}-3\psi_{j} \bigr) H^{2}, \\& B =b_{j}c_{j}-9d_{j}= ( \varepsilon_{j} \psi_{j}-9\nu_{j} ) H^{3}+ \bigl( 6 \psi_{j}-2\varepsilon_{j}^{2} \bigr) H^{2}, \\& C =c_{j}^{2}-3b_{j}d_{j}= \bigl( \psi_{j}^{2}-3\varepsilon_{j}\nu _{j} \bigr) H^{4}+ ( 9\nu_{j}-\varepsilon_{j} \psi_{j} ) H^{3}+\bigl(\varepsilon_{j}^{2}-3 \psi_{j}\bigr)H^{2}, \end{aligned}$$

and

$$\Delta_{j}=\bar{\Delta}_{j}H^{6}, $$

where

$$\bar{\Delta}_{j}=3\bigl(27\nu_{j}^{2}+4 \varepsilon_{j}^{3}\nu_{j}+4\psi _{j}^{3}-\varepsilon_{j}^{2} \psi_{j}^{2}-18\varepsilon_{j}\psi _{j}\nu _{j}\bigr). $$

It is clear that equation $F^{\prime}(\lambda)=0$ has the following two roots:

$$\lambda_{1,2}^{\ast}=\frac{1}{3} \Bigl( -b_{j}\pm\sqrt {b_{j}^{2}-3c_{j}} \Bigr) =1-\frac{H}{3} \Bigl( \varepsilon_{j}\pm\sqrt{ \varepsilon _{j}^{2}-3\psi_{j}} \Bigr). $$

If $\bar{\Delta}_{j}\leq0$, then $\Delta_{j}\leq0$; by Lemma 1, equation (10) has three real roots $\lambda_{i}$, $i=1,2,3$ (let $\lambda _{1}\leq\lambda_{2}\leq\lambda_{3}$). From this, we note that two roots $\lambda_{1,2}^{\ast}$ (let $\lambda_{1}^{\ast}\leq\lambda _{2}^{\ast}$) of equation $F^{\prime}(\lambda)=0$ also are real.

When $\bar{\Delta}_{j}>0$, namely, $\Delta_{j}>0$, by Lemma 2, we have that equation (11) has one real root $\lambda_{1}$ and a pair of conjugate complex roots $\lambda_{2,3}$. The conjugate complex roots are as follows:

$$\lambda_{2,3}=\frac{1}{6} \bigl[ \sqrt[3]{y_{1}}+ \sqrt[3]{y_{2}}-2b\pm \sqrt{3}i \bigl( \sqrt[3]{y_{1}}- \sqrt[3]{y_{2}} \bigr) \bigr] , $$

where

$$y_{1,2}=\frac{H^{3}}{2} \bigl( 2\varepsilon_{j}^{3}-9 \varepsilon _{j}\psi _{j}-27\nu_{j}\pm3\sqrt{ \bar{\Delta}_{j}} \bigr) , $$

and

$$F(1)=\nu_{j}H^{3}\quad \text{and}\quad F(-1)=-8+4\varepsilon_{j}H-2 \psi _{j}H^{2}+\nu_{j}H^{3}. $$

Now, we will introduce the stability of $E_{j}$, we have the following theorem.

Theorem 4

If the positive equilibrium point $E_{j}$ exists, then it has the following topological types of its all values of parameters:

• (1) $E_{j}$ is a sink if one of the following conditions holds:

  • (1.i) $\bar{\Delta}_{j}\leq0$, $F(1)>0$, $F(-1)<0$ and $-1<\lambda _{1,2}^{\ast}<1$,

  • (1.ii) $\bar{\Delta}_{j}>0$, $F(1)>0$, $F(-1)<0$ and $\vert \lambda_{2,3} \vert <1$.

• (2) $E_{j}$ is a source if one of the following conditions holds:

  • (2.i) $\bar{\Delta}_{j}\leq0$ and one of the following conditions holds:

    • (2.i.a) $F(1)>0$, $F(-1)>0$ and $\lambda_{2}^{\ast}<-1$ or $\lambda_{2}^{\ast}>1$,

    • (2.i.b) $F(1)<0$, $F(-1)<0$ and $\lambda_{2}^{\ast}<-1$ or $\lambda_{2}^{\ast}>1$,

  • (2.ii) $\bar{\Delta}_{j}>0$ and one of the following conditions holds:

    • (2.ii.a) $F(1)<0$ and $\vert \lambda _{2,3} \vert >1$,

    • (2.ii.b) $F(-1)>0$ and $\vert \lambda _{2,3} \vert >1$.

• (3) $E_{j}$ is a one-dimensional saddle if one of the following conditions holds:

  • (3.i) $\bar{\Delta}_{j}\leq0$ and one of the following conditions holds:

    • (3.i.a) $F(1)>0$, $F(-1)<0$ and $\lambda_{1}^{\ast}<-1$ or $\lambda_{2}^{\ast}>1$,

    • (3.i.b) $F(1)<0$, $F(-1)>0$.

  • (3.ii) $\bar{\Delta}_{j}>0$ and one of the following conditions holds:

    • (3.ii.a) $F(1)>0$, $F(-1)<0$ and $\vert \lambda _{2,3} \vert >1$,

    • (3.ii.b) $F(1)<0$ and $\vert \lambda _{2,3} \vert <1$,

    • (3.ii.c) $F(-1)>0$ and $\vert \lambda _{2,3} \vert <1$.

• (4) $E_{j}$ is a two-dimensional saddle if one of the following conditions holds:

  • (4.i) $\bar{\Delta}_{j}\leq0$ and one of the following conditions holds:

    • (4.i.a) $F(1)>0$, $F(-1)>0$ and $-1<\lambda_{2}^{\ast}<1$,

    • (4.i.b) $F(1)<0$, $F(-1)<0$ and $-1<\lambda_{1}^{\ast}<1$,

  • (4.ii) $\bar{\Delta}_{j}>0$ and one of the following conditions holds:

    • (4.ii.a) $F(-1)<0$ and $\vert \lambda _{2,3} \vert <1$,

    • (4.ii.b) $F(1)>0$ and $\vert \lambda _{2,3} \vert <1$.

• (5) $E_{j}$ is non-hyperbolic if one of the following conditions holds:

  • (5.i) $\bar{\Delta}_{j}\leq0$ and $F(1)=0$ or $F(-1)=0$,

  • (5.ii) $\bar{\Delta}_{j}>0$ and $F(1)=0$ or $F(-1)=0$ or $\vert \lambda_{2,3} \vert =1$.

Proof

Let $\bar{\Delta}_{j}\leq0$. From Lemma 2, equation (11) has three real roots $\lambda_{i}$, $i=1,2,3$. Further, we obtain that equation $F^{\prime}(\lambda)=0$ has also two real roots $\lambda_{1}^{\ast }$ and $\lambda_{2}^{\ast}$. From the expression of $F^{\prime}(\lambda)$, we have $F^{\prime}(\lambda)>0$ for all $\lambda\in ( -\infty ,\lambda _{1}^{\ast} ) \cup ( \lambda_{2}^{\ast},\infty )$ and $F^{\prime}(\lambda)<0$ for all $\lambda\in ( \lambda_{1}^{\ast },\lambda_{2}^{\ast} )$. Hence, $F(\lambda)$ is increasing for all $\lambda\in ( -\infty,\lambda_{1}^{\ast} ) \cup ( \lambda _{2}^{\ast},\infty )$ and decreasing for all $\lambda\in ( \lambda_{1}^{\ast},\lambda_{2}^{\ast} )$. Therefore, we finally obtain $F(\lambda_{1}^{\ast})\geq0$, $F(\lambda_{1}^{\ast})\leq 0$, $\lambda_{1}\in ( -\infty,\lambda_{1}^{\ast} ]$, $\lambda _{2}\in [ \lambda_{1}^{\ast},\lambda_{2}^{\ast} )$ and $\lambda_{3}\in [ \lambda_{2}^{\ast},\infty )$.

If condition (1.i) holds, then we obviously have $\lambda_{1}\in ( -1,\lambda_{1}^{\ast} ]$, $\lambda_{2}\in [ \lambda _{1}^{\ast},\lambda_{2}^{\ast} ]$ and $\lambda_{3}\in [ \lambda_{2}^{\ast},1 )$. Therefore, $E_{j}$ is a sink.

If condition (2.i.a) holds. When $\lambda_{2}^{\ast}<-1$, we have $\lambda_{1}<-1$ and $\lambda_{2}<-1$. Since $F(\lambda)$ is increasing for all $\lambda\in [ \lambda_{2}^{\ast},\infty )$ and $F(-1)>0$, we can obtain $\lambda_{3}<-1$. Therefore, $E_{j}$ is a source. When $\lambda_{2}^{\ast}>-1$, then from $F(-1)>0$ we have $\lambda _{1}<-1$. Hence $F(\lambda)>0$ for all $\lambda\in ( -1,1 )$. Consequently, $\lambda_{2}>1$ and $\lambda_{3}>1$. Therefore, $E_{j}$ is a source.

By the same way, we prove that when condition (2.i.b) holds, $E_{j}$ is also a source.

If condition (3.i.a) holds, then, when $\lambda_{1}^{\ast}<-1$ we have $\lambda_{1}<-1$ and when $\lambda_{2}^{\ast}>1$ we have $\lambda _{3}>1$. From $F(1)>0$ and $F(-1)<0$ we have $\lambda_{2}\in ( -1,1 )$. Therefore, $E_{j}$ is a one-dimensional saddle.

If condition (3.i.b) holds, then we clearly have $\lambda_{1}<-1$, $\lambda_{2}\in ( -1,1 )$ and $\lambda_{3}>1$. Therefore, $E_{j}$ is a one-dimensional saddle too.

If condition (4.i.a) holds, we have $\lambda_{2,3}\in ( -1,1 )$ and $\lambda_{1}^{\ast}\in ( -\infty,1 )$, $F(\lambda)$ is increasing for all $\lambda\in ( -\infty,\lambda_{1}^{\ast} ]$, we obtain $\lambda_{1}\in ( -\infty,-1 )$. Therefore, $E_{j}$ is a two-dimensional saddle.

By the same way, we can prove that when condition (4.i.b) holds, $E_{j}$ is also a two-dimensional saddle.

If condition (5.i) holds, then we can easily prove that $E_{j}$ is non-hyperbolic.

Now, we let $\bar{\Delta}_{j}>0$. From Lemma 2, equation (11) has one real root $\lambda_{1}$ and a pair of conjugate complex roots $\lambda_{2,3}$. If condition (1.ii) holds, then from $F(1)>0$ and $F(-1)<0$ we have that a real root $\lambda_{1}\in ( -1,1 )$. Therefore, from $\vert \lambda_{2,3} \vert <1$ we obtain that $E_{j}$ is a sink.

If condition (2.ii.a) holds, then from $F(-1)<0$ we have a real root $\lambda _{1}>1$. Therefore, from $\vert \lambda_{2,3} \vert >1$ we obtain that $E_{j}$ is a source.

By the same way, we can prove that if condition (2.ii.b) holds, then $E_{j}$ is also a source.

If condition (3.ii.a) holds, then we have a real root $\lambda_{1}\in ( -1,1 )$. Therefore, from $\vert \lambda_{2,3} \vert >1$ we have that $E_{j}$ is a one-dimensional saddle.

By the same way, we can prove that when conditions (3.ii.b) and (3.ii.c) hold, then $E_{j}$ is also a one-dimensional saddle.

If condition (4.ii.a) holds, then from $F(-1)<0$ we have a real root $\lambda _{1}>1$. Therefore, from $\vert \lambda_{2,3} \vert >1$ we have that $E_{j}$ is a two-dimensional saddle.

By the same way, we can prove that if condition (4.ii.b) holds, then $E_{j}$ is also a two-dimensional saddle.

Lastly, we can easily prove that if condition (5.ii) holds, then $E_{j}$ is non-hyperbolic. □

Theorem 5

If the positive equilibrium point $E_{j}$ exists, then $E_{j}$ loses its stability via

• (i) a saddle-node bifurcation, if one of the following conditions holds:

  • (i.1) $\bar{\Delta}_{j}\leq0$, $F(1)=0$ and $F(-1)\neq0$,

  • (i.2) $\bar{\Delta}_{j}>0$, $F(1)=0$ and $\vert \lambda _{2,3} \vert \neq1$;

• (ii) flip bifurcation, if one of the following conditions holds:

  • (ii.1) $\bar{\Delta}_{j}\leq0$, $F(-1)=0$ and $F(1)\neq0$,

  • (ii.2) $\bar{\Delta}_{j}>0$, $F(-1)=0$ and $\vert \lambda _{2,3} \vert \neq1$;

• (iii) Hopf bifurcation, if the following condition holds:

  • $\bar{\Delta}_{j}>0$, $F(-1)\neq0$, $F(1)\neq0$ and $\vert \lambda_{2,3} \vert =1$.

Proof ([29])

(i) introduced a thorough study of the main types of bifurcations for 3-D maps. In line with this study, we can see that $E_{j}$ undergoes a saddle-node bifurcation when a single eigenvalue becomes equal to 1. Therefore $E_{j}$ can lose its stability through the saddle-node bifurcation when one of $\lambda_{i}=1$, $i=1,2,3$. A saddle-node bifurcation of $E_{j}$ may occur if the parameters vary in the small neighborhood of the following sets:

$$S_{1}= \bigl\{ ( h,\alpha,\beta,\gamma,\delta,\eta,\sigma ) :\bar{\Delta}_{j}\leq0,F(1)=0 \text{ and } F(-1)\neq0 \bigr\} , $$

or

$$S_{2}= \bigl\{ ( h,\alpha,\beta,\gamma,\delta,\eta,\sigma ) :\bar{\Delta}_{j}>0,F(1)=0\text{ and }\vert \lambda _{2,3} \vert \neq1 \bigr\} . $$

By the same way, we can prove (ii).

(iii) When the Jacobian has a pair of complex conjugate eigenvalues of modulus 1, we get the Hopf bifurcation, then $E_{j}$ can lose its stability through the Hopf bifurcation when one of $\vert \lambda _{2,3} \vert =1$, and then it also implies that all the parameters locate and vary in the small neighborhood of the following set:

$$S_{3}= \bigl\{ ( h,\alpha,\beta,\gamma,\delta,\eta,\sigma ) :\bar{\Delta}_{j}>0,F(-1)\neq0,F(1)\neq0\text{ and } \vert \lambda_{2,3} \vert =1 \bigr\} . $$

 □

4.2 Numerical simulations

In this section, we give the phase portraits, the attractor of parameter β and bifurcation diagrams to confirm the above theoretical analysis and to obtain more dynamical behaviors of the palm trees, lesser date moth and predator model. Since most of the fractional-order differential equations do not have exact analytic solutions, approximation and numerical techniques must be used.

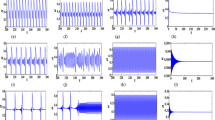
From the numerical results, it is clear that the approximate solutions depend on the fractional parameters h, α see Figure 1. The approximate solutions $x_{n}$, $y_{n}$, and $z_{n}$ are displayed in the figures below.

Figure 1

Phase portraits of model ( 4 ).

We use some documented data for some parameters like $\beta=0.5$, $\gamma =3$, $\delta=\eta=1$, and $\sigma=3$, then we have $( x_{1},y_{1},z_{1} ) = ( 0.7,0.3,0.8 )$. Other parameters will be (a) $h=0.05$, $\alpha=0.95$, (b) $h=0.07$, $\alpha=0.95$, (c) $h=0.09$, $\alpha=0.95$, and (d) $h=0.09$, $\alpha=0.75$.

Figure 1 depicts the phase portraits of model (4) according to the chosen parameter values and for various values of the fractional-order parameters h and α. We can see that, whenever the value of α is fixed and the value of h increases, then $E_{4}$ moves from the stabilized to the chaotic band. Figure 1(c) depicts the phase portrait for model (4).

By computing, we have $E_{4}\simeq ( 0.7,0.33,0.84 )$, and we can get the critical value of flip bifurcation for model (4). In Figure 1(a) we have $\bar{\Delta}_{4}=1\mbox{,}153\mbox{,}256\mbox{,}457>0$, $F(1)\simeq{0.00009>0}$, $F(-1)\simeq-7.872<0$, and $\vert \lambda_{2,3} \vert \simeq 0.999<1$. In this case we get $E_{4}$ is a sink according to case (1.ii) in Theorem 4.

In Figure 1(b) we have $\bar{\Delta}_{4}=165\mbox{,}217\mbox{,}502.2>0$, $F(1)\simeq 0.00024>0$, $F(-1)\simeq-7.8274<0$, and $\vert \lambda _{2,3} \vert \simeq0.999<1$. In this case we get $E_{4}$ is a sink according to case (1.ii) in Theorem 4.

In Figure 1(c) we have $\bar{\Delta}_{4}=38\mbox{,}548\mbox{,}982.44>0$, $F(1)\simeq 0.00049>0$, $F(-1)\simeq-7.79<0$, and $\vert \lambda_{2,3} \vert \simeq1.0002>1$. In this case we get $E_{4}$ is a one-dimensional saddle according to case (3.ii.a) in Theorem 4. We see that the fixed point $E_{4}$ loses its stability at the Hopf bifurcation parameter value $h\simeq0.086$. For $h= [ 0,0.15 ]$, there is a cascade of bifurcations. When r increases at certain values, for example, at $h=0.09$, independent invariant circles appear. When the value of h is increased (Figure 1(c)), the circles break down and some cascades of bifurcations lead to chaos.

Figures 1(c) and 1(d) explain the effect of the parameter α on the behavior of x, y, and z. Figure 2 demonstrates the sensitivity to initial conditions of system (4). We compute two orbits with initial points $( x_{1},y_{1},z_{1} )$ and $( x_{1},y_{1}+0.01,z_{1} )$, respectively. The compositional results are shown in Figure 2. From this figure it is clear that at the beginning the time series are indistinguishable; but after a number of iterations, the difference between them builds up rapidly, which shows that the model has sensitive dependence on the initial conditions of model (4), y-coordinates of the two orbits, plotted against time; the y-coordinates of initial conditions differ by 0.01, and the other coordinates do not change. In Figure 3 we use some documented data for some parameters like $\beta=0.5$, $\gamma=3$, $\delta=\eta=1$, $\sigma=3$, $\alpha=0.95$, then we have $( x_{1},y_{1},z_{1} ) = ( 0.7,0.3,0.8 )$, another parameter will be $h=0.001:0.47$. Figure 3 describes the Hopf bifurcation diagram with respect to h, we note that, as h increases, the behavior of this model (4) becomes very complicated, and the changes of parameter h has an effect on the stability of system (4). The Hopf bifurcation diagrams of system (4) in the $(h-x)$, $(h-y)$ and $(h-z)$ planes are given in Fig. 3.

Figure 2

Phase portraits of model ( 4 ).

Figure 3

Hopf bifurcation diagram with respect to h .

After calculation for the fixed point $E_{4}$ of map (4), the Hopf bifurcation emerges from the fixed point $( 0.7,0.33,0.84 )$ at $h=0.086$ and $( h,\alpha,\beta,\gamma,\delta,\eta,\sigma ) \in HB_{E_{4}}$. From Figure 3, we observe that the fixed point $E_{4}$ of map (4) loses its stability through a discrete Hopf bifurcation for $h= [ 0,0.15 ]$. In Figure 4 we use some documented data for some parameters like $\gamma=3$, $\delta=\eta=1$, $\sigma=3$, $h=0.85$, $\alpha=0.95$, other parameters will be (a) $\beta=1.55$, (b) $\beta=1.4$, (c) $\beta=1.2$, and (d) $\beta=1.15$.

Figure 4

Hopf bifurcation diagram with respect to β .

Figure 4(a) describes the stable equilibrium of model (4) according to the values of the parameters set out above. From Figure 4(f), 4(g) we can see that reducing and decreasing β causes disappearance of first-periodic orbits and increase in the chaotic attractors.

In Figure 5, we introduce the 0-1 test for detecting the chaos. Figure 5(a) indicates that, for $\beta=1.55$, one obtains $K=-0.066\approx0$. Then the dynamics is regular. Moreover, Figure 5(b) depicts bounded trajectories in the $( P_{c}(n),Q_{c}(n) )$ plane. Figure 5(c) indicates that, for $\beta=1.15$, one obtains $K=0.9658\approx1$. Then the dynamics is chaotic. Moreover, Figure 5(d) depicts Brownian-like (unbounded) trajectories in the $( P_{c}(n),Q_{c}(n) )$ plane.

Figure 5

The 0-1 test for detecting chaos.

In Figure 5(e)-5(f), we show the asymptotic growth rate K as a function of c for regular (chaotic) dynamics. In the case of regular (chaotic) dynamics, most values of c yield $K\approx0$ ($K\approx1$) as expected.

Figure 5(e)-5(f) show the two mean square displacements $M_{c}$ for system (4) with $\beta=1.55$ ($\beta=1.15$), which corresponds to regular (chaotic) dynamics.

5 Conclusion

In this paper, we consider the fractional-order model consisting of palm trees, the lesser date moth and the predator. We have got a sufficient condition for the existence and uniqueness of the system solution. We have also studied the local stability of all the equilibrium states of the discretized fractional-order system. Moreover, it has been found that the fractional parameter α has an effect on the stability of the discretized system. To support our theoretical discussion, we also present numerical simulations. We analyze the bifurcation both by theoretical point of view and by numerical simulations. One also needs to mention that when dealing with real life problems, the order of the system can be determined by using the collected data. The transformation of a classical model into a fractional one makes it very sensitive to the order of differentiation α: a small change in α may result in a big change in the final result. From the numerical results, it is clear that the approximate solutions depend continuously on the fractional derivative α.