1 Introduction

The Chaplygin gas model was first proposed by Chaplygin [1] as a model in aerodynamics with the equation of state in the form \(p=-B/\rho\) with constant \(B>0\). It was discovered in [2] that the equation of state for the Chaplygin gas was very suitable to describe the dark energy in the universe from the viewpoint of string theory. To be in more agreement with observational data, it was extended to the generalized Chaplygin gas [3] with \(p=-B/\rho^{\alpha}\) and the modified Chaplygin gas [4] with \(p=A \rho-B/\rho^{\alpha}\), where \(A,B>0\) and \(0<\alpha\leq1\). The equation of state for the modified Chaplygin gas contains two terms; the first term gives an ordinary fluid obeying a linear barotropic equation of state, and the second one is related to some power of the inverse of energy density. However, there are other barotropic fluids with quadratic or higher-order equation of state. To overcome this drawback, the modified Chaplygin gas has been further generalized by Pourhassan and Kahya [5] to the extended Chaplygin gas with the equation of state in the form \(p= \sum_{k=1} ^{n} A_{k}\rho^{k} -B/\rho^{\alpha}\). It is clear that all the Chaplygin gas models mentioned are particular cases of the extended Chaplygin gas model; see [6–9] for the related studies of the extended Chaplygin gas model.

In the present paper, we are interested in the isentropic extended Chaplygin gas dynamic system of the form

$$ \textstyle\begin{cases} \rho_{t}+(\rho u)_{x}=0, \\ (\rho u)_{t}+ (\rho u^{2}+ \sum_{k=1} ^{n} A_{k}\rho^{k}-\frac{B}{\rho} )_{x}=0, \end{cases} $$
(1.1)

where ρ and u stand for the density and velocity, respectively. The equation of state \(p= \sum_{k=1} ^{n} A_{k}\rho^{k}-B/\rho\) is chosen as a particular form of the extended Chaplygin gas with \(\alpha=1\) for the conciseness of computation, in which \(A_{k}\geq0\) (\(k=1,\ldots,n\)) and \(B>0\). In fact, the result in this paper can be generalized to the general situation (\(0<\alpha\leq1\)) with the same method by adding up a complicated computation.

If the pressure term \(p= \sum_{k=1} ^{n} A_{k}\rho^{k}-B/\rho\) tends to zero, namely the limit \(A_{k}\) (\(k=1,\ldots,n\)), \(B \rightarrow0 \) is taken, then system (1.1) formally becomes the following pressureless gas dynamic system [10–15]:

$$ \textstyle\begin{cases} \rho_{t}+(\rho u)_{x}=0, \\ (\rho u)_{t}+(\rho u^{2})_{x}=0. \end{cases} $$
(1.2)

Model (1.2) was also used to describe some important physical phenomena, such as the sticking process of free particles under collision [16, 17] and the formation of large-scale structure in the universe [18]. It is worth noticing that the universe evolution behaves as a pressureless fluid at early time of dark matter era and subsequently behaves like the cosmic fluid to mimic the cosmological constant at late time of dark energy era [6]. In this work, we investigate the transition between the two different eras of the universe by studying the process of vanishing pressure from system (1.1) to system (1.2). More precisely, we focus on the limiting relations of solutions to the Riemann problems for systems (1.1) and (1.2) with the initial data of Riemann type

$$ (u,\rho) (x,0)= \textstyle\begin{cases} (u_{-}, \rho_{-}), & -\infty< x< 0, \\ (u_{+}, \rho_{+}), & 0< x< +\infty. \end{cases} $$
(1.3)

The motivation comes from the the fact that both the δ-shock wave when \(u_{-}>u_{+}\) and the vacuum state when \(u_{-}< u_{+}\) are included in the solutions to the Riemann problem (1.2)–(1.3). Thus, the formation process of δ-shock wave and vacuum state can be observed when we consider the limit of solutions to the Riemann problem for the isentropic extended Chaplygin gas dynamic system (1.1) as the vanishing pressure \(A_{k}\) (\(k=1,\ldots,n\)), \(B\rightarrow0\). That is to say, if the limit \(A_{k}\) \((k=1,\ldots,n),B\rightarrow0\) is taken in the solution to the Riemann problem (1.1) and (1.3) when \(u_{-}>u_{+}\), then there is no solution in the space of bounded variation functions such that we must solve it in the space of distributions due to the blowup mechanism of solutions [15, 19, 20]. Specifically, we rigorously prove that the limiting solutions to the Riemann problem (1.1) and (1.3) as \(A_{k}\) (\(k=1,\ldots,n\)), \(B\rightarrow0\) are exactly identical with the corresponding ones to the pressureless gas dynamic system (1.2) with the same Riemann initial data. To be more precise, when \(u_{-}>u_{+}\), the two-shock-wave solution tends to a δ-shock wave solution as \(A_{k}\) (\(k=1,\ldots,n\)), \(B\rightarrow0\), in which the intermediate density between two shocks tends to be a weighted δ-measure. In contrast, when \(u_{-}< u_{+}\), the two-rarefaction-wave solution tends to a two-contact-discontinuity solution with a vacuum state between them, even if the initial data are far away from vacuum.

The formation of δ-shock wave and vacuum state to the Riemann problem (1.2) and (1.3) was considered initially for the isothermal [21] and isentropic [10] situations by the vanishing pressure limit approach. The result was further extended to the generalized pressureless gas dynamics model in [22], the isentropic magneto-gas-dynamics model in [23], and the Aw–Rascle model in [24]. Recently, the limiting relations of Riemann solutions from a variety of Chaplygin gas dynamic systems to the pressureless gas dynamic system have been extensively studied. More precisely, Sheng, Wang, and Yin [25] considered the asymptotic limits \(B\rightarrow0\) of Riemann solutions for the generalized Chaplygin gas \(p=-B/\rho^{\alpha}\). Furthermore, Chen and Sheng [26] have made a step further by considering the isentropic magneto-gas-dynamics Euler system for the generalized Chaplygin gas as the vanishing magnetic field. Yang and Wang made a step further by considering the modified Chaplygin gas \(p=A \rho-B/\rho^{\alpha}\) with \(\alpha =1\) in [27] and \(0<\alpha<1\) in [28]. The vanishing pressure limit problem for the Chaplygin gas \(p=-B/\rho\) and the generalized Chaplygin gas \(p=-B/\rho^{\alpha}\) with source term [29] has also been considered by Guo, Li, and Yin [30, 31]. Li and Shao [32] have generalized these results to the relativistic Euler system with the generalized Chaplygin gas \(p=-B/\rho^{\alpha}\). Also see [33–35] for the other related study about the formation of δ-shock wave. In this work, we make a step further by extending these results to the relatively more general pressure term \(p= \sum_{k=1} ^{n} A_{k}\rho^{k} -B/\rho\). In a recent paper [36], we have also considered the limiting relations of Riemann solutions from the isentropic extended Chaplygin gas dynamic system to the isentropic Chaplygin gas dynamic system when only the limit \(A_{k}\ (k=1,\ldots,n) \rightarrow0\) is taken in system (1.1). We also refer to [37–43] for other related works for the isentropic Chaplygin gas dynamic system.

The arrangement of this paper is as follows. In Sect. 2, we simply restate the solutions to the Riemann problem for the pressureless gas dynamic system (1.2) for self-consistency. In Sect. 3, we investigate in detail the basic properties of the isentropic extended Chaplygin gas dynamic system (1.1) and consequently construct the solutions to the Riemann problem (1.1) and (1.3) for all kinds of Riemann initial data. In Sect. 4, we make a step further by investigating the limit relations of Riemann solutions from the isentropic extended Chaplygin gas dynamic system (1.1) to the pressureless gas dynamic system (1.2) as the limit \(A_{k}\) (\(k=1,\ldots,n\)), \(B\rightarrow0\) is taken. The formation of δ-shock wave and vacuum state can be observed during the process of vanishing pressure limit.

2 Preliminaries

In this section, for completeness, we recall the Riemann problem for the pressureless gas dynamic system (1.2), which has been extensively investigated in [10, 14, 15]. System (1.2) is nonstrictly hyperbolic since it has a pair of coincident eigenvalues \(\lambda=u\) associated with the corresponding right eigenvector \(\overrightarrow{r}=(0,1)^{T}\). We further have \(\nabla\lambda\cdot \overrightarrow{r}=0\), where \(\nabla=(\frac{\partial}{\partial u},\frac{\partial}{\partial\rho})\), which implies that the characteristic field of λ is linear degenerate and the associated wave is contact discontinuity. For the case \(u_{-}< u_{+}\), the solution contains two contact discontinuities with vacuum state between them as follows:

$$ (u,\rho) (x,t)= \textstyle\begin{cases} (u_{-}, \rho_{-}), & -\infty< x< u_{-}t, \\ (\frac{x}{t}, 0), & u_{-}t< x< u_{+}t, \\ (u_{+}, \rho_{+}), & u_{+}t< x< +\infty. \end{cases} $$
(2.1)

For the case \(u_{-}>u_{+}\), a solution containing a weighted δ-measure supported on a curve will be taken into account. We must then introduce the definition of δ-measure [10, 15, 44] for the purpose to describe the δ-shock wave solution to the Riemann problem (1.2) and (1.3).

Definition 2.1

Let \(\Gamma=\{(x(s),t(s)):a< s< b\}\) be a parameterized smooth curve. Then a two-dimensional weighted Dirac delta function \(\omega(t)\delta_{\Gamma}\) with the support on Γ is defined by

$$ \bigl\langle \omega(s)\delta_{s},\varphi\bigl(x(s),t(s) \bigr)\bigr\rangle = \int_{a}^{b} \omega(s)\varphi\bigl(x(s),t(s)\bigr) \,ds $$
(2.2)

for any test function \(\varphi(x,t) \in C^{\infty}_{0}(R \times R_{+})\).

For completeness, we give a more general definition of δ-shock wave solution suggested by Danilov et al. [45, 46]. Suppose that \(\Gamma=\{\gamma_{i}|i\in I\}\) is a graph in the upper half-plane with the requirement \((x,t)\in R \times R_{+}\), which is comprised of Lipschitz continuous curves \(\gamma_{i}\) for \(i \in I\), where I is a finite index set. Subsequently, \(I_{0}\) is a subset of I such that the curves \(\gamma _{i}\) for \(i \in I_{0}\) start from the points on the x-axis. By \(\Gamma_{0}=\{x_{k}^{0}|k\in I_{0}\}\) we denote the set of initial points of \(\gamma_{k}\) for \(k\in I_{0}\). As is shown further, the solutions of the initial value problem for the pressureless gas dynamic system (1.2) with the δ-measure initial data are defined in the distributional sense.

Definition 2.2

Consider the initial data of δ-shock wave type

$$ (u,\rho) (x,0)= \biggl(u_{0}(x),\hat{ \rho}_{0}(x)+\sum_{k\in I_{0}} w_{k} \bigl(x^{0}_{k},0\bigr)\delta\bigl(x-x^{0}_{k} \bigr) \biggr) $$
(2.3)

with \(u_{0},\hat{\rho}_{0}\in L^{\infty}(R)\). A pair of distributions \((u,\rho)\) is called a solution of δ-shock wave type to the initial value problem (1.2) and (2.3) if the following integral identities are satisfied for every test function \(\varphi\in C_{c}^{\infty }(R\times R_{+})\):

$$\begin{aligned}& \begin{aligned}[b] & \int_{R_{+}} \int_{R} ( \hat{\rho }\varphi_{t}+\hat{\rho}u \varphi_{x} ) \,dx\,dt+\sum_{i\in I} \int_{\gamma_{i}}w_{i}(x,t)\frac{\partial \varphi(x,t) }{\partial l}\,dl \\ &\quad {}+ \int_{R} \hat{\rho}_{0}(x)\varphi(x,0) \,dx+\sum _{k\in I_{0}} w_{k}\bigl(x^{0}_{k},0 \bigr)\varphi\bigl(x^{0}_{k},0\bigr)=0, \end{aligned} \end{aligned}$$
(2.4)
$$\begin{aligned}& \begin{aligned}[b] & \int_{R_{+}} \int_{R} \bigl( \hat{\rho }u\varphi_{t}+\hat{ \rho}u^{2} \varphi_{x} \bigr) \,dx\,dt+\sum _{i\in I} \int_{\gamma_{i}}w_{i}(x,t)u_{\delta}(x,t) \frac {\partial \varphi(x,t) }{\partial l}\,dl \\ &\quad {}+ \int_{R} \hat{\rho}_{0}(x)u_{0}(x) \varphi(x,0) \,dx +\sum_{k\in I_{0}} w_{k} \bigl(x^{0}_{k},0\bigr)u_{\delta}\bigl(x^{0}_{k},0 \bigr)\varphi\bigl(x^{0}_{k},0\bigr)=0. \end{aligned} \end{aligned}$$
(2.5)

In view of these definitions, as in [10, 14, 15], if \(u_{-}>u_{+}\), then a δ-shock wave solution can be constructed for the Riemann problem (1.2) and (1.3) in the following piecewise smooth form:

$$ (u,\rho) (x,t)= \textstyle\begin{cases} (u_{-}, \rho_{-}), & x< \sigma_{\delta}t, \\ (u_{\delta}(t), \omega(t)\delta(x-\sigma_{\delta}t)), & x=\sigma _{\delta}t, \\ (u_{+}, \rho_{+}), & x>\sigma_{\delta}t, \end{cases} $$
(2.6)

in which

$$ \sigma_{\delta}=u_{\delta}(t)=\frac{\sqrt{\rho_{+}} u_{+}+\sqrt {\rho_{-}} u_{-}}{\sqrt{\rho_{+}}+\sqrt{\rho_{-}} }, \qquad \omega (t)=\sqrt{\rho_{-} \rho_{+}}(u_{-}-u_{+}) t. $$
(2.7)

In addition, the δ-shock wave solution (2.6) associated with (2.7) must satisfy the generalized Rankine–Hugoniot conditions

$$ \frac{dx}{dt}=\sigma_{\delta},\qquad \frac{d \omega(t)}{dt}=\sigma _{\delta}[\rho]-[\rho u], \qquad \frac{d (\omega(t)u_{\delta }(t))}{dt}=\sigma_{\delta}[\rho u]-\bigl[\rho u^{2}\bigr], $$
(2.8)

and the over-compressive δ-entropy condition

$$ u_{+}< \sigma_{\delta}< u_{-}. $$
(2.9)

3 The Riemann problem for the isentropic extended Chaplygin gas dynamic system (1.1)

In this section, we first analyze the properties of elementary waves and then construct the solutions to the Riemann problem (1.1) and (1.3) for all kinds of situations. System (1.1) has two distinct eigenvalues given by

$$ \lambda_{1}=u-\frac{1}{\rho}\sqrt{ \sum _{k=1} ^{n} kA_{k} \rho^{k+1}+B},\qquad \lambda_{2}=u+\frac{1}{\rho}\sqrt { \sum_{k=1} ^{n} kA_{k} \rho^{k+1}+B}. $$
(3.1)

System (1.1) is strictly hyperbolic for \(\lambda_{1}< \lambda_{2}\) when not all the \(n+1\) parameters \(A_{k}\) (\(k=1,\ldots,n\)) and B are equal to zero. The right eigenvectors corresponding to \(\lambda_{1}\) and \(\lambda _{2}\) are computed respectively by

$$ \overrightarrow{r_{1}}= \Biggl(-\frac{1}{\rho}\sqrt { \sum_{k=1} ^{n} kA_{k} \rho^{k+1}+B},\rho \Biggr)^{T},\qquad \overrightarrow{r_{2}}= \Biggl(\frac{1}{\rho}\sqrt{ \sum_{k=1} ^{n} kA_{k}\rho^{k+1}+B},\rho \Biggr)^{T}. $$
(3.2)

Let us denote \(\nabla=(\frac{\partial}{\partial u},\frac{\partial }{\partial\rho})\). Then we have

$$ \nabla\lambda_{1}\cdot\overrightarrow{r_{1}}= \frac{- \sum_{k=1} ^{n} k(k+1)A_{k}\rho^{k}}{2\sqrt{ \sum_{k=1} ^{n}kA_{k}\rho^{k+1}+B}}\neq0,\qquad \nabla\lambda_{2}\cdot \overrightarrow{r_{2}}=\frac{ \sum_{k=1} ^{n} k(k+1)A_{k}\rho^{k}}{2\sqrt{ \sum_{k=1} ^{n}kA_{k}\rho^{k+1}+B}}\neq0, $$
(3.3)

when not all the n parameters \(A_{k}\) (\(k=1,\ldots,n\)) are equal to zero. Therefore, the characteristic fields associated with \(\lambda_{1}\) and \(\lambda_{2}\) are genuinely nonlinear when not all the n parameters \(A_{k}\) (\(k=1,\ldots,n\)) are equal to zero, in which the associated waves for both of them are either shock waves or rarefaction waves.

Under uniform stretching of coordinates \((x,t)\rightarrow(\alpha x,\alpha t)\) for any constant \(\alpha>0\), both system (1.1) and initial data (1.3) remain unchanged. Hence we are looking for the self-similar solutions of the form

$$ (u,\rho) (x,t)=(u,\rho) (\xi),\quad \xi=\frac{x}{t}. $$
(3.4)

Then the Riemann problem (1.1) and (1.3) is reduced to the following system of ordinary differential equations:

$$ \textstyle\begin{cases} -\xi\rho_{\xi}+(\rho u)_{\xi}=0, \\ -\xi(\rho u)_{\xi}+(\rho u^{2}+ \sum_{k=1} ^{n}A_{k}\rho^{k}-\frac{B}{\rho})_{\xi}=0, \end{cases} $$
(3.5)

in companion with the boundary conditions at infinity given by \((u,\rho )(\pm\infty)=(u_{\pm},\rho_{\pm})\). For smooth solutions, (3.5) is simplified to be

( ρ u − ξ 2 u ρ − ξ ρ u 2 + ∑ k = 1 n k A k ρ k − 1 + B ρ 2 − ξ u ) ( d u d ρ ) = ( 0 0 ) .
(3.6)

Except for the constant states, (3.6) also provides the 1-rarefaction wave

$$ R_{1}(u_{-},\rho_{-}): \textstyle\begin{cases} \xi=\lambda_{1}=u-\frac{1}{\rho}\sqrt{ \sum_{k=1} ^{n} kA_{k}\rho^{k+1}+B}, \\ du+\frac{1}{\rho^{2}}\sqrt{ \sum_{k=1} ^{n} kA_{k}\rho^{k+1}+B} \,d\rho=0, \end{cases} $$
(3.7)

and the 2-rarefaction wave

$$ R_{2}(u_{-},\rho_{-}): \textstyle\begin{cases} \xi=\lambda_{2}=u + \frac{1}{\rho}\sqrt{ \sum_{k=1} ^{n} kA_{k}\rho^{k+1}+B}, \\ du-\frac{1}{\rho^{2}}\sqrt{ \sum_{k=1} ^{n} kA_{k}\rho^{k+1}+B} \,d\rho=0. \end{cases} $$
(3.8)

More precisely, since \(u_{\xi}=1>0\) and \(u_{\rho}=-\frac{1}{\rho ^{2}}\sqrt{ \sum_{k=1} ^{n} kA_{k}\rho^{k+1}+B}<0\) by (3.7), the 1-rarefaction wave is

$$ R_{1}(u_{-},\rho_{-}): \textstyle\begin{cases} \xi=\lambda_{1}(u,\rho)=u-\frac{1}{\rho}\sqrt{ \sum_{k=1} ^{n} kA_{k}\rho^{k+1}+B}, \\ u=u_{-}- \int_{\rho_{-}}^{\rho}\frac{1}{s^{2}}\sqrt { \sum_{k=1} ^{n} kA_{k}s^{k+1}+B}\,ds, \\ u>u_{-},\qquad \rho< \rho_{-}. \end{cases} $$
(3.9)

Similarly, since \(u_{\xi}=1>0\) and \(u_{\rho}=\frac{1}{\rho ^{2}}\sqrt{ \sum_{k=1} ^{n} kA_{k}\rho^{k+1}+B}>0\) by (3.8), the 2-rarefaction wave is

$$ R_{2}(u_{-},\rho_{-}): \textstyle\begin{cases} \xi=\lambda_{2}(u,\rho)=u+\frac{1}{\rho}\sqrt{ \sum_{k=1} ^{n} kA_{k}\rho^{k+1}+B}, \\ u=u_{-}+ \int_{\rho_{-}}^{\rho}\frac{1}{s^{2}}\sqrt { \sum_{k=1} ^{n} kA_{k}s^{k+1}+B}\,ds, \\ u>u_{-},\qquad \rho>\rho_{-}. \end{cases} $$
(3.10)

For the 1-rarefaction wave, it follows from the second equation of (3.7) that

$$ u_{\rho\rho}=-\frac{ \sum_{k=1} ^{n} k(k-3)A_{k}\rho^{k+1}-4B}{2\rho^{3}\sqrt{ \sum_{k=1} ^{n} kA_{k}\rho^{k+1}+B}}. $$
(3.11)

If \(n=1,2,3\), then we have \(u_{\rho\rho}>0\) for all the \(\rho\geq 0\). Otherwise, if \(n\geq4\), then there exists only one \(\rho_{0} \in(0,+\infty)\) such that \(u_{\rho\rho}>0\) for \(0 \leq\rho< \rho_{0}\) and \(u_{\rho\rho}<0\) for \(\rho>\rho _{0}\). In other words, the concavity or convexity of the 1-rarefaction curve changes at \(\rho =\rho_{0}\) in the \((u,\rho)\) phase plane, but it does not affect the construction of Riemann solutions. In addition, from the second equation of (3.9) we have

$$ u-u_{-}= \int_{\rho}^{\rho_{-}}\frac{1}{s^{2}}\sqrt{ \sum _{k=1} ^{n} kA_{k}s^{k+1}+B} \,ds\geq \int_{\rho}^{\rho_{-}}\frac{\sqrt{B}}{s^{2}}\,ds = \frac{\sqrt{B}}{\rho}\biggl(\frac{1}{\rho}-\frac{1}{\rho_{-}}\biggr), $$
(3.12)

which means that the limiting relation \(\lim_{\rho \rightarrow0}u=+\infty\) holds on the 1-rarefaction curve \(R_{1}\) in the \((u,\rho)\) phase plane.

Similarly, from the second equation of (3.8) we also have

$$ u_{\rho\rho}=\frac{ \sum_{k=1} ^{n} k(k-3)A_{k}\rho^{k+1}-4B}{2\rho^{3}\sqrt{ \sum_{k=1} ^{n} kA_{k}\rho^{k+1}+B}}. $$
(3.13)

With an analogous analysis as before, if \(n=1,2,3\), then we have \(u_{\rho\rho}<0\) for all \(\rho\geq0\). Otherwise, if \(n\geq4\), then there also exists only one \(\overline{\rho}_{0} \in(0,+\infty)\) such that we have \(u_{\rho\rho}>0\) for \(0 \leq\rho<\overline{\rho}_{0}\) and \(u_{\rho\rho}>0\) for \(\rho>\overline{\rho}_{0}\). In addition, from the second equation of (3.10) we also have

$$ u-u_{-}= \int_{\rho_{-}}^{\rho}\frac{1}{s^{2}}\sqrt{ \sum _{k=1} ^{n} kA_{k}s^{k+1}+B} \,ds\geq \int_{\rho_{-}}^{\rho}\frac{\sqrt{B}}{s^{2}}\,ds = \frac{\sqrt{B}}{\rho}\biggl(\frac{1}{\rho_{-}}-\frac{1}{\rho}\biggr), $$
(3.14)

which implies that the limiting relation \(\lim_{\rho \rightarrow+\infty}u=+\infty\) holds on the 2-rarefaction curve \(R_{2}\) in the \((u,\rho)\) phase space.

From now on, we focus on the shock wave, which is the other elementary wave for system (1.1). Denote by \((u_{-},\rho_{-})\) and \((u,\rho)\) the left and right states of a shock wave, respectively. The Rankine–Hugoniot conditions at a bounded discontinuity \(\xi=\sigma\) read as

$$ \textstyle\begin{cases} \sigma[\rho]=[\rho u], \\ \sigma[\rho u]=[\rho u^{2}+ \sum_{k=1} ^{n} A_{k}\rho^{k}-\frac{B}{\rho}], \end{cases} $$
(3.15)

where \([\rho]=\rho-\rho_{-}\) denotes the jump of state variable ρ across the discontinuity and so on. If \(\sigma=0\), then we can only arrive at the trivial case \((u,\rho )=(u_{-},\rho_{-})\). Otherwise, if \(\sigma\neq0\), then we have

$$ [\rho u]^{2}=[\rho] \Biggl[\rho u^{2}+ \sum _{k=1} ^{n} A_{k} \rho^{k}-\frac{B}{\rho}\Biggr], $$
(3.16)

which gives

$$ (\rho u-\rho_{-}u_{-})^{2}=(\rho- \rho_{-}) \Biggl(\rho u^{2}-\rho _{-}u_{-}^{2}+ \sum_{k=1} ^{n} A_{k}\bigl( \rho^{k}-\rho_{-}^{k}\bigr)-\frac{B}{\rho}+ \frac{B}{\rho _{-}} \Biggr). $$
(3.17)

Simplifying (3.17) yields

$$ \rho_{-}\rho(u-u_{-})^{2}=(\rho- \rho_{-}) \Biggl( \sum_{k=1} ^{n} A_{k}\bigl(\rho^{k}-\rho_{-}^{k}\bigr)+B \biggl(\frac{1}{\rho_{-}}-\frac{1}{\rho }\biggr) \Biggr), $$
(3.18)

so that we further get

$$ u-u_{-}=\pm\sqrt{ \biggl(\frac{1}{\rho_{-}}- \frac{1}{\rho} \biggr) \Biggl( \sum_{k=1} ^{n} A_{k}\bigl(\rho^{k}-\rho_{-}^{k} \bigr)+B\biggl(\frac{1}{\rho_{-}}-\frac{1}{\rho }\biggr) \Biggr)}. $$
(3.19)

In what follows, the sign in (3.19) should be determined. It is known from [47] that the 1-shock wave should satisfy the Lax entropy conditions

$$ \sigma< \lambda_{1}(u_{-}, \rho_{-}),\qquad \lambda_{1}(u,\rho)< \sigma< \lambda_{2}(u,\rho), $$
(3.20)

whereas the 2-shock wave should satisfy the Lax entropy conditions

$$ \lambda_{1}(u_{-},\rho_{-})< \sigma< \lambda_{2}(u_{-},\rho_{-}),\qquad \lambda_{2}(u,\rho)< \sigma. $$
(3.21)

It follows from the first equation of (3.15) that

$$ \sigma=\frac{\rho u-\rho_{-}u_{-}}{\rho-\rho_{-}}=u_{-}+\frac {\rho(u-u_{-})}{\rho-\rho_{-}}=u+ \frac{\rho_{-}(u-u_{-})}{\rho -\rho_{-}}. $$
(3.22)

It is deduced from (3.20) that the state set \((u,\rho)\) on the 1-shock wave curve \(S_{1}(u_{-},\rho_{-})\) must satisfy

$$ -\sqrt{ \sum_{k=1} ^{n} kA_{k}\rho^{k+1}+B}< \frac{\rho\rho_{-}(u-u_{-})}{\rho-\rho _{-}}< -\sqrt { \sum_{k=1} ^{n} kA_{k} \rho_{-}^{k+1}+B}. $$
(3.23)

Similarly, it is deduced from (3.21) that the state set \((u,\rho)\) on the 2-shock wave curve \(S_{2}(u_{-},\rho_{-})\) must satisfy

$$ \sqrt{ \sum_{k=1} ^{n} kA_{k}\rho^{k+1}+B}< \frac{\rho\rho_{-}(u-u_{-})}{\rho-\rho _{-}}< \sqrt { \sum_{k=1} ^{n} kA_{k} \rho_{-}^{k+1}+B}. $$
(3.24)

Simplifying (3.23) and (3.24), we obtain that \(\rho>\rho_{-}\) and \(u< u_{-}\) for the 1-shock wave and \(\rho<\rho_{-}\) and \(u< u_{-}\) for the 2-shock wave. Thus the minus sign should be chosen in (3.19) for both shock waves \(S_{1}(u_{-},\rho_{-})\) and \(S_{2}(u_{-},\rho_{-})\).

In summary, for the given left state \((u_{-},\rho_{-})\), the two shock waves can be expressed respectively by

$$ S_{1}(u_{-},\rho_{-}): \textstyle\begin{cases} \sigma=u_{-}+\frac{\rho(u-u_{-})}{\rho-\rho_{-}}, \\ u=u_{-}-\sqrt{(\frac{1}{\rho_{-}}-\frac{1}{\rho}) ( \sum_{k=1} ^{n} A_{k}(\rho^{k}-\rho_{-}^{k})+B(\frac{1}{\rho_{-}}-\frac{1}{\rho }) )}, \\ u< u_{-},\qquad \rho>\rho_{-}, \end{cases} $$
(3.25)

and

$$ S_{2}(u_{-},\rho_{-}): \textstyle\begin{cases} \sigma=u_{-}+\frac{\rho(u-u_{-})}{\rho-\rho_{-}}, \\ u=u_{-}-\sqrt{(\frac{1}{\rho_{-}}-\frac{1}{\rho}) ( \sum_{k=1} ^{n} A_{k}(\rho^{k}-\rho_{-}^{k})+B(\frac{1}{\rho_{-}}-\frac{1}{\rho }) )}, \\ u< u_{-}, \qquad \rho< \rho_{-}. \end{cases} $$
(3.26)

It follows from (3.25) or (3.26) that

$$ u_{\rho}=-\frac{ \sum_{k=1} ^{n}A_{k} (k\rho^{k}(\rho-\rho_{-})+\rho_{-}(\rho^{k}-\rho_{-}^{k})+ 2B\rho _{-}(\frac{1}{\rho_{-}}-\frac{1}{\rho}) )}{2\rho_{-}\rho ^{2}\sqrt{(\frac{1}{\rho_{-}}-\frac{1}{\rho_{-}}) ( \sum_{k=1} ^{n}A_{k}(\rho^{k}-\rho_{-}^{k}) +B(\frac{1}{\rho_{-}}-\frac{1}{\rho_{-}}) )}}. $$
(3.27)

We have \(u_{\rho}<0\) from \(\rho>\rho_{-}\) for the 1-shock curve and \(u_{\rho}>0\) from \(\rho<\rho_{-}\) for the 2-shock curve. The concavity or convexity of the 1-rarefaction (or 2-rarefaction) curve is similar to that for the 1-shock (or 2-shock) curve. The calculation is trivial but tedious and thus is omitted here. In addition, the limiting relation \(\lim_{\rho\rightarrow+\infty}u=-\infty \) can be established for the 1-shock curve, provided that not all the n parameters \(A_{k}\) (\(k=1,\ldots,n\)) are equal to zero. Similarly, the limiting relation \(\lim_{\rho \rightarrow0}u=-\infty\) can also be established for the 2-shock curve.

Gathering the formulae (3.9), (3.10), (3.25), and (3.26) together, we can see that if the left state \((u_{-},\rho_{-})\) is fixed, then the half-upper \((u,\rho)\) phase plane is divided into four regions denoted with I, II, III, and IV respectively by the elementary wave curves \(R_{1}(u_{-},\rho_{-})\), \(R_{2}(u_{-},\rho_{-})\), \(S_{1}(u_{-},\rho_{-})\), and \(S_{2}(u_{-},\rho_{-})\) starting from the left state \((u_{-},\rho_{-})\) (see Fig. 1). By using the method of phase plane analysis, for the given left state \((u_{-},\rho_{-})\in R\times R_{+}\), the unique solution to the Riemann problem (1.1) and (1.3) can be constructed for any right state \((u_{+},\rho_{+})\in R\times R_{+}\). More precisely, if \((u_{+},\rho_{+})\in I, \mathit{II}, \mathit{III}\), or IV, then the solution to the Riemann problem (1.1) and (1.3) can be expressed by the symbols \(R_{1}+R_{2}\), \(R_{1}+S_{2}\), \(S_{1}+R_{2}\), or \(S_{1}+S_{2}\) respectively, in which the symbol \(R_{1}+R_{2}\) is used to express a 1-rarefaction wave \(R_{1}\) followed by a 2-rarefaction wave \(R_{2}\), and so on.

Figure 1
figure 1

The elementary wave curves for system (1.1) in the \((u,\rho)\) phase plane

Full size image

4 The limits of Riemann solutions from system (1.1) to system (1.2) as \(A_{k}\) (\(k=1,\ldots,n\)), \(B \rightarrow0\)

In this section, we focus ourselves on the asymptotic limits of solutions to the Riemann problem (1.1) and (1.3) as all the parameters \(A_{k}\) (\(k=1,\ldots,n\)) and B tend to zero. Let the left state \((u_{-},\rho_{-})\) be fixed. If the limit \(A_{k}\) (\(k=1,\ldots,n\)), \(B\rightarrow0\) is taken, then it can be seen from (3.9), (3.10), (3.25), and (3.26) that all the wave curves \(R_{1}(u_{-},\rho_{-})\), \(R_{2}(u_{-},\rho_{-})\), \(S_{1}(u_{-},\rho _{-})\), and \(S_{2}(u_{-},\rho_{-})\) tend to the line \(u=u_{-}\) in the half-upper \((u,\rho)\) phase space. We further observe that the regions II and III disappear in the limit \(A_{k}\) (\(k=1,\ldots,n\)), \(B\rightarrow0\) situation. Hence, if \(u_{+}< u_{-}\), then the right state \((u_{+},\rho_{+})\) is located in the region IV for sufficiently small \(A_{k}\) (\(k=1,\ldots,n\)) and B. Otherwise, if \(u_{+}>u_{-}\), then the right state \((u_{+},\rho _{+})\) is located in the region I for sufficiently small \(A_{k}\) (\(k=1,\ldots,n\)) and B. In the special situation, if \(u_{+}=u_{-}\), then the right state \((u_{+},\rho_{+})\) is located in the region II for \(0\leq\rho_{+}<\rho_{-}\) or in the region III for \(\rho_{+}>\rho_{-}\) when all the parameters \(A_{k}\) (\(k=1,\ldots,n\)) and B are sufficiently small.

Let us first consider the situation \(u_{+}< u_{-}\), in which the right state \((u_{+},\rho_{+})\) is located in the region IV for sufficiently small \(A_{k}\) (\(k=1,\ldots,n\)) and B. In what follows, we are devoted to studying the formation of δ-shock wave solution from the solution consisting of two shock waves by studying the vanishing pressure limits of solutions to the Riemann problem (1.1) and (1.3). When \((u_{+},\rho_{+})\in \mathit{IV}\), for any fixed \(A_{k}\) (\(k=1,\ldots,n\)), \(B>0\), let \((u_{*},\rho_{*})\) be the intermediate state between two shock waves. Then \((u_{-},\rho_{-})\) and \((u_{*},\rho_{*})\) are connected by the 1-shock wave \(S_{1}\) with the speed \(\sigma_{1}\), whereas \((u_{*},\rho_{*})\) and \((u_{+},\rho_{+})\) are connected by the 2-shock wave \(S_{2}\) with speed \(\sigma_{2}\). More specifically, we have

$$ S_{1}: \textstyle\begin{cases} \sigma_{1}=\frac{\rho_{*}u_{*}-\rho_{-}u_{-}}{\rho_{*}-\rho_{-}}, \\ u_{*}=u_{-}-\sqrt{(\frac{1}{\rho_{-}}-\frac{1}{\rho_{*}}) ( \sum_{k=1} ^{n} A_{k}(\rho_{*}^{k}-\rho_{-}^{k})+B(\frac{1}{\rho_{-}}-\frac {1}{\rho_{*}}) )}, \\ u_{*}< u_{-},\qquad \rho_{*}>\rho_{-}, \end{cases} $$
(4.1)

and

$$ S_{2}: \textstyle\begin{cases} \sigma_{2}=\frac{\rho_{+}u_{+}-\rho_{*}u_{*}}{\rho_{+}-\rho_{*}}, \\ u_{+}=u_{*}-\sqrt{(\frac{1}{\rho_{*}}-\frac{1}{\rho_{+}}) ( \sum_{k=1} ^{n} A_{k}(\rho_{+}^{k}-\rho_{*}^{k})+B(\frac{1}{\rho_{*}}-\frac {1}{\rho_{+}}) )}, \\ u_{*}>u_{+},\qquad \rho_{*}>\rho_{+}. \end{cases} $$
(4.2)

In what follows, we give some lemmas to show the limiting behaviors of the solutions to the Riemann problem (1.1) and (1.3) consisting of two shock waves for the situation \(u_{+}< u_{-}\) when \(A_{k}\) (\(k=1,\ldots,n\)), \(B\rightarrow0\).

Lemma 4.1

When \(u_{+}< u_{-}\), if the solution to the Riemann problem (1.1) and (1.3) consists of two shock waves for sufficiently small \(A_{k}\) (\(k=1,\ldots,n\)) and B, then we have

$$ \lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0}\rho _{*}=+\infty,\qquad \lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0} \sum_{k=1} ^{n}A_{k}\rho_{*}^{k}= \frac{\rho_{-}\rho_{+}}{(\sqrt {\rho_{-}}+\sqrt{\rho_{+}})^{2}}(u_{-}-u_{+})^{2}. $$
(4.3)

In addition, we further have

$$ \lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0}\sigma _{1}= \lim _{A_{k}\, (k=1,\ldots,n),B\rightarrow0}\sigma _{2}= \lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0}u_{*} =\frac{\sqrt{\rho_{+}}u_{+}+\sqrt{\rho_{-}}u_{-}}{\sqrt{\rho _{+}}+\sqrt{\rho_{-}}}=\sigma_{\delta}. $$
(4.4)

Proof

It follows from (4.1) and (4.2) that

$$\begin{aligned} u_{-}-u_{+} =&\sqrt{\frac{\rho_{*}-\rho_{-}}{\rho_{*}\rho_{-}} \Biggl( \sum_{k=1} ^{n} A_{k}\bigl( \rho_{*}^{k}-\rho _{-}^{k}\bigr)+B \biggl(\frac{1}{\rho_{-}}-\frac{1}{\rho_{*}}\biggr) \Biggr)} \\ &{}+\sqrt{\frac{\rho_{+}-\rho_{*}}{\rho_{*}\rho_{+}} \Biggl( \sum _{k=1} ^{n} A_{k}\bigl(\rho_{+}^{k}- \rho_{*}^{k}\bigr) +B\biggl(\frac{1}{\rho_{*}}- \frac{1}{\rho_{+}}\biggr) \Biggr)}. \end{aligned}$$
(4.5)

If \(\lim_{A_{k}\, (k=1,\ldots,n),B \rightarrow0}\rho _{*}=M\in(\max(\rho_{-},\rho_{+}),+\infty)\), then taking the limit of (4.5) as \(A_{k}\) (\(k=1,\ldots,n\)), \(B\rightarrow0\) leads to \(u_{-}-u_{+}=0\), which contradicts with \(u_{+}< u_{-}\). Therefore, \(\lim_{A_{k}\, (k=1,\ldots,n),B \rightarrow 0}\rho_{*}=+\infty\) must be established. With this fact in mind, if we take the limit of (4.5) as \(A_{k}\) (\(k=1,\ldots,n\)), \(B\rightarrow0\) again, then we have

$$ u_{-}-u_{+}= \lim_{A_{k}\, (k=1,\ldots,n),B \rightarrow 0} \sqrt{\frac{1}{\rho_{-}} \sum_{k=1} ^{n} A_{k}\rho_{*}^{k}} + \lim _{A_{k}\, (k=1,\ldots,n),B \rightarrow0}\sqrt{\frac {1}{\rho_{+}} \sum _{k=1} ^{n} A_{k}\rho_{*}^{k}}, $$
(4.6)

which gives the second limiting relation in (4.3).

On the other hand, it can be deduced from (4.1) and (4.2) that

$$\begin{aligned}& \begin{aligned}[b] \lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0}\sigma _{1}&=\lim _{A_{k}\, (k=1,\ldots,n),B\rightarrow0}\frac{\rho_{*} u_{*}-\rho _{-} u_{-}}{\rho_{*}-\rho_{-}} \\ &=\lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow 0} \frac{u_{*}-\frac{\rho_{-} u_{-}}{\rho_{*}}}{1-\frac{\rho _{-}}{\rho_{*}}}=\lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0}u_{*}, \end{aligned} \end{aligned}$$
(4.7)
$$\begin{aligned}& \begin{aligned}[b] \lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0}\sigma_{2}&=\lim _{A_{k}\, (k=1,\ldots,n),B\rightarrow0}\frac{\rho_{+} u_{+}-\rho_{*} u_{*}}{\rho_{+}-\rho_{*}} \\ &=\lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow 0} \frac{\frac{\rho_{+} u_{+}}{\rho_{*}}-u_{*}}{\frac{\rho _{+}}{\rho_{*}}-1}=\lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0}u_{*}. \end{aligned} \end{aligned}$$
(4.8)

More precisely, from (4.1) we get

$$\begin{aligned} &\lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0}u_{*} \\ &\quad =u_{-}-\lim _{A_{k}\, (k=1,\ldots,n),B\rightarrow0} \sqrt{\biggl(\frac{1}{\rho_{-}}- \frac{1}{\rho_{*}}\biggr) \Biggl( \sum_{k=1} ^{n} A_{k}\bigl(\rho_{*}^{k}- \rho_{-}^{k}\bigr)+B\biggl(\frac{1}{\rho_{-}}- \frac {1}{\rho_{*}}\biggr) \Biggr)} \\ &\quad =u_{-}-\lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0}\sqrt{\frac{1}{\rho _{-}} \sum_{k=1} ^{n} A_{k} \rho_{*}^{k}} \\ &\quad =u_{-}-\sqrt{\frac{1}{\rho_{-}}\frac{\rho_{-}\rho_{+}}{(\sqrt {\rho_{-}}+\sqrt{\rho_{+}})^{2}}(u_{-}-u_{+})^{2}} \\ &\quad =u_{-}-\frac{\sqrt{\rho_{+}}}{\sqrt{\rho_{+}}+\sqrt{\rho _{-}}}(u_{-}-u_{+}) =\frac{\sqrt{\rho_{+}}u_{+}+\sqrt{\rho_{-}}u_{-}}{\sqrt{\rho _{+}}+\sqrt{\rho_{-}}}=\sigma_{\delta}. \end{aligned}$$

Hence the limiting relation (4.4) can also be established. The proof is completed. □

Moreover, we have the following limiting relations of mass and momentum in the limit \(A_{k}\) (\(k=1,\ldots,n\)), \(B\rightarrow0\) situation, which can be described by the following lemma.

Lemma 4.2

The limiting relations of mass and momentum between two shock waves as \(A_{k}\) (\(k=1,\ldots,n\)), \(B\rightarrow0\) are as follows:

$$\begin{aligned}& \lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0} \int_{\sigma_{1}}^{\sigma _{2}}\rho_{*}\,d\xi= \sigma_{\delta}[\rho]-[\rho u], \end{aligned}$$
(4.9)
$$\begin{aligned}& \lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0} \int_{\sigma_{1}}^{\sigma _{2}}\rho_{*} u_{*}\,d \xi=\sigma_{\delta}[\rho u]-\bigl[\rho u^{2}\bigr], \end{aligned}$$
(4.10)

in which the jump of ρ is given by \([\rho]=\rho_{+}-\rho_{-}\), and so on.

Proof

If the first equation of the Rankine–Hugoniot conditions (3.15) is carried out on the two shock waves \(S_{1}\) and \(S_{2}\), then we have

$$ \textstyle\begin{cases} \sigma_{1}(\rho_{*}-\rho_{-})=\rho_{*}u_{*}-\rho_{-}u_{-}, \\ \sigma_{2}(\rho_{+}-\rho_{*})=\rho_{+}u_{+}-\rho_{*}u_{*}, \end{cases} $$
(4.11)

which leads to

$$\begin{aligned} \lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0}(\sigma_{2}- \sigma_{1})\rho_{*}&= \lim_{A_{k}\, (k=1,\ldots,n), B\rightarrow0}(- \sigma_{1}\rho_{-}+\sigma _{2}\rho_{+}- \rho_{+}u_{+}+\rho_{-}u_{-}) \\ &= \sigma_{\delta}[\rho ]-[\rho u]. \end{aligned}$$
(4.12)

Similarly, if the second equation of the Rankine–Hugoniot conditions (3.15) is carried out on the two shock waves \(S_{1}\) and \(S_{2}\), then we also have

$$ \textstyle\begin{cases} \sigma_{1}(\rho_{*}u_{*}-\rho_{-}u_{-})=\rho_{*}u_{*}^{2}-\rho _{-}u_{-}^{2}+ \sum_{k=1} ^{n} A_{k}(\rho_{*}^{k}-\rho_{-}^{k})-B(\frac{1}{\rho_{*}}-\frac {1}{\rho_{-}}), \\ \sigma_{2}(\rho_{+}u_{+}-\rho_{*}u_{*})=\rho_{+}u_{+}^{2}-\rho _{*}u_{*}^{2}+ \sum_{k=1} ^{n} A_{k}(\rho_{+}^{k}-\rho_{*}^{k})-B(\frac{1}{\rho_{+}}-\frac {1}{\rho_{*}}), \end{cases} $$
(4.13)

which gives rise to

$$\begin{aligned} &\lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0} (\sigma_{2}-\sigma_{1})\rho _{*}u_{*} \\ &\quad = \lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0} \Biggl(-\sigma _{1}\rho_{-}u_{-}+\sigma_{2} \rho_{+}u_{+}+\rho_{-}u_{-}^{2}- \rho _{+}u_{+}^{2} \\ &\qquad {}+ \sum _{k=1} ^{n} A_{k}\bigl(\rho_{-}^{k}- \rho_{+}^{k}\bigr)+B\biggl(\frac{1}{\rho_{+}}- \frac {1}{\rho_{-}}\biggr) \Biggr) \\ &\quad = \sigma_{\delta}[\rho u]-\bigl[\rho u^{2} \bigr]. \end{aligned}$$
(4.14)

From (4.12) and (4.14) we then get

$$\begin{aligned}& \lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0} \int_{\sigma_{1}}^{\sigma _{2}}\rho_{*}\,d\xi =\lim _{A_{k}\, (k=1,\ldots,n),B\rightarrow0}(\sigma_{2}-\sigma_{1})\rho _{*}=\sigma_{\delta}[\rho]-[\rho u], \\& \lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0} \int_{\sigma_{1}}^{\sigma _{2}}\rho_{*}u_{*}\,d \xi=\lim_{A_{k}\, (k=1,\ldots,n), B\rightarrow 0}(\sigma_{2}-\sigma_{1}) \rho_{*}u_{*}=\sigma_{\delta}[\rho u]-\bigl[\rho u^{2}\bigr]. \end{aligned}$$

The proof is finished. □

Remark 4.1

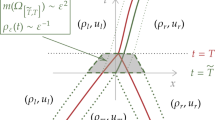
It can be concluded from the lemmas that if \(u_{+}< u_{-}\), then the shock waves \(S_{1}\) and \(S_{2}\) coincide with each other, and the intermediate density \(\rho_{*}\) becomes the singular measure of Dirac mass for the solution to the Riemann problem (1.1) and (1.3) in the limit \(A_{k}\) (\(k=1,\ldots,n\)), \(B\rightarrow0\) situation, which is just the δ-shock wave solution (2.6) associated with (2.7) to the Riemann problem for the pressureless gas dynamic system (1.2) with the same Riemann initial data (1.3) as in Sect. 2.

In what follows, for the situation \(u_{+}< u_{-}\), we use the following theorem to describe the formation of singularity of solution in the sense of distributions, which is similar to the result of Theorem 3.1 in [10].

Theorem 4.3

When \(u_{+}< u_{-}\), we assume that the solution to the Riemann problem (1.1) and (1.3) consists of two shock waves for sufficiently small \(A_{k}\) (\(k=1,\ldots,n\)) and B. Then the limit of solution as \(A_{k}\) (\(k=1,\ldots,n\)), \(B\rightarrow0\) converges to the δ-shock wave solution (2.6) associated with (2.7) in the sense of distributions, which is identical with that for the pressureless gas dynamic system (1.2). In addition, the limit of momentum ρu as \(A_{k}\) (\(k=1,\ldots,n\)), \(B\rightarrow0\) is the sum of a step function and a Dirac δ-function of the form

$$ \lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0}\rho u =\rho_{-} u_{-}+[\rho u]H(x-\sigma_{\delta} t)+\bigl(\sigma_{\delta}[ \rho u]-\bigl[\rho u^{2}\bigr]\bigr)t\delta(x-\sigma_{\delta} t). $$
(4.15)

Proof

Given \(\xi=\frac{x}{t}\), for fixed sufficiently small \(A_{k}\) (\(k=1,\ldots,n\)), \(B>0\), the solution consisting of two shock waves to the Riemann problem (1.1) and (1.3) takes the form

$$ (u,\rho) (\xi)= \textstyle\begin{cases} (u_{-}, \rho_{-}), & -\infty< \xi< \sigma_{1}, \\ (u_{*}, \rho_{*}), & \sigma_{1}< \xi< \sigma_{2}, \\ (u_{+}, \rho_{+}), & \sigma_{2}< \xi< +\infty. \end{cases} $$
(4.16)

The solution (4.16) should satisfy the following weak forms of system (3.5):

$$\begin{aligned}& - \int_{-\infty}^{+\infty}\rho(\xi) \bigl(u(\xi)-\xi\bigr) \phi'(\xi) \,d\xi + \int_{-\infty}^{+\infty}\rho(\xi)\phi(\xi) \,d\xi=0, \end{aligned}$$
(4.17)
$$\begin{aligned}& \begin{aligned}[b] &{-} \int_{-\infty}^{+\infty}\rho(\xi) u(\xi) \bigl(u(\xi)-\xi\bigr) \phi'(\xi ) \,d\xi- \int_{-\infty}^{+\infty}\Biggl( \sum _{k=1} ^{n} A_{k}\rho(\xi)^{k}- \frac{B}{\rho(\xi)}\Biggr)\phi'(\xi) \,d\xi \\ &\quad {}+ \int _{-\infty}^{+\infty}\rho(\xi) u(\xi)\phi(\xi) \,d\xi=0, \end{aligned} \end{aligned}$$
(4.18)

for arbitrary test function \(\phi(\xi) \in C_{0}^{\infty}(-\infty ,+\infty)\).

We will focus on the integral formula (4.18) only for the reason that the integral formula (4.17) has been widely investigated in [10, 24, 26, 27]. We first consider

$$\begin{aligned}& \int_{-\infty}^{+\infty}\rho(\xi) u(\xi) \bigl(u(\xi)-\xi\bigr) \phi'(\xi ) \,d\xi \\& \quad = \biggl( \int_{-\infty}^{\sigma_{1}}+ \int_{\sigma _{1}}^{\sigma_{2}}+ \int_{\sigma_{2}}^{+\infty} \biggr)\rho(\xi) u(\xi) \bigl(u(\xi)- \xi\bigr)\phi'(\xi) \,d\xi. \end{aligned}$$
(4.19)

Summing the first and third parts of (4.19), we have

$$\begin{aligned}& \lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0} \int_{-\infty}^{\sigma _{1}}\rho(\xi) u(\xi) \bigl(u(\xi)-\xi\bigr) \phi'(\xi) \,d\xi \\& \qquad {}+\lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0} \int_{\sigma _{2}}^{+\infty}\rho(\xi) u(\xi) \bigl(u(\xi)-\xi\bigr) \phi'(\xi) \,d\xi \\& \quad =\lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0} \int_{-\infty}^{\sigma _{1}}\rho_{-}u_{-}(u_{-}- \xi)\phi'(\xi) \,d\xi \\& \qquad {}+\lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0} \int_{\sigma_{2}}^{+\infty }\rho_{+}u_{+}(u_{+}- \xi)\phi'(\xi) \,d\xi \\& \quad =\bigl(\sigma_{\delta}[\rho u]-\bigl[\rho u^{2}\bigr] \bigr)\phi(\sigma_{\delta})+ \int _{-\infty}^{+\infty}\bigl(\rho_{-}u_{-}+[ \rho u]H(\xi-\sigma_{\delta })\bigr)\phi(\xi) \,d\xi, \end{aligned}$$
(4.20)

where H is the standard Heaviside function. For the second part of (4.19), we have

$$\begin{aligned}& \lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0} \int_{\sigma_{1}}^{\sigma _{2}}\rho(\xi) u(\xi) \bigl(u(\xi)-\xi\bigr) \phi'(\xi) \,d\xi \\& \quad =\lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0} \int_{\sigma_{1}}^{\sigma _{2}}\rho_{*}u_{*}(u_{*}- \xi)\phi'(\xi) \,d\xi \\& \quad =\lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0}\rho_{*}u_{*}(\sigma _{2}-\sigma_{1}) \\& \qquad {}\times \biggl( u_{*} \biggl( \frac{\phi(\sigma_{2})-\phi (\sigma_{1})}{\sigma_{2} -\sigma_{1}} \biggr)-\frac{\sigma_{2}\phi(\sigma_{2})-\sigma _{1}\phi(\sigma_{1})}{\sigma_{2}-\sigma_{1}} +\frac{1}{\sigma_{2}-\sigma_{1}} \int_{\sigma_{1}}^{\sigma _{2}}\phi(\xi) \,d\xi \biggr) \\& \quad =\bigl(\sigma_{\delta}[\rho u]-\bigl[\rho u^{2}\bigr] \bigr) \bigl(\sigma_{\delta}\phi '(\sigma_{\delta})- \sigma_{\delta}\phi'(\sigma_{\delta})-\phi ( \sigma_{\delta})+\phi(\sigma_{\delta})\bigr)=0. \end{aligned}$$
(4.21)

Summing (4.20) and (4.21) leads to

$$\begin{aligned}& \lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0} \int_{-\infty}^{+\infty}\rho (\xi) u(\xi) \bigl(u(\xi)-\xi \bigr)\phi'(\xi) \,d\xi \\& \quad =\bigl(\sigma_{\delta}[\rho u]-\bigl[\rho u^{2}\bigr] \bigr)\phi(\sigma_{\delta})+ \int _{-\infty}^{+\infty}\bigl(\rho_{-}u_{-}+[ \rho u]H(\xi-\sigma_{\delta })\bigr)\phi(\xi) \,d\xi. \end{aligned}$$
(4.22)

On the other hand, by Lemmas 4.1 and 4.2 we then have

$$\begin{aligned}& \lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0} \int_{-\infty}^{+\infty }\Biggl( \sum _{k=1} ^{n} A_{k}\bigl(\rho(\xi) \bigr)^{k}-\frac{B}{\rho(\xi)}\Biggr)\phi'(\xi) \,d\xi \\& \quad =\lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0} \biggl( \int_{-\infty}^{\sigma _{1}}+ \int_{\sigma_{1}}^{\sigma_{2}}+ \int_{\sigma_{2}}^{+\infty } \biggr) \Biggl( \sum _{k=1} ^{n} A_{k}\rho(\xi)^{k}- \frac{B}{\rho(\xi)}\Biggr)\phi'(\xi) \,d\xi \\& \quad =\lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0} \Biggl( \int_{-\infty }^{\sigma_{1}}\Biggl( \sum _{k=1} ^{n} A_{k}\rho_{-}^{k}- \frac{B}{\rho_{-}}\Biggr)\phi'(\xi) \,d\xi+ \int _{\sigma_{1}}^{\sigma_{2}}\Biggl( \sum _{k=1} ^{n} A_{k}\rho_{*}^{k}- \frac{B}{\rho_{*}}\Biggr)\phi'(\xi) \,d\xi \\& \qquad {}+ \int_{\sigma_{2}}^{+\infty}\Biggl( \sum _{k=1} ^{n} A_{k}\rho_{+}^{k}- \frac{B}{\rho_{+}}\Biggr)\phi'(\xi) \,d\xi \Biggr) \\& \quad =\lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0} \Biggl(\Biggl( \sum_{k=1} ^{n} A_{k}\rho_{-}^{k}- \frac{B}{\rho_{-}}\Biggr)\phi(\sigma_{1})+\Biggl( \sum _{k=1} ^{n} A_{k}\rho_{*}^{k} -\frac{B}{\rho_{*}}\Biggr) \bigl(\phi(\sigma_{2})-\phi( \sigma_{1})\bigr) \\& \qquad {}-\Biggl( \sum_{k=1} ^{n} A_{k}\rho_{+}^{k}- \frac{B}{\rho_{+}}\Biggr)\phi(\sigma_{2}) \Biggr) \\& \quad =0. \end{aligned}$$
(4.23)

Combining (4.18), (4.22), and (4.23), we obtain

$$\begin{aligned}& \lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0} \int_{-\infty}^{+\infty}\bigl(\rho (\xi) u(\xi)- \rho_{-}u_{-}-[\rho u] H(\xi-\sigma_{\delta})\bigr) \phi (\xi) \,d\xi \\& \quad =\bigl(\sigma_{\delta}[\rho u]-\bigl[\rho u^{2} \bigr]\bigr)\phi(\sigma_{\delta}). \end{aligned}$$
(4.24)

As in [10, 24, 26, 27], if the same method is carried out for (4.17), then we also have

$$\begin{aligned}& \lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0} \int_{-\infty}^{+\infty}\bigl(\rho (\xi)-\rho_{-}-[ \rho]H(\xi-\sigma_{\delta})\bigr)\phi(\xi) \,d\xi \\& \quad =\bigl( \sigma_{\delta}[\rho]-[\rho u]\bigr)\phi(\xi) (\sigma_{\delta}). \end{aligned}$$
(4.25)

Finally, we consider the limits of ρu and ρ. Letting \(\psi (x,t) \in C_{0}^{\infty}(R \times R_{+})\), then we have

$$\begin{aligned}& \lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0} \int_{0}^{+\infty} \int _{-\infty}^{+\infty}\rho\biggl(\frac{x}{t}\biggr)u \biggl(\frac{x}{t}\biggr)\psi(x,t)\,dx\,dt \\& \quad =\lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0} \int_{0}^{+\infty} \int _{-\infty}^{+\infty}\rho(\xi)u(\xi)\psi(\xi t,t)d(\xi t) \,dt \\& \quad = \int_{0}^{+\infty}\bigl(\sigma_{\delta}[\rho u]- \bigl[\rho u^{2}\bigr]\bigr)t\psi (\sigma_{\delta} t,t)\,dt \\& \qquad {}+ \int_{0}^{+\infty} \int_{-\infty }^{+\infty}\bigl(\rho_{-}u_{-}+[ \rho u]H(\xi-\sigma_{\delta})\bigr)t\psi (\xi t,t) \,d\xi \,dt. \end{aligned}$$
(4.26)

Therefore we can conclude that

$$\begin{aligned}& \lim_{ A_{k}\, (k=1,\ldots,n),B \rightarrow 0} \int^{\infty}_{0} \int^{\infty}_{-\infty} \biggl(\rho\biggl(\frac{x}{t} \biggr)u\biggl(\frac{x}{t}\biggr)-\rho _{-}u_{-}-[ \rho u]H(x-\sigma_{\delta}t) \biggr)\psi(x,t)\,dx \,dt \\& \quad = \int ^{\infty}_{0} \bigl(\sigma_{\delta}[\rho u]- \bigl[\rho u^{2}\bigr]\bigr)t \psi(\sigma_{\delta} t,t) \,dt. \end{aligned}$$
(4.27)

Analogously, from (4.25) we also have

$$\begin{aligned}& \lim_{A_{k}\, (k=1,\ldots,n),B \rightarrow 0} \int^{\infty}_{0} \int^{\infty}_{-\infty} \biggl(\rho\biggl(\frac{x}{t} \biggr)-\rho_{-}-[\rho ]H(x-\sigma_{\delta}t) \biggr)\psi(x,t) \,dx \,dt \\& \quad = \int^{\infty}_{0} \bigl(\sigma_{\delta}[\rho]-[\rho u] \bigr)t \psi(\sigma_{\delta} t,t)\,dt. \end{aligned}$$
(4.28)

The conclusion of the theorem can be drawn by taking into account Definition 2.1. The proof is completed. □

We are now in position to consider the situation \(u_{-}< u_{+}\), in which the solution to the Riemann problem (1.1) and (1.3) consists of two rarefaction waves for sufficiently small \(A_{k}\) (\(k=1,\ldots,n\)) and B. In the \(u_{-}< u_{+}\) situation, the formation of a vacuum state can be derived from the vanishing pressure limit of the solution consisting of two rarefaction waves to the Riemann problem (1.1) and (1.3). For fixed sufficiently small \(A_{k}\) (\(k=1,\ldots,n\)) and \(B>0\), let \((u_{*},\rho_{*})\) be the intermediate state between two rarefaction waves. Then \((u_{-},\rho_{-})\) and \((u_{*},\rho_{*})\) are connected by the 1-rarefaction wave \(R_{1}\), whereas \((u_{*},\rho_{*})\) and \((u_{+},\rho_{+})\) are connected by the 2-rarefaction wave \(R_{2}\). More specifically, we can derive from (3.9) and (3.10) that

$$ R_{1}: \textstyle\begin{cases} \xi=\lambda_{1}(u,\rho)=u-\frac{1}{\rho}\sqrt{ \sum_{k=1} ^{n} kA_{k}\rho^{k+1}+B}, \\ u-u_{-}=- \int_{\rho_{-}}^{\rho}\frac{1}{s^{2}}\sqrt { \sum_{k=1} ^{n} kA_{k}s^{k+1}+B}\,ds, \\ u_{-} \leq u \leq u_{*}, \qquad \rho_{-}\geq\rho\geq\rho_{*}, \end{cases} $$
(4.29)

and

$$ R_{2}: \textstyle\begin{cases} \xi=\lambda_{2}(u,\rho)=u+\frac{1}{\rho}\sqrt{ \sum_{k=1} ^{n} kA_{k}\rho^{k+1}+B}, \\ u_{+}-u= \int_{\rho}^{\rho_{+}}\frac{1}{s^{2}}\sqrt { \sum_{k=1} ^{n} kA_{k}s^{k+1}+B}\,ds, \\ u_{*}\leq u \leq u_{+}, \qquad \rho_{*}\leq\rho\leq\rho_{+}. \end{cases} $$
(4.30)

Theorem 4.4

When \(u_{-}< u_{+}\), if the solution to the Riemann problem (1.1) and (1.3) consists of two rarefaction waves for sufficiently small \(A_{k}\) (\(k=1,\ldots,n\)) and B, then the limit of solution as \(A_{k}\) (\(k=1,\ldots,n\)), \(B\rightarrow0\) is a two-contact-discontinuity solution with a vacuum state of the form (2.1), which is identical with that for the pressureless gas dynamic system (1.2).

Proof

From (4.29) and (4.30) we derive that

$$ \textstyle\begin{cases} u_{*}-u_{-}=- \int_{\rho_{-}}^{\rho_{*}}\frac{1}{\rho ^{2}}\sqrt{ \sum_{k=1} ^{n} kA_{k}\rho^{k+1}+B}\,d\rho, \\ u_{+}-u_{*}= \int_{\rho_{*}}^{\rho_{+}}\frac{1}{\rho ^{2}}\sqrt{ \sum_{k=1} ^{n} kA_{k}\rho^{k+1}+B}\,d\rho, \end{cases} $$
(4.31)

where \(\rho_{*}\leq\min(\rho_{-},\rho_{+})\). Therefore, we can conclude from (4.31) that

$$\begin{aligned} u_{+}-u_{-} =& \int_{\rho_{*}}^{\rho_{-}}\frac{1}{\rho^{2}}\sqrt { \sum _{k=1} ^{n} kA_{k} \rho^{k+1}+B}\,d\rho+ \int_{\rho_{*}}^{\rho_{+}}\frac{1}{\rho^{2}}\sqrt{ \sum _{k=1} ^{n} kA_{k} \rho^{k+1}+B}\,d\rho \\ \leq& \int_{\rho_{*}}^{\rho_{-}}\frac{1}{\rho_{*}^{2}}\sqrt { \sum _{k=1} ^{n} kA_{k} \rho_{-}^{k+1}+B}\,d\rho+ \int_{\rho_{*}}^{\rho_{+}}\frac{1}{\rho_{*}^{2}}\sqrt{ \sum _{k=1} ^{n} kA_{k} \rho_{+}^{k+1}+B}\,d\rho \\ \leq& \frac{\rho_{-}}{\rho_{*}^{2}}\sqrt{ \sum_{k=1} ^{n} kA_{k}\rho_{-}^{k+1}+B}+ \frac{\rho_{+}}{\rho_{*}^{2}}\sqrt{ \sum_{k=1} ^{n} kA_{k}\rho_{+}^{k+1}+B}, \end{aligned}$$
(4.32)

where we have used the fact that \(\rho_{*} \leq\min(\rho_{-},\rho_{+})\). If \(\lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0}\rho _{*}>0\), then we have \(u_{+}-u_{-}=0\) from (4.32), which contradicts the fact \(u_{-}< u_{+}\). Thus, we obtain \(\lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0}\rho_{*}=0\), which means that the intermediate state becomes vacuum in the limit \(A_{k}\) (\(k=1,\ldots,n\)), \(B\rightarrow0\) situation. In fact, the intermediate state cannot be seen as a constant state again when a vacuum state is formed. The rarefaction curve \(R_{1}\) in (4.29) turns out to be the line of contact discontinuity \(J_{1}:u=u_{-}\), whereas the rarefaction curve \(R_{2}\) in (4.30) turns out to be the line of contact discontinuity \(J_{2}:u=u_{+}\) in the the half-upper \((u,\rho)\) phase plane as \(A_{k}\) (\(k=1,\ldots,n\)), \(B\rightarrow0\). Hence we further have

$$\begin{aligned}& \lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0} \lambda_{1}(u_{-}, \rho_{-})= \lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0} \lambda_{1}(u_{*}, \rho_{*})=u_{-}, \end{aligned}$$
(4.33)
$$\begin{aligned}& \lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0} \lambda_{2}(u_{*}, \rho_{*})= \lim_{A_{k}\, (k=1,\ldots,n),B\rightarrow0} \lambda_{2}(u_{+}, \rho_{+})=u_{+}, \end{aligned}$$
(4.34)

which means that the rarefaction wave \(R_{1}\) tends to the contact discontinuity \(J_{1}\) with the speed \(u_{-}\), whereas the rarefaction wave \(R_{2}\) tends to the contact discontinuity \(J_{2}\) with the speed \(u_{+}\) as \(A_{k}\) (\(k=1,\ldots,n\)), \(B\rightarrow0\). The proof is completed. □

Finally, we are dedicating to investigating the special situation \(u_{-}=u_{+}\), in which the formation of contact discontinuity may be illustrated well by using the following theorem.

Theorem 4.5

When \(u_{-}=u_{+}\), the limit of solution to the Riemann problem (1.1) and (1.3) as \(A_{k}\) (\(k=1,\ldots,n\)), \(B\rightarrow0\) is only a contact discontinuity connecting the two constant states \((u_{-},\rho_{-})\) and \((u_{+},\rho_{+})\) directly, which is identical with that for the pressureless gas dynamic system (1.2).

Proof

Our proof is divided into two parts according to \(\rho _{+}>\rho_{-}\) or not. If \(\rho_{+}>\rho_{-}\), then we have \((u_{+},\rho_{+})\in \mathit{III}\) for any \(A_{k}\) (\(k=1,\ldots,n\)) and B. That is to say, \((u_{-},\rho_{-})\) and \((u_{*},\rho_{*})\) are connected by the 1-shock wave \(S_{1}\) with the speed \(\sigma_{1}\), whereas \((u_{*},\rho_{*})\) and \((u_{+},\rho_{+})\) are connected by the 2-rarefaction wave \(R_{2}\), which can be expressed by the formulae (4.1) and (4.30), respectively. Therefore the intermediate state \((u_{*},\rho_{*})\) between \(S_{1}\) and \(R_{2}\) is determined by

$$ \textstyle\begin{cases} u_{*}=u_{-}-\sqrt{(\frac{1}{\rho_{-}}-\frac{1}{\rho_{*}}) ( \sum_{k=1} ^{n} A_{k}(\rho_{*}^{k}-\rho_{-}^{k})+B(\frac{1}{\rho_{-}}-\frac {1}{\rho_{*}}) )}, \\ u_{+}-u_{*}= \int_{\rho_{*}}^{\rho_{+}}\frac{1}{\rho ^{2}}\sqrt{ \sum_{k=1} ^{n} kA_{k}\rho^{k+1}+B}\,d\rho, \end{cases} $$
(4.35)

where \(\rho_{-} < \rho_{*} < \rho_{+}\) and \(u_{*}< u_{-}=u_{+}\). More specifically, the solution to the Riemann problem (1.1) and (1.3) can be displayed in the form

$$ (u,\rho) (\xi)= \textstyle\begin{cases} (u_{-},\rho_{-}), & -\infty< \xi< \sigma_{1}, \\ (u_{*},\rho_{*}), & \sigma_{1}< \xi< \lambda_{2} (u_{*},\rho_{*}), \\ R_{2}, & \lambda_{2} (u_{*},\rho_{*})\leq\xi \leq\lambda_{2}(u_{+},\rho_{+}), \\ (u_{+},\rho_{+}), & \lambda_{2}(u_{+},\rho_{+})< \xi< +\infty, \end{cases} $$
(4.36)

where the propagating speed of \(S_{1}\) is given by \(\sigma_{1}=\frac{\rho_{*}u_{*} -\rho_{-}u_{-}}{\rho_{*}-\rho _{-}}\), and the state \((u,\rho)\) in \(R_{2}\) should satisfy (4.30). For \(\rho_{-} <\rho_{*}<\rho_{+}\), we directly get \(\lim_{ A_{k}\, (k=1,\ldots,n),B \rightarrow 0}u_{*}=u_{-}\) in the first equation of (4.35).

On the one hand, we can derive from the first equation of (4.35) that

$$\begin{aligned} \frac{\rho_{-}(u_{*}-u_{-})}{\rho_{*}-\rho_{-}} =&-\frac{1}{\rho _{*}}\sqrt{ \Biggl( \sum _{k=1} ^{n} A_{k}\rho_{-} \rho_{*} \biggl(\frac{\rho_{*}^{k}-\rho_{-}^{k}}{\rho _{*}-\rho_{-}} \biggr)+B \Biggr)} \\ =&-\frac{1}{\rho_{*}}\sqrt{ \Biggl( \sum_{k=1} ^{n} A_{k}\rho_{-}\rho_{*} \bigl( \rho_{*}^{k-1}+\rho_{*}^{k-2}\rho _{-}+\cdots+\rho_{-}^{k-1} \bigr)+B \Biggr)}, \end{aligned}$$
(4.37)

so that we have

$$\begin{aligned} \lim_{ A_{k}\, (k=1,\ldots,n),B \rightarrow 0}\sigma_{1} =&\lim_{ A_{k}\, (k=1,\ldots,n),B \rightarrow 0} \frac{\rho_{*}u_{*} -\rho_{-}u_{-}}{\rho_{*}-\rho_{-}} \\ =&\lim_{ A_{k}\, (k=1,\ldots,n),B\rightarrow 0} \biggl(u_{*}+\frac{\rho_{-}(u_{*} -u_{-})}{\rho_{*}-\rho_{-}} \biggr)=u_{-}. \end{aligned}$$
(4.38)

On the other hand, from (4.30) it directly follows that

$$ \lim_{ A_{k}\, (k=1,\ldots,n),B \rightarrow 0}\lambda_{2}(u_{*}, \rho_{*})=\lim_{ A_{k}\, (k=1,\ldots,n),B \rightarrow 0}\lambda_{2}(u_{+}, \rho_{+})=u_{+}=u_{-}. $$
(4.39)

In view of (4.38) and (4.39), if \(u_{-}=u_{+}\) and \(\rho_{+}>\rho _{-}\), then the limit of solution to the Riemann problem (1.1) and (1.3) as \(A_{k}\) (\(k=1,\ldots,n\)), \(B\rightarrow0\) is a contact discontinuity with the speed \(u_{-}\) connecting \((u_{-},\rho_{-})\) and \((u_{+},\rho _{+})\) directly.

Otherwise, if \(\rho_{+}<\rho_{-}\), then we have \((u_{+},\rho_{+})\in \mathit{II}\) for any \(A_{k}\) (\(k=1,\ldots,n\)) and B. In other words, \((u_{-},\rho_{-})\) and \((u_{*},\rho_{*})\) are connected by the 1-rarefaction wave \(R_{1}\), whereas \((u_{*},\rho_{*})\) and \((u_{+},\rho_{+})\) are connected by the 2-shock wave \(S_{2}\) with speed \(\sigma_{2}\), which can be expressed by the formulae (4.29) and (4.2), respectively. As before, the intermediate state \((u_{*},\rho_{*})\) between \(R_{1}\) and \(S_{2}\) is determined by

$$ \textstyle\begin{cases} u_{*}-u_{-}=- \int_{\rho_{-}}^{\rho_{*}}\frac{1}{\rho ^{2}}\sqrt{ \sum_{k=1} ^{n} kA_{k}\rho^{k+1}+B}\,d\rho, \\ u_{+}=u_{*}-\sqrt{(\frac{1}{\rho_{*}}-\frac{1}{\rho_{+}}) ( \sum_{k=1} ^{n} A_{k}(\rho_{+}^{k}-\rho_{*}^{k})+B(\frac{1}{\rho_{*}}-\frac {1}{\rho_{+}}) )}, \end{cases} $$
(4.40)

where \(\rho_{-}>\rho_{*}>\rho_{+}\) and \(u_{*}>u_{-}=u_{+}\). Analogously, the solution to the Riemann problem (1.1) and (1.3) is given by

$$ (u,\rho) (\xi)= \textstyle\begin{cases} (u_{-},\rho_{-}), & -\infty< \xi< \lambda_{1}(u_{-},\rho_{-}), \\ R_{1}, & \lambda_{1}(u_{-},\rho_{-}) \leq\xi\leq \lambda_{1}(u_{*},\rho_{*}), \\ (u_{*},\rho_{*}), & \lambda_{1}(u_{*},\rho_{*}) < \xi< \sigma_{2}, \\ (u_{+},\rho_{+}), & \sigma_{2} < \xi< \infty, \end{cases} $$
(4.41)

where the propagating speed of \(S_{2}\) is given by \(\sigma_{2}=\frac{\rho_{+}u_{+}-\rho_{*}u_{*} }{\rho_{+}-\rho _{*}}\), and the state \((u,\rho)\) in \(R_{1}\) should satisfy (4.29). For \(\rho_{-}>\rho_{*}>\rho_{+}\), we immediately obtain \(\lim_{ A_{k}\, (k=1,\ldots,n),B \rightarrow 0}u_{*}=u_{+}\) in the second equation of (4.40). With the similar method as before, we can also arrive at the limiting relations

$$ \lim_{ A_{k}\, (k=1,\ldots,n),B \rightarrow 0}\lambda_{1}(u_{-}, \rho_{-})=\lim_{ A_{k}\, (k=1,\ldots,n),B \rightarrow 0}\lambda_{1}(u_{*}, \rho_{*})=\lim_{ A_{k}\, (k=1,\ldots,n),B \rightarrow 0}\sigma_{2}=u_{+}=u_{-}. $$
(4.42)

Thus, if \(u_{-}=u_{+}\) and \(\rho_{+}<\rho_{-}\), then the limit of solution to the Riemann problem (1.1) and (1.3) as \(A_{k}\) (\(k=1,\ldots,n\)), \(B\rightarrow0\) is also a contact discontinuity connecting \((u_{-},\rho_{-})\) and \((u_{+},\rho_{+})\) directly. The proof is finished. □