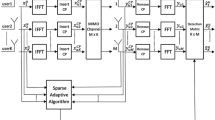
1 Introduction

The high energy and spectrum efficiency of massive multiple-input multiple-output (MIMO) systems heavily build on the premise that the base stations (BS) obtain channel state information (CSI) with reasonable quality, which is generally estimated via pilot sequences [1]. However, in the uplink massive MIMO systems, the pilot overhead demanded should be proportional to the number of users and would be prohibitively large as the number of users increase. In the uplink multicell massive MIMO, this results in pilot contamination as the same pilot sequences have to be reused by neighbor cells to serve a large number of users [2]. Moreover, the pilot contamination is a major limiting factor to system performance [3]. Hence, the massive MIMO urgently needs efficient channel estimation scheme without producing pilot contamination and requiring too much pilot overhead. Based on the estimated CSI, the signals received at base stations are typically detected through linear methods with low complexity, such as zero-forcing [4–6] and matched filter [7, 8]. However, the performances of linear detector are typically far inferior to the optimal maximum likelihood (ML) detector whose computational complexity exponentially scales up with the signal constellation size and the number of antennas [9]. Thus, the development of computationally efficient and reliable detector for massive MIMO also needs to be thoroughly addressed [10].

In the past few years, several types of schemes have been exploited to mitigate or reduce the impact of pilot contamination in multicell massive MIMO systems. (1) Semi-blind or blind approaches, such as [11–14]—the eigenvalue decomposition-based method with a short training sequence was proposed in [11]. Hu et al. [12] proposed a semi-blind method without requiring the statistical information of channels. Another low-complexity semi-blind approach was proposed in [13], which the received signal are firstly projected onto the subspace with minimal interference, then alternatively refined the channel estimation and detected the data symbols. Applying the theory of large random matrices, [14] proposed a blind pilot decontamination with subspace projection. (2) Optimization design of non-orthogonal pilot signals, such as [15–18]—when training slots are not large enough to construct the orthogonal pilot signals, [15] exploits a pilot design criterion and shows that the line packing on a complex Grassmannian manifold is the optimization scheme, which is based on minimal mean square error (MMSE) estimator. A generalized Welch-bound equality-based pilot signal design method is proposed in [16], which has low correlation coefficients and ensures the network to satisfy the requirement of user capacity. For a given pilot length, [17] proposes an alternating minimization-based pilot design algorithm. (3) The precoding-based approaches, such as [19–21]—a MMSE-based precoding is exploited in [19] to alleviate the impact of pilot contamination. A pilot contamination mitigation method along with zero-forcing precoding is proposed in [20], which can generate orthogonal pilot signals across neighboring cells through multiplying the Zadoff-Chu sequences element-wise with a specific orthogonal variable spreading factor code.

Some significant efforts have been made to reduce the pilot overhead for massive MIMO systems, which can be divided into two broad categories. (1) Low-rank channel covariance matrices based methods, such as [22–24]—the finite scattering environment and small angular spread result in high correlation of different paths between the user and the BS [25–29] and low-rank channel covariance matrix. Through exploiting the correlation characteristic of channel vectors, the joint spatial division and multiplexing (JSDM) was proposed in [23] which significantly reduced the overhead of downlink training and uplink feedback for frequency division duplexing (FDD) massive MIMO systems. When the number of pilot signals is no less than the rank of channel covariance matrix and the noise interference disappear, [24] proves that the MMSE estimator can recovery channel vectors exactly. (2) Compressed channel sensing method—exploiting the channel sparsity and applying the compressed sensing (CS) to reduce the overhead of CSI feedback has been investigated in [30–32]. A spare channel estimation method applying Gaussian-mixture Bayesian learning has been proposed in [33] to estimate the whole channel parameters including the desired and interference links, which can mitigate pilot contamination and reduce pilot overhead, but every time, the approach just can estimate the channel response at one beam.

An iterative MIMO detector with relaxed ML constraints using sparse decomposition has been proposed to preserve a low computational cost even increase the signal size, but the method just suit to detect a vector [34]. In block fading systems, the detection target at the BS usually is a multiuser data frame, i.e., a two-dimensional (2D) signal block. To detect the 2D signals, the method in [34] should run the decoding process many times or convert the 2D signal detection problem to a vector detection problem. However, the converting method will substantially increase the required memory and processing load which would make it become non-competitive when applied to massive MIMO block fading systems. For example, the converting approach can be represented as:

$$ \mathbf{Y}=\mathbf{AXB}^{T} \Longleftrightarrow \mathbf{y}=\Phi \mathbf{x} $$
(1)

with A∈R60×200, B∈R30×100, x=vec(X), and y=vec(Y), which results in Φ=B⊗A with dimensions 1800×20,000. The signs of vec() and \(\bigotimes \) denote vectorization of a matrix and Kronecker product, respectively.

In this paper, the multiuser channel estimation problem and the multiuser signal decoding problem in uplink massive MIMO systems are modelled as two-dimensional sparse signal recovery problems in compressed sensing, respectively. Although [35, 36] researched the 2D compressed sensing channel estimation schemes for massive MIMO, it is the FDD model discussed in [35, 36] which is different from the time division duplexing (TDD) multicell multiuser system model considered in this paper. The main contributions of this paper are summarized as follows:

  • We propose a channel estimation method named as 2D-SL0-CE applying the two-dimensional smoothed l0-norm compressed sensing recovery algorithm [37, 38], which are able to jointly estimate multiuser CSI. Using virtual channel representation, the 2D-SL0-CE formulates the joint channel estimation problem, comprising both the target and interference channels, as a 2D sparse signal reconstruction problem in CS, which not only can mitigate the pilot contamination but also can significantly reduce pilot overhead.

  • We propose a signal detection method named as 2D-SL0-SD using our modified 2D-SL0 algorithm, which can decode multiuser M-ary phase-shift keying (MPSK) signal block. Applying sparse decomposition, the 2D-SL0-SD models the detection problem of multiuser signal block as a 2D sparse signal reconstruction problem whose elements are binaries {0,1}. Moreover, in the high SNR scenario, through exploiting the estimated CSI of interference links, an improved 2D-SL0-SD is also proposed to remove the decoding bottleneck induced by interference from neighboring cells.

The remaining paper is organized as follows. The system model and the least square (LS) channel estimation methods are described in Section 2. Section 3 models the multicell multiuser channel estimation problem as a two-dimensional compressed sensing problem and describes the proposed channel estimation algorithm. Section 4 models the signal decoding problem of multiuser as a 2D sparse signal recovery problem and presents the steps of the proposed 2D-SL0-SD method. Section 5 gives and analyzes the numerical results. Section 6 draws a conclusion of the whole paper.

Notations: diag(x) represents a diagonal matrix with diagonal elements being the vector x. Superscripts T and † denote the transpose and pseudo-inverse, respectively. CN(0,1) denotes complex Gaussian variables with zero mean and unit variance. \(\bigotimes \) denotes Kronecker product. Vectors and matrices are denoted by boldface lowercase and uppercase letters, respectively.

2 System model

Consider a multicell massive MIMO system in which each target cell shares the same frequency band with L−1 adjacent cells. Each cell has one BS with a uniform linear array (ULA) of M antennas that serves K (K<<M) single antenna users. The uplink channel vector from the kth terminal in ith cell to jth BS is modelled as:

$$ \mathbf{h}_{jik}=\sqrt{\beta_{jik}}\mathbf{g}_{jik}, $$
(2)

where gjik is the fast fading vector, and large-scale fading factor βjik describes the quasi-static shadow fading and the path loss. Different channel vectors are assumed to be independent. Consequently, the channel matrix between the K users in ith cell and the jth BS can be represented as:

$$ \mathbf{H}_{ji}\mathbf{=G}_{ji}\mathbf{D}_{ji} $$
(3)

with Hji=[hji1,⋯,hjiK], Gji=[gji1,⋯,gjiK] and \(\mathbf {D}_{ji}=\text {diag}\left (\sqrt {\beta _{ji1}},\cdots,\sqrt {\beta _{jiK}}\right)\).

In a block fading channel, the training signal received at the jth BS becomes:

$$ \mathbf{Y}_{j}^{tr}=\sqrt{P_{tr}}\sum\limits_{i=1}^{L}\mathbf{H}_{ji}\mathbf{X}_{i}^{tr}+\mathbf{N}_{j}^{tr}, $$
(4)

where Ptr denotes the training signal-to-noise ratio (SNR), the rows of \(\mathbf {X}_{i}^{tr}\in C^{K\times T_{tr}}\) are the pilot sequences of ith cell, and \(\mathbf {N}_{j}^{tr}\) is the noise with i.i.d. elements distributed as CN(0,1).

The jth cell is assumed as the target cell. One natural choice to find a channel estimate based on the training signal without employing any prior information is the LS method which is given by:

$$\begin{array}{*{20}l} \hat{\mathbf{H}}_{jj}^{LS}&=\frac{1}{\sqrt{P_{tr}}}\mathbf{Y}_{j}^{tr}\left(\mathbf{X}_{j}^{tr}\right)^{\dag} \\ &= \mathbf{H}_{jj}+\sum\limits_{i=1,i\neq j}^{L} \mathbf{H}_{ji}+\frac{1}{\sqrt{P_{tr}}}\mathbf{N}_{j}^{tr}, \end{array} $$
(5)

where the second term denotes pilot contamination resulting in the same orthogonal pilots reused by adjacent cells.

3 2D-SL0-CE channel estimation method

The key idea of our exploited channel estimation is to explore the sparsity in the virtual channel representation, which applies spatial beams at fixed virtual directions to characterize the physical channel matrix. The virtual channel matrix \(\mathbf {G}_{ji}^{v}\) can be linked to the above described physical channel matrix Gji by the following transformation:

$$ \mathbf{G}_{ji}=\mathbf{A}_{R}\mathbf{G}_{ji}^{v}, $$
(6)

where AR=[aR(θ1),⋯,aR(θM)] with the receiver response vectors given by:

$$ \mathbf{a}_{R}(\theta_{m})=\frac{1}{\sqrt{M}}\left[1, e^{-j2\pi \theta_{m}}, \cdots, e^{-j2\pi(M-1)\theta_{m}}\right]^{T}. $$
(7)

The direction θm is related to the physical angle ϕm∈[−π/2,π/2] as θm=dsin(ϕm)/λ with λ being the carrier wavelength and d being the antenna spacing [39]. We uniformly sample the principal θ period to set the virtual spatial angles, i.e., θm=m/M, and resulting in an M×M unitary discrete Fourier transform matrix AR. The element \(\mathbf {G}_{ji,mk}^{v}\) of M×K matrix \(\mathbf {G}_{ji}^{v}\) represents the coupling gain from the kth terminal to the mth virtual receive angle θm. Therefore, the element will be zero when there is no corresponding coupling, and the \(\mathbf {G}_{ji}^{v}\) will be a sparse matrix when the number of non-zero elements is much smaller than that of the total elements.

Substituting (6) into (4) yields the following received training signal at the jth BS:

$$ \mathbf{Y}_{j}^{tr}=\sqrt{P_{tr}}\sum_{i=1}^{L}\mathbf{A}_{R}\mathbf{G}_{ji}^{v} \mathbf{D}_{ji}\mathbf{X}_{i}^{tr}+\mathbf{N}_{j}^{tr}. $$
(8)

Furthermore, taking the transpose operation to (8), we can obtain:

$$ {{} \begin{aligned} \underbrace{\frac{1}{\sqrt{P_{tr}}}(\mathbf{Y}_{j}^{tr})^{T}}_{=\mathbf{Y}} \,=\,\sum\limits_{i=1}^{L}\left(\mathbf{X}_{i}^{tr}\right)^{T}\mathbf{D}_{ji}\left(\mathbf{G}_{ji}^{v}\right)^{T}\mathbf{A}_{R}\,+\,\frac{1}{\sqrt{P_{tr}}}\left(\mathbf{N}_{j}^{tr}\right)^{T}\\ =\![\underbrace{\left(X_{1}^{tr}\right)^{T},\!\cdots\!,\left(X_{L}^{tr}\right)^{T}}_{=\mathbf{X}}] \underbrace{\left[\begin{array}{l} \mathbf{D}_{j1}\left(\mathbf{G}_{j1}^{v}\right)^{T} \\ \vdots\\ \mathbf{D}_{jL}\left(\mathbf{G}_{jL}^{v}\right)^{T} \end{array}\right]}_{=\mathbf{G}} \!\mathbf{A}_{R}\,+\,\underbrace{\frac{1}{\sqrt{P_{tr}}}\left(\mathbf{N}_{j}^{tr}\right)^{T}}_{=\mathbf{N}}. \end{aligned}} $$
(9)

Now, based on the linear model Y=XGAR+N, the channel estimation problem is modelled as a 2D sparse signal reconstruction problem in compressed sensing. Then, we estimate Hj=[Hj1,⋯,HjL] based on Y, X, and AR, using the 2D-SL0 sparse reconstruction algorithm [38]. The proposed channel estimation method 2D-SL0-CE is summarized in Algorithm 1. Different from other types of compressed sensing recovery algorithms, the SL0 and 2D−SL0 applied the following function to approximate the l0-norm of b, i.e., ||b||0.

$$ \left \{ \begin{array}{lr} \mathbf{F}_{\sigma}(\mathbf{b})=\sum_{i=1}^{M} \text{exp}\left(\frac{-b_{i}^{2}}{2\sigma^{2}}\right),\\ ||\mathbf{b}||_{0}\approx M-\mathbf{F}_{\sigma}(\mathbf{b}),\sigma\rightarrow 0, \end{array} \right. $$
(10)

where b∈RM×1 is a sparse vector, and the parameter σ determines the quality of the approximation and how smooth the function Fσ(b). Consequently, the minimum l0-norm solution can be found by maximizing Fσ(b). In Algorithm 1, steps 2–9 gradually decrease the value of σ and maximize the objective function for each value of σ.

4 2D-SL0-SD signal detection method

In a block fading scenario, the received data signal at the jth BS can be written as:

$$ \mathbf{Y}_{j}=\sqrt{P_{\text{data}}}\mathbf{H}_{jj}\mathbf{X}_{j}+\underbrace{\sqrt{P_{\text{data}}}\sum\limits_{i=1,i\neq j}^{L}\mathbf{H}_{ji}\mathbf{X}_{i}+\mathbf{N}_{j}}_{=\mathbf{W}_{j}}, $$
(11)

where \(\mathbf {Y}_{j}\in \mathcal {C}^{M\times N}\) is the received data, \(\sqrt {P_{\text {data}}}\) denotes the uplink SNR, Xi denotes the transmitted data matrix of the ith cell whose element is selected from a finite alphabet constellation defined as {s1,⋯,sQ} with Q being the finite alphabet cardinal, Nj is the noise with elements distributed as CN(01), and Wj represents the noise plus interference faced by the received data of jth BS.

The transmitted symbol of the ith cell can be sparse represented as (12) through exploiting the prior knowledge that each transmitted element Xi,mn belongs to a discrete and finite alphabet constellation:

$$ X_{i,mn}=\mathbf{s e}_{i,mn}, $$
(12)

where Xi,mn denotes the nth symbol of mth user in ith cell, s=[s1,⋯,sQ] is the discrete and finite constellation vector, and ei,mn=[ei,mn(s1),⋯,ei,mn(sQ)]T with ei,mn(sq) being equal to 1 if Xi,mn=sq or 0 otherwise (1≤q≤Q). Applying this sparse representation into all symbols, the transmitted data matrix in the ith cell can be expressed in function of a sparse matrix as:

$$ \mathbf{X}_{i}=\mathbf{B}_{s}\mathbf{E}_{i}, $$
(13)

where \(\mathbf {B}_{s}=\mathbf {I}_{K} \bigotimes \mathbf {s}\) is a block diagonal matrix of size K×KQ, and the nth column of the matrix Ei is [(ei,1n)T,⋯,(ei,Kn)T]T.

Substituting (13) into (11) generates

$$ \mathbf{Y}_{j}=\sqrt{P_{\text{data}}}\mathbf{H}_{jj}\mathbf{B}_{s}\mathbf{E}_{j}+\mathbf{W}_{j}=\mathbf{A}_{j}\mathbf{E}_{j}\mathbf{I}_{N}+\mathbf{W}_{j} $$
(14)

with \(\mathbf {A}_{j}=\sqrt {P_{\text {data}}}\mathbf {H}_{jj}\mathbf {B}_{s}\). The detection problem of signal block has been modelled as a 2D sparse binary {0,1} reconstruction problem in CS, then based on Yj, Aj, and IN, the signal block Xj can be detected using the modify 2D-SL0 algorithm which suits to reconstruct 2D sparse binary {0,1} signal. The process of 2D-SL0-SD is summarized in Algorithm 2. Because the elements of Ej needed to be recovered are 0 or 1, but the elements recovered by the original 2D-SL0 algorithm are not exactly 0 or 1, step 10 of Algorithm 2 is added to find which element of \(\hat {\mathbf {e}}_{j,mn}\) maybe 1 with highest probability and reset such element to 1 and others to 0.

In the high SNR scenario, such as Nj→0, it can be observed from (11) that the main factor restricting the decoding performance is not the noise but the interference from neighboring cells. Thus, the performance of 2D-SL0-SD will meet floor as the SNR increases. In order to resolve this problem, the CSI of interference links are exploited and an improved 2D-SL0-SD method is proposed, which does not treat the signals from neighbor cells as interference, moreover, decodes them jointly with the desired signals. Specifically, exploiting the CSI of whole links estimated by the above proposed 2D-SL0-CE method, the received data signal at the jth BS in (11) can be rewritten as:

$$\small \mathbf{Y}_{j}=\sqrt{P_{\text{data}}}[\mathbf{H}_{j1},\!\cdots\!, \mathbf{H}_{jL}][(\mathbf{X}_{1})^{T},\!\cdots\!, (\mathbf{X}_{L})^{T}]^{T}+\mathbf{N}_{j}. $$
(15)

Moreover, substituting (13) into (15) can generate:

$$ \begin{aligned} \mathbf{Y}_{j}\,=\, &\underbrace{\sqrt{P_{\text{data}}}[\mathbf{H}_{j1}\mathbf{B}_{s},\cdots\!, \mathbf{H}_{jL}\mathbf{B}_{s}]}_{=\mathbf{A}}\underbrace{[(\mathbf{E}_{1})^{T},\cdots\!, (\mathbf{E}_{L})^{T}]^{T}}_{=\mathbf{E}}\!\mathbf{I}_{N} \\ &+\mathbf{N}_{j}. \end{aligned} $$
(16)

Now, the decoding problem without multiuser interference has also been modelled as a 2D sparse {0,1} signal reconstruction problem, which has the same form as that of (14), and can be solved through the processes of Algorithm 2 whose Aj needs to be replaced by A. Hereafter, the improved 2D-SL0-SD with interference cancel is named as 2D-SL0-SD-IC. Comparing (16) with (14), it can be observed that the recovery object of the 2D-SL0-SD-IC is E, including not only the Ej of the objective cell but also the Ei of the L−1 neighbor cells (i=1,⋯L,i≠j), and the noise is the only interference source.

It is worth noting that the proposed 2D-SL0-SD is only suitable to decode constant modulus signal, such as MPSK. Since there is only one element of ei,mn in (12) equaling to 1 and the others are zeros, Algorithm 2 needs a ruler to reset the values of the estimated \(\hat {\mathbf {e}}_{i,mn}\). In step 10 of Algorithm 2, the ruler is that the element of \(\hat {\mathbf {e}}_{j,mn}\) with the largest real part is viewed as such element whose value is 1 with the highest probability. Such ruler requires that the elements of s in (12) have the same modulus.

5 Numerical results and discussion

The spectral efficiency and estimation accuracy of the proposed 2D-SL0-CE sparse channel estimation method and the decode performance of the proposed 2D-SL0-SD are investigated. A multicell scenario with L cells sharing the same frequency band is considered. The fading coefficient is modelled as βjik=zjik/(rjik/rh)α, in which \(z_{jik}\thicksim ln N\left (0,\sigma _{\text {shadow}}^{2}\right)\) is a lognormal random variable, rjik denotes the distance between the BS and the corresponding terminal, and rh is the cell-hole radius. The number of non-zero elements in each column of \(G_{ji}^{v}\), which means the number of multipath, is assumed to S, whose positions are randomly selected and values are generated through CN(0,1). The pilot sequence of each user is randomly generated using the complex normal distribution and then is normalized to unity. The normalized mean square error (NMSE) defined as \(\frac {1}{N_{\text {MC}}}{\sum \nolimits }_{i=1}^{N_{\text {MC}}}\frac {\|\hat {H_{i}}-H_{i}\|_{F}^{2}}{\|H_{i}\|_{F}^{2}}\) is used to evaluate the estimation accuracy, where NMC means the number of Monte-Carlo simulations, Hi and \(\hat {H_{i}}\) are the actual and estimated channel impulse response of ith Monte-Carlo trial, respectively. The parameters of the system and the 2D-SL0 algorithm are summarized in Table 1.

Table 1 System and algorithm parameter values
Full size table

Firstly, at the scenario of S=5, the NMSE of the 2D-SL0-CE and the bit error rate (BER) of the 2D-SL0-SD detection QPSK signals with various CSI, including perfect and estimated CSI, are investigated. The whole number of multicell users is 20×7=140; thus, the LS method should require orthogonal pilot sequences with length being not less than 140 to avoid pilot contamination. Figure 1 shows that the 2D-SL0-CE method applying random pilot sequences with a length of 12 can outperform LS with 140 pilots nearly 5 dB. Moreover, the NMSE of 2D-SL0-CE is approximate linear reducing with the SNR increasing when the pilot length is not less than 12. While in the case that 20 orthogonal pilot sequences are reused by the objective cell and neighbor cells, Fig. 1 also shows that the LS method will meet a performance floor caused by pilot contamination. In a block fading scenario with signal length N=200, Fig. 2 plots the BER performance of the 2D-SL0-SD detection QPSK signal block using various CSIs. Applying perfect CSI at 10 dB SNR, the 2D-SL0-SD can approach near to 10−2 BER. Moreover, its BER is approximate linear reducing with the SNR increasing, which shows its reliable detection ability. Using the CSI estimated through the 2D-SL0-CE, where each user applies random non-orthogonal pilot sequence with length being 32, the obtained BER of 2D-SL0-SD at 15 dB SNR is slightly better than 10−2, which shows joint the 2D-SL0-CE with 2D-SL0-SD for channel estimation and decoding QPSK signals is a feasible scheme.

Fig. 1
figure 1

NMSE performance of 2D-SL0-CE and LS methods

Full size image
Fig. 2
figure 2

BER performance of 2D-SL0-SD with various CSIs

Full size image

Then, applying perfect CSI and estimated CSI through 2D-SL0-CE, respectively, Figs. 3 and 4 show the BER of 2D-SL0-SD and its improved version 2D-SL0-SD-IC detecting various PSK data block with length N=200. In both cases, the BER of 2D-SL0-SD is better than 2D-SL0-SD-IC within a SNR threshold value. This is because the received energy of interference data is usually smaller than that of target data, which induces more difficult to decode interference data. The decoding object in 2D-SL0-SD-IC includes the target and interference data, which means the decoding result of two parts will affect each other. Thus, in the low-SNR scenario, the low correct decoding probability of interference data leads to 2D-SL0-SD-IC has higher BER than 2D-SL0-SD. With the SNR increasing and exceeding a threshold value, the 2D-SL0-SD will gradually meet a performance bound induced by interference. However, the BER of 2D-SL0-SD-IC will be still approximately linear reducing owing to gradually high correct decoding probability of interference data. In theory, with the distance of the two neighbor signal points in constellation diagram gradually reducing, it will be more difficult to decode the signals correctly. In Figs. 3 and 4, it can be observed that the BERs of QPSK, 8PSK, and 16PSK are gradually increasing at the same SNR.

Fig. 3
figure 3

BER of 2D-SL0-SD with perfect CSI

Full size image
Fig. 4
figure 4

BER of 2D-SL0-SD joint with 2D-SL0-CE

Full size image

Finally, the NMSE of 2D-SL0-CE method with fixed pilot length at various scenarios, including various sparsity and number of users in each cell, is studied in Figs. 5 and 6, respectively. In the case of each cell having 20 users, applying random pilot sequences with fixed length of 26, Fig. 5 shows that the NMSE is approximately linear reducing with the SNR increasing when the S is not larger than 20. In the case of S=5 and pilot length being 26, Fig. 6 shows that the NMSE is approximately linear reducing with the SNR increasing when the number of users in each cell is not larger than 50. In order to recovery a 1D E-sparse F-length vector successfully with high probability, [40] presents that the number of measurements needed is of order \(\mathcal {O}(E\text {log}(F/E))\). In the 2D cases, from the best performance plots in Figs. 5 and 6, it can be obtained that the number of measurements are 2.15 and 2.23 times of KLSlog(M/S), respectively, where the value of KLS is the number of non-zero elements in 2D signals. Thus, ensuring the original 2D signal can be recovered with high probability, the number of measurements needed is also of order \(\mathcal {O}(E\text {log}(F/E))\), where the E and F denote the numbers of non-zero elements and whole elements in the 2D signal, respectively. In practical, the above ruler can be used to guide for setting pilot length.

Fig. 5
figure 5

NMSE of 2D-SL0-CE with various channel sparsity

Full size image
Fig. 6
figure 6

NMSE of 2D-SL0-CE with various numbers of users

Full size image

6 Conclusions

This paper has investigated the two challenging problems for block fading massive MIMO systems. The one is to exploit efficient uplink channel estimation method that requires acceptable pilot overhead and can mitigate pilot contamination. The other one is to jointly decode multiuser data block. The joint multiuser channel estimation and data block detection problems have both been modelled and solved as a 2D sparse signal reconstruction problem in the CS framework. More specifically, through using a linear virtual channel representation for ULA, the 2D-SL0-CE compressed channel sensing method is proposed, which needs less pilot overhead than LS method, and can jointly estimate the desired and interference uplinks. Through sparse representation in a finite alphabet set for each transmitted data symbol, the 2D-SL0-SD data decoding method is proposed which can simultaneously decode a MPSK data block for multiuser. Simulation results demonstrate that joint the 2D-SL0-CE with 2D-SL0-SD to estimate channel and decode MPSK data for multiuser massive MIMO is a feasible scheme.