1 Introduction

Direction finding has gained great interest in array signal processing field over the past decades, which is widely used in radar, underwater acoustics, wireless communication, and seismic [1–3]. In this area, most of the studies have assumed that the signal follows complex circular Gaussian distribution, such as multiple signal classification (MUSIC) [4], estimation of signal parameters via rotational invariance technique (ESPRIT) [5]. However, this is not an accurate assumption; in practical application systems, many signals follow complex non-circular Gaussian distribution, such as binary phase shift keying (BPSK), Mary amplitude shift keying (MASK), and binary pulse amplitude modulated (PAM). Therefore, how to exploit the second-order non-circularity of complex signals to improve the angle estimation performance becomes an urgent issue in signal processing [6–8].

So far, a large number of subspace-based parameter estimation algorithm, which exploited the non-circular property of the signal, had been proposed in the literatures, for example, non-circular multiple signal classification (NC-MUSIC) [9], polynomial rooting NC-MUSIC (NC-Root-MUSIC) [10], fourth-order NC-Root-MUSIC (NC-Root-FO-MUSIC) [11], and unitary ESPRIT for non-circular sources (NC-unitary-ESPRIT) [12], which aim to increase degree of freedom (DoF) and improve angular estimation accuracy. For example, the work in [13] utilized the conjugation information of the partial received signal to extend the virtual aperture as well as the joint virtual array, by using a forward spatial smoothing technique in order to handle the coherent source. The main challenge for the super-resolution direction-of-arrival (DoA) estimation is to resolve the closely spaced sources with small-size sample, and even to resolve the coherent source. Compared with the conventional high-resolution estimation algorithms, source localization algorithms which based on sparse signal recovery (SSR), showed the predominant performance in the estimation accuracy [14–16]. Specifically, the authors in [17] proposed an l1-SVD algorithm which uses singular value decomposition (SVD) of the measurements to reduce the data dimension. The authors in [18] presented a subspace-weighted l2,1-SVD algorithm which exploits the MUSIC-like spectrum to design the weighted matrix. Furthermore, the authors in [19] proposed a unitary subspace-weighted l2,1-SVD algorithm by applying the spatial smoothing technique, which doubles the number of snapshots and benefits the DoA estimation accuracy. Moreover, by employing unitary transformation, the unitary l2,1-SVD algorithm puts the sparse constraint on real-data matrix and further reduces the computational complexity. For the past two decades, the non-circular SSR-based algorithms have attracted a great number of researchers’ attention, [20–22], and by exploiting the non-circular property of the signal sources, the performance of the DoA estimation algorithms can be effectively improved.

In this paper, we propose a weighted subspace mixed-norm DoA estimation algorithm for non-circular signal. The algorithm makes the most of the non-circularity of the sources and formulates the DoA estimation as a weighted subspace mixed-norm minimization problem. The offered improvement mainly displays in two aspects: For one thing, the algorithm takes advantage of the strictly non-circular sources, enhances the DoF to two times of the number of sensors, which increases the number of detectable sources and decreases the estimation error. For another, the subspace weighting scheme exploits the relationship between the over-complete dictionary and the noise subspace, which improves the reliability of weighted coefficient and further enforces the sparsity of the signal. Results verify that our proposed algorithm provides superior performance than l1-SVD and SW- l2,1-SVD algorithms under small snapshots and low SNR regime. Moreover, the proposed algorithm offers the ability to estimate DoAs in underdetermined conditions.

The rest of the paper is organized as follows. In Section 2, we introduce the system model and problem description. In Section 3, we present a weighted subspace mixed-norm DoA estimation algorithm. In Section 4, we provide the detailed experimental simulations and discussion. Finally, we conclude the whole paper in Section 6.

Notation: A vector and a matrix are denoted by a and A, respectively. For a matrix D, D∗ denotes the conjugate, DT and DH account for transpose and conjugate transpose, respectively, [D]i,k is the ith row and the kth column element in matrix D, Di,· is the elements of the ith row in D. ∥D∥F accounts for the Frobenius norm, \(\phantom {\dot {i}\!}[\textbf {u}]^{(l_{2})}\) stands for a vector u whose ith entries equals to the l2-norm of its ith row. IM denotes an M×M identity matrix. ΠM accounts for the M×M exchange matrix with elements 1s in its anti-diagonal and zeros elsewhere, and diag(u) represents a diagonal matrix, whose diagonal elements consist of the vector u.

2 System model and problem description

2.1 System model

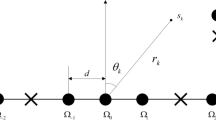
Consider an uniform linear array (ULA) with M isotropic elements, whose inter-element space is half-wavelength d=λ/2 and λ accounts for the carrier wavelength. K independent far-field narrowband sources impinge on the ULA sk(t) from the distinct directions θ1,θ2,⋯,θK, as depicted in Fig. 1. Therefore, the received signal array vector y(t) is given by

$$ \textbf{y}(t) =\sum\limits_{k = 1}^{K} {\textbf{a}(\theta_{k})} {\textbf{s}_{k}}(t)+ \textbf{n}(t) = {\textbf{A}(\pmb \theta)\textbf{s}}(t) + \textbf{n}(t), $$
(1)
Fig. 1
figure 1

Uniform linear array model

Full size image

in which A(θ)=[a(θ1),a(θ2),⋯,a(θK)] represents array manifold matrix with M×K dimension, and \(\textbf {a}(\theta _{k})=\left [1,e^{j 2{\pi } \frac {d}{\lambda }\sin (\theta _{k}) },\cdots,e^{j2{\pi }(M-1) \frac {d}{\lambda }\sin (\theta _{k})}\right ]^{T}\) accounts for an array steering vector with M×1 dimension, s(t)=[s1(t),⋯,sK(t)]T is the non-circular incident signal vector with M×1 dimension, and \(\textbf {n}(t)=[n_{1}(t),n_{2}(t),\cdots,n_{M}(t)]^{T} \in \mathbb {C}^{M \times 1} \) is the additive noise vector, whose entries follow the circularly symmetric complex Gaussian distribution (CSCG) with zero mean and variance \(\sigma _{n}^{2}\) [23–25].

For convenience, the sign t is omitted and N snapshots are collected, then the model of (1) can be expressed as a matrix form, which holds that

$$ \textbf{Y} = {\textbf{A}(\boldsymbol{\theta})\textbf{S}} + \textbf{N}, $$
(2)

in which Y=[y(1),⋯,y(N)] is a received matrix of K×N dimension, and the source symbol matrix S and the noise matrix N are defined the same way as Y.

When the received signal is a strictly second-order non-circular signal, the complex symbol amplitudes of each received signal locate on a rotated line in the complex plane. According to this property, the signal S is denoted as an array form as follows:

$$ \textbf{S}= {\boldsymbol{\Phi}}(\boldsymbol{\phi})\textbf{S}_{r}, $$
(3)

where Sr accounts for a real-valued symbol vector of K×1 dimension, and \(\pmb \Phi = \text {diag}\left \{ \left [e^{j\phi _{1}},e^{j\phi _{2}},\cdots,e^{j\phi _{K}}\right ]\right \}\), ϕk∈[0∘,180∘], and ϕ is the complex phase shift, called non-circular phase [26, 27]. Here, we just consider the strictly second-order non-circular signal case with the non-circular phase is zero.

2.2 Problem description

The conventional SSR-based algorithm for source localization depends on the array model in (2). In order to describe the DoA estimation problem through a sparse representation framework, an over-complete dictionary \( \textbf {A} (\tilde {\pmb \theta })\) with the M×P dimension needs to be constructed by discretizing the spatial angle range [−90∘,90∘] at the angular grid \( \tilde {\pmb \theta } = \left [{\tilde \theta }_{1}, {\tilde \theta }_{2},\cdots,{\tilde \theta }_{P} \right ]^{T}\), P is the number of atoms in dictionary. Assuming that the angle grid point is dense enough, in general P≫K, such that the true angle exactly lies in each grid. Then, the P×N dimensional row-sparse signal matrix \( \tilde {\textbf {S}} =[\tilde {\textbf {s}}_{1}, {\tilde {\textbf {s}}}_{2},\cdots, {\tilde {\textbf {s}}}_{P}]^{T}\) can be defined as:

$$ { \textbf{s}}_{k}^{T}= \left\{ \begin{array}{ll} \tilde{\textbf{s}}_{p}^{T} \quad &~~~~~~\text{if}~ \: \theta_{k} = \tilde \theta_{p} \\ 0 \quad & ~~~~~~\text{otherwise} \end{array}\right., $$
(4)

where the kth row corresponds to the signal comes from a source at \( {\tilde \theta }_{k} \). Obviously, when the rows of \(\tilde {\textbf {S}}\) are non-zero elements, the real DoA information can be attained. The system model in (2) can be formulated as a sparse representation problem

$$ \textbf{Y} = \textbf{A}(\tilde{{\theta}})\tilde{\textbf{S}} + \textbf{N}. $$
(5)

Under the sparse representation framework, the matrix \(\tilde {\textbf {S}}\) in (5) can be solved by using the sparse constrained minimization problem, which satisfied the following expression

$$ \begin{aligned} \underset{\tilde {\textbf{S}}} {\text{min}} \left\| \tilde {\textbf{S}} \right\|_{2,0} \; \textrm{s.t.} \; \|\textbf{Y} - \textbf{A}\left(\tilde \theta\right) \tilde {\textbf{S}} \|_{F}^{2}< \eta^{2} \end{aligned}, $$
(6)

where

$$ \|\textbf{X}\|_{2,0} \triangleq \sum_{l=1}^{L}{\delta}(\|\textbf{X}_{i,\cdot}\|_{2}>0), $$
(7)

and δ(∥Xi,·∥2>0) is an indication function,

$$ {\delta}(x) = \left\{ \begin{array}{ll} 1 \quad &~~~~~~\text{if}~ \: x>0 \\ 0 \quad & ~~~~~~\text{otherwise} \end{array}\right., $$
(8)

η is an error fitting bound and \(\eta ^{2} \geq \| \textbf {N} \|_{F}^{2}\). Here, we select the upper value of ∥N∥2 with a 99% confidence interval as the value of η.

Unfortunately, the problem in (6) is an NP-hard problem and the optimal solution can be found only with an exponential complexity. However, we can arrive at a suboptimal solution through a simpler way, by using a convex relaxation technique, which replaces the l2,0 norm by its closest convex surrogate l2,1 norm. In this case, (6) can be transformed to

$$ \begin{aligned} \underset{\tilde {\textbf{S}}} {\text{min}} \left\| \tilde {\textbf{S}} \right\|_{2,1} \; \textrm{s.t.} \; \|\textbf{Y} - \textbf{A}\left(\tilde \theta\right) \tilde {\textbf{S}} \|_{F}^{2}< \eta^{2} \end{aligned}, $$
(9)

where

$$ \|\textbf{X}\|_{2,1}\triangleq \sum_{l=1}^{L}\left(\sum_{k=1}^{K}|[\textbf{X}]_{l,k}|^{2}\right)^{\frac{1}{2}}, $$
(10)

This is a l2,1 mixed-norm which defined by the Eq. (10). The problem in (9) can be solved through standard convex optimization techniques.

Nevertheless, the SSR-based DoA algorithm in (10) does not take into account the non-circular property of the signal. It is necessary to make a deeper study on how to effectively exploit the statistic property of the sources to improve the estimation performance of the SSR-based DoA algorithm.

3 The proposed algorithm

In this section, we present a SSR-based DoA estimation algorithm which is based on weighted mixed-norm minimization. The algorithm mainly include three steps: the first step is augmenting array matrix and spatial smoothing processing, the second step is real-value matrix transformation and reducing the dimension of the matrix via SVD, and the last step is utilizing the weighted mixed-norm minimization to estimate the DoAs.

3.1 Augmented array aperture and spatial smoothing processing

In order to take full use of non-circular property of signal sources, we stack the received measurement matrix of the array and its complex conjugate counterpart and construct an augmented matrix \(\textbf {Y}^{(nc)}\in \mathbb {C}^{2M\times N}\) as:

$$ \begin{aligned} \textbf{Y}^{(nc)} &=\left[ \begin{array}{c} \textbf{Y}\\ \mathbf{\Pi}_{M}\textbf{Y}^{\ast} \end{array} \right]\\ &=\left[ \begin{array}{cl} \textbf{A}(\theta){\pmb \Phi}(\phi)\\ \mathbf{\Pi}_{M} \textbf{A}^{\ast}(\theta){{\pmb \Phi}}^{\ast}(\phi) \end{array} \right] {\textbf{S}_{0}}+\left[ \begin{array}{l} \textbf{N}\\ {{\pmb \Pi}}_{M} \textbf{N}^{\ast} \end{array}\right] \end{aligned}, $$
(11)

which can be simplified as

$$ \textbf{Y}^{(nc)} =\textbf{A}^{(nc)}(\theta,\phi)\textbf{S}_{0} +\textbf{N}^{(nc)}. $$
(12)

Under the above consideration, we consider the first element on the left of the array as the phase reference. According to the center-symmetric characteristic of the ULAs [28], it holds that

$$ \boldsymbol{\Pi}_{M} \textbf{A}^{\ast} = \textbf{A} {\Delta}_{\textbf{A}}, $$
(13)

where ΔA accounts for a unitary diagonal matrix, which is related to the phase reference of the array, whose non-zero elements consist of the last row of A. Combined with the formula (13), the array manifold matrix of augmented array can be further simplified as

$$ \textbf{A}^{(nc)}(\theta,\phi) =\left[ \begin{array}{cl} \textbf{A}(\theta){ \pmb \Phi}(\pmb \phi)\\ {\textbf{A}}(\theta) {\Delta}_{\textbf{A}} {{\pmb \Phi}}^{\ast}(\pmb \phi) \end{array} \right]. $$
(14)

Herein, we consider the case that the non-circular phase is zero, then (14) can be converted to

$$ \textbf{B}^{(nc)}(\theta) =\left[ \begin{array}{c} \textbf{A}(\theta)\\ {\textbf{A}}(\theta) {\Delta}_{\textbf{A}} \end{array} \right], $$
(15)

and (12) can be represented as:

$$ {\textbf{Y}}^{(nc)} =\textbf{B}^{(nc)}(\theta)\tilde{\textbf{S}}_{0}+\textbf{N}^{(nc)}. $$
(16)

We observe that the B(nc)(θ) has the center-symmetric characteristic, so B(nc)(θ) holds that

$$ {\boldsymbol{\Pi}}_{2M} {\textbf{B}^{(nc)}}^{\ast} = \textbf{B}^{(nc)} {\boldsymbol{\Delta}}_{\textbf{B}^{(nc)}}, $$
(17)

in which ΔB is a unitary diagonal matrix, in which the definition is the same as the definition of ΔA.

Furthermore, incorporating the spatial smoothing technique and with the help of identical formula in (17), the new measurement Y(nc) can be converted to a centro-Hermitian matrix \({\textbf {Z}}\in \mathbb {C}^{2M\times 2N}\) as:

$$ \begin{aligned} \textbf{Z} = \left[\textbf{Y}^{(nc)},\boldsymbol{\Pi}_{2M}{\textbf{Y}^{(nc)}}^{\ast}\boldsymbol{\Pi}_{T}\right] =\textbf{B}^{(nc)}\hat{\textbf{S}}_{0}+\hat{\textbf{N}}^{(nc)}, \end{aligned} $$
(18)

where

$$ \hat{\textbf{S}}_{0}=\left[\tilde{\textbf{S}}_{0},{\pmb \Delta}_{\textbf{B}^{(nc)}} \tilde{\textbf{S}}_{0}^{\ast}{{\Pi}}_{T}\right], $$
(19)

and

$$ \hat{\textbf{N}}^{(nc)}=\left[\textbf{N}^{(nc)},{\pmb\Pi}_{2M}{\textbf{N}^{(nc)}}^{\ast}{{\Pi}}_{T}\right]. $$
(20)

3.2 Unitary transformation and SVD

Aiming to reduce the computation complexity, we will utilize the centro-Hermitian of Z to convert the complex data to real data by unitary transformation. The received real-data matrix can be constructed as:

$$ \textbf{Z}^{r} \triangleq \textbf{Q}_{2M}^{H} \textbf{Z} \textbf{Q}_{2T}=\textbf{Q}_{2M}^{H}\left(\textbf{B}^{(nc)}\hat{\textbf{S}}_{0}+\hat{\textbf{N}}^{(nc)}\right)\textbf{Q}_{2T}. $$
(21)

Here, we define the even-order unitary matrix as

$$ \textbf{Q}_{2n}=\frac{1}{\sqrt{2}}\left[ \begin{array}{cl} \textbf{I}_{n} & j \textbf{I}_{n}\\ {{\pmb \Pi}}_{n} & j{{\Pi}}_{n} \end{array} \right]. $$
(22)

It is worth noting that the matrix \(\textbf {Z}^{r} \in \mathbb {R}^{{2M} \times K}\) is the real-value matrix due to the centro-Hermitian property of the matrix Z, whose unitary transformation is real matrix.

Furthermore, in order to derive a reduced 2M×K dimensional signal space, we represent the dominant component by using the K largest singular vectors of the matrix Zr, which is corresponding to the signal subspace. We perform SVD operation on the matrix Zr results to

$$ \textbf{Z}^{r} = \textbf{U}{\pmb \Sigma}\textbf{V}^{H} = [\textbf{U}_{s}, \textbf{U}_{n}]{\pmb \Sigma} [\textbf{V}_{s}, \textbf{V}_{n}]^{H}, $$
(23)

where Σ is singular value matrix with the dimension the 2M×N, U and V are called left and right singular vector matrix for Zr, respectively, which are the orthogonal matrixes. The singular vectors of matrix U corresponding to non-zero singular value form the signal subspace Us. Ideally, the number of non-zero singular value of matrix Zr is K. The 2M−K singular vectors of matrix U corresponding to the smaller singular values form the noise subspace Un.

Let

$$ \textbf{Z}_{SV} = \textbf{U}{\pmb \Sigma} \textbf{D}_{K} = \textbf{Z}^{r} \textbf{V} \textbf{D}_{K} =\textbf{Z}^{r} \textbf{V}_{s}, $$
(24)

where DK=[IK,0]T with IK being the identity matrix of K×K dimension and 0 being the zero matrix of K×(N−K) dimension. Also, we define \(\textbf {S}_{SV} =\hat {\textbf {S}}_{0}\textbf {Q}_{2T} \textbf {V}_{s}\) and \(\textbf {N}_{SV} =\textbf {Q}_{2M}^{H} {\textbf {N}^{(nc)}}\textbf {Q}_{2T} \hat {\textbf {V}}_{s}\); we can obtain

$$ \textbf{Z}_{SV}= \textbf{Q}_{2M}^{H} \textbf{B}^{(nc)} \textbf{S}_{SV} + \textbf{N}_{SV}. $$
(25)

Now, we can apply the sparse recovery framework to this model that reduces the dimension of the equation.

3.3 DoA estimation based on weighted mixed-norm minimization

The same as the discussion in Section 2.2, the array manifold dictionary \( D_{\bar {\theta }} =\left [\textbf {B}^{(nc)}\left (\bar {\theta }_{1}\right),\cdots, \textbf {B}^{(nc)}\left (\bar {\theta }_{L}\right)\right ]\) can be constructed by extending the B(nc)(θ) on spatial angular grid \(\left \{\bar {\theta }_{1},\bar {\theta }_{l},\cdots, \bar {\theta }_{L}\right \}\: (L \gg K)\). Now, the DoA estimation can be reformulated as a sparse signal recovery problem:

$$ \begin{aligned} \underset{\hat{\textbf{S}}_{SV}} {\text{min}} &\ \left\| \hat{\textbf{S}}_{SV} \right\|_{2,1} \; \\ \textrm{s.t.} &\; \|\textbf{Z}_{SV} - \textbf{D}^{(nc)} \hat{\textbf{S}}_{SV} \|_{F}^{2}< \beta^{2} \end{aligned}, $$
(26)

where \(\textbf {D}^{(nc)} = \textbf {Q}_{2M}^{H} \textbf {D}\), β is a new error fitting bound, \(\beta ^{2} \geq \|\hat {\textbf {N}}_{SV} \|_{F}^{2}\) which can be determined distribution with χ2 degrees of freedom 2M×K and 99% probability [17].

As mentioned above, the l2,1 norm is used in (26) as an approximation to l2,0 norm; therefore, the solution is suboptimal. In order to increase the accuracy of this solution, we adopt the subspace-weighted strategy. Specifically, in D(nc), there are K steering vectors which corresponded to the actual targets. Based on the orthogonality between the steering vector D(nc) and the noise subspace Un, for the true target DoA, θk holds that \( \left [{\textbf {D}^{(nc)}}^{H} \textbf {U}_{n} \right ]^{l_{2}} \rightarrow 0\) when N→∞. Then, the weighted vector is given by:

$$ \textbf{w}=\frac{\left[{ \textbf{D}^{(nc)}}^{H} \textbf{U}_{n}\right]^{(l_{2})} }{\max \left\{\left[{ \textbf{D}^{(nc)}}^{H} {\textbf{U}}_{N}\right]^{(l_{2})}\right\}}. $$
(27)

Also, the vector w can be divided into the following two parts:

$$ \textbf{w}= \left(\begin{array}{c} \textbf{w}^{s}\\ \textbf{w}^{n}\\ \end{array} \right), $$
(28)

where ws corresponds to the true DoAs, and wn consists of the remaining elements of w. The reweighted vector can be written as w=[w1,w2,⋯,w2M]T, with wi being the reweighted coefficient, and i=1,2,⋯,2M. The values in ws and wn satisfy ws(k)→0 and 0<wn(j)≤1, respectively, and ws(k)<wn(j).

Now, we can formulate a new weighted l2,1 mixed-norm minimization for the DoA estimation as:

$$ \begin{aligned} \underset{\hat{\textbf{S}}_{SV}} {\text{min}} &\ \left \| \hat{\textbf{S}}_{SV} \right \|_{\textbf{w};2,1} \\ \textrm{s.t.} &\ \|\textbf{Z}_{SV} - \textbf{D}^{(nc)} \hat{\textbf{S}}_{SV} \|_{F}^{2}< \beta^{2} \end{aligned}, $$
(29)

where

$$ \|\textbf{X}\|_{\textbf{w};2,1}\triangleq \sum_{l=1}^{L}{{ w}_{l}}\left(\sum_{k=1}^{K}|[\textbf{X}]_{l,k}|^{2}\right)^{\frac{1}{2}}, $$
(30)

wl accounts for the lth element of w. It is worth noting that (29) is treated as a second-order cone program (SOCP) problem, which is efficiently checked by utilizing standard software packages, as the CVX [29], which is used in this paper.

Once we attain the estimation of \(\hat {\textbf {S}}_{SV}\), the spatial spectrum can be caculated by averaging the rows of \(\hat {\textbf {S}}_{SV}\) (i.e., the solution of (29))

$$ \hat{p}_{l}=\frac{1}{K}\sum_{k=1}^{K}\left|\left[\hat{\textbf{S}}_{SV}\right]_{l,k}\right|^{2}. $$
(31)

The angular information \(\hat {\boldsymbol {\theta }}\) can be estimated by searching the non-zero rows of \(\hat {\textbf {S}}_{SV}\), which corresponding to the K peaks of \(\hat {\textbf {p}}\). The proposed algorithm is summarized in Algorithm 1.

3.4 Computational complexity analysis

For the subspace-based algorithm, the computational complexity of MUSIC is \(\mathcal {O}\left (M^{2} N +M^{2} L\right)\), whose main computational cost is the spectral search. The computational complexity of NC-MUSIC is \(\mathcal {O}\left (4M^{2} N + 16M^{3} -4M^{2} K + 4\left (M^{2} + 2M\right)L^{2}\right)\). For the l1-SVD algorithm, from the conclusion in [17], we know that the main computational cost is the sparse recovery process, which solves (9) via the SOCP, the computational complexity of is \(\mathcal {O}(K L)^{3}\). For the SW- l2,1-SVD algorithm, we consider the computation cost in the formulation of the weighted matrix w, which requires \( \mathcal {O}\left (M^{2} N + M^{3} + L M(M-K)\right)\). We note that the l1-SVD algorithm is realized that complex multiplication costs four times as much as that of real multiplication [12]; in the proposed algorithm, we transform the complex-valued problem into a real-valued one by the real-valued transformation, and the computational complexity is reduced by a quarter, which means that the computational cost of the sparse recovery process in (29) can be decreased as \(\mathcal {O}\left (\frac {1}{4} K L\right)^{3}\). In the proposed algorithm, we also use the weighted strategy; due to aperture expansion, the computation cost of the formulation of the weighted matrix w requires \( \mathcal {O}((2M)^{2} N + (2M)^{3} + 2LM(2M-K))\). In Table 1, we have given the computational complexity of the subspace-based algorithm and the sparse-based algorithm. From Table 1, we observe that the computational complexity of the proposed algorithm is lower than other sparse-based algorithms. Although the proposed algorithm is higher than the subspace-based algorithms, it can work in the small-size snapshots and the underdetermined case.

Table 1 Computational complexity
Full size table

4 Experimental simulations and discussion

This section provides the Monte-Carlo simulations to validate the efficiency of the subspace-weighted mixed-norm algorithm and further compares the performance with the MUSIC [4], NC-MUSIC [9], l1-SVD [17], and SW- l2,1-SVD [18]. Experimental simulations are performed by Intel(R) Core(TM) i7-7700 CPU @ 3.60 GHz, RAM 8G, MATLAB 2017a.

In simulations, an ULA with number M=10 of isotropic sensors is considered, and the inter-element spacing is half-wavelength. The non-circular signal is BPSK modulation signal. For each snapshot and individual signal at the sensor, the input SNR is defined as \(\textrm {SNR}= 10\log _{10} \left ({ \|\textbf {S}\|_{F}^{2}} /{ \| \textbf {N}\|_{F}^{2}}\ \right)\). In all algorithm, the angle grid is uniform which divided from − 90 to 90∘ with step interval 0.1∘. Unless otherwise specified, N=200 snapshots are collected.

To evaluate the DOA estimation performance, we use the root-mean-square error (RMSE) as the performance indicator, which is defined as:

$$\small {\textrm{RMSE}}= \sqrt{\frac{1}{Q}\sum\limits_{q=1}^{Q}{\sum\limits_{k=1}^{K}{\| \hat{\theta}_{i}-\theta_{i}\|}}}, $$
(32)

where \(\hat {\theta }_{i}\) and θi represent the estimated and true DoA of the ith signal in the qth trial, respectively. Q accounts for the number of Monte-Carlo trials. All simulation results derived through Q=500 Monte-Carlo trials.

We evaluate the DoA estimation performance of the proposed algorithm in the underdetermined case. In this simulation, 11 far-field narrowband BPSK signals uniformly distribute between − 55 to 55∘. The SNR is fixed to 0 dB. From Fig. 2, it can be seen that the proposed algorithm can work well in underdetermined DOA estimation, i.e., the proposed algorithm is capable of handling more sources than sensors. In general, we assume that the number of sources is smaller than the number of sensors in the subspace-based algorithms. When the number of sensors is M, the subspace-based algorithm at most identifies the M- 1 source, that is incapable of resolving more sources than sensors. From Fig. 2, we can conclude that the proposed algorithm presents better performance when the number of sources is greater than the number of sensors. The reason is that the proposed algorithm does not only increase the degree of freedom by exploiting the non-circular property of the signal source, but also employ the weighted scheme which utilizes the relationship of the noise subspace and array manifold dictionary and further enhances the reliability of the sparse DoA estimation.

Fig. 2
figure 2

Spatial spectral for NC-MUSIC, NC- l2,1-SVD, and the proposed algorithm

Full size image

Figure 3 shows the RMSE of DoA estimation against the SNR for different algorithms. Three uncorrelated narrowband BPSK-modulated signals impinge on the ULA from [ − 10∘, 0∘, 8∘]. From Fig. 3, it is observed that the proposed algorithm provides the optimal performance for the DoA estimation compared with the other algorithms since the proposed algorithm takes full advantage of the DoF of augmented array, which benefit from non-circular signal, and the proposed algorithm exploits the forward/backward spatial smoothing to improve the robust of the algorithm. We also observe that the proposed algorithm outperforms than SW- l1-SVD when the SNR is less than 0 dB; the reason for the improvement of the DoA estimation is benefited from the aperture extension and subspace weighting.

Fig. 3
figure 3

RMSEs of MUSIC, NC-MUSIC, l1−SVD, SW−l2,1−SVD, and the proposed method as a function of SNR in the Gaussian white noise for N=200

Full size image

Figure 4 shows the RMSE versus the snapshots with the different algorithms. Three uncorrelated narrowband BPSK-modulated signals are located [ − 10∘, 0∘, 8∘]. The SNR is fixed to 0 dB, and we vary the number of snapshots from 20 to 200 with the step interval 20. From Fig. 4, it can be seen that the proposed algorithm achieves better performance of angle estimation compared to other algorithms for all snapshots, even in the small-size snapshot case. This indicates that the proposed algorithm improves the DoA estimation performance for different snapshots.

Fig. 4
figure 4

RMSEs of MUSIC, NC-MUSIC, l1−SVD, SW−l2,1−SVD, and the proposed method as a function of the snapshots for SNR=0 dB

Full size image

Figure 5 depicts the RMSE of DoA estimation performance as a function of the angular separation between two targets. Two uncorrelated equal power BPSK sources is located at θ1=−10∘ and θ1=−10∘+△θ, where △θ varies from 2 to 20∘. From Fig. 5, it is shown that the performance of DoA estimation is improved with the angular separation larger compared to MUSIC, NC-MUSIC, l1-SVD, and SW- l2,1-SVD. For closely space targets, the proposed algorithm has the minimum RMSE, which indicates that the proposed algorithm can achieve higher spatial angle resolution than the other algorithms.

Fig. 5
figure 5

RMSEs of MUSIC, NC-MUSIC, l1−SVD, SW−l2,1−SVD, and the proposed method as a function of the angular separation between two source for SNR=0 dB and N=200

Full size image

Figure 6 displays the RMSE of DoA estimation performance as a function of correlation coefficient, where two correlated narrowband BPSK-modulated signals are located [ − 10∘, 8∘], the SNR is fixed to 0 dB, and the snapshot number is 100. As we can see from Fig. 6, the proposed method exhibits the best estimation performance among all the algorithms. The performance of the subspace-based algorithms, such as MUSIC and NC-MUSIC, are degrading with the correlation coefficient increasing; the performance of the other sparse-based algorithms like the l1-SVD and SW- l2,1-SVD also are affected by correlation coefficient, but the performance of the sparse-based algorithms are better than that of the subspace-based algorithms. As indicated in Fig. 6, the proposed algorithm have the best estimation performance among all the algorithms. The reason is that the proposed algorithm utilizes the spatial-smoothing process to mitigate the impact of correlated source; in addition, the sparse-based algorithm also is robust to the correlated source.

Fig. 6
figure 6

RMSE versus the correlation coefficient with the SNR=0 dB, N=100

Full size image

5 Methods

A weighted subspace mixed-norm minimization DoA estimation algorithm is proposed for strictly non-circular signal source. The proposed algorithm employs the non-circular property of signal source to extend the array aperture. Then, the spatial smoothing technique and the unitary transformation are implemented to handle the correlate source and convert the complex value matrix to real-value matrix. Furthermore, reducing the matrix dimension process is employed by SVD. In the end, the DoA estimation formulated a weighted subspace mix-norm minimization problem. The SOCP is employed to solve the convex optimization problem.

6 Conclusions

A super-resolution SSR-based DoA estimation algorithm was proposed for strictly non-circular sources in this paper, which is based on weighted subspace mixed-norm minimization. The proposed algorithm increased the degree of array freedom by exploiting the non-circular property of the signal, transformed the array data to real-value domain by utilizing the centro-Hermitian of the augmented matrix, and reduced the dimension of matrix by SVD operation which effectively lower the computational complexity. Last but not the least, we exploited the weighted strategy to enhance the liability of the sparse DoA estimation. The results showed that the proposed algorithm achieved the optimal performance of DoA estimation in the angular resolution and estimation accuracy and can well work in the underdetermined case. In the future, we will incorporate some other wireless communication techniques such as [30–34] to further improve the performance of the 5G mobile communication system.