Abstract
The detection of a known signal with unknown parameters in the presence of noise plus interferences (called total noise) whose covariance matrix is unknown is an important problem which has received much attention these last decades for applications such as radar, satellite localization or time acquisition in radio communications. However, most of the available receivers assume a second order (SO) circular (or proper) total noise and become suboptimal in the presence of SO noncircular (or improper) interferences, potentially present in the previous applications. The scarce available receivers which take the potential SO noncircularity of the total noise into account have been developed under the restrictive condition of a known signal with known parameters or under the assumption of a random signal. For this reason, following a generalized likelihood ratio test (GLRT) approach, the purpose of this paper is to introduce and to analyze the performance of different array receivers for the detection of a known signal, with different sets of unknown parameters, corrupted by an unknown noncircular total noise. To simplify the study, we limit the analysis to rectilinear known useful signals for which the baseband signal is real, which concerns many applications.
Similar content being viewed by others
I. Introduction
The detection of a known signal with unknown parameters in the presence of noise plus interferences (called total noise in the following), whose covariance matrix is unknown, is a problem that has received much attention these last decades for applications such as time or code acquisition in radio communications networks, time of arrival estimation in satellite location systems or target detection in radar and sonar.
Among the detectors currently available, a spatio-temporal adaptive detector which uses the sample covariance matrix estimate from secondary (signal free) data vectors is proposed in [1] and [2] by Brennan, Reed and Mallett. This detector is modified in [3] by Robey et al to derive a constant false-alarm rate test called the adaptive matched filter (AMF) detector, well suited for radar applications. In [4] the previous problem is reconsidered by Kelly as a binary hypothesis test: total noise only versus signal plus total noise. The Kelly's detector uses the maximum likelihood (ML) approach to estimate the unknown parameters of the likelihood ratio test, namely the total noise covariance matrix and the complex amplitude of the useful signal. This detection scheme is commonly referred to as the GLRT [5]. Extensions of the Kelly's GLRT approach assuming that no signal free data vectors are available are presented in [6] and [7] for radar and GPS applications respectively. In [8], Brennan and Reed propose a minimum mean square error detector for time acquisition purposes in the context of multiusers DS-CDMA radio communications networks. This problem is then reconsidered in [9] by Duglos and Scholtz from a GLRT approach under a Gaussian noise assumption and assuming the total noise covariance matrix and the useful propagation channel are two unknown parameters. The advantages of this detector are presented in [6] in a radar context, with regard to structured detectors that exploit an a priori information about the spatial signature of the targets.
Nevertheless, all the previous detectors assume implicitly or explicitly a second order (SO) circular [10] (or proper [11]) total noise and become suboptimal in the presence of SO noncircular (or improper [12]) interferences, which may be potentially present in radio communications, localization and radar contexts. Indeed, many modulated interferences share this feature, for example, Amplitude Modulated (AM), Amplitude Phase Shift Keying (ASK), Binary Phase Shift Keying (BPSK), Rectangular Quadrature Amplitude Modulated, offset QAM, Minimum Shift Keying (MSK) or Gaussian MSK (GMSK) [13] interferences. For this reason, the problem of optimal detection of a signal corrupted by SO noncircular total noise has received an increasing attention this last decade. In particular, a matched filtering approach in SO noncircular total noise is presented in [14] and [12] for radar and radio communications respectively, but under the restrictive assumption of a completely known signal. Alternative approaches, developed under the same restrictive assumptions, are presented in [16] and [15] using a deflection criterion and the LRT respectively. In [17] the problem of optimal detection in SO noncircular total noise is investigated but under the assumption of a noncircular random signal. In [18] a GLRT approach is also proposed to detect the noncircular character of the observations and its performance is studied in [19].
However, despite these works, the major issue of practical use consisting in detecting a known signal with unknown parameters in the presence of an arbitrary unknown SO noncircular total noise has been scarcely investigated up to now. To the best of our knowledge, it has only been analyzed recently in [20] and [21] for synchronization and time acquisition purposes in radio communications networks, assuming a BPSK, MSK or GMSK useful signal and both unknown total noise and unknown useful propagation channel. For this reason, to fill the gap previously mentioned and following a GLRT approach, the purpose of this paper is to introduce and to analyze the performance of different array receivers, associated with different sets of unknown signal parameters, for the detection of a known signal corrupted by an unknown SO noncircular total noise. To simplify the analysis, only rectilinear known useful signals are considered, i.e. useful signals whose complex envelope is real such as AM, PPM, ASK or BPSK signals, also called one dimensional signals. This assumption is not so restrictive since rectilinear signals, and BPSK signals in particular, are currently used in a large number of practical applications such as DS-CDMA radio communications networks, GNSS system [22], some IFF systems or some specific radar systems which use binary coding signal [23]. For such known waveforms, the new detectors introduced in this paper implement optimal widely linear (WL) [24] filters contrary to the detectors proposed in [1, 3, 4, 6–9] and [25] which are deduced from optimal linear filters.
Section II introduces some hypotheses, data statistics and the problem formulation. In section III, the optimal receiver for the detection of a known rectilinear signal with known parameters corrupted by a SO noncircular total noise is presented as a reference receiver, jointly with some of its performance. Various extensions of this optimal receiver, assuming different sets of unknown signal's parameters, are presented in sections IV and V from a GLRT approach for known and unknown signal steering vector, respectively. Performance of all the developed receivers are compared to each other in section VI through computer simulations, displaying, in the detection process, the great interest to take the potential noncircular feature of the total noise into account. Finally section VII concludes the paper. Note that most of the results of the paper have been patented in [20] and [26], whereas some results of the paper have been partially presented in [27] and theoretical statistical performances of some receivers have been studied in [28].
II. Hypotheses and problem formulation
A. Hypotheses
We consider an array of N Narrow-Band sensors receiving the contribution of a known rectilinear signal and a total noise composed of some potentially SO noncircular interferences and a background noise. We assume that the known rectilinear signal corresponds to a linearly modulated digital signal containing K known symbols and whose complex envelope can be written as
where the known transmitted symbols, a n (0 ≤ n ≤ K - 1) are real and deterministic, T is the symbol duration and v(t) is a real-valued pulse shaped filter verifying the Nyquist condition, i.e., such that r(nT) = v(t) ⊗ v(-t)*/ t = nT = 0 for n ≠ 0, where ⊗ is the convolution operation. The signal s(t) may correspond to the synchronization preamble of a radio communications link. For example, each burst of the military 4285 HF standard is composed of a synchronization sequence containing K = 80 known BPSK symbols, 3 × 16 known BPSK symbols for Doppler tracking and 4 × 32 QPSK information symbols. The filter v(t) corresponds to a raise cosine pulse shape filter with a roll off equal to 0.25 or 0.3. The signal s(t) may also correspond to the PN code transmitted by one satellite of a GNSS system where, in this case and as shown in Appendix A, a n and T correspond to the transmitted chips and chip duration respectively whereas v(t) is a rectangular pulse of duration T. Finally, although model (1) is generally not valid for conventional radar applications, it holds for some specific radar applications such as secondary surveillance radar (SSR), currently used for air traffic control surveillance and called Identification Friend and Foes (IFF) systems in the military domain. For example for the standardized S-mode of such systems, the signal transmitted by a target for its identification is a PPM signal which has the form (1) where v(t) is a rectangular pulse of duration T and where a n = 0 or 1. Other specific active radars transmit a series of N pulses such that each pulse is a known binary sequence (a n = ±1) of 13 chips (K = 13) corresponding to a Barker code, whereas v(t) is a rectangular pulse of duration T.
For a non frequency selective propagation channel (airborne applications for example), after a frequency offset compensation, the vector of complex envelopes of the signals at the output of the sensors is a scaled, delayed, noisy and multidimensional version of s(t) given by
where t is the propagation delay, is the zero mean total noise vector, μ s and ϕ s are real parameters controlling the amplitude and phase of the received known signal on the first sensor respectively and s is the steering vector of the known signal, such that its first component is real. For a frequency selective propagation channel, some other scaled and delayed versions of the signal, corresponding to propagation multipaths, are also received by the array but may be inserted in as our goal is to detect one main path. We deduce from (2) the following time-advanced model
from which we wish to detect s(t). To do so, using the fact that it is sufficient, under mild assumptions about the noise, to work at the symbol rate after the matched filtering operation by v(-t)*, where * is the complex conjugation operation, the sampled observation vector x v (nT) at the output of v(-t)* can be written as
where b Tv (nT) is the zero mean sampled total noise vector at the output of v(-t)*, which is assumed to be uncorrelated with a n .
B. Second order statistics of the data
The SO statistics of the data considered in the following correspond to the first and second correlation matrices of x v (nT), defined by R x (nT) ≜ E[x v (nT)x v (nT)H] and C x (nT) ≜ E[x v (nT)x v (nT)T] respectively, where T and H correspond to the transposition and transposition conjugation operation respectively. Under the assumptions of section II-A, R x (nT) and C x (nT) can be written as
where is the instantaneous power of the useful signal which should be received by an omnidirectional sensor of gain unity; R(nT) ≜ E[b Tv (nT)b Tv (nT)H] and C(nT) ≜ E[b Tv (nT)b Tv (nT)T] are the first and second correlation matrices of b Tv (nT) respectively. Note that C(nT) = 0 ∀n for a SO circular total noise vector and that the previous statistics depend on the time parameter since both the known signal (rectilinear) and the interferences (potentially digitally modulated) are not stationary.
C. Problem formulation
We consider the detection problem with two hypotheses H0 and H1, where H0 and H1 correspond to the presence of total noise only and signal plus total noise in the observation vector respectively. This problem is well-suited not only for radar applications but also for synchronization or time acquisition purposes in radio communications or in GNSS systems. Indeed, for such applications, the problem may be formulated either as a time of arrival estimation problem from observations or as a detection problem of the training sequence (radio communications) or of the spreading code (GNSS) from time advanced observations, as explained in [21]. Under these two hypotheses and (4), the observation vector x v (nT) can be written as:
The problem addressed in this paper then consists in detecting, from a GLRT approach, the known symbols or chips a n (0 ≤ n ≤ K - 1), from the observation vectors x v (nT) (0 ≤ n ≤ K - 1), for different sets of unknown parameters, assuming the total noise b Tv (nT) is potentially SO noncircular. More precisely, we assume that each of the parameters μ s , ϕ s , s, R(nT) and C(nT) may be either known or unknown, depending on the application. We first address the unrealistic case of completely known parameters in section III, while the cases of practical interest corresponding to some unknown parameters are addressed in sections IV and V from a GLRT approach. To compute all these receivers, some theoretical assumptions, which are not necessary verified and which are not required in practical situations, are made. These assumptions are not so restrictive in the sense that GLRT-based receivers derived under these assumptions still provide good detection performance even if most of the latter are not verified in practice. These theoretical assumptions correspond to
A.1: the samples b Tv (nT), 0 ≤ n ≤ K - 1, are zero mean, statistically independent, noncircular and jointly Gaussian
A.2: the matrices R(nT) and C(nT) do not depend on the symbol indice n
A.3: the samples b Tv (nT) and a m are uncorrelated ∀n, m.
The statistical independence of the samples b Tv (nT) requires in particular propagation channels with no delay spread and may be verified for temporally white interferences. The Gaussian assumption is a theoretical assumption allowing to only exploit the SO statistics of the observations from a LRT or a GLRT approach whatever the statistics of interference, Gaussian or not. The noncircular assumption is true in the presence of SO noncircular interferences but is generally not exploited in detection problems up to now. Assumption A.2 is true for cyclostationary interferences with symbol period T. Finally A.3 is verified in particular for a useful propagation channel with no delay spread. It is also verified for a propagation channel with delay spread for which the main path is the useful signal whereas the others, sufficiently delayed, are included in b Tv (nT).
III. Optimal receiver for known parameters
A. Optimal receiver
In order to compute the optimal detector of a known signal in a SO noncircular and Gaussian total noise, and also to obtain a reference receiver for the following sections, we consider in this section that parameters μ s , ϕ s , s, R(nT) and C(nT) are known. According to the statistical theory of detection [29], the optimal receiver for the detection of symbols a n from x v (nT) over the known signal duration is the LRT receiver. It consists in comparing to a threshold the function LR(x v , K) defined by
where p[x v (nT), 0 ≤ n ≤ K - 1, /H i ] (i = 0, 1) is the probability density of [x v (0), x v (T), .., x v ((K - 1)T)] under H i . Using (7) into (8), we get
Under A.1 the probability density of b Tv (nT) becomes a function of , given by [30, 31]
where det(A) means determinant of A and where is defined by
where R ≜ R(nT) and C ≜ C(nT). Note that the matrix contains the information about the SO noncircularity of the total noise through the matrix C, which is not null for SO noncircular total noise. From expression (10) and assumptions A.1 and A.2, using the fact that and taking the logarithm of (9), it is easy to verify that a sufficient statistic for the previous detection problem consists in comparing to a threshold the function OPT1(x v , K) defined by
In (12), and the vector is the (2N × 1) vector defined by
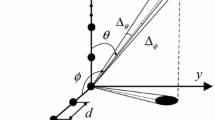
where . Vector is the so-called WL Spatial Matched Filter (SMF) [32], i.e., the WL filter which maximizes the output signal to interference plus noise ratio (SINR), whose output is a real quantity and is defined by (13) where has been replaced by y1,o(nT). Expression (14) then corresponds to the correlation of the WL SMF's output, y1,o(nT), with the known real symbols, a n , over the known signal duration, as depicted in the following Figure 1
In the particular case of a SO circular total noise (C = 0), the receiver OPT1(x v , K) reduces to the conventional one [25] defined by
where is the conventional SMF, , , , and are defined by (13) where has been replaced by x v (nT), y1,c(nT) and z1,c(nT) respectively. Expression (12) then corresponds to the correlation of the real part, z1,c(nT), of the SMF's output, y1,c(nT), with the known real symbols, a n , over the known signal duration.
B. Performance
The performance of OPT1 and CONV1 receivers are computed in terms of detection probability of the known symbols a n (0 ≤ n ≤ K - 1) for a given false alarm rate (FAR), where the FAR corresponds to the probability that OPT1(x v , K) or CONV1(x v , K) gets beyond the threshold under H0 respectively. The FAR and detection probability are computed analytically in [29] for the CONV1 receiver under the assumption of a Gaussian and circular total noise. However, in situations of practical interests which are considered in this paper, the total noise is generally neither Gaussian nor SO circular and the results of [29] are no longer valid. Nevertheless, if K does not get too small, we deduce from A.1 and the central limit theorem that the contribution of the total noise in both (12) and (14) is not far from being Gaussian. This means that the detection probability of the known signal by OPT1 and CONV1 receivers are not far from being directly related to the SINR at the output of these receivers, noted and respectively. Otherwise, this detection probability is no longer a direct function of the SINR but should still increase with the SINR. Substituting (7) into (12), we obtain
If we assume that A.1, A.2 and A.3 are verified, , which is the ratio between the expected value of the square modulus of the two terms of the right hand side of expression (15), is given by
where is the time average, over the known signal duration, of the useful signal input power received by an omnidirectional sensor and is the SINR at the output of the SMF In a similar way, it is straightforward to show that is given by
that is to say
where SINR c is the SINR at the output of the real part of the SMF w1,c. Note that for a SO circular total noise (C = 0), SINR o = SINR c = 2π s sHR-1s and we get
Computation and comparison of SINR o and SINR c are done in [32] in the presence of one rectilinear interference plus background noise and is not reported here. This comparison displays in particular the great interest of taking the SO noncircularity of the total noise into account in the receiver's computation as well as the capability of the optimal receiver to perform, in this case, single antenna interference cancellation (SAIC) of a rectilinear interference by exploiting the phase diversity between the sources. Illustrations of CONV1 and OPT1 receiver performance are presented in section VI.
IV. GLRT receivers for a known signal steering vector
In most of situations of practical interest, the parameters μ s , ϕ s , R(nT) and C(nT) are unknown while, for some applications, the steering vector s is known. This is in particular the case for radar applications for which a Doppler and a range processing currently take place at the output of a beam, which is mechanically or electronically steered in a given direction and scanned to monitor all the directions of space. In this case, the steering vector s is associated with the current direction of the beam. Another example corresponds to satellite localization for which the satellite positions are known and the vector s may be associated, in this case, with the direction of one of the satellites. Moreover, in some cases, some signal free observation vectors (called secondary observation vectors) sharing the same total noise SO statistics are available in addition to the observation vectors containing the signal to be detected plus the total noise (called primary observation vectors). For example the secondary observation vectors may correspond to samples of data associated with another range than the range of the detected target in radar or to observations in the absence of useful signal. In such situations, we will say that a total noise alone reference (TNAR) is available. In other applications, a TNAR is difficult to built, due for example to the total noise potential nonstationarity or to the presence of multipaths. For all the reasons previously described, following a GLRT approach, we introduce in sections IV-A, IV-B and IV-C several new receivers for the detection of a known real-valued signal, with different sets of unknown parameters, corrupted by a SO noncircular total noise. More precisely, these receivers assume that the parameters μ s and ϕ s are unknown, the vector s is known and the matrices R(nT ) and C(nT) are either known (section IV-A) or unknown, assuming (section IV-B) or not (section IV-C) that a TNAR is available in this latter case.
A. Unknown parameters (μ s , ϕ s ) and known total noise (R, C)
Under the assumptions A.1 and A.2, assuming known parameters R, C and s and unknown parameters μ s and ϕ s , the GLRT-based receiver for the detection of the known real-valued symbols a n (0 ≤ n ≤ K - 1) in the SO noncircular total noise characterized by R and C is given by (9) where is defined by (10) and where have to be replaced in (9) by its ML estimate. Under the previous assumptions, it is shown in Appendix B that the ML estimate, , of the (2 × 1) vector is given by
where is defined by (13) and S is the (2N × 2) matrix defined by
Inserting (20) into (9), we obtain a sufficient statistic for the previous detection problem, which is given by
In the particular case of a SO circular total noise (C = 0), we easily verify that (22) reduces to the sufficient statistic, CONV2(x v , K), found in [3] and defined by
which is proportional to the square modulus of the correlation between the SMF's output, y1,c(nT), and the known real-valued symbols, a n , over the known signal duration.
B. Unknown parameters (μ s , ϕ s ) and total noise (R, C) with a TNAR
We assume in this section that s is known, parameters μ s , ϕ s , R and C are unknown and that a TNAR is available. We denote by b Tv (nT)' (0 ≤ n ≤ K' - 1) the K' samples of the secondary data, which contain the total noise only such that R(nT)' ≜ E[b Tv (nT)'b Tv (nT)'H] = R(nT) and C(nT)' ≜ E[b Tv (nT)'b Tv (nT)'T] = C(nT). Under both this assumption and A.1, A.2, matrices R and C may be estimated either from the secondary data only or from both the primary and the secondary data, which gives rise to two different receivers.
1) Total noise estimation from secondary data only
When the matrices R and C are estimated from the secondary data only, assuming K' ≥ 2N (to ensure the invertibility of (24)) and the samples b Tv (nT)' (0 ≤ n ≤ K' - 1) also verify assumptions A.1 and A.2, the ML estimate of is given by
where . In these conditions, following a GLRT approach, we deduce from (20) that the ML estimate, , of the vector is given by
and using (25) into (9), we deduce that a sufficient statistic for the previous detection problem is given by
In the particular case of a SO circular total noise (C = 0), whose SO circularity is a priori known or assumed, (26) reduces to the well-known AMF detector, described in [3] and defined by
where is defined by (24) but with b Tv (nT)' instead of .
2) Total noise estimation from both primary and secondary data
When the matrices R and C are estimated from both the K primary and the K' secondary data, and assuming that the samples b Tv (nT)' (0 ≤ n ≤ K' - 1) also verify assumptions A.1, A.2 and K + K' ≥ 2N (to ensure the invertibility of (28) and (29)), it is shown in Appendix C that the ML estimates, and of under H0 and H1 respectively are given by
and
respectively. In these conditions, following a GLRT approach, the ML estimate, of the vector is shown in Appendix C to be given by
Using (30) into (9), we deduce that a sufficient statistic for the previous detection problem is shown in Appendix C to be given by
In the particular case of a SO circular total noise (C = 0), whose SO circularity is a priori known or assumed, (31) reduces to the conventional statistic defined by
where is defined by
Note that for K = 1 and assuming K' ≥ 2N, expression (31) reduces, after some elementary algebraic manipulations, to the following expression
where is defined by (24) with b Tv (nT)' instead of . Expression (34) is nothing else than the Kelly's detector [4], whose extensions to an arbitrary number of primary samples are given by (32) for a SO circular total noise and by (31) for both a SO noncircular total noise and a real-valued signal to be detected. Note finally that for a very large number of secondary snapshots (K' → ∞), (28) becomes equivalent to (24) and receiver (31) reduces to (26).
C. Unknown parameters (μ s , ϕ s ) and total noise (R, C) without a TNAR
We assume in this section that s is known, parameters μ s , ϕ s , R and C are unknown and that a TNAR is not available. Under both these assumptions and A.1, A.2, matrices R and C may be estimated from the K primary data only, assuming that K ≥ 2N (to ensure the invertibility of the estimated matrices). The ML estimates, and , of under H0 and H1 respectively are then given by (28) and (29) respectively for K' = 0. We then obtain
and
In these conditions, following a GLRT approach, the ML estimate, , of the vector is given by (30) for K' = 0 and can be written as
Using (37) into (9), we deduce that a sufficient statistic for the previous detection problem is given by (31) for K' = 0 and can be written as
In the particular case of a SO circular total noise (C = 0), whose SO circularity is a priori known or assumed, (38) reduces to the conventional detector described in [[6], rel.16] and defined by
where is defined by (35) with x v (nT) instead of . Note that when K becomes very large (K → ∞), (38) and (39) also correspond to (31) and (32) respectively. Moreover, for a very weak desired signal and (SINR o ≪ 1), defined by (24) with K and instead of K' and , defined by (24) with K and b Tv (nT) instead of K' and , and . We then deduce that (38) and (39) reduce to (26) and (27) respectively.
V. GLRT receiver for an unknown signal steering vector
In some situations of practical interest such as in radio communications, the steering vector s is often unknown jointly with the parameters μ s , ϕ s , R(nT) and C(nT). Moreover, in some cases, some signal free observation vectors (secondary observation vectors) sharing the same total noise SO statistics are still available in addition to the primary observation vectors and may correspond to samples of data associated with adjacent channels, adjacent time slots or guard intervals. For these reasons, we introduce in sections V-A, V-B and V-C several new receivers for the detection of a known real-valued signal, with different sets of unknown parameters and whose steering vector is unknown, corrupted by a SO noncircular total noise.
A. Unknown parameters (μ s , ϕ s , s) and known total noise (R, C)
Under the assumptions A.1 to A.4, assuming known parameters R, C and unknown parameters μ s , ϕ s , and s, the GLRT-based receiver for the detection of the known real symbols a n (0 ≤ n ≤ K - 1) in the SO noncircular total noise characterized by R and C, is given by (9) where is defined by (10). Defining the unknown desired channel vector h s by , the unknown extended (2N × 1) desired channel vector has to be replaced by its ML estimate. Under the previous assumptions, it is shown in Appendix D that the ML estimate, of is given by
Inserting (40) into (9), we obtain a sufficient statistic for the previous detection problem, given by
In the particular case of a SO circular total noise (C = 0), we easily verify that (41) reduces to the sufficient statistic, CONV6(x v , K), defined by
B. Unknown parameters (μ s , ϕ s , s) and total noise (R, C) with a TNAR
We assume in this section that parameters μ s , ϕ s , R, C and s are unknown but that a TNAR is available. We note b Tv (nT)' (0 ≤ n ≤ K' - 1) the K' samples of the secondary data, which only contain the total noise such that R(nT)' ≜ E[b Tv (nT)'b Tv (nT)'H] = R(nT) and C(nT)' ≜ E[b Tv (nT)'b Tv (nT)'T] = C(nT).
1) Total noise estimation from secondary data only
When the matrices R and C are estimated from the secondary data only and assuming that the samples b Tv (nT)' (0 ≤ n ≤ K' - 1) also verify assumptions A.1, A.2 and K + K' ≥ 2N, the ML estimate, of is given by (24) while the ML estimate, of is still given by (40). Using (24) and (40) into (9), we deduce that a sufficient statistic for the previous detection problem is given by
In the particular case of a SO circular total noise (C = 0), whose SO circularity is a priori known or assumed, (43) reduces to the detector defined by
where is defined by (24) but with b Tv (nT)' instead of .
2) Total noise estimation from both primary and secondary data
When the matrices R and C are estimated from both the K primary and the K' secondary data, and assuming that the samples b Tv (nT)' (0 ≤ n ≤ K' - 1) also verify assumptions A.1, A.2 and K + K' ≥ 2N, it has been shown in Appendix C that the ML estimates, and of under H0 and H1 respectively are given by (28) and (29) respectively, while the ML estimate, of is still given by (40). Using (28), (29) and (40) into (9), it is shown in Appendix E that a sufficient statistic for the previous detection problem is given by
In the particular case of a SO circular total noise (C = 0), whose SO circularity is a priori known or assumed, (45) reduces to the following detector
where is defined by (33). Note finally that for a very large number of secondary snapshots (K' → ∞), (45) becomes equivalent to (43) and receiver (46) reduces to (44).
C. Unknown parameters (μ s , ϕ s , s) and total noise (R, C) without a TNAR
We assume in this section that parameters μ s , ϕ s , R, C and s are unknown and that no TNAR is available. Under both these assumptions and A.1, A.2, matrices R and C may be estimated from the K primary data only, assuming that K ≥ 2N. The ML estimates, and of under H0 and H1 respectively are then given by (28) and (29) respectively for K' = 0, while the ML estimate, of is still given by (40). Using (28), (29) and (40) into (9), we deduce from (45) that a sufficient statistic for the previous detection problem is given by
which corresponds to the detector introduced in [20] and [21] for synchronization purposes in SO noncircular context. In the particular case of a SO circular total noise (C = 0), whose SO circularity is a priori known or assumed, (47) reduces to the following detector
which is nothing else than the detector introduced in [8] and [9] for synchronization purposes in SO circular contexts. Note finally that for very large values of K (K → ∞), (47) becomes equivalent to (45) and receiver (48) reduces to (46).
VI. Performances of receivers in the presence of so noncircular interferences
A. Total noise model
To be able to quantify and to compare the performance of the previous receivers, we assume in this section that the propagation channels have no delay spread and that the total noise, b Tv (kT), is composed of P interferences, potentially SO noncircular, plus a background noise. Under these assumptions, the vector b Tv (kT) can be written as
where b v (kT) is the zero mean sampled noise vector at the output of v(-t)*, which is assumed to be SO circular, spatially white and uncorrelated with the interferences; jp,v(kT) is the sampled complex envelope (or base band signal) of the interference p after the matched filtering operation, which is assumed to be uncorrelated with jq,v(kT) for q ≠ p; ϕ p and j p are respectively the carrier phase (on the first sensor) and the steering vector of the interference p, such that its first component is real-valued. Under these assumptions, the matrices R(kT) and C(kT), defined in section II-B, can be written as
where η2 is the mean power of the background noise per sensor; I is the (N × N) identity matrix; π p (kT) ≜ E[|jp,v(kT)|2] is the instantaneous power of the interference p at the output of the filter v(-t)* received by an omnidirectional sensor for a free space propagation; c p (kT) ≜ E[jp,v(kT)2] characterizes the SO noncircularity of the interference p. In particular, c p (kT) = π p (kT) for a BPSK interference p, whereas c p (kT) = 0 for a QPSK interference p.
B. Computer simulations
1) Hypotheses
To facilitate the analysis of the computer simulations presented in this section, all the introduced receivers are summarized in Table 1 with their name, their hypotheses and the associated unknown parameters they estimate. On the other hand, to illustrate the performance of the previous detectors, we consider a radio communication link for which a training sequence of K known symbols is transmitted at each burst. The BPSK useful signal is assumed to be corrupted by either one or two synchronous interferences, either BPSK or QPSK, sharing the same symbol duration and pulse shape filter as the desired signal. We consider a linear array of N omnidirectional sensors equispaced half a wavelength apart. The phase ϕ s and the direction of arrival θ s , with respect to broadside, of the desired signal are assumed to be constant over a burst. The same assumptions hold for the interference p (1 ≤ p ≤ 2) for which the phase and direction of arrival are denoted by ϕ p and θ p respectively. The input SNR is defined by SNR = π s /η2, whereas the input Interference to Noise Ratio of the interference p is defined by INR p = π p /η2 where π p = π p (kT). The performance of the previous detectors are computed in terms of Probability of Detection (P D ) of the known useful signal as a function of either its input SNR or the Probability of False Alarm (P FA ). The P D and the P FA are the probability that the considered detector gets beyond the threshold under H1 and H0 respectively. For a given detector and a given scenario, the threshold is directly related to the P FA and is computed by Monte Carlo simulations. For the simulations, the P D is computed from 100 000 bursts. When a TNAR is available, K' = K.
2) Scenarios with P= 1 interference
We first consider scenarios for which the phase and direction of arrival of the sources are constant over all the bursts, the total noise is composed of P = 1 BPSK interference plus a background noise and K = 16. The BPSK desired signal has a phase ϕ s = 0° and a direction of arrival θ s = 0° whereas the interference has a direction of arrival θ1 = 20° and an input INR such that INR = SNR + 15 dB. Under the previous assumptions, Figures 2 and 3 show the variations of the P D at the output of both the 9 optimal detectors and the 9 conventional detectors considered in this paper, as a function of the input SNR of the desired signal for a P FA equal to 0.001. On these figures, to simplify the notations, the optimal and conventional detectors are called O i (dotted lines) and C i (full lines), (1 ≤ i ≤ 9), respectively. For Figures 2a and 2b, the phase of the interference is equal to ϕ s = 15°, whereas for Figures 3a and 3b, ϕ1 = 45°. For Figures 2a and 3a, N = 1, whereas for Figures 2b and 3b, N = 2. Figures 4 and 5 show, under the same assumptions as Figure 2 and 3 respectively, the same variations of P D for the same receivers but as a function of the P FA , i.e., the receiver operating characteristic (COR), for SNR = 0 dB.
Figures 2a, 3a, 4a and 5a show, for N = 1 sensor, the poor detection of the desired signal from all the conventional detectors due to their incapability to reject the strong interference. On the contrary, the optimal detectors, which exploit the SO noncircularity of both the desired signal and the interference, perform SAIC due to the exploitation of the phase diversity between the sources. Note that SAIC is possible since the SO noncircularity of both the desired signal and interference are exploited by the receiver, which is not the case for the WL MVDR beamformer introduced in [33] which does not exploit the SO noncircularity of the desired signal. Comparison of Figures 2a and 3a or 4a and 5a shows increasing performance of the optimal detectors as the phase diversity between the sources increases. In both cases, the O1 detector, which assumes that all the parameters of the sources are known, gives the best performance. In a same way, the O9 detector, which assumes that all the parameters of the sources are unknown, has the lowest performance. Moreover, for a given set of unknown desired signal parameters, the a priori knowledge of the noise statistics (O2 and O6) increases the performance with respect to the absence of knowledge of the latter. In a same way, the knowledge of a TNAR (O3, O4, O7, O8) allows to roughly increase the performance with respect to an absence of TNAR (O5, O9). Finally, counterintuitively, the use of both primary and secondary data for the estimation of the noise correlation matrix (O4, O8) degrades the performance with respect to the use of secondary data only (O3, O7) for this estimation. This is due to the fact that contrary to the LRT receiver which is optimal for detection, GLRT receivers are sub-optimal receivers which generate estimates of the noise covariance matrix with more variance when primary data are used. More precisely, the variance of the noise covariance matrix estimate and then the associated performance degradation increases with an increasing relative weight given to the primary data with respect to secondary data in the linear combination of the two estimates, which explains the result. On the contrary, in such situations, an optimal receiver would necessarily decide to discard the primary data and to keep only the secondary data not to increase the variance of the noise covariance matrix estimate and then not to decrease the performance. However, this optimal process does not correspond to a GLRT receiver and is perhaps to invent. The same reasoning holds for OPT7, OPT8 and OPT9 receivers.
Figures 2b, 3b, 4b and 5b show that, for N = 2 sensors, all the conventional detectors have an increased detection probability with respect to the case N = 1 due to their capability to reject the interference thanks to the spatial discrimination between the sources. Moreover, we note, for a given set of estimated parameters, much better performance of the optimal detectors due to the joint spatial and phase discriminations between the sources. Comparison of Figures 2b and 3b or 4b and 5b shows again increasing performance of the optimal detectors as the phase diversity between the sources increases. We still note the best performance of the completely informed detectors (C1 and O1) and the lowest performance of the less informed detectors (C9 and O9). We note again, for a given set of unknown desired signal parameters, that better performance are obtained when the total noise is either known or estimated from secondary data only. In a same way, the knowledge of a TNAR allows to increase the performance in comparison with an absence of TNAR. Finally, for a given set of total noise parameters, the a priori knowledge of the signal steering vector s increases the performance.
3) Scenarios with P= 2 interferences
We now consider scenarios for which the total noise is composed of P = 2 interferences plus a background noise. The first interference is BPSK modulated with a direction of arrival equal to θ1 = 20°. The second interference is QPSK modulated with a phase and a direction of arrival equal to ϕ2 = 25° and θ2 = 40° respectively. The INR of both interferences is equal to INR = SNR + 15 dB. Under the previous assumptions, Figures 6a and 6b show, for N = 2 and for a P FA equal to 0.001, the variations of the P D at the output of both the 9 optimal detectors and the 9 conventional detectors considered in this paper, as a function of the input SNR of the desired signal, for ϕ1 = 15° and ϕ1 = 45° respectively. Figures 7a and 7b show, under the same assumptions as Figure 6a and 6b respectively, the same variations of the same receivers but as a function of the P FA for SNR = 0 dB.
We note the poor detection of the desired signal from all the conventional detectors compared to the optimal ones, due to their difficulty to reject the two strong interferences since the array is overconstrained (P = N = 2). On the contrary, the optimal detectors, which discriminate the sources by both the direction of arrival and the phase, succeed in rejecting these two interferences since one is rectilinear, which generates a good detection of the desired signal in most cases. More precisely, it has been shown in [33] and [32] that a BPSK source generates only one source in the extended observation vector, while a QPSK source generates two sources. The protection of the desired signal and the rejection of the two interferences then require 1 + 1 + 2 = 4 degrees of freedom, which in fact corresponds to the number of degrees of freedom, 2N = 4, effectively available, hence the result. Comparison of Figures 6a and 6b or 7a and 7b shows again increasing performance of the optimal detectors as the phase diversity between the desired signal and the BPSK interference increases. Again, the O1 detector gives the best performance while the O9 detector gives the lowest ones. Again, the a priori knowledge of the noise statistics or of a TNAR or of the desired signal steering vector allows an increase in performances.
VII. Conclusion
Several new receivers for the detection of a known rectilinear signal, with different sets of unknown parameters, corrupted by SO noncircular interferences have been presented in this paper. It has been shown that taking the potential noncircularity property of the interferences into account may dramatically improve the performance of both mono and multi-sensors receivers, due to the joint exploitation of phase and spatial discrimination between the sources. In particular, the capability of the new detectors to do SAIC of rectilinear interferences, by exploiting the phase diversity between the sources has been verified for all the new detectors. It also puts forward that the more a priori information on the signal, the better the performance.
Appendix A
In this Appendix, we show that the signal transmitted by a GNSS satellite may be written as (1). For GNSS applications, as explained in [7], the signal which is transmitted by a GNSS satellite is a known direct sequence spread-spectrum (SS) signal which can be written as
where a n = ±1, T is the symbol duration and c(t) is the SS code defined by
where T c is the chip duration, SF = T/T c is the spreading factor, u q = ±1 is the chip number q and w(t) is the rectangular pulse of duration T c . Using (A.2) into (A.1), we obtain
Defining l = q + nSF and d l = d(q + nSF) = a n u q , expression (A.3) takes the form
which has the same form as (1) where real-valued symbols a n are replaced by real-valued chips d l (±1), where T is replaced by T c and where K is replaced by K SF - 1. We easily verify that for n ≠ 0.
Appendix B
In this Appendix, we derive expressions (20) and (22) for unknown parameters (μ s , ϕ s ) and known parameters s and . To this aim, we denote as where S is defined by (21) and where . We deduce from (9), (10) and assumptions A.1, A.2 that the ML estimate of under H1 maximizes the Likelihood function given by
Using (10) into (B.1) and taking the Logarithm of , we obtain
The vector which maximizes (B.2) is thus the one which minimizes
which finally corresponds to (20). Using (10) into (9) and taking the Logarithm of (9), we obtain
Using (20) into (B.4), it is straightforward to verify that a sufficient statistics of (B.4) is given by (22).
Appendix C
In this Appendix, we derive expressions (28) to (31) for unknown parameters and a known vector s when is estimated from both K primary and K' secondary observations. We deduce from assumptions A.1 and A.2 that the ML estimate of under H1, from primary and secondary observations, maximizes the Likelihood function
In a similar way, the ML estimate of under H0, from primary and secondary observations, maximizes the Likelihood function
Using (10) into (C.1) and taking the Logarithm of , we obtain
It is well-known [9] that the ML estimate, of under H1, i.e., the matrix which maximizes (C.3) is given by (29). In a similar way, it is straightforward to show that the ML estimate, of under H0 is given by (28). On the other hand, using (29) into (C.3), we obtain under H1
where Tr[A] means Trace of matrix A. In a similar way, we obtain under H0
According to the statistical theory of detection, the optimal receiver for the detection of the K symbols a n from both the K primary data x v (nT) and the K0 secondary data b Tv (nT)' consists in comparing to a threshold the ratio between (C.1) and (C.2). Using (10) into (C.1) and (C.2), replacing by under H1, by under H0 and using (C.4) and (C.5), it is straightforward to show that the previous Likelihood receiver, , takes the form
To compute (C.6), we define the following parameters: , , , , where is the inverse of a square root, of and
Using these notations and from (28) and (29) we obtain
and then
where is an Hermitian matrix such that span {B} = span{u, v} and whose rank is equal to 2. We deduce from (C.9) that
where λ1 and λ2 are the two non zero eigenvalues of B and where Σ ≜ λ1 + λ2 and Π ≜ λ1λ2. Using (C.10) into (C.6) we obtain
A straightforward computation of λ1 and λ2 from B gives
and using the definition of v we obtain
The ML estimate of under H1 maximizes the Likelihood function (C.1) and thus the LR (C.11). It then corresponds to the quantity which minimizes (C.13). Introducing the following parameters: and , where , the vector , which minimizes (C.13) is given by
which also corresponds to (30). Inserting (C.14) into (C.13) we obtain
Applying the matrix inversion lemma to [(α -uHu)A + zzH]-1, we obtain, after straightforward computations
which proves that LR(x v , K) defined by (C.11) is an increasing function of the sufficient statistic which is finally proportional to (31).
Appendix D
In this Appendix, we derive expressions (40) and (41) for unknown parameters (μ s , ϕ s , s) and a known matrix . To this aim, we denote and . We then deduce from assumptions A.1 and A.2 that the ML estimate of under H1 maximizes the Likelihood function given by
Using (10) into (D.1) and taking the Logarithm of , we obtain
The vector which maximizes (D.2) corresponds to (40). Using (10) into (9) and taking the Logarithm of (9), we obtain
Using (40) into (B.4), it is straightforward to verify that a sufficient statistics of (D.3) is given by (41).
Appendix E
In this Appendix, we derive expression (45) for unknown parameters when is estimated from both K primary and K' secondary observations. We deduce from Appendix D and assumptions A.1 and A.2 that the ML estimate of does not depend on the total noise statistics and is still given by (40). Following the same development as the one presented in Appendix C, we deduce that the ML estimate, , of under H1, is given by (29), the ML estimate, , of under H0, is given by (28) and the Likelihood ratio receiver is given by (C.6). Moreover, using the notations introduced in Appendix C, we obtain from (28) and (29)
and we deduce from appendix C that the Likelihood ratio receiver is still given by (C.11) where
Inserting (40) into (E.2) we deduce, after straightforward manipulations, that
which proves that LR(x v , K) defined by (C.11) is an increasing function of the sufficient statistic which is finally proportional to (45).
References
Brennan LE, Reed IS: Theory of adaptive radar. IEEE Trans Aerosp Electronic Systems 1973,9(2):237-252.
Reed IS, Mallet JD, Brennan LE: Rapide convergence rate in adaptive arrays. IEEE Trans Aerosp Electronic Systems 1974,10(6):853-863.
Robey FC, Fuhrmann DR, Kelly EJ, Nitzberg R: A CFAR adaptive matched filter detector. IEEE Trans Aerosp Electronic Systems 1992,28(1):208-216. 10.1109/7.135446
Kelly EJ: An adaptive detection algorithm. IEEE Trans Aerosp Electronic Systems 1986,22(1):115-127.
Mardia KV, Kent JT, Bibby JM: Multivariate analysis. New-York, Academic; 1979.
Swindlehurst AL, Stoica P: Maximum Likelihood methods in radar array signal processing. Proc IEEE 1998,86(2):421-441. 10.1109/5.659495
Seco-Granados G, Fernandez-Rubio JA, Fernandez-Prades C: ML estimator and hybrid beamformer for multipath and interference mitigation in GNSS receivers. IEEE Trans Sign Proc 2005,53(3):1194-1208.
Brennan LE, Reed IS: An adaptive array signal processing algorithm for communications. IEEE Trans Aerosp Electronic Systems 1982,18(1):124-130.
Duglos DM, Scholtz RA: Acquisition of spread spectrum signals by an adaptive array. IEEE Trans Acou Speech Signal Proc 1989,37(8):1253-1270. 10.1109/29.31273
Pincinbono B: On Circularity. IEEE Trans Signal Processing 1994,42(12):3473-3482. 10.1109/78.340781
Neeser FD, Massey L: Proper Complex random processes with applications to information theory. IEEE Trans Information Theory 1993,39(4):1293-1302. 10.1109/18.243446
Yoon YC, Leib H: Maximizing SNR in improper complex noise and applications to CDMA. IEEE Communications Letters 1997,1(1):5-8. 10.1109/4234.552140
Proakis JG: Digital communications. Third edition. McGraw-Hill; 1995.
Brown WM, Crane RB: Conjugate linear filtering. IEEE Trans Information Theory 1969,15(4):462-465. 10.1109/TIT.1969.1054330
Amblard PO, Duvaut P: Filtrage adapté dans le cas gaussien complexe non circulaire. Proc GRETSI Juan-Les-Pins (France) 1995, 141-144.
Picinbono B, Chevalier P: Extensions of the minimum variance method. Signal Processing Elsevier 1996, 49: 1-9.
Schreier PJ, Scharf LL, Mullis CT: Detection and Estimation of improper complex random signals. IEEE Trans on Info Theory 2005,51(1):306-312. 10.1109/TIT.2004.839538
Schreier PJ, Scharf LL, Hanssen A: A Generalized likelihood ratio test for impropriety of complex signals. IEEE Signal Processing Letters 2006,13(7):433-436.
Delmas JP, Oukaci A, Chevalier P: Asymptotic distribution of GLRT improperty of complex signals. Proc ICASSP, Dallas (Texas), USA 2010.
Chevalier P, Pipon F, Delaveau F: Procédé et dispositif de synchronisation de liaisons rectilignes ou quasi-rect. en présence d'interférences de même nature. PatentFR.05.01784 2005.
Chevalier P, Pipon F, Delaveau F: Second-order optimal array receivers for synchronization of BPSK, MSK and GMSK signals corrupted by noncircular interferences. In Eurasip Journal on Advances in Signal Processing (JASP). Volume 2007. Hindawi Publishing Corporation; 2007:Article ID 45605. 16 pages
Braasch MS, Van Dierendonck AJ: GPS receiver architectures and measurements. Proc IEEE 1999,87(1):48-64. 10.1109/5.736341
Deng H: Effective CLEAN algorithms for performance-enhanced detection of binary coding radar signals. IEEE Trans Sign Proc 2004,52(1):72-78. 10.1109/TSP.2003.820075
Picinbono B, Chevalier P: Widely linear estimation with complex data. IEEE Trans Signal Processing 1995,43(8):2030-2033. 10.1109/78.403373
Monzingo RA, Miller TW: Introduction to Adaptive Arrays. John Wiley and Sons; 1980.
Delaveau F, Chevalier P, Pipon F: Procédés et dispositifs pour déterminer la réponse impulsionnelle de canaux de propagation impliquant des émetteurs, des réflecteurs et des capteurs fixes ou mobiles. Patent 07.05772 2007.
Chevalier P, Blin A, Pipon F, Delaveau F: GLRT-Based array receivers to detect a known signal corrupted by noncircular interferences. Proc EUSIPCO, Poznan (Poland) 2007.
Oukaci A, Delmas JP, Chevalier P: Performance analysis of LRT/GLRT-based array receivers for the detection of a known real-valued signal corrupted by noncircular interferences. Signal Processing 2011, 91: 2259-2267. 10.1016/j.sigpro.2011.04.007
Van Trees HL: Detection, Estimation and Modulation Theory - Part I. John Wiley and Sons; 1968.
Picinbono B: Second order complex random vectors and normal distributions. IEEE Trans Signal Processing 1996,44(10):2637-2640. 10.1109/78.539051
Van Den Bos A: The multivariate complex normal distribution - A generalization. IEEE Trans Inform Theory 1995, 41: 537-539. 10.1109/18.370165
Chevalier P, Pipon F: New Insights into optimal widely linear array receivers for the demodulation of BPSK, MSK and GMSK signals corrupted by non circular interferences - Application to SAIC. IEEE Trans Signal Processing 2006,54(3):870-883.
Chevalier P, Blin A: Widely linear MVDR beamformer for the reception of an unknown signal corrupted by noncircular interferences. IEEE Trans Signal Processing 2007,55(11):5323-5336.
Author information
Authors and Affiliations
Corresponding author
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chevalier, P., Oukaci, A. & Delmas, JP. GLRT-based array receivers for the detection of a known signal with unknown parameters corrupted by noncircular interferences. EURASIP J. Adv. Signal Process. 2011, 56 (2011). https://doi.org/10.1186/1687-6180-2011-56
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-6180-2011-56