Abstract
An adaptive example-based super-resolution (SR) using kernel principal component analysis (PCA) with a novel classification approach is presented in this paper. In order to enable estimation of missing high-frequency components for each kind of texture in target low-resolution (LR) images, the proposed method performs clustering of high-resolution (HR) patches clipped from training HR images in advance. Based on two nonlinear eigenspaces, respectively, generated from HR patches and their corresponding low-frequency components in each cluster, an inverse map, which can estimate missing high-frequency components from only the known low-frequency components, is derived. Furthermore, by monitoring errors caused in the above estimation process, the proposed method enables adaptive selection of the optimal cluster for each target local patch, and this corresponds to the novel classification approach in our method. Then, by combining the above two approaches, the proposed method can adaptively estimate the missing high-frequency components, and successful reconstruction of the HR image is realized.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.1 Introduction
In the field of image processing, high-resolution images are needed for various fundamental applications such as surveillance, high-definition TV and medical image processing [1]. However, it is often difficult to capture images with sufficient high resolution (HR) from current image sensors. Thus, methodologies for increasing resolution levels are used to bridge the gap between demands of applications and the limitations of hardware; and such methodologies include image scaling, interpolation, zooming and enlargement.
Traditionally, nearest neighbor, bilinear, bicubic [2], and sinc [3] (Lanczos) approaches have been utilized for enhancing spatial resolutions of low-resolution (LR) images. However, since they do not estimate high-frequency components missed from the original HR images, their results suffer from some blurring. In order to overcome this difficulty, many researchers have proposed super-resolution (SR) methods for estimating the missing high-frequency components, and this enhancement technique has recently been one of the most active research areas [1, 4–7]. Super-resolution refers to the task which generates an HR image from one or more LR images by estimating the high-frequency components while minimizing the effects of aliasing, blurring, and noise. Generally, SR methods are divided into two categories: reconstruction-based and learning-based (example-based) approaches [7, 8]. The reconstruction-based approach tries to recover the HR image from observed multiple LR images. Numerous SR reconstruction methods have been proposed in the literature, and Park et al. provided a good review of them [1]. Most reconstruction-based methods perform registration between LR images based on their motions, followed by restoration for blur and noise removal. On the other hand, in the learning-based approach, the HR image is recovered by utilizing several other images as training data. These motion-free techniques have been adopted by many researchers, and a number of learning-based SR methods have been proposed [9–18]. For example, Freeman et al. proposed example-based SR methods that estimate missing high-frequency components from mid-frequency components of a target image based on Markov networks and provide an HR image [10, 11]. In this paper, we focus on the learning-based SR approach. Conventionally, learning-based SR methods using principal component analysis (PCA) have been proposed for face hallucination [19]. Furthermore, by applying kernel methods to the PCA, Chakrabarti et al. improved the performance of the face hallucination [20] based on the Kernel PCA (KPCA; [21, 22]). Most of these techniques are based on global approaches in the sense that processing is done on the whole of LR images simultaneously. This imposes the constraint that all of the training images should be globally similar, i.e., they should represent a similar class of objects [7, 23, 24]. Therefore, the global approach is suitable for images of a particular class such as face images and fingerprint images. However, since the global approach requires the assumption that all of the training images are in the same class, it is difficult to apply it to arbitrary images.
As a solution to the above problem, several methods based on local approaches in which processing is done for each local patch within target images have recently been proposed [13, 25, 26]. Kim et al. developed a global-based face hallucination method and a local-based SR method of general images by using the KPCA [27]. It should be noted that even if the PCA or KPCA is used in the local approaches, all of the training local patches are not necessarily in the same class, and their eigenspace tends not to be obtained accurately. In addition, Kanemura et al. proposed a framework for expanding a given image based on an interpolator which is trained in advance with training data by using sparse Bayesian estimation [12]. This method is not based on PCA and KPCA, but calculates the Bayes-based interpolator to obtain HR images. In this method, one interpolator is estimated for expanding a target image, and thus, the image should also contain only the same kind of class. Then it is desirable that training local patches are first clustered and the SR is performed for each target local patch using the optimal cluster. Hu et al. adopted the above scheme to realize the reconstruction of HR local patches based on nonlinear eigenspaces obtained from clusters of training local patches by the KPCA [8]. Furthermore, we have also proposed a method for reconstructing missing intensities based on a new classification scheme [28]. This method performs the super-resolution by treating this problem as a missing intensity interpolation problem. Specifically, our previous method introduces two constraints, eigenspaces of HR patches and known intensities, and the iterative projection onto these constraints is performed to estimate HR images based on the interpolation of the missing intensities removed by the subsampling process. Thus, in our previous work, intensities of a target LR image are directly utilized as those of the enlarged result. Thus, if the target LR image is obtained by blurring and subsampling its HR image, the intensities in the estimated HR image contain errors.
In conventional SR methods using the PCA or KPCA, but not including our previous work [28], there have been two issues. First, it is assumed in these methods that the LR patches and their corresponding HR patches that are, respectively, projected onto linear or nonlinear eigenspaces are the same, these eigenspaces being obtained from training HR patches [8, 27]. However, these two are generally different, and there is a tendency for this assumption not to be satisfied. Second, to select optimal training HR patches for target LR patches, distances between their corresponding LR patches are only utilized.
Unfortunately, it is well known that the selected HR patches are not necessarily optimal for the target LR patches, and this problem is known as the outlier problem. This problem has also been reported by Datsenko and Elad [29, 30].
In this paper, we present an adaptive example-based SR method using KPCA with a novel texture classification approach. The proposed method first performs the clustering of training HR patches and generates two nonlinear eigenspaces of HR patches and their corresponding low-frequency components belonging to each cluster by the KPCA.
Furthermore, to avoid the problems of previously reported methods, we introduce two novel approaches into the estimation of missing high-frequency components for the corresponding patches containing low-frequency components obtained from a target LR image: (i) an inverse map, which estimates the missing high-frequency components, is derived from a degradation model of the LR image and the two nonlinear eigenspaces of each cluster and (ii) classification of the target patches is performed by monitoring errors caused in the estimation process of the missing high-frequency components. The first approach is introduced to solve the problem of the assumptions utilized in the previously reported methods. Then, since the proposed method directly derives the inverse map of the missing process of the high-frequency components, we do not rely on their assumptions. The second approach is introduced to solve the outlier problem. Obviously, it is difficult to perfectly perform classification that can avoid this problem as long as the high-frequency components of the target patches are completely unknown. Thus, the proposed method modifies the conventional classification schemes utilizing distances between LR patches directly. Specifically, the error caused in the estimation process of the missing high-frequency components by each cluster is monitored and utilized as a new criterion for performing the classification. This error corresponds to the minimum distance of the estimation result and the known parts of the target patch, and thus we adopt it as the new criterion. Consequently, by the inverse map determined from the nonlinear eigenspaces of the optimal cluster, the missing high-frequency components of the target patches are adaptively estimated. Therefore, successful performance of the SR can be expected. This paper is organized as follows: first, in Section 2, we briefly explain KPCA used in the proposed method. In Section 3, we discuss the formulation model of LR images. In Section 4, the adaptive KPCA-based SR algorithm is presented. In Section 5, the effectiveness of our method is verified by some results of experiments. Concluding remarks are presented in Section 6.
2 Kernel principal component analysis
In this section, we briefly explain KPCA used in the proposed method. KPCA was first introduced by Schölkopf et al. [21, 22], and it is a useful tool for analyzing data which contain nonlinear structures. Given target data x i (i = 1, 2, . . . , N), they are first mapped into a feature space via a nonlinear map: , where M is the dimension of x i .Then we can obtain the data mapped into the feature space, ϕ(x1), ϕ(x2), . . . , ϕ(x N ). For simplifying the following explanation, we assume these data are centered, i.e.,
For performing PCA, the covariance matrix
is calculated, and we have to find eigenvalues λ and eigenvectors u which satisfy
In this paper, vector/matrix transpose in both input and feature spaces is denoted by the superscript '.
Note that the eigenvectors u lie in the span of ϕ(x1), ϕ(x2), . . . , ϕ(x N ), and they can be represented as follows:
where Ξ = [ϕ(x1), ϕ(x2), . . . , ϕ(x N )] and α is an N × 1 vector. Then Equation 3 can be rewritten as follows:
Furthermore, by multiplying Ξ' by both sides, the following equation can be obtained:
Therefore, from Equation 2, R can be represented by , and the above equation is rewritten as
where K = Ξ'Ξ. Finally,
is obtained. By solving the above equation, α can be obtained, and the eigenvectors u can be obtained from Equation 4.
Note that (i, j)th element of K is obtained by ϕ(x i )'ϕ(x j ). In kernel methods, it can be obtained by using kernel trick [21]. Specifically, it can be obtained by some kernel functions κ(x i , x j ) using only x i and x j in the input space.
3 Formulation model of LR images
This section presents the formulation model of LR images in our method. In the common degradation model, an original HR image F is blurred and decimated, and the target LR image including the additive noise is obtained. Then, this degradation model is represented as follows:
where f and F are, respectively, vectors whose elements are the raster-scanned intensities in the LR image f and its corresponding HR image F. Therefore, the dimension of these vectors are, respectively, the number of pixels in f and F. D and B are the decimation and blur matrices, respectively. The vector n is the noise vector, whose dimension is the same as that of f. In this paper, we assume that n is the zero vector in order to make the problem easier. Note that if decimation is performed without any blur, the observed LR image is severely aliased.
Generally, actual LR images captured from commercially available cameras tend to be taken without suffering from aliasing. Thus, we assume that such captured LR images do not contain any aliasing effects. However, it should be noted that for realizing the SR, we can consider several assumptions, and thus, we focus on the following three cases:
Case 1 : LR images are captured based on the low-pass filter followed by the decimation procedure, and any aliasing effects do not occur, where this case corresponds to our assumption. Therefore, we should estimate the missing high-frequency components removed by the low-pass filter.
Case 2 : LR images are captured by only the decimation procedure without using any low-pass filters. In this case, some aliasing effects occur, and interpolation-based methods work better than our method.
Case 3 : LR images are captured based on the low-pass filter followed by the decimation procedure, but some aliasing effects occur. In this case, the problem becomes much more difficult than those of Cases 1 and 2. Furthermore, in our method, it becomes difficult to model this degradation process.
We focus only on Case 1 to realize the SR, but some comparisons between our method and the methods focusing on Case 2 are added in the experiments.
For the following explanation, we clarify the definitions of the following four images:
HR image F whose vector is F in Equation 9 is the original image that we try to estimate.
Blurred HR image whose vector is BF is obtained by applying the low-pass filter to the HR image F. Its size is the same as that of the HR image.
LR image f whose vector is f (= DBF) is obtained by applying the subsampling to the blurred HR image .
High-frequency components whose vector is F - BF are obtained by subtracting BF from F.
Note that the HR image, the blurred HR image, and the high-frequency components have the same size. In order to define the blurred HR image, the LR image, and the high-frequency components, we have to provide which kind of the low-pass filter is utilized for defining the matrix B. Generally, it is difficult to know the details of the low-pass filter and provide the knowledge of the blur matrix B. Therefore, we simply assume that the low-pass filter is fixed to the sinc filter with the hamming window in this paper. In the proposed method, high-frequency components of target images must be estimated from only their low-frequency components and other HR training images. This means when the high-frequency components are perfectly removed, the problem becomes the most difficult and useful for the performance verification. Since it is well known that the sinc filter is suitable one to effectively remove the high-frequency components, we adopted this filter. Furthermore, the sinc filter has infinite length coefficients, and thus we also adopted the hamming window to truncate the filter coefficients. The details of the low-pass filter is shown in Section 5. Since the matrix B is fixed, we discuss the sensitivity of our method to the errors in the matrix B in Section 5.
In the proposed method, we assume that LR images are captured based on the low-pass filter followed by the decimation, and aliasing effects do not occur. Furthermore, the decimation matrix is only an operator which subsamples pixel values. Therefore, when the magnification factor is determined for target LR images, the matrices B and D can be also obtained in our method. Specifically, the decimation matrix D can be easily defined when the magnification factor is determined. In addition, the blurring matrix B is also defined by the sinc function with the hamming window in such a way that target LR images do not suffer from aliasing effects. In this way, the matrices B and D can be defined, but in our method, these matrices are not directly utilized for the reconstruction. The details are shown in the following section.
As shown in Figure 1, by upsampling the target LR image f, we can obtain the blurred HR image . However, it is difficult to reconstruct the original HR image F from since the high-frequency components of F are missed by the blurring. Furthermore, the reconstruction of the HR image becomes more difficult with increase in the amount of blurring [7].
4 KPCA-based adaptive SR algorithm
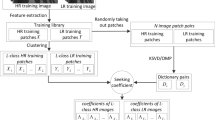
An adaptive SR method based on the KPCA with a novel texture classification approach is presented in this section. Figure 2 shows an outline of our method. First, the proposed method clips local patches from training HR images and performs their clustering based on the KPCA. Then two nonlinear eigenspaces of the HR patches and their corresponding low-frequency components are, respectively, obtained for each cluster. Furthermore, the proposed method clips a local patch from the blurred HR image and estimates its missing high-frequency components using the following novel approaches based on the obtained nonlinear eigenspaces: (i) derivation of an inverse map for estimating the missing high-frequency components of g by the two nonlinear eigenspaces of each cluster, where g is an original HR patch of and (ii) adaptive selection of the optimal cluster for the target local patch based on errors caused in the high-frequency component estimation using the inverse map in (i). As shown in Equation 9, estimation of the HR image is ill posed, and we cannot obtain the inverse map that directly estimates the missing high-frequency components. Therefore, the proposed method models the degradation process in the lower-dimensional nonlinear eigenspaces and enables the derivation of its inverse map. Furthermore, the second approach is necessary to select the optimal nonlinear eigenspaces for the target patch without suffering from the outlier problem. Then, by introducing these two approaches into the estimation of the missing high-frequency components, adaptive reconstruction of HR patches becomes feasible, and successful SR should be achieved.
Outline of the KPCA-based adaptive SR algorithm. The proposed method is composed of two procedures: clustering of training HR patches and estimation of missing high-frequency components of a target image. In the missing high-frequency component estimation algorithm, adaptive selection of the optimal cluster is newly introduced in the proposed method.
In order to realize the adaptive SR algorithm, the training HR patches must first be assigned to several clusters before generating each cluster's nonlinear eigenspaces. Therefore, the clustering method is described in detail in 4.1, and the method for estimating the missing high-frequency components of the target local patches is presented in 4.2.
4.1 Clustering of training HR patches
In this subsection, clustering of training HR patches into K clusters is described. In the proposed method, we calculate a nonlinear eigenspace for each cluster and enable the modeling of the elements belonging to each cluster by its nonlinear eigenspace. Then, based on these nonlinear eigenspaces, the proposed method can perform the clustering of training HR patches in this subsection and the high-frequency component estimation, which simultaneously realizes the classification of target patches for realizing the adaptive reconstruction, in the following subsection. This subsection focuses on the clustering of training HR patches based on the nonlinear eigenspaces.
From one or some training HR images, the proposed method clips local patches g i (i = 1, 2, . . . , N; N being the number of the clipped local patches), whose size is w × h pixels, at the same interval. Next, for each local patch, two images, and , which contain low-frequency and high-frequency components of g i , respectively, are obtained. This means , respectively, correspond to local patches clipped from the same position of (a) HR image, (b) Blurred HR image, and (d) high-frequency components shown in the previous section. Then the two vectors l i and h i containing raster-scanned elements of and , respectively, are calculated. Furthermore, l i is mapped into the feature space via a nonlinear map: [22], where the nonlinear map whose kernel function is the Gaussian kernel is utilized. Specifically, given two vectors a and b (∈ Rwh), the Gaussian kernel function in the proposed method is defined as follows:
where is a parameter of the Gaussian kernel. Then the following equation is satisfied:
Then a new vector ϕ i = [ϕ(l i )', h i ']' is defined. Note that an exact pre-image, which is the inverse mapping from the feature space back to the input space, typically does not exist [31]. Therefore, the estimated pre-image includes some errors. Since the final results estimated in the proposed method are the missing high-frequency components, we do not utilize the nonlinear map for h i (i = 1, 2, . . . , N).
From the obtained results ϕ i (i = 1, 2, . . . , N), the proposed method performs clustering that minimizes the following criterion:
where Nk is the number of elements belonging to cluster k. Generally, superscript is used to indicate the power of a number. However, in this paper, only k does not represent the power of a number. The vectors and (j = 1, 2, . . . , Nk ), respectively, represent l i and h i of g i (i = 1, 2, . . . , N) assigned to cluster k. In Equation 12, the proposed method minimizes C with respect to the belonging cluster number of each local patch g i . Each known local patch belongs to the cluster whose nonlinear eigenspace can perform the most accurate approximation of its low- and high-frequency components. Therefore, using Equation 12, we try to determine the clustering results, i.e., which cluster is the optimal for each known local patch g i .
Note that in Equation 12, and in the input space are, respectively, the results projected onto the nonlinear eigenspace of cluster k. Then, in order to calculate them, we must first obtain the projection result onto the nonlinear eigenspace of cluster k for each . Furthermore, when is defined and its projection result onto the nonlinear eigenspace of cluster k is defined as in the feature space, the following equation is satisfied:
where Ukis an eigenvector matrix of cluster k, and is the mean vector of (j = 1, 2, . . . , Nk ) and is obtained by
In the above equation, ek= [1, 1, . . . , 1]' is an Nk × 1 vector. As described above, is the projection result of onto the nonlinear eigenspace of cluster k, i.e., the approximation result of in the subspace of cluster k. Therefore, Equation 13 represents the projection of j-th element of cluster k onto the nonlinear eigenspace of cluster k. Note that from Equation 13, can be defined as . In detail, corresponds to the projection result of the low-frequency components in the feature space. Furthermore, corresponds to the result of the high-frequency components, and it can be obtained directly. However, in Equation 12 cannot be directly obtained since the projection result is in the feature space. Generally, we have to solve the pre-image estimation problem of from , i.e., , which satisfies , has to be estimated. In this paper, we call this pre-image approximation as [Approximation 1] for the following explanation. Generally, if we perform the pre-image estimation of from , estimation errors occur. In the proposed method, we adopt some useful derivations in the following explanation and enable the calculation of in Equation 12 without directly solving the pre-image problem of .
In the above equation,
is an eigenvector matrix of ΞkHkHkΞk', where Dk is the dimension of the eigenspace of cluster k, and it is set to the value whose cumulative proportion is larger than Th. The value Th is a threshold to determine the dimension of the nonlinear eigenspaces from its cumulative proportion. Furthermore, and Hkis a centering matrix defined as follows:
where Ekis the Nk × Nk identity matrix. The matrix H plays the centralizing role, and it is commonly used in general PCA and KPCA-based methods.
In Equation 15, the eigenvectors are infinite-dimensional since are eigenvectors of the vectors with the infinite dimension. This means that the dimension of the eigenvectors must be the same as that of . Then since is infinite dimensional, the dimension of is also infinite. It should be noted that since there are Dk eigenvectors , these Dk vectors span the nonlinear eigenspace of cluster k. From the above reason, Equation 13, therefore, cannot be calculated directly. Thus, we introduce the computational scheme, kernel trick, into the calculation of Equation 13. The eigenvector matrix Uksatisfies the following singular value decomposition:
where Λkis the eigenvalue matrix and Vkis the eigenvector matrix of HkΞk'ΞkHk. Therefore, Ukcan be obtained as follows:
As described above, the approximation of the matrix Ukis performed. This is a common scheme in KPCA-based methods, where we call this approximation [Approximation 2], hereafter. Since the columns of the matrix Ukare infinite-dimensional, we cannot directly use this matrix for the projection onto the nonlinear eigenspace. Therefore, to solve this problem, the matrix Ukis approximated by Equation 18 for realizing the kernel trick. Note that if Dk becomes the same as the rank of Ξk, the approximation in Equation 18 becomes equivalent relationship.
From Equations 14 and 18, Equation 13 can be rewritten as
where
Next, since we utilize the nonlinear map of the Gaussian kernel, in Equation 12 satisfies
Furthermore, given and , they satisfy . Thus, from Equation 19, in Equation 21 is obtained as follows:
Then, by using Equations 21 and 22, in Equation 12 can be obtained as follows:
Furthermore, since is calculated from Equation 19 as
in Equation 12 is also obtained as follows:
Then, from Equations 23 and 25, the criterion C in Equation 12 can be calculated. It should be noted that for calculating the criterion C, we, respectively, use Approximations 1 and 2 once through Equations 21-25.
In Equation 13, Ukis utilized for the projection onto the eigenspace spanned by their eigenvectors . Therefore, the criterion C represents the sum of the approximation errors of in their eigenspaces. This means that the squared error in Equation 12 corresponds to the distance from the nonlinear eigenspace of each cluster in the input space. Then, the new criterion C is useful for the clustering of training HR local patches. From the clustering results, we can obtain the eigenvector matrix Ukfor belonging to cluster k. Furthermore, we define and also calculate the eigenvector matrix for belonging to cluster k. Finally, we can, respectively, obtain the two nonlinear eigenspaces of HR training patches and their corresponding low-frequency components for each cluster k.
4.2 Adaptive estimation of missing high-frequency components
In this subsection, we present an adaptive estimation of missing high-frequency components based on the KPCA. We, respectively, define the vectors of g and as ϕ* = [ϕ(l)', h']' and in the same way as ϕ i and . From the above definitions, the following equation is satisfied:
where E p × q and O p × q are, respectively, the identity matrix and the zero matrix whose sizes are p × q. Furthermore, D ϕ represents the dimension of the feature space, i.e., infinite dimension in our method. The matrix is the identity matrix whose dimension is the same as that of ϕ(l) and O wh × wh represents the zero matrix which removes the high-frequency components. As shown in the previous section, our method assumes that LR images are obtained by removing their high-frequency components, and aliasing effects do not occur. This means our problem is to estimate the perfectly removed high-frequency components from the known low-frequency components. Therefore, the problem shown in this section is equivalent to Equation 9, and the solution that is consistent with Equation 9 can be obtained.
In Equation 26, since the matrix Σ is singular, we cannot directly calculate its inverse matrix to estimate the missing high-frequency components h and obtain the original HR image. Thus, the proposed method, respectively, maps ϕ* and onto the nonlinear eigenspace of HR patches and that of their low-frequency components in cluster k. Furthermore, the projection corresponding to the inverse matrix of Σ is derived in these subspaces. We show its specific algorithm in the rest of this subsection and its overview is shown in Figure 3.
Overview of the algorithm for estimating missing high-frequency components. The direct estimation of HR patches from their LR patches is infeasible since the matrix Σ is singular and its inverse matrix cannot be obtained. Thus, the proposed method projects those two patches onto the low-dimensional subspaces and enables the derivation of the projection corresponding to the inverse matrix of Σ.
First, the vector ϕ* is projected onto the Dk -dimensional nonlinear eigenspace of cluster k by using the eigenvector matrix Ukas follows:
Furthermore, the vector is also projected onto the Dk -dimensional nonlinear eigenspace of cluster k by using the eigenvector matrix as follows:
where is defined as
and . Furthermore, ϕ* is approximately calculated as follows:
In the above equation, the vector of the original HR patch is approximated in the nonlinear eigenspace of cluster k, where we call this approximation [Approximation 3]. The nonlinear eigenspace of cluster k can perform the least-square approximation of its belonging elements. Therefore, if the target local patch belongs to cluster k, accurate approximation can be realized. Then the proposed method introduces the classification procedures for determining which cluster includes the target local patch in the following explanation. Next, by substituting Equations 26 and 30 into Equation 28, the following equation is obtained:
Thus,
since
The vector corresponds to the mean vector of the vectors whose high-frequency components are removed from . Then
is derived, where .
In Equation 32, if the rank of Σ is larger than Dk , the matrix becomes a non-singular matrix, and its inverse matrix 80can be calculated. In detail, the rank of the matrices and Ukis Dk . Although the rank of Σ is not full and its inverse matrix cannot be directly obtained, the rank of becomes min (Dk , rank(Σ)). Therefore, if rank(Σ) ≥ Dk , can be calculated. Then
Finally, by substituting Equations 27 and 28 into the above equation, the following equation can be obtained:
Then we can calculate an approximation result of ϕ* from cluster k's eigenspace as follows:
Furthermore, in the same way as Equation 19, we can obtain the following equation:
where Tkis calculated as follows:
and is an eigenvector matrix of . Note that the estimation result, which we have to estimate, is the vector h of the unknown high-frequency components. Since Equation 38 is rewritten as
where . Thus, from Equations 14 and 40, the vector hk, which is the estimation result of h by cluster k, is calculated as follows:
Then, by utilizing the nonlinear eigenspace of cluster k, the proposed method can estimate the missing high-frequency components. In this scheme, we, respectively, use Approximations 2 and 3 once through Equations 31-41.
The proposed method enables the calculation of the inverse map which can directly reconstruct the high-frequency components. In the previously reported methods [8, 27], they simply project the known frequency components to the eigenspaces of the HR patches, and their schemes do not correspond to the estimation of the missing high-frequency components. Thus, these methods do not always provide the optimal solutions. On the other hand, the proposed method can provide the optimal estimation results if the target local patches can be represented in the obtained eigenspaces, correctly. This is the biggest difference between our method and the conventional methods.
Furthermore, we analyze our method in detail as follows.
It is well-known that the elements of , which are g i belonging to cluster k, can be correctly approximated in their nonlinear eigenspace in the least-squares sense. Therefore, if we can appropriately classify the target local patch into the optimal cluster from only the known parts , the proposed method successfully estimates the missing high-frequency components h by its nonlinear eigenspace. Unfortunately, if we directly utilize for selecting the optimal cluster, it might be impossible to avoid the outlier problem. Thus, in order to achieve classification of the target local patch without suffering from this problem, the proposed method utilizes the following novel criterion as a substitute for Equation 12:
where lkis a pre-image of . In the above equation, since we utilize the nonlinear map of the Gaussian kernel, ||l - lk||2 is satisfied as follows:
and is calculated from Equations 14 and 40 below.
Then, from Equations 43 and 44, the criterion in Equation 42 can be rewritten as follows:
In this derivation, Approximation 1 is used once. The criterion represents the squared error calculated between the low-frequency components lkreconstructed with the high-frequency components hkby cluster k's nonlinear eigenspace and the known original low-frequency components l.
We introduce the new criterion into the classification of the target local patch as shown in Equations 42 and 45. Equations 42 and 45 utilized in the proposed method represent the errors of the low-frequency components reconstructed with the high-frequency components by Equation 40. In the proposed method, if both of the target low-frequency and high-frequency components are perfectly represented by the nonlinear eigenspaces of cluster k, the approximation relationship in Equation 32 becomes the equal relationship. Therefore, if we can ignore the approximation in Equation 38, the original HR patches can be reconstructed perfectly. In such a case, the errors caused in the low-frequency and high-frequency components become zero. However, if we apply the proposed method to general images, the target low-frequency and high-frequency components cannot perfectly be represented by the nonlinear eigenspaces of one cluster, and the errors are caused in those two components. Specifically, the caused errors are obtained as
from the estimation results. However, we cannot calculate the above equation since the true high-frequency components h are unknown. There will always be a finite value for the last term ||h - hk||2. However, since h is unknown, we cannot know this term, and thus some assumptions become necessary. Thus, we assume that this term is constant, i.e., if we set ||h - hk||2 = 0, the result will not change. Therefore, we set ||h - hk||2 = 0 and calculate the minimum errors of . This means the proposed method utilizes the minimum errors caused in the HR result estimated by the inverse projection which can optimally provide the original image for the elements of each cluster. Then the proposed method utilizes the error in Equation 45 as the criterion for the classification. In the previously reported method based on KPCA [8], they only applied the simple k-means method to the known low-frequency components for the clustering and the classification. Thus, this approach is quite independent of the KPCA-based reconstruction scheme, and there is no guarantee of providing the optimal clustering and classification results. On the other hand, the proposed method derives all of the criteria for the clustering and the classification from the KPCA-based reconstruction scheme. Therefore, it can be expected that this difference between the previously reported method and our method provides a solution to the outlier problem.
From the above explanation, we can see in Equation 45 is a suitable criterion for classifying the target local patch into the optimal cluster kopt. Then, the proposed method regards estimated by the selected cluster kopt as the output, and becomes the estimated vector of the target HR patch g.
As described above, it becomes feasible to reconstruct the HR patches from the optimal cluster in the proposed method. Finally, we clip local patches (w × h pixels) at the same interval from the blurred HR image and reconstruct their corresponding HR patches. Note that each pixel has multiple reconstruction results if the clipping interval is smaller than the size of the local patches. In such a case, the proposed method outputs the result minimizing Equation 45 as the final result. Then, the adaptive SR can be realized by the proposed method.
5 Experimental results
In this section, we verify the performance of the proposed method. As shown in Figures 4a, 5a, and 6a, we prepared three test images Lena, Peppers, and Goldhill utilized in many papers. In order to obtain their LR images shown in Figures 4b, 5b, and 6b, we subsampled them to quarter size by using the sinc filter with the hamming window. Specifically, the filter w(m, n) of size (2L + 1) × (2L + 1) is defined as
Comparison of results (Test image "Lena", 512 × 512 pixels) obtained by using different image enlargement methods. (a) Original HR image. (b) LR image of (a). HR image reconstructed by (c) sinc interpolation, (d) reference [11], (e) reference [27], (f) reference [8], (g) reference [12], (h) reference [28], and (i) the proposed method.
Comparison of results (Test image "Peppers", 512 × 512 pixels) obtained by using different image enlargement methods. (a) Original HR image. (b) LR image of (a). HR image reconstructed by (c) sinc interpolation, (d) reference [11], (e) reference [27], (f) reference [8], (g) reference [12], (h) reference [28], and (i) the proposed method.
Comparison of results (Test image "Goldhill" (512 × 512 pixels) obtained by using different image enlargement methods. (a) Original HR image. (b) LR image of (a). HR image reconstructed by (c) sinc interpolation, (d) reference [11], (e) reference [27], (f) reference [8], (g) reference [12], (h) reference [28], and (i) the proposed method.
where s corresponds to the magnification factor, and we set L = 12. In these figures, we simply enlarged the LR images to the size of the original images. When we estimate an HR result from its LR image, the other two HR images and Boat, Girl, Mandrill are utilized as the training data. In the proposed method, we simply set its parameters as follows: w = 8, h = 8, , , Th = 0.9, is 0.075 times the variance of ||l i - l j ||2 (i, j = 1, 2, . . . , N), and K = 7. Note that the parameters and K seem to affect the performance of the proposed method. Thus, we discuss the determinations of these two parameters and their sensitivities in Appendix. In this experiment, we applied the previously reported methods and the proposed method to Lena, Peppers, and Goldhill and obtained their HR results, where the magnification factor was set to four. For comparison, we adopt the method utilizing the sinc interpolation, which is the same filter used in the downsampling process and the most traditional approach, and three previously reported methods [8, 11, 27]. Since the method in [11] is a representative method of the example-based super-resolution, we utilized this method in the experiment. Furthermore, the method [27] is also a representative method which utilizes KPCA for performing the super-resolution, and its improvement is achieved by utilizing the classification scheme in [8]. Therefore, these two methods are suitable for the comparison to verify the proposed KPCA-based method including the novel classification approach. In addition, the methods in [12, 28] have been proposed for realizing accurate SR. Therefore, since these methods can be regarded as state-of-the-art ones, we also adopted them for comparison of the proposed method.
First, we focus on test image Lena shown in Figure 4. We, respectively, show the HR images estimated by the sinc interpolation, the previously reported methods [8, 11, 12, 27, 28], and the proposed method in Figures 4c-i. In the experiments, the HR images estimated by both of the conventional methods and the proposed method were simply high-boost filtered for better comparison as shown in [27]. From the zoomed portions shown in Figures 7 and 8, we can see that the proposed method preserves the sharpness more successfully than do the previously reported methods. Furthermore, from the other two results shown in Figures 5, 6, and 9, 10, 11, 12, we can see various kinds of images are successfully reconstructed by our method. As shown in Figures 4, 5, 6, 7, 8, 9, 10, 11, 12, Goldhill contains more high-frequency components than the other two test images Lena and Peppers. Therefore, the difference of the performance between the previously reported methods and the proposed method becomes significant.
In the previously reported methods, the obtained HR images tend to be blurred in edge and texture regions. In detail, the proposed method keeps the sharpness in edge regions of test image Lena as shown in Figure 7. Furthermore, in the texture regions which are shown in Figure 8, the difference between the proposed method and the other methods becomes significant. Furthermore, in Figures 9 and 10, the center regions contain more high-frequency components compared with the other regions. Thus, the proposed method successfully reconstructs sharp edges and textures. As described above, test image Goldhill contains more high-frequency components than the other two test images, the difference of our method and the other ones is quite significant. Particularly, in Figure 11, roofs and windows can be successfully reconstructed with keeping sharpness by the proposed method. In addition, in Figure 12, the whole areas can be also accurately enhanced.
Some previously reported methods such as [12, 27] estimate one model for performing the SR. Then, if various kinds of training images are provided, it becomes difficult to successfully estimate the high-frequency components, and the obtained results tend to be blurred. Thus, we have to perform clustering of training patches in advance and reconstruct the high-frequency components by the optimal cluster. However, if the selection of the optimal cluster is not accurate, the estimation of the high-frequency components becomes also difficult. We guess that the limitation of the method in [8] occurs from this reason. The detailed analysis is shown later.
Note that our previously reported method [28] also includes the classification procedures, but its SR approach is different from our approach. This means the method in [28] performs the SR by interpolating new intensities between the intensities of LR images. Thus, the degradation model is different from that of this paper. Thus, it suffers from some degradation. On the other hand, the proposed method realizes the super-resolution by estimating missing high-frequency components removed by the blurring in the downsampling process. In detail, the proposed method derives the inverse projection of the blurring process by using the nonlinear eigenspaces. Since the estimation of the inverse projection for the blurring process is an ill-posed problem, the proposed method performs the approximation of the blurring process in the low-dimensional subspaces, i.e., the nonlinear eigenspaces, and enables the derivation of its inverse projection.
Next, in order to quantitatively verify the performance of the proposed method and the previously reported methods in Figures 4, 5, 6, we show the structural similarity (SSIM) index [32] in Table 1. Unfortunately, it has been reported that the mean squared error (MSE) peak signal-to-noise ratio and its variants may not have a high correlation with visual quality [8, 32–34]. Recent advances in full-reference image quality assessment (IQA) have resulted in the emergence of several powerful perceptual distortion measures that outperform the MSE and its variants. The SSIM index is utilized as a representative measure in many fields of the image processing, and thus, we adopt the SSIM index in this experiment. As shown in Table 1, the proposed method has the highest values for all test images. Therefore, our method realizes successful example-based super-resolution subjectively and quantitatively.
As described above, the MSE cannot reflect perceptual distortions, and its value becomes higher for images altered with some distortions such as mean luminance shift, contrast stretch, spatial shift, spatial scaling, and rotation, etc., yet negligible loss of subjective image quality. Furthermore, blurring severely deteriorates the image quality, but its MSE becomes lower than those of the above alternation. On the other hand, the SSIM index is defined by separately calculating the three similarities in terms of the luminance, variance, and structure, which are derived based on the human visual system (HVS) not accounted for by the MSE. Therefore, it becomes a better quality measure providing a solution to the above problem, and this is also confirmed in several researchers.
We discuss the effectiveness of the proposed method. As explained above, many previously reported methods, which utilize the PCA or KPCA for the SR, assume that LR patches (middle-frequency components) and their corresponding HR patches (high-frequency components) that are, respectively, projected onto linear or nonlinear eigenspaces are the same. However, there is a tendency for this assumption not to be satisfied for general images. On the other hand, the proposed method derives the inverse map, which enables estimation of the missing high-frequency components in the nonlinear eigenspace of each cluster, and solves the conventional problem. Furthermore, the proposed method monitors the error caused in the above high-frequency component estimation process and utilizes it for selecting the optimal cluster. This approach, therefore, solves the outlier problem of the conventional methods. In order to confirm the effectiveness of this novel approach, we show the percentage of target local patches that can be classified into correct clusters. Note that the ground truth can be obtained by using their original HR images. From the obtained results, the previously reported method [8] can correctly classify about 9.29% of the patches and suffers from the outlier problem. On the other hand, the proposed method selects the optimal clusters for all target patches, i.e., we can correctly classify all patches using Equation 45 even if we cannot utilize Equations 12 and 46. Furthermore, we show the results of the classification performed for the three test images in Figures 13, 14, 15. Since the proposed method assigns local images to seven clusters, seven assignment results are shown for each image. In these figures, the white areas represent the areas reconstructed by cluster k (k = 1, 2, . . . , 7). Note that the proposed method performs the estimation of the missing high-frequency components for the overlapped patches, and thus, these figures show the pixels whose high-frequency components are estimated by cluster k minimizing Equation 45. Then the effectiveness of our new approach is verified. Also, in the previously reported method [11], the performance of the SR severely depends on the provided training images, and it tends to suffer from the outline problems. Consequently, by introducing the new approaches into the estimation scheme of the high-frequency components, accurate reconstruction of the HR images can be realized by the proposed method.
Next, we discuss the sensitivity of the proposed method and the previously reported methods to the errors in the matrix B. Specifically, we calculated the LR images using the Haar and Daubechies filters and reconstructed their HR images using the proposed and conventional methods as shown in Figures 16, 17, 18. From the obtained results, it is observed that not only the previously reported methods but also the proposed method is not so sensitive to the errors in the matrix B. In the proposed method, the inverse projection for estimating the missing high-frequency components is obtained without directly using the matrix B. The previously reported methods do not also utilize the matrix B, directly. Then they tend not to suffer from the degradation due to the errors in the matrix B.
HR image reconstructed by the previously reported methods and the proposed method from the LR images obtained by the Haar and Daubechies filters (Test image "Lena"). HR image reconstructed from the LR image obtained by using the Haar filter by (a) reference [11] (SSIM index: 0.7941), (b) reference [27] (SSIM index: 0.8235), (c) reference [8] (SSIM index: 0.8159), (d) reference [12] (SSIM index: 0.8428), (e) reference [28] (SSIM index: 0.8337), and (f) the proposed method (SSIM index: 0.8542). HR image reconstructed from the LR image obtained by using the Daubechies filter by (g) reference [11] (SSIM index: 0.7950), (h) reference [27] (SSIM index: 0.8455), (i) reference [8] (SSIM index: 0.8148), (j) reference [12] (SSIM index: 0.8458), (k) reference [28] (SSIM index: 0.8320), and (l) the proposed method (SSIM index: 0.8508).
Finally, we show some experimental results obtained by applying the previously reported methods and the proposed method to actual LR images captured from a commercially available camera "Canon IXY DIGITAL 50". We, respectively, show two test images in Figures 19a and 20a and their training images in Figures 19b, c and 20b, c. The upper-left and lower-left areas in Figures 19a and 20a, respectively, correspond to the target images, and they were enlarged by the previously reported methods and the proposed method as shown in Figures 21 and 22, where the magnification factor was set to eight. It should be noted that the experiments were performed under the same conditions as those shown in Figures 4, 5, and 6. From the obtained results, we can see that the proposed method also realizes more successful reconstruction of the HR images than those of the previously reported methods. As shown in Figures 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, the difference between the proposed method and the previously reported methods becomes more significant as the amount of the high-frequency components in the target images becomes larger. In detail, regions at sculptures and characters, respectively, shown in Figures 21 and 22 have successfully been reconstructed by the proposed method.
Results obtained by applying the previously reported methods and the proposed method to the actual LR image shown in Figure 19a: (a) LR image. HR image reconstructed by (b) sinc interpolation, (c) reference [11], (d) reference [27], (e) reference [8], (f) reference [12], (g) reference [28], and (h) the proposed method. The magnification factor is set to eight, and the obtained results are 400 × 400 pixels.
Results obtained by applying the previously reported methods and the proposed method to the actual LR image shown in Figure 20a. (a) LR image. HR image reconstructed by (b) sinc interpolation, (c) reference [11], (d) reference [27], (e) reference [8], (f) reference [12], (g) reference [28], and (h) the proposed method. The magnification factor is set to eight, and the obtained results are 400 × 400 pixels.
6 Conclusions
In this paper, we have presented an adaptive SR method based on KPCA with a novel texture classification approach. In order to obtain accurate HR images, the proposed method first performs clustering of the training HR patches and derives an inverse map for estimating the missing high-frequency components from the two nonlinear eigenspaces of training HR patches and their corresponding low-frequency components in each cluster. Furthermore, the adaptive selection approach of the optimal cluster based on the errors caused in the estimation process of the missing high-frequency components enables each HR patch to be reconstructed successfully. Then, by combining the above two approaches, the proposed method realizes adaptive example-based SR. Finally, the improvement of the proposed method over previously reported methods was confirmed.
In the experiments, the parameters of our method were set to simple values from some experiments. These parameters should be adaptively determined from the observed images. Thus, we need to complement this determination algorithm.
Appendix: Determination of parameters
The determination of the parameters utilized in the proposed method is shown. The parameters which seem to affect the performance of the proposed method are and K. Therefore, we change these parameters and discuss the determination of their optimal values and their sensitivities to the proposed method. Specifically, we set to α time the variance of ||l i - l j ||2 (i, j = 1, 2, . . . , N), where α was changed as α = 0.05, 0.075, . . . , 0.2. Furthermore, K was set to K = 4, 5, . . . , 10. In the experiments, the magnification factor was set to two for the simplicity. Figure 23 shows the relationship between , K, and the SSIM index of the reconstruction results for six test images Lena, Peppers, Goldhill, Boat, Gril, and Mandrill. Note that for each test image, the other five HR images were utilized as the training images. The determination of the parameters and K and their sensitivities are shown as follows:
Parameter of the Gaussian kernel
From Figure 23, we can see the SSIM index almost monotonically increases with decreasing . When the parameter of the Gaussian kernel is set to a larger value, the expression ability of local patches tends to become worse. On the other hand, if it is set to a smaller value, the overfitting tends to occur. Therefore, from this figure, we set the parameter of the Gaussian kernel as = 0.075 × the variance of ||l i - l j ||2 since the performance of the proposed method for the three test images tends to become the highest. Note that this parameter is not so sensitive as shown in the results of Figure 23, i.e., the results are not sensitive to the parameter even if we set it to the larger or smaller values.
Number of clusters: K(= 7) From Figure 23, we can see the SSIM index of the proposed method becomes the highest value when K = 7 in several images, and the performance is not severely sensitive to the value of K. The parameter K is the number of clusters, and it should be set to the number of textures contained in the target image. However, since it is difficult to automatically find the number of textures in the target image, we simply set K = 7 in the experiments. The adaptive determination of the number of clusters will be the subject of the subsequent reports.
Abbreviations
- HR:
-
high-resolution
- KPCA:
-
kernel principal component analysis
- LR:
-
low-resolution
- PCA:
-
principal component analysis
- SR:
-
super-resolution.
References
Park SC, Park MK, Kang MG: Super-resolution image reconstruction: A technical overview. IEEE Signal Proces Mag 2003,20(3):21-36. 10.1109/MSP.2003.1203207
Keys R: Cubic convolution interpolation for digital image processing. IEEE Trans Acoust Speech Signal Proces 1981,29(6):1153-1160. 10.1109/TASSP.1981.1163711
Oppenheim AV, Schafer RW: Discrete-Time Signal Processing. 2nd edition. Prentice Hall, New Jersey; 1999.
Baker S, Kanade S, Kanade T: Limits on super-resolution and how to break them. IEEE Trans Pattern Anal Mach Intell 2002,24(9):1167-1183. 10.1109/TPAMI.2002.1033210
Farsiu S, Robinson D, Elad M, Milanfar P: Advances and challenges in super-resolution. Int J Imaging Syst Technol 2004,14(2):47-57. 10.1002/ima.20007
van Ouwerkerk JD: Image super-resolution survey. Image Vis Comput 2006,24(10):1039-1052. 10.1016/j.imavis.2006.02.026
Jiji CV, Chaudhuri S, Chatterjee P: Single frame image super-resolution: should we process locally or globally? Multidimens Syst Signal Process 2007,18(2-3):123-125. 10.1007/s11045-007-0024-1
Hu Y, Shen T, Lam KM, Zhao S: A novel example-based super-resolution approach based on patch classification and the KPCA prior model. Comput Intell Secur 2008, 1: 6-11.
Hertzmann A, Jacobs CE, Oliver BC N, Salesin DH: Image analogies. Comput Graph (Proc Siggraph) 2001, 2001: 327-340.
Freeman WT, Pasztor EC, Carmichael OT: Learning low-level vision. Int J Comput Vis 2000, 40: 25-47. 10.1023/A:1026501619075
Freeman WT, Jones TR, Pasztor EC: Example-based super-resolution. IEEE Comput Graph Appl 2002,22(2):56-65. 10.1109/38.988747
Kanemura A, Maeda S, Ishii S: Sparse Bayesian learning of filters for efficient image expansion. IEEE Trans Image Process 2010,19(6):1480-1490.
Stephenson TA, Chen T: Adaptive Markov random fields for example-based super-resolution of faces. EURASIP J Appl Signal Process 2006, 2006: 225-225.
Wang Q, Tang X, Shum H: Patch based blind image super resolution. Proceedings of ICCV 2005 2005, 1: 709-716.
Li X, Lam KM, Qiu G, Shen L, Wang S: An efficient example-based approach for image super-resolution. Proceedings of ICNNSP 2008, 2008: 575-580.
Sun J, Zheng N, Tao H, Shum H: Image hallucination with primal sketch priors. Proceedings of IEEE CVPR '03 2003, 2: 729-736.
Jiji CV, Joshi MV, Chaudhuri S: Single-frame image super-resolution using learned wavelet coefficients. Int J Imaging Syst Technol 2004,14(3):105-112. 10.1002/ima.20013
Jiji CV, Chaudhuri S: Single-frame image super-resolution through contourlet learning. EURASIP J Appl Signal Process 2006,2006(10):1-11.
Wang X, Trang X: Hallucinating face by eigentransformation. IEEE Trans Syst Man Cybern 2005,35(3):425-434. 10.1109/TSMCC.2005.848171
Chakrabarti A, Rajagopalan AN, Chellappa R: Super-resolution of face images using kernel PCA-based prior. IEEE Trans Multimedia 2007,9(4):888-892.
Schölkopf B, Smola A, Müller KR: Nonlinear principal component analysis as a kernel eigen value problem. Neural Comput 1998, 10: 1299-1319. 10.1162/089976698300017467
Schölkoph B, Mika S, Burges C, Knirsch P, Müller KR, Rätsch G, Smola A: Input space versus feature space in kernel-based methods. IEEE Trans Neural Netw 1999,10(5):1000-1017. 10.1109/72.788641
Chaudhuri S, Joshi MV: Motion-Free Super-Resolution. Springer, New York; 2005.
Turk M, Pentland A: Eigenfaces for recognition. J Cogn Neurosci 1991, 3: 71-86. 10.1162/jocn.1991.3.1.71
Bishop C, Blake A, Marthi B: Super-resolution enhancement of video. In Proceedings of 9th International Workshop on Artificial Intelligence and Statistics (AISTATS '03). Key West; 2003.
Kim KI, Kwon Y: Example-based learning for single-image super-resolution. Proceedings of the 30th DAGM Symposium on Pattern Recognition. Lecture Notes in Computer Science 2008, 456-465.
Kim KI, Schölkopf B: Iterative kernel principal component analysis for image modeling. IEEE Trans Pattern Anal Mach Intell 2005,27(9):1351-1366.
Ogawa T, Haseyama M: Missing intensity interpolation using a kernel PCA-based POCS algorithm and its applications. IEEE Trans Image Process 2011,20(2):417-432.
Datsenko D, Elad M: Example-based single document image super-resolution: a global MAP approach with outlier rejection. Multidimens Syst Signal Process 2007,18(2-3):103-121. 10.1007/s11045-007-0018-z
Elad M, Datsenko D: Example-based regularization deployed to super-resolution reconstruction of a single image. Comput J 2009, 52: 15-30.
Kwok JTY, Tsang IWH: The pre-image problem in kernel methods. IEEE Trans Neural Netw 2004,15(6):1517-1525. 10.1109/TNN.2004.837781
Wang Z, Bovik AC, Sheikh HR, Simoncelli EP: Image quality assessment: from error visibility to structural similarity. IEEE Trans Image Process 2004,13(4):600-612. 10.1109/TIP.2003.819861
Avcbas I, Sankur B, Sayood K: Statistical evaluation of image quality measures. J Elec Imaging 2003,11(2):206-223.
Staelin C, Greig D, Fischer M, Maurer R: Neural network image scaling using spatial errors. Technical Report (HP Laboratories, Israel) 2003.
Acknowledgements
This work was partly supported by Grant-in-Aid for Scientific Research (B) 21300030, Japan Society for the Promotion of Science (JSPS).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ogawa, T., Haseyama, M. Adaptive example-based super-resolution using kernel PCA with a novel classification approach. EURASIP J. Adv. Signal Process. 2011, 138 (2011). https://doi.org/10.1186/1687-6180-2011-138
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-6180-2011-138