Abstract
A two-hop amplify and forward (AF) relay system is considered where source and destination are each equipped with multiple antennas while the relay has a single antenna. Orthogonal space-time block coding (OSTBC) is employed at the source. New exact expressions for outage probability in Rayleigh fading as well as symbol error rate (SER) expressions for a variety of modulation schemes are derived. The diversity order of the system is evaluated. Monte Carlo simulations demonstrate the accuracy of the analyses presented. Results that can be extended to relay systems with a direct source-destination link are also highlighted. To put the results in context, the two-hop system performance is then compared to that of a MIMO point-to-point system. Finally, the new analysis is applied to evaluate two-hop system performance as a function of relay location.
Similar content being viewed by others
1. Introduction
Through exploiting spatial diversity, it is well known that MIMO technology can improve the reliability of wireless communication links [1]. Orthogonal space-time block coding (OSTBC) is a key component of MIMO systems that has attracted tremendous attention. First, OSTBC does not require complicated feedback links to provide channel state information at the transmitter (CSIT). Second, OSTBC methods enable maximum likelihood detection to be performed with low computational complexity [2]. As a result of its practicality, OSTBC has been incorporated into emerging MIMO standards [3].
While MIMO systems offer significant physical layer performance enhancements, a significant problem in initial wireless network deployments is obtaining adequate coverage. The concept of relaying signals through intermediate nodes has been shown to be effective at extending the coverage of networks in a power-efficient manner. In addition, very simple relaying systems have been shown to increase diversity through node collaboration. As a result, the provision for relaying has recently been adopted into recent standards [4]. This paper investigates the effect of simple relaying on MIMO system performance.
Previously, end-to-end performance of two-hop relay systems was studied in [5–7], including outage probability and average bit error rate (BER) in a variety of fading environments. However, in [5–7] all assume a single antenna at both source and destination. Recently, a two-hop amplify and forward (AF) relay system in which the source and destination are both equipped with multiple antennas while the relay has a single antenna appears in [8, 9]. In [8], an OSTBC strategy is employed at the source, and end-to-end average bit error rate (BER) was investigated. However, the method in [8] is only suitable for systems with the same numbers of antennas at the source and destination. Moreover, an exact expression for outage probability was not given, and the diversity order of the system was not evaluated analytically. In [10], system performance including outage probability and average SER is determined for the special case of multiple antennas at the source and a single antenna at the destination. Although the method used in [10] has been often used in the literature, it cannot be easily generalized to the case of multiple antennas at the destination.
In this paper, the same system model is assumed as in [8, 9]. First, exact expressions for system outage probability with both exact and ideal relay gain are derived for arbitrary antenna configurations at the source and destination. Exact average SER expressions for different modulation schemes are then derived by calculating the probability density function (PDF) and moment generation method (MGF). Generalizations of results to systems that include a direct link are also briefly indicated where applicable. The diversity order of the system is also evaluated. Monte Carlo simulations confirm the analytical results, compare performance between the proposed relaying system and a MIMO point-to-point system as well as evaluate the two-hop system performance as a function of relay location.
2. System Model
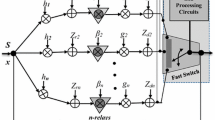
A two-hop relay system is considered where there are  antennas at the source,
antennas at the source,  antennas at the destination, and a single antenna at the relay, as shown in Figure 1. To make the relay as simple as possible, an AF relaying protocol is employed. It is also assumed that a direct communication link between source and destination is not available, as is reasonable in the case where the communication link between source and destination is in a deep fading state and/or the separation distance between them is large. In addition, half-duplex transmission is assumed; that is, the relay cannot transmit and receive simultaneously in the same time slot or frequency band.
antennas at the destination, and a single antenna at the relay, as shown in Figure 1. To make the relay as simple as possible, an AF relaying protocol is employed. It is also assumed that a direct communication link between source and destination is not available, as is reasonable in the case where the communication link between source and destination is in a deep fading state and/or the separation distance between them is large. In addition, half-duplex transmission is assumed; that is, the relay cannot transmit and receive simultaneously in the same time slot or frequency band.
OSTBC transmission containing  symbols
symbols  and block length of
and block length of  is utilized at the source to achieve space diversity. During the first time slot, the
is utilized at the source to achieve space diversity. During the first time slot, the  received vector signal at the relay can be written as
received vector signal at the relay can be written as

where  denotes a
denotes a  OSTBC transmission matrix,
OSTBC transmission matrix,  denotes the
denotes the  Rayleigh fading complex channel gain vector from the source to the relay, and
Rayleigh fading complex channel gain vector from the source to the relay, and  is the
is the  independent and identically distributed (i.i.d) complex Gaussian noise vector at the relay. During the second time slot, the
independent and identically distributed (i.i.d) complex Gaussian noise vector at the relay. During the second time slot, the  received signal at the destination can be written as
received signal at the destination can be written as

where  denotes the
denotes the  Rayleigh fading channel gain vector from the relay to the destination,
Rayleigh fading channel gain vector from the relay to the destination,  is the
is the  i.i.d noise matrix at the destination where
i.i.d noise matrix at the destination where  denotes the noise at the
denotes the noise at the  th receive antenna during the
th receive antenna during the  th symbol period, and
th symbol period, and  denotes the
denotes the  signal vector sent by the relay where
signal vector sent by the relay where  is a relay gain. As categorized in the literature, relay gains may be fixed or variable. In this paper, variable relay gain is considered. Relay gains can be further classified as exact or ideal. We denote
is a relay gain. As categorized in the literature, relay gains may be fixed or variable. In this paper, variable relay gain is considered. Relay gains can be further classified as exact or ideal. We denote  as the exact relay gain, where
as the exact relay gain, where  and
and  are average power constraints at the source and relay, respectively. If we ignore the noise at the relay,
are average power constraints at the source and relay, respectively. If we ignore the noise at the relay,  which is denoted as the ideal relay gain [5] and is amenable to mathematical manipulation. As in most of the literature, the ideal relay gain is used to compute exact average SERs of the proposed system in this paper. Later, it will be observed from simulations that the ideal relay gain provides a tight lower bound on outage probability and average SER in the case of medium-to-high SNR. Substituting
which is denoted as the ideal relay gain [5] and is amenable to mathematical manipulation. As in most of the literature, the ideal relay gain is used to compute exact average SERs of the proposed system in this paper. Later, it will be observed from simulations that the ideal relay gain provides a tight lower bound on outage probability and average SER in the case of medium-to-high SNR. Substituting  into (2) leads to the received signal at the destination given by
into (2) leads to the received signal at the destination given by

Using maximum likelihood (ML) detection of OSTBCs for the case of spatially colored noise given in [11], the received SNR is obtained as follows.
Theorem 1.
Using the exact relay gain, the received SNR of two-hop AF OSTBC transmission is given by

When the ideal relay gain is utilized, the received SNR is given by

where  ,
,  ,
,  ,
,  , and
, and  denotes the OSTBC code rate.
denotes the OSTBC code rate.
Proof.
It can be observed from (3) that the noise at the destination is temporally white but spatially colored; that is, the columns of noise matrix  are independent and Gaussian with covariance matrix
are independent and Gaussian with covariance matrix  . Also, note that system (3) under consideration is equivalent to a conventional MIMO system with an effective channel gain matrix
. Also, note that system (3) under consideration is equivalent to a conventional MIMO system with an effective channel gain matrix  . We first whiten the colored noise and then employ the ML method given in [11, 12] to decode each symbol in the OSTBC. The noise-whitening process is given by
. We first whiten the colored noise and then employ the ML method given in [11, 12] to decode each symbol in the OSTBC. The noise-whitening process is given by

where  ,
,  and
and  . After ML detection, the MIMO system in (6) can be transformed into the following
. After ML detection, the MIMO system in (6) can be transformed into the following  parallel and independent single-input and single-output (SISO) systems:
parallel and independent single-input and single-output (SISO) systems:

where  and
and  denotes the Frobenius norm of
denotes the Frobenius norm of  . Following similar arguments to [11], the received SNR for each symbol can be written as
. Following similar arguments to [11], the received SNR for each symbol can be written as

where  denotes trace of a matrix,
denotes trace of a matrix,  is inverse of matrix
is inverse of matrix  , and
, and  denotes average power of a symbol where
denotes average power of a symbol where  is assumed for OSTBCs. By substituting for
is assumed for OSTBCs. By substituting for  and
and  defined above, (8) can be written as
defined above, (8) can be written as

Using the Matrix Inversion Lemma  [13], (9) can be written as
[13], (9) can be written as

Using  , (10) can be simplified to
, (10) can be simplified to

Using the fact that  and
and  in OSTBCs, substituting the exact relay gain into (11) yields (4), and substituting the ideal relay gain into (11) yields (5).
in OSTBCs, substituting the exact relay gain into (11) yields (4), and substituting the ideal relay gain into (11) yields (5).
Remark 2.
Using maximal ratio combining (MRC) at the destination, Theorem 1 can be generalized to the case of relay systems with a direct link by including a term corresponding to the SNR of the direct link that increases the SNR by  , where
, where  is the
is the  Rayleigh fading complex channel gain matrix from source to destination and
Rayleigh fading complex channel gain matrix from source to destination and  denotes the received noise variance during the source-to-destination time slot. It is assumed that relay-to-destination communication occurs in a separate second time slot, that is, half-duplex communication.
denotes the received noise variance during the source-to-destination time slot. It is assumed that relay-to-destination communication occurs in a separate second time slot, that is, half-duplex communication.
3. Outage Probability
In this section, analytical expressions for outage probability are derived.
Theorem 3.
For the exact relay gain, the outage probability of a two-hop AF relay system when an OSTBC strategy is employed at the source is given by

where  in which
in which  denotes outage capacity and
denotes outage capacity and  denotes the modified Bessel function of second kind and order
denotes the modified Bessel function of second kind and order  . When the ideal relay gain is utilized, the outage probability is given by
. When the ideal relay gain is utilized, the outage probability is given by

Proof.
As  and
and  are complex Gaussian distributed, where
are complex Gaussian distributed, where  and
and  are elements of
are elements of  and
and  , respectively, it is readily found that
, respectively, it is readily found that  and
and  are exponentially distributed. Setting rate parameters of
are exponentially distributed. Setting rate parameters of  and
and  to be equal to
to be equal to  and
and  , respectively, the cumulative distribution function (CDF) and PDF of
, respectively, the cumulative distribution function (CDF) and PDF of  and
and  are, respectively, [14]
are, respectively, [14]




The CDF of  and
and  , in terms of the constant parameter
, in terms of the constant parameter  , is given by
, is given by

where  denotes the CDF of
denotes the CDF of  with the exact relay gain and
with the exact relay gain and  denotes the CDF of
denotes the CDF of  with the ideal relay gain. Setting
with the ideal relay gain. Setting  and substituting (14) and (17) into (18) yield
and substituting (14) and (17) into (18) yield

Moving the constant terms outside the integral and applying the binomial expansion yield

Using [15, Equation (3.324)], substituting  into (20), and through straightforward mathematical manipulations (12) with
into (20), and through straightforward mathematical manipulations (12) with  and (13) with
and (13) with  are yielded.
are yielded.
4. Exact Average SER Expressions for Different Modulation Schemes
In this section, exact SER expressions for different modulation schemes are derived assuming an ideal relay gain.
(i)First, we consider modulation schemes that have conditional SER  [16], for example, BPSK, BFSK, and MPAM.
[16], for example, BPSK, BFSK, and MPAM.
The average SER is obtained by integrating the conditional SER over the PDF of  [14]
[14]

Using integration by parts yields

where  denotes the derivative of
denotes the derivative of  and
and  denotes the CDF of
denotes the CDF of  for the ideal relay gain. Substituting (13) with
for the ideal relay gain. Substituting (13) with  into (22) yields
into (22) yields

Using integrals of combinations of Bessel functions, exponentials, and powers, for example, [15, Equation (3.381.4)] and, [15, Equation (6.621.3)], it can be shown that the following expression for average SER can be obtained from (23):

where  is the Gauss hypergeometric function,
is the Gauss hypergeometric function,  for binary phase-shift keying (BPSK),
for binary phase-shift keying (BPSK),  for binary frequency-shift keying (BFSK), and
for binary frequency-shift keying (BFSK), and  for M-ary pulse amplitude modulation (MPAM).
for M-ary pulse amplitude modulation (MPAM).
(ii)Next, we consider the modulation schemes of MPSK and MQAM.
When MPSK or MQAM is employed, we derive exact SER expressions using the well-known MGF-SER relationships given in [17]. For MPSK and MQAM, the MGF-SER relationship can be written, respectively, as

where  , and
, and

The moment generation function (MGF) of  is given by the following theorem.
is given by the following theorem.
Theorem 4.
The MGF of  is given by
is given by

Before proving Theorem 4, the probability density function (PDF) of  is first presented in the following lemma.
is first presented in the following lemma.
Lemma 5.
The PDF of  is given by
is given by

Proof of Lemma 5.
Differentiating (13), where  with respect to
with respect to  and using the expression for the modified Bessel function derivative in [15, Equation (8.486.12)]yield (28).
and using the expression for the modified Bessel function derivative in [15, Equation (8.486.12)]yield (28).
Proof of Theorem 4.
From Lemma 5, taking the Laplace transform of (28) and using [15, Equation (6.621.3)] yields (27).
Finally, from Theorem 4, substituting MGF (27) for the ideal relay gain into (25) and (26), respectively, we obtain exact average SER expressions for MPSK and MQAM.
Remark 6.
The SER expressions for MPSK and MQAM can straightforwardly be generalized to a system with a direct link. The MGF would be multiplied by the factor  , where
, where  is the rate parameter of the exponentially distributed source-to-destination gain
is the rate parameter of the exponentially distributed source-to-destination gain  .
.
5. Diversity Order Analysis
The diversity order of the system can be determined directly by the definition

Theorem 7.
The diversity order of a two-hop AF relay system is  when an OSTBC strategy is employed at the source.
when an OSTBC strategy is employed at the source.
Proof.
Since the diversity order of the system describes performance at asymptotically high SNR, the ideal relay gain assumption is used. We begin by determining the lower bound on diversity order of the system. Setting  , then when
, then when  ,
,  , it can be claimed that
, it can be claimed that  by ([18], Lemma
by ([18], Lemma  ). Substituting (15) and (17) into the previous expression yields
). Substituting (15) and (17) into the previous expression yields

According to the appendix in [19], the following expression can be obtained when  :
:

Combining (29), (30), and (31), we obtain

An upper bound on diversity order can be obtained as follows:

Combining (29), (31), and (33), we obtain

Combining (32) and (34), we conclude that the diversity order is  .
.
6. Numerical Results and Conclusions
In the following Monte Carlo simulations, without loss of generality, we assume equal transmit SNR at the source and destination:  and outage capacity
and outage capacity  . In Figures 2–4, the variances of Rayleigh fading channels
. In Figures 2–4, the variances of Rayleigh fading channels  from the source antennas to the relay and the variance of Rayleigh fading channels
from the source antennas to the relay and the variance of Rayleigh fading channels  from the relay to the destination antennas are set to 0.8 and 0.9, respectively. Also, OSTBCs with the highest code rate and minimum decoding delay are employed as given in [2]. Figure 2, showing outage probability for different antenna configurations, reveals that Monte Carlo simulations agree closely with the analysis predicted by Theorem 3. Also, the ideal relay gain provides a tight lower bound on outage probability even in the medium SNR regime. It is clear that the diversity order, observable by the slope of the outage probability curve, cannot be improved through simply adding transmit antennas only or receive antennas only for the case where an equal number of antennas is installed at the source and destination. This is as expected from Theorem 7, where the diversity order of the system is shown to be equal to
from the relay to the destination antennas are set to 0.8 and 0.9, respectively. Also, OSTBCs with the highest code rate and minimum decoding delay are employed as given in [2]. Figure 2, showing outage probability for different antenna configurations, reveals that Monte Carlo simulations agree closely with the analysis predicted by Theorem 3. Also, the ideal relay gain provides a tight lower bound on outage probability even in the medium SNR regime. It is clear that the diversity order, observable by the slope of the outage probability curve, cannot be improved through simply adding transmit antennas only or receive antennas only for the case where an equal number of antennas is installed at the source and destination. This is as expected from Theorem 7, where the diversity order of the system is shown to be equal to  .
.
Figure 3 compares Monte Carlo simulations and analytical results for modulations with conditional SER  including BPSK, BFSK, and 4 PAM as well as with QPSK and 16 QAM. Clearly, the simulations very closely match the analyses. Again, the ideal relay gain provides a tight lower bound on average SER even in the case of medium SNR.
including BPSK, BFSK, and 4 PAM as well as with QPSK and 16 QAM. Clearly, the simulations very closely match the analyses. Again, the ideal relay gain provides a tight lower bound on average SER even in the case of medium SNR.
Figure 4 shows average SER with BPSK modulation for different antenna configurations. Here, the diversity order can be observed as the slope of the average SER curve. In accordance with Theorem 7, it is observed that the diversity order cannot be improved through simply adding transmit or receive antennas for the case of equal numbers of source and destination antennas.
To assess the impact of relaying, Figure 5 compares the proposed relaying system with an MIMO point-to-point system. The relay is located between the source and destination. The normalized distance between the source and destination is assumed to be unity, so  . The path loss exponent is set to 4, and it is assumed that shadowing effects are the same for the source-relay and relay-destination links, with a standard deviation
. The path loss exponent is set to 4, and it is assumed that shadowing effects are the same for the source-relay and relay-destination links, with a standard deviation  , a value typically assumed in urban cellular environments. For a fair comparison, the transmit SNR as well as the OSTBC transmit strategy is assumed to be identical for both systems.
, a value typically assumed in urban cellular environments. For a fair comparison, the transmit SNR as well as the OSTBC transmit strategy is assumed to be identical for both systems.
Specifically, the relay is assumed to be placed halfway between the source and destination in Figure 5. Figure 5 shows how system performance trades off between the relaying and MIMO point-to-point systems. As expected, the results clearly show that the diversity order of the MIMO point-to-point system, which is known to be  , is larger than that of the relaying system for the same antenna configuration at both source and destination. In other words, as transmit SNR increases, the MIMO point-to-point system has an advantage over the relaying system. However, it can also be observed that the relaying system outperforms the MIMO point-to-point system in lower SNR regimes: for the case of
, is larger than that of the relaying system for the same antenna configuration at both source and destination. In other words, as transmit SNR increases, the MIMO point-to-point system has an advantage over the relaying system. However, it can also be observed that the relaying system outperforms the MIMO point-to-point system in lower SNR regimes: for the case of  , the relay system outperforms point-to-point MIMO systems at transmit SNRs below 6 dB. Adding a transmit antenna to the MIMO system lowers this threshold to -1 dB, while at the same time, the code rate for OSTBCs becomes 3/4. On the other hand, adding a receive antenna to the MIMO system lowers this threshold to -4 dB. Of course, the MIMO point-to-point system would be able to achieve similar system performance gain by adding transmit or receive antennas, but this would increase complexity.
, the relay system outperforms point-to-point MIMO systems at transmit SNRs below 6 dB. Adding a transmit antenna to the MIMO system lowers this threshold to -1 dB, while at the same time, the code rate for OSTBCs becomes 3/4. On the other hand, adding a receive antenna to the MIMO system lowers this threshold to -4 dB. Of course, the MIMO point-to-point system would be able to achieve similar system performance gain by adding transmit or receive antennas, but this would increase complexity.
Figure 6 shows average SER of the system for different source-relay distances with a fixed transmit SNR. It can be observed from the figure that performance is best when the relay is placed halfway between the source and destination. Although not shown here, it is found that a similar trend holds across a wide range of transmit SNR values.
7. Conclusions
The performance of a MIMO system using OSTBC transmission that encounters a simple relay in a two-hop AF configuration has been analyzed, including outage probability, SER and diversity order. These results extend those found in [8, 10]. Monte Carlo simulations are found to agree closely with the analyses. In fact, the numerical results indicate that tight lower bounds are obtainable using the ideal relay gain approximation, even at SNRs as low as 5–8 dB. In addition, Monte Carlo simulations also compare system performance between the proposed relaying system and a MIMO point-point system and assess performance as a function of location of the relay between the source and destination.
References
Gesbert D, Shafi M, Shiu D-S, Smith PJ, Naguib A: From theory to practice: an overview of MIMO space-time coded wireless systems. IEEE Journal on Selected Areas in Communications 2003, 21(3):281-302. 10.1109/JSAC.2003.809458
Tarokh V, Jafarkhani H, Calderbank AR: Space-time block codes from orthogonal designs. IEEE Transactions on Information Theory 1999, 45(5):1456-1467. 10.1109/18.771146
IEEE 802.16-2009 : Part 16: Air Interface for Broadband Wireless Access Systems. June 2009
IEEE Unapproved Draft Std P802.11s/D3.0 : Wireless LAN Medium Access Control (MAC) and PhysicalLayer (PHY) specifications Amendment 10: Mesh Networking. March 2009
Hasna MO, Alouini M-S: End-to-end performance of transmission systems with relays over Rayleigh-fading channels. IEEE Transactions on Wireless Communications 2003, 2(6):1126-1131. 10.1109/TWC.2003.819030
Tsiftsis TA, Karagiannidis GK, Takis Mathiopoulos P, Kotsopoulos SA: Nonregenerative dual-hop cooperative links with selection diversity. EURASIP Journal on Wireless Communications and Networking 2006, 2006:-8.
Suraweera HA, Louie RHY, Li Y, Karagiannidis GK, Vucetic B: Two hop amplify-and-forward transmission in mixed Rayleigh and Rician fading channels. IEEE Communications Letters 2009, 13(4):227-229.
Lee I-H, Kim D: End-to-end BER analysis for dual-hop OSTBC transmissions over Rayleigh fading channels. IEEE Transactions on Communications 2008, 56(3):347-351.
Louie RHY, Li Y, Vucetic B: Performance analysis of beamforming in two hop amplify and forward relay networks. Proceedings of the IEEE International Conference on Communications (ICC '08), 2008, Beijing, China 4311-4315.
Chen S, Wang W, Zhang X, Sun Z: Performance analysis of ostbc transmission in amplify-and-forward cooperative relay networks. IEEE Transactions on Vehicular Technology 2010, 59(1):105-113.
Larsson EG, Stoica P: Space-Time Block Coding for Wireless Communications. Cambridge University Press, Cambridge, UK; 2003.
Li X, Luo T, Yue G, Yin C: A squaring method to simplify the decoding of orthogonal space-time block codes. IEEE Transactions on Communications 2001, 49(10):1700-1703. 10.1109/26.957388
Golub GH, Loan CFV: Matrix Computations. JHU Press; 1996.
Proakis JG, Salehi M: Digital Communications. 5th edition. McGraw Hill Higher Education; 2008.
Gradshteyn IS, Ryzhik IM, Jeffrey A: Table of Integrals, Series, and Products. 6th edition. Academic Press; 2000.
Chen Y, Tellambura C: Distribution functions of selection combiner output in equally correlated Rayleigh, Rician, and Nakagami-m fading channels. IEEE Transactions on Communications 2004, 52(11):1948-1956. 10.1109/TCOMM.2004.836596
Simon MK, Alouini M: Digital Communication over Fading Channels. 2nd edition. Wiley-IEEE Press; 2004.
Yuksel M, Erkip E: Multiple-antenna cooperative wireless systems: a diversity-multiplexing tradeoff perspective. IEEE Transactions on Information Theory 2007, 53(10):3371-3393.
Laneman JN, Wornell GW: Distributed space-time-coded protocols for exploiting cooperative diversity in wireless networks. IEEE Transactions on Information Theory 2003, 49(10):2415-2425. 10.1109/TIT.2003.817829
Acknowlegment
This paper was supported in part by the Natural Sciences and Engineering Research Council of Canada Discovery (Grant no. 41731) and the Natural Science Foundation of Guangdong Province, China (Grant no. 10451009001004407).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, G., Blostein, S. & Qin, J. Performance Analysis of Two-Hop OSTBC Transmission over Rayleigh Fading Channels. J Wireless Com Network 2010, 649541 (2010). https://doi.org/10.1155/2010/649541
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/649541