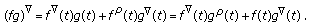Abstract
This paper deals with variational optimal-control problems on time scales in the presence of delay in the state variables. The problem is considered on a time scale unifying the discrete, the continuous, and the quantum cases. Two examples in the discrete and quantum cases are analyzed to illustrate our results.
Similar content being viewed by others
1. Introduction
The calculus of variations interacts deeply with some branches of sciences and engineering, for example, geometry, economics, electrical engineering, and so on [1]. Optimal control problems appear in various disciplines of sciences and engineering as well [2].
Time-scale calculus was initiated by Hilger (see [3] and the references therein) being in mind to unify two existing approaches of dynamic models difference and differential equations into a general framework. This kind of calculus can be used to model dynamic processes whose time domains are more complex than the set of integers or real numbers [4]. Several potential applications for this new theory were reported (see, e.g., [4–6] and the references therein). Many researchers studied calculus of variations on time scales. Some of them followed the delta approach and some others followed the nabla approach (see, e.g., [7–12]).
It is well known that the presence of delay is of great importance in applications. For example, its appearance in dynamic equations, variational problems, and optimal control problems may affect the stability of solutions. Very recently, some authors payed the attention to the importance of imposing the delay in fractional variational problems [13]. The nonlocality of the fractional operators and the presence of delay as well may give better results for problems involving the dynamics of complex systems. To the best of our knowledge, there is no work in the direction of variational optimal-control problems with delayed arguments on time scales.
Our aim in this paper is to obtain the Euler-Lagrange equations for a functional, where the state variables of its Lagrangian are defined on a time scale whose backward jumping operator is  ,
,  ,
,  . This time scale, of course, absorbs the discrete, the continuous and the quantum cases. The state variables of this Lagrangian allow the presence of delay as well. Then, we generalize the results to the
. This time scale, of course, absorbs the discrete, the continuous and the quantum cases. The state variables of this Lagrangian allow the presence of delay as well. Then, we generalize the results to the  -dimensional case. Dealing with such a very general problem enables us to recover many previously obtained results [14–17].
-dimensional case. Dealing with such a very general problem enables us to recover many previously obtained results [14–17].
The structure of the paper is as follows. In Section 2 basic definitions and preliminary concepts about time scale are presented. The nabla time-scale derivative analysis is followed there. In Section 3 the Euler-Lagrange equations into one unknown function and then in the  -dimensional case are obtained. In Section 4 the variational optimal control problem is proposed and solved. In Section 5 the results obtained in the previous sections are particulary studied in the discrete and quantum cases, where two examples are analyzed in details. Finally, Section 6 contains our conclusions.
-dimensional case are obtained. In Section 4 the variational optimal control problem is proposed and solved. In Section 5 the results obtained in the previous sections are particulary studied in the discrete and quantum cases, where two examples are analyzed in details. Finally, Section 6 contains our conclusions.
2. Preliminaries
A time scale is an arbitrary closed subset of the real line  . Thus the real numbers and the natural numbers,
. Thus the real numbers and the natural numbers,  , are examples of a time scale. Throughout this paper, and following [4], the time scale will be denoted by
, are examples of a time scale. Throughout this paper, and following [4], the time scale will be denoted by  . The forward jump operator
. The forward jump operator  is defined by
is defined by

while the backward jump operator  is defined by
is defined by

where,  (i.e.,
(i.e.,  if
if  has a maximum
has a maximum  ) and
) and  (i.e.,
(i.e.,  if
if  has a minimum
has a minimum  ). A point
). A point  is called right-scattered if
is called right-scattered if  , left-scattered if
, left-scattered if  , and isolated if
, and isolated if  . In connection we define the backward graininess function
. In connection we define the backward graininess function  by
by

In order to define the backward time-scale derivative down, we need the set  which is derived from the time scale
which is derived from the time scale  as follows. If
as follows. If  has a right-scattered minimum
has a right-scattered minimum  , then
, then  . Otherwise,
. Otherwise,  .
.
Definition 2.1 (see [18]).
Assume that  is a function and
is a function and  . Then the backward time-scale derivative
. Then the backward time-scale derivative  is the number (provided that it exists) with the property that given any
is the number (provided that it exists) with the property that given any  there exists a neighborhood
there exists a neighborhood  of
of  (i.e.,
(i.e.,  for some
for some  ) such that
) such that

Moreover, we say that  is (nabla) differentiable on
is (nabla) differentiable on  provided that
provided that  exists for all
exists for all  .
.
The following theorem is Theorem  in [19] and an analogue to Theorem
in [19] and an analogue to Theorem  in [4].
in [4].
Theorem 2.2 (see [18]).
Assume that  is a function and
is a function and  , then one has the following.
, then one has the following.
-
(i)
If
 is differentiable at
is differentiable at  then
then 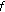 is continuous at
is continuous at 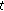 .
. -
(ii)
If
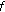 is continuous at
is continuous at 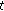 and
and 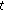 is left-scattered, then
is left-scattered, then  is differentiable at
is differentiable at 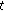 with
with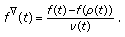 (25)
(25) -
(iii)
If
 is left-dense, then f is differentiable at
is left-dense, then f is differentiable at  if and only if the limit
if and only if the limit (26)
(26)exists as a finite number. In this case
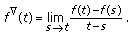 (27)
(27) -
(iv)
If
 is
is  -differentiable at
-differentiable at  , then
, then (28)
(28)
Example 2.3.
-
(i)
 or any any closed interval (the continuous case)
or any any closed interval (the continuous case) 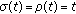 ,
,  and
and 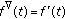 .
. -
(ii)
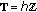 ,
, 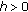 or any subset of it (the difference calculus, a discrete case)
or any subset of it (the difference calculus, a discrete case)  ,
, 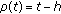 ,
, 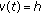 , and
, and 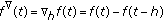 .
. -
(iii)
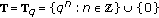 ,
, 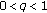 , (quantum calculus)
, (quantum calculus) 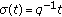 ,
, 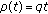 ,
, 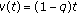 , and
, and 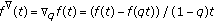 .
. -
(iv)
 ,
, 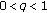 ,
,  (unifying the difference calculus and quantum calculus). There are
(unifying the difference calculus and quantum calculus). There are 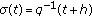 ,
,  ,
,  , and
, and  . If
. If  then
then  and so
and so 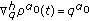 . Note that in this example the backward operator is of the form
. Note that in this example the backward operator is of the form 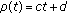 and hence
and hence 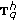 is an element of the class
is an element of the class 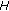 of time scales that contains the discrete, the usual, and the quantum calculus (see [17]).
of time scales that contains the discrete, the usual, and the quantum calculus (see [17]).
Theorem 2.4.
Suppose that  are nabla differentiable at
are nabla differentiable at  , then,
, then,
-
(1)
the sum
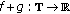 is nabla differentiable at
is nabla differentiable at 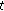 and
and 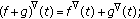
-
(2)
for any
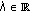 , the function
, the function 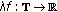 is nabla differentiable at
is nabla differentiable at 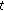 and
and  ;
; -
(3)
the product
 is nabla differentiable at
is nabla differentiable at 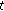 and
and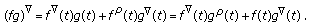 (29)
(29)For the proof of the following lemma we refer to [20].
Lemma 2.5.
Let  be an
be an  -time scale (in particular
-time scale (in particular  ),
),  two times nabla differentiable function, and
two times nabla differentiable function, and  for
for  . Then
. Then

Throughout this paper we use for the time-scale derivatives and integrals the symbol  which is inherited from the time scale
which is inherited from the time scale  . However, our results are true also for the
. However, our results are true also for the  -time scales (those time scales whose jumping operators have the form
-time scales (those time scales whose jumping operators have the form  ). The time scale
). The time scale  is a natural example of an
is a natural example of an  -time scale.
-time scale.
Definition 2.6.
A function  is called a nabla antiderivative of
is called a nabla antiderivative of  provided
provided  for all
for all  . In this case, for
. In this case, for  , we write
, we write

The following lemma which extends the fundamental lemma of variational analysis on time scales with nabla derivative is crucial in proving the main results.
Lemma 2.7.
Let  ,
,  . Then
. Then

holds if and only if

The proof can be achieved by following as in the proof of Lemma  in [9] (see also [17]).
in [9] (see also [17]).
3. First-Order Euler-Lagrange Equation with Delay
We consider the  -integral functional
-integral functional  ,
,

where

We will shortly write

We calculate the first variation of the functional  on the linear manifold
on the linear manifold  . Let
. Let  , then
, then

where

and where Lemma 2.5 and that  are used. If we use the change of variable
are used. If we use the change of variable  , which is a linear function, and make use of Theorem
, which is a linear function, and make use of Theorem  in [4] and Lemma 2.5 we then obtain
in [4] and Lemma 2.5 we then obtain

where we have used the fact that  on
on 
Splitting the first integral in (3.6) and rearranging will lead to

If we make use of part ( ) of Theorem 2.4 then we reach
) of Theorem 2.4 then we reach

In (3.8), once choose  such that
such that  and
and  on
on  and in another case choose
and in another case choose  such that
such that  and
and  on
on  , and then make use of Lemma 2.7 to arrive at the following theorem.
, and then make use of Lemma 2.7 to arrive at the following theorem.
Theorem 3.1.
Let  be the
be the  -integral functional
-integral functional

where

Then the necessary condition for  to possess an extremum for a given function
to possess an extremum for a given function  is that
is that  satisfies the following Euler-Lagrange equations
satisfies the following Euler-Lagrange equations

Furthermore, the equation:

holds along  for all admissible variations
for all admissible variations  satisfying
satisfying  ,
,  .
.
The necessary condition represented by (3.12) is obtained by applying integration by parts in (3.7) and then substituting (3.11) in the resulting integrals. The above theorem can be generalized as follows.
Theorem 3.2.
Let  be the
be the  -integral functional
-integral functional

where

Then a necessary condition for  to possess an extremum for a given function
to possess an extremum for a given function  is that
is that  satisfies the following Euler-Lagrange equations:
satisfies the following Euler-Lagrange equations:

Furthermore, the equations

hold along  for all admissible variations
for all admissible variations  satisfying
satisfying

where

4. The Optimal-Control Problem
Our aim in this section is to find the optimal control variable  defined on the
defined on the  -time scale, which minimizes the performance index
-time scale, which minimizes the performance index

subject to the constraint

such that

where  is a constant and
is a constant and  and
and  are functions with continuous first and second partial derivatives with respect to all of their arguments. To find the optimal control, we define a modified performance index as
are functions with continuous first and second partial derivatives with respect to all of their arguments. To find the optimal control, we define a modified performance index as

where  is a Lagrange multiplier or an adjoint variable.
is a Lagrange multiplier or an adjoint variable.
Using (3.11) and (3.12) of Theorem 3.2 with  (
( ,
,  ,
,  ), the necessary conditions for our optimal control are (we remark that as there is no any time-scale derivative of
), the necessary conditions for our optimal control are (we remark that as there is no any time-scale derivative of  , no boundary constraints for it are needed)
, no boundary constraints for it are needed)


and also

Note that condition (4.6) disappears when the Lagrangian  is free of the delayed time scale derivative of
is free of the delayed time scale derivative of  .
.
5. The Discrete and Quantum Cases
We recall that the results in the previous sections are valid for time scales whose backward jump operator  has the form
has the form  , in particular for the time scale
, in particular for the time scale  .
.
-
(i)
The Discrete Case
If  and
and  (of special interest the case when
(of special interest the case when  ), then our work becomes on the discrete time scale
), then our work becomes on the discrete time scale  . In this case the functional under optimization will have the form
. In this case the functional under optimization will have the form

and that  ,
,  for
for  where
where

The necessary condition for  to possess an extremum for a given function
to possess an extremum for a given function  is that
is that  satisfies the following
satisfies the following  -Euler-Lagrange equations:
-Euler-Lagrange equations:

Furthermore, the equation

holds along  for all admissible variations
for all admissible variations  satisfying
satisfying  ,
,  .
.
In this case the  -optimal-control problem would read as follows.
-optimal-control problem would read as follows.
Find the optimal control variable  defined on the time scale
defined on the time scale  , which minimizes the
, which minimizes the  -performance index
-performance index

subject to the constraint

such that

The necessary conditions for this  -optimal control are
-optimal control are


and also

Note that condition (5.9) disappears when the Lagrangian  is independent of the delayed
is independent of the delayed  derivative of
derivative of  .
.
Example 5.1.
In order to illustrate our results we analyze an example of physical interest. Namely, let us consider the following discrete action:

subject to the condition

The corresponding  -Euler-Lagrange equations are as follows:
-Euler-Lagrange equations are as follows:

We observe that when the delay is removed, that is,  , the classical discrete Euler-Lagrange equations are reobtained.
, the classical discrete Euler-Lagrange equations are reobtained.
-
(ii)
The Quantum Case
If  and
and  , then our work becomes on the time scale
, then our work becomes on the time scale  . In this case the functional under optimization will have the form
. In this case the functional under optimization will have the form

where

Using the  -integral theory on time scales, the functional
-integral theory on time scales, the functional  in (5.14) turns to be
in (5.14) turns to be

The necessary condition for  to possess an extremum for a given function
to possess an extremum for a given function  is that
is that  satisfies the following
satisfies the following  -Euler-Lagrange equations:
-Euler-Lagrange equations:

Furthermore, the equation

holds along  for all admissible variations
for all admissible variations  satisfying
satisfying  ,
,  .
.
In this case the  -optimal-control problem would read as follows.
-optimal-control problem would read as follows.
Find the optimal control variable  defined on the
defined on the  -time scale, which minimizes the performance index
-time scale, which minimizes the performance index

subject to the constraint

such that

where  is a constant and
is a constant and  and
and  are functions with continuous first and second partial derivatives with respect to all of their arguments.
are functions with continuous first and second partial derivatives with respect to all of their arguments.
The necessary conditions for this  -optimal control are
-optimal control are




and also

Note that condition (5.25) disappears when the Lagrangian  is independent of the delayed
is independent of the delayed  derivative of
derivative of  .
.
Example 5.2.
Suppose that the problem is that of finding a control function  defined on the time scale
defined on the time scale  such that the corresponding solution of the controlled system
such that the corresponding solution of the controlled system

satisfying the conditions

is an extremum for the  -integral functional (
-integral functional ( -quadratic delay cost functional):
-quadratic delay cost functional):

According to (5.24) and (5.25), the solution of the problem satisfies

and of course

When the delay is absent (i.e.,  ), it can be shown that the above system is reduced to a second-order
), it can be shown that the above system is reduced to a second-order  -difference equation. Namely, reduced to
-difference equation. Namely, reduced to

If we solve recursively for this equation in terms of an integer power series by using the initial data, then the resulting solution will tend to the solutions of the second order linear differential equation:

Clearly the solutions for this equation are  and
and  . For details see [16].
. For details see [16].
6. Conclusion
In this paper we have developed an optimal variational problem in the presence of delay on time scales whose backward jumping operators are of the form  ,
,  ,
,  , called
, called  -time scales. Such kinds of time scales unify the discrete, the quantum, and the continuous cases, and hence the obtained results generalized many previously obtained results either in the presence of delay or without. To formulate the necessary conditions for this optimal control problem, we first obtained the Euler-Lagrange equations for one unknown function then generalized to the n-dimensional case. The state variables of the Lagrangian in this case are defined on the
-time scales. Such kinds of time scales unify the discrete, the quantum, and the continuous cases, and hence the obtained results generalized many previously obtained results either in the presence of delay or without. To formulate the necessary conditions for this optimal control problem, we first obtained the Euler-Lagrange equations for one unknown function then generalized to the n-dimensional case. The state variables of the Lagrangian in this case are defined on the  -time scale and contain some delays. When
-time scale and contain some delays. When  and
and  with the existence of delay some of the results in [14] are recovered. When
with the existence of delay some of the results in [14] are recovered. When  and
and  and the delay is absent most of the results in [16] can be reobtained. When
and the delay is absent most of the results in [16] can be reobtained. When  and the delay is absent some of the results in [15] are reobtained. When the delay is absent and the time scale is free somehow, some of the results in [17] can be recovered as well.
and the delay is absent some of the results in [15] are reobtained. When the delay is absent and the time scale is free somehow, some of the results in [17] can be recovered as well.
Finally, we would like to mention that we followed the line of nabla time-scale derivatives in this paper, analogous results can be originated if the delta time-scale derivative approach is followed.
References
Rosenblueth JF: Systems with time delay in the calculus of variations: a variational approach. IMA Journal of Mathematical Control and Information 1988,5(2):125-145. 10.1093/imamci/5.2.125
Young LC: Lectures on the Calculus of Variations and Optimal Control Theory. Saunders, Philadelphia, Pa, USA; 1969:xi+331.
Hilger S: Analysis on measure chains, a unified approach to continuous and discrete calculus. Results in Mathematics 1990,18(1-2):18-56.
Bohner M, Peterson A: Dynamic Equations on Time Scales. An Introduction with Application. Birkhäuser, Boston, Mass, USA; 2001:x+358.
Atici FM, Biles DC, Lebedinsky A: An application of time scales to economics. Mathematical and Computer Modelling 2006,43(7-8):718-726. 10.1016/j.mcm.2005.08.014
Guseinov GSh: Integration on time scales. Journal of Mathematical Analysis and Applications 2003,285(1):107-127. 10.1016/S0022-247X(03)00361-5
Ferreira RAC, Torres DFM: Higher-order calculus of variations on time scales. In Mathematical Control Theory and Finance. Springer, Berlin, Germany; 2008:149-159.
Almeida R, Torres DFM: Isoperimetric problems on time scales with nabla derivatives. Journal of Vibration and Control 2009,15(6):951-958. 10.1177/1077546309103268
Bohner M: Calculus of variations on time scales. Dynamic Systems and Applications 2004,13(3-4):339-349.
Ferreira RAC, Torres DFM: Remarks on the calculus of variations on time scales. International Journal of Ecological Economics & Statistics 2007,9(F07):65-73.
Malinowska AB, Torres DFM: Strong minimizers of the calculus of variations on time scales and the Weierstrass condition. to appear in Proceedings of the Estonian Academy of Sciences
Bartosiewicz Z, Torres DFM: Noether's theorem on time scales. Journal of Mathematical Analysis and Applications 2008,342(2):1220-1226. 10.1016/j.jmaa.2008.01.018
Baleanu D, Maaraba T, Jarad F: Fractional variational principles with delay. Journal of Physics A 2008,41(31): 8.
Agrawal OP, Gregory J, Spector P: A Bliss-type multiplier rule for constrained variational problems with time delay. Journal of Mathematical Analysis and Applications 1997,210(2):702-711. 10.1006/jmaa.1997.5427
Cadzow JA: Discrete calculus of variations. International Journal of Control 1970,11(3):393-407. 10.1080/00207177008905922
Bangerezako G: Variational q-calculus. Journal of Mathematical Analysis and Applications 2004,289(2):650-665. 10.1016/j.jmaa.2003.09.004
Martins N, Torres DFM: Calculus of variations on time scales with nabla derivatives. Nonlinear Analysis: Theory, Method & Applications 2008,71(12):763-773.
Atici FM, Guseinov GSh: On Green's functions and positive solutions for boundary value problems on time scales. Journal of Computational and Applied Mathematics 2002,141(1-2):75-99. 10.1016/S0377-0427(01)00437-X
Bohner M, Peterson A: Advances in Dynamic Equations on Time Scales. Birkhäuser, Boston, Mass, USA; 2003:xii+348.
Abdeljawad T: A note on the chain rule on time scales. Journal of Arts and Sciences 2008, 9: 1-6.
Acknowledgment
This work is partially supported by the Scientific and Technical Research Council of Turkey.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Abdeljawad (Maraaba), T., Jarad, F. & Baleanu, D. Vartiational Optimal-Control Problems with Delayed Arguments on Time Scales. Adv Differ Equ 2009, 840386 (2009). https://doi.org/10.1155/2009/840386
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/840386





 is differentiable at
is differentiable at  then
then 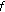 is continuous at
is continuous at 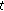 .
.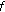 is continuous at
is continuous at 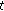 and
and 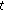 is left-scattered, then
is left-scattered, then  is differentiable at
is differentiable at 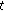 with
with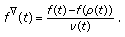
 is left-dense, then f is differentiable at
is left-dense, then f is differentiable at  if and only if the limit
if and only if the limit
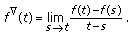
 is
is  -differentiable at
-differentiable at  , then
, then
 or any any closed interval (the continuous case)
or any any closed interval (the continuous case) 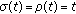 ,
,  and
and 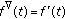 .
.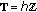 ,
, 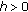 or any subset of it (the difference calculus, a discrete case)
or any subset of it (the difference calculus, a discrete case)  ,
, 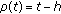 ,
, 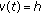 , and
, and 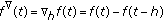 .
.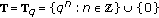 ,
, 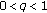 , (quantum calculus)
, (quantum calculus) 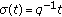 ,
, 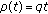 ,
, 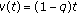 , and
, and 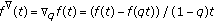 .
. ,
, 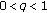 ,
,  (unifying the difference calculus and quantum calculus). There are
(unifying the difference calculus and quantum calculus). There are 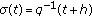 ,
,  ,
,  , and
, and  . If
. If  then
then  and so
and so 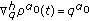 . Note that in this example the backward operator is of the form
. Note that in this example the backward operator is of the form 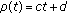 and hence
and hence 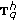 is an element of the class
is an element of the class 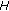 of time scales that contains the discrete, the usual, and the quantum calculus (see [
of time scales that contains the discrete, the usual, and the quantum calculus (see [ is nabla differentiable at
is nabla differentiable at 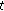 and
and 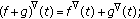
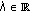 , the function
, the function 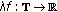 is nabla differentiable at
is nabla differentiable at  and
and  ;
; is nabla differentiable at
is nabla differentiable at  and
and