1 Introduction

General Relativity (GR) is one of the cornerstones of modern physics being stated as the standard model of gravitation and cosmology. However, in the last years, shortcomings came out in the Einstein’s theory and the investigations whether GR is the fundamental theory capable of explaining the gravitational interaction in different regimes initiated.

Combined data from Cosmic Microwave Background Radiation (CMB) [2] and from Baryonic Acoustic Oscillations (BAO), indicate that the Universe is spatially flat, it is in accelerated expansion [3, 4], and it is composed of \(96\%\) of unknown matter-energy, commonly known as dark matter and dark energy, respectively. It is widely accepted that the reason for the present accelerated expansion phase of the Universe is due dark energy [5,6,7], while that an invisible matter (or dark matter) accounts for the galaxies’ rotation curves flatness [8, 9].

To overcome this situation different researchers came up with more sophisticated gravity theories by modifying the Einstein–Hilbert action, which gave arise a new avenue known as modified or extended theories of gravity. The extended theories of gravity have born out as an opportunity to solve problems which are still without explanation within GR framework. The f(R) theory of gravity is one of the most well studied theories, and consists of choosing a more general action to replace the Einstein–Hilbert one, assuming that the gravitational action is an arbitrary function of the Ricci scalar, R as discussed in Refs. [10, 11].

In this work, we are particularly interested in the f(R, T) theory of gravity that is a generalization of f(R) type theories. The f(R, T) gravity, proposed by Harko et al. [12], consists of choosing a gravitational action as an arbitrary function of the Ricci scalar and also the trace of the energy–momentum tensor, T. Moraes [1] has used \(f(R,T)= R + f(T)\) to calculate the trace of the f(R, T) gravity field equations. In this case, the author describes only a minimal coupling between the Ricci tensor and an arbitrary function of the energy–momentum tensor, i.e., a specific model. Here, we are going further in calculating the trace of the f(R, T) gravity field equations and also deriving a new field equation for the theory that does not depend on the matter Lagrangian. In our approach matter and curvature can have a more complex coupling, i.e., it is a general approach. As pointed by [13], a more rich phenomenology could arise from a non-minimal geometry-matter coupling, what is within the motivations behind the present work.

This new general approach eliminates the Lagrangian ambiguity choice. We argue that the trace of the energy–momentum tensor is the macroscopic description of the more fundamental gravity structure, i.e., it is the quantity that encodes the degree of freedom of the matter to the scalar curvature. We show that our proposal resolves two limitations: the Lagrangian choice, and the fact that the energy–momentum tensor cannot be the perfect fluid. From this novel approach we consider that the trace of the energy–momentum tensor is an “unknown” variable, and thus, the trace of the field equations can be exploited to eliminate it.

This article is organized as follows: Sect. 2 presents a basic overview on general properties of the f(R, T) gravity, in Sect. 3 we derive the traceless field equations for a generic f(R, T) functional, in Sect. 4 we present a consistent approach for the Lagrangian ambiguity choice, in Sect. 5 we apply the theory to describe the matter era of cosmology and show that a transition between a decelerated Universe to an accelerated one is possible in f(R, T) cosmology and finally in Sect. 6 we conclude and discuss possible applications of the theory presented here.

2 f(R, T) gravity

The f(R, T) gravity is derived by adopting the following gravitational action [12]

$$\begin{aligned} S=\int \mathrm{d}^4 x \sqrt{-g} \left( \frac{f(R,T)}{16\pi }+\mathscr {L}\right) , \end{aligned}$$
(1)

where f(R, T) is a generic function of the Ricci scalar R, and to the trace T of the energy–momentum tensor \(T_{\mu \nu }\). \(\mathscr {L}\) represents the matter Lagrangian density. Natural units are adopted and metric signature -2.

By variation of the action (1) with respect to the metric tensor \(g_{\mu \nu }\), one obtains the field equations of the f(R, T) gravity theory as follows

$$\begin{aligned}&f_R R_{\mu \nu }-\frac{1}{2} g_{\mu \nu }f + (g_{\mu \nu }\Box - \nabla _\mu \nabla _\nu )f_R \nonumber \\&\quad = 8\pi T_{\mu \nu } + f_T( T_{\mu \nu } - g_{\mu \nu }\mathscr {L}), \end{aligned}$$
(2)

where \(\Box \) is the D’Alambertian operator, \(R_{\mu \nu }\) is the Ricci tensor and \(\nabla _\mu \) represents the covariant derivative associated with the Levi–Civita connection of \(g_{\mu \nu }\). For sake of simplicity, we defined \(f_R \equiv \frac{\partial {f(R,T)}}{\partial R}\) and \(f_T \equiv \frac{\partial {f(R,T)}}{\partial T}\).

3 Traceless f(R, T) gravity

Taking the trace of (2) we obtain

$$\begin{aligned} \mathscr {L}= \frac{f_T T- f_R R+2f-3 \Box f_R + 8\pi T}{4f_T}. \end{aligned}$$
(3)

Combining (2) with (3) yields

$$\begin{aligned}&\left( R_{\mu \nu }- \frac{1}{4}g_{\mu \nu } R+\frac{1}{4}g_{\mu \nu }\Box - \nabla _\mu \nabla _\nu \right) f_R \nonumber \\&\quad = 8\pi T_{\mu \nu }- 2\pi g_{\mu \nu } T + f_T\left( T_{\mu \nu }-\frac{1}{4}g_{\mu \nu }T\right) . \end{aligned}$$
(4)

The covariant derivative of the stress–energy tensor is given by

$$\begin{aligned} \nabla ^\mu T_{\mu \nu }= & {} \frac{f_T}{8\pi +f_T}\Bigg [ (g_{\mu \nu }\mathscr {L}-T_{\mu \nu })\nabla ^\mu {\ln }f_T \nonumber \\&-\frac{1}{2}g_{\mu \nu }\nabla ^\mu T +g_{\mu \nu }\nabla ^\mu \mathscr {L}\Bigg ], \end{aligned}$$
(5)

where \(\mathscr {L}\) can be eliminated from Eq. (3). As one can see, the four-divergence is non-null and in a traceless formulation of the field equations, the f(R, T) shares a similarity with the unimodular gravity as will see ahead.

3.1 f(R, T) gravity and unimodular gravity, connection through energy–momentum violation

Trying to deal with elementary particles in a geometrical framework, Einstein proposed [14, 15] in 1919 a trace-free field equation

$$\begin{aligned} R_{\mu \nu }-\frac{1}{4}g_{\mu \nu }R=8 \pi \left( T_{\mu \nu }-\frac{1}{4}g_{\mu \nu }T\right) . \end{aligned}$$
(6)

The formulation derived from the Einstein–Hilbert was persuaded in order to have an understanding in the right-hand side of the field equations of General Relativity. The gravitational field equations involve only traceless parts of the Riemann/energy–momentum tensor.

Nowadays, this formulation was reborn as “unimodular gravity”, due to a fixation on the metric determinant -det\(g_{\mu \nu }\equiv g=1\), and it is applied to solve the problem of the discrepancy between the vacuum energy density and the observed value of the cosmological constant [16,17,18,19,20].

In Eq. (6), the Bianchi identity still holds for the Einstein tensor, \(\nabla ^\mu G_{\mu \nu }=0\), but the vanishing of the four-divergence of energy–momentum tensor, \(\nabla ^\mu T_{\mu \nu }=0\), is not a geometrical consequence. As have been shown, the difference between the field equations in unimodular and in GR is a scalar stress \(1/4(T+R/8\pi )g^{\mu \nu }\) [16].

The field equations are derived by restricting the variations preserving the volume form. These restrictions lead to violations of the energy–momentum conservation. For a conservative case, the condition

$$\begin{aligned} \nabla ^{\mu }\left( 8\pi T_{\mu \nu } - \frac{8\pi }{4}g_{\mu \nu }T - \frac{1}{4}g_{\mu \nu }R\right) =0, \end{aligned}$$
(7)

must be satisfied and it leads to GR with cosmological constant, i.e., dark energy.

In the case of f(R, T) gravity, which is a theory with a presence of coupling in the gravitational field, the non-vanishing of the energy–momentum tensor, Eq. (5), arises without restrictions in the variations and it is associated with particle creation in a quantum level, being plausible that gravitational field theories intrinsically contain effective particle creation in a phenomenological description [21]. Particle creation is a feature in quantum field theories described in curved spacetime and in noncommutative quantum field theories, which is field theory in a noncommutative spacetime and can be interpreted as a low energy limit of a quantum gravity theory. As we stated in a previous work [22], the energy nonconservation in a four dimensional spacetime can be related to a noncommutative compact extra dimension with circular topology. In this regard, a letter by Josset et al. [23] considered the unimodular gravity with violation of the conservation of energy–momentum, investigating sources of nonconservation in quantum mechanics. In a first scenario studied by them, is evoked a Markovian equation (used to describe creation and evolution of black holes) of the density matrix \(\hat{\rho }\). This leads to a non-constant average energy \(\langle {E}\rangle \equiv {{\,\mathrm{Tr}\,}}[\hat{\rho }, \hat{H}]\). In the second scenario the nonconservation arises naturally from quantum gravity. In a more recently letter [24], exploring this second case, they showed that the nonconservation arises from the discreteness at the Planck level, similar to our line of thought [22]. They have shown that these quantum phenomena are relevant in a cosmological scale, i.e., the underline granularity of the spacetime would lead to the emergence of an effective dark energy. The relevance of the discreteness arises by the interaction of the gravity with scale-invariance-breaking fields (massive fields could interact with quantum gravity structure and exchange energy with it). The quantity that would describe macroscopically the phenomenon is the trace of the energy–momentum tensor T, which for a perfect fluid is given by \(T = \rho - 3p\), the trace characterizes the breaking of the conformal and scale invariance [25], and it is related to the scalar curvature, therefore captured geometrically by scalar curvature R. A non-vanishing of trace leads to a trace anomaly [26, 27].

As we can see, the trace is an important ingredient in the quantum and gravitational level description, and it is intrinsically associated with energy violations. We will use it in a more consistent approach to the Lagrangian ambiguity issue in f(R, T) gravity in the next section.

4 A more consistent approach to the Lagrangian ambiguity choice

In this section we present a new approach to the Lagrangian ambiguity problem in f(R, T) gravity. Our approach consists of considering the trace of the energy–momentum tensor as a variable of the field equations.

Taking the general definition [13] of the energy–momentum tensor given by

$$\begin{aligned} T_{\mu \nu }=(p+\rho )u_\mu u_\nu +g_{\mu \nu }\mathscr {L}, \end{aligned}$$
(8)

and calculating the trace we obtain that

$$\begin{aligned} \mathscr {L}=\frac{T-(p+\rho )}{4}, \end{aligned}$$
(9)

then, the field equations become

$$\begin{aligned}&f_R R_{\mu \nu }-\frac{1}{2} g_{\mu \nu }f + (g_{\mu \nu }\Box - \nabla _\mu \nabla _\nu )f_R \nonumber \\&\quad =8\pi T_{\mu \nu } + f_T\left( T_{\mu \nu } - \frac{g_{\mu \nu }}{4}(T-(p+\rho ))\right) . \end{aligned}$$
(10)

In this way, the field equations become independent of the matter Lagrangian. In a flat spacetime limit, the trace is free of anomaly, however, considering a coupling, we can have trace anomaly, i.e., correction terms to energy–momentum tensor, which would lead to phenomenological implications as pointed by Perez and Sudarsky [24].

Rewriting the energy–momentum tensor we have

$$\begin{aligned} T_{\mu \nu }=(p+\rho )u_\mu u_\nu +g_{\mu \nu }\left( \frac{T-(p+\rho )}{4}\right) . \end{aligned}$$
(11)

We can also calculate the four divergence of the energy–momentum tensor by replacing (9) into Eq. (5). One must realize that, from now on, field equations depend only on energy–momentum tensor and its trace, rather than matter Lagrangian. In previous works in f(R, T) gravity the trace of the energy–momentum tensor depends on matter Lagrangian, being not well-defined. Assuming the trace to be an unknown entity, we can treat it as a variable of the f(R, T) theory. To solve this issue one can take the trace of the field equations to obtain

$$\begin{aligned} 8\pi T +2f +f_T(p+\rho )= f_R R+ 3\Box f_R. \end{aligned}$$
(12)

When taking the trace of the field equations one more equation is added to the problems to be solved. It is worth to quote that in this approach the trace, T, will have a similar role as the curvature scalar, R, in f(R) gravity theories. This approach has two major advances: it solves the Lagrangian choice problem; and it also respects the fact that in f(R, T) gravity the energy–momentum tensor cannot be the one for perfect fluids. As the energy–momentum tensor is not well-defined as in GR our proposed approach solves this issue by coupling the trace of the field equation to themselves.

5 Cosmology in the general approach for the Lagrangian ambiguity

5.1 Model I: \(f(R,T)=R+\lambda T\)

Taking (10) and using \(f(R,T)=R+\lambda T\), which is an extensively studied case, one obtains the field equations

$$\begin{aligned} G_{\mu \nu }=(8\pi +\lambda )T_{\mu \nu } +g_{\mu \nu }\frac{\lambda }{4}(T+p+\rho ). \end{aligned}$$
(13)

Therefore, the trace of the energy–momentum tensor becomes

$$\begin{aligned} T=-\frac{R+\lambda (p+\rho )}{8\pi +2\lambda }, \end{aligned}$$
(14)

which states that the trace, T not only depends on pressure and energy density but it also depends on the curvature scalar, R.

Defining an effective energy–momentum tensor

$$\begin{aligned} T_{\mu \nu {\ \mathrm I}}^\mathrm{eff}= \left( 1+\frac{\lambda }{8\pi }\right) T_{\mu \nu }+\frac{\lambda }{32\pi }(T+p+\rho )g_{\mu \nu }, \end{aligned}$$
(15)

we write the field equations in a compact form \(G_{\mu \nu }=8\pi T_{\mu \nu \, I}^\mathrm{eff}\). Considering the FLRW metric for these field equations we have

$$\begin{aligned} R=-6(\dot{H}+2H^2) \end{aligned}$$
(16)

and

$$\begin{aligned}&3 H^{2}=8 \pi \rho ^{\mathrm {eff}}_\mathrm{I}, \end{aligned}$$
(17)
$$\begin{aligned}&2 \dot{H}+3 H^{2}=-8 \pi p^{\mathrm {eff}}_\mathrm{I}, \end{aligned}$$
(18)

where H is the Hubble parameter.

Substituting (16) into (14), and then this result into (15), we get

$$\begin{aligned} \rho ^\mathrm{eff}_\mathrm{I}=\frac{(3\lambda +24\pi )(p+\rho )+R}{32\pi }, \end{aligned}$$
(19)

and

$$\begin{aligned} p^\mathrm{eff}_\mathrm{I}=\frac{(\lambda +8\pi )(p+\rho )+R}{32\pi }. \end{aligned}$$
(20)

From (17) and (18), we obtain

$$\begin{aligned} \dot{H}=-\frac{1}{2}(\lambda +8\pi )(p+\rho ) . \end{aligned}$$
(21)

By assuming that pressure and energy density must be positive, Eq. (21) provides that, if \(\lambda >-8\pi \) the Hubble parameter is decreasing, if \(\lambda <-8\pi \), H is increasing, and in case of \(\lambda =-8\pi \), H becomes a constant in time.

Considering the matter era (\(p=0\)) and isolating \(\rho \) in both (17) and (18) and combining the results, one can arrive at

$$\begin{aligned} \dot{H}=-2H^2, \end{aligned}$$
(22)

whose solution is straightforward

$$\begin{aligned} \frac{1}{H(t_0)}-\frac{1}{H(t)}=2(t_0-t). \end{aligned}$$
(23)

This equation gives a new model for the evolution of the Hubble constant with time, where H(t) is noticeably a decreasing function.

By solving \(a(t)=a_0\exp \left[ \int _{t_0}^t Hdt \right] \) the solution for the scale parameter is

$$\begin{aligned} a(t)=a_0(2H_0 t-2H_0 t_0 +1), \end{aligned}$$
(24)

which gives the deceleration parameter \(q=-\ddot{a}a/\dot{a}^2=-8\). So, in this linear case, the theory does not predict a transition between a decelerated Universe to an accelerated one. This indicates that a linear functional on T (a well studied case in the literature) cannot explain the observational data. However, the f(R, T) theory is still possible from the point of view of others functional, as we are going to show.

5.2 Model II: \(f(R,T)=R+\lambda T^2\)

Assuming now that \(f(R,T)=R+\lambda T^2\), one can obtain the field equations as \(G_{\mu \nu }=8\pi T_{\mu \nu }^\mathrm{eff}\), where \(T_{\mu \nu }^\mathrm{eff}\) reads now

$$\begin{aligned} T_{\mu \nu {\ \mathrm II}}^\mathrm{eff}=\left( 1+\frac{\lambda T}{4\pi }\right) T_{\mu \nu }+\frac{\lambda T}{16\pi } (p+\rho )g_{\mu \nu }. \end{aligned}$$
(25)

In this case, the effective energy density and pressure are given by

$$\begin{aligned} \rho ^\mathrm{eff}_\mathrm{II}= & {} \left( 1+\frac{\lambda T}{4\pi }\right) \left[ (p+\rho )+\frac{T-(p+\rho )}{4}\right] \nonumber \\&+\frac{\lambda T}{16\pi } (p+\rho ) \end{aligned}$$
(26)
$$\begin{aligned} p^\mathrm{eff}_\mathrm{II}= & {} -\left( 1+\frac{\lambda T}{4\pi }\right) \left( \frac{T(p+\rho )}{4}\right) -\frac{\lambda T}{16\pi } (p+\rho ). \end{aligned}$$
(27)

The modified Friedmann equations are

$$\begin{aligned}&3 H^{2}=8 \pi \rho ^{\mathrm {eff}}_\mathrm{II}, \end{aligned}$$
(28)
$$\begin{aligned}&2 \dot{H}+3 H^{2}=-8 \pi p^{\mathrm {eff}}_\mathrm{II}. \end{aligned}$$
(29)

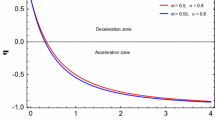
To solve (28) and (29), we use (27) and (26) and assume the matter era. Solving this numerically gives us the solutions for the Hubble parameter and energy density, \(\rho \). From the solution one can obtain the evolution of the scale parameter and, hence, obtain the deceleration parameter, q. The initial conditions for the solutions used in this work were: \(H_0=67.4\) km s\(^{-1}\) Mpc\(^{-1}\) and \(\rho _0=6\times 10^{-16}\) kg m\(^{-3}\) [28].

Fig. 1
figure 1

Evolution of the deceleration parameter with time. A change of signal on q is presented, therefore, the theory, for \(f(R, T)=R+\lambda T^2\), predicts a transition between a decelerated Universe to an accelerated one, without the need for dark energy

Full size image

The result for q is shown on Fig. 1, which indicates that the f(R, T) gravity can predict a transition between a decelerated Universe to an accelerated one for \(\lambda \approx 1.6\pi \). In this second model, we have an agreement with the observational data, which shows a transition between a decelerated Universe to an accelerated one.

6 Discussion

The f(R, T) gravity has attracted a lot of researchers attention in the last few years  [29,30,31,32,33,34,35,36,37,38,39,40,41,42,43]. Nevertheless, a few works have addressed the Lagrangian choice problem in the f(R, T) gravity and modified theories of gravity [1, 13, 44,45,46]. In general, choices for matter Lagrangian among those works are \(\mathscr {L}=\rho \) or \(\mathscr {L}=-p\). In some works it is shown that Lagrangian may be an arbitrary function of pressure and energy density, \(\mathscr {L}=\mathscr {L}(p,\rho )\), or considering an equation of state the dependence on pressure can be eliminated to give \(\mathscr {L}=\mathscr {L}(\rho )\).

Moraes [1] has provided a solution for the Lagrangian choice problem by deriving a field equation for the f(R, T) gravity that does not depend on the matter Lagrangian. However, he considered the specific case \(f(R,T)=R+f(T)\). The case studied by Moraes is an advance on f(R, T) gravity research field, in the sense that now researchers have the possibility to study f(R, T) gravity with no need for choosing a specific matter Lagrangian, thus, working on a general basis. In addition to Moraes’ approach, we consider in this letter a generalization of his seminal idea. Here, we work with no specific case, so, the f(R, T) functional remains as arbitrary as possible. This study was inspired by the work of Fisher and Carlson [13], where they studied the on-shell Lagrangian problem in f(R, T) gravity. In their work, they suggest that only cross terms between matter and geometry could survive as a theory which brings new insights for the gravitational theory. Our work here is then presented as a possible way to eliminate the matter LagrangianFootnote 1 as a variable of the field equations. This is done for any f(R, T) functional, and hence it is also valid for cross terms between matter and geometry.

Another way to remove the matter Lagrangian form field equations is also presented here. Our approach was again motivated by the work of Fisher and Carlson [13], in the sense that they have shown that the energy–momentum tensor cannot be given by the perfect fluid definition. In this work, we take the general definition of the energy–momentum tensor to remove the dependence on matter Lagrangian of the field equations. We also argued that trace of the energy–momentum tensor becomes an unknown variable that can be obtained from the trace of the field equations. Hence, this approach unfolds two problems of the f(R, T) gravity, which are the Lagrangian choice one and the energy–momentum tensor that becomes not well-defined.

Finally, we have applied our results to cosmology, considering two specific cases: model I and model II. In the case of model I, we have shown the cosmological inviability of the functional, i.e., the linear case cannot explain a transition between a decelerated Universe to an accelerated one. Nevertheless, for the case II, where we have \(f(R,T)=R+\lambda T^2\), we found a viable functional which predicts a transition between an decelerated era to an accelerated one, being in agreement with the cosmological data without the introduction of dark energy.

Forthcoming applications of our approaches can be applied to flat rotation curves of galaxies, astrophysical systems and so on. Others functional are also encouraged.