1 Introduction

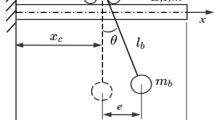
In recent years, more and more often, with the help of ships and vessels, they carry out the transportation of large-sized and heavy cargoes (loads), which, in the process of loading/unloading on board ships, require rather complex systems for suspending the cargo to the hook of the lifting device. Such a two-chain suspension system (arrangement) is shown in the Fig. 1 as an example. The arrangement in which the primary and secondary slings are fixed to the spreader at the same points (Figs. 1, 2) might be called as an arrangement with normal placement of the primary pivots or, simply, normal two-chain suspension arrangement. From the standpoint of the classical theory of stability of complex mechanical systems (Lagrange stability concept), such a two-chain suspension arrangements, due to the presence of several (two) degrees of freedom, are less stable than, for example, traditional (single-chain) load suspension systems.

Fig. 1
figure 1

Typical two-chain suspension arrangement of the load with normal placement of the primary pivots

Full size image
Fig. 2
figure 2

Flat model of the two-chain cargo suspension arrangement with normal placement of the primary pivots

Full size image

The issues of static and tip-over stability of the normal two-chain suspension arrangements of loads (Figs. 1, 2) have been explored by Kaps [1,2,3] and later, in detail, by Nikitin [4, 5]. Specifically, it has been shown that, such a spatial system (Fig. 1) is capable (for various reasons) of swinging (oscillating) relative to the suspension point in any direction (vertical plane). Nevertheless, as a first approximation, it can be assumed that the oscillations (rocking) of such a system mainly occur in two vertical and mutually perpendicular planes. Moreover, the line of intersection of the planes passes through the suspension point S (Fig. 2). Under these assumptions, the analysis of vibrations and stability of the spatial suspension system can be reduced to the study of its movement in these two planes, for which the real system can be replaced by two flat ones (as shown in Fig. 2).

In article [4], by the use of the Lagrange–Dirichlet stability concept [6,7,8,9,10], it has been proved that the stable equilibrium (or simply, static stability) of such flat two-chain suspension arrangement (system) can be ensured only on the condition that the gravity center of the load—GCL (point G in Fig. 2) is located inside a certain allowable area. In fact, this area is an isosceles triangle CDT (Fig. 2) called as stability triangle with the base CD and the height of which (zm) is not less than the height of the primary suspension chain (distance v in Fig. 2).

Note 1 In fact, the allowable area for the GCL position is not limited to the base CD, but extends below. In fact, this is not a triangle, but a sector with the center T bounded by the sides of the ST (Fig. 2). Since from a practical point of view the position of the GCL below the base CD is barely impossible, it is logical to limit the allowed area to the triangle CDT.

Note 2 Sometimes the load is not placed on the CD platform, but is attached to the secondary slings (Fig. 1). In this case, the segment connecting the CD attachment points plays the role of a platform.

During lifting operations, it is quite often when the pivots of the primary slings are placed narrower (Fig. 3) or wider (Fig. 4) than the pivots of the secondary slings. This occurs for various reasons, including due to a misunderstanding that this can reduce (worsen) the stability of the suspension system. Indeed, if the primary slings are fixed on the spreader AB close enough [in the limiting case—at the same point (Fig. 5)], then it is intuitively clear that this kind of suspension system will be very sensitive to the slightest transverse offset of the GCL, then is practically unstable. Nevertheless, there are a number of guidelines and articles [1, 2] following which it can be assumed that the distance (in particular, small distances) between the primary pivots does not have any effect on the stability of the suspension system as a whole. Therefore, the main purpose of this article is to fully clarify whether the distance between the primary pivots affects the stability of a two-chain suspension arrangement of a load or not.

Fig. 3
figure 3

Suspension arrangement with narrow placement of the primary pivots

Full size image
Fig. 4
figure 4

Suspension arrangement with wide placement of the primary pivots

Full size image
Fig. 5
figure 5

Limiting case: original position of the suspension system with narrow primary pivots (the primary pivots coincide each other and the stability triangle degenerates to the line segment OT)

Full size image

The manuscript includes several subsections: Sect. 1: Introduction (summarizes the relevance and main purpose of the article); Sect. 2: Methodology (outlines the basic techniques and methods to achieve the goal); Results (formulas are obtained for calculating the dimensions of the stability triangle for a narrow and wide position of the primary pivots, conditions are determined under which the narrow position of the primary pivots does not affect the stability of the system in comparison with the normal system); Sect. 3: Discussion (a comparative analysis of suspension systems with a narrow, normal and wide position of the primary pivots is carried out, the limiting case (when the distance between the primary pivots is zero) is also analyzed, a numerical example is considered as a demonstration); Sect. 4: Conclusion (general conclusions and proposals for further research are formulated).

2 Methodology

The study of the influence of the distance between the primary pivots on the stability of two-chain suspension systems will be carried out on the basis of the approach and results presented in [4, 5]. In our opinion, this is quite logical, since the stability of a system with a narrow or wide position of the primary pivots fits well into the general concept of stability of mechanical systems used in manuscripts [4, 5] and in this sense does not represent anything fundamentally new.

In work [4] and in this same, a study of the stability of the suspension was carried out under the next assumptions:

  1. 1.

    a system with a load was considered as a flat mechanical system of bodies with ideal restraints, having two degrees of freedom relative to a fixed suspension point S;

  2. 2.

    all flexible slings of the system (primary and secondary) are weightless and inelastic;

  3. 3.

    the load is securely fixed on the CD platform (base), therefore, both the load and the platform are considered in the analysis as one body, the mass of which is equal to their total mass (weight).

Under the above assumptions, using the Lagrange–Dirichlet theorem, the equations have been obtained that determine the necessary and sufficient conditions for a stable equilibrium of the system. These equations connect the main mass-dimensional characteristics of the suspension system \(\left( {v, \frac{p}{{P_{c} }}} \right)\), the coordinates of the GCL (x, z) with the tilting (slewing) angles of the primary (\(\propto\)) and secondary (\(\beta\)) suspension chains. These equations look as follows:

$$tg \propto = \frac{y}{{v\left( {\frac{p}{{P_{c} }} + 1} \right) - z}}$$
(1)
$$\beta = 0$$
(2)

Equations (1, 2) show that under conditions of stable equilibrium of the system [and regardless of the tilting angle of the primary suspension (SAB)—\(\propto\)], the slewing angle of the secondary suspension \((\beta )\) is always zero, that is, the secondary slings will be vertical. In addition, these equations do not include such a quantity as the length of the secondary slings (r). This means that their length has no effect on the stability of the two-chain suspension system. Thus, the necessary and sufficient conditions for the stable equilibrium of the system can be described by only one equation (1). Following the methodology outlined in [4], to assess the stability of the suspension system (no matter what the distance between the primary slings), it is necessary to determine the so-called stability triangle (ST): the permissible area of the position of the GCL relative to the suspension system. For this, it is necessary to put the latter in the so-called critical equilibrium position (conditions for the maximum deviation of the primary suspension chain (\(\propto_{m} )\) relative to the suspension point S). Specifically, for the normal suspension system the height of the ST (zm) as well as maximum tilting angle of the primary chain (\(\propto_{m} )\) can be calculated under condition that: y = l and z = 0 as follows [4]:

$$z_{m} = \left( {\frac{p}{{P_{c} }} + 1} \right)v$$
(3)
$$\propto_{m} = {\text{arctg}}\left[ {\frac{l}{{\left( {\frac{p}{{P_{c} }} + 1} \right)v}}} \right] = {\text{arctg}}\left[ {\frac{ctg\varphi }{{\left( {\frac{p}{{P_{c} }} + 1} \right)}}} \right]$$
(4)

In the comparative analysis of the stability of various suspension systems, it is assumed to use a fairly simple and obvious rule: the larger the area of the stability triangle, the higher it is, the better the stability of the suspension system.

3 Results

First, let us to explore the stability of a two-chain suspension arrangement with narrow placement of the primary pivots that shown in Fig. 3. Following the above methodology, put the suspension system in a critical position of stable equilibrium. This is possible if the GCL is placed at point G (\(y = y_{m}^{nr} ;z = 0)\) as shown in Fig. 6. The maximum tilting angle of the primary chain and base CD \({-} \propto_{m}^{nr}\) (as long as \(\beta = 0)\) cannot be more than the primary slings angle \(\varphi^{nr}\). (Otherwise, the integrity of linkages and constraints of the arrangement as a mechanical system will be destroyed, and the equilibrium stability will be lost as well.) So, the next inequity must be valid:

$$\propto_{m}^{nr} \le \varphi^{nr}$$
(5)
Fig. 6.
figure 6

Critical position of the stable equilibrium of the arrangement with narrow placement of the primary pivots (inequity 8 is valid)

Full size image

Taking into account inequity (5), the maximum transverse offset of the GCL (\(y_{m}^{nr}\)) can be determined from Eq. 1 (under condition that z = 0 and \(\propto = \varphi_{{}}^{nr}\)) as follows:

$$y_{m}^{nr} = v\left( {\frac{p}{{P_{c} }} + 1} \right){\text{tg}}\varphi^{nr}$$
(6)

As long as \((v \times {\text{tg}}\varphi^{nr} = l^{nr}\))—is half the distance between primary pivots (Fig. 3), then Eq. (6) might be represented as follows:

$$y_{m}^{nr} = \frac{{A^{nr} B^{nr} }}{2}\left( {\frac{p}{{P_{c} }} + 1} \right) = l^{nr} \left( {\frac{p}{{P_{c} }} + 1} \right)$$
(7)

If value of \(y_{m}^{nr}\) calculated by (6 or 7) is less than the half of the base CD (l), i.e.:

$$y_{m}^{nr} = l^{nr} \left( {\frac{p}{{P_{c} }} + 1} \right) < l$$
(8)

then, the maximum tilting angle:

$$\propto_{m}^{nr} = \varphi^{nr}$$
(9)

In addition, as long as: \(\varphi^{nr} < \varphi\), then angle \(\propto_{m}^{nr}\) is also less than the maximum tilting angle \(\propto_{m}^{{}}\) (calculated for the normal arrangement by Eq. 4).

For the arrangement with narrow primary pivots and provided that inequity (8) is valid (Fig.6), the base segment of the stability triangle (ST) is equaled to \(2y_{m}^{nr}\), i.e. might be determined as follows:

$$2y_{m}^{nr} = 2v\left( {\frac{p}{{P_{c} }} + 1} \right) = 2l^{nr} \left( {\frac{p}{{P_{c} }} + 1} \right)$$
(10)

and the height of this ST (Fig. 6):

$$z_{m}^{nr} = y_{m}^{nr} {\text{ctg}}\varphi^{nr} = v\left( {\frac{p}{{P_{c} }} + 1} \right) = l\left( {\frac{p}{{P_{c} }} + 1} \right){\text{ctg}}\varphi$$
(11)

Equation (11) is completely identical to Eq. (3) that determines the height of the ST for the normal arrangement.

If value of \(y_{m}^{nr}\) calculated by (6 or 7) is equaled to the half of the base CD (the GCL is placed at point D—Fig.7), then the maximum tilting angle of the system with narrow pivots is the same as for the normal suspension system (\(\propto_{m}^{nr} = \propto_{m} ).\) Consequently it might be calculated by Eq. (4). In other words, when inequity (8) is not valid, then the stability of the suspension system with narrow pivots is precisely the same as for a normal one.

Fig. 7.
figure 7

Critical position of stable equilibrium of the arrangement with narrow (or normal) placement of the primary pivots providing that equity (8) is not valid

Full size image

Second, let us to explore the stability of a two-chain suspension arrangement with wide placement of the primary pivots that shown in Fig. 4. Again, following the accepted methodology, put the suspension system in a critical position of stable equilibrium that shown in Fig. 8 (here, the GCL is placed at point C so that: \(y = l;\, z = 0).\) Such a position is really critical one with respect to stable equilibrium of the arrangement with wide primary pivots because any further offset of the GCL (from point C to the left) will cause the violation of linkages, constraints and integrity of the arrangement as a mechanical system; therefore, the loss of balance and stability.

Fig. 8.
figure 8

Critical position of the stable equilibrium of the arrangement with wide primary pivots placement

Full size image

Providing that all mass and geometric parameters of the arrangements with wide and normal primary pivots (except for the spreader length) are the same, the height of the ST (\(z_{m}^{w}\)) and maximum tilting angle \(\alpha_{m}^{w}\) of the primary chain of the arrangement with wide primary pivots can be determined by Eqs. (3) and (4) as follows:

$$z_{m}^{w} = z_{m} = \left( {\frac{p}{{P_{c} }} + 1} \right)v$$
(12)
$$\alpha_{m}^{w} = \propto_{m} = {\text{arctg}}\left[ {\frac{l}{{\left( {\frac{p}{{P_{c} }} + 1} \right)v }}} \right] ,$$
(13)

The base segment of the ST will be exactly the same as for the normal suspension system hence it will be equaled to length of the base CD (2l).

4 Discussion

Let us begin the discussion with an analysis of the stability of systems with narrow primary pivots. Equations (10), (11) show that, if inequity (8) is valid, then the ST area of the arrangement is less than for the normal arrangement. It happens due to reduction in the length of the base segment of the ST while the heights of both triangles are the same (Fig. 6).

From Eq. (10), it follows that the narrower the primary pivots are (the smaller the value of \(l^{nr}\)), then the smaller the base and the area of the ST and the narrower the stability triangle will be. Therefore, the stability of the system will be worse. Moreover, in the limiting case, when the distance between the primary pivots is zero [they are attached to the same point of the spreader AB (Fig. 5)], the ST degenerates into a line segment of length zm, the area of which is zero. In this case, it becomes quite obvious that with the slightest transverse offset of the GCL, the suspension system (with “rather narrow” pivots) becomes unstable. This limiting case shows how important it is to evaluate not only the permissible height of the GCL (zm), as was done in [1,2,3], but also the entire area of the permissible position of the GCL, that is, the dimensions of the stability triangle.

Note Examples of practical application of a suspension system with very little stability (almost zero area of the stability triangle) can be the lifting of a copy of the Santa Maria ship (Fig. 1.4) or the lifting of a catamaran hull (Fig. 1.6) given in [2].

Transforming inequity (8), it is possible to get the next:

$$\frac{{l^{nr} }}{l}\left( {\frac{p}{{P_{c} }} + 1} \right) < 1\;{\text{or}}\;\frac{l}{{l^{nr} }} > \left( {\frac{p}{{P_{c} }} + 1} \right)$$
(14)

The last expression shows that if the weight of the spreader AB is much less than the cargo weight [\(p \ll P_{c}\) and \(\left( {\frac{p}{{P_{c} }} + 1} \right) \approx 1]\), then inequities (14) and (8) as well are valid (due to \(\frac{l}{{l^{nr} }} > 1\)). That is, the stability of a system with narrow primary pivots, especially when the weight of spreader is much less than the weight of the load, is always worse than for a normal system.

On the other hand, the heavier the spreader AB, the more difficult it is to keep inequalities (8) and (14). In other words, as the weight of the spreader increases, then the stability of the system with narrow pivots more and more approaches the stability of the system with normal pivots. That is, the weight of the spreader plays a stabilizing role for the two-chain suspension system, regardless of the distance between the primary pivots.

As mentioned above, if the maximum transverse offset of the GCL (at which a system with narrow pivots can remain in stable equilibrium—Fig. 7) is equaled to the half-length of the base CD, then such a system has stability equal to that of a normal system.

Note Ratio \(\frac{l}{{l^{nr} }}\) might be less than \(\left( {\frac{p}{{P_{c} }} + 1} \right)\). This means that the GCL is located to the left of sling AC (to the left from point C of the base CD—Fig. 6) or to the right of sling BD (\(y_{m}^{nr} > l\)). In this case, the entire arrangement after its hanging will be definitely destroyed. Therefore, this case is not taken into account.

Thus, the decisive rule for determining whether the stability of a system with narrow pivots is the same as for a normal system is the observance of inequalities (8) or (14). It is noteworthy that for the same geometric dimensions (\(v, l, l^{nr} , \varphi , \varphi^{nr}\)) and the weight of the load (P), the fulfillment (or non-fulfillment) of inequality (8) depends on the mass (weight) of the spreader (p). The higher the mass of the spreader, the more likely it is that inequality (8) will not hold, and hence the stability of the suspension system will correspond to the normal system. And vice versa, with an insignificant weight of the spreader, inequality (8) will most likely be fulfilled, which means that the stability of the system will be less, since the ST will have a smaller base, and it must be calculated by formula (10).

As for the suspension system with wide primary pivots, then Eqs. (12) and (13) show even though the distance between primary pivots (2lw) is longer than secondary pivots distance (2l), there is no any effect on the stability of the arrangement at all. Consequently, using the spreader that is longer than the distance between secondary slings makes no sense. Nevertheless, if the spreader AwBw is not only longer than AB, but also heavier than the last one (\(p^{w} > p\)), then the stability of the arrangement with wide primary pivots is higher than the stability of the normal arrangement. Really, in this case, the ST height \(z_{m}^{w}\) (calculated by Eq. 12) is bigger than \(z_{m}^{{}}\) as long as:

$$\left( {\frac{{p^{w} }}{{P_{c} }} + 1} \right) > \left( {\frac{p}{{P_{c} }} + 1} \right)$$
(15)

Maximum tilting angle \(\alpha_{m}^{w}\) of the arrangement with wide primary pivots (calculated by Eq. 13) is smaller than for the normal arrangement due to inequity (15), too.

For greater clarity of the comparative analysis and demonstration of the practical application of the obtained methods for calculating the stability of systems with a narrow, normal and wide position of the primary pivots, consider a numerical example. The initial data on the mass-dimensional characteristics of the systems are presented in Table 1 (lines 1–7). It is necessary to determine:

  1. 1.

    the allowable area of the GCL placement (base side and height of the ST) and the maximum tilting angle \(\propto_{m}\) at which each of the systems will still hold the balance and stability;

  2. 2.

    the minimal primary slings angle \(\varphi_{min}^{nr}\) and the minimal distance between primary slings (\(2l_{min}^{nr}\)) at which the stability of the arrangement with narrow primary pivots will be the same as for the normal arrangement;

  3. 3.

    to carry out a comparative analysis of the stability of the considered systems, while answering the question of whether it was justified with such initial data to use a system with narrow primary pivots.

Table 1 Initial numerical data and the main results of calculating the stability of suspension arrangements with a normal, narrow and wide position of the primary pivots
Full size table

Solution

  1. 1.

    For the system with narrow pivots:

    • Using Eq. (6), value of \(y_{m}^{nr}\) is to be calculated as follows:

      $$y_{m}^{nr} = v\left( {\frac{p}{{P_{c} }} + 1} \right){\text{tg}}\varphi^{nr} = 4.44\left( {\frac{300}{{1600}} + 1} \right){\text{tg}}18^{0} = 1.713{\text{m}}.$$

    • As long as: \(y_{m}^{nr} = 1.713{\text{m}} < 4m\), then inequity (8) is valid. It means that the maximum tilting angle at which the suspension arrangement will still hold the balance and stability is: \(\propto_{m}^{nr} = \varphi^{nr} = 18^{0}\).

    • The height of the ST is to be calculated by Eq. (11) as follows:

      $$z_{m}^{nr} = y_{m}^{nr} {\text{ctg}}\varphi^{nr} = 1.713{\text{ctg}}18^{0} = 5.272{\text{m}}$$

      and its base side: \(2y_{m}^{nr} = 1.713 \times 2 = 3.426{\text{m}}\)

    • Minimal primary slings angle \(\varphi_{min}^{nr}\) at which the stability of the arrangement will be the same as for the normal arrangement might be calculated by Eq. (6):

      $$\varphi_{min}^{nr} = \propto_{m} = {\text{arctg}}\left[ {\frac{l}{{v\left( {\frac{p}{{P_{c} }} + 1} \right)}}} \right] = {\text{arctg}}\left[ {\frac{4}{5.2725}} \right] = 37,18^{0} .$$

    • The minimal distance between primary slings (\(2l_{min}^{nr}\)) at which the stability of the arrangement will be the same as for the normal one is to be calculated by Eq. (14):

      \(2l^{nr} = \frac{2l}{{\left( {\frac{p}{{P_{c} }} + 1} \right)}} = \frac{2 \times 4}{{\left( {\frac{30}{{160}} + 1} \right)}} = 6.74{\text{m}}\).

  1. 2.

    For the systems with normal and wide pivots:

    • by the use of Eqs. (3) and (12), the height of the ST is to be calculated as follows:

      \(z_{m} = z_{m}^{w} = \left( {\frac{p}{{P_{c} }} + 1} \right)v = \left( {\frac{300}{{1600}} + 1} \right)4.44 = 5.27{\text{m}}\).

    • The length of the ST base is the same as length of base AB, so it will be \(2l = 2 \times 4 = 8{\text{m}}\).

    • Maximum tilting angle at which the systems will be still stable are to be calculated by Eqs. (4) or (13):

      $$\propto_{m} = {\text{arctg}}\left[ {\frac{l}{{\left( {\frac{p}{{P_{c} }} + 1} \right)v}}} \right] = {\text{arctg}}\left[ {\frac{4}{{\left( {\frac{300}{{1600}} + 1} \right)4.44}}} \right] = 37.2^{0}$$

All numerical results calculated above are represented in Table 1 (lines 8–12). From these numbers, it might be seen that the area of the ST for the arrangement with narrow primary pivots is more than twice less than for the normal system (base of the ST: \(2y_{m}^{nr} = 3.426\;{\text{m}} < 2l = 8\;{\text{m}}\)). The minimal distance between primary pivots at which the arrangement will have the same stability as the normal one is 6.74 m (instead of 2.89 m according to the example).

Thus, our numerical example shows, that stability of the systems with normal and wide primary pivots are the same, and it is almost twice better than the stability of the system with narrow primary pivots. So, with such initial data, the use of a system with narrow primary pivots is hardly justified.

5 Conclusion

Thus, the study shows that the distance between the primary pivots of two-chain suspension systems can be important for its stability. Especially, this is critical when the primary pivots are located narrower than the secondary ones. Our study also shows how important it is when assessing the stability of two-chain suspension systems to calculate not only the maximum height of the safe position of the GCL (zm), but also the entire area where it can be located (that is, the dimensions of the stability triangle).

The research carried out also demonstrates the importance of the height of the primary chain of suspension (v) and the mass of the spreader AB (p) for ensuring the stability of the suspension system as a whole (regardless of what is the distance between the primary pivots). The higher primary chain of suspension (v) and the greater the mass of the spreader (more precisely, the ratio \(\frac{p}{{P_{c} }}\)), the greater the height and the area of the ST, which means the higher the stability of the system as a whole.

Further research in the field of studying the stability of two-chain suspension systems should be aimed at taking into account such factors as possible sudden offsets of the suspension point S (or its periodic oscillations), which is associated with the inclination (rolling) of the vessel, since in this and previous works the suspension point of the system was taken to be fixed.

In addition, since in this work suspension systems were studied only with parallel secondary slings, then in the future (if necessary) it is possible to continue studies of stability, taking into account the fact that the secondary slings may not initially be parallel.

Finally, in the future, not only static, but also dynamic stability of complex (multi-chain) load suspension systems should be considered and evaluated.