1 Introduction

Single ended primary inductance converter (SEPIC) is a switching mode DC–DC power converter which has the ability to reduce or boost the input voltage. It is comprised of 2 capacitor and 2 inductors as passive components and 2 active switching elements which are manipulated to control the output voltage. System input is a signal that is applied to the active switch. The applied continuous signal is passed through an PWM block and resulted signal is directly used to control the circuit. Input voltage and output current deviation from their steady-state values are considered to be disturbance signals due to the fact that in most cases those are not the signals that the system designer have control over [1, 2]. Besides being utilized in DC power conditioning, as it is the case in battery charging applications, SEPIC is also used in Active Power Factor Correction (APFC) and Total harmonic distortion (THD) minimization in AC systems by drawing the current that is determined by the control algorithm. Another prevalent utilization of SEPIC is Maximum Power Point Tracking (MPPT) application which is gaining more attention due to the increase in investments in the PV studies. SEPIC, as many power converters, has discontinuous nonlinear mathematical model [3, 4]. In addition to the nonlinearity that is inherent in the plant, a linear state space model from the duty cycle to the output voltage that is obtained by approximating the system about a determined operating point is non-minimum phase which constrains the closed loop bandwidth that is achievable which is also the case in boost converter. These factors contribute to the problem of state estimation. For system monitoring and for employing feedback control algorithms, states of the plant are required to be estimated reliably [5].

DC–DC converters depending on the application can have a critical role in the power conditioning systems and to prevent a possible fault which can result in the disruption of the whole system, thereby causing financial loss, it is crucial for some of the signals that are not directly measurable to be predicted. To prevent this kind of possible faults from occurring, system monitoring techniques which includes state estimation methods may be considered. State estimation is also required for control algorithms where states of the plant is required to generate the input signals to drive the error to zero. Although, there are advanced robust output feedback control algorithms [6,7,8,9] available in the literature where there is no demand for a state information, in the case of state being available gives the designer flexibility in producing a linear or nonlinear control laws. State estimators can also be employed to estimate the critical parameters of the plant where the parameters are considered to be additional states and the state vector is augmented [10]. Simultaneous state and parameter estimation if the model of the plant is reliable across a wide range of frequencies, can lead to adaptive control algorithms which are known to be robust to parameter variations.

SEPIC is often modeled as a 4-dimensional system which operates under CCM (continuous conduction mode) where the current in the inductors cannot attain to zero. For completely DC based applications, CCM mode assumption is made which leads to simple derivation process, as for systems where AC voltage is present either on the supply or the load side such as APFC, DCM (Discontinuous conduction mode) operation is considered and a model is derived based on that operation [11]. SEPIC can be modeled in such a way that not only the inductor currents and voltages across the capacitors are specified as states but in more advanced harmonic based modeling techniques, by considering the switching frequency, the harmonics of the current and voltage signals are considered as states of the plant as well which leads to the models where the current and voltage ripples can be accurately estimated and more complex behaviors of the plant can be investigated [12]. However, besides resonant converter applications where the switching frequency parameter can have a determining impact on the system, harmonic based modeling techniques are mainly employed in AC systems such as inverters, rectifiers and THD minimization systems, and their applications in DC circuits are limited [13]. To obtain a linear model, SSA (State space averaging) methods are used where all of the circuit configurations are modeled and state space representations are derived, then these state space models are averaged using the switching time period. Standard SSA results in linear state space models for the systems where the inputs are known to be such that the nonlinear dynamics are not triggered, this model can be preferred [14]. Another prevalent modeling technique, GSSA focuses on the effects of the switching frequency on the system which achieves that by considering the harmonic components, often truncating at second terms. In this paper, an extended version of SSA method is discussed, where the nonlinear small signal (deviation from steady state point) terms are not considered to be negligible to have a better estimate of the nonlinear dynamics which can be apparent when a fast-varying input signals are applied [15].

After the model is available, the state estimator can be designed. Since the model to be obtained is nonlinear, to have a better estimate of the states a nonlinear observer is studied. There are many robust nonlinear observers in the literature such as High Gain (HG) observer and Sliding Mode Observer (SMO). HG observers are designed by deriving transfer functions from nonlinear model uncertainty to estimation error and minimizing the \({\mathcal{H}}_{\infty }\) norm of this transfer function through the observer parameters [16]. Another nonlinear observer type, SMO uses switching functions to suppress the nonlinear terms and forces the error dynamics to be linear after a certain point [17]. Despite their performance, the design processes of the mentioned observers become intractable for the high dimensional systems. Another prevalent nonlinear observer EKF uses KF algorithms, where the disturbance signals are assumed to be gaussian in nature which in turn leads to significant simplifications in guaranteeing the observer convergence and the resulting model is easy to derive. EKF uses KF state estimation techniques, to generate the state space matrices which are used to update the error covariance matrix, in each time step the nonlinear model is linearized around the estimated states which is computed in a previous time step [18]. Although, this procedure requires the state matrices to be derived analytically before the design, unlike sigma point Kalman filter (SPKF) observers where there is not analytical derivation is required [19], for the relatively small dimensional systems this is not a considerable problem. In this paper, EKF is studied and the derivation is detailed for SEPIC. The performance of EKF is demonstrated by means of MATLAB based numerical simulations. Finally, to highlight the need for EKF over a linear state estimator for SEPIC, a comparative simulation is also presented.

This paper is organized as follows, in the Sect. 2, SEPIC approximated nonlinear small signal model is derived and discretization is addressed. In the Sect. 3, Kalman filter and EKF design steps are detailed and implementation for SEPIC is addressed. To present the EKF closed loop performance, LQI (linear Quadratic Integral) controller is explained. The simulations to present the operation of the observers are given in the Sect. 4. In addition to the nominal open-loop simulations, a series of separate simulations where the values of the circuit parameters are perturbed as the KF and EKF design left unchanged which is based on the nominal parameter values are detailed to examine the robustness properties of the estimators. Finally, the assessment of the observers and overall system performance are discussed in the Sect. 5.

2 Plant model

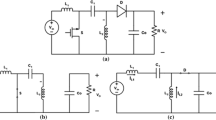
SEPIC converter is generally modeled as 3 input and 1 output system where the inputs can be stated as input voltage, output current and duty cycle of the signal that drives the active switch. The first two signals manifest themselves as disturbances due to the fact that in many applications these signals are generated by external factors such as, a supply line deviation and load variation. The SEPIC circuit diagram is given in Fig. 1.

Fig. 1
figure 1

SEPIC converter circuit [24]

Full size image

As it can be seen from the illustration, considering the inductor currents and the capacitance voltages, SEPIC is modeled as a 4-dimensional system. Due to the present discontinuity caused by the discrete component in the circuit, a complete and accurate mathematical model is not feasible for linear control-based applications. To obtain a more tractable model, traditionally state space averaging is employed. SSA method is detailed in [20], and obtained average large signal model is derived as,

$$\begin{aligned} & \frac{d}{dt}\left[ {\begin{array}{*{20}c} {i_{L1} } \\ {i_{L2} } \\ {v_{C1} } \\ {v_{C2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 & 0 & { - \frac{{\left( {1 - d} \right)}}{{L_{1} }}} & { - \frac{{\left( {1 - d} \right)}}{{L_{1} }}} \\ 0 & 0 & {\frac{d}{{L_{2} }}} & { - \frac{{\left( {1 - d} \right)}}{{L_{2} }}} \\ {\frac{{\left( {1 - d} \right)}}{{C_{1} }}} & { - \frac{d}{{C_{1} }}} & 0 & 0 \\ {\frac{{\left( {1 - d} \right)}}{{C_{2} }}} & {\frac{{\left( {1 - d} \right)}}{{C_{2} }}} & 0 & { - \frac{1}{{RC_{2} }}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{L1} } \\ {i_{L2} } \\ {v_{C1} } \\ {v_{C2} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\frac{1}{{L_{1} }}} & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & { - \frac{1}{{C_{2} }}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {v_{g} } \\ {i_{Load} } \\ \end{array} } \right], \\ & v_{o} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{L1} } \\ {i_{L2} } \\ {v_{C1} } \\ {v_{C2} } \\ \end{array} } \right] \\ \end{aligned}$$
(1)

which can be expressed in a compact form as,

$$\dot{x}_{ALSM} = A_{ALSM} x_{ALSM} + B_{ALSM} w_{ALSM}$$
(2)

where \(A_{ALSM}\) contains \(d\) term which denotes the large signal duty cycle term. It is also expected that \(B_{ALSM}\) to have \(d\) term, however for SEPIC, this is not the case, but this will lead to some simplifications further ahead. The subscript stands for average large signal model. To obtain the small signal dynamics, the following substitution is carried out,

$$A_{ALSM} = A_{D} + A_{{\Delta d}}$$
(3)
$$B_{ALSM} = B_{D} + B_{{{{\Delta }}d}}$$
(4)
$$x_{ALSM} = X + {{\Delta }}x$$
(5)
$$w_{ALSM} = \left[ {\begin{array}{*{20}c} {V_{g} } \\ {I_{Load} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\Delta v_{g} } \\ {\Delta i_{Load} } \\ \end{array} } \right]$$
(6)
$$d = D + {{\Delta }}d$$
(7)

where ALSM components are decomposed to their steady state and small signal parts. This leads to the following,

$$\frac{d}{dt}\left[ {X + {{\Delta }}x} \right] = \left[ {A_{D} + A_{{{{\Delta }}d}} } \right]\left[ {X + {{\Delta }}x} \right] + \left[ {B_{D} + B_{{{{\Delta }}d}} } \right]\left( {\left[ {\begin{array}{*{20}c} {V_{g} } \\ {I_{Load} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\Delta v_{g} } \\ {\Delta i_{Load} } \\ \end{array} } \right]} \right)$$
(8)

where the matrices are given explicitly as follows,

$$A_{D} = \left[ {\begin{array}{*{20}c} 0 & 0 & { - \frac{{\left( {1 - D} \right)}}{{L_{1} }}} & { - \frac{{\left( {1 - D} \right)}}{{L_{1} }}} \\ 0 & 0 & {\frac{D}{{L_{2} }}} & { - \frac{{\left( {1 - D} \right)}}{{L_{2} }}} \\ {\frac{{\left( {1 - D} \right)}}{{C_{1} }}} & { - \frac{D}{{C_{1} }}} & 0 & 0 \\ {\frac{{\left( {1 - D} \right)}}{{C_{2} }}} & {\frac{{\left( {1 - D} \right)}}{{C_{2} }}} & 0 & { - \frac{1}{{RC_{2} }}} \\ \end{array} } \right],A_{{{{\Delta }}d}} = \left[ {\begin{array}{*{20}c} 0 & 0 & {\frac{{{{\Delta }}d}}{{L_{1} }}} & {\frac{{{{\Delta }}d}}{{L_{1} }}} \\ 0 & 0 & {\frac{{{{\Delta }}d}}{{L_{2} }}} & {\frac{{{{\Delta }}d}}{{L_{2} }}} \\ {\frac{{ - {{\Delta }}d}}{{C_{1} }}} & {\frac{{ - {{\Delta }}d}}{{C_{1} }}} & 0 & 0 \\ {\frac{{ - {{\Delta }}d}}{{C_{2} }}} & {\frac{{ - {{\Delta }}d}}{{C_{2} }}} & 0 & 0 \\ \end{array} } \right]$$
(9)
$$B_{D} = \left[ {\begin{array}{*{20}c} {\frac{1}{{L_{1} }}} & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & { - \frac{1}{{C_{2} }}} \\ \end{array} } \right],B_{{{{\Delta }}d}} = \left[ {\begin{array}{*{20}c} 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ \end{array} } \right]$$
(10)
$$X = \left[ {\begin{array}{*{20}c} {I_{{L_{1} }} } \\ {I_{{L_{2} }} } \\ {V_{{C_{1} }} } \\ {V_{{C_{2} }} } \\ \end{array} } \right],{{\Delta }}x = \left[ {\begin{array}{*{20}c} {\Delta i_{{L_{1} }} } \\ {\Delta i_{{L_{2} }} } \\ {\Delta v_{{C_{1} }} } \\ {\Delta v_{{C_{2} }} } \\ \end{array} } \right]$$
(11)

where \(I_{{L_{1} }} ,I_{{L_{2} }} ,V_{{C_{1} }}\) and \(V_{{C_{2} }}\) are the steady state values of the states. The steady state terms are obtained as,

$$X = - A_{D}^{ - 1} B_{D} \left[ {\begin{array}{*{20}c} {V_{g} } \\ {I_{Load} } \\ \end{array} } \right]$$
(12)

Using this expression leads to the following,

$$\frac{d}{dt}\left[ {{{\Delta }}x} \right] = A_{D} {{\Delta }}x + A_{{{{\Delta }}d}} X + A_{{{{\Delta }}d}} {{\Delta }}x + B_{D} \left[ {\begin{array}{*{20}c} {\Delta v_{g} } \\ {\Delta i_{Load} } \\ \end{array} } \right]$$
(13)

where the 2nd and 3rd terms are explicitly can be written as,

$$\begin{aligned} & A_{\Delta d} X = \left[ {\begin{array}{*{20}c} {\left( {\frac{{V_{{C_{1} }} }}{{L_{1} }} + \frac{{V_{{C_{2} }} }}{{L_{1} }}} \right)} \\ {\left( {\frac{{V_{{C_{1} }} }}{{L_{2} }} + \frac{{V_{{C_{2} }} }}{{L_{2} }}} \right)} \\ { - \left( {\frac{{I_{{L_{1} }} }}{{C_{1} }} + \frac{{I_{{L_{2} }} }}{{C_{1} }}} \right)} \\ { - \left( {\frac{{I_{{L_{1} }} }}{{C_{2} }} + \frac{{I_{{L_{2} }} }}{{C_{2} }}} \right)} \\ \end{array} } \right]\Delta d, \\ & A_{\Delta d} \Delta x = \left[ {\begin{array}{*{20}c} {\frac{1}{{L_{1} }}\left( {\Delta v_{{C_{1} }} + \Delta v_{{C_{2} }} } \right)\Delta d} \\ {\frac{1}{{L_{2} }}\left( {\Delta v_{{C_{1} }} + \Delta v_{{C_{2} }} } \right)\Delta d} \\ {\frac{ - 1}{{C_{1} }}\left( {\Delta i_{{L_{1} }} + \Delta i_{{L_{2} }} } \right)\Delta d} \\ {\frac{ - 1}{{C_{2} }}\left( {\Delta i_{{L_{1} }} + \Delta i_{{L_{2} }} } \right)\Delta d} \\ \end{array} } \right] \\ \end{aligned}$$
(14)

By expanding individual terms, small signal dynamics are obtained as,

$$\frac{d}{dt}\left[ {\begin{array}{*{20}c} {\Delta i_{{L_{1} }} } \\ {\Delta i_{{L_{2} }} } \\ {\Delta v_{{C_{1} }} } \\ {\Delta v_{{C_{2} }} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 & 0 & { - \frac{{\left( {1 - D} \right)}}{{L_{1} }}} & { - \frac{{\left( {1 - D} \right)}}{{L_{1} }}} \\ 0 & 0 & {\frac{D}{{L_{2} }}} & { - \frac{{\left( {1 - D} \right)}}{{L_{2} }}} \\ {\frac{{\left( {1 - D} \right)}}{{C_{1} }}} & { - \frac{D}{{C_{1} }}} & 0 & 0 \\ {\frac{{\left( {1 - D} \right)}}{{C_{2} }}} & {\frac{{\left( {1 - D} \right)}}{{C_{2} }}} & 0 & { - \frac{1}{{RC_{2} }}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\Delta i_{{L_{1} }} } \\ {\Delta i_{{L_{2} }} } \\ {\Delta v_{{C_{1} }} } \\ {\Delta v_{{C_{2} }} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\left( {\frac{{V_{{C_{1} }} }}{{L_{1} }} + \frac{{V_{{C_{2} }} }}{{L_{1} }}} \right)} \\ {\left( {\frac{{V_{{C_{1} }} }}{{L_{2} }} + \frac{{V_{{C_{2} }} }}{{L_{2} }}} \right)} \\ { - \left( {\frac{{I_{{L_{1} }} }}{{C_{1} }} + \frac{{I_{{L_{2} }} }}{{C_{1} }}} \right)} \\ { - \left( {\frac{{I_{{L_{1} }} }}{{C_{2} }} + \frac{{I_{{L_{2} }} }}{{C_{2} }}} \right)} \\ \end{array} } \right]{{\Delta }}d + \left[ {\begin{array}{*{20}c} {\frac{1}{{L_{1} }}\left( {{{\Delta }}v_{{C_{1} }} + {{\Delta }}v_{{C_{2} }} } \right)\Delta d} \\ {\frac{1}{{L_{2} }}\left( {{{\Delta }}v_{{C_{1} }} + {{\Delta }}v_{{C_{2} }} } \right)\Delta d} \\ {\frac{ - 1}{{C_{1} }}\left( {{{\Delta }}i_{{L_{1} }} + {{\Delta }}i_{{L_{2} }} } \right)\Delta d} \\ {\frac{ - 1}{{C_{2} }}\left( {{{\Delta }}i_{{L_{1} }} + {{\Delta }}i_{{L_{2} }} } \right)\Delta d} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\frac{1}{{L_{1} }}\Delta v_{g} } \\ 0 \\ 0 \\ {\frac{ - 1}{{C_{2} }}\Delta i_{Load} } \\ \end{array} } \right]$$
(15)

For a complete linear model, the third term is ignored. From now on, the following notational changes are introduced to simplify the manipulations further ahead,

$$\left[ {x_{1} x_{2} x_{3} x_{4} } \right]^{T} \text{ := }\left[ {{{\Delta }}i_{{L_{1} }} {{\Delta }}i_{{L_{2} }} {{\Delta }}v_{{C_{1} }} {{\Delta }}v_{{C_{2} }} } \right]^{T}$$
(16)
$$\left[ {w_{1} w_{2} } \right]^{T} \text{ := }\left[ {{{\Delta }}v_{g} {{\Delta }}i_{Load} } \right]^{T}$$
(17)
$$u\text{ := }{{\Delta }}d$$
(18)

Using the given substitutions, the ZOH discretized version of the approximated nonlinear small signal model for SEPIC is obtained explicitly as,

$$x_{1} \left( {k + 1} \right) = \left[ {\left( { - \frac{{\left( {1 - D} \right)}}{{L_{1} }}} \right)x_{3} \left( k \right) + \left( { - \frac{{\left( {1 - D} \right)}}{{L_{1} }}} \right)x_{4} \left( k \right) + \left( {\frac{{V_{{C_{1} }} }}{{L_{1} }} + \frac{{V_{{C_{2} }} }}{{L_{1} }}} \right)u\left( k \right) + \left( {\frac{1}{{L_{1} }}} \right)w_{1} \left( k \right) + \left( {\frac{1}{{L_{1} }}} \right)\left( {x_{3} \left( k \right) + x_{4} \left( k \right)} \right)u\left( k \right)} \right]T_{s} + x_{1} \left( k \right)$$
(19)
$$x_{2} \left( {k + 1} \right) = \left[ {\left( {\frac{D}{{L_{2} }}} \right)x_{3} \left( k \right) + \left( { - \frac{{\left( {1 - D} \right)}}{{L_{2} }}} \right)x_{4} \left( k \right) + \left( {\frac{{V_{{C_{1} }} }}{{L_{2} }} + \frac{{V_{{C_{2} }} }}{{L_{2} }}} \right)u\left( k \right) + \left( {\frac{1}{{L_{2} }}} \right)\left( {x_{3} \left( k \right) + x_{4} \left( k \right)} \right)u\left( k \right)} \right]T_{s} + x_{2} \left( k \right)$$
(20)
$$x_{3} \left( {k + 1} \right) = \left[ {\left( {\frac{{\left( {1 - D} \right)}}{{C_{1} }}} \right)x_{1} \left( k \right) + \left( {\frac{ - D}{{C_{1} }}} \right)x_{2} \left( k \right) - \left( {\frac{{I_{{L_{1} }} }}{{C_{1} }} + \frac{{I_{{L_{2} }} }}{{C_{1} }}} \right)u\left( k \right) + \left( {\frac{ - 1}{{C_{1} }}} \right)\left( {x_{1} \left( k \right) + x_{2} \left( k \right)} \right)u\left( k \right)} \right]T_{s} + x_{3} \left( k \right)$$
(21)
$$x_{4} \left( {k + 1} \right) = \left[ {\left( {\frac{{\left( {1 - D} \right)}}{{C_{2} }}} \right)x_{1} \left( k \right) + \left( {\frac{{\left( {1 - D} \right)}}{{C_{2} }}} \right)x_{2} \left( k \right) + \left( {\frac{ - 1}{{RC_{2} }}} \right)x_{4} \left( k \right) - \left( {\frac{{I_{{L_{1} }} }}{{C_{2} }} + \frac{{I_{{L_{2} }} }}{{C_{2} }}} \right)u\left( k \right) + \left( {\frac{ - 1}{{C_{2} }}} \right)w_{2} \left( k \right) + \left( {\frac{ - 1}{{C_{2} }}} \right)\left( {x_{1} \left( k \right) + x_{2} \left( k \right)} \right)u\left( k \right)} \right]T_{s} + x_{4} \left( k \right)$$
(22)

where \(T_{s}\) is sample period. This is written in a compact form as,

$$x\left( {k + 1} \right) = f\left( {x\left( k \right),u\left( k \right),w\left( k \right)} \right)$$
(23)
$$\begin{aligned} y\left( k \right) & = g\left( {x\left( k \right),u\left( k \right),w\left( k \right)} \right) \\ & = x_{4} + v \\ \end{aligned}$$
(24)

where \(v\) is defined as the sensor noise, \(f\) is nonlinear state function, \(g\) is measurement function, \(y\) is the measurement.

3 Observer design

3.1 KF design

Before discussing the EKF, in this subsection KF is discussed to facilitate the explanation of EKF. For a discrete linear system whose dynamics are given as,

$$x\left( k \right) = A\left( {k - 1} \right)x\left( {k - 1} \right) + B\left( {k - 1} \right)u\left( {k - 1} \right) + B_{w} \left( {k - 1} \right)w\left( {k - 1} \right)$$
(25)
$$y\left( k \right) = C\left( k \right)x\left( k \right) + D\left( k \right)u\left( k \right) + D_{v} \left( k \right)v\left( k \right)$$
(26)

where \(A,B,C,D,B_{w} ,D_{v}\) matrices are state matrices. The KF equations for the given linear system are given as,

$$\hat{x}\left( {k|k - 1} \right) = A\left( {k - 1} \right)\hat{x}\left( {k - 1} \right) + B\left( {k - 1} \right)u\left( {k - 1} \right)$$
(27)
$$P\left( {k|k - 1} \right) = A\left( {k - 1} \right)P\left( {k - 1} \right)A^{T} \left( {k - 1} \right) + B_{w} \left( {k - 1} \right)Q\left( {k - 1} \right)B_{w}^{T} \left( {k - 1} \right)$$
(28)
$$K\left( k \right) = P\left( {k|k - 1} \right)C^{T} \left( k \right)\left[ {C\left( k \right)P\left( {k|k - 1} \right)C^{T} \left( k \right) + D_{v} \left( k \right)R\left( k \right)D_{v}^{T} \left( k \right)} \right]^{ - 1}$$
(29)
$$\hat{x}\left( k \right) = \hat{x}\left( {k|k - 1} \right) + K\left( k \right)\left[ {y\left( k \right) - C\left( k \right)\hat{x}\left( {k|k - 1} \right)} \right]$$
(30)
$$P\left( k \right) = \left[ {I - K\left( k \right)C\left( k \right)} \right]P\left( {k|k - 1} \right)$$
(31)

where \(A\left( {k - 1} \right),B\left( {k - 1} \right),C\left( {k - 1} \right)\) matrices are standard state marices, this variable names are chosen to prevent any confusion between the state matrices that are given in the previous section and the state matrices that are generated by the EKF in the next subsection. In (Eq. 25), the state time update is performed. The (Eq. 26) describes the state error covariance matrix time update. In (Eq. 27), the Kalman gain is computed which is the gain factor of the error between the KF output estimated and real measured output, which is called innovation term given in (Eq. 28). In the final step, the state error covariance matrix is corrected considering the calculated Kalman gain. \(Q\) and \(R\) are KF parameters to be chosen, known as process noise covariance and sensor noise covariance matrices, respectively. They are determined considering the effect of each noise term on the estimation performance. In addition to those 2 parameters, initial state estimate, \(\hat{x}\left( 0 \right)\) and initial state error covariance matrix, \(P\left( {k - 1} \right)\) are selected [21].

3.2 EKF design

The nonlinear discrete time system, whose dynamics are given as,

$$x\left( k \right) = f\left( {x\left( {k - 1} \right),u\left( {k - 1} \right),w\left( {k - 1} \right)} \right)$$
(32)
$$y\left( k \right) = g\left( {x\left( k \right),u\left( k \right),v\left( k \right)} \right)$$
(33)

where the state equation and measurement equation are both considered to be nonlinear. In addition to that, the effects of the process and sensor noises on the system are considered to be nonlinear by using this general form. The linearized version of the dynamics is given as,

$$x\left( k \right) = \underbrace {{\left[ {\left. {\frac{\partial f}{\partial x}} \right|_{{\begin{array}{*{20}c} {x = x\left( {k - 1} \right)} \\ {u = u\left( {k - 1} \right)} \\ {w = w\left( {k - 1} \right)} \\ \end{array} }} } \right]}}_{{\hat{A}\left( {k - 1} \right)}}x\left( {k - 1} \right) + \underbrace {{\left[ {\left. {\frac{\partial f}{\partial u}} \right|_{{\begin{array}{*{20}c} {x = x\left( {k - 1} \right)} \\ {u = u\left( {k - 1} \right)} \\ {w = w\left( {k - 1} \right)} \\ \end{array} }} } \right]}}_{{\hat{B}\left( {k - 1} \right)}}u\left( {k - 1} \right) + \underbrace {{\left[ {\left. {\frac{\partial f}{\partial w}} \right|_{{\begin{array}{*{20}c} {x = x\left( {k - 1} \right)} \\ {u = u\left( {k - 1} \right)} \\ {w = w\left( {k - 1} \right)} \\ \end{array} }} } \right]}}_{{\hat{B}_{w} \left( {k - 1} \right)}}w\left( {k - 1} \right)$$
(34)
$$y\left( k \right) = \underbrace {{\left[ {\left. {\frac{\partial f}{\partial x}} \right|_{{\begin{array}{*{20}c} {x = x\left( k \right)} \\ {u = u\left( k \right)} \\ {w = w\left( k \right)} \\ \end{array} }} } \right]}}_{{\hat{C}\left( k \right)}}x\left( k \right) + \underbrace {{\left[ {\left. {\frac{\partial f}{\partial u}} \right|_{{\begin{array}{*{20}c} {x = x\left( k \right)} \\ {u = u\left( k \right)} \\ {w = w\left( k \right)} \\ \end{array} }} } \right]}}_{{\hat{D}\left( k \right)}}u\left( k \right) + \underbrace {{\left[ {\left. {\frac{\partial f}{\partial v}} \right|_{{\begin{array}{*{20}c} {x = x\left( k \right)} \\ {u = u\left( k \right)} \\ {w = w\left( k \right)} \\ \end{array} }} } \right]}}_{{\hat{D}_{v} \left( k \right)}}v\left( k \right)$$
(35)

The EKF steps are given as,

$$\hat{A}\left( {k - 1} \right) = \left. {\frac{\partial f}{\partial x}} \right|_{{\begin{array}{*{20}c} {x = \hat{x}\left( {k - 1} \right)} \\ {u = u\left( {k - 1} \right)} \\ {w = \bar{w}} \\ \end{array} }} ,\;\hat{B}_{w} \left( {k - 1} \right) = \left. {\frac{\partial f}{\partial w}} \right|_{{\begin{array}{*{20}c} {x = \hat{x}\left( {k - 1} \right)} \\ {u = u\left( {k - 1} \right)} \\ {w = \bar{w}} \\ \end{array} }}$$
(36)
$$\hat{x}\left( {k|k - 1} \right) = f\left( {\hat{x}\left( {k - 1} \right),u\left( {k - 1} \right),\bar{w}} \right)$$
(37)
$$P\left( {k|k - 1} \right) = A\left( {k - 1} \right)P\left( {k - 1} \right)A^{T} \left( {k - 1} \right) + B_{w} \left( {k - 1} \right)Q\left( {k - 1} \right)B_{w}^{T} \left( {k - 1} \right)$$
(38)
$$\hat{C}\left( k \right) = \left. {\frac{\partial g}{\partial x}} \right|_{{\begin{array}{*{20}c} {x = \hat{x}\left( {k|k - 1} \right)} \\ {u = u\left( k \right)} \\ {w = \bar{w}} \\ \end{array} }} ,\;\hat{D}_{v} \left( k \right) = \left. {\frac{\partial g}{\partial v}} \right|_{{\begin{array}{*{20}c} {x = \hat{x}\left( {k|k - 1} \right)} \\ {u = u\left( k \right)} \\ {w = \bar{w}} \\ \end{array} }}$$
(39)
$$K\left( k \right) = P\left( {k|k - 1} \right)C^{T} \left( k \right)\left[ {C\left( k \right)P\left( {k|k - 1} \right)C^{T} \left( k \right) + D_{v} \left( k \right)R\left( k \right)D_{v}^{T} \left( k \right)} \right]^{ - 1}$$
(40)
$$\hat{x}\left( k \right) = \hat{x}\left( {k|k - 1} \right) + K\left( k \right)\left[ {y\left( k \right) - g\left( {x\left( k \right),u\left( k \right),\bar{v}} \right)} \right]$$
(41)
$$P\left( k \right) = \left[ {I - K\left( k \right)C\left( k \right)} \right]P\left( {k|k - 1} \right)$$
(42)

where \(\bar{w}\) and \(\bar{v}\) are the estimated mean values of the process and sensor noise signals, in most application they are assumed to be zero, but if there is a prior knowledge about their mean values, the information can be contributed these terms. In (Eq. 36), the \(\hat{A}\left( {k - 1} \right)\) and \(\hat{B}_{w} \left( {k - 1} \right)\) matrices are computed using the input to the system and state value estimate which is computed in the previous time step. In (Eq. 37), the state prediction is performed using the system nonlinear model information only. In (Eq. 38), state error covariance matrix is updated using the state matrices that are computed in (Eq. 36). (Equation 38) is used to compute measurement equation matrices around the state prediction and input values. Kalman filter gain is calculated in (Eq. 39) as this is the case in KF, given in (Eq. 29). Finally, state estimate using the Kalman filter gain weighted innovation value and state error covariance matrix is updated [22].

The linearized system state matrices for SEPIC, using the discrete time small signal approximated nonlinear functions, given in (Eq. 32) and (Eq. 33) are derived explicitly as,

$$\hat{A}\left( {k - 1} \right) = \left. {\left[ {\begin{array}{*{20}c} 1 & 0 & { - \frac{{\left( {1 - D} \right)}}{{L_{1} }}T_{s} + \frac{1}{{L_{1} }}T_{s} u} & { - \frac{{\left( {1 - D} \right)}}{{L_{1} }}T_{s} + \frac{1}{{L_{1} }}T_{s} u} \\ 0 & 1 & {\frac{D}{{L_{2} }}T_{s} + \frac{1}{{L_{2} }}T_{s} u} & { - \frac{{\left( {1 - D} \right)}}{{L_{2} }}T_{s} + \frac{1}{{L_{2} }}T_{s} u} \\ {\frac{{\left( {1 - D} \right)}}{{C_{1} }}T_{s} + \frac{ - 1}{{C_{1} }}T_{s} u} & { - \frac{D}{{C_{1} }}T_{s} + \frac{ - 1}{{C_{1} }}T_{s} u} & 1 & 0 \\ {\frac{{\left( {1 - D} \right)}}{{C_{2} }}T_{s} + \frac{ - 1}{{C_{2} }}T_{s} u} & {\frac{{\left( {1 - D} \right)}}{{C_{2} }}T_{s} + \frac{ - 1}{{C_{2} }}T_{s} u} & 0 & 1 \\ \end{array} } \right]} \right|_{\begin{subarray}{l} x = \hat{x}(k - 1) \\ u = u(k - 1) \end{subarray} }$$
(43)
$$\hat{B}_{w} \left( {k - 1} \right) = \left[ {\begin{array}{*{20}c} {\frac{1}{{L_{1} }}T_{s} } & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & { - \frac{1}{{C_{2} }}T_{s} } \\ \end{array} } \right]$$
(44)
$$\hat{C}\left( k \right) = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 1 \\ \end{array} } \right]$$
(45)
$$\hat{D}_{v} \left( k \right) = \left[ 1 \right]$$
(46)

This state matrices are computed numerically in each time step in order to update the Kalman gain, state and state error covariance matrices in EKF.

3.3 LQI design

Linear quadratic regulator uses a static gain matrix and determines an input to be supplied to the plant that is controlled. For a given linear discrete time system,

$$x\left( {k + 1} \right) = Ax\left( k \right) + Bu\left( k \right)$$
(47)
$$y\left( k \right) = Cx\left( k \right)$$
(48)

The control law is given as,

$$u\left( k \right) = - K_{LQR} x\left( k \right)$$
(49)

where \(K_{LQR}\) is the static state feedback gain matrix. The closed loop dynamics resulting in employing this control law is given as,

$$x\left( {k + 1} \right) = \left[ {A - BK_{LQR} } \right]x\left( k \right)$$
(50)

Consequently, by changing the \(K_{LQR}\) static gain matrix, eigenvalues of the closed loop state matrix \(\left[ {A - BK_{LQR} } \right]\) can be assigned, therefore the control is achieved. As for the Linear Quadratic Integral controller, for reference tracking applications and to suppress the non-zero mean disturbance signals, integral of error between the desired output signal and measured output signal is introduced. Integrated error state is denoted by \(x_{i} \left( k \right)\) [23]. System states \(x\left( k \right)\) are augmented as

$$x_{a} \left( k \right) = \left[ {\begin{array}{*{20}c} {x\left( k \right)} \\ {x_{i} \left( k \right)} \\ \end{array} } \right]$$
(51)

Again, for reference tracking and for the closed system to have an integral control type of property, augmented state vector is considered.

By applying the same procedure, and augmented static gain matrix is calculated, so that the eigenvalues of the augmented dynamics are located at the desired locations, therefore the control and reference tracking is achieved. The procedure is illustrated by the block diagram given in Fig. 2.

Fig. 2
figure 2

State observer based LQI control for SEPIC [24]

Full size image

4 Numerical simulations

4.1 About the system simulated

In this section, to assess the performance of the EKF whose design process are detailed in the previous section, an open loop and close loop simulations are carried out.

The parameters of the SEPIC simulated are given in the Table 1 above [24]. The parameters are used, and the simulation is carried out using MATLAB/powersim toolbox.

Table 1 The circuit parameters
Full size table

4.2 Open loop simulations

In the first simulation, the system is subjected to the input signal that is a sinusoidal whose frequency increases as time progresses. The initial frequency of this chirp input signal is \(10 \,{\text{Hz}}\) and this frequency is increased linearly. At the \(t = 0.1\,{\text{s}}\), the frequency reaches at \(100\,{\text{Hz}}\). The real small signal states are compared with the estimated ones by the linear and nonlinear estimators. The results are given in Fig. 3.

Fig. 3
figure 3

Comparison of EKF and KF in estimating the SEPIC states a x1, b x2, c x3, d x4

Full size image

As it can be illustrated in the figures, the initial performances of the KF and EKF estimators are close and these estimators are able to accurately estimate the real states. However, as the frequency of the input signal gradually increases over time, since this fast changing input signal is capable of triggering the nonlinear dynamics to become apparent, KF estimated states drifts from the true states, whereas EKF is able to accurately estimate even when these nonlinear dynamics becomes prominent. The performance differences of the estimators especially become clear for the \(x_{1}\) and \(x_{2}\) states.

4.3 Open loop simulations under parameter uncertainty

In this section, to assess the robustness of the estimators to parameter variations, values of the parameters of the circuit is perturbed up to 30%. The parameters that are perturbed are \(L_{1} , L_{2} , C_{1} ,C_{2} ,R,D\). To test the accuracy of the estimators, EKF and KF are built on the parameters that are listen in Table 1, and simulated on the same SEPIC circuit whose parameter values deviate up to 30%. To illustrate the results of these simulations, in Fig. 5, estimation error of each state is given for the KF and EKF. To induce the nonlinear dynamics, a chirp signal input is applied to the SEPIC, which is given in Fig. 4.

Fig. 4
figure 4

The applied input signal to the SEPIC

Full size image

This input signal is chosen to cause the small nonlinear terms to become more prominent. As these nonlinear terms increase, the estimation performance of EKF over KF becomes clear (Fig. 5).

Fig. 5
figure 5

State estimation errors of the EKF and KF under a series of simulations to test parameter uncertainty

Full size image

It is also important to indicate that after \(t = 0.07\,{\text{s}}\), as the frequency of the applied input increases and the nonlinear terms dominate the dynamics, the estimation performance of the KF degrades significantly as the performance level of the EKF stays steady.

4.4 Closed loop simulations

In this section, the EKF performance is also tested in a closed loop where a discrete time LQI control law is employed. Simulation scenario can be summarized as follows, at \(t = 2 \,{\text{s}}\), input voltage is changed from \(12 \,{\text{V}}\) to \(14 \,{\text{V}}\), at \(t = 4 \,{\text{s}}\), the current that is drawn from the converter is increased from \(1.33 \,{\text{A}}\) to \(1.53 A\), and finally, at \(t = 6 \,{\text{s}}\), the reference output voltage that the converter outputs is increased from \(15 \,{\text{V}}\) to \(18 \,{\text{V}}\). \(Q\) and \(R\) are as identity matrices of suitable dimensions as the controller parameters and the rationale behind this is addressed in [24].

The output signal as a large signal is given in Fig. 6, where it is apparent that the control law in cooperation with the EKF is capable of maintaining the stable operation, despite of the disturbances and reference change applied to the system during the operation.

Fig. 6
figure 6

Comparison of output and reference voltages as the system is disturbed

Full size image

5 Conclusion

In this study, SEPIC converter approximate nonlinear model is derived by using the conventional state space averaging technique and considering the nonlinear small signal terms that are usually neglected for the sake of obtaining a completely linear model. The resulted approximated nonlinear small signal model, then is used to design an EKF to estimate the plant states during the operation. To assess the performance of the EKF, open loop as well as closed loop simulations are conducted, where in the closed-loop simulations, a liner control algorithm is employed. To explain the need for an EKF over KF whose design process is detailed in section IV, an open loop simulation is set up where a chirp signal injected to the system. As the frequency of this small signal duty cycle is increased linearly, KF performance degrades due to the fact that this increase in the frequency causes the nonlinear dynamics to be apparent, which is not considered by the KF. Unlike KF, EKF performance remains steady since it is designed such a way that the neglected nonlinear dynamics are considered to a degree in the design procedure of EKF. In the final simulation, to demonstrate that the utilization of the EKF into the closed loop does not cause any instability, LQI control law is also used and the output voltage level is controlled through the control algorithm. As seen from the results, the closed loop system is capable of suppressing the effects of the disturbances. Although, EKF has a higher computational cost compared with a KF, since in addition to the standard operations of KF, EKF also linearizes the model in order to obtain the state matrices, in each time step. For the more critical and expensive active power factor correction applications, where the state monitoring is of crucial importance and the normally neglected nonlinearities may have a determining effect on the operation, these types of more elaborate designs to estimate the states may be warranted.