Free vibration analysis of infinitely long thick-walled hollow elliptical cylinder

Abstract

Various shell theories have been used in the past to study the free vibration of the elliptic cylindrical shells. However, as the thickness ratio of the shell increases, the accuracy of the results for shear deformation theories declines. In this article, the classical theory of elasticity is employed to study the free vibration of a thick cylinder with an elliptic cross-section. The milestone of the analytically established model is based on Navier’s equation, Helmholtz decomposition and Mathieu equations. The new model would specifically be applicable to the high thickness ratios where the structure response becomes highly complex and the high-order shell theories fail to obtain accurate results. Numerical example have been conducted in order to show the key effect of the cylinder’s aspect ratio on the dispersion curve and deformed mode shape of the elliptical cylinder. Finally, the validity of the proposed analytical solution was compared to a finite element simulation in Comsol Multiphysics.

1 Introduction

The majority of literature regarding the free vibration of shells are limited to specific shapes such as sphere, cylinder, and plate [1,2,3,4,5,6,7]. Recently, multidisciplinary research has drawn scientists’ attention to investigate other complex structural shapes [8,9,10,11]. For instance, the biomedical practice of vibration of bone modeling has necessitated using non-circular cylindrical shells.

In this regard, Ethier and Simmons [12], Kelley [13] considered the reflection of waves in the branching of blood vessels. Casciaro et al. [14], Jaganathan et al. [15] worked on hemodynamic computational modeling by wave propagation in blood vessels. Papathanasiou et al. [16], Auricchio et al. [17] compared the natural frequencies of different types of metallic structure of heart stent. Mesh-free method has been also used to handle complicated geometries [18,19,20]. Tanaka et al. [21] used the mixed-mode stress resultant intensity factors (SRIFs) to study a cracked folded structures.

An encyclopedic treatment of vibration of circular and non-circular cylindrical shell expresses more than 500 references for circular cylindrical shells while only a few references dealing with non-circular cylindrical shells [22]. Donnell [23] presented a new theory for thin shell buckling during axial compression and bending. The theory has been applicable for many projects done by researchers. Karman [24] considered the stability of circular cylindrical shells by experiment and analytical solution. The results show that the linear modeling is not reliable to predict buckling phenomena. Conversely, nonlinear analysis can create a safe design.

Amabili et al. [25, 26] considered free and forced vibration of circular cylindrical shells for the case of those empty and filled by fluid. Their results express the traveling wave response close to resonance. There is a good agreement between their numerical results with the work of other researchers in this field [27,28,29]. Amabili et al. [30,31,32,33] used Donnell’s nonlinear shell theory to investigate the forced vibration of circular cylindrical shells with simply supported boundary conditions. Amabili [34] studied vibration of cylindrical shells for large deformation along with excitation near lowest resonance. Amabili et al. [35], Pellicano et al. [36] considered internal resonance problems for a shell filled with water using both modal point excitations.

Laing et al. [37], Foale et al. [38], Amiro and Prokopenko [39] considered the vibration of circular cylindrical panel under radial loading. Three different methods such as the Galerkin method, the nonlinear Galerkin method and the post-processed Galerkin method have been used in this study. As a result, the post-processed Galerkin method is known as the best method compared to other methods. Kubenko and Kovalchuk [40] studied vibration of the circular cylindrical shell by following Donnell’s theory along with Galerkin method. They included driven and companion modes in their study, but they did not investigate axisymmetric terms in the mode expansion. Nagal and Yamaguchi [41] considered shallow cylindrical panels by performing an accurate study of chaotic motion. A complete literature review regarding vibration of cylindrical shells with circular-cross section has been performed by Leissa [22], Kumar et al. [42].

The vibration modeling of cylindrical shells with the non-circular cross-section is important due to its application in some structures such as aircraft wings, acoustic mufflers, acoustic transducers, and fuselages. Pusey and Sewall [43] studied experimental and numerical analysis of the elliptical cylindrical shell. The eccentricities of shells change from zero to 0.916. The results show a good agreement between mode shapes and frequencies of experimental and analytical work.

Shirakawa and Morita [44] presented a free vibration of an elliptical cylinder under external pressure. They used the composition of two circular arcs to show the elliptical cross-section. The effect of out-of-roundness on natural frequency is investigated. Suzuki [45] proposed a new method to analyze the vibration of a non-circular cross-section of cylindrical shells. The method is applicable to in-flight structure, chemical plants, and nuclear plants. It also can be applied to various types of non-circular cylindrical shells. For freely supported ends, they obtained natural frequencies and mode shapes. Yamada et al. [46] worked on tabulating of natural frequencies of elliptical cylindrical shells by six boundary condition combinations. Hayek and Boisvert [47] derived the vibration equation of an elliptical cylindrical shell using the Ritz approach. They used an assumption in the thickness of the shell to allow the feasibility of numerical results. The assumption was acceptable for a specific range of frequencies but not for all.

Suzuki and Leissa [48] used an exact solution to solve free vibration of non-circular cylindrical shells by variation in circumferential thickness. For those elliptical cylindrical shells which have a thickness variation of second degree, the natural frequencies are obtained. Rosen and Singer [49] worked on the effect of circularity deviation of cylindrical shells. They showed that the vibration frequencies change significantly by imperfections in the circularity of the order of shell thickness. Bentley and Firth [50], Firth [51] considered the experimental studies of shells filled with fluid. They expressed that asymmetric shell modes can be excited by axisymmetric of acoustic modes, but such phenomena are influenced by circumferential variation of thickness or material properties. These superficial conclusions motivated more additional research by Yousri and Fahy [52], Tonin and Bies [53].

Hasheminejad and Sanaei [54] used the theory of elasticity to study the ultrasonic scattering from a cylinder with the elliptical cross-section. Hayek and Boisvert [47] used higher-order shell theories that included the effect of rotary inertia and shear deformation along with benefiting from the Ritz approach to study the vibration of elliptical shells. Tornabene et al. [55] used the generalized differential quadrature method (GDQM) and different shell theories to investigate the free vibration of composite oval and elliptical cylindrical shell. Later on, they used the same method to investigate the free vibration of elliptical shells made of composite materials [56]. Zhao et al. [57] used the first-order shear deformation theory to study the effect of general boundary conditions such as elastic and classical boundary on the free vibration of elliptical cylindrical shells.

1.1 Motivation and objective of this work

The above review shows that while there have been many investigations regarding the free vibration of infinite elliptical shells using thin shell theories of different orders, there has been no rigorous analytical study for an infinite elliptical cylindrical body with arbitrary thickness using the classical three-dimensional theory of elasticity. The current work would specifically be applicable to the high thickness ratios where the structure response becomes highly complex and nonlinear. In addition, while the shell theories give infinite numbers of natural frequencies as the circumferential mode number, n, and axial mode number, m, increase, they give a finite number of modes at specific n and m. However, the three-dimensional theory of elasticity gives infinite numbers of natural frequencies in any circumferential and axial mode numbers. Accordingly, the main goal of this manuscript is to engage Navier’s equation, Helmholtz decomposition, radial and angular Mathieu functions with a suitable technique to enforce boundary conditions in order to develop an analytical solution for an infinite elliptical cylinder based on the linear theory of elasticity. Namely, here for the first time the relation between the non-dimensional natural frequency and aspect ratio is investigated for an infinite hollow elliptical cylindrical shell. The suggested solution in conjunction with an inverse technique may also be used to monitor the ellipticity in different mechanical elements. The validity of the proposed solution is checked via finite element simulations in Multiphysics COMSOL package.

Fig. 1

Schematic of elliptical shell

2 Problem description

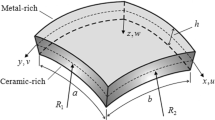
The geometry of an elliptical hollow cylinder is depicted in Fig. 1. The elliptic cylindrical coordinates $(\zeta ,\eta )$ are defined according to the transformation $x+i y=a \ \mathrm{cos}h[(\zeta + i \ \eta )]$ in which, the $\eta$ coordinate is the asymptotic angle of confocal hyperbolic cylinders with symmetric axis y=0, while the $\zeta$ coordinate is confocal elliptic cylinders centered on the origin. The semi major and minor axes of elliptic cylinders are parallel with the x-axis and y-axis, respectively. The explicit relations between the Cartesian coordinates (x, y) and the elliptic cylindrical coordinates $(\zeta ,\eta )$ are given by [58]

$$\begin{aligned} x&=a\ \mathrm{cos}h(\zeta )\ \mathrm{cos}(\eta ),\end{aligned}$$

(1a)

$$\begin{aligned} y&=a\ \mathrm{sin}h(\zeta ) \ \mathrm{sin}(\eta ), \end{aligned}$$

(1b)

where $\zeta$ is a radial coordinate with a non-negative real number, $\zeta \in [0,\infty )$ and the coordinate $\eta$ is the angular coordinate ranging from $[0,2 \pi ]$. Furthermore, a is the semi-focal length of the cylinder elliptical cross section. The curvilinear axes are the confocal ellipses and hyperbolae with two foci located at $\pm\, a$ as it depicted in Fig. 1. Moreover, the surface of the internal ellipse can be defined by $\zeta =\zeta _0$ with the major and minor axes of $R_1=a \ \mathrm{cos}h(\zeta _0)$ and $R_2=a \ \mathrm{sin}h(\zeta _0)$, respectively. Likewise, the surface of the external ellipse can be describe by $\zeta =\zeta _1$ with the major and minor axis of $R_1^{'}=a \ \mathrm{cos}h(\zeta _1)$ and $R_2^{'}=a \ \mathrm{sin}h(\zeta _1)$, respectively. Here we should note that as simultaneously the values of a and $\zeta$ converge to zero and infinity, respectively, the focal points approach to each other which this case is the transition to the limiting case of the circular cylinder shell.

2.1 Constitutive relations

The constitutive relations for a linear homogeneous isotropic elliptical cylinder can be given as [59]

$$\begin{aligned} {[}\sigma _{ij}]=\lambda \ [\delta _{ij}] \epsilon _{kk} + 2 \mu \ [\epsilon _{ij}], \end{aligned}$$

(2)

in which $[\delta _{ij}]$, $[\sigma _{ij}]$ and $[\epsilon _{ij}]$ are Kronecker delta function, second order Green–Cauchy stress and strain tensors, respectively. Furthermore $\lambda$ and $\mu$ are Lame constants.

2.2 Kinematic assumptions

The Green–Cauchy strain tensor is related to the pertinent material displacement vectors via the linearized kinematic relation as [60]

$$\begin{aligned} \pmb {\Gamma }&=\frac{1}{2}\left( \nabla \mathbf{u }+ \nabla \mathbf{u }^{\text {T}}\right) , \end{aligned}$$

(3)

where $\mathbf{u }=[ u_{\zeta } \, \, u_{\eta } \, \, u_{z} ]^{T}$ and $\pmb {\Gamma }$ are the Lagrangian displacement vector and Green–Cauchy strain tensor, respectively. In addition, the superscript “T” denotes the transpose of a matrix which flips a matrix over its diagonal. The expanded form of Eq. 3 is given in Eq. 27.

2.3 Elastodynamics

In the absence of body forces, the wave equation of motion in the isotropic solid medium is expressed by the classical Navier’s equation as follows [61]

$$\begin{aligned} \mu \nabla ^2 \mathbf{u }+ (\mu +\lambda ) \nabla (\nabla \ . \ \mathbf{u })= \rho \frac{\partial ^2 \mathbf{u } }{\partial t^2}, \end{aligned}$$

(4)

where $\rho$ is the unperturbed material density. Moreover, the gradient operator, $\nabla$ in the elliptical coordinate system can be defined as [62]

$$\begin{aligned} \nabla = (\partial / \partial \zeta \ \hat{\mathbf{e }}_{\zeta }+ \partial / \partial \eta \ \hat{\mathbf{e }}_{\eta })/ a J(\zeta ,\eta ), \end{aligned}$$

where $J(\zeta ,\eta )=\sqrt{\frac{ \mathrm{cos}h( 2 \zeta )-\mathrm{cos}(2 \eta )}{2}\ }$. In addition, $\hat{\mathbf{e }}_{\zeta }$ and $\hat{\mathbf{e }}_{\eta }$ are the orthogonal unit vectors in the radial and tangential directions, respectively.

2.4 Helmholtz decomposition in elliptical coordinate

Helmholtz partial differential equations can be obtained by equating the material displacement, $\mathbf{u }$ as the sum of the irrotational and solenoidal part as [62]

$$\begin{aligned} \mathbf{u }= \nabla \Phi + \nabla \times \pmb {\Psi }, \end{aligned}$$

(5)

in which $\pmb {\Psi } =\Psi ( \zeta ,\eta ) {\hat{\mathbf{e }}}_{z}$ with the gauge condition, $\pmb \nabla . \pmb {\Psi }=0$ applied to the solenoidal part. Next, the Lagrangian displacement of the elliptical cylinder can be obtained using the definition of gradient of $\Phi$ and curl of $\pmb {\Psi }$ for an elliptical cylindrical coordinate in Euclidean space. Then the Eq. 5 can be rewritten as [63]

$$\begin{aligned} u_{\zeta }&= \frac{1}{a J(\zeta , \eta )} \left( \frac{\partial \Phi }{\partial \zeta }+\frac{\partial \Psi }{\partial \eta } \right) \end{aligned}$$

(6a)

$$\begin{aligned} u_{\eta }&=\frac{1}{a J(\zeta , \eta )} \left( \frac{\partial \Phi }{\partial \eta }-\frac{\partial \Psi }{\partial \zeta } \right) \end{aligned}$$

(6b)

Next, substituting Eq. 5 into the Navier’s equation of motion, Eq. 4, two sets of fully uncoupled wave equations can be obtained as [54, 64]

$$\begin{aligned} (\nabla ^2+k_{i}^2) \Omega =0; \ \ i=c,s, \end{aligned}$$

(7)

where $\Omega$ could be any of $\Psi$ or $\Phi$. Furthermore, $k_{c}^2$ and $k_s^2$ are given as [65]

$$\begin{aligned} k_{c}^2=\frac{\omega ^2}{c_p^2}; \ k_s^2= \frac{\omega ^2 }{c_s}, \end{aligned}$$

in which $c_{p}=(\lambda +2 \mu )/\rho$ and $c_{s}=\mu /\rho$ are propagation velocities of distortional and dilatational waves in the solid medium.

Using the Laplacian operator,$\nabla ^2$ in the elliptic cylindrical coordinate, Eq. 7 result in [58]

$$\begin{aligned} \frac{1}{a^{2} J^2(\zeta ,\eta )} \left( \frac{\partial ^2 \Omega }{\partial \zeta ^{2}}+\frac{\partial ^2 \Omega }{\partial \eta ^{2}}\right) + k^{2}_{i} \ \Omega =0, \end{aligned}$$

(8)

substituting $\Omega (\eta ,\zeta )=\Omega _{\zeta }(\zeta ) \ \Omega _{\eta }(\eta )$ into the Eq. 8, after rewriting equations in the way that each of two variables appears on a separate side of equations (Separation of variables), the partial differential Eq. 8 will be transformed to two sets of ordinary differential equations in which $\Omega _{\zeta }(\zeta )$ and $\Omega _{\eta }(\eta )$ are satisfying the ordinary (angular) Mathieu’s differential equation and modified (radially) Mathieu’s differential equation, respectively [58],

$$\begin{aligned} \frac{d^{2} \Omega _{\zeta }(\zeta )}{d \zeta ^2} -[\beta -2q\ \mathrm{cos}h(2\zeta )]\ \Omega _{\zeta }(\zeta )=0, \end{aligned}$$

(9)

$$\begin{aligned} \frac{d^{2} \Omega _{\eta }(\eta )}{d \eta ^2} +[\beta -2q\ \mathrm{cos}(2\eta )] \ \Omega _{\eta }(\eta )=0, \end{aligned}$$

(10)

where, $q=\frac{k_{i}^2 a^2}{4}$ is a pre-defined constant and $\beta$ is a separation constant. The computation of the angular Mathieu function will be discussed next.

2.5 Angular Mathieu function and its derivatives

According to the Floquet theory, for a set of discrete values of $\beta$, namely the roots of characteristic equation, Eq. 10 admits periodic solutions. It can be simply distinguished that there are four kinds of countable set of eigenvalues of $\beta$ in the way that angular Mathieu functions of even indices are $\pi$-periodic while those of the odd indices are $2\pi$-periodic. For every eigenvalue, there is a set of transcendental functions related to each eigenvalue. These infinite set of transcendental functions are associated with four classes of modified solutions satisfying [66]

$$\begin{aligned} 1 \qquad&even{-}even{:} \ \ Ce_{2n}(\eta ,q)= \sum _{m=0}^{\infty } A_{2m}^{2n}(q) \ \mathrm{cos}(2 m \eta ), \end{aligned}$$

(11a)

$$\begin{aligned} 2 \qquad&even{-}odd{:} \ Ce_{2n+1}(\eta ,q)= \sum _{m=0}^{\infty } A_{2m+1}^{2n+1}(q) \ \mathrm{cos}[(2m+1) \eta ], \end{aligned}$$

(11b)

$$\begin{aligned} 3 \qquad&odd{-}even{:} \ \ \ \ Se_{2n}(\eta ,q)= \sum _{m=1}^{\infty } B_{2m}^{2n}(q) \ \mathrm{sin}(2 m \eta ), \end{aligned}$$

(11c)

$$\begin{aligned} 4 \qquad&odd{-}odd{:} \ \ \ Se_{2n+1}(\eta ,q)= \sum _{m=0}^{\infty } B_{2m+1}^{2n+1}(q) \ \mathrm{sin}[(2m+1) \eta ], \end{aligned}$$

(11d)

in which $A^{n}_{m}$ and $B^{n}_{m}, n,m=0,1,\ldots ,\infty$ are the expansion coefficients for the even and odd Mathieu functions. In addition, Ce and Se are even and odd radial Mathieu functions, respectively. Substitution of Eq. 11 into the Eq. 10, result in the following recurrence relations, respectively, as [66]

$$\begin{aligned}&even{-}even{:} \nonumber \\&\quad \beta A^{2n}_{0} - q A^{2n}_{2}=0, \nonumber \\&\quad -2 q A^{2n}_{0}+ (\beta -4) A^{2n}_{2}- q A^{2n}_{4}=0, \nonumber \\&\quad -q A^{2n}_{2m-2}+[\beta -4m^2] A^{2n}_{2m} -q A^{2n}_{2m+2}=0, \qquad m=2,3,4, \ldots \end{aligned}$$

(12a)

$$\begin{aligned}&even{-}odd{:} \nonumber \\&\quad (\beta -1-q) A^{2n+1}_1-q A^{2n+1}_{3}=0,\nonumber \\&\quad -q A^{2n+1}_{2m-1}+[\beta -(2m+1)^2] A^{2n+1}_{2m+1}-q A^{2n+1}_{2m+3}=0, \qquad m=1,2,3, \ldots \end{aligned}$$

(12b)

$$\begin{aligned}&odd{-}even{:} \nonumber \\&\quad (\beta -4) B^{2n}_{2}- q B^{2n}_{4}=0, \nonumber \\&\quad -q B^{2n}_{2m-2}+[\beta -4m^2] B^{2n}_{2m}-q B^{2n}_{2m+2}=0, \qquad m=2,3,4, \ldots \end{aligned}$$

(12c)

$$\begin{aligned}&odd{-}odd{:} \nonumber \\&\quad (\beta -1+q)\ B^{2n+1}_{1}-a B^{2n+1}_{3}=0, \nonumber \\&\quad -q B^{2n+1}_{2m-1}+ [\beta -(2m+1)^2] B^{2n+1}_{2m+1}- q B^{2n+1}_{2m+3}=0, \qquad m=1,2,3, \ldots \end{aligned}$$

(12d)

the recurrence relations can be rewritten in the form of eigenvalue problems with four sets of characteristic values and characteristic vectors. The expanded form of eigenvalue problems is given in “Appendix 2”. After calculating the characteristic values and characteristic vectors of the infinite tridiagonal matrices, the modified angular Mathieu functions are normalized by implementing the following relations [66]

$$\begin{aligned}&even{-}even{:} \qquad \sum _{m=0}^{\infty } A^{2n}_{2m}(q)=1, \end{aligned}$$

(13a)

$$\begin{aligned}&even{-}odd{:} \qquad \sum _{m=0}^{\infty } A^{2n+1}_{2m+1}(q)=1, \end{aligned}$$

(13b)

$$\begin{aligned}&odd{-}even{:} \qquad \sum _{m=1}^{\infty } 2m B^{2n}_{2m}(q)=1, \end{aligned}$$

(13c)

$$\begin{aligned}&odd{-}even{:} \qquad \sum _{m=0}^{\infty } (2m+1) B^{2n+1}_{2m+1}(q)=1. \end{aligned}$$

(13d)

Next, the orthogonality of angular Mathieu functions will be achieved according to McLachlan normalization [67] as

$$\begin{aligned} \int _{0}^{2 \pi } S_{m}(\eta ,q) \ S_{m'}(\eta ,q) \ d\eta = \pi \delta _{mm'}, \qquad S=Ce,Se, \end{aligned}$$

(14)

where $\delta _{mm'}$ is the Kronecker delta function. Substitution of Eq. 11 into the Eq. 14, result in the following normalized relations as [66]

$$\begin{aligned}&even{-}even{:} \qquad 2 (A^{2n}_{0}(q))^2+\sum _{m=1}^{\infty } (A^{2n}_{2m}(q))^2=1, \end{aligned}$$

(15a)

$$\begin{aligned}&even{-}odd{:} \qquad \sum _{m=0}^{\infty } A^{2n+1}_{2m+1}(q)=1, \end{aligned}$$

(15b)

$$\begin{aligned}&odd{-}even{:} \qquad \sum _{m=1}^{\infty } B^{2n}_{2m}(q)=1, \end{aligned}$$

(15c)

$$\begin{aligned}&odd{-}odd{:} \qquad \sum _{m=0}^{\infty } B^{2n+1}_{2m+1}(q)=1. \end{aligned}$$

(15d)

Once the characteristic coefficients are calculated, the angular Mathieu functions and its derivatives can be determined. The derivatives of the angular Mathieu functions can be obtained by taking differentiation of Eq. 11 as [66]

$$\begin{aligned}&even{-}even{:} \quad \frac{d Ce_{2n}(\eta ,q)}{d\eta }= -\sum _{m=1}^{\infty } 2m A^{2n}_{2m}(q)\ \mathrm{sin}(2m \eta ), \end{aligned}$$

(16a)

$$\begin{aligned}&even{-}odd{:} \quad \frac{d Ce_{2n+1}(\eta ,q)}{d\eta }=-\sum _{m=0}^{\infty } (2m+1) A^{2n+1}_{2m+1}(q) \ \mathrm{sin}[(2m+1)\eta ], \end{aligned}$$

(16b)

$$\begin{aligned}&odd{-}even{:} \quad \frac{d Se_{2n}(\eta ,q)}{d\eta }=\sum _{m=1}^{\infty } 2 m B^{2n}_{2m}(q) \ \mathrm{cos}(2m\eta ), \end{aligned}$$

(16c)

$$\begin{aligned}&odd{-}odd{:} \quad \frac{d Se_{2n+1}(\eta ,q)}{d\eta }= \sum _{m=0}^{\infty } (2m+1) B^{2n+1}_{2m+1}(q) \ \mathrm{cos}[(2m+1)\eta ]. \end{aligned}$$

(16d)

The higher derivatives of angular Mathieu functions can be obtained with the same manner.

2.6 Radial Mathieu function of the first kind and it’s derivatives

Solution of Eq. 9 can be expressed in the form of four distinct classes of modified Mathieu functions of the first kind as [66]

$$\begin{aligned} even{-}even{:} \, Mc_{2n}(\zeta ,q)=&\frac{\sqrt{2 \pi }}{2 A^{2n}_{0}(q)} \sum _{m=0}^{\infty } (-1)^{(m+n)} A_{2m}^{2n}(q) J_{m}(\sqrt{q} e^{-\zeta }) J_{m}(\sqrt{q} e^{\zeta }), \end{aligned}$$

(17a)

$$\begin{aligned} even{-}odd{:} \, Mc_{2n+1}(\zeta ,q)=&\frac{\sqrt{2 \pi }}{2 A^{2n+1}_{1}(q)} \sum _{m=0}^{\infty } (-1)^{(m+n)} A^{2n+1}_{2m+1}(q)[J_{m}(\sqrt{q}e^{-\zeta }) \nonumber \\&J_{m+1}(\sqrt{q} e^{\zeta }) + J_{m}(\sqrt{q} e^{\zeta }) J_{m+1}(\sqrt{q} e^{-\zeta })], \end{aligned}$$

(17b)

$$\begin{aligned} odd{-}even{:}\, Ms_{2n}(\zeta ,q)=&\frac{\sqrt{2 \pi }}{2 B^{2n}_{2}(q)} \sum _{m=1}^{\infty } (-1)^{m+n} B^{2n}_{2m}(q) [J_{m-1}(\sqrt{q} e^{-\zeta }) \nonumber \\&J_{m+1}(\sqrt{q} e^{\zeta })] -J_{m-1}(\sqrt{q} e^{\zeta }) J_{m+1}(\sqrt{q} e^{-\zeta })], \end{aligned}$$

(17c)

$$\begin{aligned} odd{-}odd{:} \, Ms_{2n+1}(\zeta ,q)=&\frac{\sqrt{2 \pi }}{2 B^{2n+1}_{1}(q)} \sum _{m=0}^{\infty } (-1)^{(m+n)} B^{2n+1}_{2m+1}(q) [J_{m}(\sqrt{q} e^{-\zeta }) \nonumber \\&J_{m+1}(\sqrt{q} e^{\zeta })- J_{m}(\sqrt{q} e^{\zeta }) J_{m+1}(\sqrt{q} e^{-\zeta })], \end{aligned}$$

(17d)

where, Mc and Ms are even and odd radial modified Mathieu functions, respectively. In addition $J_{m}(x)$ is the Bessel function of the first kind which satisfies the ordinary differential equation $x^2 \frac{d^2{y(x)}}{dx^2}+x \frac{dy(x)}{dx}+(x^2-m^2)y(x)=0$. Subsequently, the first derivatives of the modified Mathieu function can be obtained as [66]

$$\begin{aligned}&even{-}even{:} \nonumber \\&\quad \frac{dMc_{2n}(\zeta ,q)}{d\zeta }= \frac{\sqrt{2 \pi }}{2 A^{2n}_{0}(q)} \sum _{m=0}^{\infty } (-1)^{(m+n)} A_{2n}^{2m}(q) [\sqrt{\zeta } e^{-\zeta } J_{m+1}(\sqrt{q} e^{-\zeta })\nonumber \\&\quad J_{m}(\sqrt{q} e^{\zeta })- \sqrt{q} e^{\zeta } J_{m}(\sqrt{q} e^{-\zeta }) J_{m+1}(\sqrt{q} e^{\zeta })], \end{aligned}$$

(18a)

$$\begin{aligned}&even{-}odd{:} \nonumber \\&\quad \frac{dMc_{2n+1}(\zeta ,q)}{d\zeta }= \frac{\sqrt{2 \pi }}{2 A^{2n}_{1}(q)} \sum _{m=0}^{\infty } (-1)^{(m+n)} A^{2n+1}_{2m+1}(q) \{(\sqrt{q}e^{\zeta }- \sqrt{q} e^{-\zeta }) [J_{m}(\sqrt{q} e^{-\zeta }) \nonumber \\&\quad J_{m}(\sqrt{q} e^{\zeta })- J_{m+1}(\sqrt{q} e^{-\zeta }) J_{m+1}(\sqrt{q} e^{\zeta })+ (2m+1) \nonumber [J_{m+1}(\sqrt{q} e^{-\zeta }) J_{m}(\sqrt{q} e^{\zeta })\nonumber \\&\quad -J_{m}(\sqrt{q} e^{-\zeta } J_{m+1}(\sqrt{q} e^{\zeta }) ) ] \} \end{aligned}$$

(18b)

$$\begin{aligned}&odd{-}even{:} \nonumber \\&\quad \frac{dMs_{2n}(\zeta ,q)}{d\zeta }= \frac{\sqrt{2 \pi }}{2 B^{2n}_{2}(q)} \sum _{m=0}^{\infty } (-1)^{(m+n)} B^{2n}_{2m+2}(q) (4m+4) \{J_{m}(\sqrt{q} e^{-\zeta }) \nonumber \\&\quad J_{m}(\sqrt{q} e^{\zeta })+ \mathrm{cos}h(2 \zeta )\ J_{m+1}(\sqrt{q} e^{-\zeta } ) J_{m+1} (\sqrt{q} e^{\zeta } ) - (m+1) [ \frac{1}{\sqrt{q} e^{-\zeta }} \nonumber \\&\quad J_{m+1}(\sqrt{q} e^{- \zeta }) J_{m}(\sqrt{q} e^{\zeta } )+ \frac{1}{\sqrt{q} e^{\zeta }} J_{m}(\sqrt{q} e^{-\zeta }) J_{m+1}(\sqrt{q} e^{\zeta })) ] \end{aligned}$$

(18c)

$$\begin{aligned}&odd{-}odd{:} \nonumber \\&\quad \frac{dMs_{2n+1}(\zeta ,q)}{d\zeta }= \frac{\sqrt{2 \pi }}{2 B^{2n+1}_{1}(q)} \sum _{m=0}^{\infty } (-1)^{(m+n)} B_{2m+1}^{2n+1}(q) \{(\sqrt{q} e^{-\zeta } + \sqrt{q} e^{\zeta }) \nonumber \\&\quad [J_{m}(\sqrt{q} e^{-\zeta }) J_{m}(\sqrt{q} e^{\zeta })+ J_{m+1} (\sqrt{q} e^{-\zeta }) J_{m+1} (\sqrt{q} e^{\zeta })- (2m+1) [ J_{m+1} (\sqrt{q} e^{-\zeta }) \nonumber \\&\quad J_{m} (\sqrt{q} e^{\zeta })+ J_{m} (\sqrt{q} e^{-\zeta }) J_{m+1} (\sqrt{q} e^{\zeta })\}. \end{aligned}$$

(18d)

The higher derivatives of radial Mathieu functions can be obtained with the same manner.

2.7 Longitudinal and transverse waves

The strain components inside the elastic elliptical cylinder can be expressed in terms of compressional and shear waves potential functions by substitution of Eq. 6 into Eq. 3 as

$$\begin{aligned} \epsilon _{\zeta \zeta }&=\frac{ \sin (2 \eta )}{2a^2 J^4(\zeta ,\eta )}\left( \frac{\partial \Phi }{\partial \eta } -\frac{\partial \Psi }{\partial \zeta } \right) , \end{aligned}$$

(19a)

$$\begin{aligned} \epsilon _{\zeta \eta }&= \frac{-\mathrm{sin}(2\eta )}{4a^{2} J^4(\zeta ,\eta ) } \left( \frac{\partial \Phi }{\partial \zeta }+\frac{\partial \Psi }{\partial \eta }\right) + \frac{\mathrm{sin}h(2\zeta )}{4a^{2} J^{4}(\zeta ,\eta ) } \left( \frac{\partial \Psi }{\partial \zeta }- \frac{\partial \Phi }{\partial \eta } \right) , \end{aligned}$$

(19b)

$$\begin{aligned} \epsilon _{\eta \eta }&= \frac{\mathrm{sin}h(2\zeta )}{2a^{2} J^4(\zeta ,\eta )} \left( \frac{\partial \Phi }{\partial \zeta }+\frac{\partial \Psi }{\partial \eta }\right) . \end{aligned}$$

(19c)

The tangential and radial stress components in the elastic elliptical cylinder may be expressed by substituting Eq. 19 into the constitutive relations isotropic materials, i.e. Eq. 2 for isotropic materials as

$$\begin{aligned} \sigma _{\zeta \zeta }&= \frac{1}{a^2 J^4(\zeta ,\eta )} \left[ 2\mu J^2(\zeta ,\eta ) \frac{\partial ^2 \Psi }{\partial \zeta \partial \eta }+\mu \ \mathrm{sin}(2 \eta ) \left( \frac{\partial \Phi }{\partial \eta }- \frac{\partial \Psi }{\partial \zeta }\right) - \mu \ \mathrm{sin}h(2\zeta ) \right. \nonumber \\&\left. \quad \left( \frac{\partial \Phi }{\partial \zeta }+ \frac{\partial \Psi }{\partial \eta }\right) + (\lambda + 2 \mu ) J^2(\zeta ,\eta ) \frac{\partial ^{2} \Phi }{\partial \zeta ^{2}}+ \lambda J^2(\zeta ,\eta ) \frac{\partial ^{2} \Phi }{\partial \eta ^{2}} \right] , \end{aligned}$$

(20a)

$$\begin{aligned} \sigma _{\zeta \eta }&= -\frac{1}{a^2 J^4(\zeta ,\eta ) } \left[ \mu \ J^2(\zeta ,\eta )\left( -2 \frac{\partial ^2 \Phi }{\partial \zeta \partial \eta } +\frac{\partial ^2\Psi }{\partial \zeta ^2}-\frac{\partial ^2 \Psi }{\partial \eta ^2} \right) +\mu \ \mathrm{sin}(2\eta ) \right. \nonumber \\&\quad \left. \left( \frac{\partial \Phi }{\partial \zeta }+\frac{\partial \Psi }{\partial \eta }\right) + \mu \ \mathrm{sin}h(2\zeta ) \left( \frac{\partial \Phi }{\partial \eta }-\frac{\partial \Psi }{\partial \zeta }\right) \right] . \end{aligned}$$

(20b)

Finally, using Eqs. 10 and 9, the longitudinal and transverse wave potential functions in the elastic elliptical cylinder can be written respectively, as

$$\begin{aligned} \Phi (\zeta ,\eta ,\omega )&= \sum _{n=0}^{\infty } [e_{n}(\omega ) Mc_{n}(\zeta ,q_{c}) Ce_n(\eta ,q_{c})+ f_{n} (\omega ) Ms_{n}(\zeta ,q_{c}) Se_{n}(\eta ,q_{c})], \end{aligned}$$

(21a)

$$\begin{aligned} \Psi (\zeta ,\eta ,\omega )&=\sum _{n=0}^{\infty }[g_{n}(\omega ) Mc_n(\zeta ,q_{s}) Ce_{n}(\eta ,q_{s})+ h_{n}(\omega ) Ms_{n}(\zeta ,q_{s}) Se_{n}(\eta ,q_{s})], \end{aligned}$$

(21b)

in which $e_{n}(\omega ),f_{n}(\omega ), g_{n}(\omega )$ and $h_{n}(\omega )$ are unknown modal coefficients. Furthermore, $q_{i}=k_i^{2} a^2/4;\ i=c,s.$

2.8 Mechanical boundary conditions

The appropriate mechanical boundary conditions that must be held on the internal and external surfaces of the elliptical cylinder can be written as

$$\begin{aligned} \sigma _{\zeta \zeta }|_{\zeta =\zeta _{i}}=0, \quad \sigma _{\zeta \eta }|_{\zeta =\zeta _{i}}=0; \quad i=0,1, \end{aligned}$$

(22)

substitution of Equation 21 into the field equations Eq. 20, and resubstituting the ensuing results into the mechanical boundary Eq. 22, result in

$$\begin{aligned}&\sigma _{\zeta \zeta } \nonumber \\&\quad =\sum _{n=0}^{\infty } \frac{1}{a^2 J^4(\zeta _{i},\eta )} \left\{ \left[ \lambda J^2(\zeta _{i},\eta ) \frac{d^{2} Ce_{n}(\eta ,q_c) }{d \eta ^2}\ Mc_{n}(\zeta _{i},q_c)+ \mu \ \mathrm{sin}(2\eta ) \frac{d Ce_{n}(\eta ,q_c) }{d \eta } \right. \right. \nonumber \\&\qquad \left. \left. Mc_{n}(\zeta _{i},q_c)+(\lambda +2\mu ) J^2(\zeta _{i},\eta )\ Ce_{n}(\eta ,q_{c}) \frac{d^2 Mc_{n}(\zeta _i,q_c)}{d \zeta ^2} -\mu \ \mathrm{sin}h(2\zeta _i) Ce_{n}(\eta ,q_c) \right. \right. \nonumber \\&\qquad \left. \left. \frac{d Mc_{n}(\zeta _i,q_c)}{d \zeta }\right] \ e_n(\omega )+\left[ (\lambda +2 \mu ) J^2(\zeta _{i},\eta ) \frac{d^2 Mc_{n}(\zeta _i,q_c)}{d \zeta ^2} Se_{n}(\eta ,q_c) +\lambda J^2(\zeta _i,\eta )\right. \right. \nonumber \\&\qquad \left. \left. Ms_{n}(\zeta _i,q_c) \frac{d^2 Se_{n}(\eta ,q_c)}{d \eta ^2} - \mu \mathrm{sin}h(2\zeta _i) \frac{d Ms_n(\zeta _i,q_c)}{d \zeta } \ Se_{n}(\zeta _i,q_c)+\mu \ \mathrm{sin}(2\eta ) \right. \right. \nonumber \\&\qquad \left. \left. Ms_n(\zeta _i,q_c) \frac{d Se_n(\eta ,q_c)}{d \eta } \right] f_n(\omega )+ \left[ 2 \mu \ J^2(\zeta _i,\eta ) \frac{d Ce_n(\eta ,q_s)}{d \eta } \frac{d Mc_n(\zeta _i,q_s)}{d \zeta }- \mu \right. \right. \nonumber \\&\qquad \left. \left. \mathrm{sin}h(2\zeta _i) \frac{d Ce_{n}(\eta ,q_s)}{d \eta } Mc_n(\zeta _i,q_s)-\mu \mathrm{sin}(2\eta ) Ce_n(\eta ,q_s) \frac{d Mc_n(\zeta _i,q_s)}{d \zeta } \right] g_n(\omega ) \right. \nonumber \\&\qquad \left. + \left[ 2 \mu J^2(\zeta _i,\eta ) \frac{d Ms_n(\zeta _i,q_s)}{d \zeta } \frac{d Se_n(\eta ,q_c)}{d \eta }-\mu \ \mathrm{sin}(2\eta ) \frac{d Ms_n(\zeta _i,q_s)}{d \zeta } Se_{n}(\eta ,q_s)- \mu \right. \right. \nonumber \\&\qquad \left. \left. \mathrm{sin}h(2\zeta _i) Ms_n(\zeta _i,q_s) \frac{d Se_n(\eta ,q_c)}{d \eta }\right] h_n( \omega )\right\} =0;\ \ i=0,1, \end{aligned}$$

(23a)

$$\begin{aligned}&\sigma _{\zeta \eta }\nonumber \\&\quad = \sum _{n=0}^{\infty } \left\{ \left[ 2 J^2(\zeta _i,\eta ) \frac{d Ce_n(\eta ,q_c)}{d \eta } \frac{d Mc_n(\zeta _i,q_c)}{d \zeta }-\, \mathrm{sin}h(2\zeta _i) \frac{d Ce_n(\eta ,q_c)}{d \eta } Mc_n(\zeta _i,q_c)\right. \right. \nonumber \\&\qquad \left. -\, \mathrm{sin}(2\eta ) Ce_n(\eta ,q_c) \frac{d Mc_n(\zeta _i,q_c)}{d \zeta } \right] e_n(\omega )+\left[ 2 J^2(\zeta _i,\eta ) \frac{d Ms_n(\zeta _i,q_c)}{d \zeta } \frac{d Se_n(\eta ,q_c)}{d \eta }\right. \nonumber \\&\qquad \left. - \mathrm{sin}(2\eta ) \frac{d Ms_n(\zeta _i,q_c)}{d \zeta } Se_n(\eta ,q_c)- \mathrm{sin}h(2\zeta _i) Ms_n(\zeta _i,q_c) \frac{d Se_n(\eta ,q_c)}{d \eta }\right] f_n(\omega )\nonumber \\&\qquad +\left[ J^2(\zeta _i,\eta ) \frac{d^2 Ce_n(\eta ,q_s)}{d \eta ^2} Mc_n({\zeta _i,q_s})-\mathrm{sin}(2\eta ) \frac{d Ce_n(\eta ,q_s)}{d \eta }Mc_n({\zeta _i,q_s})- J^2(\zeta _i,\eta ) \right. \nonumber \\&\qquad \left. Ce_n(\eta ,q_s) \frac{d^2 Mc_n(\zeta _i,q_c)}{d \zeta ^2}+ \mathrm{sin}h(2\zeta _i) Ce_n(\eta ,q_s) \ \frac{d Mc_n(\zeta _i,q_c)}{d \zeta } \right] g_n(\omega )+ \left[ J^2(\zeta _i,eta) \right. \nonumber \\&\qquad Ms_n(\zeta _i,q_s) \ \frac{d^2 Se_n(\eta ,q_s)}{d \eta ^2}\ -\ J^2(\zeta _i,\eta ) \ \frac{d^2 Mc_n(\zeta _i,q_c)}{d \zeta ^2} \ Se_n(\zeta ,q_s) \, + \mathrm{sin}h(2\zeta _i) \nonumber \\&\qquad \left. \left. \frac{d Ms_n(\zeta _i,q_c)}{d \zeta } Se_{n}(\eta ,q_s)- \mathrm{sin}(2\eta ) Ms_{n}(\zeta _i,q_s) \frac{d Se_n(\eta ,q_s)}{d \eta }\right] h_n(\omega ) \right\} =0;\ \ i=0,1. \end{aligned}$$

(23b)

The boundary conditions given in Eq. 23 cannot be satisfied as the angular Mathieu functions and their derivatives do not construct an orthogonal set due to the existence of even and odd Mathieu function with different wave numbers in their arguments. Thereby, the classical wave-function expansion technique cannot be employed to explicitly satisfy the mechanical boundary conditions on the inner and outer surfaces of the elliptical shell. The complexity in the boundary condition emerges due to the presence of variable $\eta$ in the terms such as $\sin (2\eta )$ and $J^2(\zeta _i,\eta )$. The complexity can be advantageously avoided by benefiting from the transcendental expansion of even and odd angular Mathieu functions given in Eq. 11.

Equation 23 which are intensively complex formulas, can be transformed into a new system of independent linear equations in terms of unknown modal coefficients. To this end, Equation 11 are substituted into Equation 23 and the ensuing equations are separately multiplied by the factors $\mathrm{cos}(k\eta )$ and $\sin (k\eta )$ , $k=0,1,2,3,\ldots$ and are integrated from 0 to $2\pi$ as [68, 69]

$$\begin{aligned} \mathbf{D }_n\ \pmb {v} =0, \end{aligned}$$

(24)

where

$$\begin{aligned} \pmb {v}^{\mathbf{T }}=[e_0,\ldots ,e_N;\;f_0,\ldots ,f_N;\;g_0,\ldots ,g_N;\;h_0,\ldots ,h_N ] , \end{aligned}$$

(25)

wherein, the entries of the matrix $\mathbf{D }_n$ are given in “Appendix 3”. The natural frequencies of the elliptical shell can be obtained by solving the eigenvalue problem of Eq. 24, as

$$\begin{aligned} |\mathbf{D }_n|=0, \end{aligned}$$

(26)

where $|\mathbf{D }_n|$ is the determinant of Matrix $\mathbf{D }$.

3 Model validation

In order to check the validity of the current solution, a general Matlab$^\circledR$ code was first developed to calculate the characteristic values and characteristic vectors given in Eq. 28 for radial and angular Mathieu functions. Then the characteristic values and vectors are used to calculate the even and odd Mathieu and modified Mathieu functions. In addition, the first and second derivatives of angular and radial Mathieu functions were achieved by taking differentiation of Eqs. 11 and 17. The reliability and accuracy of calculation of radial and angular Mathieu functions were finally checked by comparing with the result given in Ref. [67].

Figure 2a compares the results given in Ref. [67] for the even angular Mathieu function of orders 0–5 with respect to $\eta$ for a fixed value of $q=1$. Figure 2b illustrates the results for the odd Mathieu functions of orders 1–5 with respects to $\eta$ for a fixed value of $q=1$. Figure 2c displays the radial Mathieu function of the first kind with order zero for different value of q. Figure 2d displays the first derivative of the radial Mathieu function of the first kind with order zero for different values of q. The results show perfect accuracy of the current Matlab$^\circledR$ code and result given in Ref. [67].

Fig. 2

Comparison between Matlab$^\circledR$ code written based on Cojocaru [66] and result provided by Abramowitz et al. [67] for angular Mathieu functions and it’s derivatives

After precise calculation of angular and radial Mathieu functions and it’s derivatives, a second Matlab$^\circledR$ script file (M-file) was constructed to calculate the elements of matrix D given in Eq. 24 and its determinant in order to find the resonance frequencies and mode shapes as a function of aspect ratio. Calculation of Bessel function of the first kind (BesselJ) is accomplished by using Matlab$^\circledR$ special function, besselj. A very efficient and robust root-finding method based on the interval halving technique was utilized to calculate the resonance frequencies of the system. The roots can be obtained by repeatedly bisecting extremely small frequency intervals and then selecting the sub-interval in which the sign of characteristic equations changes because the selected interval must have a root to cause a sign change. The same procedure was applied to all different aspect ratios utilizing extremely small aspect ratio steps. Subsequently, any disappeared resonance frequencies were determined and directly included. Due to the slow nature of the interval halving method, calculation of roots will be very computationally time-consuming. Therefore, Matlab$^\circledR$ Parallel Computing $\hbox {Toolbox}^{\mathrm{TM}}$ was engaged to increase the speed of calculation by taking advantage of computers with multicore processors and additional GPUs. By executing Matlab$^\circledR$ M-file that can perform independent iterations in parallel on multicore processors, the Matlab$^\circledR$ operations could speed up significantly in order to manage the drawback of the interval halving method.

Table 1 Comparison of first nine natural frequencies, $f=\omega /2 \pi \ (Hz)$ calculated by finite element model using Comsol Multiphysics$^\circledR$ simulation software with the analytical Matlab$^\circledR$ code for selected aspect ratios of a hollow steel elliptical cylinder

After evaluating the natural frequencies of the elliptic cylinder by the above-discussed method, each frequency is then inserted back into Eq. 24, and subsequently the corresponding shape modes is calculated by employing Matlab$^\circledR$ Null space function which gives an orthonormal basis for the null space of $D_{n}$. The calculation was executed on a server computer with number of terms of truncated series $N=200$ in order to guarantee reliable results in high-frequency ranges and high aspect ratios while keeping the running time in a reasonable scale. The convergence of the suggested solution was assured by using a general method of trial and failure, by increasing the attempt variable of mode number, n, while searching for reliable natural frequencies.

Fig. 3

Selected two dimensional deformed mode shapes related to the first nine clusters of natural frequencies associated with natural frequencies given in Table 1 for various aspect ratios

In order to check the accuracy of the current solution, our Matlab$^\circledR$ code was employed to calculate the first nine clusters of resonance frequencies, $f=\omega /2 \pi$ for different aspect ratios, $e=\zeta _1 / \zeta _0$ while the thickness ratio along y-axis, $\gamma =(R_2^{'}-R_2)/a$ were kept constant($\gamma =0.5$). The elliptic cylinder is assumed to be made of steel $(\lambda =7.67\times 10^{10}\ N/m^2, \mu =7\times 10^{10}\ N/m^2,\rho =7900\ kg/m^3).$ Table 1 clearly shows a perfect agreement between the results calculated by our Matlab$^\circledR$ code with the numerical calculations performed by utilizing finite element package Comsol Multiphysics 5.3 $^\circledR$ [70]. The natural frequencies provided by the current model and FEM were very close for the first few frequencies. However, in higher frequencies and modes, the analytical model is deemed more accurate. It is worth mentioning that the finite element model used for the latter verification consists of 4284 domain elements and 970 boundary elements. In addition, the mapped meshed was used due to the high aspect ratio of geometry. We note that the repeated deformed mode shapes were omitted for the sake of brevity.

Fig. 4

The variation of dimensionless natural frequencies $(\Omega )=\omega a/c_p$ with aspect ratio parameter, e for selected circumferential mode number of elliptical cylinder

4 Effect of aspect ratio: results and discussion

In order to explain the behavior and nature of the suggested solution, a few example with different aspect ratios will be considered. The material properties and geometry of the elliptical cylinder were assumed to be equal to the values given in Sect. 3.

Figure 3 illustrates the two-dimensional deformed mode shapes related to the first nine clusters of natural frequencies given in Table 1 for various aspect ratios $(e=1.06,1.13,1.29,1.5)$. As it can be readily seen, the mode shapes associated with low aspect ratios $(e.g.\ e=1.06)$ for the elliptic cylinder is very similar to the case of circular cylindrical shell regardless of the value of the wave number (Hamidzadeh and Jazar [71]). As the value of aspect ratio increases, the change in the deformed mode shape progressively developed into a more corrupted shape, especially for the breathing mode $(n=0)$ in which the cylinder radius expands and contracts, all parts of the cylinder moving inward or outward at the same rate. Another interesting observation can be seen for the lobar modes $(n>1)$ in which the number of lobes matches the value of wavenumber while as the aspect ratio, e increases, the lobes become more distorted, especially in the high value of circumferential wave number. Such mode shapes (0 and 1) could not be predicted via any of the common shear theory methods [47, 47].

Figure 4 shows the dispersion curve of the non-dimensional resonance frequencies $(\Omega )=\omega a/c_p$ versus the aspect ratio parameter e for the selected circumferential mode number of the elliptical cylinder. It is worth mentioning that that the thickness ratio of $\gamma$ was kept constant $(\gamma =0.5)$ for all calculations. The associated circumferential mode number, n is also described in the plot. The dispersion curve of the elliptical cylinder displays very unique features. When the aspect ratio is not very high (e.g. e=1) the elliptical cylinder is perfectly symmetric and the vibration modes can appear with the same value of repeated resonance frequencies. As the aspect ratio, e increases, the elliptical geometry of the cylinder can cause the curve of repeated resonance frequencies to be divided into modes with different natural frequencies. As it can be clearly seen the level of curve bifurcation is very dependent on the circumferential mode number and aspect ratio. For instance, the high level of curve bifurcation can be seen for lower modes such as $n=1$ and $n=2$ especially for the high aspect ratio numbers while the bifurcation decreases for the high value of circumferential wave number $(e.g.\ n=3)$ and low value of aspect ratio. Another interesting observation is that the natural frequency associated with the breathing mode $(n=0)$ remains single value regardless of the value of aspect ratio. Consequently, it can be concluded that the repeated double roots of the elliptic cylinder with a low value of aspect ratio $(e=1)$ displays a unique decoupling of symmetric and anti-symmetric modes [1]. Another interesting observation that can be seen from Fig. 4 is the cross over of resonance frequencies associated with different circumferential mode numbers (e.g. note the breathing mode $n=0$ and lobar mode $n=4$ cross each other at the aspect ratio $e=1.3$). This indicates that beyond the aspect ratio of $e=1.3$, the stiffness of elliptical cylinder in the breathing mode $(n=0)$ will increase in comparison with mode number $(n=4)$.

5 Concluding remarks

This paper illustrated an exact two-dimensional analytical solution for free vibration of an infinitely long thick-walled hollow elliptical cylinder. Solution of the classical Navier’s equation by taking advantage of the Helmholtz decomposition yielded to the angular and radial Mathieu functions of the first kind. The displacement and stress fields were calculated using both even and odd forms of the radial and angular Mathieu function. It is important to note that the angular form of Mathieu function on the boundary conditions does not create an orthogonal set. Hence, the difficulty was tackled by using the trigonometric expansion of the even and odd angular Mathieu functions, leading to a linearly independent set of equations in terms of the unknown modal coefficients. The prime interests was to study the effect of the cylinder’s ellipticity on the resonance frequencies, deformed mode shapes and dispersion curves of an elliptical cylinder. Numerical studies were investigated for a stainless steel elliptical cylinder at different ranges of aspect ratios.

The results revealed that the mode shapes associated with low aspect ratios display similar behavior to the case of a circular cylindrical shell regardless of the value of circumferential wave number. While, by increasing the value of aspect ratios, the change in the deformed mode shape progressively developed into a more corrupted shape, especially for the breathing mode. As the elliptical shape of the cylinder increases, the curve of repeated natural frequencies bifurcates into two identical branches. The separation of natural frequencies is more apparent for the lowest modes. In general, the magnitude of separation is dependent on the value of aspect ration and mode number. In addition, the natural frequency associated with breathing mode remains single value regardless of the value of aspect ratio. Another interesting observation was the cross over of natural frequencies associated with different mode numbers. Two different types of modes may share the same value of resonance frequency at the crossover point. The associated modes were found to switch the values across the crossover point. Finally, it is worth noting that, compared to the shear theories, the presented modeling framework would be more applicable to the problems with high shell thickness ratios where the structures response becomes complex and highly nonlinear [72, 73]. In addition, depending on the order, the shell theories only provide finite number of natural frequencies, while the employed theory of elasticity gives infinite number of natural frequencies [74]. It is worth noting that for other solution methods such as finite element analysis, as the thickness of the cylinder increases, the mesh size should be refined, and hence the computational time will parabolically increase, in order to obtain a reliable approximation of natural frequencies and mode shapes; however using the developed analytical solution, the exact results can be obtained fairly fast (e.g. for initial design trials) for any given thickness of the given structure.

Appendices

Appendix 1: Kinematic relations

The expanded matrix form of Cauchy-Green infinitesimal strain tensor for the plane-strain case in the elliptical coordinate system becomes

$$\begin{aligned} \begin{pmatrix} \epsilon _{\zeta \zeta } & \epsilon _{\zeta \eta } \\ \epsilon _{\eta \zeta } & \epsilon _{\eta \eta } \end{pmatrix} =\begin{pmatrix} \frac{u_{\eta } \sin (2 \eta )}{2 a J^3(\zeta ,\eta )} & -\frac{u_{\zeta } \sin (2 \eta )+u_{\eta } \mathrm{sin}h (2 \zeta )}{4 a J^3(\zeta ,\eta )} \\ &\\ . & \frac{u_{\zeta } \mathrm{sin}h (2 \zeta )}{2 a J^3(\zeta ,\eta )} \end{pmatrix}. \end{aligned}$$

(27)

Equation 27 corresponds to the one of Eq. 3.

Appendix 2: Characteristic values and characteristic vectors of Mathieu function

In a linear algebra, the recurrence Eq. 12, can be rewritten in the form of eigenvalue problems as follows [75]

$$\begin{aligned}&even{-}even: \qquad \begin{pmatrix} -\beta & q & 0 & 0 & 0 & 0 & \ldots \\ \\ 2q & 4-\beta & q & 0 & 0 & 0 & \ldots \\ \\ 0 & q & 16-\beta & q & 0 & 0 & \ldots \\ \\ 0 & 0 & q & 36-\beta & q & 0 & \ldots \\ \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \ddots \end{pmatrix} \begin{pmatrix} A^{2n}_{0}\\ \\ A^{2n}_{2}\\ \\ A^{2n}_{4}\\ \\ A^{2n}_{6}\\ \\ \vdots \end{pmatrix}=0, \end{aligned}$$

(28a)

$$\begin{aligned}&even{-}odd: \qquad \begin{pmatrix} 1+q-\beta & q & 0 & 0 & 0 & 0 & \ldots \\ \\ q & 9-\beta & q & 0 & 0 & 0 & \ldots \\ \\ 0 & q & 25-\beta & q & 0 & 0 & \ldots \\ \\ 0 & 0 & q & 49-\beta & q & 0 & \ldots \\ \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \ddots \end{pmatrix} \begin{pmatrix} A^{2n+1}_{1}\\ \\ A^{2n+1}_{3}\\ \\ A^{2n+1}_{5}\\ \\ A^{2n+1}_{7}\\ \\ \vdots \end{pmatrix}=0, \end{aligned}$$

(28b)

$$\begin{aligned}&odd{-}even: \qquad \begin{pmatrix} 4-\beta & q & 0 & 0 & 0 & 0 & \ldots \\ \\ q & 16-\beta & q & 0 & 0 & 0 & \ldots \\ & & & & & & \\ 0 & q & 36-\beta & q & 0 & 0 & \ldots \\ \\ 0 & 0 & q & 64-\beta & q & 0 & \ldots \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \ddots \end{pmatrix} \begin{pmatrix} B^{2n}_{2}\\ \\ B^{2n}_{4}\\ \\ B^{2n}_{6}\\ \\ B^{2n}_{8}\\ \\ \vdots \end{pmatrix}=0, \end{aligned}$$

(28c)

$$\begin{aligned}&odd{-}odd: \qquad \begin{pmatrix} 1-q-\beta & q & 0 & 0 & 0 & 0 & \ldots \\ \\ q & 9-\beta & q & 0 & 0 & 0 & \ldots \\ \\ 0 & q & 25-\beta & q & 0 & 0 & \ldots \\ \\ 0 & 0 & q & 49-\beta & q & 0 & \ldots \\ \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \ddots \end{pmatrix} \begin{pmatrix} B^{2n+1}_{1}\\ \\ B^{2n+1}_{3}\\ \\ B^{2n+1}_{5}\\ \\ B^{2n+1}_{7}\\ \\ \vdots \end{pmatrix}=0, \end{aligned}$$

(28d)

Equation 28 is corresponding to the recurrence Eq. 12. Excluding the Eq. 28b, all the left-hand side matrices are symmetric, tridiagonal with non-imaginary matrix entries.

Appendix 3: The Block Matrix of known Coefficients

The element of the known matrix given in Eq. 24 can be obtained as

$$\begin{aligned} D_n&=\begin{bmatrix} \Xi ^{(1,1)}_{n,k}&\pmb {0}&\pmb {0}&\Xi ^{(1,4)}_{n,k} \\ \pmb {0}&\Xi ^{(2,2)}_{n,k}&\Xi ^{(2,3)}_{n,k}&\pmb {0} \\ \pmb {0}&\Xi ^{(3,2)}_{n,k}&\Xi ^{(3,3)}_{n,k}&\pmb {0} \\ \Xi ^{(4,1)}_{n,k}&\pmb {0}&\pmb {0}&\Xi ^{(4,4)}_{n,k} \end{bmatrix},\nonumber \\ \Xi ^{(1,1)}_{n,k}&=\xi ^1_{n,k}+\xi ^2_{n,k}+\xi ^3_{n,k}+\xi ^4_{n,k}, \end{aligned}$$

(29)

where,

$$\begin{aligned} \xi ^1_{n,k}= & {} {\left\{ \begin{array}{ll} 2\pi \lambda A^n_{(k+2)}(q_c)\ Mc_n(\zeta _i,q_c) \Gamma (k,n), &{} k=0,\\ \\ \lambda \left\{ \frac{9}{4} \pi A^n_{(k+2)}(q_c)+\frac{1}{4} A^n_{k}(q_c)\left[ \pi -2 \pi \ \mathrm{cos}h(2\zeta _i)\right] \right\} \\ \qquad \qquad \qquad \qquad \qquad Mc_n(\zeta _i,q_c)\Gamma (k,n), &{} k=1,\\ \\ \lambda \left[ \frac{1}{4} (-2+k)^2 \pi A^n_{(k-2)}(q_c) -\frac{k^2}{2}\pi \ \mathrm{cos}h(2\zeta _i) A^n_k(q_c)\right. \\ \left. \qquad \qquad \qquad +\frac{(2+k)^2}{4} \pi A^n_{(k+2)}(q_c)\right] Mc_n(\zeta _i,q_c) \Gamma (k,n), &{} k\ge 2, \end{array}\right. } \end{aligned}$$

$$\begin{aligned} \xi ^2_{n,k}= & {} {\left\{ \begin{array}{ll} -2\pi \mu \ A^n_{(k+2)}(q_c) \ Mc_n(\zeta _i,q_c) \ \Gamma (k,n), &{} k=0,\\ \\ \mu \ \left[ - \frac{\pi }{2} A^n_{k}(q_c)-\frac{3}{2} \pi A^n_{k+2}(q_c) \right] \\ \qquad \qquad \qquad \qquad Mc_n(\zeta _i,q_c)\ \Gamma (k,n) , &{} k=1,\\ \\ \mu \left[ \frac{(-2+k)}{2} \pi A^n_{(k-2)}(q_c)-\frac{(k+2)}{2}\pi A^n_{(k+2)}(q_c) \right] \\ \qquad \qquad \qquad \qquad Mc_n(\zeta _i,q_c) \ \Gamma (k,n), &{} k\ge 2,\end{array}\right. } \end{aligned}$$

$$\begin{aligned} \xi ^3_{n,k}= & {} (\lambda +2 \mu ) \Gamma (k,n) {\left\{ \begin{array}{ll} \left[ -\frac{\pi }{2} A^n_{(k+2)}(q_c) +\pi \ \mathrm{cos}h(2 \zeta _i) A^n_k(q_c) \right] \\ \qquad \qquad \frac{d^2 Mc_n(\zeta _i,q_c)}{d\zeta ^2}, &{} k=0,\\ \\ \left\{ -\frac{\pi }{4} A^n_{(k+2)}(q_c)+\frac{\pi }{4} A^n_{k}(q_c) \left[ -1+\right. \right. \\ \left. \left. \qquad \qquad 2 \ \mathrm{cos}h(2\zeta _i)\right] \right\} \frac{d^2 Mc_n(\zeta _i,q_c)}{d\zeta ^2}, &{} k=1, \\ \\ \left[ -\frac{\pi }{2} A^n_{(k-2)}(q_c) -\frac{\pi }{4} A^n_{(k+2)}(q_c) +\right. \\ \left. \qquad \qquad \frac{\pi }{2} A^n_{k}(q_c) \ \mathrm{cos}h(2\zeta _i) \right] \frac{d^2 Mc_n(\zeta _i,q_c)}{d\zeta ^2}, &{} k=2,\\ \\ \left[ -\frac{\pi }{4} A^2_{(k-2)}(q_c) +\frac{\pi }{2} \mathrm{cos}h(2\zeta _i) A^n_{k}(q_c) \right. \\ \left. \qquad \qquad -\frac{\pi }{4} A^{n}_{(k+2)}(q_c)\right] \frac{d^2 Mc_n(\zeta _i,q_c)}{d\zeta ^2}, &{} k\ge 3, \end{array}\right. } \end{aligned}$$

$$\begin{aligned} \xi ^{4}_{n,k}= & {} \mu \pi \frac{d Mc_n(\zeta _i,q_c)}{d \zeta } \ \Gamma (k,n) {\left\{ \begin{array}{ll} -2 \ \mathrm{sin}h(2\zeta _i) A^n_{k}(q_c), &{} k=0,\\ -\mathrm{sin}h(2 \zeta _i) A^n_{k}(q_c), &{} k\ge 1, \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned} \Gamma (k,n)&={\left\{ \begin{array}{ll} 1, &{} (k \& n)=(2j+1),\\ 1, &{} (k \& n)=(2j),\\ 0, &{} else, \end{array}\right. } \end{aligned}$$

in which $j=0,1,2,\ldots ,N$.

$$\begin{aligned} \Xi ^{(1,4)}_{n,k}&=\alpha ^1_{n,k}+\alpha ^2_{n,k}+\alpha ^3_{n,k},\\ \alpha ^1_{n,k}&= \pi \mu \frac{d Ms_n(\zeta _i,q_s)}{d \zeta } \Gamma (k,n) {\left\{ \begin{array}{ll} -2 B^n_{(k+2)}(q_s), &{} k=0,\\ \\ \frac{1}{2} \left\{ -3 B^n_{(k+2)}(q_s) \right. \\ \\ +\left. B^n_{k}(q_s) [-1+2 \mathrm{cos}h(2 \zeta _i) ] \right\} , &{} k=1, \\ \\ 2\left[ \frac{(2-k)}{4} B^n_{(k-2)}(q_s) +\frac{k}{2}\ \mathrm{cos}h(2 \zeta _i)\right. \\ \left. \qquad B^n_{k}(q_s) -\frac{(2+k)}{4} B^n_{(k+2)}(q_s) \right] , &{} k\ge 2, \end{array}\right. } \end{aligned}$$

$$\begin{aligned} \alpha ^{2}_{n,k}&= \pi \mu \frac{d Ms_n(\zeta _i,q_s)}{d \zeta } \Gamma (k,n) {\left\{ \begin{array}{ll} -B^n_{(k+2)}(q_s), &{} k=0,\\ \\ \frac{-1}{2} B^n_{(k+2)}(q_s), &{} 1\le k\le 2 ,\\ \\ \left[ \frac{1}{2} B^n_{(k-2)}(q_s)-\frac{1}{2} B^n_{(k+2)}(q_s)\right] , &{} k\ge 3 ,\\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} \alpha ^3_{n,k}&= Ms_n(\zeta _i,q_s) \mu \Gamma (k,n) {\left\{ \begin{array}{ll} 0, &{} 0 \le k \le 1,\\ -2 B^n_{k} \mathrm{sin}h(2\zeta _i), &{} k=2, \\ -k B^n_{k} \mathrm{sin}h(2\zeta _i), &{} k\ge 3, \end{array}\right. } \end{aligned}$$

$$\begin{aligned} \Xi ^{(2,2)}_{n,k}= \Delta ^1_{n,k}+\Delta ^2_{n,k}+\Delta ^3_{n,k}, \end{aligned}$$

(30)

$$\begin{aligned} \Delta ^1_{n,k}&= \pi \frac{d Ms_n(\zeta _i,q_c)}{d \zeta } \Gamma (k,n) {\left\{ \begin{array}{ll} -2 B^n_{k+2}(q_c), &{} k=0,\\ \\ \frac{1}{2}\left\{ -3 B^n_{(k+2)}(q_c)+\right. \\ \left. \qquad B^n_k(q_c) [-1+2\ \mathrm{cos}h(2\zeta _i)] \right\} , &{} k=1,\\ \\ \left[ \frac{(2-k)}{2} B^n_{(k-2)}(q_c) + k\ \mathrm{cos}h(2\zeta _i)\right. \\ \left. \qquad B^n_k(q_c) -\frac{(k+2)}{2} B^n_{(k+2)}(q_c)\right] , &{} k\ge 2, \end{array}\right. } \end{aligned}$$

$$\begin{aligned} \Delta ^2_{n,k}&= \pi \frac{d Ms_n(\zeta _i,q_c)}{d \zeta } \Gamma (k,n) {\left\{ \begin{array}{ll} - B^n_{(k+2)}(q_c), &{} k=0, \\ \\ -\frac{1}{2} \left[ B^n_{k}(q_c)+B^n_{(k+2)}(q_c)\right] , &{} k=1,\\ \\ \frac{-1}{2} B^n_{(k+2)}(q_c), &{} k=2,\\ \\ \left[ \frac{1}{2}B^n_{(k-2)}(q_c)-\frac{1}{2}B^n_{(k+2)}(q_c)\right] , &{} k\ge 3, \end{array}\right. } \end{aligned}$$

$$\begin{aligned} \Delta ^3_{n,k}&=-\,\pi k B^n_{k}(q_c) Ms_n(\zeta _i,q_c) \Gamma (k,n),\\ \Xi ^{(2,3)}_{n,k}&= \vartheta ^1_{n,k}+ \vartheta ^2_{n,k}+ \vartheta ^3_{n,k} + \vartheta ^4_{n,k}, \end{aligned}$$

$$\begin{aligned} \vartheta ^1_{n,k}&=\pi Mc_n(\zeta _i,q_s) \Gamma (k,n) {\left\{ \begin{array}{ll} 2 A^n_{(k+2)}(q_s), &{} k=0,\\ \\ \frac{1}{4} \left\{ 9 A^n_{(k+2)}(q_s)+ A^n_{k}(q_s)\right. \\ \qquad \left. \left[ 1-2 \ \mathrm{cos}h(2\zeta _i)\right] \right\} , &{} k=1, \\ \\ \left[ \frac{1}{4} (k-2)^2 A^n_{(k-2)}(q_s) -\frac{k^2}{2} \mathrm{cos}h(2\zeta _i)\right. \\ \qquad A^n_k(q_s) \left. +\frac{(k+2)^2}{4} A^n_{k+2}(q_s) \right] , &{} k\ge 2, \end{array}\right. } \end{aligned}$$

$$\begin{aligned} \vartheta ^2_{n,k}&= \pi Mc_n(\zeta _i,q_s) \Gamma (k,n) {\left\{ \begin{array}{ll} -2 A^n_{(k+2)}(q_s), &{} k=0, \\ \\ \frac{-1}{2} \left[ A^n_k(q_s) +3 A^n_{(k+2)}(q_s) \right] , &{} k=1, \\ \left[ \frac{(k-2)}{2} A^n_{(k-2)} (q_s) -\frac{(k+2)}{2} A^n_{(k+2)} (q_s) \right] , &{} k\ge 2, \end{array}\right. } \end{aligned}$$

$$\begin{aligned} \vartheta ^3_{n,k}&= \pi \frac{d^2 Mc_n(\zeta _i,q_s)}{d\zeta ^2} \Gamma (k,n) \left\{ \begin{array}{ll} \left[ \frac{1}{2} A^n_{(k+2)}(q_s)- A^n_{k}(q_s) \mathrm{cos}h(2\zeta _i)\right] , &{} k=0,\\ \\ \frac{1}{4}\left\{ A^n_{(k+2)}(q_s) +\right. \\ \\ \left. \qquad A^n_{k}(q_s) \left[ 1-2\ \mathrm{cos}h(2\zeta _i)\right] \right\} , &{} k=1,\\ \\ \left[ \frac{1}{4} A^n_{(k-2)}(q_s) -\frac{1}{2} \right. \\ \left. \mathrm{cos}h(2 \zeta _i) A^n_{k}(q_s) +\frac{1}{4} A^n_{(k+2)}(q_s) \right] ,&{} k\ge 2, \end{array}\right. \end{aligned}$$

$$\begin{aligned} \vartheta ^4_{n,k}&=\pi \frac{d Mc_n(\zeta _i,q_s)}{d \zeta } \Gamma (k,n) \left\{ \begin{array}{ll} 2 A^n_{k}(q_s)\ \mathrm{sin}h(2\zeta _i), &{} k=0,\\ 2 A^n_{k}(q_s)\ \mathrm{sin}h(2\zeta _i), &{} k\ge 1, \end{array}\right. \\ \Xi ^{(3,2)}_{n,k}&= \iota ^1_{n,k}+\iota ^2_{n,k}+\iota ^3_{n,k}+\iota ^4_{n,k}, \end{aligned}$$

$$\begin{aligned} \iota ^1_{n,k}&=\pi (\lambda +2\mu ) \frac{d^2 Ms(\zeta _i,q_c)}{d\zeta ^2} \Gamma (k,n) \left\{ \begin{array}{ll} \frac{1}{4} \left\{ - B^n_{(k+2)}(q_c) + B^n_{k}(q_c)\right. \\ \qquad \left. \left[ 1+2 \ \mathrm{cos}h(2\zeta _i)\right] \right\} , &{} k=1, \\ \\ -\frac{1}{4} \left[ B^n_{(k+2)}(q_c) \right. \\ \left. \qquad -2 B^n_{k}(q_c)\ \mathrm{cos}h(2\zeta _i)\right] , &{} k=2,\\ \\ \frac{-1}{4} \left[ B^n_{(k-2)}(q_c)+B^n_{(k+2)}(q_c)\right. \\ \qquad \left. -2 B^n_{k}(q_c) \mathrm{cos}h(2\zeta _i)\right] , &{} k\ge 3, \end{array}\right. \end{aligned}$$

$$\begin{aligned} \iota ^2_{n,k}&= \pi \lambda Ms_n(\zeta _i,q_c) \Gamma (k,n) \left\{ \begin{array}{ll} -\frac{1}{4} \left\{ -9 B^n_{(k+2)}(q_c) +\right. \\ \left. \qquad B^n_{k}(q_c) [1+2 \ \mathrm{cos}h(2\zeta _i) \right\} , &{} k=1, \\ \\ \left[ 4 B^n_{(k+2)}(q_c)- 2 B^n_{k}(q_c) \ \mathrm{cos}h(2 \zeta _i) \right] , &{} k=2,\\ \\ \left[ \frac{(k-2)^2}{4} B^n_{(k-2)} (q_c) -\frac{k^2}{2} \right. \\ \left. \quad \mathrm{cos}h(2\zeta _i) B^n_{k}(q_c) \frac{(k+2)^2}{4} B^n_{(k+2)}(q_c) \right] , &{} k\ge 3, \end{array}\right. \end{aligned}$$

$$\begin{aligned} \iota ^3_{n,k}&=- \pi \mu \frac{d Ms_n(\zeta _i,q_c)}{d \zeta } \ \mathrm{sin}h(2\zeta _i) \Gamma (k,n) B^n_{k}(q_c) , \end{aligned}$$

$$\begin{aligned} \iota ^4_{n,k}&=\pi \mu Ms_n(\zeta _i,q_c) \Gamma (k,n) \left\{ \begin{array}{ll} \frac{1}{2} [ B^n_{k}(q_c)-3 B^n_{k+2}(q_c) ], &{} k=1,\\ \\ \frac{(k-2)}{2} B^n_{(k-2)}(q_c) -\frac{(2+k)}{2} B^n_{(k+2)}(q_c), &{} k \ge 2, \end{array}\right. \end{aligned}$$

$$\begin{aligned} \Xi ^{(3,3)}_{n,k}&=\Theta ^{1}_{n,k}+\Theta ^{2}_{n,k}+\Theta ^{3}_{n,k},\\ \Theta ^1_{n,k}&= \pi \mu \frac{d Mc_n(\zeta _i,q_s)}{d \zeta } \Gamma (k,n) {\left\{ \begin{array}{ll} -\frac{1}{2} \left\{ -3 B^{n}_{(k+2)}(q_s)+ \right. \\ \qquad \left. B^n_{k}(q_s) [1+2 \ \mathrm{cos}h(2 \zeta _i) ] \right\} , &{} k=1, \\ \\ \\ \left[ \frac{(k-2)}{2} B^n_{(k-2)}(q_s)-k B^n_{k}(q_s) \right. \\ \left. \qquad \mathrm{cos}h(2\zeta _i)+\frac{(k+2)}{2} B^n_{(k+2)}(q_s) \right] , &{} k\ge 2, \end{array}\right. } \end{aligned}$$

$$\begin{aligned} \Theta ^2_{n,k}&=-\mu \ k \ \pi \ \mathrm{sin}h(2\zeta _i)\ Mc_n(\zeta _i,q_s) A^n_{k}(q_s)\ \Gamma (k,n),\\ \Theta ^3_{n,k}&= \mu \frac{d Mc_n(\zeta _i,q_s)}{d \zeta } \Gamma (k,n) {\left\{ \begin{array}{ll} -\frac{1}{2} \left[ A^n_{k}(q_s)-A^n_{(k+2)}(q_s) \right] , &{} k=1, \\ \\ -\left[ A^n_{(k-2)}(q_s)-\frac{1}{2} A^n_{(k+2)}(q_s) \right] , &{} k=2,\\ \\ -\frac{1}{2} \left[ A^n_{(k-2)}(q_s)-A^n_{(k+2)}(q_s) \right] , &{} k \ge 2,\end{array}\right. } \end{aligned}$$

$$\begin{aligned} \Xi ^{(4,1)}_{n,k}&=\Pi ^1_{n,k}+\Pi ^2_{n,k}+\Pi ^3_{n,k},\\ \Pi ^1_{n,k}&=\pi \frac{d Mc_n(\zeta _i,q_c)}{d \zeta } \Gamma (k,n) {\left\{ \begin{array}{ll} \frac{-1}{2} \left\{ -3 A^n_{(k+2)}(q_c) +A^n_{k}(q_c)\right. \\ \qquad \left. [1+2 \mathrm{cos}h(2\zeta _i) ] \right\} , &{} k=1, \\ \\ \left[ \frac{(k-2)}{2} A^n_{k-2}(q_c) -k \ \mathrm{cos}h(2\zeta _i) A^n_k(q_c) \right. \\ \left. \qquad \frac{(k+2)}{2} A^n_{(k+2)}(q_c) \right] , &{} k\ge 2, \end{array}\right. } \end{aligned}$$

$$\begin{aligned} \Pi ^2_{n,k}&=k \pi A^n_{k}(q_c) \ \mathrm{sin}h(2\zeta _i) \ \Gamma (k,n) Mc_n(\zeta ,q_c)\ ,\\ \Pi ^3_{n,k}&= \pi \frac{d Mc_n(\zeta _i,q_c)}{d \zeta } \Gamma (k,n) {\left\{ \begin{array}{ll} \frac{-1}{2} [A^n_{k}(q_c) -A^n_{(k+2)} ], &{} k=1,\\ \\ -A^n_{(k-2)}(q_c) +\frac{1}{2} A^n_{(k+2)}(q_c), &{} k=2, \\ \\ \frac{-1}{2} A^n_{(k-2)}(q_c)+\frac{1}{2} A^n_{(k+2)}(q_c), &{} k\ge 3, \end{array}\right. } \end{aligned}$$

$$\begin{aligned} \Xi ^{(4,4)}_{n,k}&=\Upsilon ^1_{n,k}+\Upsilon ^2_{n,k} +\Upsilon ^3_{n,k}+\Upsilon ^4_{n,k},\\ \Upsilon ^1_{n,k}&= \pi \frac{d^2 Ms_n(\zeta _i,q_s)}{d\zeta ^2} \Gamma (k,n) {\left\{ \begin{array}{ll} \frac{-1}{4} \left\{ - B^n_{(k+2)}(q_s)\right. \\ \qquad \left. +B^n_{k}(q_s) [1+2 \ \mathrm{cos}h(2\zeta _i) ]\right\} , &{} k=1,\\ \\ \frac{1}{4} [ B^n_{(k+2)}(q_s)\\ \qquad - 2 B^n_{k}(q_s) \ \mathrm{cos}h(2\zeta _i) ], &{} k=2, \\ \\ \left[ \frac{1}{4} B^n_{(k-2)}(q_s) +\frac{1}{4} B^n_{(k+2)}(q_s)\right. \\ \left. \qquad \qquad -\frac{1}{2} B^n_{k}(q_s) \ \mathrm{cos}h(2 \zeta _i) \right] , &{} k\ge 3,\end{array}\right. } \end{aligned}$$

$$\begin{aligned} \Upsilon ^2_{n,k}&= \pi Ms_n(\zeta _i,q_s) \Gamma (k,n) {\left\{ \begin{array}{ll} -\frac{1}{4} \left\{ -9 B^n_{k+2}(q_s) + \right. \\ \left. \qquad B^n_{k}(q_s) [1+2 \ \mathrm{cos}h(2 \zeta _i) ] \right\} , &{} k=1,\\ \\ \left[ \frac{(k-2)^2}{4} B^n_{(k-2)}(q_s) -\frac{k^2}{2} \mathrm{cos}h(2\zeta _i)\right. \\ \qquad \left. B^n_{k}(q_s) +\frac{(k+2)^2}{4} B^n_{(k+2)}(q_s) \right] , &{} k\ge 2, \end{array}\right. } \end{aligned}$$

$$\begin{aligned} \Upsilon ^3_{n,k}&= \pi \frac{d Ms_n(\zeta ,q_s)}{d \zeta } \Gamma (k,n) B^n_{k}(q_s),\\ \Upsilon ^4_{n,k}&= \pi Ms_n(\zeta _i,q_s) \Gamma (k,n) {\left\{ \begin{array}{ll} -\frac{1}{2} [ B^n_{k}(q_s) -3 B^n_{(k+2)}(q_s)], &{} k=1,\\ \\ \left\{ (\pi -\frac{k \pi }{2}) B^n_{(k-2)} (q_s)\right. \\ \left. \qquad +(\pi +\frac{k \pi }{2}) B^n_{(k+2)} (q_s) \right\} , &{} k\ge 2, \end{array}\right. } \end{aligned}.$$

where $k=0,1,2,3,\ldots$ and $i=1,2$.