Abstract
We generalize the notion of strong quasi-continuity for real functions of real variable, given by Grande (Real Anal Exchange 21(1):236–243, 1995/1996), to the case of multifunctions in topological spaces. We introduce a differentiation base in a metric space and show that a strong quasi-continuous multifunction with respect to this differentiation base is almost everywhere continuous.
Similar content being viewed by others
1 Introduction
The notion of quasi-continuity, introduced by Kempisty [10] for real functions, has been studied intensively. There are various reasons for the interest in this notion. Perhaps the main ones are its applications in mathematical analysis and topology. There are also some connections to probability and, of course, to other generalized continuity concepts such as cliquishness [3, 22], semi-continuity [14], and \(\alpha \)-continuity (called also strong quasi-continuity) [18, 19].
Kempisty’s definition of quasi-continuity was reformulated for general topological spaces by Neubrunn [18] and generalized to the case of multifunctions by Popa [20]. Many new features evolved in this case. Afterwards, quasi-continuity of multifunctions has been widely considered by many authors, we refer to Neubrunn [17, 18], Ewert [2], Ewert and Neubrunn [4], Holá and Holý [9], and Matejdes [16]. The special case of quasi-continuous functions of two real variables was investigated by Grande in [5, 7, 8].
As we have alluded earlier, strong quasi-continuity has been considered in the literature first by Noiri [19] for functions and then by Neubrunn for multifunctions [18]; under a different name—continuity with respect to the \(\alpha \)-topology of a topological space.
Strong quasi-continuity of real functions was also considered by Grande in [6] but in a different sense. His definition is based on the density topology in the space of real numbers. We generalize this notion to the case of multifunctions (in abstract spaces) and show that a multifunction which is strongly quasi-continuous is almost everywhere continuous.
2 Preliminaries
We will use standard notation. The sets of positive integers and real numbers will be denoted by \({{\mathbb {N}}}\) and \({{\mathbb {R}}}\), respectively. \({{\mathbb {R}}}^n\), \(n\in {{\mathbb {N}}}\), will denote the n-dimensional Euclidean space. Let \((S,{{\mathcal {T}}}(S))\) and \((Z,{{\mathcal {T}}}(Z))\) be topological spaces. For a set  and
and  will denote the closure and the interior of A, respectively. Moreover, if \(s_0\in S\), then \({{\mathcal {B}}}(s_0)\subset {{\mathcal {T}}}(S)\) will denote the family of all neighbourhoods of \(s_0\).
will denote the closure and the interior of A, respectively. Moreover, if \(s_0\in S\), then \({{\mathcal {B}}}(s_0)\subset {{\mathcal {T}}}(S)\) will denote the family of all neighbourhoods of \(s_0\).
Kempisty’s definition of quasi-continuity of a function \(f:X\rightarrow Y\) was given for the case \(X={{\mathbb {R}}}^n\) and \(Y={{\mathbb {R}}}\) [10]. For general topological spaces it can be reformulated in the following way [18]: A function \(f:S\rightarrow Z\) is called quasi-continuous at\(s_0\in S\) if for any open sets U and V such that \(s_0\in U\) and \(f(s_0)\in V\) there exists a nonempty open set \(G\subset U\) such that \(f(G)\subset V\); f is called quasi-continuous if it is quasi-continuous at any point \(s\in S\).
Clearly any continuous function is quasi-continuous. The converse is of course not true. Any left or right continuous function \(f:{{\mathbb {R}}}\rightarrow {{\mathbb {R}}}\) is quasi-continuous.
By a multifunction (set-valued map) from S to Z we mean a map which assigns to every point of S a nonempty subset of Z. If \(\Phi \) is a multifunction from S to Z, we denote it by \(\Phi :S \leadsto Z\).
If \(\Phi :S\leadsto Z\) and \(G\subset Z\) are given, then we define

Note that

A function \(f:S\rightarrow Z\) may be considered as a multifunction assigning to \(s\in S\) the singleton \(\{f(s)\}\). It is clear that in this case for \(G\subset Z\) we have
A multifunction \(\Phi :S\leadsto Z\) is called upper (resp. lower) semicontinuous at a point\(s_0\in S\) if for any open set \(G\subset Z\) such that \(\Phi (s_0)\subset G\) (resp. \(\Phi (s_0)\cap G\ne \varnothing \)), there exists \(U(s_0)\in {{\mathcal {B}}}(s_0)\) such that \(U(s_0)\subset \Phi ^+(G)\) (resp. \(U(s_0)\subset \Phi ^-(G))\); \(\Phi \) is called continuous at\(s_0\in S\) if it is both upper and lower semicontinuous at \(s_0\). \(\Phi \) is called continuous or upper (resp. lower) semicontinuous if it is continuous or upper (resp. lower) semicontinuous at each \(s\in S\).
Following Neubrunn [18], a multifunction \(\Phi :S\leadsto Z\) is lower (resp. upper) quasi-continuous at a point\(s_0\in S\) if for any set \(G\in {{\mathcal {T}}}(Z)\) such that \(s_0\in \Phi ^-(G)\) (resp. \(s_0\in \Phi ^+(G)\)) and for any set \(U(s_0)\in {{\mathcal {B}}}(s_0)\) there exists a nonempty open set \(V\subset U(s_0)\) such that \(V\subset \Phi ^-(G)\) (resp. \(V\subset \Phi ^+(G)\)); \(\Phi \) is said to be lower (resp. upper) quasi-continuous if it is lower (resp. upper) quasi-continuous at every point \(s\in S\).
Note that in the case of single-valued function the notions of lower quasi-continuity and upper quasi-continuity coincide with quasi-continuity.
A multifunction \(\Phi :S\leadsto Z\) is said to be quasi-continuous at a point\(s_0\in S\) if for arbitrary sets \(G\in {{\mathcal {T}}}(Z)\) and \(H\in {{\mathcal {T}}}(Z)\) such that \(s_0\in \Phi ^-(G)\cap \Phi ^+(H)\) and for every set \(U(s_0)\in {{\mathcal {B}}}(s_0)\) there exists a nonempty open set \(V\subset U(s_0)\) such that \(V\subset \Phi ^-(G)\cap \Phi ^+(H)\).
Clearly a quasi-continuous multifunction is both lower quasi-continuous and upper quasi-continuous. The converse is not true (see [18, Example 1.2.7]). Also, any lower (resp. upper) semicontinuous multifunction is lower (resp. upper) quasi-continuous while the converse is not true.
A set \(A\subset S\) is said to be quasi-open [18] (semi-open [14]) if there is an open set O such that \(O\subset A\subset \mathrm{Cl}(O)\).
Theorem 2.1
([18]) A multifunction \(\Phi :S\leadsto Z\) is lower (resp. upper) quasi-continuous if and only if for any set \(G\in {{\mathcal {T}}}(Z)\) the set \(\Phi ^-(G)\) (resp. \(\Phi ^+(G)\)) is quasi-open.
3 Main results
Let us assume that \((S,d,{{\mathcal {M}}}(S),\mu )\) is a measure metric space with metric d, with a \(\sigma \)-finite complete and \({{\mathcal {G}}}_{\delta }\)-regular measure \(\mu \) defined on a \(\sigma \)-field \({{\mathcal {M}}}(S)\) containing Borel sets; \(\mu ^*\) will denote the outer measure generated by \(\mu \), i.e.,  for a set \(A\subset S\). Moreover
for a set \(A\subset S\). Moreover  will denote the topology in S generated by the metric d.
will denote the topology in S generated by the metric d.
A multifunction \(\Phi :S\leadsto Z\) is called upper (resp. lower) \({{\mathcal {M}}}(S)\)-measurable if \(\Phi ^+(G)\in {{\mathcal {M}}}(S)\) (resp. \(\Phi ^-(G)\in {{\mathcal {M}}}(S)\)) for any set \(G\in {{\mathcal {T}}}(Z)\).
In general the families of all upper \({{\mathcal {M}}}(S)\)-measurable multifunctions and of all lower \({{\mathcal {M}}}(S)\)-measurable multifunctions are independent (see [12, Proposition 1]). While in the case of single-valued functions the notions of upper \({{\mathcal {M}}}(S)\)-measurability and lower \({{\mathcal {M}}}(S)\)-measurability coincide with the usual notion of \({{\mathcal {M}}}(S)\)-measurability of a function.
Let \({{\mathcal {F}}}\subset {{\mathcal {M}}}(S)\) be a family of sets with nonempty interiors of positive and finite measure \(\mu \), the boundaries of which are \(\mu \)-negligible. Let  and \(s\in S\). We write
and \(s\in S\). We write  to mean that for each
to mean that for each  and the diameter of \(I_n\) tends to zero as n runs to infinity. We assume that for every \(s\in S\), there exists a sequence \((I_n)_{n\in {{\mathbb {N}}}}\) of sets from \({\mathcal {F}}\) such that
and the diameter of \(I_n\) tends to zero as n runs to infinity. We assume that for every \(s\in S\), there exists a sequence \((I_n)_{n\in {{\mathbb {N}}}}\) of sets from \({\mathcal {F}}\) such that  .
.
The pair \(({{\mathcal {F}}},\rightarrow )\) is called a differentiation basis for the space \((S,d,{{\mathcal {M}}}(S),\mu )\) in accordance with Bruckner’s terminology [1, p. 30].
Let \(A\subset S\) and \(s\in S\). The upper outer density of the set Aat the pointswith respect to\({\mathcal {F}}\) is equal to the supremum of the set of numbers
(whenever exist) taken for all the sequences \((I_n)_{n\in {{\mathbb {N}}}}\) selected from \({\mathcal {F}}\) and converging to s. Replacing supremum by infimum we obtain the lower outer density of Aat\(s\in S\)with respect to\({\mathcal {F}}\). These densities we will denote by \(D^*_{\mathrm{u}}(A,s)\) and \(D^*_{\mathrm{l}}(A,s)\), respectively. If these densities coincide, then their common value is called the outer density of the set Aatswith respect to\({\mathcal {F}}\) and is denoted by \(D^*(A,s)\). If \(A\in {{\mathcal {M}}}(S)\), then the outer density of the set A at \(s\in S\) with respect to \({\mathcal {F}}\) is called the density ofAatswith respect to\({\mathcal {F}}\) and is denoted by D(A, s).
A point \(s\in S\) is called the density point of a set \(A\subset S\)with respect to\({\mathcal {F}}\) if there exists a set \(B\in {{\mathcal {M}}}(S)\) such that \(B\subset A\) and the density of B at s with respect to \({\mathcal {F}}\) is equal to 1. We will write \(D(A,s)=1\).
We will assume that
-
(DP)
\({\mathcal {F}}\) has the density property, i.e., every set \(A\subset S\) satisfies the following condition:
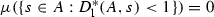 .
.
By the density property of \({\mathcal {F}}\), it is clear that
Lemma 3.1
A set \(A\subset S\), whose \(\mu \)-almost every point is its density point with respect to \({\mathcal {F}}\), is \({\mathcal M}(S)\)-measurable.
An \({{\mathcal {M}}}(S)\)-measurable set is called homogeneous with respect to\({\mathcal {F}}\) if its density with respect to \({\mathcal {F}}\) is 1 at each of its points. The space S can be topologized by taking the homogeneous sets with respect to \({\mathcal {F}}\) as open sets (see [11, p. 232]). This topology we will denote by  . Note that
. Note that  is finer than
is finer than  . The interior of A with respect to
. The interior of A with respect to  is denoted by
is denoted by  -
- .
.
From now on let \((S,d,{{\mathcal {M}}}(S),\mu )\) be a measure metric space with the differentiation basis \(({{\mathcal {F}}},\rightarrow )\) with the density property (DP), and let \((Z,{{\mathcal {T}}}(Z))\) be a topological space.
Definition 3.2
A multifunction \(\Phi :S\leadsto Z\) is called strongly lower (resp. upper) quasi-continuous at a point\(s_0\in S\)with respect to\({\mathcal {F}}\) if for any set \(G\in {{\mathcal {T}}}(Z)\) such that \( s_0 \in \Phi ^-(G)\) (resp. \( s_0 \in \Phi ^+(G)\)) and for any set  containing \(s_0\) there exists a nonempty open set \(V\subset S\) such that \(V\cap U\ne \varnothing \) and \(V\cap U\subset \Phi ^-(G)\) (resp. \(V\cap U\subset \Phi ^+(G)\)); \(\Phi \) is said to be strongly lower (resp. upper) quasi-continuous with respect to\({\mathcal {F}}\) if it is strongly lower (resp. upper) quasi-continuous with respect to \({\mathcal {F}}\) at every point \(s\in S\).
containing \(s_0\) there exists a nonempty open set \(V\subset S\) such that \(V\cap U\ne \varnothing \) and \(V\cap U\subset \Phi ^-(G)\) (resp. \(V\cap U\subset \Phi ^+(G)\)); \(\Phi \) is said to be strongly lower (resp. upper) quasi-continuous with respect to\({\mathcal {F}}\) if it is strongly lower (resp. upper) quasi-continuous with respect to \({\mathcal {F}}\) at every point \(s\in S\).
Observe that replacing in the above definition the density topology with the topology generated by the metric d, we obtain the notion of lower (resp. upper) quasi-continuity of \(\Phi \). Since  -open sets are
-open sets are  -open, we have
-open, we have
Lemma 3.3
If a multifunction \(\Phi :S\leadsto Z\) is strongly lower (resp. upper) quasi-continuous with respect to \({\mathcal {F}}\), then \(\Phi \) is lower (resp. upper) quasi-continuous.
The converse is not true.
By analogy with the definition of quasi-continuity we define strong quasi-continuity of a multifunction.
Definition 3.4
A multifunction \(\Phi :S\leadsto Z\) is called strongly quasi-continuous with respect to\({\mathcal {F}}\)at a point\(s_0\in S\) if for arbitrary sets \(G\in {{\mathcal {T}}}(Z)\) and \(H\in {{\mathcal {T}}}(Z)\) such that \(s_0\in \Phi ^-(G)\cap \Phi ^+(H)\) and for each set  containing \(s_0\) there exists a nonempty open set \(V\subset S\) such that \(V\cap U\ne \varnothing \) and \(V\cap U\subset \Phi ^-(G)\cap \Phi ^+(H)\).
containing \(s_0\) there exists a nonempty open set \(V\subset S\) such that \(V\cap U\ne \varnothing \) and \(V\cap U\subset \Phi ^-(G)\cap \Phi ^+(H)\).
Clearly a multifunction \(\Phi :S\leadsto Z\) which is strongly quasi-continuous with respect to \({\mathcal {F}}\) is quasi-continuous. Furthermore, if \(\Phi \) is strongly quasi-continuous with respect to \({\mathcal {F}}\), then it is both strongly lower quasi-continuous and strongly upper quasi-continuous with respect to \({\mathcal {F}}\).
Some connections between the quasi-continuity and the Denjoy property of real functions were considered by Šalát [21]. We establish now more general properties for multifunctions.
Definition 3.5
A multifunction \(\Phi :S\leadsto Z\) is said to have the \(D^-\) (resp. \(D^+\)) property if for any set \(G\in {{\mathcal {T}}}(Z)\) and for any nonempty open set \(U\subset S\) the set \(U\cap \Phi ^-(G)\) (resp. \(U\cap \Phi ^+(G)\)) is either empty or \(\mu ^* (U\cap \Phi ^-(G))>0\) (resp. \(\mu ^*(U\cap \Phi ^+(G))>0\)).
Proposition 3.6
If a multifunction \(\Phi :S\leadsto Z\) is lower (resp. upper) quasi-continuous, then \(\Phi \) has the \(D^-\) (resp. \(D^+)\) property.
Proof
Let \(G\in {{\mathcal {T}}}(Z)\) and let \(U\subset S\) be a nonempty open set. By the lower (resp. upper) quasi-continuity of \(\Phi \), the set \(\Phi ^-(G)\) (resp. \(\Phi ^+(G)\)) is quasi-open (see Theorem 2.1). Then the set \(U\cap \Phi ^-(G)\) (resp. \(U\cap \Phi ^+(G)\)) is either empty or its interior is nonempty, i.e., \(\mu ^*(U\cap \Phi ^-(G))>0\) (resp. \(\mu ^*(U\cap \Phi ^+(G))>0\)).\(\square \)
For a multifunction \(\Phi \) we denote by \(D(\Phi ), D_{\mathrm{l}}(\Phi )\) and \(D_{\mathrm{u}}(\Phi )\) the sets of all its discontinuity, lower semidiscontinuity and upper semidiscontinuity points, respectively. The following lemma will be useful.
Lemma 3.7
([13, p. 182]) Let \((S,{{\mathcal {T}}}(S))\) be a topological space and let \((Z,{{\mathcal {T}}}(Z))\) be a second countable topological space with a base  . Then for a multifunction \(\Phi :S\leadsto Z\) we have:
. Then for a multifunction \(\Phi :S\leadsto Z\) we have:
-
(i)
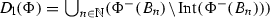 .
. -
(ii)
If \((Z,{{\mathcal {T}}}(Z))\) is \(T_1\) regular and \(\Phi \) is compact valued, then
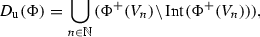
where \((V_n)_{n\in {{\mathbb {N}}}}\) is a sequence of all finite unions of sets from \({\mathcal {B}}\).
Theorem 3.8
If the space \((Z,{{\mathcal {T}}}(Z))\) is regular and second countable, a multifunction \(\Phi :S\leadsto Z\) is strongly lower quasi-continuous with respect to \({\mathcal {F}}\) and it has the \(D^+\) property, then \(\mu (D_{\mathrm{l}}(\Phi ))=0\).
Proof
We first prove that

Suppose, on the contrary, that there is a set \(G\in {\mathcal T}(Z)\) such that \(s\in \Phi ^-(G)\) and  . Let
. Let

Then  . We can assume that \(A\ne \varnothing \). Since \(s\in \Phi ^-(G)\), there is a point \(z\in \Phi (s)\cap G\). By the regularity of Z, there is an open set V containing z such that
. We can assume that \(A\ne \varnothing \). Since \(s\in \Phi ^-(G)\), there is a point \(z\in \Phi (s)\cap G\). By the regularity of Z, there is an open set V containing z such that  . Then \(s\in \Phi ^-(V)\). Let
. Then \(s\in \Phi ^-(V)\). Let

Observe that \(W\ne \varnothing \), since \(A\ne \varnothing \) and \(A\subset W\). Therefore, by the \(D^+\) property of \(\Phi ,\mu ^*(W)>0\). Since  and
and  , it follows that
, it follows that  .
.
Let  -
- . Then
. Then  . Since \(\Phi \) is strongly lower quasi-continuous at s with respect to \({\mathcal {F}}\), for the sets V and B there is a nonempty open set \(U\subset S\) such that
. Since \(\Phi \) is strongly lower quasi-continuous at s with respect to \({\mathcal {F}}\), for the sets V and B there is a nonempty open set \(U\subset S\) such that
On the other hand, however, \(U\cap B\cap W\ne \varnothing \), i.e.,

which contradicts (2), and (1) is proved.
Now we prove that \(\mu (D_{\mathrm{l}}(\Phi ))=0\). Suppose, on the contrary, that \(\mu ^*(D_{\mathrm{l}}(\Phi ))>0\). Let  be a base of \({{\mathcal {T}}}(Z)\). Then, by Lemma 3.7 (i), there is \(n\in {{\mathbb {N}}}\) such that
be a base of \({{\mathcal {T}}}(Z)\). Then, by Lemma 3.7 (i), there is \(n\in {{\mathbb {N}}}\) such that

Let

Since \(\mu ^*(C)>0\), by the assumption (DP), it follows that there is a point \(s\in C\) such that \(D_{\mathrm{l}}^*(C,s)=1\). Note that \(C\subset \Phi ^-(B_n)\). So, \(s\in \Phi ^-(B_n)\) and, by (1), we have  . Thus
. Thus  .\(\square \)
.\(\square \)
Similar proof works for a dual theorem.
Theorem 3.9
Let the space \((Z,{{\mathcal {T}}}(Z))\) be regular. If a multifunction \(\Phi :S\leadsto Z\) is compact-valued strongly upper quasi-continuous with respect to \({\mathcal {F}}\) and it has the \(D^-\) property, then \(\mu (D_{\mathrm{u}}(\Phi ))=0\).
By Lemma 3.3, Proposition 3.6, Theorems 3.8 and 3.9, we have the following result.
Proposition 3.10
If the space \((Z,{{\mathcal {T}}}(Z))\) is regular and if a multifunction \(\Phi :S\leadsto Z\) is compact-valued strongly lower quasi-continuous and strongly upper quasi-continuous with respect to \({\mathcal {F}}\), then \(\Phi \) is \(\mu \)-almost everywhere continuous.
Proposition 3.11
If the space \((Z,{{\mathcal {T}}}(Z))\) is regular and if \(\Phi :S\leadsto Z\) is a compact-valued multifunction strongly lower quasi-continuous and strongly upper quasi-continuous with respect to \({\mathcal {F}}\), then \(\Phi \) is lower \({{\mathcal {M}}}(S)\)-measurable and upper \({{\mathcal {M}}}(S)\)-measurable.
Proof
By Proposition 3.10, the multifunction \(\Phi \) is \(\mu \)-almost everywhere continuous. Let \(G\in {{\mathcal {T}}}(Z)\) and \(s_0\in S\). If \(s_0\) is a continuity point of \(\Phi \), then \(d(\Phi ^+(G),s_0)=1\) and \(d(\Phi ^-(G),s_0)=1\). Hence the sets \(\Phi ^-(G)\) and \(\Phi ^+(G)\) have density 1 with respect to \({\mathcal {F}}\) at \(\mu \)-almost every point. By Lemma 3.1, the sets \(\Phi ^-(G)\) and \(\Phi ^+(G)\) are \({{\mathcal {M}}}(S)\)-measurable, i.e., \(\Phi \) is lower \({{\mathcal {M}}}(S)\)-measurable and upper \({{\mathcal {M}}}(S)\)-measurable. \(\square \)
Remark 3.12
It is known that there is a quasi-continuous function  which is not Lebesgue measurable [15, Example (x), p. 49]. So, if we suppose that the multifunction \(\Phi \), considered in Proposition 3.11, is both lower quasi-continuous and upper quasi-continuous, then \(\Phi \) need not be neither upper \({{\mathcal {M}}}(S)\)-measurable nor lower \({{\mathcal {M}}}(S)\)-measurable.
which is not Lebesgue measurable [15, Example (x), p. 49]. So, if we suppose that the multifunction \(\Phi \), considered in Proposition 3.11, is both lower quasi-continuous and upper quasi-continuous, then \(\Phi \) need not be neither upper \({{\mathcal {M}}}(S)\)-measurable nor lower \({{\mathcal {M}}}(S)\)-measurable.
References
Bruckner, A.M.: Differentiation of Integrals. American Mathematical Monthly, vol. 78(9), Part II. American Mathematical Society, Providence (1971)
Ewert, J.: On quasicontinuous and cliquish maps with values in uniform spaces. Bull. Polish Acad. Sci. Math. 32(1–2), 81–88 (1984)
Ewert, J., Lipiński, J.S.: On relations between continuity, quasi-continuity and cliquishness of maps. In: Frolík, Z. (ed.) General Topology and its Relations to Modern Analysis and Algebra, vol. VI. Research and Exposition in Mathematics, vol. 16, pp. 177–185. Heldermann, Berlin (1988)
Ewert, J., Neubrunn, T.: On quasi-continuous multivalued maps. Demonstratio Math. 21(3), 697–711 (1988)
Grande, Z.: Measurability, quasicontinuity and cliquishness of functions of two variables. Real Anal. Exchange 20(2), 744–752 (1994/1995)
Grande, Z.: On strong quasi-continuity of functions of two variables. Real Anal. Exchange 21(1), 236–243 (1995/1996)
Grande, Z.: Quasicontinuity, cliquishness and the Baire property of functions of two variables. Tatra Mt. Math. Publ. 24(1), 29–35 (2002)
Grande, Z.: Quasicontinuity and measurability of functions of two variables. Real Anal. Exchange 28(1), 7–14 (2002/2003)
Holá, L., Holý, D.: Pointwise convergence of quasicontinuous mappings and Baire spaces. Rocky Mountain J. Math. 41(6), 1883–1894 (2011)
Kempisty, S.: Sur les fonctions quasicontinues. Fund. Math. 19, 184–197 (1932)
Kwiecińska, G.: Measurability and approximate continuity of multivalued functions. Tatra Mt. Math. Publ. 19(2), 229–238 (2000)
Kwiecińska, G., Ślęzak, W.: On complete measurability of multifunctions defined on product spaces. Acta Math. Univ. Comenian. 66(2), 293–305 (1997)
Kuratowski, K.: Topology, vol. I. Mir, Moscow (1966) (in Russian)
Levine, N.: Semi-open sets and semi-continuity in topological spaces. Amer. Math. Monthly 70, 36–41 (1963)
Marcus, S.: Sur les fonctions quasicontinues au sens de S. Kempisty. Colloq. Math. 8(1), 47–53 (1961)
Matejdes, M.: Quelques remarques sur la quasi-continuité des multifunctions. Math. Slovaca 37(3), 267–271 (1987)
Neubrunn, T.: On quasicontinuity of multifunctions. Math. Slovaca 32(2), 147–154 (1982)
Neubrunn, T.: Quasi-continuity. Real. Anal. Exchange 14(2), 259–306 (1988/1989)
Noiri, T.: On \(\alpha \)-continuous functions. Časopis. Pěst. Mat. 109(2), 118–126 (1984)
Popa, V.: On a decomposition of quasicontinuity for multifunctions. Stud. Cerc. Mat. 27(3), 323–328 (1973) (in Romanian)
Šalát, T.: Some generalizations of the notion of continuity and Denjoy property of functions. Časopis. Pěst. Mat. 99, 380–385 (1974)
Thielman, H.P.: Types of functions. Amer. Math. Monthly 60, 156–161 (1953)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kwiecińska, G. A note on strong quasi-continuity of multifunctions. European Journal of Mathematics 5, 186–193 (2019). https://doi.org/10.1007/s40879-018-0239-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-018-0239-8



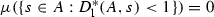 .
.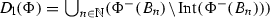 .
.