Introduction

The susceptible–infected–susceptible (SIS) model is one of the most well-known type of epidemic models. These models are appropriate for some infections, for instance, common cold and influenza, or bacterial diseases such as meningitis and cholera, or sexually transmitted diseases, that do not cause permanent immunity after recovery. To immunize individuals from infection and control the infectious diseases, vaccination is usually preferred because of its efficiency compared with other drug and non-drug interventions. There are many epidemic models [1, 3, 8, 13, 14, 16, 19] and also some SIS epidemic models in which temporary or permanent vaccination has been included [6, 9,10,11, 17, 22]. These models may be deterministic [10, 11] or stochastic [4, 6, 22], with constant [10, 13] or variable [9] population size, and with general incidence [7, 21] or a particular incidence such as standard, bilinear, and saturated [2, 5, 13]. In this paper, we introduce an SIS epidemic model with vaccination and standard incidence. In the next section, we first describe the model and then some basic properties of it will be given. Sections “Local asymptotical stability” and “Global asymptotical stability” are devoted to investigating the local and global stability of endemic equilibrium of the model, respectively. Finally, we summarize the conclusions in section “Conclusions”, after a numerical consideration in section “Numerical examples”.

Model description

Consider the following system:

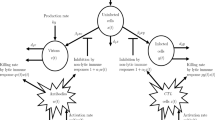
$$\begin{aligned} \frac{{\text{d}}S}{{\text{d}}t}&= (1-\vartheta )\varLambda - \frac{\beta S I}{N} - (\delta + \sigma )S + \eta I + \xi V,\nonumber \\ \frac{{\text{d}}I}{{\text{d}}t}&= \frac{\beta S I}{N} - (\delta + \eta + \alpha )I,\nonumber \\ \frac{{\text{d}}V}{{\text{d}}t}&= \vartheta \varLambda + \sigma S - (\delta + \xi )V. \end{aligned}$$
(1)

Here, the population has been divided into three subpopulations as susceptible, infected, and vaccinated individuals. The size of population in each class at time t is denoted by S, I, and V, respectively, whereas the number of all individuals in this time is given by \(N=S+I+V\). The recruiting is done by entering a number of \(\varLambda\) individuals into population per unit time that may be either immigrants or newborns. The vaccination program is applied on the new members by a proportion \(\vartheta\). A proportion \(\sigma\) of susceptible individuals are also vaccinated, and the rate of losing immunity of vaccination is \(\xi\). The vaccine is supposed to be completely effective, and no vaccinated individual becomes infected. Susceptible individuals become infected at standard incidence rate \(\frac{\beta S I}{N},\) where \(\beta\) is transmission coefficient, whereas the rate of recovery is \(\eta\). The rate of natural death in population is \(\delta\) , and the mortality due to disease is also included in the model with a rate \(\alpha\). All values in the model are nonnegative except \(\varLambda\) and \(\delta\) that are assumed positive.

From system (1), it can be seen that the total number of members N is not fixed in general and it is expressed by the following equation:

$$\begin{aligned} \frac{{\text{d}}N}{{\text{d}}t} = \varLambda - \delta N -\alpha I. \end{aligned}$$
(2)

We have \(\frac{{\text{d}}N}{{\text{d}}t} \le \varLambda - \delta N\), and thus, \(\mathop {\limsup N(t)}\limits _{t\rightarrow \infty } \le \frac{\varLambda }{\delta }\). This also states that I, S, and V are bounded. We can see that the feasible region

$$\begin{aligned} \varGamma =\left\{ (I, S, V)\in {\mathbb {R}}^3_{+}: I+S+V \le \frac{\varLambda }{\delta }\right\} \end{aligned}$$

is a positively invariant set for system (1), and the system is well posed for mathematical and epidemiological considerations in \(\varGamma\).

The equilibria of the model (1) are obtained by solving the following equations:

$$\begin{aligned}&(1 - \vartheta )\varLambda - \frac{\beta \bar{S} \bar{I}}{\bar{N}} - (\delta + \sigma )\bar{S} + \eta \bar{I} + \xi \bar{V} =0,\nonumber \\&\left( \frac{\beta \bar{S}}{\bar{N}}-(\delta + \eta + \alpha )\right) \bar{I} = 0,\nonumber \\&\vartheta \varLambda + \sigma \bar{S} - (\delta + \xi )\bar{V} =0. \end{aligned}$$
(3)

The system has two solutions: When \(\bar{I}=0\) , the disease-free equilibrium (DFE) \(E^0\)

$$\begin{aligned} E^0=(I^0,S^0,V^0)=\left( 0, \frac{\varLambda (\delta (1 - \vartheta ) + \xi )}{\delta (\delta + \xi + \sigma )}, \frac{\varLambda (\delta \vartheta + \sigma )}{\delta (\delta + \xi + \sigma )}\right) , \end{aligned}$$
(4)

and when \(\bar{I}>0\), the endemic equilibrium \(E^*=(I^*,S^*,V^*)\), where

$$\begin{aligned}&I^*=\frac{\varLambda ({\mathcal {R}}_0-1)}{\delta \widetilde{{\mathcal {R}}}_0+\alpha (\widetilde{{\mathcal {R}}}_0-1)},\nonumber \\&S^*=\frac{\varLambda (\delta +\eta +\alpha )}{\beta \delta } \left( 1-\frac{\alpha ({\mathcal {R}}_0-1)}{\delta \widetilde{{\mathcal {R}}}_0+\alpha (\widetilde{{\mathcal {R}}}_0-1)}\right) ,\nonumber \\&V^*=\frac{\vartheta \varLambda }{\delta +\xi } \left( 1+\frac{\sigma (\delta +\alpha \vartheta +\xi )/\vartheta (\delta +\sigma +\xi )}{\delta \widetilde{{\mathcal {R}}}_0+\alpha (\widetilde{{\mathcal {R}}}_0-1)}\right) . \end{aligned}$$
(5)

Here,

$$\begin{aligned} {{\mathcal {R}}}_0&= \frac{ \beta (\delta (1 - \vartheta ) + \xi )}{(\delta +\eta +\alpha ) (\delta +\xi +\sigma )},\\ \widetilde{\mathcal {R}}_0&= \frac{\beta (\delta +\xi )}{(\delta +\eta +\alpha ) (\delta +\xi +\sigma )}, \end{aligned}$$

and thus, we have

$$\begin{aligned} \widetilde{\mathcal {R}}_0 - {\mathcal {R}}_0 = \frac{\beta \delta \vartheta }{(\delta +\eta +\alpha ) (\delta +\xi +\sigma )}. \end{aligned}$$

The quantity \({\mathcal {R}}_0\) is called the basic reproduction number of the model. Furthermore, the total population sizes at two equilibria \(E^0\) and \(E^*\) are obtained, respectively, as follows:

$$\begin{aligned} N^0 = \frac{\varLambda }{\delta }, \end{aligned}$$

and

$$\begin{aligned} N^* = \frac{\varLambda }{\delta } \left( 1-\frac{\alpha ({\mathcal {R}}_0-1)}{\delta \widetilde{\mathcal {R}}_0 + \alpha (\widetilde{\mathcal {R}}_0-1)}\right) . \end{aligned}$$

In the following sections, we investigate dynamics of the model (1) at the endemic equilibrium \(E^*\) and its asymptotic stability will be obtained. The next section is devoted to consider the local asymptotic stability.

Local asymptotical stability

Letting \(F = \frac{\beta S I}{N}\), the Jacobian matrix of the model (1) at \(E^*\) has the following form:

$$\begin{aligned} J^* = \left( \begin{array}{ccc} a_1-(\delta + \eta + \alpha ) &{} a_2 &{} a_3 \\ -a_1 + \eta &{} -a_2-(\delta + \sigma )&{} -a_3+\xi \\ 0 &{} \sigma &{} -(\delta + \xi ) \\ \end{array}\right) , \end{aligned}$$
(6)

in which

$$\begin{aligned} a_1&= \frac{\partial F}{\partial I}\vert _{E^*} = \frac{\beta S^*}{{N^*}^2}(N^*-I^*),\\ a_2&= \frac{\partial F}{\partial S}\vert _{E^*} = \frac{\beta I^*}{{N^*}^2}(N^*-I^*),\\ a_3&= \frac{\partial F}{\partial V}\vert _{E^*} = -\frac{\beta S^* I^*}{{N^*}^2}. \end{aligned}$$

The characteristic equation of matrix \(J^*\) is

$$\begin{aligned} p(\lambda ) = \lambda ^3 + b_1 \lambda ^2 + b_2 \lambda + b_3, \end{aligned}$$
(7)

where

$$\begin{aligned} b_1= & {} -tr(J^*) = -a_1+a_2+(\delta +\eta +\alpha )+(2\delta +\sigma +\xi ),\\ b_2= & {} -\frac{1}{2}(tr({J^*}^2)-tr^2(J^*))\\= & {} -a_1(2\delta +\sigma +\xi )+a_2(2\delta +\alpha +\xi )+a_3\sigma \\&+\delta (\delta +\sigma +\xi )+(\delta +\eta +\alpha )(2\delta +\sigma +\xi ),\\ b_3= & {} -det(J^*) =-a_1\delta (\delta +\sigma +\xi )\\&+a_2(\delta +\alpha )(\delta +\xi )+a_3\sigma (\delta +\alpha )\\&+\delta (\delta +\eta +\alpha )(\delta +\sigma +\xi ). \end{aligned}$$

We have

$$\begin{aligned} a_1&= (\delta +\eta +\alpha )\left( 1-\frac{\delta ({\mathcal {R}}_0-1)}{\delta \widetilde{{\mathcal {R}}}_0+\alpha (\widetilde{{\mathcal {R}}}_0-{\mathcal {R}}_0)}\right) ,\nonumber \\ a_2&= \delta (\beta -(\delta +\eta +\alpha ))\left( \frac{{\mathcal {R}}_0-1}{\delta \widetilde{{\mathcal {R}}}_0+\alpha (\widetilde{{\mathcal {R}}}_0-{\mathcal {R}}_0)}\right) ,\nonumber \\ a_3&= -\delta (\delta +\eta +\alpha )\left( \frac{{\mathcal {R}}_0-1}{\delta \widetilde{{\mathcal {R}}}_0+\alpha (\widetilde{{\mathcal {R}}}_0-{\mathcal {R}}_0)}\right) . \end{aligned}$$
(8)

Obviously \(a_3 < 0\) and \(a_1 = (\delta +\eta +\alpha )\left( \frac{(\delta +\alpha )(\widetilde{{\mathcal {R}}}_0-{\mathcal {R}}_0)+\delta }{\delta \widetilde{{\mathcal {R}}}_0+\alpha (\widetilde{{\mathcal {R}}}_0-{\mathcal {R}}_0)}\right) >0\). Moreover, notice that the equilibrium \(E^*\) exists if \({\mathcal {R}}_0 > 1\) and this implies

$$\begin{aligned} \beta> \beta \left( \frac{\delta (1-\vartheta )+\xi }{\delta +\sigma +\xi }\right) >(\delta +\eta +\alpha ), \end{aligned}$$

and thus, \(a_2>0\).

Using (8), we obtain

  1. (I)

    \(-a_1+a_2 = -(\delta +\eta +\alpha )+\delta \beta \left( \frac{{\mathcal {R}}_0-1}{\delta \widetilde{{\mathcal {R}}}_0 +\alpha (\widetilde{{\mathcal {R}}}_0-{\mathcal {R}}_0)}\right);\) thus,

    $$\begin{aligned} b_1=\delta \beta \left( \frac{{\mathcal {R}}_0-1}{\delta \widetilde{{\mathcal {R}}}_0 +\alpha (\widetilde{{\mathcal {R}}}_0-{\mathcal {R}}_0)}\right) +(2\delta +\sigma +\xi )>0. \end{aligned}$$
  2. (II)

    We can see that

    $$\begin{aligned}&-a_1(2\delta +\sigma +\xi ) + a_3\sigma +(\delta +\eta +\alpha )(2\delta +\sigma +\xi )\\&\quad = (\delta +\eta +\alpha ) \left( \frac{\delta ({\mathcal {R}}_0-1)}{\delta \widetilde{{\mathcal {R}}}_0+\alpha (\widetilde{{\mathcal {R}}}_0-{\mathcal {R}}_0)}\right) (2\delta +\xi ), \end{aligned}$$

    and therefore,

    $$\begin{aligned} b_2&= (\delta +\eta +\alpha ) \left( \frac{\delta ({\mathcal {R}}_0-1)}{\delta \widetilde{{\mathcal {R}}}_0+\alpha (\widetilde{{\mathcal {R}}}_0-{\mathcal {R}}_0)}\right) (2\delta +\xi )\\&+ a_2(2\delta +\alpha +\xi ) + \delta (\delta +\sigma +\xi )>0. \end{aligned}$$
  3. (III)

    We have

    $$\begin{aligned} b_3= & {} \delta (\delta +\sigma +\xi )(\delta +\eta +\alpha ) \left( \frac{\delta ({\mathcal {R}}_0-1)}{\delta \widetilde{{\mathcal {R}}}_0+\alpha (\widetilde{{\mathcal {R}}}_0-{\mathcal {R}}_0)}\right) \\&+(\beta (\delta +\xi )\\&-(\delta +\sigma +\xi )(\delta +\eta +\alpha ))\delta (\delta +\alpha ) \left( \frac{{\mathcal {R}}_0-1}{\delta \widetilde{{\mathcal {R}}}_0+\alpha (\widetilde{{\mathcal {R}}}_0-{\mathcal {R}}_0)}\right) \\&+\delta (\delta +\sigma +\xi )(\delta +\eta +\alpha ). \end{aligned}$$

    Besides, \(\widetilde{{\mathcal {R}}}_0>{\mathcal {R}}_0\) and \({\mathcal {R}}_0>1\) implies \(\beta (\delta +\xi )>(\delta +\sigma +\xi )(\delta +\eta +\alpha )\). Therefore,

    $$\begin{aligned} b_3>\delta (\delta +\sigma +\xi )(\delta +\eta +\alpha )\left( 1+\frac{\delta ({\mathcal {R}}_0-1)}{\delta \widetilde{{\mathcal {R}}}_0+\alpha (\widetilde{{\mathcal {R}}}_0-{\mathcal {R}}_0)}\right) >0. \end{aligned}$$
  4. (IV)
    $$\begin{aligned} b_1b_2-b_3&= (\delta +\xi )(b_2-a_2(\delta +\alpha )) \\&\quad+(\delta +\eta +\alpha )(b_2-\delta (\delta +\sigma +\xi ))\\&\quad+ (-a_1+a_2+\delta +\sigma )b_2\\&\quad+a_1\delta (\delta +\sigma +\xi )-a_3\sigma (\delta +\alpha )\\&= (\delta +\xi )(b_2-a_2(\delta +\alpha ))\\&\quad+((\delta +\eta +\alpha )-a_1)(b_2-\delta (\delta +\sigma +\xi ))\\&\quad+(a_2+\delta +\sigma )b_2-a_3\sigma (\delta +\alpha ). \end{aligned}$$

    We see that \(a_1 = (\delta +\eta +\alpha ) \left( 1-\frac{\delta ({\mathcal {R}}_0-1)}{\delta \widetilde{{\mathcal {R}}}_0+\alpha (\widetilde{{\mathcal {R}}}_0-{\mathcal {R}}_0)}\right) < (\delta +\eta +\alpha ),\) and as a result,

    $$\begin{aligned} b_1b_2-b_3> (\delta +\xi )(b_2-a_2(\delta +\alpha ))+(a_2+\delta +\sigma )b_2-a_3\sigma (\delta +\alpha ) >0. \end{aligned}$$

In preceding relations, we got \(b_1>0\), \(b_2>0\), \(b_3>0\) and \(b_1b_2-b_3>0\); thus, by using Routh–Hurwitz criterion the real part of all eigenvalues of the Jacobian matrix \(J^*\) must be negative. Therefore, the following theorem has been proven:

Theorem 1

For epidemic model (1), the endemic state \(E^*\) exists and is stable if \({\mathcal {R}}_0>1\).

Corollary 1

The endemic state \(E^*\) is stable if parameter values \(\vartheta\) and \(\sigma\) lie under the following line in the \(\vartheta\)-\(\sigma\) plane:

$$\begin{aligned} (\beta \delta ) \vartheta +(\delta +\eta +\alpha ) \sigma = (\beta -(\delta +\eta +\alpha ))(\delta +\xi ). \end{aligned}$$
(9)

Corollary 1 gives minimum amount of vaccination proportions that is needed to the vaccine be effective. Indeed, those values of \(\vartheta\) and \(\sigma\) that lie above the mentioned line in (9) are sufficient to the disease eradicated from population. When the proportion of vaccination in new members and in susceptibles is equal, i.e., \(\tau =\vartheta =\sigma\), this optimum amount of vaccination will be as

$$\begin{aligned} \tau ^*=\frac{(\beta -(\delta +\eta +\alpha ))(\delta +\xi )}{(\delta +\eta +\alpha )+\beta \delta }. \end{aligned}$$
(10)

Global asymptotical stability

The global asymptotical stability of the endemic state \(E^*\) is discussed in this section. The analysis of the global stability of epidemic models is generally a difficult task, and the methods introduced for carrying this out are scant. To analyze the global asymptotic stability of the endemic state, we employ a geometric method developed by Li and Muldowney [12] and used by many authors [2, 15, 18,19,20, 23]. The following result has been proved in [12].

Theorem 2

Assume that f is a \(C^1\) function on a simply connected open set \(D\subset \mathbb {R}^n\), the system \(x'=f(x)\) has a unique equilibrium \(\bar{x}\) in D, and there exists a compact absorbing set \(\varTheta \subset D\). Then, \(\bar{x}\) is globally stable in D if

$$\begin{aligned} \mathop {\limsup }\limits _{t \rightarrow \infty } \mathop {\sup }\limits _{x_0\in \varTheta } \frac{1}{t}\int _0^t \varPsi (\varUpsilon (x(r,x_0)))dr <0, \end{aligned}$$

in which \(\varUpsilon =\varSigma _f\varSigma ^{-1}+\varSigma J^{[2]}\varSigma ^{-1}\). Here, \(\varSigma\) is an \(\left( {\begin{array}{c}n\\ 2\end{array}}\right) \times \left( {\begin{array}{c}n\\ 2\end{array}}\right)\) matrix-valued function, \(J^{[2]}\) is the second additive compound matrix of the Jacobian matrix J, \(\varSigma _f\) is obtained by \((\sigma _{ij})_f=\left( \frac{\partial \sigma _{ij}}{\partial x}\right) ^\top . f(x)\), and \(\varPsi (\varUpsilon )\) is the Lozinski\(\breve{\imath }\) measure of \(\varUpsilon\) with respect to a vector norm |.| in \(\mathbb {R}^m\), with \(m=\left( {\begin{array}{c}n\\ 2\end{array}}\right)\), defined by \(\varPsi (\varUpsilon )= \mathop {\lim }\limits _{h \rightarrow 0^+} \frac{|I+h\varUpsilon |-1}{h}\).

The global stability of the endemic state is expressed in the next theorem.

Theorem 3

When \({\mathcal {R}}_0>1\) and \(\delta +\sigma >\xi\), the endemic equilibrium \(E^*\) is globally asymptotic stable if \(\delta +\xi > \max \{\sigma , \alpha \}+ \eta\).

Proof

Considering the feasible region \(\varGamma\), we see that interior and boundary of \(\varGamma\) are \(\mathop {\varGamma }\limits ^{\circ } = \{(I, S, V)\in \varGamma : I>0 \}\) and \(\partial \varGamma = \varGamma \setminus \mathop {\varGamma }\limits ^{\circ } = \{(I, S, V)\in \varGamma : I=0 \}\), respectively. When \({\mathcal {R}}_0>1\), there exists an unique endemic state \(E^*\) , and moreover, the disease-free equilibrium (DFE) \(E^0 \in \partial \varGamma\) is unstable. Now, using Acyclicity Theorem similar to the proof of Theorem 3.2 in [18] we find that when \({\mathcal {R}}_0>1\), system (1) is uniformly persistent. On the other hand, we know that the solutions are bounded because the total population size N is bounded. Considering this with the uniform persistence of the system, it can be concluded that there exists a compact absorbing set \(\varTheta \subset \varGamma\).

The Jacobian matrix of the system at \(E^*\) was given by (6), and thus, its second additive compound matrix is

$$\begin{aligned} {J^*}^{[2]} = \left( \begin{array}{ccc} a_1-a_2-n_1 &{} -a_3+\xi &{} -a_3 \\ \sigma &{} a_1-n_2 &{} a_2 \\ 0 &{} -a_1+\eta &{} -a_2-n_3 \\ \end{array}\right) , \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} n_1&=2\delta +\eta +\alpha +\sigma ,\\ n_2&=2\delta +\eta +\alpha +\xi ,\\ n_3&=2\delta +\sigma +\xi . \end{aligned} \end{aligned}$$

Matrix \(\varSigma\) in Theorem 2 acts as a Lyapunov function. So, for the method to be applicable and efficient, this matrix must be chosen suitable. Now, we choose matrix \(\varSigma\) as \(\varSigma =\frac{S}{I}\mathbb {I}_3\), where \(\mathbb {I}_3\) is the \(3\times 3\) identity matrix. Then, \(\varSigma ^{-1}=\frac{I}{S}\mathbb {I}_3\), \(\varSigma _f=\left( \frac{\frac{{\text{d}}S}{{\text{d}}t}}{I}-\frac{S\left( \frac{{\text{d}}I}{{\text{d}}t}\right) }{I^2}\right) \mathbb {I}_3\) and \(\varSigma _f\varSigma ^{-1}=\left( \frac{\frac{{\text{d}}S}{{\text{d}}t}}{S}-\frac{\frac{{\text{d}}I}{{\text{d}}t}}{I}\right) \mathbb {I}_3\).

Therefore,

$$\begin{aligned} \begin{aligned} \varUpsilon&=\varSigma _f\varSigma ^{-1}+\varSigma {J^*}^{[2]}\varSigma ^{-1} \\&=\left( \begin{array}{ccc} \frac{\frac{{\text{d}}S}{{\text{d}}t}}{S}-\frac{\frac{{\text{d}}I}{{\text{d}}t}}{I}+a_1-a_2-n_1 &{} -a_3+\xi &{} -a_3 \\ \sigma &{} \frac{\frac{{\text{d}}S}{{\text{d}}t}}{S}-\frac{\frac{{\text{d}}I}{{\text{d}}t}}{I}+a_1-n_2 &{} a_2 \\ 0 &{} -a_1+\eta &{} \frac{\frac{{\text{d}}S}{{\text{d}}t}}{S}-\frac{\frac{{\text{d}}I}{{\text{d}}t}}{I}-a_2-n_3 \\ \end{array}\right) . \end{aligned} \end{aligned}$$
(11)

The matrix \(\varUpsilon\) can be written in the block form as \(\varUpsilon =\left( \begin{array}{cc} \varUpsilon _{11} &{} \varUpsilon _{12} \\ \varUpsilon _{21} &{} \varUpsilon _{22} \\ \end{array} \right) ,\) in which

$$\begin{aligned} \begin{aligned} \varUpsilon _{11}&=\frac{\frac{{\text{d}}S}{{\text{d}}t}}{S}-\frac{\frac{{\text{d}}I}{{\text{d}}t}}{I}+a_1-a_2-n_1,\\ \varUpsilon _{12}&=(\begin{array}{cc} -a_3+\xi ,&-a_3 \end{array}),\\ \varUpsilon _{21}&=\left( \begin{array}{c} \sigma \\ 0 \\ \end{array}\right) ,\\ \varUpsilon _{22}&=\left( \begin{array}{cc} \frac{\frac{{\text{d}}S}{{\text{d}}t}}{S}-\frac{\frac{{\text{d}}I}{{\text{d}}t}}{I}+a_1-n_2 &{} a_2 \\ -a_1+\eta &{} \frac{\frac{{\text{d}}S}{{\text{d}}t}}{S}-\frac{\frac{{\text{d}}I}{{\text{d}}t}}{I}-a_2-n_3 \\ \end{array} \right) . \end{aligned} \end{aligned}$$

Considering the vector norm \(| (\mu _1,\mu _2,\mu _2) | = \max \{ | \mu _1 |,| \mu _2 | + | \mu _3 |\}\) for all \((\mu _1, \mu _2, \mu _3) \in \mathbb {R}^3\) as in [12], we have

$$\begin{aligned} \varPsi (\varUpsilon ) \le \sup \{\varOmega _1, \varOmega _2 \}, \end{aligned}$$

where

$$\begin{aligned} \varOmega _1=\varPsi (\varUpsilon _{11})+| \varUpsilon _{12} | \quad \mathrm {and} \quad \varOmega _2=\psi (\varUpsilon _{22})+| \varUpsilon _{21} |. \end{aligned}$$

Thus, we obtain

$$\begin{aligned} \varPsi (\varUpsilon _{11})=\frac{\frac{{\text{d}}S}{{\text{d}}t}}{S}-\frac{\frac{{\text{d}}I}{{\text{d}}t}}{I}+a_1-a_2-n_1,\quad | \varUpsilon _{12} |=-a_3+\xi , \quad | \varUpsilon _{21} |=\sigma \end{aligned}$$

and

$$\begin{aligned} \varPsi (\varUpsilon _{22})&= \max \left\{ \frac{\frac{{\text{d}}S}{{\text{d}}t}}{S}-\frac{\frac{{\text{d}}I}{{\text{d}}t}}{I}+\eta -n_2, \frac{\frac{{\text{d}}S}{{\text{d}}t}}{S}-\frac{\frac{{\text{d}}I}{{\text{d}}t}}{I}-n_3 \right\} \\&=\max \left\{ \frac{\frac{{\text{d}}S}{{\text{d}}t}}{S}-\frac{\frac{{\text{d}}I}{{\text{d}}t}}{I}-(2\delta +\alpha +\xi ), \frac{\frac{{\text{d}}S}{{\text{d}}t}}{S}-\frac{\frac{{\text{d}}I}{{\text{d}}t}}{I}-(2\delta +\sigma +\xi )\right\} \\&=\frac{\frac{{\text{d}}S}{{\text{d}}t}}{S}-\frac{\frac{{\text{d}}I}{{\text{d}}t}}{I}-(2\delta +\xi )-\min \{\alpha , \sigma \}. \end{aligned}$$

From the second equation in system (1)

$$\begin{aligned} \frac{\frac{{\text{d}}I}{{\text{d}}t}}{I}=\frac{\beta S}{N}-(\delta +\eta +\alpha ). \end{aligned}$$

Therefore, we have

$$\begin{aligned} \varOmega _1&= \frac{\frac{{\text{d}}S}{{\text{d}}t}}{S}-\frac{\frac{{\text{d}}I}{{\text{d}}t}}{I}+a_1-a_2-n_1-a_3+\xi \\&= \frac{\frac{{\text{d}}S}{{\text{d}}t}}{S}-\frac{\beta I}{N}\left( 1-\frac{S}{N}\right) -(\delta +\sigma -\xi )\\&\le \frac{\frac{{\text{d}}S}{{\text{d}}t}}{S}-(\delta +\sigma -\xi ), \end{aligned}$$

and

$$\begin{aligned} \varOmega _2&=\frac{\frac{{\text{d}}S}{{\text{d}}t}}{S}-\frac{\frac{{\text{d}}I}{{\text{d}}t}}{I}-(2\delta +\xi )-\min \{\alpha , \sigma \}+\sigma \\&\le \frac{\frac{{\text{d}}S}{{\text{d}}t}}{S}-(\min \{\alpha , \sigma \}-(\eta +\sigma +\alpha )+(\delta +\xi )). \end{aligned}$$

Hence, assuming

$$\begin{aligned} d = \min \{\delta +\sigma -\xi , (\delta +\xi )-(\max \{\sigma ,\alpha \}+\eta )\}>0, \end{aligned}$$

yields to

$$\begin{aligned} \varPsi (\varUpsilon ) \le \frac{\frac{{\text{d}}S}{{\text{d}}t}}{S}-d. \end{aligned}$$

Thus, for each solution \((I(0), S(0), V(0))\in \varTheta\), we have

$$\begin{aligned} \frac{1}{t}\int _0^t\varPsi (B)dr\le \frac{1}{t}\int _0^t \left( \frac{\frac{{\text{d}}S}{{\text{d}}t}}{S}-d\right) dr=\frac{1}{t}\ln \frac{S(t)}{S(0)}-d, \end{aligned}$$

which implies

$$\begin{aligned} \mathop {\limsup }\limits _{t \rightarrow \infty } \sup \frac{1}{t}\int _0^t \varPsi (B)dr< -\frac{d}{2} <0. \end{aligned}$$

Therefore, the conditions of Theorem 2 are hold and this concludes that \(E^*\) is globally asymptotically stable. \(\square\)

Numerical examples

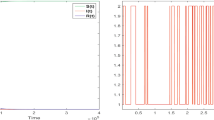
Suppose the parameters in model (1) as \(\varLambda =30\), \(\beta =0.8\), \(\delta =0.2\), \(\alpha =0.1\), \(\eta =0.1\) , and \(\xi =0.2\). For these values, the mentioned line in (9) is shown in Fig. 1. The ordered pair \((\vartheta , \sigma )=(0.2, 0.1)\) lies below the line and by corollary 1 the endemic state \(E^*=(I^*, S^*, V^*)=(34.74, 66.32, 31.58)\) is stable. The point \((\vartheta , \sigma )=(0.4, 0.5)\) lies above the line. In this case, the disease-free equilibrium \(E^0=(I^0, S^0, V^0)=(0, 53.33, 96.67)\) is stable and the infection will be wiped out from population. Besides, for these values for \((\vartheta , \sigma )\) we have \({\mathcal {R}}_0= 1.44>1\) and \({\mathcal {R}}_0=0.71<1\), respectively. Thus, these results can be confirmed also by Theorem 1. Now, if it is supposed that the vaccination proportions in new members and in susceptibles are equal, then the optimal value of such quantity is given by relation (10) as \(\tau ^*=0.286\). For \(\tau =0.05<\tau ^*\) , the infection will remain in the population and the endemic state is stable, while for \(\tau =0.4>\tau ^*\) the number of infected individuals vanishes and the disease-free state is stable (see Fig. 2). Figures 3 and 4 describe the behavior of the model for various initial values and show the solutions are stable. Figure 3 shows the number of infected individuals (sub-figure (a)) and the phase diagram of I(t) and S(t) (sub-figure (b)) when \(\tau =0.4\), and it can be seen that \(E^0\) is stable. Figure 4 shows that I(t) does not vanish when \(\tau =0.05\), and in this case, \(E^*\) is stable .

Fig. 1
figure 1

The line of optimal proportions of vaccine. For those values of \(\vartheta\) and \(\sigma\) that lie below the line, \(E^*\) is stable (red point), and for such values that lie above the line, \(E^0\) is stable (blue point)

Full size image
Fig. 2
figure 2

Solutions of model (1) for \(\tau =0.05\) (left) and \(\tau =0.4\) (right)

Full size image
Fig. 3
figure 3

Solutions of I(t) (a) and the phase diagram of I(t) and S(t) (b) for \(\tau =0.4\) with different initial values in each subpopulation. In this case, \({\mathcal {R}}_0=0.80<1\) and disease will be extinct with \(I^0=0, S^0=53.33, V^0=96.67\)

Full size image
Fig. 4
figure 4

Diagrams of I(t) (a) and the phase diagram of I(t) and S(t) (b) for \(\tau =0.05\) with different initial values. This gives \({\mathcal {R}}_0=1.73>1\) , and disease will persist with \(I^*=34.74, S^*=66.32, V^*=31.58\)

Full size image

Conclusions

In this paper, a deterministic SIS epidemic model with temporary vaccination was studied. Vaccination includes both susceptible and new members, and disease transmission takes place at standard incidence rate. The number of individuals which are added to the population per unit time is constant and differs from the number of individuals that die and leave the population per unit time. Thus, the total population size is variable. Dynamics of the model at the endemic equilibrium were determined by the basic reproduction number \({\mathcal {R}}_0\); when \({\mathcal {R}}_0 >1\) , the unique endemic equilibrium \(E^*\) is locally asymptotically stable and uniformly persists. In addition, it was shown that in this case \(E^*\) is globally asymptotically stable under some conditions by employing a geometric approach and second additive compound matrix method. A numerical discussion was also performed to support the theoretical results.