Introduction

Nowadays, modelling different problems in different issues of science leads to stochastic equations [1]. These equations arise in many fields of science such as mathematics and statistics [2,3,4,5,6,7], finance [8,9,10], physics [11,12,13], mechanics [14, 15], biology [16,17,18], and medicine [19, 20]. Whereas most of them do not have an exact solution, the role of numerical methods and finding a reliable and accurate numerical approximation have become highlighted [21].

In recent years, different orthogonal basic functions and polynomials have been used to find a numerical solution for integral equations such as block pulse functions [2, 21, 22], hat functions [23], hybrid functions [24, 25], wavelet methods [26,27,28], triangular functions [3, 29], and Bernstein polynomials [30]. In this paper, MHFs will be applied to find an approximate solution for the following stochastic Itô–Volterra integral equation with multi-stochastic terms,

$$\begin{aligned}&X(t)=f(t)+\int _0^t\mu (s,t)X(s)\,\hbox {d}s\\&\qquad +\sum _{j=1}^n\int _0^t\sigma _j(s,t)X(s)\,dB_j(s), \end{aligned}$$

where \(t\in D=[0,T), X, f, \mu\) and \(\sigma _j,\,j=1,2,\dots ,n\), for \(s,t\in D\) are the stochastic processes defined on the same probability space (\(\Omega ,F,P\)) and X is unknown. Also \(\int _0^t\sigma _j(s,t)X(s)\,dB_j(s)\,,\,j=1,2,\dots ,n\) are Itô integrals and \(B_1(t), B_2(t),\dots \, B_n(t)\) are the Brownian motion processes [31, 32].

The paper is organized as follows: In “MHFs and their properties” section, the MHFs and their properties are described. In “Operational matrices” section, the operational matrices are found. In “Solving stochastic Itô–Volterra integral equation with multi-stochastic terms by the MHFs” section, the sets and operational matrices are applied in the above equation and the approximate solution is found. In “Error analysis” section, the error analysis of the present method is discussed. In the “Numerical examples” section, some numerical examples are solved by using this method. And finally, the last section concludes the paper.

MHFs and their properties

In this section, we recall the definition and properties of modified hat functions [33]. Let \(m\ge 2\) be an even integer and \(h=\frac{T}{m}\). Also assume that the interval [0, T) is divided into \(\frac{m}{2}\) equal subintervals \([ih,(i+2)h], i=0, 2,\dots , (m-2)\) and let \(X_m\) be the set of all continuous functions that are quadratic polynomials when restricted to each of the above subintervals. Because each element of \(X_m\) is completely determined by its values at the \((m+1)\) nodes \(ih, i=0, 1,\dots , m\), the dimension of \(X_m\) is \((m+1)\). Considering that \(f\in \chi =C^3(D)\) can be approximated by its expansion with respect to the following set functions, \((m+1)\) set of MHFs are defined over D as

$$\begin{aligned} h_0 (t)=&{\left\{ \begin{array}{ll} \frac{1}{2h^2}(t-h)(t-2h), & \quad 0 \le t \le 2h \\ 0 , & \quad \hbox {otherwise}. \end{array}\right. } \end{aligned}$$

If i is odd and \(1\le i\le (m-1)\),

$$\begin{aligned} h_i (t)=&{\left\{ \begin{array}{ll} \frac{-1}{h^2}(t-(i-1)h)(t-(i+1)h), &{} (i-1)h \le t \le (i+1)h \\ 0, &{} \hbox {otherwise}. \end{array}\right. } \end{aligned}$$
(1)

If i is even and \(2 \le i \le (m-2)\),

$$\begin{aligned} h_i (t)=&{\left\{ \begin{array}{ll} \frac{1}{2h^2}(t-(i-1)h)(t-(i-2)h), &{} (i-2)h \le t \le ih \\ \frac{1}{2h^2}(t-(i+1)h)(t-(i+2)h), &{} ih \le t \le (i+2)h \\ 0, &{} \hbox {otherwise}, \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} h_m (t)=&{\left\{ \begin{array}{ll} \frac{1}{2h^2}(t-(T-h))(t-(T-2h)), &{} T-2h \le t \le T \\ 0, &{} \hbox {otherwise}. \end{array}\right. } \end{aligned}$$

Properties of the MHFs

By considering the above definition, the following properties come as a result.

$$\begin{aligned} 1)\, h_i (jh)=&{\left\{ \begin{array}{ll} 1, & \quad i=j \\ 0, & \quad i\ne j \end{array}\right. } . \end{aligned}$$
$$\begin{aligned} 2)\, h_i(t)h_j(t)&= {\left\{ \begin{array}{ll} 0, & \quad i \text { even and }|i-j|\ge 3 \\ 0, & \quad i \text { odd and }|i-j|\ge 2 \end{array}\right. }. \end{aligned}$$

3) They are linearly independent.

$$\begin{aligned} 4)\,\sum _{i=0}^m h_i(t)=&1.&\end{aligned}$$

Suppose

$$\begin{aligned} \mathbf H (t)= [h_0(t) , h_1(t) ,\dots , h_m(t)]^T, \end{aligned}$$
(2)

by applying the second property and considering definition (1), we obtain

$$\begin{aligned} 5)\,\mathbf H (t)\mathbf H ^T(t)\simeq&\begin{pmatrix} h_0(t) &{} 0 &{} \dots &{} 0 \\ 0 &{} h_1(t) &{} \dots &{} 0 \\ \vdots &{} \vdots &{}\ddots &{} \vdots \\ 0 &{} 0 &{} 0 &{} h_m(t) \end{pmatrix}.&\end{aligned}$$
$$\begin{aligned} 6)\,{\mathbf {H}}(t){\mathbf {H}}(t)^T\mathbf X \simeq&diag(\mathbf X ){\mathbf {H}}(t),&\end{aligned}$$

7) Let \(\mathbf {A}\) be an \((m+1)\times (m+1)\) matrix and \({\mathbf {H}}(t)\) be the vector of \((m+1)\)-MHFs defined in (2) then \({\mathbf {H}}(t)^T\mathbf {A}{\mathbf {H}}(t)\simeq {\mathbf {H}}(t)^T\tilde{\mathbf {A}}\) , where \(\tilde{\mathbf {A}}\) is a column vector with \((m+1)\) entries equal to the diagonal entries of the matrix \(\mathbf {A}\).

Function approximation

An arbitrary real function f on D can be expanded by these functions as [34]

$$\begin{aligned} f(t)\simeq \sum _{i=0}^m f_i h_i(t)= \mathbf F ^T \mathbf H (t)=\mathbf H ^T(t)\mathbf F , \end{aligned}$$
(3)

where \(\mathbf F = [f_0 , f_1 , \dots , f_m]^T\) and \(\mathbf H (t)\) is defined in relation (2) and the coefficients in (3) are given by \(f_i=f(ih), i=0,1,\dots ,m.\)

Similarly, an arbitrary real function of two variables g(s, t) on \(D \times D\) can be expanded by these basic functions as

$$\begin{aligned} g(s,t)\simeq \mathbf H ^T(s)\,\mathbf G \,\mathbf I (t), \end{aligned}$$
(4)

where \(\mathbf H (s),\mathbf I (t)\)  are, respectively, \((m_1+1)\)- and \((m_2+1)\)-dimensional MHFs vectors. \(\mathbf G\) is the \((m_1+1)\times (m_2+1)\) MHFs coefficient matrix with entries \(G_{ij} ,i=0,1,2,\dots ,m_1\, , j=0,1,2,\dots ,m_2\) and \(G_{ij}=g(ih,jk),\) where \(h=\frac{T}{m_1}\) and \(k=\frac{T}{m_2}.\) For convenience, we put \(m_1=m_2=m\).

Operational matrices

In this section, we present both operational matrix of integrating the vector \({\mathbf {H}}(t)\), denoted by \(\mathbf P\), and stochastic operational matrix of Itô integrating the vector \({\mathbf {H}}(t)\), denoted by \(\mathbf P _s\). Therefore, by integrating the vector \({\mathbf {H}}(t)\) defined in (2), we have [34, 35]

$$\begin{aligned} \int _0^t{\mathbf {H}}(\tau )\,\hbox {d}\tau =\mathbf P {\mathbf {H}}(t), \end{aligned}$$
(5)

where \(\mathbf P\) is the following  \((m+1)\times (m+1)\) operational matrix of integration of MHFs

$$\begin{aligned} \mathbf P =\frac{h}{12} \begin{pmatrix} 0 &{} 5 &{} 4 &{} 4 &{} 4 &{} \dots &{} 4 &{} 4 &{} 4 &{} 4 \\ 0 &{} 8 &{} 16 &{} 16&{} 16 &{} \dots &{} 16 &{}16&{}16&{}16 \\ 0 &{} -1 &{} 4 &{} 9 &{} 8 &{} \dots &{} 8 &{} 8 &{} 8 &{} 8\\ &{}&{}\ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} &{} &{} \\ &{} &{} &{}\ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} &{} \\ &{} &{} &{} &{}\ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \\ &{} &{} &{} &{} &{}\ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots \\ 0 &{} 0 &{} 0 &{} 0 &{} 0&{}\dots &{} -1 &{} 4&{}9&{}8 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \dots &{}0&{}0&{}8&{}16\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \dots &{}0&{}0&{}-1&{}4 \end{pmatrix}. \end{aligned}$$

Theorem 1

Let \({\mathbf {H}}(t)\) be the vector defined in (2), the Itô integral of \({\mathbf {H}}(t)\) can be expressed as

$$\begin{aligned} \int _0^t{\mathbf {H}}(\tau )\,dB(\tau )=\mathbf P _s{\mathbf {H}}(t), \end{aligned}$$
(6)

where \(\mathbf P _s\) is the following \(\,(m+1)\times (m+1)\,\) stochastic operational matrix of integration

$$\begin{aligned} \left\{ \begin{array}{llllllllll} 0 &{} \gamma _1 &{} \gamma _2 &{} \gamma _2 &{} \gamma _2 &{} \dots &{} \gamma _2 &{} \gamma _2 &{} \gamma _2 &{}\gamma _2 \\ 0 &{} B(h)+\theta _{1,1} &{} \theta _{2,1} &{} \theta _{2,1}&{} \theta _{2,1} &{} \dots &{} \theta _{2,1} &{}\theta _{2,1}&{}\theta _{2,1}&{}\theta _{2,1} \\ 0 &{} \eta _{1,2} &{} B(2h)+\eta _{2,2} &{} \eta _{3,2} &{} \eta _{4,2} &{} \dots &{} \eta _{4,2} &{} \eta _{4,2} &{} \eta _{4,2} &{} \eta _{4,2}\\ &{}&{}\ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} &{} &{} \\ &{} &{} &{}\ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} &{} \\ &{} &{} &{} &{}\ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \\ &{} &{} &{} &{} &{}\ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots \\ 0 &{} 0 &{} 0 &{} 0 &{} 0&{}\dots &{} \eta _{1,m-2} &{} B(T-2h)+\eta _{2,m-2}&{}\eta _{3,m-2}&{}\eta _{4,m-2} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \dots &{}0&{}0&{}B(T-h)+\theta _{1,m-1}&{} \theta _{2,m-1}\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \dots &{}0&{}0&{}\eta _{1,m}&{}B(T)+\eta _{2,m} \end{array} \right. \end{aligned}$$
(7)

with

$$\begin{aligned} \gamma _1= & {} -\displaystyle \int _0^h \frac{1}{2h^2}(2\tau -3h)B(\tau )\,\hbox {d}\tau \\ \gamma _2= & {} -\displaystyle \int _0^{2h} \frac{1}{2h^2}(2\tau -3h)B(\tau )\,\hbox {d}\tau ,\\ \theta _{1,i}= & {} \displaystyle \int _{(i-1)h}^{ih}\frac{1}{h^2}(2\tau -2ih)B(\tau )\,\hbox {d}\tau ,\\ \theta _{2,i}= & {} \displaystyle \int _{(i-1)h}^{(i+1)h}\frac{1}{h^2}(2\tau -2ih)B(\tau )\,\hbox {d}\tau ,\\ \eta _{1,i}= & {} -\displaystyle \int _{(i-2)h}^{(i-1)h}\frac{1}{2h^2}(2\tau -(2i-3)h)B(\tau )\,\hbox {d}\tau ,\\ \eta _{2,i}= & {} -\displaystyle \int _{(i-2)h}^{ih}\frac{1}{2h^2}(2\tau -(2i-3)h)B(\tau )\,\hbox {d}\tau ,\\ \eta _{3,i}= & {} -\displaystyle \int _{(i-2)h}^{ih}\frac{1}{2h^2}(2\tau -(2i-3)h)B(\tau )\,\hbox {d}\tau \\&\quad -\int _{ih}^{(i+1)h}\frac{1}{2h^2}(2\tau -(2i+3)h)B(\tau )\,\hbox {d}\tau , \end{aligned}$$

and

$$\begin{aligned} \eta _{4,i}=-\displaystyle \int _{(i-2)h}^{ih} \frac{1}{2h^2}(2\tau -(2i-3)h)B(\tau )\,\hbox {d}\tau -\int _{ih} ^{(i+2)h}\frac{1}{2h^2}(2\tau -(2i+3)h)B(\tau )\,\hbox {d}\tau . \end{aligned}$$

Proof

By considering definitions of \(h_i(t), i= 0, 1,\dots , m\) and integrating by parts, we have

$$\begin{aligned} \displaystyle \int _0^t h_i(\tau )dB(\tau ) &= h_i(t)B(t)-h_i(0)B(0)-\int _0^t h_i'(\tau )B(\tau )\hbox {d}\tau \\ \displaystyle &= h_i(t)B(t)-\int _0^t h_i'(\tau )B(\tau )\hbox {d}\tau , \end{aligned}$$

expanding \(\int _0^t h_i(\tau )dB(\tau )\) in terms of MHFs yields

$$\begin{aligned} \int _0^t h_i(\tau )dB(\tau )\simeq \sum _{j=0}^m a_{ij}h_j(t) \end{aligned}$$

and

$$\begin{aligned} a_{ij} &= \int _0^{jh} h_i(\tau )dB(\tau ),\\= & \, h_i(jh)B(jh)-\int _0^{jh} h_i'(\tau )B(\tau )\hbox {d}\tau \end{aligned}$$

so we obtain

$$\begin{aligned} a_{0j}=&{\left\{ \begin{array}{ll} 0, &\quad j=0 \\ -\int _0^h\frac{1}{2h^2}(2s-3h)B(s)\hbox {d}s , &\quad j=1\\ -\int _0^{2h}\frac{1}{2h^2}(2s-3h)B(s)\hbox {d}s , &\quad j\ge 2. \end{array}\right. } \end{aligned}$$

If i is odd and \(1\le i\le (m-1)\)

$$\begin{aligned} a_{ij}=&{\left\{ \begin{array}{ll} 0, &{} j \le i-1 \\ B(ih)-\int _{(i-1)h}^{ih}\frac{-1}{h^2}(2s-2ih)B(s)\hbox {d}s , &{} j=i\\ -\int _{(i-1)h}^{(i+1)h}\frac{-1}{h^2}(2s-2ih)B(s)\hbox {d}s , &{} j\ge i+1. \end{array}\right. } \end{aligned}$$

If i is even and \(2\le i\le (m-2)\),

$$\begin{aligned} a_{ij}=&{\left\{ \begin{array}{ll} 0, &{} j \le i-2 \\ -\int _{(i-2)h}^{(i-1)h}\frac{1}{2h^2}(2s-(2i-3)h)B(s)\hbox {d}s , &{} j=i-1\\ B(ih)-\int _{(i-2)h}^{ih}\frac{1}{2h^2}(2s-(2i-3)h)B(s)\hbox {d}s , &{} j=i\\ -\int _{(i-2)h}^{ih}\frac{1}{2h^2}(2s-(2i-3)h)B(s)\hbox {d}s\\ -\int _{ih}^{(i+1)h}\frac{1}{2h^2}(2s-(2i+3)h)B(s)\hbox {d}s, &{} j=i+1\\ -\int _{(i-2)h}^{ih}\frac{1}{2h^2}(2s-(2i-3)h)B(s)\hbox {d}s\\ -\int _{ih}^{(i+2)h}\frac{1}{2h^2}(2s-(2i+3)h)B(s)\hbox {d}s , &{} j \ge i+2. \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} a_{mj}=&{\left\{ \begin{array}{ll} 0, &{} j \le m-2 \\ -\int _{(T-2h)}^{(T-h)}\frac{1}{2h^2}(2s-2T+3h)B(s)\hbox {d}s , &{} j=m-1\\ B(T)-\int _{(T-2h)}^{T}\frac{1}{2h^2}(2s-2T+3h)B(s)\hbox {d}s , &{} j=m. \end{array}\right. } \end{aligned}$$

Putting the obtained components in the matrix form ends the proof. \(\square\)

Solving stochastic Itô–Volterra integral equation with multi-stochastic terms by the MHFs

Our problem is to define the MHFs coefficients of X(t) in the following linear stochastic Itô–Volterra integral equation with several independent white noise sources,

$$\begin{aligned}&X(t)=f(t)+\int _0^t\mu (s,t)X(s)\,\hbox {d}s\nonumber \\&\qquad +\sum _{j=1}^n\int _0^t\sigma _j(s,t)X(s)\,dB_j(s),\,t\in D, \end{aligned}$$
(8)

where \(X,f,\mu\) and \(\sigma _j, j=1,2,\dots ,n\) for \(s,t\in D\), are stochastic processes defined on the same probability space\((\Omega ,F,P)\). Also \(B_1(t), B_2(t),\dots , B_n(t)\) are Brownian motion processes, and \(\int _0^t \sigma _j(s,t)\,dB_j(s)\,,j = 1,2,\dots ,n\) are the Itô integrals.

We replace \(X(t),f(t),\mu (s,t)\) and \(\sigma _j(s,t)\,,j=1,2,\dots ,n\) by their approximations which are obtained by MHFs:

$$\begin{aligned}&\quad X(t)\simeq {\mathbf {X}}^T{\mathbf {H}}(t)={\mathbf {H}}(t)^T{\mathbf {X}}, \end{aligned}$$
(9)
$$\begin{aligned}&\quad f(t)\simeq \mathbf {F}^T{\mathbf {H}}(t)={\mathbf {H}}(t)^T\mathbf {F}, \end{aligned}$$
(10)
$$\begin{aligned} \mu (s,t)\simeq & \quad {\mathbf {H}}(t)^T{\mu}^T{\mathbf {H}}(s) ={\mathbf {H}}(s)^T{\mu }{\mathbf {H}}(t), \end{aligned}$$
(11)
$$\begin{aligned}&\sigma_j(s,t)\simeq {\mathbf {H}}(t)^T\mathbf {\Delta }_j^T{\mathbf {H}}(s) = {\mathbf {H}}(s)^T\mathbf {\Delta }_j{\mathbf {H}}(t),\nonumber \\&\quad j=1,2,\dots ,n, \end{aligned}$$
(12)

where \({\mathbf {X}}\) and \(\mathbf {F}\) are stochastic MHFs coefficient vectors and \({\mu }\) and \(\mathbf {\Delta }_j\,,j=1,2,\dots ,n\) are stochastic MHFs coefficient matrices. Substituting (9)–(12) in relation (8), we obtain

$$\begin{aligned}&{\mathbf {H}}(t)^T {\mathbf {X}} \simeq {\mathbf {H}}(t)^T \mathbf {F}+\left( \int _0^t{\mathbf {H}}(t)^T {\mu }^T {\mathbf {H}}(s) {\mathbf {H}}(s)^T {\mathbf {X}}\,\hbox {d}s \right) \nonumber \\&\qquad +\sum _{j=1}^n \left( \int _0^t {\mathbf {H}}(t)^T \mathbf {\Delta _j}^T {\mathbf {H}}(s) {\mathbf {H}}(s)^T {\mathbf {X}}\,dB_j(s)\right) . \end{aligned}$$
(13)

Using the 6-th property in relation (13), we get

$$\begin{aligned}&{\mathbf {H}}(t)^T {\mathbf {X}} \simeq {\mathbf {H}}(t)^T \mathbf {F}+{\mathbf {H}}(t)^T {\mu }^T diag({\mathbf {X}}) \left( \int _0^t {\mathbf {H}}(s)\,\hbox {d}s \right) \nonumber \\&\quad +\sum _{j=1}^n {\mathbf {H}}(t)^T \mathbf {\Delta _j}^T diag({\mathbf {X}}) \left( \int _0^t {\mathbf {H}}(s) \,dB_j(s)\right) . \end{aligned}$$
(14)

Utilizing operational matrices defined in relations (5) and (6) in (14), we have

$$\begin{aligned}&{\mathbf {H}}(t)^T {\mathbf {X}} \simeq {\mathbf {H}}(t)^T \mathbf {F}+{\mathbf {H}}(t)^T {\mu }^T diag({\mathbf {X}}) \mathbf {P} {\mathbf {H}}(t)\nonumber \\&\quad +\sum _{j=1}^n {\mathbf {H}}(t)^T \mathbf {\Delta _j}^T diag({\mathbf {X}}) \mathbf {P_s} {\mathbf {H}}(t). \end{aligned}$$
(15)

Let \(\mathbf {A}={\mu }^Tdiag({\mathbf {X}})\mathbf {P}\) and \(\mathbf {B}_j=\mathbf {\Delta _j}^Tdiag({\mathbf {X}})\mathbf {P_s}, j=1,2,\dots ,n.\) Applying property (7) in relation (15) yields

$$\begin{aligned} {\mathbf {H}}(t)^T {\mathbf {X}} \simeq {\mathbf {H}}(t)^T \mathbf {F}+ {\mathbf {H}}(t)^T \tilde{\mathbf {A}}+\sum _{j=1}^n {\mathbf {H}}(t)^T \tilde{\mathbf {B}}_j, \end{aligned}$$

therefore, by using the third property and replacing \(\simeq\) by \(=\), we have

$$\begin{aligned} {\mathbf {X}}=\mathbf {F}+\tilde{\mathbf {A}}+\sum _{j=1}^{n}\tilde{\mathbf {B}}_j, \end{aligned}$$

which is a linear system of equations that gives the approximation of X with the help of MHFs.

Error analysis

In this section, the error analysis is studied. We propose some conditions to show that the rate of convergence for this method is \(O(h^3)\).

Theorem 2

[34] Let \(t_j=jh , j=0,1,\dots ,m , f\in \chi\) and \(f_m\) be the MHFs expansion of f defined as \(f_m(t)=\sum _{j=0}^{m}f(t_j)h_j(t)\) and also assume that \(e_m(t)=f(t)-f_m(t)\) , for \(t \in D\) , then we have

$$\begin{aligned} \Vert e_m\Vert \le \frac{h^3}{9\sqrt{3}}\Vert f^{(3)}\Vert , \end{aligned}$$

and hence \(\Vert e_m\Vert =O(h^3)\) . Where \(\Vert .\Vert\) denotes the sup-norm for which any continuous function f is defined on the interval [0, T) by

$$\begin{aligned} \Vert f\Vert =\sup _{t\in [0,T)}|f(t)|. \end{aligned}$$

Theorem 3

[34] Let \(s_i=t_i=ih , i=0,1,\dots ,m , \mu \in C^3(D \times D)\) and \(\mu _m(s,t)=\sum _{i=0}^{m}\sum _{j=0}^{m}\mu (s_i,t_j)h_i(s)h_j(t),\) be the MHFs expansion of \(\mu (s,t),\) and also assume that \(e_m(s,t)=\mu (s,t)-\mu _m(s,t),\) then we have

$$\begin{aligned}&\Vert e_m\Vert \le \frac{h^3}{9\sqrt{3}}\left( \Vert \mu _s^{(3)}\Vert +\Vert \mu _t^{(3)}\Vert \right) \\&\quad +\frac{h^6}{243}\Vert \mu _{s,t}^{(3+3)}\Vert , \end{aligned}$$

and so \(\Vert e_m\Vert = O(h^3).\)

Theorem 4

Let X be the exact solution of (8) and \(X_m\) be the MHFs series approximate solution of (8) , and also assume that

$$\begin{aligned}&H_1:\,\Vert X\Vert \le \rho , \\& H_2:\,\Vert \mu \Vert \le K,\\& H_3:\,\Vert \sigma _j\Vert \le M_j, j=1,2,\dots ,n,\\& H_4:\,T(K+\gamma (h))+\sum _{j=1}^n(M_j+\lambda _j(h))\Vert B_j\Vert < 1, \end{aligned}$$

then

$$\begin{aligned} \Vert X-X_m\Vert \le \frac{\Gamma (h)+T\rho \gamma (h)+\rho \sum \limits _{j=1}^n \lambda _j(h)\Vert B_j\Vert }{1-\left( T(K+\gamma (h)) +\sum \limits _{j=1}^n(M_j+\lambda _j(h))\Vert B_j\Vert \right) }, \end{aligned}$$

and \(\Vert X-X_m\Vert =O(h^3)\,,\) where

$$\begin{aligned}&\Gamma (h)=\frac{h^3}{9\sqrt{3}}\Vert f^{(3)}\Vert ,\\&\quad \gamma (h)=\frac{h^3}{9\sqrt{3}}\left( \Vert \mu _s^{(3)}\Vert +\Vert \mu _t^{(3)}\Vert \right) \\&\quad +\frac{h^6}{243}\Vert \mu _{s,t}^{(3+3)}\Vert ,\\&\quad \lambda _j(h)= \frac{h^3}{9\sqrt{3}}\left( \Vert \sigma _{j_s}^{(3)}\Vert +\Vert \sigma _{j_t}^{(3)}\Vert \right) \\&\quad +\frac{h^6}{243}\Vert \sigma _{j_{s,t}}^{(3+3)}\Vert ,\\&\quad j=1, 2,\dots , n. \end{aligned}$$

Proof

From relation (8), we have

$$\begin{aligned}&X(t)-X_m(t)=f(t)-f_m(t)\\&\quad +\int _{0}^{t}\left( \mu (s,t)X(s)-\mu _m(s,t)X_m(s)\right) \,\hbox {d}s\\&\quad +\sum _{j=1}^{n}\int _{0}^{t}\\&\quad \left( \sigma _j(s,t)X(s)-\sigma _{jm}(s,t)X_m(s)\right) \,dB_j(s), \end{aligned}$$

now the following relation is concluded

$$\begin{aligned} |X(t)-X_m(t)|\le |f(t)-f_m(t)|+tN +\sum _{j=1}^n |B_j(t)|N_j, \end{aligned}$$
(16)

where

$$\begin{aligned} N= \sup \limits _{s,t\in [0,T)}|\mu (s,t)X(s)-\mu _m(s,t)X_m(s)|, \end{aligned}$$

and

$$\begin{aligned} N_j= \sup \limits _{s,t\in [0,T)}|\sigma _j(s,t)X(s)-\sigma _{jm}(s,t)X_m(s)|, \end{aligned}$$

using Theorems 2 and 3, we also have

$$\begin{aligned}&N \le \Vert \mu \Vert \Vert X-X_m\Vert +\Vert \mu -\mu _m\Vert \left( \Vert X-X_m\Vert +\Vert X\Vert \right) \nonumber \\&\quad \le \Vert X-X_m\Vert (K+\gamma (h))+ \gamma (h)\rho ,\quad \,\, \end{aligned}$$
(17)

and

$$\begin{aligned}&\quad N_j \le \Vert \sigma _j\Vert \Vert X-X_m\Vert +\Vert \sigma _j-\sigma _{jm}\Vert (\Vert X-X_m\Vert +\Vert X\Vert )\nonumber \\&\le (M_j+\lambda _j(h))\Vert X-X_m\Vert +\lambda _j(h)\rho , \end{aligned}$$
(18)

j= 1, 2, ..., n.

By substituting (17) and (18) in relation (16), we obtain

$$\begin{aligned}&\Vert X-X_m\Vert \le \Gamma (h)+T((K+\gamma (h))\Vert X-X_m\Vert +\rho \gamma (h))\\&\quad +\sum _{j=1}^{n}\Vert B_j\Vert \left( (M_j+\lambda _j(h))\Vert X-X_m\Vert +\rho \lambda _j(h)\right) , \end{aligned}$$

and so

$$\begin{aligned} \Vert X-X_m\Vert \le \frac{\Gamma (h)+T\rho \gamma (h)+\rho \sum \limits _{j=1}^{n}\lambda _j(h)\Vert B_j(t)\Vert }{1-\left( T(K+\gamma (h)) +\sum \limits _{j=1}^{n}(M_j+\lambda _j(h))\Vert B_j(t)\Vert \right) }, \end{aligned}$$

which means \(\Vert X-X_m\Vert =O(h^3)\,\). Thus, the proof is complete. \(\square\)

Numerical examples

In this section, we use our algorithm to solve stochastic Itô–Volterra integral equation with multi-stochastic terms stated in “Solving stochastic Itô–Volterra integral equation with multi-stochastic terms by the MHFs” section. In order to compare it with the method proposed in [22, 23], we consider some examples. The computations associated with the examples were performed using Matlab 7 and [36].

Example 1

Consider the following linear stochastic Itô–Volterra integral equation with multi-stochastic terms [22]

$$\begin{aligned}&X(t)= X_0+\int _0^trX(s)\,\hbox {d}s\\&\quad +\sum _{j=1}^n\int _0^t\alpha _jX(s)dB_j(s),\, s,t \in [0,1), \end{aligned}$$

with the exact solution

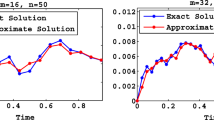
$$\begin{aligned} X(t)=X_0e^{(r-\frac{1}{2}\sum _{j=1}^{n}\alpha _j^2)t +\sum _{j=1}^{n}\alpha _jB_j(t)}, \end{aligned}$$

for \(0\le t< 1\) where X is the unknown stochastic process, defined on the probability space \((\Omega ,F,P)\) and \(B_1(t), B_2(t),\dots , B_n(t)\) are the Brownian motion processes. The numerical results for \(X_0=\frac{1}{200}, r=\frac{1}{20}, \alpha _1=\frac{1}{50}, \alpha _2=\frac{2}{50}, \alpha _3=\frac{4}{50}, \alpha _4 = \frac{9}{50}\) are shown in Table  1. Also curves in Figs. 1 and 2 show the exact and approximate solutions computed by this method for \(m=10\) and \(m=40\). Figures 3 and 4 represent the errors of the present method.

Table 1 Numerical results for Example 1
Full size table
Fig. 1
figure 1

Numerical results for Example 1 with \(m=10\)

Full size image
Fig. 2
figure 2

Numerical results for Example 1 with \(m=40\)

Full size image
Fig. 3
figure 3

Error curve of the method for Example 1 with \(m=10\)

Full size image
Fig. 4
figure 4

Error curve of the method for Example 1 with \(m=40\)

Full size image

Example 2

Let [22]

$$\begin{aligned} X(t)= X_0+\int _0^tr(s)X(s)\,\hbox {d}s\\ \quad +\,\sum _{j=1}^n\int _0^t\alpha _j(s)X(s)dB_j(s),\,s,t \in [0,1), \end{aligned}$$

be a linear stochastic Itô–Volterra integral equation with multi-stochastic terms with the exact solution

$$\begin{aligned} X(t)=X_0e^{(\int _0^tr(s)-\frac{1}{2}\sum _{j=1}^{n}\alpha _j^2(s)\hbox {d}s+\sum _{j=1} ^{n}\int _0^t\alpha _j(s)dB_j(s))} \end{aligned}$$

for \(0\le t< 1,\) where X is the unknown stochastic process defined on the probability space \((\Omega ,F,P)\) and \(B_1(t), B_2(t),\dots , B_n(t)\) are the Brownian motion processes. The numerical results for \(X_0=\frac{1}{12}, r=\frac{1}{30}, \alpha _1=\frac{1}{10}, \alpha _2(s)=s^2, \alpha _3(s)=\frac{\sin (s)}{3}\) are inserted in Table 2. Also curves in Figs. 5 and 6 show the exact and approximate solutions computed by this method for \(m=10\) and \(m=40\). Figures 7 and 8 represent the errors of the present method.

Table 2 Numerical results for Example 2
Full size table
Fig. 5
figure 5

Numerical results for Example 2 with \(m=10\)

Full size image
Fig. 6
figure 6

Numerical results for Example 2 with \(m=40\)

Full size image
Fig. 7
figure 7

Error curve of the method for Example 2 with \(m=10\)

Full size image
Fig. 8
figure 8

Error curve of the method for Example 2 with \(m=40\)

Full size image

Conclusion

Finding an analytical exact solution for stochastic equations usually seems impossible. Therefore, it is convenient to use stochastic numerical methods to find some approximate solutions. The MHFs, as a simple and suitable basis, adopt to solve stochastic Itô–Volterra integral equations with multi-stochastic terms. With this choice, the vector and matrix coefficients are found easily. This method results in a linear system of equations that can be solved simply. Numerical results of the examples show that the MHFs tend to more accurate solutions than the BPFs and GHFs do.