First Error

In Eq. (17) in Hayat et al. (2018) the boundary condition for the non-dimensional concentration is \(\varphi (\infty ) = 0\).

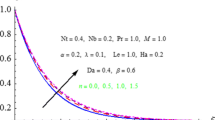
In Fig. 1 of the present work we show schematically a dimensionless concentration profile from Hayat et al. (2018), taken from their Fig. 16 and a second concentration profile proposed by the present author (sketch). It is seen that the concentration profile presented by Hayat et al. (2018) does not approach the ambient condition asymptotically but intersects the horizontal axis with a steep angle. At the same figure it is shown a correct concentration profile which extends to high values of transverse component \(\xi\) and approaches smoothly the ambient condition. In Fig. 16 in Hayat et al. (2018) the calculations have been restricted to a maximum \(\xi\) equal to 4 (\(\xi_{\max } = 4\)). It is obvious that this calculation domain is insufficient to capture the real shape of profiles and a higher value of \(\xi\) is needed. According to above analysis all concentration profiles in Figs. 16, 17, 18, 19 and 20 in Hayat et al. (2018) are truncated and wrong. More information on the truncation error is given by Pantokratoras (2009), Pantokratoras (2019).

Fig. 1
figure 1

The existing dimensionless concentration profile is given by Hayat et al. (2018) in their Fig. 16 (blue profile). The proposed profile is in agreement with the boundary condition \(\varphi (\infty ) = 0\). The existing profile violates the boundary condition \(\varphi (\infty ) = 0\)

Full size image

In Eq. (21) in Hayat et al. (2018) the following equation appears

$$\frac{Sh}{{\sqrt {\text{Re}} }} = - \sqrt {\frac{n + 1}{2}} \varphi ^{\prime}(0)$$
(1)

From Fig. 1 it is clear that the values \(\varphi ^{\prime}(0)\) in the truncated profiles are also wrong and consequently the quantity \(\frac{Sh}{{\sqrt {\text{Re}} }}\) is wrong.

Second Error

The transformed momentum Eq. (14) in Hayat et al. (2018) is as follows

$$\begin{array}{c}{f}^{{\prime}{\prime}{\prime}}-\left(\frac{2n}{n+1}\right){\left({f}^{\prime}\right)}^{2}+f{f}^{{\prime}{\prime}}-\left(\frac{2}{n+1}\right){(Ha)}^{2}\left({f}^{\prime}-\lambda \right)-\left(\frac{2}{n+1}\right)(Da)\left({f}^{\prime}-\lambda \right)\\ -\left(\frac{2}{n+1}\right)\beta \left({f}^{{\prime}2}-{\lambda }^{2}\right)+\left(\frac{2n}{n+1}\right){\lambda }^{2}=0\\ \end{array}$$
(2)

The parameters \(Ha\), \(\lambda\), \(Da\), \(\beta\), are defined as follows (Eq. 21 in Hayat et al. 2018)

$$Ha = \sqrt {\frac{\sigma }{\rho a}} B_{0}$$
(3)
$$\lambda = \frac{d}{a}$$
(4)
$$Da = \frac{\varepsilon \nu }{{ka(x + b)^{n - 1} }}$$
(5)
$$\beta = \frac{{C_{b} \varepsilon (x + b)}}{\sqrt k }$$
(6)

There is an essential difference between parameters \(Ha,\lambda\) and \(Da,\beta\). The parameters \(Da,\beta\) are functions of coordinate x whereas the \(Ha,\lambda\) are not. The dependence of x means that the transformed momentum Eq. (2) is a non-similar equation because the fluid velocity depends on x and changes along the coordinate x. This change along x must be expressed with derivatives with respect to x.

Let us give an example of how the non-similar method works. If in Eq. (2) the parameters \(Da,\beta\) are absent the Eq. (2) will take the following form

$$\begin{array}{c}{f}^{{\prime}{\prime}{\prime}}-\left(\frac{2n}{n+1}\right){\left({f}^{\prime}\right)}^{2}+f{f}^{{\prime}{\prime}}-\left(\frac{2}{n+1}\right){(Ha)}^{2}\left({f}^{\prime}-\lambda \right)+\left(\frac{2n}{n+1}\right){\lambda }^{2}=0\\ \end{array}$$
(7)

In Eq. (7) the coordinate x has disappeared and this equation is a classical similar equation (an ordinary differential equation). If in Eq. (2) the parameter \(Da\) is absent the Eq. (2) will take the following form

$$\begin{aligned}{f}^{{\prime}{\prime}{\prime}}&-\left(\frac{2n}{n+1}\right){\left({f}^{\prime}\right)}^{2}+f{f}^{{\prime}{\prime}}-\left(\frac{2}{n+1}\right){(Ha)}^{2}\left({f}^{\prime}-\lambda \right)\\&-\left(\frac{2}{n+1}\right)\beta \left({f}^{{\prime}2}-{\lambda }^{2}\right)+\left(\frac{2n}{n+1}\right){\lambda }^{2}=0\\ \end{aligned}$$
(8)

In Eq. (8) the parameter \(\beta = \frac{{C_{b} \varepsilon (x + b)}}{\sqrt k }\) is a function of x and this parameter acts as a transformed coordinate x. Thus the fluid velocity depends on \(\beta = \frac{{C_{b} \varepsilon (x + b)}}{\sqrt k }\) and changes along \(\beta\). In Eq. (8) except of derivatives with respect to \(\xi\) (\(f{\prime} = \frac{\partial f}{{\partial \xi }}\)), derivatives with respect to \(\beta\) (\(\frac{\partial f}{{\partial \beta }}\)) must be included. The following Eqs. (9) and (10) have been taken from Minkowycz and Cheng (1982) and represent a non-similar problem

$$\frac{{\partial^{2} \theta }}{{\partial \eta^{2} }} + \frac{f}{2}\frac{\partial \theta }{{\partial \eta }} = \frac{\xi }{2}\left( {\frac{\partial f}{{\partial \eta }}\frac{\partial \theta }{{\partial \xi }} - \frac{\partial f}{{\partial \xi }}\frac{\partial \theta }{{\partial \eta }}} \right)$$
(9)

where the parameter \(\xi\) is a function of \(x\)

$$\xi = \frac{{2v_{w} }}{a}\left[ {\frac{\mu ax}{{\rho_{\infty } g\beta K(T_{w} - T{}_{\infty })}}} \right]^{1/2}$$
(10)

In Eq. (9) there are derivatives of \(f\) both on \(\eta\) and \(\xi\). In the local-similarity method the streamwise derivatives are omitted and for that reason the local-similarity method, used in Hayat et al. (2018), is not correct. Cui et al. (2021) compared the results between local-similarity and non-similarity method and found differences up to 257%. In addition in the similarity method, ordinary differential equations are used, whereas in the non-similarity method partial differential equations are used. More information is given in Pantokratoras (2019).

Third Error

The dimensionless Hartmann number \(Ha = \sqrt {\frac{\sigma }{\rho a}} B_{0}\) is wrong because it is dimensional with units \(m^{{\frac{n - 1}{2}}} (length)^{{\frac{n - 1}{2}}}\) and the results for \(n \ne 1\) are wrong.