Skip to main content
SpringerLink
Log in

Numerical Simulation for Magneto Nanofluid Flow Through a Porous Space with Melting Heat Transfer

  • Original Article
  • Published:
Microgravity Science and Technology Aims and scope Submit manuscript

A Research to this article was published on 19 October 2023

Abstract

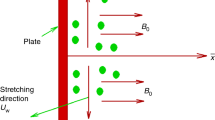
Melting heat transfer and non-Darcy porous medium effects in MHD stagnation point flow toward a stretching surface of variable thickness are addressed. Brownian motion and thermophoresis in nanofluid modeling are retained. Zero mass flux condition for concentration at surface is imposed. The problem of ordinary differential system are analyzed numerically through shooting technique. Graphically results of various physical variables on the velocity, temperature and concentration are studied. Skin friction coefficient local Nusselt number and Sherwood number are also addressed through tabulated values. The results described here illustrate that the velocity field is higher via larger melting parameter. However reverse situation is examined for Hartman number. Moreover the influence of thermophoresis parameter on temperature and concentration is noted similar.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20

Similar content being viewed by others

References

  • Abbas, T., Bhatti, M.M., Ayub, M.: Aiding and opposing of mixed convection Casson nanofluid flow with chemical reactions through a porous Riga plate. Proc. Inst. Mech. Eng Part E J. Process Mech. Eng. (2017a) https://doi.org/0954408917719791

  • Abbas, T., Hayat, T., Ayub, M., Bhatti, M.M., Alsaedi, A.: Electromagnetohydrodynamic nanofluid flow past a porous Riga plate containing gyrotactic microorganism. Neural Comput. Appl. (2017b) https://doi.org/10.1007/s00521-017-3165-7

  • Azmi, W.H., Hamid, K.A., Mamat, R., Sharma, K.V., Mohamad, M.S.: Effects of working temperature on thermo-physical properties and forced convection heat transfer of TiO2 nanofluids in water – Ethylene glycol mixture. Appl. Thermal Eng. 106, 1190–11997 (2016)

    Article  Google Scholar 

  • Babu, M.J., Sandeep, N.: 3D MHD slip flow of a nanofluid over a slendering stretching sheet with thermophoresis and Brownian motion effects. J. Mol. Liq. 222, 1003–1009 (2016)

    Article  Google Scholar 

  • Bhatti, M.M., Abbas, M.A., Rashidi, M.M.: A robust numerical method for solving stagnation point flow over a permeable shrinking sheet under the influence of MHD. Appl. Math. Comput. 316, 381–389 (2018)

    MathSciNet  Google Scholar 

  • Choi, S.U.S., Eastman, J.A.: Enhancing thermal conductivity of fluids with nanoparticles. In: The Proceedings of the 1995 ASME International Mechanical Engineering Congress and Exposition, San Francisco, USA, ASME FED 231/MD, vol. 66, pp 99–105 (1995)

  • Choi, S.U.S., Zhang, Z.G., Yu, W., Lockwood, F.E., Grulke, E.A.: Anomalously thermal conductivity enhancement in nanotube suspensions. Appl. Phys. Lett. 79, 2252–2254 (2001)

    Article  Google Scholar 

  • Darcy, H.: Les Fontaines Publiques De La Ville De Dijon. Victor Dalmont Paris (1856)

  • Dhanai, R., Rana, P., Kumar, L.: Multiple solutions of MHD boundary layer flow and heat transfer behavior of nanofluids induced by a power-law stretching/shrinking permeable sheet with viscous dissipation. Powder Technol. 273, 62–70 (2015)

    Article  Google Scholar 

  • Epstein, M., Cho, D.H.: Melting heat transfer in steady laminar flow over a flat plate. J. Heat Transf. 98, 531–533 (1976)

    Article  Google Scholar 

  • Forchheimer, P.: Wasserbewegung durch boden. Zeitschrift Ver D. Ing. 45, 1782–1788 (1901)

    Google Scholar 

  • Gireesha, B.J., Mahanthesh, B., Manjunatha, P.T., Gorla, R.S.R.: Numerical solution for hydromagnetic boundary layer flow and heat transfer past a stretching surface embedded in non-Darcy porous medium with fluid-particle suspension. J. Nigerian Math. Soc. 34, 267–285 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  • Gireesha, B.J., Mahanthesh, B., Shivakumara, I.S., Eshwarappa, K.M.: Melting heat transfer in boundary layer stagnation-point flow of nanofluid toward a stretching sheet with induced magnetic field. Eng. Sci. Tech. Int. J. 19, 313–321 (2016)

    Article  Google Scholar 

  • Haghighi, E.B., Utomo, A.T., Ghanbarpour, M., Zavareh, A.I.T., Poth, H., Khodabandeh, R., Pacek, A., Palm, B.E.: Experimental study on convective heat transfer of nanofluids in turbulent flow: methods of comparison of their performance. Exp. Thermal Fluid Sci. 57, 378–387 (2014)

    Article  Google Scholar 

  • Haq, R.U., Noor, N.F.M., Khan, Z.H.: Numerical simulation of water based magnetite nanoparticles between two parallel disks. Adv. Powder Technol. 27, 1568–1575 (2016)

    Article  Google Scholar 

  • Hayat, T., Muhammad, T., Shehzad, S.A., Alsaedi, A.: Simultaneous effects of magnetic field and convective condition in three-dimensional flow of couple stress nanofluid with heat generation/absorption. J. Braz. Soc. Mech. Sci. (2015) https://doi.org/10.1007/s40430-016-0632-5 https://doi.org/10.1007/s40430-016-0632-5

  • Hayat, T., Waqas, M., Shehzad, S. A., Alsaedi, A.: A model of solar radiation and Joule heating in magnetohydrodynamic (MHD) convective flow of thixotropic nanofluid. J. Mol. Liq. 215, 704–710 (2016a)

  • Hayat, T., Waqas, M., Khan, M.I., Alsaedi, A.: Analysis of thixotropic nanomaterial in a doubly stratified medium considering magnetic field effects. Int. J. Heat Mass Transf. 102, 1123–1129 (2016b)

  • Hayat, T., Waqas, M., Shehzad, S.A., Alsaedi, A.: On model of Burgers fluid subject to magneto nanoparticles and convective conditions. J. Mol. Liq. 222, 181–187 (2016c)

  • Hayat, T., Qayyum, S., Alsaedi, A., Shehzad, S.A.: Nonlinear thermal radiation aspects in stagnation point flow of tangent hyperbolic nanofluid with double diffusive convection. J. Mol. Liq. 223, 969–978 (2016d)

  • Hayat, T., Bashir, G., Waqas, M., Alsaedi, A.: MHD 2D flow of Williamson nanofluid over a nonlinear variable thicked surface with melting heat transfer. J. Mol. Liq. 223, 836–844 (2016e)

  • Hayat, T., Khan, M.I., Alsaedi, A., Khan, M.I.: Homogeneous-heterogeneous reactions and melting heat transfer effects in the MHD flow by a stretching surface with variable thickness. J. Mol. Liq. 223, 960–968 (2016f)

  • Hayat, T., Khan, M.I., Farooq, M., Alsaedi, A., Waqas, M., Yasmeen, T.: Impact of Cattaneo-Christov heat flux model in flow of variable thermal conductivity fluid over a variable thicked surface. Int. J. Heat Mass Transf. 99, 702–710 (2016g)

  • Hayat, T., Zubair, M., Ayub, M., Waqas, M., Alsaedi, A.: Stagnation point flow towards nonlinear stretching surface with Cattaneo-Christov heat flux. Eur. Phys. J. Plus (in press) (2016h)

  • Hayat, T., Shah, F., Alsaedi, A., Hussain, Z.: Outcome of homogeneous and heterogeneous reactions in Darcy-Forchheimer flow with nonlinear thermal radiation and convective condition. Res. Phys. 7, 2497–2505 (2017a)

  • Hayat, T., Hussain, Z., Alsaedi, A., Ahmad, B.: Numerical study for slip flow of carbon–water nanofluids. Comput. Methods Appl. Mech. Eng. 319, 366–378 (2017b)

  • Ibrahim, W., Haq, R.U.: Magnetohydrodynamic (MHD) stagnation point flow of nanofluid past a stretching sheet with convective boundary condition. J. Braz. Soci. Mech. Sci. Eng. 38, 1155–1164 (2016)

    Article  Google Scholar 

  • Imran Khan, M., Ijaz Khan, M., Waqas, M., Hayat, T., Alsaedi, A.: Chemically reactive flow of Maxwell liquid due to variable thicked surface. Int. Commun. Heat Mass Transf. 86, 231–238 (2017)

    Article  Google Scholar 

  • Kameswaran, P.K., Hemalatha, K., Madhavi, M.V.D.N.S.: Melting effect on convective heat transfer from a vertical plate embedded in a non-Darcy porous medium with variable permeability. Adv. Powder Technol. 27, 417–425 (2016)

    Article  Google Scholar 

  • Khader, M.M., Megahed, A.M.: Numerical solution for boundary layer flow due to a nonlinearly stretching sheet with variable thickness and slip velocity. Eur. Phys. J. Plus 100, 128 (2013)

    Google Scholar 

  • Khan, W.A., Pop, I.: Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 53, 2477–2483 (2010)

    Article  MATH  Google Scholar 

  • Khan, M., Khan, W.A., Alshomrani, A.S.: Non-linear radiative flow of three-dimensional Burgers nanofluid with new mass flux effect. Int. J. Heat Mass Transf. 101, 570–576 (2016)

    Article  Google Scholar 

  • Khan, M.I., Waqas, M., Hayat, T., Alsaedi, A., Khan, M.I.: Significance of nonlinear radiation in mixed convection flow of magneto Walter-B nanoliquid. Int. J. Hydrog. Energy 42, 26408–26416 (2017)

    Article  Google Scholar 

  • Mahanthesh, B., Gireesha, B.J., Gorla, R.S.R., Abbasi, F.M., Shehzad, S.A.: Numerical solutions for magnetohydrodynamic flow of nanofluid over a bidirectional non-linear stretching surface with prescribed surface heat flux boundary. J. Magn. Magn. Mater. 417, 189–196 (2016a)

  • Mahanthesh, B., Gireesha, B.J., Gorla, R.S.R.: Nonlinear radiative heat transfer in MHD three-dimensional flow of water based nanofluid over a non-linearly stretching sheet with convective boundary condition. J. Nigerian Math. Soc. 35, 178–198 (2016b)

  • Malekzadeh, S., Roohi, E.: Investigation 333 of different droplet formation regimes in a T-junction microchannel using the VOF technique in OpenFOAM. Microgravity Sci. Technol. 27, 231–243 (2015)

    Article  Google Scholar 

  • Malvandi, A., Ghasemi, A., Ganji, D.D., Pop, I.: Effects of nanoparticles migration on heat transfer enhancement at film condensation of nanofluids over a vertical cylinder. Adv. Powder Tech. (2016) https://doi.org/10.1016/j.apt.2016.06.025

  • Muskat, M.: The Flow of Homogeneous Fluids through Porous Media. Edwards MI (1946)

  • Nanjundappa, C.E., Shivakumara, I.S., Lee, J.: Effect of coriolis force on Bénard-Marangoni convection in a rotating ferrofluid layer with MFD viscosity. Microgravity Sci. Technol. 27, 27–37 (2015)

    Article  Google Scholar 

  • Navas, J., Coronilla, A.S., Martin, E.I., Teruel, M., Gallardo, J.J., Aguilar, T., Villarejo, R.G., Alcantara, R., Lorenzo, C.F., Pinero, J.C., Calleja, J.M.: On the enhancement of heat transfer fluid for concentrating solar power using Cu and Ni nanofluids: an experimental and molecular dynamics study. Nano Energy 27, 213–224 (2016)

    Article  Google Scholar 

  • Pandy, A.K., Kumar, M.: Natural convection and thermal radiation influence on nanofluid flow over a stretching cylinder in a porous medium with viscous dissipation. Alex Eng. (2016) https://doi.org/10.1016/j.aej.2016.08.035

  • Qiang, L.Y., Hui, C.W., Ling, L.: Numerical simulation of capillary flow in fan-shaped asymmetric interior corner under microgravity. Microgravity Sci. Technol. 29, 65–79 (2015)

    Article  Google Scholar 

  • Sadiq, M.A., Waqas, M., Hayat, T.: Importance of Darcy-Forchheimer relation in chemically reactive radiating flow towards convectively heated surface. J. Mol. Liq. 248, 1071–1077 (2017)

    Article  Google Scholar 

  • Salman, B.H., Mohammed, H.A., Kherbeet, A.Sh.: Numerical and experimental investigation of heat transfer enhancement in a microtube using nanofluids. Int. Commun. Heat Mass Transf. 59, 88–100 (2014)

    Article  Google Scholar 

  • Seddeek, M.A.: Influence of viscous dissipation and thermophoresis on Darcy-Forchheimer mixed convection in a fluid saturated porous media. J. Coll. Interf. Sci. 293, 137–142 (2006)

    Article  Google Scholar 

  • Shehzad, S.A., Abbasi, F.M., Hayat, T., Alsaedi, A.: Cattaneo-Christov heat flux model for Darcy-Forchheimer flow of an Oldroyd-B fluid with variable conductivity and non-linear convection. J. Mol. Liq. (2016) https://doi.org/10.1016/j.molliq.2016.09.109

  • Sheikholeslami, M., Bhatti, M.M.: Active method for nanofluid heat transfer enhancement by means of EHD. Int. J. Heat Mass Transf. 109, 115–122 (2017a)

  • Sheikholeslami, M., Bhatti, M.M.: Forced convection of nanofluid in presence of constant magnetic field considering shape effects of nanoparticles. Int. J. Heat Mass Transf. 111, 1039–1049 (2017b)

  • Smirnov, N.N., Nikitin, V.F., Norkin, A.V., Kudryavtseva, O.V., Legros, J.C., Istasse, E., Shevtsova, V.M.: Capillary driven filtration in porous media. Microgravity Sci. Technol. 7, 23–35 (1999)

    Google Scholar 

  • Smirnov, N.N., Legros, J.C., Nikitin, V.F., Istasse, E., Schramm, L., Wassmuth, F., Hart, D.: Filtration in artificial porous media and natural sands under microgravity conditions. Microgravity Sci. Technol. 14, 3–28 (2003)

    Article  Google Scholar 

  • Wahed, M.S.A., Elbashbeshy, E.M.A., Emam, T.G.: Flow and heat trasfer over a moving surface with nonlinear velocity and variable thickness in a nanofluids in the presence of Brownian motion. Appl. Math. Comput. 254, 49–62 (2015)

    MathSciNet  Google Scholar 

  • Waqas, M., Farooq, M., Khan, M.I., Alsaedi, A., Yasmeen, T.: Magnetohydrodynamic (MHD) mixed convection flow of micropolar liquid due to nonlinear stretched sheet with convective condition. Int. J. Heat Mass Transf. 102, 766–772 (2016)

    Article  Google Scholar 

  • Waqas, M., Khan, M.I., Hayat, T., Alsaedi, A.: Numerical simulation for magneto Carreau nanofluid model with thermal radiation: a revised model. Comput. Methods Appl. Mech. Eng. 324, 640–653 (2017)

    Article  MathSciNet  Google Scholar 

  • Waqas, M., Hayat, T., Shehzad, S.A., Alsaedi, A.: Transport of magnetohydrodynamic nanomaterial in a stratified medium considering gyrotactic microorganisms. Phys. B: Condens. Matter 529, 33–40 (2018)

    Article  Google Scholar 

  • Xie, H., Zheng, Z., Zhang, L., Yokota, Y., Kawazoe, Y., Yoshikawa, A.: Simulation on thermocapillary-driven drop coalescence by hybrid Lattice Boltzmann method. Microgravity Sci. Technol. 28, 67–77 (2016)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Quaid-I-Azam University, 45320, Islamabad, 44000, Pakistan

    T. Hayat, Faisal Shah & M. Waqas

  2. Nonlinear Analysis and Applied Mathematics (NAAM) Research Group, Department of Mathematics, Faculty of Science, King Abdulaziz University, P. O. Box 80257, Jeddah, 21589, Saudi Arabia

    T. Hayat & A. Alsaedi

Authors
  1. T. Hayat
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Faisal Shah
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. A. Alsaedi
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. M. Waqas
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. Waqas.

Ethics declarations

Conflict of interest

The authors declare they have no conflict of interest.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hayat, T., Shah, F., Alsaedi, A. et al. Numerical Simulation for Magneto Nanofluid Flow Through a Porous Space with Melting Heat Transfer. Microgravity Sci. Technol. 30, 265–275 (2018). https://doi.org/10.1007/s12217-018-9595-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12217-018-9595-8

Keywords

Search

Navigation