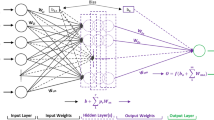
Abstract
The martensite start temperature (Ms) is a critical parameter when designing high-performance steels and their heat treatments. It has, therefore, attracted significant interest over the years. Numerous methodologies, such as thermodynamics-based, linear regression and artificial neural network (ANN) modeling, have been applied. The application of data-driven approaches, such as ANN modeling, or the wider concept of machine learning (ML), have shown limited technical applicability, but considering that these methods have made significant progress lately and that materials data are becoming more accessible, a new attempt at data-driven predictions of the Ms is timely. We here investigate the usage of ML to predict the Ms of steels based on their chemical composition. A database of the Msvs alloy composition containing 2277 unique entries is collected. It is ensured that all alloys are fully austenitic at the given austenitization temperature by thermodynamic calculations. The ML modeling is performed using four different ensemble methods and ANN. Train-test split series are used to evaluate the five models, and it is found that all four ensemble methods outperform the ANN on the current dataset. The reason is that the ensemble methods perform better for the rather small dataset used in the present work. Thereafter, a validation dataset of 115 Ms entries is collected from a new reference and the final ML model is benchmarked vs a recent thermodynamics-based model from the literature. The ML model provides excellent predictions on the validation dataset with a root-mean-square error of 18, which is slightly better than the thermodynamics-based model. The results on the validation dataset indicate the technical usefulness of the ML model to predict the Ms in steels for design and optimization of alloys and heat treatments. Furthermore, the agility of the ML model indicates its advantage over thermodynamics-based models for Ms predictions in complex multicomponent steels.
Similar content being viewed by others
1 Introduction
Materials development is currently undergoing large changes with a transition from the previously dominating empirical development methodologies toward methodologies with more computational components. This development can be divided loosely into two paths with one focusing on replacing some of the experimental input with physically based modeling on different length- and timescales, often referred to as integrated computational materials engineering (ICME).[1] The other direction is the use of data and machine learning (ML),[2,3,4,5] a branch of artificial intelligence. Key for both these areas is the use of databases where the ICME methods to a large extent rely on the so-called CALPHAD databases that collect thermodynamic and kinetic data essential for the modeling of phase transformations and related phenomena, while the ML approaches are more flexible to use any database that contains data of relevance for the parameter that should be predicted. It is clearly also possible to combine elements from the two areas and both rely on the materials genomics field where the Materials Genome Initiative[6] has provided extra thrust to the development of open materials databases.
In steel research and development, it is vital to be able to predict microstructures based on alloy composition and heat treatment cycle. One constituent that is important in high-performance steels is the hard martensite constituent, which is a part of, e.g., tool steels, dual-phase steels, quenching and partitioning steels, transformation-induced plasticity steels, and martensitic stainless steels. In the alloy and heat treatment design process, the martensite start temperature (Ms) is a critical parameter. Therefore, significant attention has been paid to the modeling of martensite and Ms in the literature.[7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30] These models use different methodologies such as linear regression,[7,8] thermodynamics-based modeling, which relies on CALPHAD databases and semiempirical fitting of the required driving force to initiate martensitic transformation,[9,10,11,12,13,14,15,16,17,18,19] and artificial neural network (ANN) modeling, which uses nonlinear fitting to the available experimental data.[21,22,23,24,25,26,27,28,29] The data-driven approaches, where the ANN modeling is one, have developed significantly recently.[31,32,33,34] From here on, these methods are referred to as ML, which can be simply described as computational techniques that enable the computer to learn from data and recognize patterns in the data. The datasets can be of many different sizes and big data is another important concept describing the use of huge datasets. However, so far in ANN modeling of the Ms,[21,22,23,24,25,26,27,28,29] the datasets are more accurately described as rather small datasets (about 1000 entries) and big data is generally not accessible for most empirical work in materials engineering. It is more common in computer science.
ML techniques can be applied also to small and intermediate datasets with successful outcomes, but it is critical which specific ML techniques are applied. To the authors’ knowledge, all previous work to predict the Ms using ML approaches has applied ANN modeling, which is very accurate for sufficiently large data due to its high nonlinearity. However, for smaller datasets, other ML techniques may be more suitable.[35] Hence, in the present work, we explore the opportunities provided by different state-of-the-art ML techniques to predict the Ms in steels. The data are taken from the open literature starting with the dataset made openly available by prior works of Capdevila and Andrés,[25] Capdevila et al.,[26] and Garcia Matteo and co-workers,[27,28,29] whom developed ANN models for the prediction of the Ms. Prior works, however, have not been able to predict the Ms for a large set of steel grades without significant scattering of the predictions, and to date, thermodynamics-based models with the mature commercial CALPHAD databases have been providing the most reliable predictions. We challenge this in the present work.
2 Methodology
2.1 Data Collection, Preprocessing, and Cleaning
A good database is key for ML and the size of the database needed depends on factors such as number of independent variables (features), complexity of correlations, and requested accuracy of predictions. When a sufficiently large database has been collected, the data must be properly normalized, and finally, the data must be cleaned to make sure that the database is correct. It should be noted that the cleaning does not involve removal of natural outliers in the dataset, related to measurement uncertainty. This is something that will be picked up during the training of the ML model. The prior consecutive works by Capdevila and Andrés[25], Capdevila et al.[26] and Garcia Matteo et al.[27,28,29] to predict the Ms of steels using the same database exemplify the importance of data cleaning. In the first work, mistakes related to the conversion of units and other issues led to some quite unreliable and wild spike predictions. By cleaning the original database and by introducing a minor change to constrain the wild spike predictions, Garcia Matteo and co-workers were able to significantly improve the predictions.
The dataset used in the present study is partly derived from the same database that was used by Capdevila and Andrés,[25] Capdevila et al.,[26] and Garcia Matteo and co-workers.[27,28,29] These data have been made available as an open source database within the materials algorithm project (MAP),[36,37] and they are based on the data published in References 10 and 38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60, through 61 We have further supplemented the MAP database by collecting additional Ms data from References 59, 62,63,64,65,66,67,68,69,70,71,72,73, through 74.
The entries in the database were screened using thermodynamic calculations to try and make sure that the steel alloys were fully austenitic at the given austenitization temperature, i.e., before the quenching. These calculations were performed under the assumption that phase equilibria have been obtained. In some cases, the austenitization temperature was not reported in the original reference and, in those cases, a standard austenitization temperature was assumed. The thermodynamic calculations were performed using the software Thermo-Calc[75] with the database TCFE9.[76] Taking this approach with fully austenitic structures before quenching meant that many entries in the original MAP database[37] were removed during cleaning. It should be mentioned, though, that the methodology is not limited to fully austenitic structures; it is only important to have good information about the austenitization temperature, to include that as a feature, and to assure a sufficient number of entries in the database. However, we have chosen to only treat 100 pct austenite in the present work, since the current database is somewhat limited when it comes to the representation of highly alloyed steels with austenitization temperature given where secondary phases, such as carbides, are expected to form. Further cleaning was performed to make sure that errors in the raw data, e.g., missing, undefined, mixed-mode, redundant, outlier, and duplicate data, were removed. Part of this data cleaning was performed by statistical techniques to identify data entries with the same chemical composition but with completely different measured Ms values, i.e., obviously incorrect entries not related to statistical variations. After cleaning, the database contained 2277 entries of Msvs chemical composition for binary, ternary, and multicomponent steel alloys. The chemical composition data from the steel alloys include the following elemental species: Fe (bal), C, Mn, Si, Cr, Ni, Mo, V, Co, Al, W, Cu, Nb, Ti, N, S, P, and B.
2.2 Feature Selection
Feature selection is another key step in the data analysis procedure and will largely influence the outcome of the ML. Without identifying all the features that contribute to the predictions of the dependent variable, it is not possible to develop a reliable model. At the same time, including irrelevant features will lead to an overly complex model by adding unnecessary coefficients. This means that it is more difficult to develop a reliable model and also that a larger dataset is needed for training of the model. One important tool that can be used in the selection of features is to investigate linear correlations in the dataset. Features that are uncorrelated with the dependent variable are good candidates to exclude from the dataset before training the model. There are many measures to determine correlations, but one of the simplest methods for understanding the relation between features and the dependent variable is the Pearson’s correlation coefficient. It evaluates the linear correlation between two variables and the resulting value lies between − 1 and 1. Negative values mean negative correlation (i.e., when the value of the feature increases, the dependent variable decreases), while on the other hand, positive values mean the opposite; 0 means that there is no linear correlation between the two variables. The Pearson’s correlation coefficient for the Ms dataset is represented as a heat map in Figure 1. It can be seen that C and Ni are strongly negatively correlated with the Ms, whereas Mn and Mo have a positive correlation with the Ms. For C and Ni, this is as expected, since they are both known to lower the Ms. However, this is more questionable when it comes to Mn and Mo. The reported effect of Mn and Mo is that they both nonlinearly lower Ms when the effect of incremental additions has been studied.[77,78] Mn has even been reported to be more effective than Ni in lowering the Ms.[77] However, it seems that the linear analysis is not able to capture this general trend, possibly because of the limited database and the simplistic linear approach. In particular, it can be noted that there are only seven binary entries for Fe-Mn and no binary entries for Fe-Mo in the current database, which clearly complicates the linear analysis. Nonetheless, this is not the purpose of this exercise; instead, it is the purpose to evaluate whether some elements have negligible correlation with the Ms and, thus, can be excluded from the ML modeling. We can see that some of the elements, e.g., B, S, and P, have values quite close to zero and should have a minor influence on the Ms. These three features, therefore, were excluded in the present modeling. It should be noted, though, that when the alloy is not fully austenitic during austenitization, it will be important to also consider, e.g., B and S since they can contribute to the formation of borides and sulfides.
The final database showing the distribution of alloying content for all individual elements is given in Figure 2. Table I includes a simple classification of the steel alloys included in the database.
2.3 ML Approach
In general, training an ML algorithm can be explained as searching a vector space X of hypotheses to identify the best hypothesis where f:X → y. A key problem arises during ML when the amount of training data available is too small compared to the size of the hypothesis space. Without sufficient data, the ML algorithm can find many different hypotheses in X that all give the same accuracy on the training data. This problem can be solved effectively by using ensemble algorithms, where the algorithm can take one of the votes (predictions) and find a good approximation of the true target function y.
In the present work, supervised ML was used to model the Ms based on the chemical composition of the alloys. Previous ML models for the Ms have all used ANN, which is often a suitable approach but it has limitations. We, therefore, have evaluated ANN modeling vs ensemble methods, which are suitable for smaller datasets, as explained previously.
Various methods have been proposed to generate accurate, yet diverse, sets of models for constructing ensembles. Bagging,[3] Boosting,[2] and their variants are the most popular examples of this methodology. In Boosting, an iterative approach to minimize the loss function (error function) is used, whereas in Bagging, the learning is performed simultaneously and then the outcome is averaged. In general, Boosting is effective in generating accurate predictions close to the experimental data, but it can be susceptible to overfitting, which will be further explained subsequently. On the other hand, Bagging is less sensitive to overfitting, but it can be sensitive to changes in the data, which can lead to large changes in the predictions. The following four different ML ensemble techniques were applied:
-
(a)
Random forests (RFs)
-
(b)
Extremely randomized trees: Extra Trees (ExT)
-
(c)
Gradient boosting (GB), and
-
(d)
Adaboost (AdB)
where (a) and (b) can be categorized as Bagging methods and (c) and (d) as Boosting methods.
For ANN modeling, a multilayer perceptron (MLP) approach, which learns using backpropagation techniques, was employed:
-
(e)
Multilayer perceptron
The Python Data Analysis Library Pandas,[79] an open source library providing data structures and data analysis tools for the Python programming language, was used for the implementation of methods (a) through (e). Pandas DataFrame was applied to analyze the data and visualization was performed using the Matplotlib package in Python. The ML models for predicting the Ms were developed based on Scikit-learn: ML tools in Python.
In ML, it is critical to make sure that the fitting of the model to the data is balanced. The power of ML is that it is not necessary to know how the features relate to the dependent variable beforehand; these relationships are discovered automatically. In the case of simple linear regression, the development of the model and the evaluation of the accuracy of the model are both, in general, evaluated on the entire dataset. While this approach in most cases works well for simple linear regression, it is susceptible to overfitting in a nonlinear ML model. Hence, it can indicate overly optimistic accuracy of the nonlinear ML model. A nonlinear ML model can, in principle, learn every single point in the dataset to yield 100 pct accuracy on that dataset, but this model would most likely not work well on unseen data. Therefore, the accuracy of ML models must be evaluated based on unseen data. A simple way to do this is to build the model using a random subset of the data and then to use the remaining subset for the evaluation of the accuracy of the model. This approach is called the train-test split approach or cross-validation. A balanced fitting as well as models that underfit and overfit the data is illustrated in Figure 3. The balanced model should be able to predict unseen data, whereas the other two should not be able to give good predictions on unseen data.
Illustration of statistical fitting of data: (a) the model is underfitting, i.e., a linear model is fitted to a nonlinear dataset; (b) the fitting is balanced, i.e., the model fits the nonlinear data well; and (c) the model is overfitting, i.e., the model fits more-or-less all datapoints during training, but the predictability is likely poor for unseen data
2.4 Evaluation of Predictability for Statistical Modeling
The evaluation of the predictive power of the ML models must be performed before concluding on their reliability. This can be achieved by statistical evaluation metrics. There are many different metrics to evaluate the statistical accuracy of the predictions, and in the present work, we use four different quality metrics.
First, the coefficient of determination (R2) is always a value between 0 and 1, where 1 is a perfect agreement between the model and experiments. \( \hat{y}_{i} \) is the value of the ith prediction, and yi is the corresponding measured value. R2 is estimated over the sampling size nsamples and is defined as
where
Second, another measure that provides an absolute number on the average discrepancy between the model and experiments is the mean square error (MSE), which is defined as
And, the root-mean-square error is
Similarly, the mean absolute error (MAE) is
Finally, the explained variation (EV) measures the proportion to which a statistical model accounts for the variation of a given dataset. EV is evaluated as follows:
where Var is the variance.
We use these quality metrics to assess the predictive power of the ML models for training, testing, and benchmarking.
3 Results and Discussion
3.1 Model Evaluation
The performance of the ensemble methods and the MLP method is presented in Figure 4. The quality metrics defined in Section II–D are used to evaluate their performance; the left-hand column shows the quality metric for the training data using the different methods, whereas the right-hand column shows the quality metric for the test data for the same method. It can be seen that the ensemble methods consistently perform better than the MLP method based on all the different quality metrics. The ensemble methods all perform well and there are only small differences between them, but the AdB method performs slightly better than the others. The regression results using the AdB model are included in Figure 5(a) where the measured Ms is presented vs the predicted Ms. The Ms datasets were split into training and test data by random sampling; 10 pct of the data was used for the testing. The blue points represent the training data, whereas the orange points represent the test data. It can be seen that the fit vs both training and test data is excellent. This is promising, but in light of the description under Section II–C regarding overfitting, one should question whether this could be an overfitted model. In Figure 5(b), we also give the results from the training and test data for the RF model, and it can be seen that the scatter of the datapoints is somewhat larger using RF and this may appear as a more balanced model. However, it should be noted that both models give excellent predictions according to the quality metrics in Figure 4 with only quite small differences.
Evaluation of the five models (RF, ExT, GB, AdB, and MLP) described in Section II–C using (a) through (d) the four quality metrics defined in Section II–D. The left-hand column is for the training data and the right-hand column is for the test data. It can be seen that the ensemble ML methods consistently perform better than the MLP model and that AdB generally performs best among the ensemble methods
To increase the reliability of the ML modeling even further, we implemented an additional scheme in the model. For each prediction, we evaluate the predictions from all four ensemble models; then, we take the two predictions that are closest to each other and calculate the average of these predictions. Considering the quality metrics, it is highly unlikely that two of the ensemble models would perform badly for a certain prediction and, thus, this further assures high-quality predictions and ensures limiting of any influence of overfitting from a certain single ML model. This add-on is implemented in the ML final predictor model that is used for the benchmarking vs the thermodynamics-based model predictions in Section III–C.
From the quality metrics in Figure 4 and the predictions in Figure 5, it is clear that the ML approach can reliably model the Ms dataset. This implies that the ML final predictor model has the potential to predict the Ms of steel alloys based on their chemical composition; in this case, it is assured that the austenitization temperature and time give a fully austenitic structure before quenching. It is also possible to add additional effects to the model, such as parent grain size[18] and secondary phases, provided those data are available.
It should be noted that in the present work, the ML ensemble models perform well on the relatively small dataset. A basic requirement when using regression schemes for data-driven modeling is that the training dataset needs to be sufficiently large. A relatively large dataset allows sufficient partitioning into training and testing sets, thus leading to reasonable validation on the dependent variable. A small training dataset, compared to data dimensionality, can result in inaccurate predictions and unstable and biased models. Except the dataset size, the quality of the dataset and careful feature selection schemes are of great importance for effective ML and, subsequently, for accurate Ms predictions. An informed decision on the feature subset for training the model increases the likelihood of a robust model. One can also compare with prior works using ANN modeling (MLP in the present work) where the dataset has always been smaller than the dataset in the present work. From a statistical modeling perspective, the smaller datasets and less efficient ML methodology (ANN) can explain some of the prediction uncertainty in prior works. Another important improvement in the present work is the usage of a clean dataset with only fully austenitic structures prior to quenching. This helps to limit the required size of the dataset. Some of the problems in prior works were probably also related to unclean datasets. While collecting and cleaning the data for the present work, we could identify some further errors in the MAP database, in addition to the ones that have already been pointed out in the works by Garcia Matteo and coworkers.[27,28,29]
3.2 Interactions in Data and Physical Interpretation
The normalized nonlinear interactions for the AdB model relating the chemical species and the Ms values are presented in Figure 6. These interactions can be compared with the linear interactions that were presented in the Pearson correlation plot in Figure 1. C and Ni are the two elements that have the strongest interaction with the Ms; this is similar to the linear interactions (Figure 1) prior to developing the model. Thereafter, in the linear interaction plot (Figure 1), Mn and Mo are the third and fourth most significant interaction parameters, but for the AdB model, we can see that Mn, Cr, Si, and Mo are the third through sixth strongest interactions, in the given order. Hence, nonlinear interactions are clearly important to model the Ms dataset in the present work.
It is well known that C plays the strongest role in decreasing the Ms; also, Ni and Mn are austenite-stabilizing elements, and it is reasonable that these elements have a major effect on the Ms. A similar tendency was reported by Capdevila and Andrés[25] in their ANN modeling study. The effect of Cr on the Ms, here, is comparable to the effect of Mn, showing a stronger effect of Cr than in Capdevila and Andrés. Mo is also found to be a more important feature than other strong carbide forming elements, such as W, V, Nb, and Ti, for the present dataset. It is, however, important to keep in mind that the feature importance is a combination of the effect of the element and the range of compositions for that element in the modeled dataset. For example, N is considered to have a similar effect as C in binary alloys (e.g., Ishida and Nishizawa[41]). The difference in the present work can be explained by the different distribution of C compositions in the datasets in comparison with N compositions. It is clear from Figure 1 that the feature importance of C is predicted to be dominant in the present dataset where the C range is between about 0 and 2 wt pct, whereas the N range is between about 0 and 0.1 wt pct. In order to further investigate such effects, it is necessary to include more nonzero compositions for N in the database. The same is true for strong carbide forming elements such as W, V, Nb, and Ti. In the present database, the alloys containing large fractions of these elements were removed, since the carbides formed with these elements are not fully dissolved in the austenite matrix at the austenitization temperature, as predicted by the thermodynamic calculations. Thus, only steels with low fractions of W, V, Nb, and Ti were included in the database; then, the effect on the Ms is quite low. It is believed that this situation will change when the database is extended with further data on highly alloyed steels such as tool steels and high-speed steels. It can also be interesting to note that in a global model perspective, only two elements, Al and Co, increase the Ms when they are added to the alloy; all other elements lower the Ms when they are added to the alloy.
3.3 Benchmarking of ML Model with Thermodynamics-Based Models
The ML final predictor model developed in this work was benchmarked vs a thermodynamics-based model from Stormvinter et al.[16] The thermodynamics-based model was implemented using the Matlab interface of Thermo-Calc[75] and the database TCFE6,[80] which was used to develop the barrier equation in Stormvinter et al. Only the lath martensite expression was implemented; therefore, the barrier of transformation was calculated for both lath and plate martensite to make sure that only entries where lath martensite forms according to the thermodynamics-based model were included in the benchmarking database. 115 unseen data entries were included in the benchmarking database. These data come from the same reference that was used to validate the thermodynamics-based model, all in order to try and make sure that it is an unbiased comparison. The comparison is presented in Figure 7, and it can be seen that both models provide quite accurate predictions of the Ms. The ML model predictions are slightly better, and the blue dashed lines indicate a predictive capability of ±18 K, which is the RMS for the ML final predictor model.
4 Conclusions
-
(1)
An ML model using ensemble learning and a database of 2277 entries for chemical composition and Ms in steels has been developed to predict the Ms of steels.
-
(2)
The ML final predictor model provides accurate predictions on unseen data for similar steels as included in the database. The model is agile and can easily incorporate a larger distribution of steel categories and additional features as long as a more extensive database is developed.
-
(3)
The ML final predictor model was compared to a recent thermodynamics-based model for the Ms using unseen data. Both models give quite accurate and reliable predictions, but the ML model performs slightly better.
References
S.S. Sahay: in Integrated Computational Materials Engineering (ICME) for Metals, M.F. Horstemeyer, ed.; Mater. Manufact. Processes, 2015, vol. 30 (4), pp. 569–70.
L. Breiman: Mach. Learn., 1996, vol. 24, pp. 123–40.
L. Breiman: Mach. Learn., 2001, vol. 45, pp. 5–32.
F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot, and E. Duchesnay: J. Mach. Learn. Res., 2011, vol. 12, pp. 2825–30.
C.E. Rasmussen and C.K.I. Williams: Gaussian Processes for Machine Learning, MIT Press, Cambridge, MA, 2006.
https://www.mgi.gov/sites/default/files/documents/materials_genome_initiative-final.pdf.
P. Payson and C.H. Savage: Trans. ASM, 1947, vol. 39, pp. 403–52.
K.W. Andrews: J. Iron Steel Inst., 1965, vol. 203, pp. 721–27.
H.K.D.H. Bhadeshia: Met. Sci., 1981, vol. 15 (4), pp. 178–80.
G. Ghosh and G.B. Olson: Acta Metall. Mater., 1994, vol. 42 (10), pp. 3361–70.
G. Ghosh and G.B. Olson: Acta Metall. Mater., 1994, vol. 42 (10), pp. 3371–79.
V. Raghavan and D. Antia: Metall. Mater. Trans. A, 1996, vol. 27A, pp. 1127–32.
C.Y. Kung and J.J. Rayment: Metall. Mater. Trans. A, 1982, vol. 13A, pp. 328–31.
A. Borgenstam and M. Hillert: Acta Mater., 1997, vol. 45 (5), pp. 2079–91.
S.J. Lee and K.S. Park: Metall. Mater. Trans. A, 2013, vol. 44A, pp. 3423–27.
A. Stormvinter, A. Borgenstam, and J. Ågren: Metall. Mater. Trans. A, 2012, vol. 43A, pp. 3870–79.
F. Huyan, P. Hedström, L. Höglund, and A. Borgenstam: Metall. Mater. Trans. A, 2016, vol. 47A, pp. 4404–10.
S.M.C. van Bohemen and L. Morsdorf: Acta Mater., 2017, vol. 125, pp. 401–15.
A. Kumar: Master’s Thesis, KTH Royal Institute of Technology, Stockholm, 2018.
D. Barbier: Adv. Eng. Mater., 2014, vol. 16 (1), pp. 122–27.
W.G. Vermeulen, P.F. Morris, A.P. De Weijer, and S. Van der Zwaag: Ironmaking Steelmaking, 1996, vol. 23 (5), pp. 433–37.
J. Wang, P.J. van der Wolk, and S. van der Zwaag: ISIJ Int., 1999, vol. 39, pp. 1038–46.
J. Wang, P.J. van der Wolk, and S. van der Zwaag: Mater. Trans. JIM, 2000, vol. 41, pp. 761–68.
J. Wang, P.J. van der Wolk, and S. van der Zwaag: Mater. Trans. JIM, 2000, vol. 41, pp. 769–76.
C. Capdevila and C.G. de Andrés: ISIJ Int., 2002, vol. 42 (8), pp. 894–902.
C. Capdevila, F.G. Caballero, and C. Garcia de Andres: Mater. Sci. Technol., 2003, vol. 19 (5), pp. 581–86.
T. Sourmail and C. Garcia-Mateo: Comp. Mater. Sci., 2005, vol. 34, pp. 323–34.
T. Sourmail and C. Garcia-Mateo: Comp. Mater. Sci., 2005, vol. 34 (2), pp. 213–18.
C. Garcia-Mateo, C. Capdevila, F.G. Caballero, and C.G. de Andrés: J. Mater. Sci., 2007, vol. 42 (14), pp. 5391–97.
M.J. Peet: Mater. Sci. Technol., 2015, vol. 31, pp. 1370–75.
H.K.D.H. Bhadeshia: ISIJ Int., 1999, vol. 39 (10), pp. 966–79.
H.K.D.H. Bhadeshia, R.C. Dimitriu, S. Forsik, J.H. Pak, and J.H. Ryu: Mater. Sci. Technol., 2009, vol. 25 (4), pp. 504–10.
H.K.D.H. Bhadeshia: ASA Data Sci. J., 2009, vol. 1, pp. 296–305.
Z.W. Yu: Appl. Mech. Mater., 2010, vol. 20 (23), pp. 1211–16.
O Sagi, L Rokach (2018) Adv Rev WIREs Data Mining Knowl Discov 8 (4):1–18.
Materials Algorithms Project (MAP): https://www.phase-trans.msm.cam.ac.uk/map/data/data-index.html#neural. Accessed June 1, 2017.
MAP_DATA_STEEL_MS_2004: https://www.phase-trans.msm.cam.ac.uk/map/data/materials /Ms_data_2004.html. Accessed June 1, 2017.
A.B. Greninger: Trans. ASM, 1942, vol. 30, pp. 1–26.
T.G. Digges: Trans. ASM, 1940, vol. 28, pp. 575–607.
T. Bell and W.S. Owen: Trans. TMS-AIME, 1967, vol. 239, pp. 1940–49.
K. Ishida and T. Nishizawa: Trans. Jpn. Inst. Met., 1974, vol. 15 (3), pp. 217–24.
M. Oka and H. Okamoto: Metall. Mater. Trans. A, 1988, vol. 19A, pp. 447–52.
J.S. Pascover and S.V. Radcliffe: Trans. TMS-AIME, 1968, vol. 242 (4), pp. 673–82.
R.B.G. Yeo: Trans. TMS-AIME, 1963, vol. 227, pp. 884–89.
A.S. Sastri and D.R.F. West: J. Iron Steel Inst., 1965, vol. 203, pp. 138–45.
U.R. Lenel and B.R. Knott: Metall. Trans. A, 1987, vol. 18A, pp. 767–75.
W. Steven: J. Iron Steel Inst., 1956, vol. 203, pp. 349–59.
R.H. Goodenow and R.F. Hehemann: Trans. AIME, 1965, vol. 233, pp. 1777–86.
R.A. Grange and H.M. Stewart: Trans. AIME, 1946, vol. 167, pp. 467–94.
M.M. Rao and P.G. Winchel: Trans. AIME, 1967, vol. 239 (7), pp. 956–60.
E.S. Rowland and S.R. Lyle: Trans. ASM, 1946, vol. 37, pp. 27–47.
Atlas of Continuous Cooling Transformation Diagrams for Vanadium Steels, Vanitec, Kent, June 1985.
Atlas zur Warmebehaendlung der Staehle, Verlag Stahleisen mbH, Duesseldorf, Germany 1954.
W.W. Cias: Phase Transformation Kinetics and Hardenability of Medium-Carbon Alloy Steels, Climax Molybdenum Company, Greenwich, CT, 1973.
M. Atkins: Atlas of Continuous Cooling Transformation Diagrams for Engineering Steels, British Steel Corporation, London, 1980.
M. Economopoulos, N. Lambert, and L. Habraken: Diagrames de Transformation Desaciers Fabriques dans le Benelux, Centre National de Recherches Metallurgiques, 1967.
Atlas of Isothermal Transformation Diagrams of B.S. EN Steels, Special Report No. 40, The British Iron and Steel Research Association, 1949.
Atlas of Isothermal Transformation Diagrams of B.S. EN Steels, 2nd ed., Special Report No. 56, The British Iron and Steel Research Association, 1956.
Atlas of Isothermal Transformation and Cooling Transformation Diagrams, American Society for Metals, Metals Park, OH, 1977.
DP Koistinen, RE Marburger (1959) Acta Metall 7 (1):59–60
AJ Goldman, WD Robertson (1954) Acta Metall 12(11):1265–75.
NIMS Materials Database (MatNavi): http://mits.nims.go.jp/index_en.html. Accessed June 20, 2017.
G.F. Vander Voort, ed., Atlas of Time-Temperature Diagrams for Irons and Steels, ASM International, Materials Park, OH, 1991.
Atlas of Isothermal Transformation Diagrams, United States Steel, Pittsburgh, PA, 1953.
Z. Zhang and R.A. Farrar, eds., An Atlas of Continuous Cooling Transformation Diagrams Applicable to Low Carbon Low Alloy Weld Metals, 1995.
D.A. Mirzayev, M.M. Shteynberg, T.N. Ponomareva, and V.M. Schastlivtsev: Phys. Met. Metallogr., 1980, vol. 47, pp. 102–11.
M. Oka and H. Okamoto: Metall. Trans. A, 1988, vol. 19A, pp. 447–52.
D.A. Mirzayev, O.P. Morozov, and M.M. Shteynberg: Phys. Met. Metallogr., 1973, vol. 6, pp. 99–105.
D.A. Mirzayev, V.N. Karzunov, V.N. Schastlivtsev, I.I. Yakovleva, and Y.V. Kharitonova: Phys. Met. Metallogr., 1986, vol. 61, pp. 114–22.
E.A. Wilson: Doctoral Thesis, University of Liverpool, Liverpool, 1965.
M.M. Shteynberg, D.A. Mirzayev, and T.N. Ponomareva: Phys. Met. Metallogr., 1977, vol. 43, pp. 143–49.
W.D. Swanson and J.G. Parr: J. Iron Steel Inst., 1964, vol. 204, pp. 104–06.
D.A. Mirzayev, S.Y. Karzunov, V.M. Schastlivtsev, I.L. Yakovleva, and Y.V. Kharitonova: Phys. Met. Metallogr., 1986, vol. 62, pp. 100–09.
G.E. Totten, ed., Steel Heat Treatment Handbook: Metallurgy and Technologies, 2nd ed., CRC Press, Boca Raton, FL, 2006.
J.-O. Andersson, T. Helander, L. Höglund, P. Shi, and B. Sundman: CALPHAD, 2002, vol. 26, pp. 273–312.
TCFE9: TCS Steels/Fe-Alloys Database Version 9.0, Thermo-Calc Software AB, Sweden, 2017.
M. Izumiyama, M. Tsuchiya, and Y. Imai: J. Jpn. Inst. Met., 1970, vol. 34, pp. 105–115.
M. Okamoto and R. Odaka: Tetsu-to-Hagané, 1953, vol. 39 (4), pp. 426–32.
Python Data Analysis Library–Pandas: Python Data Analysis Library, http://pandas.pydata.org/.
TCFE6: TCS Steels/Fe-Alloys Database Version 6.2, Thermo-Calc Software AB, Sweden, 2009.
Acknowledgments
The support provided by KTH Innovation, in particular, Daniel Carlsson, and the funding from Vinnova VFT-1 are gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding authors
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Manuscript submitted May 15, 2018.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Rahaman, M., Mu, W., Odqvist, J. et al. Machine Learning to Predict the Martensite Start Temperature in Steels. Metall Mater Trans A 50, 2081–2091 (2019). https://doi.org/10.1007/s11661-019-05170-8
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11661-019-05170-8