Abstract
The principal cultivated potato (Solanum tuberosum) has mainly been vegetatively propagated through its tubers. Potato breeders have therefore made planned artificial hybridizations to generate genetically unique seedlings and their clonal descendants from which to select new cultivars for tuber propagation. After the initial hybridizations, no more sexual reproduction was required to produce a successful new cultivar, which depended on choosing the correct breeding objectives and the ability to recognize a clone that met those objectives. Any impact of the new science of genetics after 1900 needed to be through the production of parental material of known genetic constitution and predictable offspring. This included making use of the many wild tuber-bearing relatives of the potato in Central and South America, as well as the abundance of landraces in South America. This review looks at the history of how potato geneticists: 1) established that the principal cultivated potato is a tetraploid that displays tetrasomic inheritance (2n = 4x = 48); 2) developed progeny tests to determine the dosage of major genes for qualitative traits in potential parents, and also progeny tests for their general combining abilities for quantitative traits; and 3) provided molecular markers for the marker assisted selection of major genes and quantitative trait alleles of large effect, and for the genomic selection of many alleles of small effect. It is argued that the concepts of population genetics are required by breeders, once a number of cycles of hybridization and cultivar production are considered for the genetic improvement of potato crops.
Similar content being viewed by others
Introduction
William Bateson was one of the first scientists to appreciate the potential impact on animal and plant breeding of Mendel’s paper Experiments in Plant Hybridisation (Mendel 1865). This can be seen in Bateson’s book, Mendel’s Principles of Heredity, published in 1902, and including the English translation of Mendel’s paper of 1865 (Bateson and Mendel 1902). Bateson concluded his book: “The breeder, whether of plants or of animals, no longer trudging in the old paths of tradition, will be second only to the chemist in resource and in foresight. Each conception of life in which heredity bears a part-and which of them is exempt-must change before the coming rush of facts.” The way genetics impacted on plant breeding turned out to depend upon the mating system of the crop species, as might have been anticipated from Darwin’s book of 1876 on The Effects of Cross and Self Fertilisation in the Vegetable Kingdom (Darwin 1876). The world’s four most important food crops, wheat, rice, maize and potatoes, provide good examples of the three main types of mating system and their consequences for plant breeding.
Wheat (Triticum aestivum) and rice (Oryza sativa), like Mendel’s peas (Pisum sativum), are species that naturally reproduce by self-pollination but in which the breeder can artificially perform cross-pollinations. The breeder can thus select true breeding lines with complementary traits, hybridize them, and then seek new true breeding combinations over the subsequent generations of self-pollination. As Mendel pointed out, the number of constant combinations for his seven differentiating characters is given by 27 = 128. Whatever the subsequent complexities of dealing with quantitative as well as qualitative traits, the Mendelian method could be seen in successful wheat and rice breeding programmes, including those of the Green Revolution of the 1950s to the 1970s, which made use of the dwarfing alleles from Norin 10 wheat and Dee-geo-woo-gen (DGWG) rice (Riley 1969).
Maize (Zea mays), in contrast, is a species that naturally reproduces by cross-pollination, primarily but not exclusively as a result of having separate male and female flowers on the same plant (monoecious). However, it is also easy to self-pollinate and proved suitable for both genetical and plant breeding research. The former can be seen in the early linkage studies of Bregger (1918) and the proof by Creighton and McClintock (1931) that during meiosis the cytological (physical) crossing-over of homologous chromosomes is accompanied by genetic crossing-over of genes in the same linkage group. By the 1950s, textbooks of genetics (e.g. Sinnott et al. 1958) were showing the locations of several hundred gene loci on the 10 linkage groups of maize corresponding to its 10 microscopically visible pairs of chromosomes. The breeding research on the effects of inbreeding and crossbreeding in maize by East (1908), Shull (1908, 1909) and Jones (1918) resulted in hybrid maize, one of the great success stories of plant breeding in the twentieth century (Kingsbury 2009). The purpose of the inbreeding was not to produce inbred line cultivars, but rather to find lines that combined well with other lines, and ultimately to find the best combination for a single-cross hybrid. As a consequence of the large numbers involved, the concepts and practice emerged of first selecting lines for their general combining ability and then for their specific combining ability (Sprague and Tatum 1942). Furthermore, quantitative geneticists became interested in the genetic basis of heterosis (hybrid vigour) and mating designs were conceived to estimate the average degree of dominance, such as the three North Carolina Designs (Comstock and Robinson 1948, 1952) and the Diallel Designs (Griffing 1956). The designs also allowed the genetical variation in populations to be analysed and the results applied to the selection of quantitative traits, as was happening in animal breeding; for example, as seen in Lerner’s book Population Genetics and Animal Improvement as Illustrated by the Inheritance of Egg Production (Lerner 1950).
Potatoes (Solanum tuberosum), in a further contrast, naturally reproduce by both sexual and asexual means. The natural pollination of potato flowers by insects capable of buzz pollination results in true (botanical) potato seeds (TPS) in berries. The genetically unique seedlings that arise from these seeds produce tubers which can sprout and grow into new potato plants, giving rise to a complicated mixed sexual/clonal system of reproduction. In the late nineteenth century, potato breeders started to switch from using natural open-pollinations to planned artificial hybridizations, to generate genetically unique seedlings and their clonal descendants from which to select new cultivars for tuber propagation. Hence, after the initial hybridizations, no more sexual reproduction was required to produce a new cultivar and therefore, in a sense, no knowledge of genetics was required. As a consequence, any impact of genetics needed to be through the production of parental material of known genetic constitution and predictable offspring. This included making use of the many wild tuber-bearing relatives of the potato in Central and South America, as well as the abundance of landraces in South America. The numerous potato-collecting expeditions to Central and South America, pioneered by the Russians in the 1920s, led to the establishment of a number of potato germplasm collections (gene banks) worldwide, including those established in Europe and North America in the 1940s and 1950s, and the world collection at the International Potato Centre (CIP) in Peru in 1971. The book by Hawkes, The Potato: Evolution, Biodiversity & Genetic Resources, provides a useful summary of the germplasm that had become available to breeders by 1990, and the relevant knowledge that had accumulated to aid its utilization (Hawkes 1990).
In this review paper, the focus is on the impact of potato genetics on the breeding of potato cultivars for propagation by tubers, and the paper concentrates on the principal cultivated potato, tetraploid S. tuberosum (2n = 4x = 48), without considering any specific programme aimed at a target environment and end use. A much wider coverage of potato breeding, including breeding cultivars for propagation through true potato seed, genetic transformation and gene editing, can be found in my recent book Potato Breeding: Theory and Practice (Bradshaw 2021). It will be argued that the concepts of population genetics are required by breeders, once a number of cycles of hybridization and cultivar production are considered for the genetic improvement of potato crops. In contrast, breeding a successful new cultivar depends more on choosing the correct breeding objectives and the ability to recognize a clone that meets those objectives, than on understanding the complexities of potato genetics.
The Early Years of Potato Breeding and Genetics: 1901 to 1937
One of the key figures in England in the early years of potato breeding and genetics was Redcliffe N. Salaman, who trained as a doctor but contracted tuberculosis in 1903. On his recovery, with guidance from his friend William Bateson and at the suggestion of his gardener, he turned to the scientific study of the potato (Reader 2008; Weintraub 2019). He started his breeding and genetics experiments in 1906 in the garden of his home in Barley in Hertfordshire, and published his seminal paper on potato genetics in the first issue of the Journal of Genetics (Salaman 1910). He summarized the results of his work at Barley in 1926 in his book Potato Varieties (Salaman 1926). His work then transferred to the new Potato Virus Research Institute in Cambridge where he became its founding director, a position he held until his retirement in 1939.
Salaman’s book contains a chapter on “the application of genetics to variety raising” which considers genetic factors for immunity to wart disease; for resistance to leaf roll and mosaic disease (caused by viruses); for red, purple and white skin colour; for the distribution of colour on the tuber surface; for yellow and white flesh colour; for eye depth; for tuber shape; and for plant growth habit. Other traits thought to have a strong genetic component were maturity and yield, but more work was required on cooking quality (waxy and floury) and flavour. The genetic factors (alleles) for all of the traits he considered, with one notable exception, were present in potato cultivars being grown in Great Britain. Examples of Mendelian ratios could be found for skin colour and immunity to wart [Synchytrium endobioticum, pathotype 1(D1)] on the assumption of disomic inheritance. In summary, Salaman was able to offer guidance on the choice of parents and what to expect in their offspring, but could not go further with the limited genetic knowledge acquired by 1926 and the lack of understanding of meiosis in potatoes. He also worked on the breeding of one extremely important trait that was not present in the cultivars being grown in Great Britain, nor in other European countries and North America, namely resistance to late blight.
Resistance to Late Blight (Phytophthora infestans) from Solanum demissum
In 1906, Salaman requested tubers of Solanum maglia from Kew Gardens (Reader 2008; Weintraub 2019). The mislabelled tubers that he received were in fact S. edinense, a natural hybrid of S. demissum and S. tuberosum which had arisen in the botanic garden in Edinburgh. At Barley, S. edinense proved highly but not completely resistant to late blight in the years 1906 to 1910. Salaman was able to self-pollinate S. edinense and in 1909 raised a family of 40 plants, 7 of which proved resistant to the bad blight attacks of that year and the next. One clone was allowed to remain in the kitchen garden at Barley for 17 consecutive years and remained completely resistant. In 1910, Salaman made crosses between the resistant clones and domestic cultivars. He also secured S. demissum itself, confirmed that it was resistant, and from 1911 hybridized it as female parent with domestic cultivars. He crossed some of the resistant offspring with the resistant stocks he had previously established. By 1926 he had a number of clones combining blight resistance with other desirable traits. However, in 1932 some previously resistant material showed signs of being attacked by blight, an omen that was also experienced on similarly derived material in Scotland (Weintraub 2019).
The work in Scotland was being done by William Black, the first and longest serving (1926 to 1968) potato breeder at the Scottish Plant Breeding Station (SPBS). SPBS had been founded in 1920 and had inherited a collection of potato breeding material from John H. Wilson of St Andrews University who had died that year. The material included derivatives of Wilson’s breeding experiments with blight resistance from S. edinense and S. demissum. Selections from this material initially remained free of blight but in 1932 succumbed to a new race of blight, whereas the original S. demissum source remained resistant. Hence, in 1932, Black started afresh with a breeding programme to introduce new resistance factors from S. demissum. but soon found that progenies bred only from S. demissum and S. tuberosum gave segregation ratios that bore little resemblance to standard Mendelian ratios, as might have been expected from the cytological studies (chromosome numbers) of Miss Campin, as described by Salaman (Salaman 1926). Eventually in 1937 the cross S. rybinii × S. demissum (S. rybinii = S. phureja) provided breeding material in which Mendelian expectations were realized, and after three backcrosses to cultivars Gladstone, Pepo and Craigs Defiance, resulted in cultivar Pentland Ace in 1951 and a scientific paper in 1952 (Black 1952). In this work we see Black the breeder wanting a successful cultivar and Black the geneticist wanting Mendelian ratios.
As a result of similar work in other countries, in 1953, Black, Mastenbroek, Mills and Petersen were able to establish an international system for the nomenclature of races of Phytophthora infestans in which physiological races of P. infestans were numbered to indicate their virulence towards the four R genes recognized by 1947, with all four genes present in SPBS clone 2070(54) (Black et al. 1953). Thus, late blight of potato provided another early example of a dominant host resistance (R) gene interacting with a dominant pathogen avirulence (Avr) gene to provide race-specific hypersensitive resistance, as conceived of in Flor’s original gene-for-gene hypothesis (Flor 1942). By Black’s retirement in 1968 eleven R genes had been discovered, but it was already clear from race surveys that they would not provide durable resistance, either singly or in combination, due to the evolution of new races of P. infestans (Malcolmson and Black 1966; Malcolmson 1969). Nevertheless, S. demissum features in the pedigrees of 58 out of the 72 potato cultivars bred at the Scottish Plant Breeding Station and the Scottish Crop Research Institute from 1926 to 2008 (Bradshaw 2009).
Assessment of Yield and Other Quantitative Traits
Potato breeders needed to assess the clones from their hybridizations for economically important traits. Salaman devoted four chapters of his book (Salaman 1926) to the yield of potatoes in which he clearly recognized that yield was affected by both genetic and environmental factors, with implications for the conduct of yield trials. He also had an intuitive feel for the combining ability of parents with respect to yield, but was unable to progress the genetics of yield. He quoted the paper by Fisher and Mackenzie (1923) on the manurial response of different potato varieties. Their experiment was done at Rothamsted Experimental Station in England and comprised an assessment of the yield of 12 varieties (average yields over manurial treatments ranged from 8.86 to 21.47 lbs/plot) in 6 manurial treatments (average yields over varieties ranged from 4.47 to 20.12 lbs/plot). The experiment had three replications and through a novel analysis of variance, the authors were able to demonstrate that the differences between varieties and the differences between manurial treatments were statistically significant but that the varieties by manurial treatments interactions could have arisen by chance. Potatoes went on to feature in Fisher’s famous book The Design of Experiments (Fisher 1935).
Hence, before 1937, potato breeders did not know that the potato is a tetraploid that displays tetrasomic inheritance, but they did know how to assess and analyse yield and other quantitative traits over clonal generations in randomized and replicated trials. I have argued elsewhere (Bradshaw 2021) that such multistage, multi-trait selection would benefit from the application of multistage selection theory, as first proposed by Finney (1958), and the use of a selection index, such as the optimum index of Smith (1936). However, practical considerations prevailed in what potato breeders did, and arose from the limited amount of planting material of each clone in each generation, and the overall resources that could be allocated to a breeding programme (Bradshaw 2021).
Acceptance and Consequences of Tetrasomic Inheritance: 1937 to 1962
Acceptance of Tetrasomic Inheritance
As early as 1927, in a paper primarily concerned with male sterility, Fukuda (1927) counted 48 chromosomes in the metaphase of somatic nuclear division in the root tips of 29 potato cultivars. In the same year Smith (1927) reported haploid chromosome numbers of 12 for S. jamesii and S. chacoense, 24 for S. fendleri and 36 for S. demissum. Hence, it looked as though the tuber-bearing Solanum species formed a polyploid series with a base number of 12 and that the cultivars were tetraploid. It appears however that geneticists assumed that the potato behaved genetically as a diploid (disomic inheritance) until the publication of Lunden’s comprehensive paper in 1937. Lunden (1937) identified seven (unlinked) genes connected with colour inheritance, five of which showed without doubt tetrasomic inheritance, and concluded that the potato is an autotetraploid. Cadman (1942) added the dominant Nx gene for race-specific resistance to Potato virus X (PVX) as another example. He also gave a clear account of the difficulties of distinguishing the disomic inheritance of an allotetraploid and the tetrasomic inheritance of an autotetraploid using segregation ratios. Firstly, if one considers a single pair of alleles A and a, when simplex (A1a1a1a1) autotetraploids (one locus) and simplex (A1a2/a1a2) allotetraploids (two unlinked loci) are backcrossed to the recessive genotype and also selfed, they both give the same 1:1 and 3:1 ratios of dominants to recessives. In contrast, duplex (A1A1a1a1) autotetraploids give 5:1 and 35:1 ratios, respectively, whereas duplex (A1A2/a1a2) allotetraploids give 3:1 and 15:1 ratios, respectively, assuming that A1 and A2 are identical in function but not necessarily identical by descent. Hence these ratios should distinguish tetrasomic from disomic inheritance, provided enough offspring are raised to avoid similarity by chance. However, Cadman (1942) realised from the work of Mather (1936) on segregation and linkage in autotetraploids, that the phenomenon of double reduction could reduce the 5:1 and 35:1 ratios in the direction of 3:1 and 15:1 (with maximum double reduction they are 3½:1 and 19¼:1). Therefore, a lot of additional progeny testing was required to be certain of tetrasomic inheritance. Ideally this would be complemented with cytological determinations of the frequency of quadrivalents, the pairings of four chromosomes which can give rise to double reduction in which sister chromatids end up in the same diploid gamete, the frequency depending on the distance of the locus from the spindle attachment (centromere). Swaminathan (1954) studied the nature of polyploidy in some 48-chromosome tuber-bearing Solanum species. In Tuberosum cultivars he found a maximum of five and a mean of two to three quadrivalents per metaphase I plate. He concluded from all of the cytological and genetical evidence that tetraploid S. tuberosum probably arose as an autotetraploid and is essentially an autotetraploid, but that for all practical purposes current commercial cultivars are segmental allotetraploids. In contrast, Gottschalk (1958) studied the pachytene stage of meiosis and concluded that the potato is a true autotetraploid with four identical or almost identical genomes. Then Lunden (1960) provided more genetic evidence of tetrasomic inheritance from further results on the inheritance of tuber and flower colour in some potato cultivars. Tetrasomic inheritance with double reduction provided a better explanation of segregation ratios than disomic inheritance. In his book Principles of Plant Breeding, Allard (1960) includes the potato in his list of major crop species that may be autotetraploid, before considering the cytology of autotetraploids and Mendelian ratios with and without double reduction. In summary, the gametic output of an autotetraploid with two alleles A and a is shown in Table 1, where α is the coefficient of double reduction, defined as the probability of two sister chromatids going to the same gamete (Fisher and Mather 1943), and normally has a value between 0 and
 (see for example Bradshaw 1994).
(see for example Bradshaw 1994).
It can be seen that each locus has its own unique Mendelian ratios depending on the frequency of double reduction, but constrained within the limits of the coefficient of double reduction which increases with the distance of the locus from the centromere.
Today more detailed information on chromosome pairing, quadrivalent formation and crossover events can be obtained from the segregation of molecular markers (Bourke et al. 2015) and the use of Fluorescence In Situ Hybridisation (FISH) to differentiate individual meiotic chromosomes (Choudhary et al. 2020). A summary can be found in my book on potato breeding (Bradshaw 2021), but the results show that the cytogeneticists did come to the right conclusions about tetrasomic inheritance over 60 years ago.
Consequences for Potato Breeding
Cadman (1942) had recognized that individuals quadruplex (four copies) for a dominant resistance allele were recoverable from selfing simplex (single copy) and then duplex (two copies) genotypes and would be most useful in breeding since all the gametes from such plants would carry the dominant allele. Toxopeus (1953) explained and discussed in more detail this method for breeding parents that were multiplex (more than one copy) for major dominant genes for resistance to important diseases and pests of potato. When Salaman started his work in 1906, the major diseases were wart, late blight and viruses, whereas the cyst nematodes started to become a serious problem in Europe in the early 1950s and are still a problem today, particularly Globodera pallida. By 1953, in tetraploid Tuberosum, a number of effective major dominant genes were either available to breeders, or becoming available from landraces and wild relatives of the potato, and the number has continued to increase over the years, although not all have provided durable resistance (Bradshaw 2021). As most of the initially available resistant breeding material appeared to be simplex for the dominant resistance gene, the method of producing multiplex genotypes was as shown in Table 2 (Toxopeus 1953), and had not changed by 2005 (Mackay 2005).
A clone which is simplex for the R gene is either selfed or crossed to another clone which is also simplex for the R gene. The frequency of (RRRR + RRRr + RRrr) in the offspring is about 0.25, although the desired RRRR or RRRr genotype only occurs through double reduction, and then at a very low frequency. The duplex genotype (RRrr) is recognized in a testcross to a susceptible clone rrrr by resistant to susceptible proportions of between 0.83 to 0.17 (α = 0) and 0.78 to 0.22 (α =
 ), whereas the proportions for a simplex genotype (Rrrr) are between 0.50 to 0.50 (α = 0) and 0.46 to 0.54 (α =
), whereas the proportions for a simplex genotype (Rrrr) are between 0.50 to 0.50 (α = 0) and 0.46 to 0.54 (α =
 ). One can work out the minimum testcross progeny size to distinguish these proportions with a very high probability: Toxopeus (1953) concluded as few as 26 offspring for a probability of 97.5%.
). One can work out the minimum testcross progeny size to distinguish these proportions with a very high probability: Toxopeus (1953) concluded as few as 26 offspring for a probability of 97.5%.
Next a clone which is duplex for the R gene is either selfed or crossed to another clone which is also duplex for the R gene. The desired RRRR or RRRr genotype occurs at a frequency of at least 0.25 and the triplex genotype (RRRr) is recognized in a testcross to a susceptible clone rrrr either by all resistant progeny (α = 0) or a resistant proportion of at least 0.96 (α =
 ). In the absence of double reduction, a triplex clone cannot be distinguished from a quadruplex one (RRRR), both giving all resistant offspring as desired.
). In the absence of double reduction, a triplex clone cannot be distinguished from a quadruplex one (RRRR), both giving all resistant offspring as desired.
In summary, if a simplex resistant parent is crossed to a susceptible parent, in the absence of double reduction, half of the progeny will be susceptible and discarded, however good they are for other traits, and if there are as many as eight unlinked genes segregating in the cross, every 255 out of 256 offspring will need to be discarded as lacking at least one resistance gene. However, if the parent is duplex, just one sixth of the progeny will be susceptible and discarded, although with eight unlinked genes segregating, every 77 out of 100 offspring would need to be discarded. Finally, if the parent is triplex, there will be no susceptible offspring to discard, and the same will be true no matter how many loci are segregating. When double reduction occurs, there are slightly more susceptible offspring, but duplex parents are still clearly superior to simplex ones and triplex parents are superior to duplex ones. It is clear that breeders needed to increase the frequencies of multiplex parents available for crossing, but this could only be done through progeny testing until the advent of diagnostic molecular markers and methods to determine allele dosage. Furthermore, Toxopeus (1953) pointed out that these multiplex parents need to be built up in such a way as to ensure the quality of the parents for other traits (i.e. the parents should have commercial value). This raises the issue of whether this should be done in a separate parental line breeding programme or by careful choice of parents in programmes aimed at producing finished cultivars. A good example of a separate parental line breeding programme is the one that operated at the Młochów Research Centre in Poland for over 50 years from 1961 until recently (Zimnoch-Guzowska and Flis 2021), and contributed parents to 72 Polish cultivars. A good example of careful choice of parents in breeding finished cultivars is the use of the H1 gene for resistance to G. rostochiensis in the SPBS/SCRI programme, starting with the cross of Pentland Javelin with Maris Piper in 1971 (for pedigrees see Bradshaw 2009). Interestingly, Vos et al. (2015) have used SNP markers to provide an insight into introgression breeding history since 1945 in Europe and North America. Some of the introgression segments (haplotypes) introduced soon after 1945 had reached frequencies of up to 19% compared with 4% for recently introduced ones. The former means that the introgressed gene is absent in 43% of cultivars, present as a single copy in 40%, and as two copies in 14%, assuming the equilibrium frequencies for the genotypes shown later in Table 3. The latter means absent in 85% of cultivars and present as single copy in 14%. Clearly breeders have not yet increased the frequencies of multiplex genotypes to an appreciable extent, and hence the frequencies of desirable combinations of major genes remains low.
Yield and Other Quantitative Traits
Although Salaman (1926) expressed an intuitive feel for the combining ability of parents, it was the period from 1962 until the mid-1990s that saw the extensive use of combining ability analysis for quantitative traits. One of the first papers was by Plaisted et al. (1962) in the Plant Breeding Department at Cornell University, on combining ability for total plot yield, and opens with the aim of such an analysis for potato breeders which did not change over the following 30 years: “To conduct a successful potato breeding programme for a character such as yielding ability, it is necessary to select parental lines capable of transmitting yielding ability to their offspring. Parental lines which transmit superior yielding ability to their offspring when crossed with a wide variety of other clones are said to have good general combining ability (GCA). The deviation of a specific cross from what is expected on the basis of the GCA of the parents is called specific combining ability (SCA).” The authors secured 190 progenies out of a possible set of 270 from attempting to cross 45 female lines with six tester lines, the minimum number they recommended as representative of the germplasm under consideration. The progenies plus 10 checks were assessed at three sites in rectangular lattice trials with six replicates and ten-hill (plant) plots. The authors estimated the components of variance for lines (GCA lines), for testers (GCA testers) and for the lines × testers interactions (SCA) and found that the SCA item was larger than each of the two GCA items at all three sites, and in an analysis over the three sites, the same was true for the interactions with sites. Nevertheless, they identified four lines with good general combining ability for future use as parents.
Bradshaw and Mackay (1994) summarized the combining ability results for 23 quantitative traits from 15 papers over the period 1962 to 1992, but I (Bradshaw 2021) decided not to produce an updated table for two reasons. Firstly, the results strictly only apply to the particular breeding material under consideration and cannot be generalized. Secondly, if the GCA variance is larger than the SCA variance, there is usually a high correlation between parental GCAs and parental phenotypes, whereas if the SCA variance is larger than the GCA variance, neither the parental GCAs nor the mid-parent value is a good predictor of the offspring mean; but the mid-parent value is all that is available before the cross is made. Hence breeders tended to continue to select parents based on their complementary phenotypes rather than their combining abilities. Nevertheless, the breeder can see in the books by Kempthorne (1957), Wricke and Weber (1986) and Gallais (2003), the development of relevant population and quantitative genetics theory under tetrasomic inheritance, and the genetic basis of general combining ability and progress over a number of cycles of crossing and selecting.
Population and Quantitative Genetics Theory Under Tetrasomic Inheritance
Kempthorne (1955, 1957) provided the general method of subdivision of the genetic variance in randomly mating populations through the fitting of the effects of single alleles and their successively higher orders of interaction by least squares. However, with four different alleles at a single locus in a population there are 35 different genotypes compared with 5 different genotypes with two alleles. Fortunately, the two-allele model with chromosomal segregation (no double reduction) provides useful information for breeders, and Li (1957) showed that for this special case the components of the genetic variance can be found as the variances associated with successive terms in a polynomial regression of genotype value on to allele frequency. In other words, as much as possible of the regression of genotype value on the allele frequency in each genotype is first explained by the effects of single alleles, then as much as possible of the residual variation is explained by the interactions of two alleles, then as much as possible of the residual variation still remaining is explained by the interactions of three alleles, leaving the rest to be explained by the interactions of four alleles. Wright (1979) went on to show that the polynomial regression is equivalent to a Taylor series and that the components of genetic variance can be expressed as simple functions of the various differential coefficients of the population mean. The two-allele model for a single locus in genetic equilibrium with two alleles A and a at frequencies p and q, respectively, and chromosomal segregation (no double reduction), is shown in Table 3 using the notation of Wright (1979), but with d replaced by a and h replaced by d, which is confusing but in line with the modern notation for diploids.
The four parameters a, d, v and w in the genotypic values are sufficient to generate all possible genotypic values for the five genotypes; for example: when a = 1 and d = v = w = 0, the values are 2, 1, 0, -1 and -2, and we have a simple additive model; when a = 1, d =
 and v = w = 0, the values are 2, 2, 1
and v = w = 0, the values are 2, 2, 1
 , 0 and -2, and we have what looks like an unusual kind of dominance; when a = 1, d = ½, v = -1 and w = ½, the values are 2, 2, 2, 2 and -2, and we have a more recognizable form of dominance; and when a = 1, d = ½, v = 1 and w = ½, the values are 2, 4, 2, 0 and -2, and we have a form of overdominance. Hence care is required in interpreting the meanings of d, v and w. The population mean and the partitioning of the genetic variance are as follows (Wright 1979), where αt = the average effect of the allele substitution (A for a) and βt, γt and δt are the interactions between two, three and four alleles, respectively, with t denoting tetraploid.
, 0 and -2, and we have what looks like an unusual kind of dominance; when a = 1, d = ½, v = -1 and w = ½, the values are 2, 2, 2, 2 and -2, and we have a more recognizable form of dominance; and when a = 1, d = ½, v = 1 and w = ½, the values are 2, 4, 2, 0 and -2, and we have a form of overdominance. Hence care is required in interpreting the meanings of d, v and w. The population mean and the partitioning of the genetic variance are as follows (Wright 1979), where αt = the average effect of the allele substitution (A for a) and βt, γt and δt are the interactions between two, three and four alleles, respectively, with t denoting tetraploid.
It can be seen that a, d, v and w contribute to αt; d, v and w to βt; v and w to γt; and w to δt; although the extent depends on the allele frequencies. In Gallais (2003) α = αt, β = -2βt, γ = -2γt and δ = -8δt so that VG = 4pqα2 + 6p2q2β2 + 4p3q3γ2 + p4q4δ2.
The General Combining Abilities (GCAs) and breeding values are shown in Table 4. The GCAs of the genotypes are the means of their offspring from mating at random with gametes from the equilibrium population (p2 AA, 2pq Aa, q2 aa), minus the population mean. In practice, this will probably be a random sample of pollen from the population of breeding material under consideration. The breeding values (Breeding Value 2 in Table 4) of the genotypes are the sums of the average effects in the population of all the alleles they contain and which they transmit to the next generation, as explained in more detail in my book (Bradshaw 2021). These breeding values can also be obtained from the regression of the genotypic values in Table 3 on the frequencies of A, taking into account the frequencies of the genotypes, again as explained in more detail in my book under genomic selection (Bradshaw 2021). The same is true for the regression of phenotypic values provided there is no covariation between the environmental variation and the frequencies of A (in other words, the genotypes are randomized over the environments). Twice the GCA value provides an estimate of the breeding value (Breeding Value 1 in Table 4) that includes a contribution from the diallelic interactions that arise from diploid gametes but are not maintained in an equilibrium population. With the simple two-allele model, it is assumed that one can add the variances, GCAs and breeding values across all loci contributing to the genetic variation to get their total contributions (individual GCAs and breeding values can be positive or negative, whereas variances are always positive). However, non-allelic interactions (epistasis) can occur between loci and contribute to the totals. Kempthorne’s general method (Kempthorne 1957) can be extended to take account of them, but results in 14 components of variance when interactions between two loci are taken into account, which is far more than can be estimated.
The other factor that the simple model ignores is double reduction. For a given chromosome, the coefficient of double reduction α increases from zero at the centromere to a maximum value of
 at the distal end of the chromosome. If loci affecting a quantitative trait like yield are distributed along the chromosome, the effect of double reduction will be most marked at the distal end, and this effect is inbreeding, as shown by Crow and Kimura (1970) in their book An Introduction to Population Genetics Theory. For our two allele model the diploid equilibrium gamete frequencies are [(1 – f)p2 + fp]AA, [2(1 – f)pq]Aa and [(1 – f)q2 + fq]aa, where p and q are the frequencies of alleles A and a, respectively, and f = 3α/(2 + α). The tetraploid equilibrium genotype frequencies for our random mating population are obtained by multiplying together all combinations of the gamete frequencies. When α equals one seventh, we have what is called random chromatid segregation, despite meiosis involving two cell divisions, and f equals one fifth which is the equivalent of 20% inbreeding. We can see this in the genotype frequencies; for example, with p = q = ½ we have the results shown in Table 5. Also given in the table are the equilibrium frequencies under mixed selfing and random mating where the proportion of selfing is one fifth and the figures were obtained using the formula given by Haldane (1930). As expected, the frequencies with chromatid segregation and with 20% selfing are virtually the same and result in higher frequencies of the two homozygotes and lower frequencies of the three heterozygotes, which will affect the population mean and variance to an extent determined by the differences in genotype frequencies. Nevertheless, theoretical considerations which ignore the effects of double reduction should still be of value.
at the distal end of the chromosome. If loci affecting a quantitative trait like yield are distributed along the chromosome, the effect of double reduction will be most marked at the distal end, and this effect is inbreeding, as shown by Crow and Kimura (1970) in their book An Introduction to Population Genetics Theory. For our two allele model the diploid equilibrium gamete frequencies are [(1 – f)p2 + fp]AA, [2(1 – f)pq]Aa and [(1 – f)q2 + fq]aa, where p and q are the frequencies of alleles A and a, respectively, and f = 3α/(2 + α). The tetraploid equilibrium genotype frequencies for our random mating population are obtained by multiplying together all combinations of the gamete frequencies. When α equals one seventh, we have what is called random chromatid segregation, despite meiosis involving two cell divisions, and f equals one fifth which is the equivalent of 20% inbreeding. We can see this in the genotype frequencies; for example, with p = q = ½ we have the results shown in Table 5. Also given in the table are the equilibrium frequencies under mixed selfing and random mating where the proportion of selfing is one fifth and the figures were obtained using the formula given by Haldane (1930). As expected, the frequencies with chromatid segregation and with 20% selfing are virtually the same and result in higher frequencies of the two homozygotes and lower frequencies of the three heterozygotes, which will affect the population mean and variance to an extent determined by the differences in genotype frequencies. Nevertheless, theoretical considerations which ignore the effects of double reduction should still be of value.
In summary, the practically estimated general combining abilities were considered of value to the breeder, despite including departures from the assumptions used to determine the theoretical ones, particularly departures in breeders’ germplasm from the idealized (imagined) random mating population in equilibrium.
Hence by 1962 the geneticist could provide the breeder with the genetic basis for breeding parents that were multiplex for major dominant genes, and for choosing parents with good general combining ability for quantitative traits such as yield, as well as predicting progress over cycles of crossing and selecting, as we shall see in the next section. The breeder, however, didn’t need to understand tetrasomic inheritance in order to make appropriate crosses and to do relevant progeny tests.
Potato Breeding from 1962 to 1989
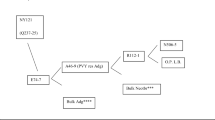
Potato breeding, particularly since the 1960s, can be summarized and described as follows (Fig. 1). Potato breeders make crosses to generate genetic variation from which they seek new cultivars over a number of generations of clonal selection. A cross may be between two cultivars, or between a cultivar and a breeder’s clone that did not become a cultivar, or between two such clones. The outcome will be a few new cultivars, at best, and some improved clones which can also be used as parents in a new cycle of crosses. Parental clones may also be the outcome of the introgression of major dominant genes for disease and pest resistance from landraces and wild tuber-bearing Solanum species, and will have one or more copies of the R gene. They may also be the outcome of attempts at a more general base broadening of the breeding programme with desirable alleles (e.g. Q in Fig. 1) for quantitative traits, mainly but not exclusively from landraces. One further important point to make is that the shorter the time between one set of crosses and the next set, the faster the overall progress in the programme.
Breeding of Finished Cultivars
Since the 1960s, breeders have felt the need to increase the sizes of their programmes in order to assess more traits in more environments. Hence starting with 100,000 seedlings each year from 200 to 300 crosses became the norm and is still common today, as reviewed by Bradshaw (2021). Continued progress was made through cycles of such hybridization and selection, usually among the developing elite germplasm. Furthermore, as the parents for the next round of hybridizations were usually selected on phenotype, rather than on combining ability, the response to such clonal selection each cycle could be predicted with the simple form of the breeder’s equation. The response could be divided by the generation cycle time in years (T) to obtain the response per year (R). In Scotland at SPBS/SCRI, for example, the average generation cycle time from 1927 to 2005 was about 7 years (Bradshaw 2009).
where i is the intensity of selection, rAP is the correlation between the breeding values and the phenotypic values of the parental clones, which is the square root (hn) of the narrow-sense heritability (hn2), and σA is the square root of the additive genetic variance VA. The narrow-sense heritability is VA/VP where VP is the phenotypic variance between parental clones. In other words
where VE is the environmental variation between parental clones.
It is not entirely clear who was the first person to derive the breeder’s equation, but Walsh and Lynch (2018) attribute its popularization in animal breeding to Lush (1937) and the equation is discussed in the book by Lerner (1950) mentioned in the introduction. Walsh and Lynch also explain why the response equals the mean breeding value of the selected parents.
Potato breeders achieved a high intensity of selection for visual selection of seedlings in a glasshouse, spaced plants at a seed-site and small unreplicated plots at the seed-site. The visual selection reduced the number of potential cultivars from 100,000 seedlings to 1000 clones entering replicated yield trials. However, research in the 1980s confirmed that this visual selection was not very effective; but there was no general consensus on how to address the problem, and such visual selection is still common practice, but unable to affect most economically important traits which are quantitative in nature (see for example: Plaisted et al. 1984; Swiezynski 1984; Tai and Young 1984; Brown et al. 1988; Neele et al. 1989; Gopal et al. 1992). Furthermore, as breeders increased the sizes of their programmes, they increased the number of generations of clonal selection for a new cultivar to as many as eight, and as a consequence, lengthened the time to selecting a new set of parents for crossing. In other words, they increased the cycle time in years (T) and hence reduced the response to selection per year (R). In theory, breeders could have increased the narrow-sense heritability by reducing the environmental variation through increased replication in their trials, but were limited in this respect by the number of tubers available for trials. Furthermore, they had no control over the amount of non-additive genetic variation (VD + VT + VQ). Breeders could estimate the narrow-sense heritability from the regression of offspring on mid-parent values, as well as the additive genetic variance (VA). They could also do this from diallel or North Carolina mating designs. They could therefore predict their likely progress over a number of cycles of crossing and selection and compare it with their actual progress. However, from the beginning of the 1960s, primarily from a consideration of domestication and the global history of the potato crop, they convinced themselves that faster progress would come from the use of landraces and potato wild relatives to broaden the genetic base of their programmes (i.e. to increase σA), as well as for the introgression of specific genes. Interestingly, and controversially, Simmonds in his 1995 review (Simmonds 1995) put the emphasis on a general base-broadening (incorporation) from Andigena landraces as the way forward, as he had done in his paper of 1969 (Simmonds 1969). Indeed, he had first argued in 1962 (Simmonds 1962) that there was a need to go beyond introgression to widen the genetic bases of diverse crops, either narrow at the start of domestication or seriously narrowed by subsequent selection. A summary of the genetic principles of incorporation can be found in the review by Spoor and Simmonds (2001). But let us first look at introgression breeding.
Introgression Breeding
The aim was to cross cultivated Tuberosum with a wild species carrying a desirable resistance gene R and then to backcross the R gene into the cultivated Tuberosum, in theory eliminating all of the wild species’ genome except the R gene. In practice the backcrossing would stop with the production of a commercially acceptable clone, if not an actual cultivar. The breeder would not worry about how much of the wild species’ genome actually remained. It was assumed that few backcrosses meant that the remaining genome contained desirable genes whereas many backcrosses meant the need to break linkages between the R gene and undesirable genes (linkage drag). The expected remaining wild species’ genome could be predicted from the number of backcrosses: the wild species contribution falling by one half with each backcross, starting with 50% in the initial tetraploid hybrid and reaching 6.25% after three backcrosses and 0.78% after six backcrosses (see for example Bradshaw 2021).
The crossability of wild and cultivated species was determined by artificial pollinations and could be explained primarily but not exclusively in terms of Endosperm Balance Number (EBN). This can be regarded as the effective rather than the actual ploidy of the species (Johnston et al. 1980). Hybridizations are usually successful between species with the same EBN number. Five groups of species can be recognized based on ploidy and EBN as follows (Hawkes and Jackson 1992), where the number of species uses those recognized in the taxonomic classification of Hawkes (1990).
Potato breeders found that they could achieve their desired gene transfers from wild and primitive cultivated species by manipulation of ploidy with due regard to EBN (Ortiz 1998, 2001), with the option of somatic (protoplast) fusion to achieve difficult or impossible sexual hybridizations (Veilleux 2005). However, from time-to-time unexpected successes and failures did occur. Examples from the literature of successful introgression schemes can be found in my book (Bradshaw 2021), where it was still only necessary to consider 32 of the 219 wild species. There proved to be two main introgression routes depending on the ploidy and EBN of the wild species, namely the diploid and hexaploid/pentaploid routes.
The relatively difficult introgressions ultimately involved a common hexaploid/pentaploid route. Somatic hybridization of tetraploid Tuberosum (T) with a diploid wild (W) species, chromosome manipulation of diploid 1EBN and tetraploid 2EBN species, as well as the hexaploid species themselves, can all result in a hexaploid as starting material. This is crossed to a tetraploid Tuberosum cultivar to give a pentaploid hybrid (2n = 5x = 60) of chromosome composition WTTTT, WWTTT or WWWTT, depending on the previous chromosome manipulations. Backcrosses to tetraploid Tuberosum cultivars should, but may not, result in a loss of 12 chromosomes and a return to a stable tetraploid (2n = 4x = 48). It is assumed that the 11 wild species chromosomes not carrying the major dominant R gene of interest will be lost. If the chromosome with the R gene does not pair with a Tuberosum chromosome, then the whole of this chromosome will be selected along with the R gene. However, if this chromosome does pair with the Tuberosum chromosomes, then physical and genetic crossing-over can occur and the R gene can recombine into the Tuberosum chromosome along with a few linked genes from the wild species (linkage drag). Today molecular cytogenetics techniques, such as Genomic In Situ hybridization (GISH), Fluorescence In Situ hybridization (FISH) and species-specific molecular markers, can be used to monitor introgressions, and to select for the desired R gene but against the rest of the wild species genome (Gavrilenko 2011). However, the breeder may still in practice choose to backcross to tetraploid potato cultivars with selection for resistance until commercially acceptable clones are secured. As a consequence, the breeder may benefit from the serendipitous inclusion of other desirable genes from the wild species.
The relatively easy introgressions involved the diploid 2EBN species which are the vast majority of wild species. It is assumed that these taxonomic species have evolved by means of geographical and ecological isolation rather than by genetic incompatibility, and that their chromosomes (W) will pair normally with those of cultivated Tuberosum (T). There are two methods of introgression. The first uses colchicine to double the chromosome complement, thus producing a tetraploid 4EBN species (WWWW) which will cross with tetraploid potato cultivars (TTTT) to give tetraploid offspring (WWTT). Those selected for resistance will be RRrr or possibly Rrrr if the wild species parent was heterozygous for R. The breeder then simply backcrosses to tetraploid potato cultivars with selection for resistance until a backcross produces a commercially acceptable clone, most likely with a single copy of the R gene. Different potato cultivars are usually used over the backcross generations to avoid inbreeding.
The second method became possible with the production of haploids (also called dihaploids) of S. tuberosum, from 1958 onwards (Hougas and Peloquin 1958; Hougas et al. 1958), which are diploid 2EBN and hence cross with other diploid 2EBN species. It was developed by Peloquin and his co-workers (Hermundstad and Peloquin 1987; Jansky et al. 1990; Ortiz and Peloquin 1994) as a novel breeding strategy both to introgress specific characteristics and to broaden the genetic base of potato. The former usually involves hybrids between dihaploids and diploid wild species and the latter hybrids between dihaploids and diploid cultivated species (i.e. groups Phureja and Stenotomum), but both types of hybrid can be used for both purposes. Here we are just concerned with the introgression that is possible when the resistant hybrids (WT, Rr) produce 2n gametes in crosses with tetraploid Tuberosum cultivars (TTTT). The outcome is tetraploid offspring with approximately 25% of the wild species genes. Selection for resistance will result in either RRrr or Rrrr genotypes, depending on whether the 2n gamete was RR or Rr. We shall see below that depending on the mechanism of 2n gamete formation and the position of the locus relative to the centromere, the frequency of RR plus Rr gametes from a resistant hybrid Rr can vary between 50 and 100%. Hence at least 50% of the tetraploid offspring will be resistant. Again, the breeder then simply backcrosses to tetraploid potato cultivars with selection for resistance.
In all of the introgression schemes the outcome has been determined by chromosome pairing and the distribution of chiasmata along the chromosomes during the meioses leading to the final genotype. However, the breeder has simply backcrossed to tetraploid potato cultivars with selection for resistance to achieve a commercially acceptable clone, not to understand potato genetics in the way of a geneticist.
Production of 2n Gametes
Before moving on to base broadening, we do need to consider the production of 2n gametes from diploid species and dihaploid-species hybrids as the mechanisms involved affect their combining abilities with tetraploid clones. The different mechanisms result from genetic mutations that affect the outcomes of meiosis in microsporogenesis and megasporogenesis and can be classified genetically into first division restitution (FDR) or second division restitution (SDR), as reviewed by Peloquin et al. (1999). Hybridizations between 4x and 2x parents (4x-2x and 2x-4x crosses) give rise to almost entirely 4x progeny due to a ‘triploid block’ mechanism, whereas those between 2x parents (2x-2xcrosses) produce 2xand 4x offspring, the frequencies being cross dependent (Mendiburu and Peloquin 1977). It was Mendiburu and Peloquin (1977) who found a large difference in yield between the offspring of 4x-2x and 2x-4x crosses involving 7 diploid Tuberosum-Phureja hybrids and 7 tetraploid cultivars, assessed at two locations in Wisconsin, USA. As a group, the 14 4x-2x families averaged 4.4 lbs/hill, while the mean of all seven cultivars was 4.0 lbs/hill and the mean of the two male diploids was 2.8 lbs/hill, giving a mid-parent mean of 3.4 lbs/hill. In contrast, the 35 2x-4x families averaged 3.8 lbs/hill, while the mean of all seven cultivars was 4.0 lbs/hill and the mean of the five female diploids was 3.9 lbs/hill, giving a mid-parent mean of 4.0 lbs/hill. The two male parents had been cytologically shown to produce 2n gametes by FDR whereas the method of 2n megasporogenesis was not known at the time, but presumed to be different (i.e. SDR). Significant differences were established among the general combining abilities of the diploid parents and among the general combining abilities of the tetraploid parents, in each of the two locations and in the combined analysis. Specific combining abilities were not significant in either location, but they were detected in the analysis combined over locations. The authors concluded that progeny testing in their material was an efficient tool to evaluate the breeding value for tuber yield of both tetraploid and diploid parents in 4x-2x crosses. Although a practical breeder does not need to understand the genetical basis of the differences in combining ability, an explanation can be found in the products of FDR and SDR.
The genetical differences between 2n gametes produced by FDR and SDR are the frequencies of the heterozygote (Aa) and the two homozygotes (AA and aa contributing equally) and how they change with the distance of the locus from the centromere. Diagrams of FDR and SDR and their genetic consequences can be found in the book chapter by Tai (1994), who also reviewed the progress that had been made in developing high-quality 2n gamete-producing parents for use in the breeding of tetraploid cultivars. For any chosen scheme, the breeder either selected tetraploid and diploid parents for crossing on the basis of their phenotypes or, preferably, on their general combining abilities, which involved progeny testing the potential parents as advocated by Mendiburu and Peloquin (1977). As loci affecting quantitative traits are likely to be distributed along each chromosome, the mechanism of 2n gamete formation will influence combining ability if the proportion of heterozygous genotypes is important.
Figure 2 shows the percentage of heterozygous (Aa) gametes expected from FDR and SDR for a chromosome arm with two chiasmata distributed at random and hence an arm length of 100 cM (Bradshaw 2016). With FDR the level of heterozygosity falls from 100% at the centromere to 75% one third the way along, to 66.7% two thirds the way along, and back to 75% at the end of the chromosome arm; with an average value of near 75% for the whole arm. With SDR, the level of heterozygosity increases from 0% at the centromere to 50% one third the way along, to 66.7% two thirds the way along, and back to 50% at the end of the chromosome arm; with an average value of near 50% for the whole arm. If there is just one chiasma per chromosome arm, and hence an arm length of 50 cM, assumptions about the positions of centromeres and chiasmata for potato chromosomes leads to the often-quoted figures of average heterozygosity of 80% and 40% for FDR and SDR, respectively (Tai 1994; Peloquin et al. 1999). Hence, Fig. 2 provides an explanation for the higher general combining abilities found for yield for diploid hybrids producing 2n gametes by FDR (Mendiburu and Peloquin 1977).
The other issue faced by breeders is whether or not to subsequently select the ‘unadapted’ 2x parents for further improvement based on per se performance, or combining ability with the ‘adapted’ 4x parents, assuming that the overall aim is incorporation of novel germplasm into a 4x × 4x breeding programme rather than into a separate 4x × 2x one also aimed at producing finished cultivars. Whatever the theoretical arguments, breeders tended to opt for per se performance, as well as ability to produce 2n gametes.
Base Broadening
In the 1960s, potato breeders in Europe and North America started to use the cultivated landraces of South America to broaden the genetic base of their breeding programmes. The strategy was to use population improvement schemes to produce adapted parents for feeding into the breeding of finished cultivars. The breeders demonstrated that through simple mass selection under northern latitude, long-day summer conditions, Group Andigena will adapt and produce ‘Neotuberosum’ parents suitable for direct incorporation into European and North American potato breeding programmes (Simmonds 1969; Glendinning 1975; Rasco et al. 1980; Munoz and Plaisted 1981; Tarn and Tai 1983; Maris 1989). Likewise, Carroll (1982) and Haynes (Haynes and Lu 2005) produced populations of Group Phureja/Group Stenotomum adapted to long-day conditions in Europe and North America, respectively. The improved diploid populations were incorporated into tetraploid potato cultivars via unreduced pollen grains (4x × 2x crosses) (Carroll and De Maine 1989). Brief accounts of these breeding programmes can be found in my book on potato breeding (Bradshaw 2021). Then on its establishment in 1971, the International Potato Centre (CIP) in Lima, Peru, recognized the need to make broad-based germplasm and candidate cultivars available to National Programmes in developing countries (Mendoza 1989). Details of the population improvement schemes for quantitative resistance to late blight under high endemic disease pressure in the Andean highlands (B populations), and for virus resistance in the lowland tropics (LTVR), together with other desirable traits, can be found in the book chapter by Bonierbale et al. (2020). Furthermore, in the Central Potato Research Institute of India there was interest in Tuberosum (female) × short-day Andigena hybrids in breeding for the sub-tropical plains where the potato crop is grown under short days (Gopal et al. 2000; Kumar and Kang 2006).
All of these programmes were in essence population improvement schemes and the methods of quantitative genetics could be used to assess the genetic variation present in the populations and to predict responses to selection (e.g. Mendoza 1989). However, what was the genetic makeup of the parents that fed into the breeding of finished cultivars, and what was the impact of potato genetics on potato breeding in this context? The main features of incorporation are shown in Fig. 3.
Although the aim of the population improvement schemes was parents for use in the breeding of finished cultivars, the populations were selected for per se performance, not combining ability with adapted clones.
If crosses between clones from the improved populations and adapted clones produced clones as good as the ones from adapted-by-adapted crosses in terms of commercial worth, then they would enter the breeding programmes aimed at finished cultivars as seen in the theoretical example in Fig. 4 (based on binomial distribution) where commercial worth is assessed on a 1 to 9 scale of increasing worth. The 256 clones from the Clone × Adapted Clone cross have a mean of 5 and variance of 2, whereas those from the Adapted Clone × Adapted Clone cross have a higher mean of 6 and lower variance of 1.5. If the breeder selects clones with a commercial worth of 8 or more, 9 would come from the incorporation cross and 28 from the breeding programme cross. In other words, about ¼ would be incorporated and now considered adapted clones, with a higher variance compensating for a lower mean. Furumoto et al. (1991) confirmed for Neotuberosum that it was better to practise population improvement for yield on the unadapted population before attempting incorporation. Although yield heterosis was often seen in crosses between Clones and Adapted Clones so that their population means were higher than those between Adapted Clones and Adapted Clones, the reverse was true for overall commercial worth (e.g. Sanford and Hanneman 1982), and Neotuberosum and long-day-adapted diploid populations required further improvement in addition to yield (Bradshaw 2021).
Genetics of Base Broadening
If we consider a single locus, we can think of the incorporation as introducing a desirable allele A (say for higher yield) into a breeding programme that had been all allele a. What happens over subsequent rounds of crosses with Adapted Clones and Cultivars? The breeder simply selects higher yielding clones and makes crosses between them. But what are the consequences? Let us consider two examples where the genotypes have the two sets of values shown in Table 6.
In the first example, the addition of each copy of allele A increases the yield (simple additive model). Selection over generations results in a linear increase in the mean of each generation, a steady increase in the frequency of A in each generation of clones, and eventually fixation of A when all clones have genotype AAAA and the genetic variation is exhausted, having been at a maximum when the frequency of A was 0.5 (Fig. 5).
The effect of increase in frequency p of allele A on the mean and additive genetic variance of a locus where a = 1 and d = v = w = 0 (from Table 3)
In the second example, genotype AAAA is superior to aaaa, but AAAa is the best genotype (form of overdominance). The consequences of selection over generations are more complicated, as can be seen in Fig. 6. There is an approximately linear increase in the mean of each generation until the frequency of A is about 0.5, and an increase in the additive genetic variance to a maximum which occurs between a frequency of 0.3 and 0.4. Then the population mean approaches a maximum value when the frequency of A is very close to 0.8, at which frequency there is no additive genetic variance and no more progress can be made in subsequent generations. An equilibrium has been reached. There is however non-additive genetic variation present (VD = 1.007, VT = 0.168 and VQ = 0.010), as can be seen in Fig. 6. All five genotypes are present, but the two most frequent genotypes are AAAA and AAAa (Table 7), and the breeder will select AAAa as the best and clonally multiply it as a new cultivar. It can also be seen in Table 7 that Aaaa was the most frequent genotype when the additive genetic variance was at a maximum.
The effect of increase in frequency p of allele A on the mean and components of genetic variance [VA (additive effect), VD (digenic), VT (trigenic) and VQ (quadrigenic interactions)] of a locus where a = 1, d = ½, v = 1 and w = ½ (from Table 3)
By exploiting the additive genetic variance, the breeder has over sexual generations increased the mean of the available clones by 4.762 units (from -2.000 to 2.762), and then by selecting the best clone in the equilibrium population, achieved a further increase of 1.238 to 4.000 (genotypic value of AAAa). Figure 7 and Table 7 show that between an allele frequency of 0.6 and 0.8, the mean plus one standard deviation is between 3.81 and 3.93, and that the best genotype (AAAa) is the most frequent. In practice, with many loci segregating for yield, the best genotype may not exist in a moderate sized population, and the mean plus two standard deviations may be a realistic target.
The effect of increase in frequency p of allele A on the mean and the mean + (VG)½ where VG is the total genotypic variance of a locus where a = 1, d = ½, v = 1 and w = ½ (from Table 3)
We have just considered two examples, the second of which was the more realistic one for a trait like yield. A more extensive range of models can be found in the book by Gallais (2003), but the following pattern still holds. When the frequency of A is low, most of the genetic variation is additive genetic; but as the frequency of A increases, the non-additive components start to contribute varying amounts to the total variation. Furthermore, this means that the relative importance of GCA and SCA depends on the allele frequency and hence is unique to the breeding material under consideration. More than two alleles at a locus introduces the possibility of many more interactions, but if there are relatively large differences between the homozygotes, the additive genetic variance will still be the major component of genetic variation at low allele frequencies. The importance of trigenic and quadrigenic interactions between alleles at higher frequencies has been the subject of much debate, as has the superiority or otherwise of genotypes carrying four different alleles (A1A2A3A4), and hence the genetic basis of heterosis in tetraploid potatoes.
Maximum Heterozygosity
Mendoza and Haynes (1974) put forward a model of overdominant gene action to explain heterosis for yield in autotetraploids in which loci with multiple alleles and a maximum heterotic value for quadrigenic genotypic structures (A1A2A3A4) were postulated. Analysis of various experimental results showing the importance of specific combining ability, and the different results from crosses between diploids (offspring lower yields than parents) and crosses between chromosome doubled diploids (offspring higher yields than parents), suggested a close positive correlation between heterozygosity and yield. They concluded that increasing the genetic diversity of the parental clones in potato breeding should result in a substantial genetic advance in yield. However, they also concluded that alien sources of germplasm should first undergo selection for adaptation to achieve a proper balance between heterozygosity and adaptation, mainly to photoperiod, and hence to maximize the heterosis for yield. Nearly 50 years later the issue of the importance of overdominance and maximum heterozygosity has not been resolved (Muthoni et al. 2019), even with the advent of molecular markers for Quantitative Trait Locus (QTL) analysis, because of the large number of possible genotypes at each locus. For a single locus with four different alleles, there are 35 different genotypes in a large random mating population in equilibrium and with equal allele frequencies, 1 in 64 genotypes are mono-allelic, 12 are di-allelic with one and three copies of the two alleles, 9 are di-allelic with two copies of each allele, 36 are tri-allelic and 6 are tetra-allelic. In contrast, with two diploid inbred lines, there are two alleles at each locus, and for every QTL (Q) linked to a molecular marker, the degree of dominance (dQ/aQ) can be estimated from a North Carolina Design III experiment (Cockerham and Zeng 1996). I concluded in my book (Bradshaw 2021) from a review of the literature and key papers that the superiority of tetraploid potatoes comes primarily from their genetic makeup, rather than polyploidy per se (chromosome doubled diploids do not outyield their diploid parents; Maris 1990; diploid and tetraploid plants have similar gene expression patterns; Stupar et al. 2007), and is not simply a matter of maximum heterozygosity (4x Tuberosum × 2x Tuberosum-Phureja hybrids are as good as 4x Tuberosum-Andigena × 2x Tuberosum-Phureja hybrids for yield; Sanford and Hanneman 1982; importance of specific combinations of individual molecular-marker fragments; Bonierbale et al. 1993). Nevertheless, it is worth remembering that Uijtewaal et al. (1987) found an increase in vigour from x to homozygous 2x that was much larger than the increase from 2x to homozygous 4x but for tuber weight per plant the increase from 2x to 4x was larger than from x to 2x. However, breeders do not actually need to know the genetic basis of heterosis in a clonally propagated crop. Having incorporated increased allelic diversity into their breeding material, they simple select and inter-cross the best clones each generation until the additive genetic variance runs out. Then they select the best clone from that generation and clonally multiply it as a new cultivar. It will certainly be heterozygous and exploit any heterosis available, but as for maximum heterozygosity, the breeder will not know and will not care.
Use of Molecular Markers 1989 to 2021
Potato Genetics
During the last 30 years, potato genetics has been able to have a greater impact on potato breeding through molecular markers for both qualitative and quantitative traits. Some of the key steps in progress in potato genetics were as follows. The first molecular-marker maps became available in 1988 (Bonierbale et al. 1988) and 1989 (Gebhardt et al. 1989). Additional mapping work by Gebhardt et al. (1991) and Tanksley et al. (1992) allowed the linkage maps of potato and tomato to be aligned and the numbering of the 12 chromosomes (linkage groups) to be agreed. Twenty years later, Mann et al. (2011) reviewed the progress that had been made with linkage maps and summarized 16 significant maps for potato and its wild relatives in terms of mapping population type (F1 or BC1), parents, number of progeny (49 to 246), marker type and number, and map length (403 to 1170 cM). A cross between two diploid heterozygous S. tuberosum clones (SH83-92–488 and RH89-039–16) with 130 usable F1 offspring clones, was used to produce an ultra-high density (UHD) genetic map of 10,365 AFLP markers (van Os et al. 2006). The UHD map accelerated gene isolation by map-based cloning and provided a genome wide physical map through the anchoring of BAC (bacterial artificial chromosomes) contigs. Although RH89-039–16 (RH) was used in the sequencing of the potato genome, most of the sequence came from whole genome shotgun sequencing of a doubled monoploid of Group Phureja DM1-3 516 R44 (DM). On 14 July 2011, in Nature, the Dutch-led global consortium published 86 per cent of the sequence of the 844 Mb-genome of the potato, with a prediction of 39,031 protein-coding genes (Potato Genome Sequencing Consortium 2011). Reference chromosome-scale pseudomolecules were then constructed for the potato, integrating the potato reference genome with genetic and physical maps (Sharma et al. 2013). Clone DM was subsequently compared with 12 ‘monoploid’ genotypes by Hardigan et al. (2016) to define a core potato gene set (pan-genome) of 30,401 genes (77.4%) required for potato growth and development, the rest being dispensable genes that can be missing in individual potato genotypes.
Major genes underlying qualitative traits can be and have been mapped directly onto the dense molecular-marker maps as individuals can be classified into distinct categories for both trait and marker. Most of the mapping has been done at the diploid level, but the results can then be used at the tetraploid level as the gene order is the same. Quantitative trait loci (QTLs) can be mapped indirectly through associations between trait scores and molecular markers. Again, most of the mapping has been done at the diploid level, although it can be done at the tetraploid level, for a biparental F1 population (Hackett et al. 2017), and through Genome Wide Association Studies (GWAS) for a diverse set of genotypes in a collection of interest to the breeder (Rosyara et al. 2016). Today single nucleotide polymorphisms (SNPs) are the marker of choice for mapping. SNPs discovery was made possible by the use of next-generation sequencing (Hamilton et al. 2011; Uitdewilligen et al. 2013) and the development of SNP arrays such as the Infinium 8300 (8303) array used by Hackett et al. (2013) and the 20 K SolSTW array used by Vos et al. (2015, 2017). As SNP panels for arrays are chosen to target single copy regions of the genome, the majority of SNPs can be assigned a unique genomic location in the published potato genome sequence, and this ‘map to genome’ link used in the identification of candidate genes at trait loci. Today a major goal of potato geneticists is the confirmation of candidate genes as causal genes, with successes being achieved with genes for disease resistance and key genes in biosynthetic pathways such as those for carotenoids and anthocyanins, including purple (P) and red (R) skin colour. The P locus on chromosome 11 codes for flavonoid 3’, 5’–hydroxylase (Jung et al. 2005); the R locus (drf) on chromosome 2 codes for dihydroflavonol 4-reductase (Zhang et al. 2009); and the I locus on chromosome 10 encodes an R2R3 MYB transcription factor that regulates expression of multiple anthocyanin structural genes in the tuber skin (Jung et al. 2009) and was originally referred to as D for developer by Salaman (1910). But how does this help the potato breeder?
Major Genes in Potato Breeding
Let us return to a typical breeding programme aimed at producing new cultivars, and let us look at the offspring from one bi-parental cross. Furthermore, let us look at a short section of one of the 12 sets of four homologous chromosomes (Fig. 8). Let us start with the resistance gene R which is present in the resistant parent (1). We would like to know that there are two copies (duplex) of the gene in the parent without having to do any progeny testing. We could then anticipate that one sixth of the offspring would also have two copies of the resistance gene. We would like to identify these offspring and use the best of them in terms of overall commercial worth as parents in the next round of crossing and selecting, whereas the best clone, with one or two copies of the resistance gene, could be selected as a new cultivar. If we had a suitable diagnostic marker for the resistance gene, we would not need to do any disease testing. We could identify the desired plants as seedlings in a glasshouse, or better still, as tiny seedlings before they were planted in pots and grown in the glasshouse. The frequency of the desired allele could be rapidly increased over cycles of crossing and selection on an annual basis. The desired allele could be its own molecular marker, or be extremely tightly linked to a diagnostic molecular marker, or lie between closely linked flanking markers.
The marker technology is now available; for example, with SNPs, the number of alleles (dosage) can be inferred from allele signal intensity ratios (Voorrips et al. 2011; Hackett et al. 2013; Uitdewilligen et al. 2013), and called using software such as the R package fitTetra (Voorrips et al. 2011). So today, breeders can practise marker-assisted selection (MAS) for a number of major genes of commercial importance. The most widely used genes are the Ryadg, Rychc and Rysto genes for extreme resistance to PVY and the Rx1 gene for extreme resistance to PVX, the R1 and R2 genes for resistance to Phytophthora infestans, and the Gro1 and the H1 genes for resistance to the nematode Globodera rostochiensis (Ortega and Lopez-Vizcon 2012; Mori et al. 2015; Meade et al. 2019, 2020). However, once the number of segregating alleles in any given cross increases to twelve and beyond, the frequency of the desired combination of alleles becomes a limiting factor in the breeding programme (Bradshaw 2017, 2021). With 12 unlinked simplex alleles (e.g. one per chromosome) the frequency is 1 in 4096, whereas by 24 alleles it is 1 in 16,777,216. Hence, one rapidly comes to appreciate the need to produce multiplex parents and more generally to increase allele frequencies by recurrent selection on a short annual cycle time as part of an overall breeding strategy. This means doing the MAS on the seedling generation rather than the second field generation, as is the current practice, which was recommended by Slater et al. (2013) as cost effective at the time. MAS is also an attractive proposition for recessive alleles such as zeaxanthin epoxidase (zep) allele 1, which when homozygous and combined with dominant β-carotene hydroxylase 2 (Chr2) allele 3, produces orange-fleshed tubers with large amounts of zeaxanthin (Wolters et al. 2010); an otherwise challenging task for potato breeders.
Finally, De Jong et al. (2003) have provided a nice example of how a fluorogenic 5’ nuclease assay for marker dosage allowed them to rapidly determine the dosage of the dominant red allele at the R locus in many potato cultivars, something that would have been far too onerous to do by monitoring segregation ratios. Such a technique is of value to practical potato breeders for assessing potential parents for use in their hybridization programmes.
Quantitative Traits in Potato Breeding
Let us return to Fig. 8. The two parents together could have eight different alleles at each of the loci shown. In practice the number is likely to be less and for the markers will be known. Indeed, with SNPs there may just be two alleles to consider. The challenge in QTL analysis is to find the chromosomal locations of the QTLs contributing to the quantitative variation through their linkage to the molecular markers and to work out the genotypes at the QTL locus. In Fig. 8, we have a simple and ideal situation where the flanking markers A and B and the marker M are diagnostic of the QTL allele Q, and in the offspring, we can identify and compare the genotypes QQqq, Qqqq, and qqqq. In practice we need a lot of computing power to reach this conclusion. Computer software is now available to do this at the tetraploid level for each linkage group separately in a full sib family, either assuming no double reduction (TetraploidSNPMap, Hackett et al. 2017) or taking account of quadrivalents and double reduction (Chen et al. 2020). It is also available for Genome Wide Association Studies (GWAS) on a diverse set of genotypes in a collection of interest to the breeder, where QTLs for more traits and better mapping resolution were anticipated (R package GWASpoly, Rosyara et al. 2016). The unwanted effects of population structure and kinship on the marker-trait associations can be removed from the GWAS analysis through use of a general mixed model (Rosyara et al. 2016).
As discussed in my book (Bradshaw 2021), there is one striking feature of all of the published marker work, namely the contrast between the increases in the number of markers and the increases in population sizes over the last 30 years. The first map had 135 markers whereas today maps can have thousands, or even millions, of SNPs markers. In contrast, mapping populations have only increased from 49 to 272 genotypes in bi-parental populations and from 95 to 537 genotypes in panels for genome wide association studies (GWAS). In other words, there is a lack of statistical power for detecting alleles of small effect. Population size is the main limiting factor in full sib families (Hackett et al. 2014), but dense marker coverage on all four homologues of a chromosome is required for both QTL detection power and precision (ability to locate true position) (Bourke et al. (2019). The same is true for GWAS (Rosyara et al. 2016). Hence with population sizes of 200 to 400, and SNP array sizes of 8000 to 20,000, only QTL alleles of large effect have been detected, accounting for about 10% to 50% of the trait variation (Bradshaw 2021). Nevertheless, provided diagnostic markers are available for these QTL alleles of large effect, breeders can handle them the same way as markers for major genes, but may now have even more alleles to consider. As a consequence, the frequencies of the desirable combination of alleles for a new cultivar will be even lower. Therefore, breeders must think in terms of increasing allele frequencies through population improvement. Geneticists can if they wish seek causal genes for the QTLs and a better understanding of the genetic basis of the trait(s). But what are breeders going to do about all of the undetected alleles of small effect?
Many Alleles of Small Effect
Let us look at the theoretical example in Fig. 9 where we have a population of 256 clones. The total variation in the trait scores was generated by segregation at 12 unlinked loci (one on each chromosome), each of which explains 8.33% of the variation (Qqqq × qqqq) (there is no environmental variation). One of the QTL can be detected because it contains a molecular marker M which therefore also explains 8.33% of the variation (Mmmm × mmmm). The means of the two groups with and without the marker are 6.124 and 5.307 (difference 0.8165 ± 0.169), respectively, the between group variance is 0.167 and the within group variance is 1.833 (total 2.0). The difference between the two groups is one twelfth of the difference between the highest and lowest clones (difference of 9.798), which are the two extreme genotypes with all of the alleles of increasing and decreasing effects, respectively. However, they are unlikely to occur in a population of 256 clones as their expected numbers are each 0.0625 (i.e. much less than 1) whereas the numbers with 11 increasing and 11 decreasing alleles are each 0.75 (almost 1), and their trait scores are 2.89 standard deviations from the population mean. The difference between the two groups is statistically significant (t = 4.82, P < 0.001, 254 df; Bulmer 1967).
If we keep the population size and variance the same, at 256 and 2, respectively, and keep increasing the number of loci segregating, our molecular marker explains less and less of the variance and there comes a point where its effect is no longer statistically significant. For example, with 128 loci segregating, each with the same effect, our molecular marker now explains just 0.78% of the variance. The between group and within group variances are 0.015625 and 1.984375, respectively, and the difference between the means of the two groups is 0.25 ± 0.176, which is not statistically significant (t = 1.42, P > 0.10, 254 df; Bulmer 1967). The genetic difference is real but too small to be statistically significant in a population of size 256. In other words, we lack the power to detect the difference.
Now let us consider a real situation where we have a very large number of molecular markers but don’t know how many QTLs are segregating in our population. There will be molecular markers in causal genes (alleles) of sufficiently large effect for the marker differences to be statistically significant, others in causal genes of smaller effect so that the marker differences are not statistically significant, and yet others that are not in causal genes but have associations with them (various degrees of linkage) which may result in statistically significant differences between the marker classes. Where differences in marker classes result from causal genes, they are expected to hold in different populations whereas looser or chance associations may be population specific and of little value to the breeder. So how does the potato breeder make use of the molecular markers? The answer that has been provided by geneticists is to use them for genomic selection in which robust prediction equations are used to estimate breeding values (genomic estimated breeding values) (Slater et al. 2016; Endelman et al. 2018), as first proposed more generally by Meuwissen et al. (2001).
Genomic Selection
There are three main stages in the development and use of genomic selection which are explained in more detail in my book (Bradshaw 2021). First the population of clones of interest to the breeder, or a subset of the population (reference or training population), is both phenotyped as accurately as possible and genotyped with molecular markers to see how much of the phenotypic variation can be explained by the markers. The phenotypes will be economically important quantitative traits such as yield. The traits may be considered individually or combined into an index of overall merit for selection purposes. Sufficient molecular markers need to be used to adequately cover the whole genome for the purpose of detecting tight associations with all of the quantitative trait loci affecting the traits. This depends on the extent of linkage disequilibrium between pairs of markers at different distances apart (Slater et al. 2016; Vos et al. 2017; Sharma et al. 2018). Single nucleotide polymorphism (SNP) markers with two alleles (M or m) are commonly used with 8000 to 20,000 SNPs considered adequate.
In the second stage, the data are used to estimate the breeding values of the individuals. In order to obtain robust prediction equations, cross-validation is required to choose the best method of estimating the breeding values. Hence, the training population is divided into two subgroups, one for generating the equation to predict the breeding values (estimation set, ES), the other to validate the predictions and assess their accuracy (test set, TS), with five-fold cross-validation (TS = 20%) commonly used. This ensures that we avoid chance associations in the estimation set that do not occur in the test set (i.e. we do not over-fit the data). As a result, the best prediction equation is chosen for use. In theory we do a standard multiple regression analysis in which the phenotypic values are regressed on to all of the marker genotypes (coded for 4, 3, 2, 1 or 0 copies of allele M) at all of the marker loci (Meuwissen et al. 2001), as done earlier for a single locus, quantitative genetics model (Tables 3 and 4). The markers do not individually have to be statistically significant nor do they have to be in the causal genes; collectively they simply need to make good predictions. In practice, the analysis needs to deal with the problem of the number of markers being considerably larger than the number of genotypes under consideration, either through some type of variable selection or shrinkage estimation procedure, details of which can be found in the review by de los Campos et al. (2013).
Finally, in the third stage, the rest of the individuals in the population, or those in a newly derived one (breeding population), are genotyped for the molecular markers and the best prediction equation used to estimate their breeding values. Individuals are then selected as parents of the next generation on the basis of their estimated breeding values rather than their phenotypes. Traits may be considered separately or combined into an index.
The simple example in Table 8 may be of help to the reader. Table 8 shows the results for a locus A with genotypic values 2, 4, 2, 0 and -2 for genotypes with 4, 3, 2, 1 and 0 alleles of increasing effect (a = 1, d = ½, v = 1 and w = ½), when p = 0.5 and the five genotypes are in the exact ratios of 1:4:6:4:1. There is no environmental variation, αt = a + ½v = 1½, VA = 2.25, VG = 2.9375 and narrow sense heritability hn2 = VA/VG = 0.766. In extending the results to three identical loci, A, B and C, all combinations of genotypes in the correct frequencies need to be considered, making a population of 4096 genotypes (clones).
where y is the observed yield, say, and ŷ is the estimated yield. The b’s are the regression coefficients for the predictors (X’s) which take the values 0.5, 0.25, 0, -0.25 and -0.5 for the frequencies of the A, B and C alleles in each genotype minus the mean frequencies which are all 0.5. The e’s are the residual deviations. The b’s are estimated to minimize ∑(y—ŷ)2 (least squares estimate). In matrix algebra we have:
All the b’s have a value of 6 which is 4αt as expected.
Hence genotype AAAABBBbCCcc has a genotypic value of 2.75 (0.25 + 2.25 + 0.25) and a breeding value of 4.5 (3 + 1.5 + 0.0) (Table 8). The matrices are simple because all combinations of genotypes are considered in the correct proportions for an equilibrium population.
Research is still being done on GS in potatoes. Hence, the advice from geneticists to breeders may change in terms of using either next-generation sequencing or SNP arrays, which SNP array to use, the size and makeup of the training population required to achieve adequate genomic prediction accuracy, and the best method for determining the GS equation (Slater et al. 2016; Habyarimana et al. 2017; Sverrisdóttir et al. 2017; Endelman et al. 2018). Interestingly, Sverrisdóttir et al. (2017) found that using GWAS selected (significant) SNPs did not improve prediction accuracy when predicting the performance of individuals in the test panel, and has the disadvantage of requiring a separate marker set for each trait. They also concluded that the training population should comprise potential parents (clones and cultivars) that are relevant to the breeding programme. Training populations will probably be between 500 and 5000 in size. However, practical breeders will mainly want a set of markers and computer software to produce genomic estimated breeding values that result in better responses to selection than can be achieved through phenotypic selection or progeny testing.
The response to genomic selection (GS) based on estimated breeding values from markers (M) depends on the correlation (rMA) between these estimated values and the true values (A), termed the accuracy of genomic selection. The theory of the accuracy of genomic selection has developed from pioneering papers such as those of Daetwyler et al. (2008, 2010) and Goddard (2009). The response to GS can also be obtained by considering the response to genomic selection as a correlated response to selection based on markers (Falconer and Mackay 1996).
where i is the intensity of selection and σA is the square root of the additive genetic variance.
We cannot determine rMA (prediction accuracy) directly because we do not know the true breeding values. However, we can determine the correlation (rMP) between the estimated breeding values and the phenotypic values (prediction ability) in the subgroup of the training population used for cross-validation. Then, we can use the following simple relationship, the derivation of which can be found in the theoretical paper of Rabier et al. (2016).
where hn is the square root of the narrow-sense heritability.
The practical breeder wants R = irMAσA/T (where T is the generation cycle time in years) to be greater than R = irAPσA/T (where rAP is the correlation between the true breeding values and the phenotypic values). Prospects are good, and will improve as the cost of genome-wide assays reduces, because GS can be done on the seedling generation and hence the generation cycle time could be as low as one year, whereas phenotypic selection requires assessment of clones in field plots and preferably in replicated trials. Indeed, it may be possible to combine genomic selection (GS) and marker-assisted selection (MAS) of major genes and QTL alleles of large effect in a single genotyping platform, as suggested by Byrne et al. (2020). It may also be possible to increase the intensity of selection, but the more traits being considered, the lower the intensity of selection for each trait, and this will continue be a limiting factor for each trait. Nevertheless, so long as rMA is similar to rAP (hopefully at least 0.5), progress through genomic selection should be much faster than with phenotypic selection, as shown in theory by Slater et al. (2016), and hence of substantial benefit to practical potato breeders. And that just leaves σA, the square root of the additive genetic variance, and the final overall message of this paper: progress in potato breeding over generations for economically important quantitative traits depends on the amount of additive genetic variation.
References
Allard RW (1960) Principles of Plant Breeding. Wiley International, New York, p 485
Bateson W, Mendel G (1902) Mendel’s principles of heredity. Digitally printed version 2009, Cambridge University Press, Cambridge, p 212
Black W (1952) Inheritance of resistance to blight (Phytophthora infestans) in potatoes: Interrelations of genes and strains. Proceedings of the Royal Society of Edinburgh, Section B 64:312–352
Black W, Mastenbroek C, Mills WR, Peterson LC (1953) A proposal for an international nomenclature of races of Phytophthora infestans and of genes controlling immunity in Solanum demissum derivatives. Euphytica 2:173–179
Bonierbale MW, Plaisted RL, Tanksley SD (1988) RFLP maps based on a common set of clones reveal modes of chromosomal evolution in potato and tomato. Genetics 120(4):1095–1103
Bonierbale MW, Plaisted RL, Tanksley SD (1993) A test of the maximum herterozygosity hypothesis using molecular markers in tetraploid potatoes. Theor Appl Genet 86:481–491
Bonierbale MW, Amoros WR, Salas E, de Jong W (2020) Potato breeding. In: Campos H, Ortiz O (eds) The potato crop: its agricultural, nutritional and social contribution to humankind. Springer, ebook, pp 163–218
Bourke PM, Voorrips RE, Visser RGF, Maliepaard C (2015) The double-reduction landscape in tetraploid potato as revealed by a high-density linkage map. Genetics 201:853–863. https://doi.org/10.1534/genetics.115.181008
Bourke PM, Hackett CA, Voorrips RE, Visser RGF, Maliepaard C (2019) Quantifying the power and precision of QTL analysis in autopolyploids under bivalent and multivalent genetic models. G3: Genes|Genomes|Genetics 9:2107–2122. https://doi.org/10.1534/g3.119.400269
Bradshaw JE (1994) Quantitative genetics theory for tetrasomic inheritance. In: Bradshaw JE, Mackay GR (eds) Potato Genetics. CAB International, Wallingford, pp 71–99
Bradshaw JE (2009) Potato breeding at the Scottish Plant Breeding Station and the Scottish Crop Research Institute: 1920–2008. Potato Res 52:141–172
Bradshaw JE (2016) Plant breeding: past, present and future. Springer, Switzerland, p 693
Bradshaw JE (2017) Review and analysis of limitations in ways to improve conventional potato breeding. Potato Res 60:171–193. https://doi.org/10.1007/s11540-017-9346-z
Bradshaw JE (2021) Potato breeding: theory and practice. Springer, Switzerland, p 563
Bradshaw JE, Mackay GR (1994) Breeding strategies for clonally propagated potatoes. In: Bradshaw JE, Mackay GR (eds) Potato genetics. CAB International, Wallingford, pp 467–497
Bregger T (1918) Linkage in maize: the C aleurone factor and waxy endosperm. Am Nat 52:57–61
Brown J, Caligari PDS, Dale MFB, Swan GEL, Mackay GR (1988) The use of cross prediction methods in a practical potato breeding programme. Theor Appl Genet 76:33–38
Bulmer MG (1967) Principles of statistics, 2nd edn. Oliver & Boyd, Edinburgh, p 252
Byrne S, Meade F, Mesiti F, Griffin D, Kennedy C, Milbourne D (2020) Genome-wide association and genomic prediction for fry color in potato. Agronomy 10:90. https://doi.org/10.3390/agronomy10010090
Cadman CH (1942) Autotetraploid inheritance in the potato: some new evidence. J Genet 44:33–52
Carroll CP (1982) A mass-selection method for the acclimatization and improvement of edible diploid potatoes in the United Kingdom. J Agric Sci Camb 99:631–640
Carroll CP, De Maine MJ (1989) The agronomic value of tetraploid F1 hybrids between potatoes of group Tuberosum and group Phureja/Stenotomum. Potato Res 32:447–456
Chen J, Leach L, Yang J, Zhang F, Tao Q, Dang Z, Chen Y, Luo Z (2020) A tetrasomic inheritance model and likelihood-based method for mapping quantitative trait loci in autotetraploid species. N Phytol. https://doi.org/10.1111/nph.16413
Choudhary A, Wright L, Ponce O, Chen J, Prashar A, Sanchez-Moran E, Luo Z, Compton L (2020) Varietal variation and chromosome behaviour during meiosis in Solanum tuberosum. Heredity 125:212–226. https://doi.org/10.1038/s41437-020-0328-6
Cockerham CC, Zeng Z-B (1996) Design III with marker loci. Genetics 143:1437–1456
Comstock RE, Robinson HF (1948) The components of genetic variance in populations of biparental progenies and their use in estimating the average degree of dominance. Biometrics 4:254–266
Comstock RE, Robinson HF (1952) Estimation of average dominance of genes. In: Gowen JW (ed) Heterosis. Iowa State College Press, Ames, Iowa, pp 494–516
Creighton HB, McClintock B (1931) A correlation of cytological and genetic crossing-over in Zea mays. Proc Natl Acad Sci 17:492–497
Crow JF, Kimura M (1970) An introduction to population genetics theory. Harper and Row, New York, p 591
Daetwyler HD, Villanueva B, Woolliams JA (2008) Accuracy of predicting the genetic risk of disease using a genome-wide approach. PLoS One 3(10):e3395
Daetwyler HD, Pong-Wong R, Villanueva B, Woolliams JA (2010) The impact of genetic architecture on genome-wide evaluation methods. Genetics 185(3):1021–1031
Darwin C (1876) The effects of cross and self fertilisation in the vegetable kingdom. Digitally printed 2009, Cambridge University Press, Cambridge, p 482
De Jong WS, De Jong DM, Bodis M (2003) A fluorogenic 5′ nuclease (TaqMan) assay to assess dosage of a marker tightly linked to red skin color in autotetraploid potato. Theor Appl Genet 107:1384–1390. https://doi.org/10.1007/s00122-003-1420-z
de los Campos G, Hickey JM, Pong-Wong R, Daetwyler HD, Calus MPL (2013) Whole-genome regression and prediction methods applied to plant and animal breeding. Genetics 193:327–345
East EM (1908) Inbreeding in corn. pp. 419–428. In Connecticut Agricultural Experiments Station Report 1907
Endelman JB, Schmitz Carley CA, Bethke PC, Coombs JJ, Clough ME, da Silva WL, De Jong WS, Douches DS, Frederick CM, Haynes KG, Holm DG, Miller JC, Muñoz PR, Navarro FM, Novy RG, Palta JP, Porter GA, Rak KT, Sathuvalli VR, Thompson AL, Craig Yencho G (2018) Genetic variance partitioning and genome-wide prediction with allele dosage information in autotetraploid potato. Genetics 209(1):77–87. https://doi.org/10.1534/genetics.118.300685
Falconer DS, Mackay TFC (1996) Introduction to quantitative genetics, 4th edn. Longman, Harlow, p 464
Finney DJ (1958) Plant selection for yield improvement. Euphytica 7:83–106
Fisher RA (1935) The design of experiments. Oliver and Boyd, Edinburgh, p 252
Fisher RA, Mackenzie WA (1923) Studies in crop variation. II. The manurial response of different potato varieties. J Agric Sci 13:311–320
Fisher RA, Mather K (1943) The inheritance of style length in Lythrum salicaria. Ann Eugen 12:1–23
Flor HH (1942) Inheritance of pathogenicity in Melampsora lini. Phytopathology 32:653–659
Fukuda Y (1927) Cytological studies on the development of pollen grains in different races of S. tuberosum with special reference to sterility. Botanical Magazine (Tokyo) 61:459–476
Furumoto O, Plaisted RL, Ewing EE (1991) Comparison of two techniques for introgression of unadapted andigena germplasm into temperate germplasm. Am Potato J 68:391–404
Gallais A (2003) Quantitative genetics and breeding methods in autopolyploid plants. INRA, Paris, p 515
Gavrilenko T (2011) Application of molecular cytogenetics in fundamental and applied research of potato. In: Bradeen JM, Kole C (eds) Genetics, genomics and breeding of potato. Science Publishers, Enfield, pp 184–206
Gebhardt C, Ritter E, Debener T, Schachtschabel U, Walkemeier B, Uhrig H, Salamini F (1989) RFLP analysis and linkage mapping in Solanum tuberosum. Theor Appl Genet 78(1):65–75
Gebhardt C, Ritter E, Barone A, Debener T, Walkemeier B, Schachtschabel U, Kaufmann H, Thompson RD, Bonierbale MW, Ganal MW, Tanksley SD, Salamini F (1991) RFLP maps of potato and their alignment with the homoeologous tomato genome. Theor Appl Genet 83(1):49–57
Glendinning DR (1975) Neo-Tuberosum: new potato breeding material. 2. A comparison of Neo-Tuberosum with unselected Andigena and with Tuberosum. Potato Res 18:343–350
Goddard M (2009) Genomic selection: prediction of accuracy and maximisation of long term response. Genetica 136:245–257. https://doi.org/10.1007/s10709-008-9308-0
Gopal J, Gaur PC, Rana MS (1992) Early generation selection for agronomic characters in a potato breeding programme. Theor Appl Genet 84:709–713
Gopal J, Chahal GS, Minocha JL (2000) Progeny mean, heterosis and heterobeltiosis in Solanum tuberosum × tuberosum and S. tuberosum × andigena families under a short day sub-tropic environment. Potato Res 43:61–70
Gottschalk W (1958) Über die Anwendung cytologischer Methoden für die Bearbeitung phylogenetischer Fragestellungen bei den Solanaceen. Eine Erwiderung. Zeitschr für Pftanzenzücht 39:47–70
Griffing B (1956) Concept of general and specific combining ability in relation to diallel crossing systems. Aust J Biol Sci 9:463–493
Habyarimana E, Parisi B, Mandolino G (2017) Genomic prediction for yields, processing and nutritional quality traits in cultivated potato (Solanum tuberosum L.). Plant Breed 136:245–252. https://doi.org/10.1111/pbr.12461
Hackett CA, McLean K, Bryan GJ (2013) Linkage analysis and QTL mapping using SNP dosage data in a tetraploid potato mapping population. PLoS ONE 8(5):e63939. https://doi.org/10.1371/journal.pone.0063939
Hackett CA, Bradshaw JE, Bryan GJ (2014) QTL mapping in autotetraploids using SNP dosage information. Theor Appl Genet 127:1885–1904. https://doi.org/10.1007/s00122-014-2347-2
Hackett CA, Boskamp B, Vogogias A, Preedy K, Milne I (2017) TetraploidSNPMap: Software for linkage analysis and QTL mapping in autotetraploid populations using SNP dosage data. J Heredity 108:438–442. https://doi.org/10.1093/jhered/esx022
Haldane JBS (1930) Theoretical genetics of autotetraploids. J Genet 22:359–372
Hamilton JP, Hansey CN, Whitty BR, Buell CR (2011) Single nucleotide polymorphism discovery in elite North American potato germplasm. BMC Genomics 12(1):302. https://doi.org/10.1186/1471-2164-12-302
Hardigan MA, Crisovan E, Hamilton JP, Kim J, Laimbeer P, Leisner CP, Manrique-Carpintero NC, Newton L, Pham GM, Vaillancourt B, Yang X, Zeng Z, Douches DS, Jiang J, Veilleux RE, Buell CR (2016) Genome reduction uncovers a large dispensable genome and adaptive role for copy number variation in asexually propagated Solanum tuberosum. Plant Cell 28:388–405. https://doi.org/10.1105/tpc.15.00538
Hawkes JG (1990) The potato: evolution, biodiversity & genetic resources. Belhaven Press, London, p 259
Hawkes JG, Jackson MT (1992) Taxonomic and evolutionary implications of the endosperm balance number hypothesis in potatoes. Theor Appl Genet 84:180–185
Haynes KG, Lu W (2005) Improvement at the diploid species level. In: Razdan MK, Mattoo AK (eds) Genetic improvement of Solanaceous crops, volume I: potato. Science Publishers Inc, Enfield, pp 101–114
Hermundstad SA, Peloquin SJ (1987) Breeding at the 2x level and sexual polyploidization. In: Jellis GJ, Richardson DE (eds) The production of new potato varieties. Cambridge University Press, Cambridge, pp 197–210
Hougas RW, Peloquin SJ (1958) The potential of potato haploids in breeding and genetic research. Am Potato J 35:701–707
Hougas RW, Peloquin SJ, Ross RW (1958) Haploids of the common potato. J Hered 49:103–107
Jansky SH, Yerk GL, Peloquin SJ (1990) The use of potato haploids to put 2x wild species germplasm into a usable form. Plant Breed 104:290–294
Johnston SA, der Nijs TPM, Peloquin SJ, Hanneman RE Jr (1980) The significance of genic balance to endosperm development in interspecific crosses. Theor Appl Genet 57:5–9
Jones DF (1918) The effects of inbreeding and crossbreeding upon development. Connecticut Agric Exp Stn Bull 207:5–100
Jung CS, Griffiths HM, De Jong DM, Cheng S, Bodis M, De Jong WS (2005) The potato P locus codes for flavonoid 3’,5’–hydroxylase. Theor Appl Genet 110:269–275
Jung CS, Griffiths HM, De Jong DM, Cheng S, Bodis M, Kim TS, De Jong WS (2009) The potato developer (D) locus encodes an R2R3 MYB transcription factor that regulates expression of multiple anthocyanin structural genes in tuber skin. Theor Appl Genet 120:45–57
Kempthorne O (1955) The correlation between relatives in a simple autotetraploid population. Genetics 40:168–174
Kempthorne O (1957) An introduction to genetic statistics. Wiley, New York, p 545
Kingsbury N (2009) Hybrid: the history & science of plant breeding. The University of Chicago Press, Chicago and London, p 493
Kumar R, Kang GS (2006) Usefulness of Andigena (Solanum tuberosum ssp. andigena) genotypes as parents in breeding early bulking potato cultivars. Euphytica 150:107–115
Lerner IM (1950) Population genetics and animal improvement. Cambridge University Press, Cambridge, p 342
Li CC (1957) The genetic variance of autotetraploids with two alleles. Genetics 42:583–592
Lunden AP (1937) Arvelighetsundersøkelser i potet (Inheritance studies in the potato), Solanum tuberosum L. Meld Fra Norges Landbrukshøiskole 1937:1–156
Lunden AP (1960) Some more evidence of autotetraploid inheritance in the potato (Solanum tuberosum). Euphytica 9:225–234
Lush JL (1937) Animal breeding plans. Iowa State University Press, Ames, Iowa
Mackay GR (2005) Propagation by traditional breeding methods. In: Razdan MK, Mattoo AK (eds) Genetic improvement of Solanaceous crops, vol I. potato. Science Publishers, Enfield, pp 65–81
Malcolmson JF (1969) Races of Phytophthora infestans occurring in Great Britain. Trans Br Mycol Soc 53:417–423
Malcolmson JF, Black W (1966) New R genes in Solanum demissum Lindl. and their complementary races of Phytophthora infestans (Mont.) de Bary. Euphytica 15:199–203
Mann H, Iorizzo M, Gao L, D’Agostino N, Carputo D, Chiusano ML, Bradeen JM (2011) Molecular linkage maps: strategies, resources and achievements. In: Bradeen JM, Kole C (eds) Genetics, genomics and breeding of potato. Science Publishers, Enfield, pp 68–89
Maris B (1989) Analysis of an incomplete diallel cross among three ssp. tuberosum varieties and seven long-day adapted ssp. andigena clones of the potato (Solanum tuberosum L.). Euphytica 41:163–182
Maris B (1990) Comparison of diploid and tetraploid potato families derived from Solanum phureja x dihaploid S. tuberosum hybrids and their vegetatively doubled counterparts. Euphytica 46:15–33
Mather K (1936) Segregation and linkage in autotetraploids. J Genet 32:287–314
Meade F, Byrne S, Griffin D, Kennedy C, Mesiti F, Milbourne D (2020) Rapid development of KASP markers for disease resistance genes using pooled whole genome resequencing. Potato Res 63(1):57–73. https://doi.org/10.1007/s11540-019-09428-x
Mendel G (1865) Experiments in plant hybridisation. English translation with introduction by R.A. Fisher, 1965, Oliver & Boyd, Edinburgh, p 95
Mendiburu AO, Peloquin SJ (1977) The significance of 2n gametes in potato breeding. Theor Appl Genet 49:53–61
Mendoza HA (1989) Population breeding as a tool for germplasm enhancement. Am Potato J 66:639–653
Mendoza HA, Haynes FL (1974) Genetic basis of heterosis for yield in autotetraploid potato. Theor Appl Genet 45:21–25
Meuwissen TH, Hayes BJ, Goddard ME (2001) Prediction of total genetic value using genome-wide dense marker maps. Genetics 157:1819–1829
Mori K, Asano K, Tamiya S, Nakao T, Mori M (2015) Challenges of breeding potato cultivars to grow in various environments and to meet different demands. Breed Sci 65(1):3–16. https://doi.org/10.1270/jsbbs.65.3
Munoz FJ, Plaisted RL (1981) Yield and combining abilities in Andigena potatoes after six cycles of recurrent phenotypic selection for adaptation to long day conditions. Am Potato J 58:469–479
Muthoni J, Shimelis H, Melis R (2019) Production of hybrid potatoes: Are heterozygosity and ploidy levels important? AJCS 13(05):687–694. https://doi.org/10.21475/ajcs.19.13.05.p1280
Neele AEF, Nab HJ, de Jongh de Leeuw MJ, Vroegop AP, Louwes KM (1989) Optimising visual selection in early clonal generations of potato based on genetic and economic considerations. Theor Appl Genet 78:665–671
Ortega F, Lopez-Vizcon C (2012) Application of molecular marker-assisted selection (MAS) for disease resistance in a practical potato breeding programme. Potato Res 55:1–13
Ortiz R (1998) Potato breeding via ploidy manipulations. In: Janick J (ed) Plant Breed Revs, vol 16. John Wiley & Sons, New York, pp 15–86
Ortiz R (2001) The state of the use of potato genetic diversity. In: Cooper HD, Spillane C, Hodgkin T (eds) Broadening the genetic base of crop production. CAB International, Wallingford, pp 181–200
Ortiz R, Peloquin SJ (1994) Use of 24-chromosome potatoes (diploids and dihaploids) for genetical analysis. In: Bradshaw JE, Mackay GR (eds) Potato genetics. CAB International, Wallingford, pp 133–154
Peloquin SJ, Boiteux LS, Carputo D (1999) Meiotic mutants in potato: Valuable variants. Genetics 153:1493–1499
Plaisted RL, Sandford L, Federer WT, Kehr AE, Peterson LC (1962) Specific and general combining ability for yield in potatoes. Am Potato J 39:185–197
Plaisted RL, Thurston HD, Brodie BB, Hoopes RW (1984) Selecting for resistance to diseases in early generations. Am Potato J 61:395–403
Potato Genome Sequencing Consortium (2011) Genome sequence and analysis of the tuber crop potato. Nature 475:189–195
Rabier C-E, Barre P, Asp T, Charmet G, Mangin B (2016) On the accuracy of genomic selection. PLoS ONE 11(6):e0156086. https://doi.org/10.1371/journal.pone.0156086
Rasco ET, Plaisted RL, Ewing EE (1980) Photoperiod response and earliness of S. tuberosum ssp. Andigena after six cycles of recurrent selection for adaptation to long days. Am Potato J 57:435–448
Reader J (2008) Propitious esculent. William Heinemann, London, p 315
Riley R (1969) Plant genetics in the service of man. In: Jinks J (ed) Fifty years of genetics. Oliver and Boyd, Edinburgh, pp 37–55
Rosyara U, De Jong W, Douches D, Endelman J (2016) Software for genome-wide association studies in autopolyploids and its application to potato. Plant Genome 9:1–10
Salaman RN (1910) The inheritance of colour and other characters in the potato. J Genet 1:7–46
Salaman RN (1926) Potato varieties. Cambridge University Press, Cambridge, p 378
Sanford J, Hanneman R (1982) A possible heterotic threshold in potato and its implications for breeding. Theor Appl Gen 61:151–159
Sharma SK, Bolser D, de Boer J, Sønderkaer M, Amoros W, Carboni MF, D’Ambrosio JM, de la Cruz G, Di Genova A, Douches DS, Eguiluz M, Guo X, Guzman F, Hackett CA, Hamilton JP, Li G, Li Y, Lozano R, Maass A, Marshall D, Martinez D, McLean K, Mejía N, Milne L, Munive S, Nagy I, Ponce O, Ramirez M, Simon R, Thomson SJ, Torres Y, Waugh R, Zhang Z, Huang S, Visser RGF, Bachem CWB, Sagredo B, Feingold SE, Orjeda G, Veilleux RE, Bonierbale M, Jacobs JME, Milbourne D, Martin DMA, Bryan GJ (2013) Construction of reference chromosome-scale pseudomolecules for potato: integrating the potato genome with genetic and physical maps. G3 (Bethesda) 3:2031–2047
Sharma SK, MacKenzie K, McLean K, Dale F, Daniels S, Bryan GJ (2018) Linkage Disequilibrium and Evaluation of Genome-Wide Association Mapping Models in Tetraploid Potato G3(8):3185–3202. https://doi.org/10.1534/g3.118.20037
Shull GH (1908) The composition of a field of maize. Am Breeders’ Assoc Rep 4:296–301
Shull GH (1909) A pure-line method of corn breeding. Am Breeders’ Assoc Rep 5:51–59
Simmonds NW (1962) Variability in crop plants, its use and conservation. Biol Rev 37:422–465
Simmonds NW (1969) Prospects of potato improvement. Scottish Plant Breeding Station Forty-Eighth Annual Report 1968–69:18–38
Simmonds NW (1995) Potatoes. In: Smartt J, Simmonds NW (eds) Evolution of crop plants, 2nd edn. Longman Scientific & Technical, Harlow, pp 466–471
Sinnott EW, Dunn LC, Dobzhansky T (1958) Principles of Genetics, 5th edn. McGraw-Hill, New York, p 459
Slater AT, Cogan NOI, Forster JW (2013) Cost analysis of the application of marker-assisted selection in potato breeding. Mol Breed 32:299–310
Slater AT, Cogan NOI, Forster JW, Hayes BJ, Daetwyler HD (2016) Improving genetic gain with genomic selection in autotetraploid potato. Plant Genome 9. https://doi.org/10.3835/plantgenome2016.02.0021
Smith HB (1927) Chromosome counts in the varieties of S. tuberosum and allied wild species. Genetics 12:84–92
Smith HF (1936) A discriminant function for plant selection. Ann Eugen 7:240–250
Spoor W, Simmonds NW (2001) Base-broadening: introgression and incorporation. In: Cooper HD, Spillane C, Hodgkin T (eds) Broadening the genetic base of crop production. CAB International, Wallingford, pp 71–79
Sprague GF, Tatum LA (1942) General vs. specific combining ability in single crosses of corn. J Amer Soc Agron 34:923–932
Stupar RM, Bhaskar PB, Yandell BS, Rensink WA, Hart AL, Ouyang S, Veilleux RE, Busse JS, Erhardt RJ, Buell CR, Jiang J (2007) Phenotypic and transcriptomic changes associated with potato autopolyploidization. Genetics 176:2055–2067
Sverrisdóttir E, Byrne S, Sundmark HER, Johnsen HØ, Kirk HG, Asp T, Janss L, · Kåre L. Nielsen KL, (2017) Genomic prediction of starch content and chipping quality in tetraploid potato using genotyping-by-sequencing. Theor Appl Genet 130:2091–2108. https://doi.org/10.1007/s00122-017-2944-y
Swaminathan MS (1954) Nature of polyploidy in some 48-chromosome species of the genus Solanum, section tuberarium. Genetics 39:59–76
Swiezynski KM (1984) Early generation selection methods used in Polish potato breeding. Am Potato J 61:385–394
Tai GCC (1994) Use of 2n gametes. In: Bradshaw JE, Mackay GR (eds) Potato genetics. CAB International, Wallingford, pp 109–132
Tai GC, Young DA (1984) Early generation selection for important agronomic characteristics in a potato breeding population. Am Potato J 61:419–434
Tanksley SD, Ganal MW, Prince JP, de-Vicente MC, Bonierbale MW, Broun P, Fulton TM, Giovannoni JJ, Grandillo S, Martin GB, Messeguer R, Miller JC, Miller L, Paterson AH, Pineda O, Roder MS, Wing RA, Wu W, Young ND, (1992) High density molecular linkage maps of the tomato and potato genomes. Genetics 132(4):1141–1160
Tarn TR, Tai TCC (1983) Tuberosum × Tuberosum and Tuberosum × Andigena potato hybrids: comparisons of families and parents, and breeding strategies for Andigena potatoes in long-day temperate environments. Theor Appl Genet 66:87–91
Toxopeus HJ (1953) On the significance of multiplex parental material in breeding for resistance to some diseases in the potato. Euphytica 2:139–146
Uijtewaal BA, Jacobsen E, Th. Hermsen JG (1987) Morphology and vigour of monohaploid potato clones, their corresponding homozygous diploids and tetraploids and their heterozygous diploid parent. Euphytica 36:745–753
Uitdewilligen JGAML, Wolters A-MA, D’hoop BB, Borm TJA, Visser RGF, van Eck HJ (2013) A next generation sequencing method for genotyping-by-sequencing of highly heterozygous autotetraploid potato. PLoS ONE 8(5):e62355. https://doi.org/10.1371/journal.pone.0062355
van Os H, Andrzejewski S, Bakker E, Barrena I, Bryan GJ, Caromel B, Ghareeb B, Isidore E, de Jong W, van Koert P, Lefebvre V, Milbourne D, Ritter E, Rouppe van der Voort JNAM, Rousselle-Bourgeois F, van Vliet J, Waugh R, Visser RGF, Bakker J, van Eck HJ (2006) Construction of a 10,000-marker ultradense genetic recombination map of potato: providing a framework for accelerated gene isolation and a genomewide physical map. Genetics 173(2):1075–1087. https://doi.org/10.1534/genetics.106.055871
Veilleux RE (2005) Cell and tissue culture of potato (Solanaceae). In: Razdan MK, Mattoo AK (eds) Genetic improvement of Solanaceous crops, vol I. potato. Science Publishers Inc, Enfield, pp 185–208
Voorrips RE, Gort G, Vosman B (2011) Genotype calling in tetraploid species from bi-allelic marker data using mixture models. BMC Bioinformatics 12:172. https://doi.org/10.1186/1471-2105-12-172
Vos PG, Uitdewilligen JGAML, Voorrips RE, Visser RGF, van Eck HJ (2015) Development and analysis of a 20K SNP array for potato (Solanum tuberosum): an insight into the breeding history. Theor Appl Genet 128:2387–2401
Vos PG, Paulo MJ, Voorrips RE, Visser RGF, van Eck HJ, van Eeuwijk FA (2017) Evaluation of LD decay and various LD-decay estimators in simulated and SNP-array data of tetraploid potato. Theor Appl Genet 130:123–135. https://doi.org/10.1007/s00122-016-2798-8
Walsh B, Lynch M (2018) Evolution and selection of quantitative traits. Oxford University Press, Oxford, p 1459
Weintraub B (2019) Redcliffe Nathan Salaman (1874–1955) and the first potato plant with “genuine resistance” to late blight. The Israel Chemist and Chemical Engineer 5:28–34
Wolters AMA, Uitdewilligen JGAML, Kloosterman BA, Hutten RCB, Visser RGF, van Eck HJ (2010) Identification of alleles of carotenoid pathway genes important for zeaxanthin accumulation in potato tubers. Plant Mol Biol 73:659–671. https://doi.org/10.1007/s11103-010-9647-y
Wricke G, Weber WE (1986) Quantitative genetics and selection in plant breeding. Walter de Gruyter, Berlin, p 406
Wright AJ (1979) The use of differential coefficients in the development and interpretation of quantitative genetic models. Heredity 43:1–8
Zhang Y, Cheng S, De Jong D, Griffiths H, Halitschke R, De Jong W (2009) The potato R locus codes for dihydroflavonol 4-reductase. Theor Appl Genet 119:931–937
Zimnoch-Guzowska E, Flis B (2021) Over 50 years of potato parental line breeding program at the Plant Breeding and Acclimatization Institute in Poland. Potato Res. https://doi.org/10.1007/s11540-021-09503-2
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The author declares no conflict of interest, no funding source, no human or animal rights issues, and compliance with ethical standards.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bradshaw, J.E. A Brief History of the Impact of Potato Genetics on the Breeding of Tetraploid Potato Cultivars for Tuber Propagation. Potato Res. 65, 461–501 (2022). https://doi.org/10.1007/s11540-021-09517-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11540-021-09517-w