Sediment–Water Interface Flow with the Multiparticle Collision Dynamics

Abstract

Multiparticle collision dynamics is a relatively new algorithm of fluid flow simulations that has been applied mostly to flows around simple objects. One might ask how it behaves in more complex flows. We extend the basic algorithm to handle flows in porous media. For this, we introduce a particle-level drag force. The force hinders the flow, which results in global resistance to flow and decrease of permeability. The extended algorithm is validated in the flow through a porous channel and compared with an analytical solution. Some basic properties of the solver are investigated. Finally, we use the solver to capture solutions in the sediment–water interface flow.

1 Introduction

Porous media flows are ubiquitous in nature. An example is a flow through porous sediments that occur at the ocean bottom, where sandy sediment is exposed to bottom current flows (Huettel et al. 1996; Guo and Zhao 2002). There, the transport of the water in porous media is important for many natural processes, including $\hbox {CO}_2$ storage and denitrification (Gao et al. 2012). In situ experiments in such systems require the usage of complex experimental techniques (Lin et al. 2015), and thus, numerical simulations are often the best option.

Numerically, porous media are modelled either at the microscopic or macroscopic level. In microscale, the porous matrix exists explicitly as a system of interconnected void areas (pores) between solids. In this description, the system size is limited mostly by the computer memory required for the numerical mesh. In the macroscale, the Navier–Stokes equation may be extended by a resistant term (Guo and Zhao 2002) to simulate effect of porous media.

In general, fluids are often modelled by integration of the Navier–Stokes equations discretized using numerical grids. There are many numerical methods of this type, and they require a tedious task of numerical mesh generation that is limited by both the acceptable time and available computational resources, especially in complex geometries. Another option is to describe the system at the mesoscopic level with the lattice Boltzmann Method velocity distribution function defined on a regular grid. One may also use particles that are driven by the flow. An example is the multiparticle collision dynamics (MPCD). This method, originally used for systems that include thermal fluctuations, may be used for standard hydrodynamics as well (Angelis et al. 2012). Recently, MPCD was used in hydrodynamical applications, see, e.g. vortex shedding in the flow past cylinder (Malevanets and Kapral 1999), flow over fish-like objects (Daniel et al. 2009), slip and no-slip steady flow past cylinders (Salil Bedkihal 2013). The advantage of MPCD over standard solvers is a relative simplicity of its implementation and no need to use a numerical mesh.

The aim of this work is to utilize advantages of MPCD and extend the original algorithm so as it can be used to simulate flows in macroscopic porous media (without explicit geometry of pores). We show that after extension of the standard method with velocity rescaling procedure we are able to obtain correct numerical profiles in a porous channel. The numerical results are convergent with decreasing time step in the model. We show that Darcy’s law holds in the model and test the basic numerical properties of the model. Finally, we use the extended MPC solver to simulate a porous sediment–water flow.

2 The Model

In MPCD, the fluid is represented by point particles. The simulations consist of two steps: streaming and collision. No explicit particle–particle interaction potential exists, which distinguishes the model from other particle-based methods such like smoothed particle hydrodynamics and molecular dynamics.

In the streaming step, the i-$\hbox {th}$ particle moves at a constant velocity:

$$\begin{aligned} \mathbf {r}_i(t+h)=\mathbf {r}_i(t)+h\mathbf {v}_i(t), \end{aligned}$$

(1)

where $\mathbf {r}_i(t)$ is its position at time t, $\mathbf {v}_i$ is its velocity assumed to be constant at the time interval h.

Fig. 1

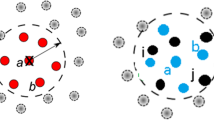
Scheme of MPC collision step. Rotation of velocities of particles grouped in a single cell in the moving frame of reference. The velocity of the frame $\mathbf {u}$ is an average taken over all particles in the cell. Vectors before rotation are drawn with light grey. All particles are rotated by the same, random angle $\alpha$

To perform the collision step, particles are grouped into a regular grid. Grid resolution is adjusted, so that on average there are 70 particles in a single cell (particle positions are initialized as random). The velocity of the i-th particle is rotated in the frame of reference moving with the average velocity $\mathbf {u}$ computed as the average over all its neighbours in the cell (see Fig. 1):

$$\begin{aligned} \mathbf {v}_i(t+h)=\mathbf {u}+s\mathbf {R}(\theta )(\mathbf {v}_i-\mathbf {u}), \end{aligned}$$

(2)

where $\mathbf {R}(\alpha )$ is the rotation matrix by the angle $\theta$ and s is the scaling variable representing a thermostat (which we calculate individually for each cell). For MPCD particles of equal unit mass, we use the following expression:

$$\begin{aligned} s=\sqrt{\frac{k_{B}Td(n-1)}{\sum _{i=1}^n |\mathbf {v}_i-\mathbf {u}|^2}}, \end{aligned}$$

(3)

where $k_B$ is the Boltzmann constant, T is the temperature, d is the number of dimensions, n is the number of particles in a single cell, and the sum goes over all particles in the cell (Bolintineanu et al. 2012; Wysocki et al. 2010).

To ensure the Galilean invariance of the model, the cell borders are shifted randomly after each computational step (Wysocki et al. 2010). For this, at each step, we draw two random numbers $r_x\in (-r/2,r/2)$ and $r_y\in (-r/2,r/2)$ and use the shifted coordinates of cells in the grouping procedure. Here, r denotes the width and height of a cell in the grid; thus, they are shifted by at most half of their linear size in each direction.

2.1 Porous Media

To simulate effect of porous media on the flow, we use a similar approach to that reported in Dardis and McCloskey (1998). There, velocity of the fluid was locally damped. But, in contrast to Dardis and McCloskey (1998), where the velocity distribution function is used, our model works on particles and their velocities.

To model porous media, we assume that the velocity of the fluid in the pore-space is low and the Reynolds number $Re<1$. We assume the following particle-level drag force:

$$\begin{aligned} \mathbf {f}_i = -C\mathbf {v}_i, \end{aligned}$$

(4)

where C is the drag coefficient—a function of porosity and geometry of the porous matrix. If we start from the second Newton’s law and discretize it with our drag force (Eq. 4), we get:

$$\begin{aligned} \mathbf {v}_i = \mathbf {v}_i(1 - hC)=\lambda \mathbf {v}_i, \end{aligned}$$

(5)

where h is the discretization time step (we assume first-order approximation and mass $m=1$ for each particle). Thus, to include drag, we have to rescale the velocity by a single factor $\lambda =1-hC$. The time step must be small enough to ensure that $0<\lambda <1$, and we suggest to use $0<h<1/C$ limit. The procedure is applied to all particles that flow in the porous domain at each simulation step. In general, the drag coefficient C may be space and/or time dependent ($C=C(\mathbf {r},t)$), which leads to many applications, including coupled fluid–porous and porous–porous systems with a variable porosity (not considered in the paper).

3 Results

3.1 Porous Channel

The velocity scaling described with Eq. (5) modifies the permeability of the modelled medium. To investigate properties of the permeability, I simulated the fluid flow in a straight, 2D rectangular channel filled with a homogeneous porous medium. Such a system may be solved analytically with the damped Stokes model (Dardis and McCloskey 1998; Balasubramanian et al. 1987):

$$\begin{aligned} \nu \frac{\mathrm{d}^2u}{\mathrm{d}x^2}-\alpha u=\frac{1}{\varrho }\frac{\mathrm{d}p}{\mathrm{d}y}. \end{aligned}$$

(6)

The exact solution reads (Dardis and McCloskey 1998):

$$\begin{aligned} u(x)=-\frac{1}{\varrho \alpha }\frac{\mathrm{d}p}{\mathrm{d}y}\left[ 1-\frac{\cosh \left[ r(x-W/2)\right] }{\cosh (rW/2)} \right] , \end{aligned}$$

(7)

where x is the horizontal position in the channel, $\alpha$ is a parameter related to the damping force, r is a free parameter, $\frac{\mathrm{d}p}{\mathrm{d}y}$ is the pressure gradient along the vertical direction, and W is the channel width.

We started with a flow through a fully porous channel. We used the no-slip condition at the top and bottom walls. The vertical boundary was periodic. The gravity was applied to simulate the flow in the vertical direction. We used a regular grid of $64\times 64$ cells in the collision step. On average, 70 particles are initially placed in each cell at random positions. In the collision step, angle $\theta =\pm 160^\circ$ was used. In the thermostat, Eq. (3), we kept $k_BT=0.01$ (Lamura et al. 2001). To verify our solutions, we used the least square fitting of Eq. (7) to simulation data.

Our first test was to check the minimum time necessary for the solution to converge to the stationary state. To this end, we measured the total kinetic energy in our simulation. Because the flow was driven by gravity, we expected it to converge to the stationary state. The resulting plots revealed that at least 10,000 time steps are required for $h=0.001$ to achieve the steady solutions (data not shown). Thus, in all our simulations the total number of 10,000 time steps was used in each case. Moreover, we averaged the macroscopic profiles of the velocity starting from step 5000 with the $n=200$ interval.

In the next numerical test, we verified convergence of the numerical solutions with a decreasing time step h. We simulated the flow in the channel at a fixed drag coefficient $C=1$. Thus, the scaling factor $\lambda (h)$ varied with h according to Eq. (5). The resulting velocity profiles at varying h are plotted in Fig. 2. From these data, the minimum useful time step was estimated as $h=0.01$ and we used this value in the remaining part of the study.

Fig. 2

Convergence test of the velocity profiles in a fully porous channel for time steps $h=0.1, 0.05, 0.01, 0.001$ and 0.0005. Data points represent our MPCD simulation results, and solid lines are the numerical fits of Eq. 7

Next, we investigated the relation between the two main parameters of the model: r and $\alpha$ from Eq. (7). We used the data from the least square fits to the numerical profiles of the velocity. The test was repeated several times for varying $\lambda$. Numerical profiles of the velocity profiles with fitted analytical profiles are plotted in Fig. 3. The numerical data agree with the theoretical curves well. Due to discrete nature of the model, statistical noise appears in all data (see Fig. 2). For example, at $\lambda =0.7$ some points at x/L near 0.2 and 0.65 are laying relatively far from the theoretical profile (see Fig. 3).

Fig. 3

Velocity profiles in the flow through a porous channel. Data points represent MPCD simulation, and solid lines are fits to Eq. 7

Fig. 4

Numerical test of the power law Eq. 8 based on the parameters from numerical fitting of Eq. 7 to simulation data (open circles). Simulations were done at $\lambda$ from $\lambda =1-1\times 10^{-7}$ to $\lambda =0.7$. Solid lines represent Eq. 8 for $b\approx 0.5$, $\nu \approx 7\times 10^{-4}$ (thick line) and $b\approx 0.17$, $\nu \approx 6\times 10^{-10}$ (thin line)

The values of r and $\alpha$ corresponding to all velocity profiles measured in Fig. 3 are plotted in Fig. 4. We investigated if the power law:

$$\begin{aligned} r \propto (\alpha / \nu )^{b}, \end{aligned}$$

(8)

holds and found two distinct scaling regimes. We found $b\approx 0.17$ for $\alpha >1$ and $b\approx 0.5$ for $0.05< \alpha < 1$ using least square fitting of Eq. 8 to numerical data. There $\nu$ is the model viscosity, and $\alpha$ is the drag coefficient from Eq. 7. Note that uniform scaling at $b=0.5$ was reported previously in the similar study based on the lattice Boltzmann porous media model (Dardis and McCloskey 1998) at relatively higher numerical viscosity.

3.2 Permeability

To study the permeability in our system, we integrated the velocity along the horizontal direction. The resulting plot of the flux q at varying gravity is expected to be linear, and, in fact, linearity is seen in almost the whole range of gravity (see Fig. 5).

Fig. 5

Test of Darcy’s law $q\propto g$—the dependency of the numerical flux q on the gravity in the porous channel flow. $\lambda$ was fixed at 0.99

To measure the dependency of permeability on $\lambda$, we used directly the information hold in profiles in Fig. 3. We integrated the velocity in the profile to get the total flux q. We did this for each $\lambda$ and plotted the results in Fig. 6. Based on the results in Fig. 3 and the previous observation that Darcy law ($q\propto k$) holds in our system, we may now write that:

$$\begin{aligned} q\propto (1-\lambda )^{-1}. \end{aligned}$$

(9)

Fig. 6

Numerical fit of the numerical MPCD data to the function $k\propto 1/(1-\lambda$)

3.3 Sediment–Water Flow

The MPCD model can be used to study flows in systems with heterogeneous porosity distributions as well. Those are difficult simulations from the point of view of numerical methods. Special difficulties occur at the boundary of two phases with different porosities.

Fig. 7

Scheme of the sediment–water interface flow

Here, we perform the simulation of the flow in two-phase porous media. For this, we use horizontal channel partially filled by porous media (see Fig. 7). The top half of the media is completely filled by fluid ($\varphi =1$), and the bottom half has uniform porosity $\varphi = \varphi _b$. The fluid is driven by external horizontal gravity in the whole domain.

Resulting velocity profile in Fig. 8 has a typical shape of transition flow between two phases (see e.g. Tao et al. 2013). The Poiseuille-like profile emerges in the top half which is then deformed near sediment–water interface (SWI). The momentum from free flow penetrates through the media accelerating the skin region around $10\%$ below the SWI. Deep in the porous part the profile flats and the solution to Darcy model emerges. The drop of the velocity near the bottom ($y/L = 0$) is probably due to the no-slip condition used for the bottom.

Fig. 8

Numerical velocity profile (closed circles) and shear rate (inset, open circles) in the fluid flow over porous sediment. Results averaged over 500 MPCD simulation time steps. The sharp transition at $y=0.5$ is clearly noticeable

In order to quantify shape of the velocity profile at the SWI, we computed the shear stress directly from horizontal velocity profile. Assuming Newtonian flow, we do this by numerical derivation of the velocity:

$$\begin{aligned} \tau = \mu \frac{\partial u}{\partial y}, \end{aligned}$$

(10)

where $\mu$ was the viscosity of the fluid. We divided stress by its max value and plot along with the velocity profile in the Fig. 8. Stress undergoes standard linear increase in the Poiseuille-flow region. This is natural for channel flow and was observed before (Backer et al. 2005). What is interesting here is the sudden change of its behaviour at the SWI (y/L = 0.5) where it starts to decrease nonlinearly.

4 Summary

We extended the standard MPCD solver to account for porous media as a source of an additional force acting on a fluid. We confirmed that the extended model can reproduce the analytical solution to the damped Stokes model with the power law correlation between its two main parameters. We showed that the model correctly recovers the Darcy’s law. Our work has several interesting consequences. In principle, MPCD allows to include extra particles in the flow using molecular dynamics. Thus, the applications of our model may include other types of media, i.e. polymer flows, diluted particles transport, all in porous media. Also, due to the possibility of modelling spatial changes in permeability of the model by varying $\lambda$ in space, it is possible to simulate various types and shapes of porous structures, i.e. transport through rippled sea bed (Huettel et al. 1996; Kharab 1990) layered porous media or porous particles (Kindler et al. 2010) which we confirmed in the flow over porous sediment scenario.