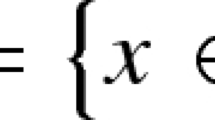Second-Order Optimality Conditions in Locally Lipschitz Inequality-Constrained Multiobjective Optimization

Abstract

The main goal of this paper is to give some primal and dual Karush–Kuhn–Tucker second-order necessary conditions for the existence of a strict local Pareto minimum of order two for an inequality-constrained multiobjective optimization problem. Dual Karush–Kuhn–Tucker second-order sufficient conditions are provided too. We suppose that the objective function and the active inequality constraints are only locally Lipschitz in the primal necessary conditions and only strictly differentiable in sense of Clarke at the extremum point in the dual conditions. Examples illustrate the applicability of the obtained results.

1 Introduction

Nonsmooth multiobjective optimization receives a lot of attention nowadays (see, for instance, [1,2,3,4,5,6,7,8]) because it has practical applications to mathematical sciences, economics, engineering, etc.

In this paper, we derive second-order optimality conditions for a nonsmooth multiobjective optimization problem (P) with inequality constraints.

This problem has been considered in many recent papers, but the data are at least continuously differentiable (for instance, in [9,10,11,12,13,14,15,16,17]). The papers, which deal with optimization problems with locally Lipschitz data, give first-order optimality conditions [1, 6, 18, 19]. The articles concerning second-order conditions for optimization problems with locally Lipschitz data are scarce and deal mostly with scalar problems [2, 4, 5, 20,21,22,23].

We give primal and dual second-order necessary conditions and dual second-order sufficient conditions for a strict local Pareto minimum of order two for problem (P) with locally Lipschitz data. We get our optimality conditions without assuming any kind of second-order differentiability.

Thus, we extend to locally Lipschitz multiobjective optimization problems and improve the second-order necessary conditions for a local minimum and for a strict (or isolated) local minimum of order two of Constantin [21] for inequality-constrained scalar problems with locally Lipschitz data, and of Ivanov [23] for inequality-constrained scalar problems with locally Lipschitz data and some second-order Hadamard differentiable data.

Our necessary conditions for a strict local Pareto minimum of order two are obtained in terms of the second-order Zangwill constraint qualification (ZSCQ). This constraint qualification was introduced by Ivanov [14], where continuously differentiable functions have been studied. It was generalized to locally Lipschitz functions in terms of Páles and Zeidan’s second-order directional derivative by Xiao et al. [5]. We show by means of examples that (ZSCQ) is not related to several regularity conditions introduced in [1, 18, 19]. Our dual necessary conditions are of Karush–Kuhn–Tucker type (i.e., the multipliers in the dual necessary conditions are not all equal to zero), and they are obtained under an hypothesis inspired by a condition due to Luu [4].

We derive Karush–Kuhn–Tucker dual sufficient conditions for a strict local Pareto of order two under weaker hypotheses than the ones required in the recent sufficient conditions due to Feng–Li [10].

After some preliminaries in Sect. 2, we give primal necessary conditions in Sect. 3, dual necessary conditions in Sect. 4, and dual sufficient conditions in Sect. 5.

2 Preliminaries

2.1 About Weak Solutions

In this section, we will discuss some applications of weak Pareto solutions to bioinformatics and computational biology. The paper [24] reviews five different contexts that give rise to multiple objectives in biology. It outlines the wide applicability of multiobjective optimization in biological problem domains (see sections 4–8, [24]). In [24], the optimum solutions to the multiobjective problems modeling those contexts are Pareto solutions. One of those five contexts concerns alignment problems (sections 3.2 and 6, [24]). Reference [25] deals with a particular type of alignment problem, namely the structural RNA sequence alignment, which is also known as an inverse problem of the RNA folding, or the RNA inverse folding (see [26]).

The ribonucleic acid (RNA) and the deoxyribonucleic acid (DNA) are nucleic acids present in all living cells. The principal role of RNA is to act as a messenger carrying instructions from DNA for controlling the synthesis of proteins. In some viruses, RNA rather than DNA carries the genetic information. Such a virus is SARS-CoV-2 as it is written in [27] “the existence of SARS-CoV-2 in aerosol samples was determined through the quantification of its genetic material (RNA).” The presence of RNA belonging to SARS-CoV-2 allowed the authors of [27] to propose that SARS-CoV-2 may have the potential to be transmitted via aerosols.

“Sequence alignment is a fundamental technology for various biological analyses such as gene prediction and phylogenetic inference” [25]. It has been applied to protein, DNA, and RNA. The structural RNA sequence alignment is important due to the “increase in the number of known biological functions of noncoding RNAs” [25], and also due to the need “to create artificial RNA molecules which have a desired function. In such artificial applications of RNA sequence, we have to design an RNA sequence that folds into a desired structure (target structure) to realize a desired function” [26].

The structural RNA sequence alignment problem is a multi-objective optimization problem because it involves two competing objective functions, sequence similarity score s and secondary structure score P (see section 2.1, [25]). As explained in [25], those objective functions are competing because “at a low sequence similarity, it is difficult to discriminate an accidental sequence similarity and evolutionary conserved nucleotides; hence, nonstructural alignment methods can give an inaccurate alignment due to accidental matches of nucleotides; on the other hand, if we construct an RNA alignment by maximizing a secondary structure score alone, the alignment can have a reduced sequence similarity score compared to the alignment obtained by a nonstructural alignment method.” The secondary structure score is also known as structure stability score (see [26]).

In [25, 26], the author finds useful the weak Pareto optimal solutions of the structural RNA sequence alignment problem. The reason is that “the solutions with the highest P or highest s are of interest. For example, when multiple solutions have the highest P in a solution set and they have values of s different from each other, only one solution (with the highest s) of the solutions with the highest P is included in Pareto optimal solutions, whereas weak Pareto optimal solutions contain all solutions with the highest P in the solution set. When we align RNA sequences with a very low sequence identity, the solutions with a low s and the highest P also can contain a good alignment since the sequence identity becomes less reliable in such a case” ([25], pp. 2384).

It is further emphasized in [26] that “not only very stable RNA structures, but also those with a lower stability can be candidates for artificial functional RNA sequences.” In [26], the similarity score ranges from 0 to 1.0, and a similarity score of 1.0 indicates a perfect consensus between two structures. To obtain a set of the RNA sequences that fold into the target structure, and have a wide range of stability scores, the weak Pareto optimal solutions are useful. “In weak Pareto optimal solutions of the RNA sequence alignment problem, multiple solutions are allowed to have a similarity score of 1.0 in contrast to the case of the Pareto optimal solutions, where only one solution is allowed to have a similarity score of 1.0. Thus, weak Pareto optimal solutions can give more a comprehensive solution set for RNA inverse folding” ([26], pp. 10).

2.2 Notations and Definitions

In this paper, we deal with the following multiobjective optimization problem

$$\begin{aligned} \text {Minimize} \;f(x)\;\text {subject to}\; x\in D=\{x\in U:\;g_i(x)\le 0, \;i=1,2, ..., m\}, \qquad (\text {P}) \end{aligned}$$

where X is a Banach space, $f=(f_1,...,f_p):U\rightarrow \mathbb {R}^p$, $g_i:U\rightarrow \mathbb {R}$, $i=1,...,m$, and U is an open set in X.

In this paper, we accept $0\times (-\infty )=0$ and $0\times \infty =0$.

Denote $I:=\{1, 2, \ldots , m\}$, $K:=\{1, 2, \ldots , p\}$. For a subset A, $\text {cl} \,A$ and $\text {conv}\, A$ denote the closure of A, and the convex hull of A, respectively.

Definition 2.1

• (a) A point $\bar{x}\in D$ is a weak local Pareto minimum, if there exists a neighborhood V of $\bar{x}$ such that no $x\in V\cap D$ satisfies $f_k(x)< f_k(\bar{x})$ for all $k=1,\ldots , p$.

• (b) (Jiménez [29]) A point $\bar{x}\in D$ is a strict local Pareto minimum of order two for (P), or of f on D, if there exists a constant $\alpha >0$ and a neighborhood V of $\bar{x}$ such that $(f(x)+\mathbb {R}^p_+)\cap B(f(\bar{x}),\alpha \Vert x-\bar{x}\Vert ^2)=\emptyset ,\;\forall \,x\in D\cap V,\; x\ne \bar{x}.$

• (c) (Jimenez [29]) A point $\bar{x}\in D$ is a strict local Pareto minimum for (P), if there exists a neighborhood V of $\bar{x}$ such that $f(x)-f(\bar{x})\notin - \mathbb {R}^p_+$, $\forall \,x\in D\cap V,\; x\ne \bar{x}$.

Here, $B(f(\bar{x}),\alpha \Vert x-\bar{x}\Vert ^2)$ denotes the open ball of center $f(\bar{x})$ and radius $\alpha \Vert x-\bar{x}\Vert ^2$, $\mathbb {R}^p$ denotes the p-dimensional Euclidean space, and $\mathbb {R}^p_{+}=\{x=(x_1,\ldots ,x_p)\in \mathbb {R}^p:\; x_k\ge 0,\;k=1,\ldots ,p\}$.

If $\bar{x}$ is a strict local Pareto minimum of order two, then $\bar{x}$ is a strict local Pareto minimum, and thus, $\bar{x}$ is a weak local Pareto minimum.

Definition 2.2

Let F be a real-valued locally Lipschitz mapping on an open set U of X, and $x \in U$. Then,

• (a) [30] Clarke’s generalized derivative of F at x is defined by

  $$\begin{aligned} F^{\circ }(x;v):=\displaystyle \limsup _{(u,t)\rightarrow (x,0^+)}\frac{F(u+tv)-F(u)}{t}, \;v\in X. \end{aligned}$$

• (b) [31] Páles and Zeidan’s second-order upper generalized directional derivative of F at x is defined as an element of $\overline{\mathbb {R}}=\mathbb {R}\cup \{\infty \}\cup \{-\infty \}$ by

  $$\begin{aligned} F^{\circ \circ }(x;v):=\displaystyle \limsup _{t\rightarrow 0^+}2\frac{F(x+tv)-F(x) -tF^{\circ }(x;v)}{t^2},\;v\in X. \end{aligned}$$

• (c) [23] Ivanov’s second-order lower generalized directional derivative of F at x in the direction $v\in X$ is defined as an element of $\overline{\mathbb {R}}$ by

  $$\begin{aligned} (F)^{\prime \prime }_-(x;v):=\displaystyle \liminf _{(t,v^{\prime })\rightarrow (0^+,v)}2\frac{F(x+tv^{\prime })-F(x)-tF^{\circ }(x;v)}{t^2}. \end{aligned}$$

• (d) Ivanov’s second-order upper generalized directional derivative of F at x in the direction $v\in X$ is defined as an element of $\overline{\mathbb {R}}$ by

  $$\begin{aligned} (F)^{\prime \prime }_+(x;v):=\displaystyle \limsup _{(t,v^{\prime })\rightarrow (0^+,v)}2\frac{F(x+tv^{\prime })-F(x)-tF^{\circ }(x;v)}{t^2}. \end{aligned}$$

Under the hypotheses of Definition 2.2, $F^{\circ }(\bar{x};v)$ is finite for all $v\in X$. Thus, the second-order upper and lower generalized derivatives considered above are well defined as elements of $\overline{\mathbb {R}}$.

Definition 2.3

Let F map the Banach space X to another Banach space Y. Then, F is strictly differentiable at $\bar{x}$ (in sense of Clarke) [30], if there exists an element of the space $\mathcal {L}(\text {X},\text {Y})$ of continuous linear functionals from X to Y denoted by $\nabla F(\bar{x})$, such that for each v, the following holds

$$\begin{aligned} \displaystyle \lim _{(x,t)\rightarrow (\bar{x},0^+)}\frac{F(x+tv)-F(x)}{t}=\nabla F(\bar{x})(v), \end{aligned}$$

and the convergence is uniform for v in compact sets. (This last condition is automatic if F is Lipschitz near $\bar{x}$.)

If F is strictly differentiable at x, then F is Lipschitz near x (Proposition 2.2.1, [30]). If F is continuously Gâteaux differentiable at x, then F is strictly differentiable at x, and hence, F is Lipschitz near x [30]. In general, the pointwise notions of Fréchet and strict differentiability are not comparable. Strict differentiability implies Fréchet differentiability when X is finite-dimensional, but this implication vanishes when X is infinite-dimensional.

Remark 2.1

If $F:U\rightarrow \mathbb {R}$ is locally Lipschitz near x, regular in the sense of Clarke and Gâteaux differentiable at x with the Gâteaux derivative $F^{\prime }(x)(v)$, then by Proposition 2.3.6, [30], Clarke’s subdifferential of F at x reduces to a singleton. So, by Proposition 2.2.4, [30], F is strictly differentiable in sense of Clarke. If, in addition, X is a finite-dimensional normed space, then F is Fréchet differentiable at x, and $F^{\circ }(x;v)=\nabla F(x)(v)=F^{\prime }(x)(v)$, for all $v\in X$.

The contingent cone $T_{\bar{x}}S$ to a set $S\subseteq X$ at $\bar{x}\in \text {cl}\,S$ is defined by

$$\begin{aligned} T_{\bar{x}}S:=\{v\in X:\; \exists \, t_n\rightarrow 0^+\; \;\exists \,x_n\rightarrow \bar{x} \; \text {such that}\; \bar{x}+t_n x_n\in S,\,\forall \,n\ge 1\}. \end{aligned}$$

For any $\bar{x}\in D$, let $I(\bar{x}):=\{i\in I:\; g_i(\bar{x})=0\}$ be the set of active constraints.

The functions $f_k$, $k\in K$, and $g_i$, $i\in I(\bar{x})$, are assumed to be locally Lipschitz on U. For fixed vectors $\bar{x}\in U$ and $v\in X$, let us denote

$I(\bar{x};v):=\{i\in I(\bar{x}):\; g_i^{\circ }(\bar{x};v)=0\}$, and $K(\bar{x};v):=\{k\in K:\; f_k^{\circ }(\bar{x};v)=0\}.$

A direction v is called critical at the point $\bar{x}\in D$, if $f_k^{\circ }(\bar{x};v)\le 0$ for all $k\in K$ and $g_i^{\circ }(\bar{x};v)\le 0$ for all $i\in I(\bar{x})$.

In Xiao et al. [5] the Zingwill second-order constraint qualification (ZSCQ) has been considered: $B(\bar{x},v)\subseteq \text {cl}\, A(\bar{x}, v),$

where $\bar{x}$ is a feasible point for (P), v is a direction in X,

$$\begin{aligned} A(\bar{x}, v):= & {} \{w\in \! X:\forall \,i\in I(\bar{x};v)\;\,\exists \, \epsilon _i>0\; g_i\left( \bar{x}+tv+\displaystyle \frac{1}{2}t^2w\right) \le 0,\,\forall \, t\in ]0,\epsilon _i[\},\\ B(\bar{x}, v):= & {} \{w\in X:\, g_i^{\circ }(\bar{x};w)+g_i^{\circ \circ }(\bar{x};v)\le 0,\; \forall \, i\in I(\bar{x};v)\}. \end{aligned}$$

By definition, $A(\bar{x}, v)=B(\bar{x}, v)=X$ if $I(\bar{x};v)=\emptyset$.

In [21], we applied the condition $B(\bar{x}, v)\subseteq A_0(\bar{x}, v)$ where the set $A_0(\bar{x},v)$ was defined like $A(\bar{x},v)$ with $I(\bar{x})$ instead of $I(\bar{x};v)$. It is a generalization of a condition introduced in [13] for functions that are differentiable and second-order directionally differentiable. Clearly, the condition $B(\bar{x},v)\subseteq A_0(\bar{x}, v)$ implies the constraint qualification (ZSCQ).

3 Primal Necessary Conditions

In this section, we give primal second-order necessary conditions for a strict local Pareto minimum of order two.

Theorem 3.1

Suppose that $\bar{x}\in D$ is a strict local Pareto minimum of order two for problem (P), the functions $g_i$, $i\notin I(\bar{x})$ are continuous at $\bar{x}$, and the functions $f_k$, $k\in K$ and $g_i$, $i\in I(\bar{x})$ are locally Lipschitz on U. Then, for every nonzero critical direction $v\in X$ satisfying $B(\bar{x}, v)\subseteq \text {cl}\, A(\bar{x}, v)$, it follows that there is no $w\in X$ which solves the system

$$\begin{aligned} \left\{ \begin{array}{l} f_k^{\circ }(\bar{x};w)+f_k^{\circ \circ }(\bar{x};v)\le 0,\;k\in K(\bar{x};v),\\ g_i^{\circ }(\bar{x};w)+g_i^{\circ \circ }(\bar{x};v)\le 0,\;i\in I(\bar{x};v).\end{array}\right. \end{aligned}$$

(3.1)

Proof

Suppose the contrary that there exists a nonzero critical direction v satisfying $B(\bar{x}, v)\subseteq \text {cl}\, A(\bar{x}, v)$, such that system (3.1) has a solution $w\in X$. Consider the three possible cases concerning the constraints:

(1) For every $i\in I(\bar{x};v)$, we have $g_i^{\circ }(\bar{x};w)+g_i^{\circ \circ }(\bar{x};v)\le 0$. Thus, $w\in B(\bar{x},v)$. Due to the assumption $B(\bar{x},v) \subseteq \text {cl}\, A(\bar{x},v)$, there exists a sequence $w_r\rightarrow w$ with $w_r\in A(\bar{x};v)$. Let us fix a nonnegative integer r. Then, there exists $\epsilon _i^r>0$ such that for all $t\in ]0,\epsilon _i^r[$, $g_i(\bar{x}+tv+\displaystyle \frac{1}{2}t^2w_r)\le 0.$

(2) For every $i\in I(\bar{x})\setminus I(\bar{x};v)$, we have $g_i^{\circ }(\bar{x};v)<0$. Then, there exists $\epsilon _i^r>0$ such that for all $t\in ]0,\epsilon _i^r[$, $g_i(\bar{x}+tv+\displaystyle \frac{t^2}{2}w_r)<g_i(\bar{x})=0.$ To show this inequality, we suppose by contradiction that, for any $\epsilon >0$, there is $0<t(\epsilon )<\epsilon$ such that $g_i(\bar{x}+t(\epsilon )v+\displaystyle \frac{t^2(\epsilon )}{2}w_r)\ge g_i(\bar{x})$. Let $\{\epsilon _n\}_{n\ge 1}$ be a sequence, $\epsilon _n\rightarrow 0^+$ as $n\rightarrow \infty$, and $t_n\in ]0,\epsilon _n[$ with $g_i(\bar{x}+t_nv+\displaystyle \frac{t_n^2}{2}w_r)- g_i(\bar{x})\ge 0$. Then,

$$\begin{aligned} 0\le & {} \limsup _{n\rightarrow \infty }\displaystyle \frac{g_i(\bar{x}+t_nv+\displaystyle \frac{t_n^2}{2}w_r)- g_i(\bar{x})}{t_n}\\\le & {} \displaystyle \limsup _{n\rightarrow \infty }\frac{1}{t_n}[g_i(\bar{x}+t_nv)-g_i(\bar{x})]\\&+ \displaystyle \limsup _{n\rightarrow \infty }\frac{1}{t_n}\left[ g_i\left( \bar{x}+t_nv+\frac{t_n^2}{2}w_r\right) - g_i(\bar{x}+t_nv)\right] . \end{aligned}$$

Then, $0\le g_i^{\circ }(\bar{x};v)+\displaystyle \limsup _{n\rightarrow \infty }\frac{1}{2}L_it_n\Vert w_r\Vert$, as $g_i$ is locally Lipschitz of constant $L_i>0$. Therefore, $g_i^{\circ }(\bar{x};v)\ge 0$, which contradicts $i\notin I(\bar{x};v)$.

(3) For every $i\in I\setminus I(\bar{x})$, $g_i(\bar{x})<0$. Hence, by continuity, there exists $\epsilon _i^r>0$ such that $g_i(\bar{x}+tv+\displaystyle \frac{1}{2}t^2w_r)<0$, for all $t\in ]0,\epsilon _i^r[$.

Cases (1), (2), and (3) imply that $\displaystyle g_i(\bar{x}+t v+\displaystyle \frac{1}{2}t^2w_r)\le 0$, for all $i\in \{1,2,\ldots ,m\}$, and for all $t\in ]0,\tilde{\epsilon }[$, where $\tilde{\epsilon }=\displaystyle \min _{i\in \{1,2,\ldots ,m\}}\epsilon _i^r$. Thus, the point $\displaystyle \bar{x}+t v+\frac{1}{2}t^2w_r$ is feasible for all $t\in ]0,\tilde{\epsilon }[$.

Since $\bar{x}$ is a strict local Pareto minimum of order two of f on D, by Theorem 3.7, a) [29], there exist $\alpha >0$, $\bar{U}$ a neighborhood of $\bar{x}$, and at most p sets $V_k$, $k\in K^{\prime }\subset K$ such that $\{V_k:\;k\in K^{\prime }\}$ is a covering of $D\cap \bar{U}\setminus \{\bar{x}\}$ and $f_k(x)>f_k(\bar{x})+\alpha \Vert x-\bar{x}\Vert ^2, \forall \, x\in \bar{D}_k\setminus \{\bar{x}\}$, where $\bar{D}_k=(D\cap \bar{U}\cap V_k)\cup \{\bar{x}\}$.

For every positive sequence $\{t_n\}_{n\ge 1}$, $t_n\rightarrow 0^+$ as $n\rightarrow \infty$, there exists an index $k\in K^{\prime }\subset K$ and an infinite subsequence, which we can denote again by $\{t_n\}_{n\ge 1}$, such that $\bar{x}+t_nv+\displaystyle \frac{t_n^2}{2}w_r\in \bar{D}_k$ for any positive integer $n\ge \bar{n}$ for some $\bar{n}\ge 1$ because $\{V_k:\;k\in K^{\prime }\}$ is a covering of $D\cap \bar{U}\setminus \{\bar{x}\}$.

Then, for all $n\ge \bar{n}$, we have

$$\begin{aligned} f_k(\bar{x}+t_nv+\displaystyle \frac{t_n^2}{2}w_r)>f_k(\bar{x})+\alpha \Vert t_nv+\displaystyle \frac{t_n^2}{2}w_r\Vert ^2. \end{aligned}$$

(3.2)

There are two possible cases concerning a function $f_k$, $k\in K^{\prime }$:

(i) If $k\in K^{\prime }$ and $k\notin K(\bar{x};v)$, then there exists $\tilde{n}\ge \bar{n}$ such that

$$\begin{aligned} f_k\left( \bar{x}+t_nv+\displaystyle \frac{t_n^2}{2}w_r\right) <f_k(\bar{x}), \;\forall \,n\ge \tilde{n}. \end{aligned}$$

(3.3)

To show this, suppose by contradiction that there exists a subsequence of $\{t_n\}_{n\ge \bar{n}}$, which, for simplicity, we denote by $\{t_n\}_{n\ge \bar{n}}$ too, such that

$f_k(\bar{x}+t_nv+\displaystyle \frac{t_n^2}{2}w_r)\ge f_k(\bar{x}), \;\text {for all}\;n\ge \bar{n}$. From the previous inequality, as in case 2), we get $f_k^{\circ }(\bar{x};v)\ge 0$, and then $f_k^{\circ }(\bar{x};v)=0$ because v is a critical direction. This contradicts $k\notin K(\bar{x};v)$. Thus, inequality (3.3) holds, which contradicts inequality (3.2).

(ii) If $k\in K^{\prime }$ and $k\in K(\bar{x};v)$, we have $f_k^{\circ }(\bar{x};v)=0$. Inequality (3.2) implies that the following inequality holds for all $n\ge \bar{n}$

$$\begin{aligned} \alpha t_n^2\Vert v+\displaystyle \frac{t_n}{2}w_r\Vert ^2\le & {} \displaystyle \frac{t_n^2}{2}\left[ \frac{2}{t_n^2}\left( f_k(\bar{x}+t_nv+\displaystyle \frac{t_n^2}{2}w_r\right) - f_k(\bar{x}+t_nv))\right] \\&+\displaystyle \frac{t_n^2}{2}\left[ \displaystyle \frac{2}{t_n^2}\left( f_k(\bar{x}+t_nv)-f_k(\bar{x}\right) -t_n f_k^{\circ }(\bar{x};v))\right] . \end{aligned}$$

Since $v\ne 0$ and $\alpha >0$, after dividing the above inequality by $t_n^2/2$ and taking the upper limit as $n\rightarrow \infty$, we obtain

$$\begin{aligned} 0<2\alpha \Vert v\Vert ^2\le & {} \displaystyle \limsup _{n\rightarrow \infty }\left\{ \left[ \frac{2}{t_n^2}\left( f_k(\bar{x}+t_nv+\frac{t_n^2}{2}w_r\right) - f_k(\bar{x}+t_nv))\right] \right. \\&\left. +\left[ \displaystyle \frac{2}{t_n^2}(f_k(\bar{x}+t_nv)-f_k(\bar{x})-t_n f_k^{\circ }(\bar{x};v))\right] \right\} \\\le & {} \displaystyle \limsup _{n\rightarrow \infty }\left[ \frac{2}{t_n^2}(f_k\left( \bar{x}+t_nv+\frac{t_n^2}{2}w_r\right) - f_k(\bar{x}+t_nv))\right] \\&+\displaystyle \limsup _{n\rightarrow \infty }\left[ \frac{2}{t_n^2}(f_k(\bar{x}+t_nv)-f_k(\bar{x})-t_n f_k^{\circ }(\bar{x};v))\right] \le f_k^{\circ }(\bar{x};w_r)+f_k^{\circ \circ }(\bar{x};v). \end{aligned}$$

Letting $r\rightarrow \infty$, and taking into account that the function $u\rightarrow f_k^{\circ }(\bar{x};u)$ is locally Lipschitz on X (Proposition 2.1.1., b), [30]), we get

$0<2\alpha \Vert v\Vert ^2\le f_k^{\circ }(\bar{x};w)+f_k^{\circ \circ }(\bar{x};v)$, which contradicts the assumption that w is a solution of system (3.1).

Since we arrived at contradictions in both possible cases concerning $f_k$, $k\in K^{\prime }$, there is no critical direction $v\ne 0$ for which (3.1) has a solution. $\square$

The theorem below can be proved using some arguments of the proof of Theorem 3.1. This result can also be derived by means of Proposition 3.1, i), and Theorem 4.2 [5], but under the additional hypothesis $K(\bar{x};v)\ne \emptyset$. This hypothesis is embedded in the definition of a critical direction used in [5], where v is a critical direction, if it satisfies $f_k^{\circ }(\bar{x};v)\le 0$ for all $k\in K$, $f_k^{\circ }(\bar{x};v)=0$ for at least one $k\in K$, and $g_i^{\circ }(\bar{x};v)\le 0$ for all $i\in I(\bar{x})$. Theorem 3.2 is used in Examples 3.1 and 4.1.

Theorem 3.2

Suppose that $\bar{x}\in D$ is a weak local Pareto minimum for problem (P), the functions $g_i$, $i\notin I(\bar{x})$ are continuous at $\bar{x}$, and the functions $f_k$, $k\in K$, and $g_i$, $i\in I(\bar{x})$, are locally Lipschitz on U.

Then, for every critical direction $v\in X$ satisfying (ZSCQ), there is no $w\in X$ which solves the system

$$\begin{aligned} \left\{ \begin{array}{l} f_k^{\circ }(\bar{x};w)+f_k^{\circ \circ }(\bar{x};v)< 0,\;k\in K(\bar{x};v),\\ g_i^{\circ }(\bar{x};w)+g_i^{\circ \circ }(\bar{x};v)\le 0,\;i\in I(\bar{x};v).\end{array}\right. \end{aligned}$$

(3.4)

Remark 3.1

By Corollary 1 [2], if $\bar{x}$ is a local weak Pareto minimum, then $K(\bar{x};v)\cup I(\bar{x};v)\ne \emptyset$. A strict local Pareto minimum of order two is a weak local Pareto minimum. Thus, under the hypotheses of Theorems 3.1 and 3.2, systems (3.1) and (3.4) exist, respectively.

In Theorem 3.2, we generalize to the nonsmooth multiobjective inequality-constraint optimization problem (P) with locally Lipschitz data the primal necessary conditions of Theorem 4.1 [14] given for problem (P) with continuously differentiable data. If the stronger assumptions of Theorem 4.1 [14] hold, then our assumptions hold too, and the conclusion of our result is the same as the conclusion of Ivanov’s result.

The scalar case of Theorem 3.2 gives stronger second-order necessary conditions than those in Theorem 2 [21] for scalar problems with locally Lipschitz data, and those in Theorem 5 [11] for scalar problems with continuously differentiable data and some second-order directionally differentiable data (see also Remark 2, [21]). The reason is that in Theorem 2 [21] and in Theorem 5 [11], in the unsolvable system, the inequalities corresponding to the inequality constraint functions are strict, but in Theorem 3.2 those inequalities are nonstrict. In Theorem 3.2, we require (ZSCQ), but in Theorem 2 [21] and Theorem 5 [11], no constraint qualification condition or regularity condition was imposed.

Example 3.1

Let $f=(f_1,f_2):\mathbb {R}^2\rightarrow \mathbb {R}^2$, $f_1(x_1,x_2)=|x_1-2x_2|-3x_2+x_1^2+2$, $f_2(x_1,x_2)=|x_1-x_2|+(x_1-x_2)^2+x_2^6+1$, subject to $x\in D=\{x\in \mathbb {R}^2:\;g_1(x)=|x_1|-x_2-x_1^3\le 0,\;g_2(x)=|x_2|-x_1-x_2^4\le 0\}$.

The point $\bar{x}=(0,0)\in D$ is a strict local Pareto minimum of f on D as $f_2(x)>f_2(\bar{x})$ for all $x\in \mathbb {R}^2$, $x\ne \bar{x}$. The critical directions $v=(v_1,v_2)\in \mathbb {R}^2$ at $\bar{x}\in D$ verify $v_1=v_2\ge 0$. For any critical direction v, $I(\bar{x};v)=\{1,2\}$, $K(\bar{x};v)=\{2\}$ if $v\ne 0$, and $K(\bar{x};v)=\{1, 2\}$ if $v=0$.

The second-order necessary conditions for a weak local Pareto minimum are verified at $\bar{x}$ as for a critical direction $v\ne 0$, the systems in Theorem 3 [2] and in Theorem 3.2 have no solution $w=(w_1,w_2)\in \mathbb {R}^2$ because they both contain the inequality $f_2^{\circ }(\bar{x};w)+f_2^{\circ \circ }(\bar{x};v)=|w_1-w_2|+2(v_1-v_2)^2< 0$.

Let v be any critical direction. Since $g_i^{\circ \circ }(\bar{x};v)=0$, $i=1,2$, we have $B(\bar{x}, v)=\{w\in \mathbb {R}^2:\;|w_1|-w_2\le 0,\; |w_2|-w_1\le 0\}=\{w\in \mathbb {R}^2;\; w_1=w_2\ge 0\},$$A(\bar{x}, v)=\{w\in \mathbb {R}^2:\;\exists \,\epsilon >0,\; g_i(tv+\frac{1}{2}t^2w)\le 0,\, i=1,2,\;\forall \,t\in ]0,\epsilon [\}.$ If w is any direction in $B(\bar{x}, v)$, then the inequalities in the definition of the set $A(\bar{x}, v)$ become $|tv_1+\displaystyle \frac{1}{2}t^2w_1|-(tv_1+\displaystyle \frac{1}{2}t^2w_1)-(tv_1+\displaystyle \frac{1}{2}t^2w_1)^3\le 0$ and $|tv_1+\displaystyle \frac{1}{2}t^2w_1|-(tv_1+\displaystyle \frac{1}{2}t^2w_1)-(tv_1+\displaystyle \frac{1}{2}t^2w_1)^4\le 0$, which are both satisfied for any $t>0$ because $tv_1+\displaystyle \frac{1}{2}t^2w_1\ge 0$. So w belongs to the set $A(\bar{x}, v)$ too, and thus, $B(\bar{x}, v)\subseteq A(\bar{x}, v)$. Therefore, (ZSCQ) holds for every critical direction.

For a critical direction $v\ne 0$, i.e., for $v\in \mathbb {R}^2$ with $v_1=v_2>0$, we can find a vector $w\in \mathbb {R}^2$ (for example, $w=(1,1)$), which is a solution of the system formed by the inequalities $f_2^{\circ }(\bar{x};w)+f_2^{\circ \circ }(\bar{x};v)=|w_1-w_2|+2(v_1-v_2)^2\le 0$, $g_1^{\circ }(\bar{x};w)+g_1^{\circ \circ }(\bar{x};v)=|w_1|-w_2\le 0$, $g_2^{\circ }(\bar{x};w)+g_2^{\circ \circ }(\bar{x};v)=|w_2|-w_1\le 0$. Thus, our second-order necessary conditions of Theorem 3.1 are not verified, and (0, 0) is not a strict local Pareto minimum of order two of f on D.

The primal and the dual second-order necessary conditions for a weak local Pareto minimum for (P), given in Theorems 4.1 and 4.2 [14], Theorems 3.2 and 3.3 [12], Theorems 4.1 and 4.2 [16], Theorem 4.1 [17] are not applicable to Example 3.1 because the functions $f_1$, $g_1$, and $g_2$ are not continuously differentiable near $\bar{x}$.

We will show by means of examples that the constraint qualification (ZSCQ) is not related to any of the regularity conditions (GGRC) and (GARC) of [1], the (GACQ) and (GGCQ) of [19], and the Basic Regularity Condition of [18].

Example 3.2

Let us consider the function $f=(f_1,f_2)$, subject to $x\in D=\{(x_1,x_2)\in \mathbb {R}^2:\; g_1(x)\le 0, \;g_2(x)\le 0\}$, where $f_1(x)=x_1^2+x_2^2$, $f_2(x)=x_2^6+x_1^3$, $g_1(x_1,x_2)=|x_1|-x_2-x_1^3$, $g_2(x)=|x_2|-x_1-x_2^4$, and $f_1,\;f_2,\; g_1, \;g_2:\mathbb {R}^2\rightarrow \mathbb {R}$.

The point $\bar{x}=(0,0)\in D$ is a strict local Pareto minimum of order two of $f_1$ on $\mathbb {R}^2$ and thus on D. It follows using Proposition 3.4 [29] that $\bar{x}$ is a strict local Pareto minimum of order two of f on D.

Any critical direction v must verify $|v_1|-v_2\le 0$, $|v_2|-v_1\le 0$, and so, $v_1=v_2\ge 0$. As in Example 3.1, (ZSCQ) is verified for any critical direction.

Let us find the sets $Q^i$, $i=1,2$ considered in [19] and the sets $M^i$, $i=1,2$ considered in [1]. We have $Q^2=M^1=\{x=(x_1,x_2)\in {\mathbb {R}}^2: \,f_1(x)\le 0,\, g_1(x)\le 0,\, g_2(x)\le 0 \}= \{\bar{x}\}$, and $Q^1=M^2=\{x=(x_1,x_2)\in {\mathbb {R}}^2: \,f_2(x)\le 0,\, g_1(x)\le 0, \, g_2(x)\le 0 \}$. Then, $\{\bar{x}\}\subseteq T(M^2,\bar{x})\subseteq \{v=(v_1,v_2)\in \mathbb {R}^2:\,v_1^3\le 0, \; |v_1|-v_2\le 0,\;|v_2|-v_1\le 0\}$. So $T(M^2,\bar{x})=\{\bar{x}\}$. Also, $T(M^1,\bar{x})=\{\bar{x}\}$. We have $Q=M=M_1\cap M_2$, $L(M,\bar{x})=\{v\in \mathbb {R}^2:\, f_1^{\circ }(\bar{x};v)\le 0,\; f_2^{\circ }(\bar{x};v)\le 0,\; g_1^{\circ }(\bar{x};v)\le 0,\, g_2^{\circ }(\bar{x};v)\le 0\}$, and $L(Q,\bar{x})=L(M,\bar{x}) =\{v=(v_1,v_2)\in \mathbb {R}^2:\, v_1=v_2\ge 0\}$.

It follows $L(M,\bar{x})\nsubseteq \text { cl}\,\text {conv}\,T(M^1,\bar{x})$ and $L(M,\bar{x})\nsubseteq \text {cl}\,\text {conv}\,T(M^2,\bar{x})$. So (GGRC) introduced in [1] does not hold at $\bar{x}$. Also, $L(M; \bar{x})\nsubseteq \cap _{i=1}^{2} T(M^i, \bar{x})$. Thus, (GARC) introduced in [1] is not verified at $\bar{x}$.

Since $L(Q,\bar{x})\nsubseteq \cap _{i=1}^2T(Q^i, \bar{x})$, (GACQ) of [19] is not satisfied at $\bar{x}$. Also, $L(Q,\bar{x})\nsubseteq \cap _{i=1}^2\,\text {cl}\,\text {conv}\,T(Q^i, \bar{x})$. Thus, (GGCQ) of [19] is not verified at $\bar{x}$.

In this example, the Basic Regularity Condition introduced by Chandra et. al. ((4) in [18]) is not satisfied at $\bar{x}$ as for any $k\in \{1,2\}=K$, there exist nonzero $\lambda _l\ge 0$, $l\in \{1,2\}$, $l\ne k$, and $\mu _i\ge 0$, $i\in I(\bar{x})$ such that $0\in \sum \nolimits _{l\in K,\, l\ne k}\lambda _l\partial f_l (\bar{x})+\sum \nolimits _{i\in I(\bar{x})}\mu _i\partial g_i(\bar{x})$. Here, for a locally Lipschitz function $F:\mathbb {R}^2\rightarrow \mathbb {R}$, $\partial F(\bar{x}):=\{\xi \in \mathbb {R}^2:\;<\xi ,v>\le F^{\circ }(\bar{x};v),\;\forall \, v\in \mathbb {R}^2 \}$, and $<\xi ,v>$ denotes the dot product of $\xi$ and v. For $k=1$, $\lambda _2=1>0$ and $\mu _1=\mu _2=\displaystyle \frac{1}{2}$ satisfy $0\in \lambda _2\nabla f_2(\bar{x})+\mu _1 \partial g_1(\bar{x})+\mu _2 \partial g_2(\bar{x})$. Similarly, for $k=2$, $\lambda _1=1>0$ and $\mu _1=\mu _2=\displaystyle \frac{1}{2}$ satisfy $0\in \lambda _1\nabla f_1(\bar{x})+\mu _1\partial g_1(\bar{x})+\mu _2 \partial g_2(\bar{x})$.

Example 3.3

Let us consider the function $f=(f_1,f_2):\mathbb {R}^2\rightarrow \mathbb {R}^2$, subject to $x\in D=\{(x_1,x_2)\in \mathbb {R}^2:\; g_1(x)\le 0\}$, where $g_1(x_1,x_2)=|x_1|-x_2-x_1^3$, $f_1(x)=|x_2|$, and $f_2(x)=2x_2+x_2^2+5x_1$.

The point $\bar{x}=(0,0)\in D$ is a local Pareto minimum of f on D. We get $L(M,\bar{x})=\{v\in \mathbb {R}^2: f_1^{\circ }(\bar{x};v)\le 0,\, f_2^{\circ }(\bar{x};v)\le 0,\, g_1^{\circ }(\bar{x};v)\le 0\}=\{\bar{x}\}$, and $L(Q,\bar{x})=L(M,\bar{x})$. Since $\bar{x}\in T(S, \bar{x})$ for any set $S\ne \emptyset$ with $\bar{x}\in S$, the regularity conditions (GGRC), (GARC) we introduced in [1], and the regularity conditions (GACQ) and (GGCQ) due to Giorgi et al. [19] are verified at $\bar{x}$.

The Basic Regularity Condition due to Chandra et al. [18] holds at $\bar{x}$ because for $k=1$, $0\in \lambda _2\nabla f_2(\bar{x})+\mu _1\partial g_1(\bar{x})$ only if $\lambda _2=\mu _1=0$.

The only critical direction at $\bar{x}$ is $v=(0,0)$. We have

$B(\bar{x},v)=\{w=(w_1,w_2)\in \mathbb {R}^2:\;|w_1|-w_2\le 0 \}$. Let $\bar{w}=(-2,2)\in B(\bar{x},v)$. We show that $\bar{w}\notin cl\, A(\bar{x},v)$. Suppose by contradiction that there exists $w_n\in A(\bar{x},v)$ such that $\displaystyle \lim _{n\rightarrow \infty }w_n=\bar{w}$. We have that there exists $\bar{\epsilon }>0$ such that $|w_{1n}|-w_{2n}-\displaystyle \frac{1}{4} t^4w_{1n}^3\le 0$, $\forall \, t\in ]0,\bar{\epsilon }[$. Letting $n\rightarrow \infty$, we obtain $2t^4\le 0$, $\forall \, t\in ]0,\bar{\epsilon }[$, and we arrived at a contradiction. Thus, $\bar{w}\notin \text { cl}\,A(\bar{x},v)$. Therefore, $B(\bar{x},v)\nsubseteq \text {cl}\,A(\bar{x},v)$, i.e., (ZSCQ) does not hold at $\bar{x}$ in the direction v.

4 Dual Necessary Conditions

In this section, we derive dual second-order necessary conditions for a strict local Pareto minimum of order two.

Let the functions $f_k$, $k\in K$, $g_i$, $i\in I(\bar{x})$ locally Lipschitz on U.

We consider the hypotheses below that we introduced in [2]:

$(\text {H}_1)$::

$f_k^{\circ \circ } (\bar{x};v)<\infty$, $k\in K(\bar{x};v)$, $g_i^{\circ \circ } (\bar{x};v)<\infty$, $i\in I(\bar{x};v)$.

$(\text {H}_2)$::

We say that a given direction $v\in X$ verifies hypothesis $(\text {H}_2)$, if there exists a vector $w\in X$ such that $g_i^{\circ }(\bar{x};w)+g_i^{\circ \circ }(\bar{x};v)\le 0$, for all $i\in I(\bar{x};v)$.

Hypothesis $(\text {H}_2)$ is a modification of the constraint qualification (CQ1) due to Luu [4], which extended to locally Lipschitz functions the Ben-Tal constraint qualification [28] for twice continuously differentiable functions.

Theorem 4.1

Consider problem (P) with X a finite-dimensional normed space. Suppose that $\bar{x}\in D$ is a strict local Pareto minimum of order two for problem (P), the functions $g_i$, $i\notin I(\bar{x})$ are continuous at $\bar{x}$, and the functions $f_k$, $k\in K$, and $g_i$, $i\in I(\bar{x})$, are strictly differentiable at $\bar{x}$.

Then, for every nonzero critical direction v verifying (ZSCQ) and ($\text {H}_1$), there exist nonnegative multipliers $\lambda _k$, $k\in K$, $\mu _i$, $i\in I$, $\{\lambda _k,\, \mu _i:\; k\in K, \,i\in I(\bar{x})\}$ not all zeroes, such that $\mu _ig_i(\bar{x})=0,\; i\in I$,

$$\begin{aligned}&\sum _{k\in K}\lambda _k\nabla f_k(\bar{x})+\sum _{i\in I(\bar{x})}\mu _i\nabla g_i(\bar{x})=0, \end{aligned}$$

(4.1)

$$\begin{aligned}&\mu _i\nabla g_i(\bar{x})(v)=0,\, i\in I(\bar{x}),\; \,\lambda _k\nabla f_k(\bar{x})(v)=0,\, k\in K, \end{aligned}$$

(4.2)

$$\begin{aligned}&\sum _{k\in K}\lambda _k f_k^{\circ \circ }(\bar{x}; v)+\sum _{i\in I(\bar{x})}\mu _i g_i^{\circ \circ }(\bar{x}; v)> 0. \end{aligned}$$

(4.3)

Moreover, for any nonzero critical direction v verifying ($\text {H}_1$), ($\text {H}_2$) and (ZSCQ), the multipliers $\{\lambda _k:\;k\in K\}$ are not all equal to zero.

Proof

Let $v\ne 0$ be an arbitrary fixed critical direction satisfying (ZSCQ) and ($\text {H}_1$). By Theorem 3.1, the system below is inconsistent:

$$\begin{aligned} \left\{ \begin{array}{l} \nabla f_k(\bar{x})(w)+f_k^{\circ \circ }(\bar{x};v)\le 0,\;k\in K(\bar{x};v),\\ \nabla g_i(\bar{x})(w)+g_i^{\circ \circ }(\bar{x};v)\le 0,\;i\in I(\bar{x};v).\end{array}\right. \end{aligned}$$

We remove all the inequalities from the above system for which the corresponding second-order upper generalized directional derivative is $-\infty$.

Consider the matrix $\mathbf {A}$ with the rows $\{\nabla f_k(\bar{x}): \; k\in K(\bar{x},v)\}$ and $\{\nabla g_i(\bar{x}): \; i\in I(\bar{x},v)\}$, and the vector $\mathbf {b}$ with the components $\{f_k^{\circ \circ }(\bar{x}; v):\;k\in K(\bar{x};v)\}$ and $\{g_i^{\circ \circ }(\bar{x}; v): \;i\in I(\bar{x};v)\}$.

With these notations, it follows that the linear system $\mathbf {Az}+\mathbf {b}\leqq \mathbf {0}$ has no solution $w\in X$, which is equivalent to the fact that the linear program $\min \{y:\; \mathbf {Aw}+\mathbf {b}\leqq \hat{\mathbf {y}}\}$, where by $\hat{\mathbf {y}}$ is denoted the vector with all the components equal to y, has a positive optimal solution, according to condition ($\text {H}_1$). An equivalent form of the last program is $\min \{y:\;\mathbf {-Aw}+\hat{\mathbf {y}}\geqq \mathbf {b}\}$. By the duality theorem, the dual program $\max \{\mathbf {b}^{T}\varvec{\delta }:\; -\mathbf {A}^{T}\varvec{\delta }=0,\; \sum \nolimits \delta _i=1, \;\delta _i\ge 0\}$ has a positive optimal value, which means that the system $\mathbf {A}^{T}\varvec{\delta }=0, \; \mathbf {b}^{T}\varvec{\delta }> 0$, $\varvec{\delta }\geqq \mathbf {0}, \; \varvec{\delta }\ne \mathbf {0}$, has a solution. Here, the vector $\varvec{\delta }=(\varvec{\lambda }, \varvec{\mu })$ has the same dimension as the vector $\mathbf {b}$ (say n), $\varvec{\lambda }$ has the components $\{\lambda _k:\,k\in K(\bar{x};v)\}$, $\varvec{\mu }$ has the components $\{\mu _i:\;i\in I(\bar{x};v)\}$, $\varvec{A}^T$ is the transpose of the matrix $\varvec{A}$, and $\varvec{\delta }=(\delta _1,\ldots , \delta _n)\geqq \mathbf {0}$ means $\delta _l\ge 0$ for all $l\in \{1,\ldots ,n\}$.

We obtained that there exist $\lambda _k\ge 0$, $k\in K(\bar{x};v)$, $\mu _i\ge 0$, $i\in I(\bar{x};v)$, $\{\lambda _k,\, \mu _i:\;k\in K(\bar{x};v), \,i\in I(\bar{x};v)\}$ not all equal to zero, such that

$$\begin{aligned}&\displaystyle \sum _{k\in K(\bar{x};v)}\lambda _k\nabla f_k(\bar{x})+\sum _{i\in I(\bar{x};v)}\mu _i\nabla g_i(\bar{x})=\mathbf {A}^{T}\mathbf {\delta }=0, \end{aligned}$$

(4.4)

$$\begin{aligned}&\displaystyle \sum _{k\in K(\bar{x};v)}\lambda _k f_k^{\circ \circ }(\bar{x}; v)+\sum _{i\in I(\bar{x};v)}\mu _i g_i^{\circ \circ }(\bar{x}; v)=\mathbf {b}^{T}\mathbf {\delta }> 0. \end{aligned}$$

(4.5)

We take $\lambda _k=0$ for $k\in K\setminus K(\bar{x};v)$, and $\mu _i=0$ for $i\in I(\bar{x})\setminus I(\bar{x};v)$ and for $i\notin I(\bar{x})$. Also, we take $\lambda _k=0$ and $\mu _i=0$ if $k\in K(\bar{x};v)$, $i\in I(\bar{x};v)$, and the corresponding second-order generalized derivative is equal to $-\infty$.

The multipliers $\lambda _1, \ldots , \lambda _p$ verify the equation $\lambda _k\nabla f_k(\bar{x})(v)=0$, for all $k\in K$ because $\lambda _k=0$ for $k\in K\setminus K(\bar{x};v)$, and if $k\in K(\bar{x};v)$, then according to the definition of the set $K(\bar{x};v)$, we have $\nabla f_k(\bar{x})(v)=f_k^{\circ }(\bar{x};v)=0$ because the functions $f_k$, $k\in K$ are assumed to be strictly differentiable at $\bar{x}$. For similar reasons, the multipliers $\mu _1,\ldots ,\mu _m$ verify $\mu _i\nabla g_i(\bar{x})(v)=0,\, i\in I(\bar{x})$.

Next, we want to show that, for any nonzero critical direction v verifying ($\text {H}_1$), ($\text {H}_2$), and (ZSCQ), at least one of the multipliers $\lambda _k$, $k\in K$ is positive. Suppose the contrary, i.e., that there exists such a critical direction v for which all $\{\lambda _k:\;k\in K\}$ are equal to zero. Let w be the vector guaranteed by ($\text {H}_2$). From (4.1) and (4.3), the inequality below follows

$$\begin{aligned} \sum _{k\in K}\lambda _k(\nabla f_k(\bar{x})(w)+ f_k^{\circ \circ }(\bar{x}; v))+\sum _{i\in I(\bar{x})}\mu _i(\nabla g_i(\bar{x})(w) +g_i^{\circ \circ }(\bar{x}; v))> 0. \end{aligned}$$

If we suppose that all $\{\lambda _k:\;k\in K\}$ are equal to zero, then

$$\begin{aligned} \sum _{i\in I(\bar{x})}\mu _i(\nabla g_i(\bar{x})(w)+ g_i^{\circ \circ }(\bar{x}; v))> 0. \end{aligned}$$

Since $\mu _i=0$ for $i\in I(\bar{x})\setminus I(\bar{x};v)$ and $\{\lambda _k,\, \mu _i:\;k\in K(\bar{x};v), \,i\in I(\bar{x};v)\}$ are not all equal to zero, it follows that, for the critical direction v as above, at least one $\mu _i, \,i\in I(\bar{x};v)$ must be positive. Then, due to $(\text {H}_2)$, we arrive at a contradiction. $\square$

Remark 4.1

Theorem 3.1 extends to locally Lipschitz multiobjective problems the primal second-order necessary conditions of Theorem 3 [13] and Theorem 6 [23] for scalar optimization problems. In Theorem 3 [13], all functions are continuously differentiable data, and the active inequality constraint functions are second-order directionally differentiable at $\bar{x}$ in every critical direction. In Theorem 6 [23], the objective function and the active inequality constraint functions are locally Lipschitz near $\bar{x}$, regular and Gâteaux differentiable at $\bar{x}$, and the active inequality constraint functions are second-order Hadamard differentiable at $\bar{x}$ in every critical direction.

In view of Remark 2.1, the scalar cases of Theorems 3.1 and 4.1 improve Theorems 5 and 6, Constantin [21], respectively. In Theorem 6 [21], the objective function and the active inequality constraint functions are locally Lipschitz near $\bar{x}$, regular and Gâteaux differentiable at $\bar{x}$. If the stronger hypotheses of Theorems 5 and 6 [21] hold, then the hypotheses of the scalar cases of Theorems 3.1 and 4.1 hold, respectively, and the conclusions of the corresponding results are the same. In addition, in Theorem 4.1, we derive conditions for at least one of the multipliers corresponding to the objective functions to be strictly positive, but in Theorem 6 [21], we did not give conditions that guarantee that the objective coefficient is different from zero. In Theorems 3.1 and 4.1, we require the weaker condition $B(\bar{x}, v)\subseteq \text {cl}\, A(\bar{x}, v)$ to be satisfied for some critical directions $v\ne 0$, but in Theorems 5 and 6 [21], we required the stronger condition $B(\bar{x}, v)\subseteq A_0(\bar{x}, v)$ to hold for any critical direction $v\ne 0$.

Example 4.1

Let us consider the function $f=(f_1,f_2)$, subject to $x\in D=\{(x_1,x_2)\in \mathbb {R}^2:\; g_1(x)\le 0\}$, where $f_1(x)=(x_1-x_2)^2+x_1^4+2$, $f_2(x)=-x_1^{{4/3}}-x_2^{{6/5}}+x_2^6+x_1$, $g_1(x_1,x_2)=x_1-x_2-x_1^4$, and $f_1,\, f_2:\mathbb {R}^2\rightarrow \mathbb {R}$.

The point $\bar{x}=(0,0)\in D$ is a strict local Pareto minimum of f on $\mathbb {R}^2$, and thus, on D as $f_1(x)>f_1(\bar{x})$ for all $x\in \mathbb {R}^2$, $x\ne \bar{x}$. We want to show that $\bar{x}$ is not a strict local Pareto minimum of order two of f on D.

We have $I(\bar{x})=\{1\}$. The functions $f_1$, $f_2$, and $g_1$ are strictly differentiable at $\bar{x}$, because they are continuously differentiable near $\bar{x}$. The function $f_2$ is not twice differentiable at $\bar{x}$.

The critical directions at $\bar{x}$ are the vectors $v=(v_1,v_2)\in \mathbb {R}^2$ with $v_1\le v_2$, $v_1\le 0$. We get $K(\bar{x},v)=\{1\}$ if $v_1\ne 0$ and $K(\bar{x},v)=\{1,\,2\}$ if $v_1=0$.

For any critical direction v, we have $(f_k)^{\circ \circ } (\bar{x};v)< +\infty ,\;k\in K(\bar{x},v)$ and $(g_i)^{\circ \circ } (\bar{x};v)< +\infty ,\;i\in I(\bar{x},v)$ as $f_1$ and $g_1$ are twice differentiable, $(f_2)^{\circ \circ } (\bar{x};v)=-\infty$ if $v\ne 0$, and $(f_2)^{\circ \circ } (\bar{x};v)=0$ if $v=0$. The point $\bar{x}$ verifies $\displaystyle \sum \nolimits _{k\in K}\lambda _k\nabla f_k(\bar{x})+\displaystyle \sum \nolimits _{i\in \cup I(\bar{x})}\mu _i\nabla g_i(\bar{x})=0$, $\lambda _k\nabla f_k(\bar{x})(v)=0, k\in K$, and $\mu _i\nabla g_i(\bar{x})(v)=0$, $i\in I(\bar{x})$ with any $\lambda _1>0$, $\lambda _2=0$, and $\mu _1=0$.

Let v be a nonzero critical direction such that $v_1=v_2$. Then, $I(\bar{x}, v)=\{1\}$. We have $B(\bar{x}, v)=\{w=(w_1,w_2)\in \mathbb {R}^2:\;w_1-w_2\le 0\}$ as $g_1^{\circ \circ }(\bar{x};v)=0$. Also, $A(\bar{x}, v)=\{w\in \mathbb {R}^2:\;\exists \delta >0, g_1(tv+\displaystyle \frac{1}{2}t^2w)\le 0\; \forall \, t\in ]0,\delta [\}$. If w is any direction in $B(\bar{x}, v)$, then the inequality in the definition of the set $A(\bar{x}, v)$ becomes $(tv_1+\displaystyle \frac{1}{2}t^2w_1)-(tv_2+\displaystyle \frac{1}{2}t^2w_2)-(tv_1+\displaystyle \frac{1}{2}t^2w_1)^4\le 0$, which is obviously satisfied for any $t>0$. Thus, $w\in A(\bar{x}, v)$, and so $B(\bar{x}, v)\subseteq A(\bar{x}, v)$. Therefore, $B(\bar{x}, v)\subseteq \text {cl}\, A(\bar{x}, v)$ for any nonzero critical direction with $v_1=v_2$. (ZSCQ) holds for a critical direction v with $v_1<v_2$ as $I(\bar{x},v)=\emptyset$.

The first-order necessary conditions for a weak local Pareto minimum are satisfied at $\bar{x}$, as the systems of Theorems 4.1 [5] and Theorem 2 [2] have no solution $v\in \mathbb {R}^2$ because they both contain the inequality $f_1^{\circ }(\bar{x};v)<0$. The second-order necessary conditions for a weak local Pareto minimum are verified at $\bar{x}$, as for a critical direction $v\ne 0$, the systems of Theorem 3 [2] and of Theorem 3.2 have no solution $w\in \mathbb {R}^2$ because they both contain the inequality $f_1^{\circ }(\bar{x};w)+f_1^{\circ \circ }(\bar{x};v)=2(v_1-v_2)^2< 0$.

Our second-order necessary condition for a strict local Pareto minimum of order two of Theorem 4.1 is not verified as the second-order expression $\displaystyle \sum \nolimits _{k\in K}\lambda _k (f_k)^{\circ \circ }(\bar{x}; v)+\displaystyle \sum \nolimits _{i\in I(\bar{x})}\mu _i (g_i)^{\circ \circ }(\bar{x}; v)=2\lambda _1(v_1-v_2)^2$ is not strictly positive for any nonzero critical direction v with $B(\bar{x}, v)\subseteq \text {cl} A(\bar{x}, v)$ because $2\lambda _1(v_1-v_2)^2=0$ for any nonzero critical direction v with $v_1=v_2$. Therefore, $\bar{x}$ is not a strict local Pareto minimum of order two of f on D.

In this example, condition (C) of [14] is not verified because for $v=(0,v_2)$, $v_2>0$, which verifies $\nabla f_2(\bar{x})(v)=0$, the second-order directional derivative $f_2^{\prime \prime }(\bar{x},v):=\displaystyle \lim _{t\rightarrow 0^+}\frac{2}{t^2}[f_2(\bar{x}+tv)-f_2(\bar{x})-t\nabla f_2(\bar{x}(v)]=-\infty$, so $f_2^{\prime \prime }(\bar{x},v)$ does not exist as an element of $\mathbb {R}$. Thus, the dual necessary conditions of Theorem 4.2 [14] for a weak local Pareto minimum of problem (P) with inequality constraints and continuously differentiable data are not applicable here. $\square$

5 Sufficient Conditions

In this section, we obtain second-order sufficient conditions for a strict local Pareto minimum of order two.

Theorem 5.1

Consider problem (P) with X a finite-dimensional normed space. Suppose that $\bar{x}\in D$, the functions $g_i$, $i\notin I(\bar{x})$ are continuous at $\bar{x}$, and the functions $f_k$, $k\in K$, and $g_i$, $i\in I(\bar{x})$, are strictly differentiable at $\bar{x}$. Suppose that for every nonzero critical direction $v\in T_{\bar{x}}D$, it holds $(f_k)^{\prime \prime }_+(\bar{x}; v)<\infty$, for all $k\in K$, $(g_i)^{\prime \prime }_+(\bar{x}; v)<\infty$ for all $i\in I(\bar{x})$, and there exist nonnegative multipliers $\lambda _k$, $k\in K$, and $\mu _i$, $i\in I$, not all $\{\lambda _k:\; k\in K\}$ equal to zero with

$$\begin{aligned}&\sum _{k\in K}\lambda _k\nabla f_k(\bar{x})+\sum _{i\in I(\bar{x})}\mu _i\nabla g_i(\bar{x})=0, \end{aligned}$$

(5.1)

$$\begin{aligned}&\sum _{k\in K}\lambda _k (f_k)^{\prime \prime }_-(\bar{x}; v)+\sum _{i\in I(\bar{x})}\mu _i (g_i)^{\prime \prime }_-(\bar{x}; v)> 0. \end{aligned}$$

(5.2)

Then, $\bar{x}$ is a strict local Pareto minimum of order two for problem (P).

Proof

Suppose by contradiction that $\bar{x}\in D$ is not a strict local Pareto minimum of order two for problem (P). By Proposition 3.5, b) [29], there exists a sequence $\{x_n\}_{n\ge 1}\subset D\setminus \{\bar{x}\}$, $x_n\rightarrow \bar{x}$, such that $\displaystyle \lim _{n\rightarrow \infty }\frac{x_n-\bar{x}}{\Vert x_n-\bar{x}\Vert }=v$, $v\in T_{\bar{x}}D$, $\Vert v\Vert =1$, and

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{f(x_n)-f(\bar{x})}{\Vert x_n-\bar{x}\Vert ^2}={d}\in [-\infty ,0]^p. \end{aligned}$$

We denote $t_n=\Vert x_n-\bar{x}\Vert \rightarrow 0^{+}$, and $v_n=\displaystyle \frac{x_n-\bar{x}}{\Vert x_n-\bar{x}\Vert }\rightarrow v$. It follows that $x_n=\bar{x}+t_nv_n\in D$. Then, for ${d}=({d}_1,\ldots , {d}_p)$ and $k\in K$, it holds

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{f_k(x_n)-f_k(\bar{x})}{\Vert x_n-\bar{x}\Vert ^2}={d}_k\in [-\infty ,0]. \end{aligned}$$

If $d_k=-\infty$, then $f_k(x_n)-f_k(\bar{x})<0$, for all n sufficiently large, and $\nabla f_k(\bar{x})(v)=\displaystyle \lim _{n\rightarrow \infty }{[t_n^{-1}}(f_k(x_n)-f_k(\bar{x}))]\le 0$. If $d_k\in \mathbb {R}$, $d_k\le 0$, then $\nabla f_k(\bar{x})(v)=\displaystyle (\lim _{n\rightarrow \infty }t_n)\lim _{n\rightarrow \infty }[t_n^{-2}(f_k(x_n)-f_k(\bar{x}))]=0$.

Moreover, due to the fact that $g_i(x_n)\le 0$, as $x_n\in D$ for all n, we get $\nabla g_i(\bar{x})(v)=\displaystyle \lim _{n\rightarrow \infty }t_n^{-1}(g_i(x_n)-g_i(\bar{x}))=\displaystyle \lim _{n\rightarrow \infty }(t_n^{-1}g_i(x_n))\le 0$. Since the functions are strict differentiable, we get $f_k^{\circ }(\bar{x};v)=\nabla f_k(\bar{x})(v)\le 0$, for all $k\in K$, and $g_i^{\circ }(\bar{x};v)=\nabla g_i(\bar{x})(v)\le 0$, for all $i\in I(\bar{x})$. So v is a critical direction. Then,

$$\begin{aligned}&\sum _{k\in K}\lambda _k (f_k)^{\prime \prime }_-(\bar{x}; v)+\sum _{i\in I(\bar{x})}\mu _i (g_i)^{\prime \prime }_-(\bar{x}; v)\\&\quad \le \sum _{k\in K}\lambda _k \liminf _{n\rightarrow \infty }\left( \frac{2}{t_n^2}(f_k(\bar{x}+t_nv_n)-f_k(\bar{x})-t_n\nabla f_k(\bar{x})(v)\right) \\&\qquad +\sum _{i\in I(\bar{x})}\mu _i\liminf _{n\rightarrow \infty } 2t_n^{-2}(g_i(\bar{x}+t_nv_n)-g_i(\bar{x})-t_n\nabla g_i(\bar{x})(v))\\&\quad \le \liminf _{n\rightarrow \infty }2t_n^{-2}\left[ \sum _{k\in K}\lambda _kf_k(\bar{x}+t_nv_n)-\sum \lambda _kf_k(\bar{x})-t_n\sum _{k\in K}\lambda _k\nabla f_k(\bar{x})(v)\right. \\&\qquad \left. +\sum _{i\in I(\bar{x})}\mu _ig_i(\bar{x}+t_nv_n)-\sum _{i\in I(\bar{x})}\mu _ig_i(\bar{x})-t_n\sum _{i\in I(\bar{x})}\mu _i\nabla g_i(\bar{x})(v)\right] \\&\quad = \liminf _{n\rightarrow \infty }2t_n^{-2}\left[ \sum _{k\in K}\lambda _kf_k(\bar{x}+t_nv_n)-\sum \lambda _kf_k(\bar{x})+\sum _{i\in I(\bar{x})}\mu _ig_i(\bar{x}+t_nv_n)\right] \\&\quad \le \liminf _{n\rightarrow \infty }2t_n^{-2}\left[ \sum _{k\in K}\lambda _kf_k(\bar{x}+t_nv_n)-\sum \lambda _kf_k(\bar{x})\right] \\&\quad =\sum _{k\in K}\lambda _k\left\{ \lim _{n\rightarrow \infty }2t_n^{-2}\left[ f_k(\bar{x}+t_nv_n)-f_k(\bar{x})\right] \right\} =2\sum _{k\in K}\lambda _kd_k\le 0, \end{aligned}$$

as $d_k\in [-\infty ,0]$, $k\in K$, and $\lambda _k\ge 0$, $k\in K$. We arrived at a contradiction. $\square$

Remark 5.1

The existence of nonnegative multipliers $\lambda _k$, $k\in K$, and $\mu _i$, $i\in I$, verifying conditions (5.1) and $\mu _ig_i(\bar{x})=0$, $i\in I$, implies that $\lambda _k\nabla f_k(\bar{x})(v)=0$, $k\in K$ and $\mu _i\nabla g_i(\bar{x})(v)=0$, $i\in I$, for any critical direction v.

Remark 5.2

In view of Remark 2.1, the scalar case of Theorem 5.1 improves Theorem 4 [23], for scalar optimization problems with locally Lipschitz, regular, and Gâteaux differentiable objective and active constraint functions, and with second-order Hadamard differentiable active inequality constraint functions. In [23], a locally Lipschitz function $F:X\rightarrow \mathbb {R}$ is second-order Hadamard directionally differentiable at $\bar{x}$ in a direction $v\in X$, if there exists the limit $F_I^{\prime \prime }(x;v):=\displaystyle \lim _{(t,v^{\prime })\rightarrow (0^+,v)}2t^{-2}[F(x+tv^{\prime })-F(x)-tF^{\circ }(x;v)]$ as an element of $\mathbb {R}$. In our results, we do not require any of the functions to be second-order differentiable in any sense. If the functions involved verify all the additional hypotheses of Theorem 4 [23], then the conclusion of the scalar case of Theorem 5.1 coincides to the conclusion of Ivanov’s result.

Recently, Feng–Li [10] have presented second-order sufficient conditions for a strict local Pareto minimum of order two for multiobjective optimization problems with equality and inequality constraints. In Feng–Li [10], all the functions are continuously differentiable with stable derivatives and radial second-order directional derivatives in any critical contingent direction. In Feng–Li [10] as in Ivanov [14], the second-order radial directional derivative of a function $f:X\rightarrow \mathbb {R}^p$, that is Fréchet differentiable at $\bar{x}$, is defined as an element of $\mathbb {R}^p$ by $f^{\prime \prime }(\bar{x},v):=\displaystyle \lim _{t\rightarrow 0^+}{2}t^{-2}[f(\bar{x}+tv)-f(\bar{x})-t\nabla f(\bar{x})(v)]$. We require only strict differentiability in sense of Clarke of the data, so our sufficient conditions improve the ones due to Feng–Li [10] in the case of multiobjective problems with inequality constraints.

Example 5.1

Let us consider the function $f=(f_1,f_2):\mathbb {R}^2\rightarrow \mathbb {R}$ subject to $x\in D=\{x\in \mathbb {R}^2:\; g(x)=-x_1^{{6/5}}+x_2^6-x_2^{{4/3}}\le 0\}$, where $f_1(x)=-|x_2|$ and $f_2(x)=x_1^2+x_2^2$.

Clearly, $\bar{x}=(0,0)$ is a strict local Pareto minimum of order two of $f_2$ on $\mathbb {R}^2$, and thus, on D. The scalar case of Theorem 5.1 is applicable to the scalar problem of minimizing $f_2$ over D because $f_2$ and g are continuously differentiable, so strictly differentiable, $(f_2)^{\prime \prime }_{+}(\bar{x};v)=2v_1^2+2v_2^2<\infty$, for any $v=(v_1,v_2)\in \mathbb {R}^2$, and $(g)^{\prime \prime }_{+}(\bar{x};v)=-\infty <\infty$, for any $v\ne 0$. There exist nonnegative multipliers $\mu =0$ and $\lambda$ any positive real number such that $\lambda \nabla f_2(\bar{x})+\mu \nabla g(\bar{x})=0$ and $\lambda (f_2)^{\prime \prime }_-(\bar{x}; v)+\mu (g)^{\prime \prime }_-(\bar{x}; v)=2(v_1^2+v_2^2)> 0$ for any nonzero $v=(v_1,v_2)\in \mathbb {R}^2$, and, in particular, for any contingent critical direction $v\ne 0$. Here, $\mu =0$ because $(g)^{\prime \prime }_-(\bar{x}; v)=-\infty$ if $v\ne 0$, and we accept $0\times (-\infty )=0$. Thus, the scalar case of Theorem 5.1 helps us recognize $\bar{x}$ as a strict local Pareto minimum of order two of $f_2$ on D. Then, due to Proposition 3.4 [29], $\bar{x}$ is a strict local Pareto minimum of order two of f on D.

This example cannot be analyzed by means of the theory developed in Bigi [32], because g is not twice differentiable at $\bar{x}$. The necessary and sufficient second-order conditions due to Feng–Li (Theorems 4.1, 4.2, 5.1, 5.2, [10]) cannot be applied because $f_1$ is not continuously differentiable near $\bar{x}$ with stable derivative at $\bar{x}$, $g^{\prime \prime }(\bar{x},v)$ does not exist as an element of $\mathbb {R}$, and $f_1$ does not possess a radial second-order directional derivative. $\square$

6 Conclusions

We obtained optimality conditions for a strict local Pareto minimum of order two for an inequality-constrained multiobjective problem with locally Lipschitz data. All our conditions are of second-order and do not require the data to be second-order differentiable in any sense. We have extended some results from [10, 14, 21, 23]. We analyzed examples which cannot be solved using the results from [1, 2, 4, 12,13,14,15,16,17,18,19,20,21,22,23, 32].