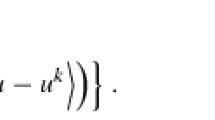Cauchy Noise Removal by Nonconvex ADMM with Convergence Guarantees

Abstract

Image restoration is one of the essential tasks in image processing. In order to restore images from blurs and noise while also preserving their edges, one often applies total variation (TV) minimization. Cauchy noise, which frequently appears in engineering applications, is a kind of impulsive and non-Gaussian noise. Removing Cauchy noise can be achieved by solving a nonconvex TV minimization problem, which is difficult due to its nonconvexity and nonsmoothness. In this paper, we adapt recent results in the literature and develop a specific alternating direction method of multiplier to solve this problem. Theoretically, we establish the convergence of our method to a stationary point. Experimental results demonstrate that the proposed method is competitive with other methods in visual and quantitative measures. In particular, our method achieves higher PSNRs for 0.5 dB on average.

1 Introduction

In many imaging applications, images inevitably contain natural non-Gaussian noises, such as impulse noise, Poisson noise, multiplicative noise, and Cauchy noise. At the same time, the images may have been blurred by the point spread function (PSF) during their acquisition. Therefore, the image restoration problem is an essential task. Researchers have proposed many methods to deblur and denoise images; see [12, 16, 17, 27, 35, 36, 41, 54] and references therein. In this paper, we focus on recovering images corrupted by blurring and Cauchy noise. Cauchy noise usually arises in echo of radar, in the presence of low-frequency atmospheric noise, and in underwater acoustic signals [26, 31, 40]. According to [44, 45], it follows Cauchy distribution and is impulsive.

We assume that the original gray-scale image u is defined on a connected bounded domain $\Omega \subset {\mathbb {R}}^2$ with a compacted Lipschitz boundary. The observed image with blurs and Cauchy noise is given as follows:

$$\begin{aligned} f = Ku + \eta , \end{aligned}$$

(1)

where $f\in L^2(\Omega )$ denotes the observed image, $K\in {\mathcal {L}}(L^1(\Omega ),L^2(\Omega ))$ represents a known linear and continuous blurring (or convolution) operator, and $\eta \in L^2(\Omega )$ denotes Cauchy noise. Our goal is to recover u from the observed image f.

In recent years, much attention has been given to Cauchy noise removal, and several methods have been proposed. In [13], the authors applied a recursive algorithm based on the Markov random field to reconstruct images and retain sharp edges. In 2005, Achim and Kuruoǧlu utilized a bivariate maximum a posteriori estimator (BMAP) to propose a new statistical model in the complex wavelet domain for removing Cauchy noise [1]. In [34], Loza et al. proposed a statistical approach based on non-Gaussian distributions in the wavelet domain for tackling the image fusion problem. Their method achieved a significant improvement in fusion quality and noise reduction. In [46], Wan et al. developed a novel segmentation method for RGB images that are corrupted by Cauchy noise. They combined statistical methods with denoising techniques and obtained a satisfactory performance. Since TV regularization is able to preserve edges effectively while still suppressing noise satisfactorily [21], Sciacchitano et al. proposed a convex TV-based variational method for recovering images corrupted by Cauchy noise in [42]. The variational model in this method is as follows:

$$\begin{aligned} \min _{u\in BV(\Omega )} \int _\Omega |Du|+ \frac{\lambda }{2}\left( \int _\Omega \log \left( \gamma ^2+(u-f)^2\right) dx+\alpha \Vert u-\tilde{u}\Vert _2^2\right) , \end{aligned}$$

(2)

where $\gamma >0$ is the scale parameter of Cauchy distribution, and $BV(\Omega )$ is the space of functions of bounded variation. Here, $u\in BV(\Omega )$ if $u\in L^1(\Omega )$ and its total variation (TV)

$$\begin{aligned} \int _\Omega |Du|\triangleq \sup \bigg \{\int _\Omega u\;\mathrm {div} \mathbf {v} \; dx:\mathbf {v}\in \left( C_0^\infty (\Omega )\right) ^2,\Vert \mathbf {v}\Vert _{\infty }\le 1\bigg \} \end{aligned}$$

is finite, where $(C_0^\infty (\Omega ))^2$ is the space of vector-valued functions with compact support in $\Omega$. The space $BV(\Omega )$ endowed with the norm $\Vert u\Vert _{BV(\Omega )}=\Vert u\Vert _{L^1(\Omega )}+\int _\Omega |Du|$ is a Banach space; see, e.g., [21]. In (2), $\lambda$ denotes the positive regularization parameter, which controls the trade-off between TV regularization and the fitting to f and $\tilde{u}$, $\tilde{u}$ is the result obtained by the median filter, and $\alpha$ is a positive penalty parameter. Note that if $8\alpha \gamma ^2\ge 1$, the objective functional in (2) is strictly convex and leads to a unique solution. Because of strict convexity, the model avoids the common issues of nonconvex optimization: the solutions depend on the numerical methods and how they are initialized. But the last term in (2) in fact pushes the solution close to the median filter result, and the median filter does not always provide satisfactory removals of Cauchy noise. Hence, in this paper we turn our focus back to a nonconvex model.

Recently, researchers have discovered some useful convergence properties of the optimization algorithms for solving nonconvex minimization problems [24, 47, 48, 53]. In particular, the paper [48] established the global convergence (to a stationary point) of the alternating direction method of multipliers (ADMM) for nonconvex nonsmooth optimization with linear constraints. To take advantages of the recent results, in this paper we develop the ADMM algorithm to solve the following nonconvex variational model directly for denoising and deblurring simultaneously:

$$\begin{aligned} \min _{u\in BV(\Omega )} \int _\Omega |Du|+ \frac{\lambda }{2}\int _\Omega \log \left( \gamma ^2+(Ku-f)^2\right) dx. \end{aligned}$$

(3)

We prove that our algorithm starting from any initialization is globally convergent to a stationary point under certain conditions. Furthermore, we compare our proposed method to the state-of-the-art method proposed in [42] and show the effectiveness of our method in terms of restoration quality and noise reduction.

The outline of the paper is summarized as follows. In the next section, we analyse some fundamental properties of Gaussian distribution, Laplace distribution and Cauchy distribution. In Sect. 3, we illustrate the nonconvex variational model for denoising and deblurring, and prove the existence and uniqueness of the solution. In Sect. 4, we develop our algorithm for the proposed nonconvex model and present the convergence results. In Sect. 5, we demonstrate the performance of our algorithm by comparing with other existing algorithms. Finally, we conclude the paper with some remarks in Sect. 6.

2 Statistical Properties for Cauchy Distribution

The Cauchy distribution is a special kind of the $\alpha$-stable distributions with $\alpha =1$ and is important as a canonical example of the “pathological” case [3, 15, 29]. It is closed under linear fractional transformations with real coefficients [30]. However, different from most $\alpha$-stable distributions, it possesses a probability density function that can be expressed analytically [19, 28] as:

$$\begin{aligned} P_C(x)=\frac{\gamma }{\pi \left( (x-\mu )^2+\gamma ^2\right) }, \end{aligned}$$

where the parameter $\mu$ specifies the location of the peak and the parameter $\gamma >0$ decides the half-width at half-maximum. Here, we let $\mathcal {C}(\mu ,\gamma )$ denote the Cauchy distribution. Its mode and median are both $\mu$ while the mean, variance, and higher moments are undefined. In addition, the Cauchy distribution is infinitely divisible, that is, for every positive integer n, there exist n independent identically distributed (i.i.d.) random variables $X_{n1},X_{n2},\ldots X_{nn}$ such that $X_{n1}+X_{n2}+\cdots +X_{nn}$ follows the Cauchy distribution. Due to their infinite divisibility, random variables following the Cauchy distribution obey the generalized central limit theorem [37].

The Cauchy distribution is closely related to some other probability distributions. The Cauchy distribution is heavy-tailed, and its tail’s heaviness is determined by the scale parameter $\gamma$. In particularly, if X and Y are two independent Gaussian random variables with mean 0 and variance 1, then the ratio X / Y follows the standard Cauchy distribution $\mathcal {C}(0,1)$ [6, 38]. In Sect. 5, we will apply this property to simulate images corrupted by Cauchy noise.

Further to show the statistical properties of the Cauchy distribution, we compare it with two most commonly used probability distributions: the Gaussian distribution (${\mathcal {N}}(\mu ,\sigma ^2)$ with mean $\mu$ and variance $\sigma ^2$) and the Laplace distribution ${\mathcal {L}}(\mu ,b)$ with mean $\mu$ and variance $2b^2$. Since the Gaussian and Cauchy distributions are $\alpha$-stable distributions with $\alpha =2$ and $\alpha =1$, respectively, they are both bell-shaped. Moreover, we can easily obtain the following relation between them at $x=0$.

Proposition 2.1

Let $X_{1}$ and $X_{2}$ be two independent random variables. Assume that $X_{1}\sim {\mathcal {N}}(0,1)$ and $X_{2}\sim \mathcal {C}(0,\sqrt{\frac{2}{\pi }})$. Then the values of their probability density functions (PDFs) at $x=0$ are equal.

In addition, both the Laplace and Cauchy distributions are heavy-tailed distributions. We demonstrate their relation by the tails of their distribution curves in the following proposition.

Proposition 2.2

Let $P_{G}$, $P_{L}$ and $P_{C}$ denote the PDFs for ${\mathcal {N}}(0,\sigma ^{2})$, ${\mathcal {L}}(0,b)$ and $\mathcal {C}(0,\sqrt{\frac{2}{\pi }})$, respectively. Then, the followings hold:

• 1. At $x=\sigma =b=\gamma$, the ratio of $P_G$, $P_L$ and $P_C$ is $1:\sqrt{\frac{\pi }{2e}}:\sqrt{\frac{e}{2\pi }}$;

• 2. At $x=3\sigma =3b=3\gamma$, the ratio of $P_G$, $P_L$ and $P_C$ is $1:\sqrt{\frac{\pi }{2}}e^{\frac{3}{2}}:\sqrt{\frac{1}{50\pi }}e^{\frac{9}{2}}$.

Based on Proposition 2.2, we can see that the probability density value of the Gaussian distribution at a rather small x, saying $x=\sigma =b=\gamma$, is the largest, which shows that the additive Gaussian noise tends to mainly produce small perturbations. However, at larger x, saying $x=3\sigma =3b=3\gamma$, the density of the Laplace distribution is more than 5 times that of the Gaussian distribution, and the density of the Cauchy distribution is even more than 7 times. Hence, the Laplace and Cauchy distributed additive noise tend to corrupt images with high perturbations.

Fig. 1

Comparison for probability density functions of ${\mathcal {N}}(0,1)$, ${\mathcal {L}}(0,\sqrt{\frac{2}{\pi }})$ and $\mathcal {C}(0,\sqrt{\frac{2}{\pi }})$. a The plots of three distributions, b the zoomed-in portion of the curves around the peaks, c the zoomed-in portion of the curves around the tails

Figure 1 depicts the PDFs of the Gaussian, Laplace, and Cauchy distributions. From Fig. 1a, we see that these three distributions have different behaviours at the peaks and tails. See the details in the zoom-ins. Figure 1b depicts the portion around the peaks of the three distributions. The Gaussian distribution has the same peak as the Cauchy distribution while the density of the Gaussian distribution is slightly higher on both sides of the peak. Figure 1c depicts the portion around the tails of the three distributions. The tail of the Laplace distribution is closer to that of the Cauchy distribution than Gaussian distribution, but there still exists a big gap between the densities of the Laplace and Cauchy distributions. Therefore, the Cauchy distribution cannot be simply replaced with the Gaussian or Laplace distribution during image restoration.

3 Nonconvex Variational Model

This section describes our model of deblurring and denoising. In [42], a variational model for denoising was proposed. To make our exposition self-contained, we deduce a similar nonconvex variational model for deblurring and denoising based on the maximum a posteriori (MAP) estimator and Bayes’ rule.

3.1 Nonconvex Variational Model Via MAP Estimator

We consider f(x) and u(x) as random variables for each $x\in \Omega$. The MAP estimator of u is the most likely value of u given f, i.e., $u^*=\arg \max _u P(u|f)$. Based on Bayes’ rule and the independence of u(x) and f(x) for all $x\in \Omega$, we obtain

$$\begin{aligned} \begin{aligned} \mathop {\arg \max }_u P(u|f)&=\mathop {\arg \max }_u \frac{P(f|u)P(u)}{P(f)}\\&= \mathop {\arg \min }_u -\log P(f|u)-\log P(u)\\&=\mathop {\arg \min }_u -\int _{\Omega } \log P(f(x)|u(x))\ dx -\log P(u), \end{aligned} \end{aligned}$$

(4)

where the term $\log P(f(x)|u(x))$ describes the degradation process that produces f from u based on (1), and $\log P(u)$ is the prior on u. Since $\eta (x)$ follows $\mathcal {C}(0,\gamma )$ for each $x\in \Omega$, we have

$$\begin{aligned} P(f(x)|u(x))=\frac{\gamma }{\pi \left( ((Ku)(x)-f(x))^2+\gamma ^2\right) }. \end{aligned}$$

In addition, we use the prior $P(u)=\exp (-\frac{2}{\lambda } \int _\Omega |Du|)$. Then, we arrive at the variational model for deblurring and denoising:

$$\begin{aligned} \min _{u\in BV(\Omega )} \frac{\lambda }{2}\int _\Omega \log \left( (Ku-f)^2+\gamma ^{2}\right) \ dx+\int _\Omega |Du|, \end{aligned}$$

(5)

where $\lambda >0$ is the regularization parameter. Although $\int _\Omega |Du|$ is convex, due to the logarithm in the data-fitting term, $\int _\Omega \log \left( \gamma ^2+(Ku-f)^2\right) \ dx$ is nonconvex. Therefore, the numerical solution of (5) depends on the numerical approach and how it is initialized.

3.2 Solution Existence and Uniqueness of the Model (5)

According to the properties of the total variation, we prove that there exists at least one solution for the nonconvex variational problem in the BV space.

Theorem 3.1

Assume that $\Omega$ is a connected bounded set with compacted Lipschitz boundary and $f\in L^2(\Omega )$. Suppose that $K\in {\mathcal {L}}(L^1(\Omega ),L^2(\Omega ))$ is nonnegative and linear with $K\mathbf {1}\ne 0$. Then the model (5) has at least one solution $u^*\in BV(\Omega )$.

Proof

Let $E(u)=\int _\Omega |Du|+ \frac{\lambda }{2}\int _\Omega \log \left( \gamma ^2+(Ku-f)^2\right) \ dx$. Obviously, E(u) is bounded from below. For a minimizing sequence $\{u^k\}$, we know that $E(u^k)$ is bounded, so both $\left\{ \int _\Omega |Du^k|\right\}$ and $\int _\Omega \log \left( \gamma ^2+(Ku^k-f)^2\right) \ dx$ are bounded.

Now we apply proof by contradiction to show that $\{Ku^k\}$ is bounded in $L^2(\Omega )$ and therefore also bounded in $L^1(\Omega )$. Assume that $\Vert Ku^k\Vert _{2}=+\infty$, so there exists a set $E\subset \Omega$, whose measure is not zero, such that for any $x\in E$ we have $Ku^{k}(x)=+\infty$. Then, with $f\in L^{2}(\Omega )$ we will also have $\log \left( \gamma ^2+(Ku^k(x)-f(x))^2\right) =+\infty$ for all $x\in E$, which derives a contradiction with $\int _\Omega \log \left( \gamma ^2+(Ku^k-f)^2\right) \ dx<+\infty$.

Based on $\left\{ \int _\Omega |Du^k|\right\}$ being bounded, by the Poincaré inequality [2], we have

$$\begin{aligned} \Vert u^k-m_\Omega (u^k)\Vert _2\le C\int _\Omega \left| D\left( u^k-m_\Omega (u^k)\right) \right| =C\int _\Omega |Du^k|, \end{aligned}$$

(6)

where $m_\Omega (u^k)=\frac{1}{|\Omega |}\int _\Omega u^kdx$, C is a positive constant, and $|\Omega |$ represents the measure of $\Omega$. As $\Omega$ is bounded, $\Vert u^k-m_\Omega (u^k)\Vert _2$ and $\Vert u^k-m_\Omega (u^k)\Vert _1$ are bounded for each k. Because $K\in {\mathcal {L}}(L^1(\Omega ),L^2(\Omega ))$ is continuous, we have that $\{K(u^k-m_\Omega (u^k))\}$ is bounded in $L^2(\Omega )$ and $L^1(\Omega )$. Thus, we conclude

$$\begin{aligned} |m_\Omega (u^k)|\cdot \Vert K\mathbf {1}\Vert _1\le \left\| K\left( u^k-m_\Omega (u^k)\right) \right\| _1+\Vert Ku^k\Vert _1. \end{aligned}$$

Due to $K\mathbf {1}\ne 0$, $m_\Omega (u^k)$ is uniformly bounded. Combining with (6), this gives that the sequence $\{u^k\}$ is bounded in $L^2(\Omega )$ and in $L^1(\Omega )$. Recalling that $\left\{ \int _\Omega |Du^k|\right\}$ is bounded, we obtain the boundedness of $\{u^k\}$ in $BV(\Omega )$.

Therefore, there exists a subsequence $\{u^{n_k}\}$ in $BV(\Omega )$ that converges strongly in $L^1(\Omega )$ to some $u^*\in BV(\Omega )$ as $k\rightarrow \infty$, while $\{Du^{n_k}\}$ converges weakly as a measure to $Du^*$. Since K is linear and continuous, $\{Ku^{n_k}\}$ converges strongly to $Ku^*$ in $L^2(\Omega )$. By the lower semicontinuity of total variation and Fatou’s lemma, we conclude that $u^*$ is a solution of the model (5). $\square$

Although the objective function in (5) is nonconvex, we are still able to obtain a result on the uniqueness of the solution.

Theorem 3.2

Assume that $f\in L^2(\Omega )$ and K is injective. Then, the model (5) has a unique solution $u^*$ in $\Omega _U:=\{u\in BV(\Omega ): f(x)-\gamma<(Ku)(x)<f(x)+\gamma \text{ for } \text{ all } x\in \Omega \}$.

Proof

For each fixed $x\in \Omega$, we define a function $g: {\mathbb {R}}\rightarrow {\mathbb {R}}$:

$$\begin{aligned} g(t)=\log \left( \gamma ^2+(t-f(x))^2\right) . \end{aligned}$$

Since the second order derivative of g:

$$\begin{aligned} g''(t)=\frac{2\left( \gamma ^2-(t-f(x))^2\right) }{\left( \gamma ^2+(t-f(x))^2\right) ^2} \end{aligned}$$

is positive when $f(x)-\gamma<t<f(x)+\gamma$, g is strictly convex in this case. Since K is injective, we have that, if $f(x)-\gamma<(Ku)(x)<f(x)+\gamma$, g((Ku)(x)) is strictly convex. By the convexity of TV and linearity of K, the objective function of the model (5) is strictly convex in $\Omega _U$. Hence, there exists a unique solution for the model (5) in $\Omega _U$. $\square$

Note that Cauchy noise is so impulsive that, even with a small $\gamma$, many points in f are still heavily corrupted and thus some impulsive noise is still left in the images in $\Omega _U$. If we also take the smoothing property of K into account, then the unique solution in $\Omega _U$ will not be satisfactory. In Sect. 5.1, we will demonstrate this point numerically.

4 Proposed ADMM Algorithm

Due to the nonconvexity of the variational model (5), different numerical algorithms and initializations may yield different solutions. Taking advantage of the recent result in [48], in this section we apply the ADMM algorithm to the minimization problem (5), which restores images degraded by blurring and Cauchy noise. Then, we prove that the proposed algorithm is globally convergent to a stationary point.

4.1 The ADMM Algorithm for Nonconvex and Nonsmooth Problem

We briefly review the ADMM algorithm and its recent convergence result under nonconvexity and nonsmoothness.

Let $\mathbf {x}=[x_1^\top , \cdots , x_s^\top ]^\top \in {\mathbb {R}}^N$ and $\mathbf {A}=[A_1,\cdots ,A_s]\in {\mathbb {R}}^{M\times N}$ where $x_i\in {\mathbb {R}}^{n_i}$, $A_i\in {\mathbb {R}}^{M\times n_i}$, $\sum _{i=1}^s n_i=N$. We consider the minimization problem formulated as:

$$\begin{aligned}&\min _{\mathbf {x},y} \mathcal {F}(\mathbf {x})+\mathcal {G}(y)\\&\quad \text {s.t. } \mathbf {A}\mathbf {x}+By=0, \nonumber \nonumber \end{aligned}$$

(7)

where $\mathcal {F}(\mathbf {x})$ is a continuous function, $\mathcal {G}(y)$ is a differentiable, and $y\in {\mathbb {R}}^L$ is a variable with the corresponding coefficient $B\in {\mathbb {R}}^{M\times L}$. In general, $\mathcal {F}$ can be nonsmooth and nonconvex, and $\mathcal {G}$ can be nonconvex (but is differentiable as stated). By introducing a Lagrangian multiplier $w\in {\mathbb {R}}^M$ for the linear constraint $\mathbf {A}\mathbf {x}+By=0$, we obtain the augmented Lagrangian:

$$\begin{aligned} {\mathcal {L}}_\beta (\mathbf {x},y;w)=\mathcal {F}(\mathbf {x}) +\mathcal {G}(y)+w^\top (\mathbf {A}\mathbf {x}+By)+ \frac{\beta }{2}\Vert \mathbf {A}\mathbf {x}+By\Vert _2^2, \end{aligned}$$

where $\beta >0$ is a penalty parameter.

Extending from the classic ADMM [7, 20], the multi-block ADMM generates the iterates $(\mathbf {x}^{k+1},y^{k+1})$ by

$$\begin{aligned} \left\{ \begin{aligned}\ x_1^{k+1}&\in \mathop {\arg \min }_{x_1} {\mathcal {L}}_\beta \left( x_1,x_2^k,\cdots ,x_s^k,y^k;w^k\right) \\ \vdots \quad&\in \quad \vdots \qquad \vdots \\ x_s^{k+1}&\in \mathop {\arg \min }_{x_s}{\mathcal {L}}_\beta \left( x_1^{k+1}, x_2^{k+1},\cdots ,x_s,y^k;w^k\right) \\ y^{k+1}&\in \mathop {\arg \min }_{y} {\mathcal {L}}_\beta \left( \mathbf {x}^{k+1},y;w^k\right) \\ w^{k+1}&=w^k+\beta \left( \mathbf {A}\mathbf {x}^{k+1}+By^{k+1}\right) , \end{aligned} \right. \end{aligned}$$

(8)

where we use $\in \mathop {\arg \min }$ when minimizers are not necessarily unique (in which case, any minimizer is fine). The general assumption is that all subproblems have minimizers. The convergence result of the ADMM algorithm under nonconvexity and nonsmoothness is summarized as follows [48]. We present the conditions that are simplified to fit our need yet more restrictive than those in [48].

Theorem 4.1

Let $\mathcal {D}=\left\{ (\mathbf {x},y)\in {\mathbb {R}}^{N+L}:\mathbf {A}\mathbf {x}+By=0\right\}$ be a nonempty feasible set. Assume $\mathcal {F}(\mathbf {x})+\mathcal {G}(y)$ is $\mathcal {D}$-coercive, that is, for $(\mathbf {x},y)\in \mathcal {D}$, $\mathcal {F}(\mathbf {x})+\mathcal {G}(y)\rightarrow \infty$ as $\Vert (\mathbf {x},y)\Vert \rightarrow \infty$. Also, assume that $\mathbf {A}$, B have full column rank¹ and $Im(\mathbf {A})\subset Im(B)$. Further assume that $\mathcal {F}(\mathbf {x})$ is either restricted prox-regular² or piecewise linear, and $\mathcal {G}(y)$ is Lipschitz differentiable with the constant $L_{\nabla \mathcal {G}}>0$. Then, for any $\beta$ larger than a certain constant $\beta _0$ and starting from any initialization $(\mathbf {x}^0,y^0,w^0)$, ADMM (8) produces a sequence of iterates that has a convergent subsequence, whose limit is a stationary point $(\mathbf {x}^*,y^*,w^*)$ of the augmented Lagrangian ${\mathcal {L}}_\beta (\mathbf {x},y;w)$. If in addition ${\mathcal {L}}_\beta$ satisfies the Kurdyka–Łojasiewicz (KL) inequality [4, 8, 32, 33], then the result improves to global convergence to that stationary point.

4.2 The ADMM Algorithm for Solving (5)

Taking advantage of the ADMM convergence result, we apply it to solve the nonconvex variational model in (5) for simultaneous denoising and deblurring. Hereafter, we switch to the discrete form, but, for the sake of simplicity, we still use the same letters defined in the continuous context. We assume that the discrete image domain $\Omega$ contains $n\times n$ pixels. The discrete minimization nonconvex model of (5) is formulated as follows:

$$\begin{aligned} \min _{u\in {\mathbb {R}}^{{n^{2}}}} \Vert \nabla u\Vert _1+\frac{\lambda }{2}\left\langle \log \left( \gamma ^2+(Ku-f)^2\right) ,\mathbf {1}\right\rangle , \end{aligned}$$

(9)

where $f\in {\mathbb {R}}^{n^2}$ is obtained by stacking the columns of the corresponding $n\times n$ gray-scale image, and $K\in {\mathbb {R}}^{n^2\times n^2}$. The TV regularization $\Vert \nabla u\Vert _1$ is defined as:

$$\begin{aligned} \Vert \nabla u\Vert _1=\sum _{i=1}^{n^2}\sqrt{(\nabla _x u)_{i}^2+(\nabla _y u)_{i}^2}, \end{aligned}$$

where $\nabla _x\in {\mathbb {R}}^{n^2\times n^2}$ and $\nabla _y\in {\mathbb {R}}^{n^2\times n^2}$ are the discrete first order forward differences in the x- and y-directions, respectively. The discrete gradient of u, $\nabla u$, is defined as $\nabla u=[(\nabla _x u)^{\top }, (\nabla _y u)^{\top }]^{\top }\in {\mathbb {R}}^{2n^2}$.

To derive the ADMM algorithm for our model, we introduce a new auxiliary variable $v\in {\mathbb {R}}^{n^2}$ and obtain the following constrained nonconvex minimization problem:

$$\begin{aligned}&\min _{u, v\in {\mathbb {R}}^{n^2}} \Vert \nabla u\Vert _1+\frac{\lambda }{2}\left\langle \log \left( \gamma ^2+(v-f)^2\right) , \mathbf {1}\right\rangle \\&\quad \text {s.t. } Ku=v. \nonumber \end{aligned}$$

(10)

Let $w\in {\mathbb {R}}^{n^2}$ be the Lagrangian multiplier for the constraint $Ku=v$. Then we have the corresponding augmented Lagrangian:

$$\begin{aligned} {\mathcal {L}}_{\beta }(u,v,w)=\Vert \nabla u\Vert _1+\frac{\lambda }{2}\left\langle \log \left( \gamma ^2+(v-f)^2\right) , \mathbf {1}\right\rangle + \left\langle w,Ku-v\right\rangle +\frac{\beta }{2}\Vert Ku-v\Vert _2^2, \end{aligned}$$

where $\beta >0$ is a penalty parameter. The whole algorithm for restoring the blurred images corrupted by Cauchy noise is given in Algorithm 1.

In Algorithm 1, the dominant computation is the steps to solve the two minimization subproblems in (11) and (12). The u-subproblem (11) can be efficiently solved by many methods, for instance, the dual algorithm [10], the split-Bregman algorithm [9, 23, 43, 50], the primal-dual algorithm [11, 18], the infeasible primal-dual algorithm of semi-smooth Newton-type [25], the ADMM algorithm [14, 52], as well as the max-flow algorithm [22]. Here, we apply the dual algorithm proposed in [10]. Since the objective function in (12) is twice continuously differentiable, we can utilize the Newton method to solve it efficiently. Inspired by [48], as a special case of (7), we have the following convergence result for Algorithm 1. In addition, taking some specific properties of the variational model (9) into account, we provide a relatively simple proof.

Theorem 4.2

Let $(u^0,v^0,w^0)$ be any initial point and $\{(u^k,v^k,w^k)\}$ be the sequence of iterates generated by Algorithm 1. Then, if $\beta >\tfrac{\lambda }{\gamma ^2}$ and K has full column rank, the sequence $\{(u^k,v^k,w^k)\}$ converges globally to a point $(u^*,v^*,w^*)$, which is a stationary point of ${\mathcal {L}}_{\beta }$.

In order to prove Theorem 4.2, based on the model in (7), we define the following functions:

$$\begin{aligned} \mathcal {F}:{\mathbb {R}}^{n^2}\rightarrow {\mathbb {R}},\qquad \mathcal {F}(u)= & {} \Vert \nabla u\Vert _1 \nonumber \\ \mathcal {G}:{\mathbb {R}}^{n^2}\rightarrow {\mathbb {R}},\qquad \mathcal {G}(v)= & {} \frac{\lambda }{2}\left\langle \log \left( \gamma ^2+(v-f)^2\right) ,\mathbf {1}\right\rangle . \end{aligned}$$

(14)

The feasible set is $\Omega _{F}=\{(u,v)\in {\mathbb {R}}^{n^2}\otimes {\mathbb {R}}^{n^{2}}: Ku-v=0\}$. First, we give some useful lemmas that will be used in the main proof.

Lemma 4.1

The iterates of Algorithm 1 satisfy:

• 1. for all $k\in \mathbb {N}$, $\nabla \mathcal {G}(v^k)=w^k$;

• 2. $\Vert w^k-w^{k+1}\Vert \le \frac{\lambda }{\gamma ^{2}} \Vert v^k-v^{k+1}\Vert$.

Proof

Substituting (13) on $w^{k}$ into the first-order optimality condition of the v-subproblem on $v^k$: $\nabla \mathcal {G}(v^k)-w^{k-1}+\beta (v^k-Ku^k)=0$, we have $\nabla \mathcal {G}(v^k)=w^k$ for all $k\in \mathbb {N}$.

Since $\mathcal {G}$ is smooth, we can calculate its second derivative

$$\begin{aligned} \nabla ^{2}_{v_{i}}\mathcal {G}=\lambda \frac{\gamma ^{2}-(v_{i}-f)^{2}}{(\gamma ^{2}+(v_{i}-f)^{2})^{2}} \le \frac{\lambda }{\gamma ^{2}}, \end{aligned}$$

(15)

and thus $L_{\nabla \mathcal {G}}=\frac{\lambda }{\gamma ^{2}}$ is a Lipschitz constant for $\nabla \mathcal {G}$. Consequently, we obtain the bound

$$\begin{aligned} \Vert w^k-w^{k+1}\Vert =\Vert \nabla \mathcal {G}(v^k)-\nabla \mathcal {G} (v^{k+1})\Vert \le L_{\nabla \mathcal {G}}\Vert v^k-v^{k+1}\Vert . \end{aligned}$$

$\square$

Lemma 4.2

Let $\{(u^k, v^k, w^k)\}$ be the sequence of iterates generated by Algorithm 1. If $\beta >\tfrac{\lambda }{\gamma ^2}$, then $\{(u^k, v^k, w^k)\}$ satisfies:

• 1. ${\mathcal {L}}_{\beta }(u^k,v^k,w^k)$ is lower bounded and nonincreasing for all $k\in \mathbb {N}$;

• 2. $\{(u^k,v^k,w^k)\}$ is bounded.

Proof

According to the optimality condition of the u-subproblem (11), we define

$$\begin{aligned} d^{k+1}:=-\left( K^\top w^k+\beta K^\top (Ku^{k+1}-v^k)\right) \in \partial \mathcal {F}(u^{k+1}). \end{aligned}$$

(16)

From (11) and the definition of subgradient $\mathcal {F}$, it follows

$$\begin{aligned}&{\mathcal {L}}_{\beta }(u^k,v^k,w^k)-{\mathcal {L}}_{\beta }(u^{k+1},v^k,w^k) \nonumber \\&\quad =\mathcal {F}(u^k)-\mathcal {F}(u^{k+1})+\langle w^k,Ku^k-Ku^{k+1} \rangle +\frac{\beta }{2}\Vert Ku^k-v^k\Vert ^2 -\frac{\beta }{2}\Vert Ku^{k+1}-v^k\Vert ^2\nonumber \\&\quad =\mathcal {F}(u^k)-\mathcal {F}(u^{k+1})+\langle K^\top w^k +\beta K^\top (Ku^{k+1}-v^k),u^k-u^{k+1}\rangle + \frac{\beta }{2}\Vert Ku^k-Ku^{k+1}\Vert ^2\nonumber \\&\quad =\mathcal {F}(u^k)-\mathcal {F}(u^{k+1})-\langle d^{k+1}, u^k-u^{k+1}\rangle +\frac{\beta }{2}\Vert Ku^k-Ku^{k+1}\Vert ^2\nonumber \\&\quad \ge \frac{\beta }{2}\Vert Ku^k-Ku^{k+1}\Vert ^2 \end{aligned}$$

(17)

where the second equality follows from the cosine rule: $\Vert b+c\Vert ^2-\Vert a+c\Vert ^2=\Vert b-a\Vert ^2+2\langle a+c,b-a\rangle$ and the last inequality follows from the convexity of $\mathcal {F}(u)$.

For the updates of $v^{k+1}$, $w^{k+1}$, by the cosine rule and Lemma 4.1, we have

$$\begin{aligned}&{\mathcal {L}}_{\beta }(u^{k+1},v^k,w^k)-{\mathcal {L}}_{\beta }(u^{k+1},v^{k+1},w^{k+1}) \nonumber \\&\quad =\mathcal {G}(v^k)-\mathcal {G}(v^{k+1})+\langle w^{k+1},v^{k+1}-v^{k}\rangle - \beta \Vert Ku^{k+1}-v^{k+1}\Vert ^2+\frac{\beta }{2}\Vert v^{k}-v^{k+1}\Vert ^2\nonumber \\&\quad =\mathcal {G}(v^k)-\mathcal {G}(v^{k+1})-\langle \nabla \mathcal {G}(v^{k+1}),v^{k}-v^{k+1}\rangle - \frac{1}{\beta }\Vert w^{k}-w^{k+1}\Vert ^2+\frac{\beta }{2}\Vert v^{k}-v^{k+1}\Vert ^2\nonumber \\&\quad \ge -\frac{L_{\nabla \mathcal {G}}}{\beta }\Vert v^k-v^{k+1}\Vert ^2+\frac{\beta }{2}\Vert v^k-v^{k+1}\Vert ^2\nonumber \\&\quad =C\Vert v^k-v^{k+1}\Vert ^2 \end{aligned}$$

(18)

where we have applied the inequality

$$\begin{aligned} \mathcal {G}(v)-\mathcal {G}(v')-\langle \nabla \mathcal {G}(v'),v-v'\rangle \ge 0 \end{aligned}$$

and used the constant $C=\frac{\beta }{2}-\frac{L_{\nabla \mathcal {G}}}{2}$. In order to ensure $C>0$, we need the penalty parameter $\beta$ to satisfy:

$$\begin{aligned} \beta > L_{\nabla \mathcal {G}} \mathop {=}\limits ^{(15)} \frac{\lambda }{\gamma ^2}. \end{aligned}$$

According to (17) and (18), we have

$$\begin{aligned} {\mathcal {L}}_{\beta }(u^{k},v^k,w^k)-{\mathcal {L}}_{\beta }(u^{k+1},v^{k+1},w^{k+1})\ge C\Vert v^k-v^{k+1}\Vert ^2+\frac{\beta }{2}\Vert Ku^k-Ku^{k+1}\Vert ^2. \end{aligned}$$

This means that ${\mathcal {L}}_{\beta }(u^{k},v^k,w^k)$ is nonincreasing in $k\in \mathbb {N}$.

As K has full column rank, there exists $\hat{v}$ such that $Ku^k-\hat{v}=0$. Therefore, we have

$$\begin{aligned} \mathcal {F}(u^k)+\mathcal {G}(\hat{v})\ge \min _{u,v} \{\mathcal {F}(u)+\mathcal {G}(v):Ku-v=0\}>-\infty . \end{aligned}$$

Thus, we arrive at

$$\begin{aligned} {\mathcal {L}}_{\beta }(u^{k},v^k,w^k)&=\mathcal {F}(u^k)+\mathcal {G}(v^k)+\langle w^k,Ku^k-v^k\rangle + \frac{\beta }{2}\Vert Ku^k-v^k\Vert ^2 \\&=\mathcal {F}(u^k)+\mathcal {G}(v^k)+\langle \nabla \mathcal {G}(v^k),\hat{v}-v^k\rangle +\frac{\beta }{2}\Vert Ku^k-v^k\Vert ^2\\&\ge \mathcal {F}(u^k)+\mathcal {G}(\hat{v})-\frac{L_{\nabla \mathcal {G}}}{2} \Vert \hat{v}-v^k\Vert ^2+\frac{\beta }{2}\Vert Ku^k-v^k\Vert ^2\\&= \mathcal {F}(u^k)+\mathcal {G}(\hat{v})+\frac{\beta -L_{\nabla \mathcal {G}}}{2}\Vert Ku^k-v^k\Vert ^2>-\infty . \end{aligned}$$

Since ${\mathcal {L}}_{\beta }(u^{k},v^k,w^k)$ is upper bounded by ${\mathcal {L}}_{\beta }(u^{0},v^0,w^0)$ and obviously $\mathcal {F}(u)+\mathcal {G}(v)$ is coercive over $\Omega _{F}$, we conclude that $\{u^k\}$ and $\{v^k\}$ are bounded. By Lemma 4.1, $\{w^k\}$ is also bounded. $\square$

Lemma 4.3

Let $\partial {\mathcal {L}}(u^{k+1},v^{k+1},w^{k+1})=(\partial _{u} {\mathcal {L}},\nabla _v {\mathcal {L}}, \nabla _w {\mathcal {L}})$. Then, there exists a constant $C_1>0$ such that, for all $k\ge 1$, for some $p^{k+1}\in \partial {\mathcal {L}}(u^{k+1},v^{k+1},w^{k+1})$ we have $\Vert p^{k+1}\Vert \le C_1\Vert v^k-v^{k+1}\Vert$.

Proof

Because $\nabla _w{\mathcal {L}}=Ku^{k+1}-v^{k+1}=\frac{1}{\beta }(w^{k+1}-w^k)$ and $\nabla _{v}{\mathcal {L}}=w^{k+1}-w^{k}$, based on Lemma 4.1, we have

$$\begin{aligned} \Vert \nabla _w{\mathcal {L}}\Vert&\le \frac{L_{\nabla \mathcal {G}}}{\beta }\Vert v^k-v^{k+1}\Vert , \end{aligned}$$

(19)

$$\begin{aligned} \Vert \nabla _v {\mathcal {L}}\Vert&\le L_{\nabla \mathcal {G}}\Vert v^k-v^{k+1}\Vert . \end{aligned}$$

(20)

By the definition of the subgradient, we have

$$\begin{aligned} \begin{aligned} \partial _{u} {\mathcal {L}}&=\partial \mathcal {F}(u^{k+1})+K^\top w^{k+1} +\beta K^\top (Ku^{k+1}-v^{k+1}) \\&=\partial \mathcal {F}(u^{k+1})+K^\top w^k+\beta K^\top (Ku^{k+1}-v^k)\\&\quad +K^\top (w^{k+1}-w^k)+\beta K^\top (v^k-v^{k+1}).\\ \end{aligned} \end{aligned}$$

(21)

Thus, according to the optimal condition $0\in \partial \mathcal {F}(u^{k+1})+K^\top w^k+\beta K^\top (Ku^{k+1}-v^k)$, we have $K^\top (w^{k+1}-w^k)+\beta K^\top (v^k-v^{k+1})\in \partial _{u} {\mathcal {L}}$. Letting

$$\begin{aligned} p^{k+1}\triangleq \left( K^\top (w^{k+1}-w^k)+\beta K^\top (v^k-v^{k+1}),\frac{1}{\beta }(w^{k+1}-w^k),w^{k+1}-w^{k}\right) \end{aligned}$$

and combining (19), (20), (21), and Lemma 4.1, we arrive at

$$\begin{aligned} \begin{aligned} \Vert p^{k+1}\Vert&\le \left( L_{\nabla \mathcal {G}}\left( 1+\frac{1}{\beta }+\Vert K\Vert \right) +\beta \Vert K\Vert \right) \Vert v^k-v^{k+1}\Vert \\&=C_1\Vert v^k-v^{k+1}\Vert \end{aligned} \end{aligned}$$

where $C_1=\left( L_{\nabla \mathcal {G}}(1+\frac{1}{\beta }+\Vert K\Vert )+\beta \Vert K\Vert \right)$. $\square$

Now we give the proof to our main convergence theorem.

Proof of Theorem 4.2

As K has full column rank, the feasible set $\Omega _{F}$ is nonempty. By Lemma 4.2, the iterative sequence $\{(u^k,v^k,w^k)\}$ is bounded, so there exists a convergent subsequence $\{(u^{n_k},v^{n_k},w^{n_k})\}$, i.e., $(u^{n_k},v^{n_k},w^{n_k})$ converges to $(u^*,v^*,w^*)$ as k goes to infinity. Since ${\mathcal {L}}_\beta (u^k,v^k,w^k)$ is nonincreasing and lower-bounded, we have $\Vert K(u^k-u^{k+1})\Vert \rightarrow 0$ and $\Vert v^k-v^{k+1}\Vert \rightarrow 0$ as $k\rightarrow \infty$. According to Lemma 4.3, there exists $p^k\in \partial {\mathcal {L}}_\beta (u^k,v^k,w^k)$ such that $\Vert p^k\Vert \rightarrow 0$. Further, this leads to $\Vert p^{n_k}\Vert \rightarrow 0$ as $k\rightarrow \infty$. Based on the definition of the general subgradient [39], we obtain that $0\in \partial {\mathcal {L}}_\beta (u^*,v^*,w^*)$, i.e., $(u^*,v^*,w^*)$ is a stationary point.

Referring to [47, 51], the function $\mathcal {F}(u)$ is semi-algebraic, and $\mathcal {G}(v)$ is a real analytic function. Thus, we conclude that ${\mathcal {L}}_{\beta }$ satisfies the KL inequality [8]. Then, as in the proof of Theorem 2.9 in [5], we can deduce that the iterative sequence $\{(u^k,v^k,w^k)\}$ is globally convergent to $(u^*,v^*,w^*)$. $\square$

Remark 1

In Theorem 4.2 we need K to have full column rank. Since K is a blurring matrix in our problem, this requirement is satisfied.

5 Numerical Experiments

In this section, we present the results of several numerical experiments to demonstrate the performance of the proposed method for restoring images corrupted by blurs and Cauchy noise. Here, we use ten 8-bit 256-by-256 gray-scale test images, see Fig. 2. All numerical results are performed under Windows 10 and Matlab Version 7.10 (R2012a) running on a Lenovo laptop with a 1.7 GHz Intel Core CPU and 4GB RAM.

Fig. 2

Original images a Parrot, b Cameraman, c Baboon, d Boat, e Bridge, f House, g Leopard, h Plane, i Test, j Montage

We utilize the peak signal-to-noise ratio (PSNR) and the structural similarity index (SSIM) [49] as performance measures, which are respectively defined as

$$\begin{aligned} \text {PSNR}=20\log 10\left( \frac{255n}{\Vert \tilde{u}-u\Vert _2}\right) , \quad \text {SSIM}=\frac{2\mu _{\tilde{u}}\mu _u(2\sigma +c_2)}{(\mu _{\tilde{u}}^2+ \mu _u^2+c_1)(\sigma _{\tilde{u}}^2+\sigma _u^2+c_2)}, \end{aligned}$$

where $\tilde{u}$ is the restored image, u is the original image, $\mu _{\tilde{u}}$ and $\mu _u$ denote their respective means, $\sigma _{\tilde{u}}^2$ and $\sigma _u^2$ represent their respective variances, $\sigma$ is the covariance of $\tilde{u}$ and u, and $c_1, c_2>0$ are constants. PSNR is a good measure of the human subjective sensation, and a higher PSNR implies better quality of the restored image. SSIM conforms with the quality perception of the human visual system (HVS). If the SSIM value is closer to 1, the characteristic (edges and textures) of the restored image is more similar to the original image.

Table 1 PSNR and SSIM for the test images “Parrot” and “Cameraman” with different initial values

Fig. 3

Comparison of different initial values for removing Cauchy noise in the image “Parrot”, with $\gamma =5$ (in the 1st row) and 10 (in the 2nd row). a Noisy images, b restored images of (I), c restored images of (II), d restored images of (III)

In our method, we set the stopping condition based on the following relative improvement inequality:

$$\begin{aligned} \left| \frac{E(u^{k+1})-E(u^k)}{E(u^{k+1})}\right| <\epsilon , \end{aligned}$$

(22)

where E is the objective function in (9) and $\epsilon =5\times 10^{-5}$. In addition, since the regularization parameter $\lambda$ balances the trade-off between fitting f and TV, we manually tune it in order to obtain the highest PSNRs of the restored images. The selection method of $\lambda$ is out of the scope in this paper. The parameter $\beta$ in Algorithm 1 affects the convergent speed. Based on Theorem 4.2, we round $\beta >\tfrac{\lambda }{\gamma ^2}$ up to the nearest value with two digits after the decimal point as $\beta$. In addition, we set the iteration number for the Newton method while solving the v-subproblem as 3. The iteration number for solving the u-subproblem equals 5 in denoising and 10 in simultaneous deblurring and denoising.

Fig. 4

Plots of the objective function values versus iterations for the noisy images “Parrot” and “Cameraman” with $\gamma =5$ (in the 1st row) and 10 (in the 2nd row). a I b II c III

Table 2 PSNR and SSIM for the noisy images and the restored images by applying different methods ($\gamma =5$)

5.1 Different Initializations

Since our model (9) is nonconvex, though we are able to prove that the ADMM algorithm converges globally to a stationary point from any given starting point $(u^{0}, v^{0}, w^{0})$, the local minimizers that we obtained may still depend on the initial points. To study the influence of initializations and obtain better restorations, in this section we test three different choices of $u^{0}$ in denoising:

$$\begin{aligned} (I):&u^0=\max (0,\min (f,255)); \\ (II):&u^0=medfile2(f); \\ (III):&u^0=f, \\ \end{aligned}$$

where medfile2(f) denotes the result from the median filter with window size 3. Note that due to the impulsive feature of Cauchy noise, the median filter usually provides fairly good results. In addition, based on Theorem 3.2 with $u^{0}$ in case (III), we obtain the unique solution in $\Omega _{U}$.

In Table 1, we list PSNRs and SSIMs for different initial points for the test images “Parrot” and “Cameraman” at the noise levels $\gamma =5$ and 10. The noisy images are obtained via $f=u+\gamma \frac{\eta _1}{\eta _2}$, where $\eta _1$ and $\eta _2$ are independent random variables following the Gaussian distribution with mean 0 and variance 1. It is obvious that both PSNRs and SSIMs are highest in the case (I), and are lowest in the case (III), which shows that the unique solution in $\Omega _{U}$ is not a satisfactory local minimizer.

Table 3 PSNR and SSIM for the noisy images and the restored images by applying different methods ($\gamma =10$)

Fig. 5

Comparison of different methods for removing Cauchy noise, with $\gamma =5$. a Noisy image:19.20, b Median:27.18, c conRE:27.91, d Ours:29.06, e Noisy image:18.98, f Median:25.94, g conRE:26.51, h Ours:28.72, i Noisy image:17.74, j Median:19.18, k conRE:21.18, l Ours:22.56, m Noisy image:18.01, n Median:25.94, o conRE:27.03, p Ours:27.94, q Noisy image:17.37, r Median:25.09, s conRE:25.83, t Ours:27.25

Fig. 6

Comparison of different methods for removing Cauchy noise, with $\gamma =10$. a Noisy image:16.35, b Median:25.51, c conRE:26.74, d Ours:27.12, e Noisy image:16.06, f Median:24.68, g conRE:25.68, h Ours:26.67, i Noisy image:14.87, j Median:18.79, k conRE:20.27, l Ours:20.96, m Noisy image:15.11 n Median:24.39, o conRE:25.71, p Ours:25.79, q Noisy image:14.49, r Median:23.64, s conRE:24.85, t Ours:25.25

Fig. 7

Zoomed version of the restored images in Fig. 5. a original images; b the median filter; c the “conRe” model; d our method

Fig. 8

Zoomed version of the restored images in Fig. 6. a Original images; b the median filter; c the “conRe” model; d our method

Figure 3 depicts the restored “Parrot” images in order to compare the visual performance due to different initial points. Figure 3d shows the unique solution in $\Omega _{U}$, and we can see that there is still some noise left in the restored images. The reason is that Cauchy noise is so impulsive that by corrections in a small range, $[-\gamma , \gamma ]$, it is not enough to remove all noise. Compared with the results from (II), the ones from (I) include clearer features and less noise, especially in the region around the eye and black stripes of “Parrot”. Hence, we choose (I) as initialization in our remaining numerical experiments.

Theorem 4.2 demonstrate that with any given initial points, Algorithm 1 converges globally to a stationary point. Figure 4 depicts the plots of the objective function values in (9) versus the number of iteration in order to observe the convergence of our method. It is clear that the objective function value keeps decreasing over the iterations. Furthermore, our method converges very fast except in case (III), which does not provide good restorations.

5.2 Comparisons of Image Deblurring and Denoising

In order to demonstrate the superior performance of our proposed method, we compare it with two other well-known methods: the median filter (matlab function ‘medfilt2’) with window size 3 and the convex variational method in [42] (“conRE” for short). For fair comparison, we use the same stopping rule in the convex variational method and adjust the two parameters in the model for highest PSNRs.

First, we compare the three methods for Cauchy noise removal, i.e., by setting K as the identity matrix. Tables 2 and 3 list the PSNRs and SSIMs of the restored images at the noise levels $\gamma =5$ and $\gamma =10$, respectively. Obviously, comparing to the two variational methods, the median filter provides the worst PSNRs and SSIMs. Our method always yields the highest PSNRs. Especially at the lower noise level ($\gamma =5$), our PSNRs are about 1dB higher than the convex method [42]. Furthermore, in most cases, our SSIMs are also higher than others.

Table 4 PSNR and SSIM for the images degraded by Gaussian blur and Cauchy noise ($\gamma =5$) and the restored images by different methods

In Figs. 5 and 6, we present the results from different methods for removing Cauchy noise from the images “Parrot”, “Cameraman”, “Baboon”, “Boat” and “Plane”. Although the median filter effectively removes Cauchy noise, it also oversmooths the edges and destroys many details. It is obvious that two variational methods outperform the median filter. Comparing to the convex method, our nonconvex method can provide better balance between preserving detail and removing noise. To further illustrate the performance of our method, we show the zoomed regions of the restored images “Parrot”, “Baboon” and “Boat” in Figs. 7 and 8, where we can clearly see the difference among the results from the three methods, e.g., the stripes around the eye in “Parrot”, the nose and whiskers of “Baboon”, and the ropes and iron pillars of “Boat”.

In the following experiments, we compare the three methods on recovering images corrupted by blurs and Cauchy noise. Here, we consider the Gaussian blur with size 7 and standard deviation 3, and the out-of-focus blur with size 5. Further, Cauchy noise with $\gamma =5$ is added into the blurry images. Tables 4 and 5 list the PSNRs and SSIMs by applying different methods to the images “Parrot”, “Cameraman”, “Plane” and “Test”. Figures 9 and 10 show the restored images.

From Tables 4 to 5, we find that our method provides the highest PSNRs and SSIMs. Comparing with the convex method, our method can improve by at least 0.36dB on PSNR. In Figs. 9 and 10, it is easy to see that the restored images by the median filter are oversmoothing as the median filter does not deblur. The convex method can recover edges and textures, but some noise is not removed. However, our method not only preserves the fine features but also effectively removes Cauchy noise, which can be clearly seen in the zoomed regions in Fig. 11.

Table 5 PSNR and SSIM for the images degraded by the out-of-focus blur and Cauchy noise ($\gamma =5$) and the restored images by different methods

Fig. 9

Comparison of the restored results by applying different methods for deblurring and denoising the images degraded by a Gaussian blur (G, 7, 3) and Cauchy noise $(\gamma =5)$. a Degraded images; b the median filter; c the “conRe” model; d our method

Fig. 10

Comparison of the restored results by applying different methods for deblurring and denoising the images degraded by the out-of-focus blur (A, 5) and Cauchy noise $(\gamma =5)$. a Degraded images; b the median filter; c the “conRe” model; d our method

Fig. 11

Zoomed version of the restored results for the image “Parrot” degraded by the Gaussian blur (in the 1st row) and the out-of-focus blur (in the 2nd row), respectively. a Degraded images; b the median filter; c the “conRe” model; d our method

6 Conclusion

In this paper, we have reviewed and analyzed the statistic properties of the Cauchy distribution by comparing it with the Gaussian and Laplace distributions. Based on the MAP estimator, we have developed a nonconvex variational model for restoring images degraded by blurs and Cauchy noise. Taking advantage of a recent result in [48], the alternating direction method of multiplier (ADMM) algorithm is applied to solve the nonconvex variational optimization problem with a convergence guarantee. Numerical experiments show that the proposed method outperforms two well-known methods in both qualitative and quantitative comparisons.