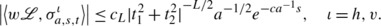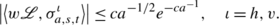Abstract
Recently, compressed sensing techniques in combination with both wavelet and directional representation systems have been very effectively applied to the problem of image inpainting. However, a mathematical analysis of these techniques which reveals the underlying geometrical content is missing. In this paper, we provide the first comprehensive analysis in the continuum domain utilizing the novel concept of clustered sparsity, which besides leading to asymptotic error bounds also makes the superior behavior of directional representation systems over wavelets precise. First, we propose an abstract model for problems of data recovery and derive error bounds for two different recovery schemes, namely ℓ 1 minimization and thresholding. Second, we set up a particular microlocal model for an image governed by edges inspired by seismic data as well as a particular mask to model the missing data, namely a linear singularity masked by a horizontal strip. Applying the abstract estimate in the case of wavelets and of shearlets we prove that—provided the size of the missing part is asymptotic to the size of the analyzing functions—asymptotically precise inpainting can be obtained for this model. Finally, we show that shearlets can fill strictly larger gaps than wavelets in this model.










Similar content being viewed by others
References
Aharon, M., Elad, M., Bruckstein, A.: K-SVD: an algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process. 54, 4311–4322 (2006)
Ballester, C., Bertalmio, M., Caselles, V., Sapiro, G., Verdera, J.: Filling-in by joint interpolation of vector fields and gray levels. IEEE Trans. Image Process. 10(8), 1200–1211 (2001)
Bertalmio, M., Bertozzi, A., Sapiro, G.: Navier-Stokes, fluid dynamics, and image and video inpainting. In: Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition 2001 (CVPR 2001), pp. I355–I362. IEEE Press, New York (2001)
Bertalmío, M., Sapiro, G., Caselles, V., Ballester, C.: Image inpainting. In: Proceedings of SIGGRAPH 2000, New Orleans, pp. 417–424 (2000)
Cai, J.F., Cha, R.H., Shen, Z.: Simultaneous cartoon and texture inpainting. Inverse Probl. Imaging 4(3), 379–395 (2010)
Cai, J.F., Dong, B., Osher, S., Shen, Z.: Image restoration: Total variation, wavelet frames, and beyond. J. Am. Math. Soc. 25, 1033–1089 (2012)
Candès, E.J., Donoho, D.L.: New tight frames of curvelets and optimal representations of objects with piecewise C 2 singularities. Commun. Pure Appl. Math. 57(2), 219–266 (2004)
Candès, E.J., Donoho, D.L.: Continuous curvelet transform. I. Resolution of the wavefront set. Appl. Comput. Harmon. Anal. 19(2), 162–197 (2005)
Chan, T.F., Kang, S.H.: Error analysis for image inpainting. J. Math. Imaging Vis. 26(1–2), 85–103 (2006)
Chan, T.F., Kang, S.H., Shen, J.: Euler’s elastica and curvature based inpainting. SIAM J. Appl. Math. 63(2), 564–592 (2002)
Chan, T.F., Shen, J.: Mathematical models for local nontexture inpaintings. SIAM J. Appl. Math. 62(3), 1019–1043 (2002) (electronic)
Christensen, O.: An Introduction to Frames and Riesz Bases. Applied and Numerical Harmonic Analysis. Birkhäuser, Boston (2003)
Chui, C.K., Shi, X.L.: Inequalities of Littlewood-Paley type for frames and wavelets. SIAM J. Math. Anal. 24(1), 263–277 (1993)
Daubechies, I.: Ten Lectures on Wavelets. CBMS-NSF Regional Conference Series in Applied Mathematics, vol. 61. SIAM, Philadelphia (1992)
Dong, B., Ji, H., Li, J., Shen, Z., Xu, Y.: Wavelet frame based blind image inpainting. Appl. Comput. Harmon. Anal. 32(2), 268–279 (2012)
Donoho, D.L., Elad, M.: Optimally sparse representation in general (nonorthogonal) dictionaries via l 1 minimization. Proc. Natl. Acad. Sci. USA 100(5), 2197–2202 (2003) (electronic)
Donoho, D.L., Huo, X.: Uncertainty principles and ideal atomic decomposition. IEEE Trans. Inf. Theory 47(7), 2845–2862 (2001)
Donoho, D.L., Kutyniok, G.: Microlocal analysis of the geometric separation problem. Commun. Pure Appl. Math. 66, 1–47 (2013)
Drori, I.: Fast ℓ 1 minimization by iterative thresholding for multidimensional NMR spectroscopy. EURASIP J. Adv. Signal Process. 2007, 020248 (2007)
Elad, M., Bruckstein, A.M.: A generalized uncertainty principle and sparse representation in pairs of bases. IEEE Trans. Inf. Theory 48(9), 2558–2567 (2002)
Elad, M., Starck, J.L., Querre, P., Donoho, D.L.: Simultaneous cartoon and texture image inpainting using morphological component analysis (MCA). Appl. Comput. Harmon. Anal. 19(3), 340–358 (2005)
Engan, K., Aase, S., Hakon Husoy, J.: Method of optimal directions for frame design. In: IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP ’99), vol. 5, pp. 2443–2446 (1999)
Foucart, S.: Recovering jointly sparse vectors via hard thresholding pursuit. In: Proceedings of SampTA 2011, Singapore (2011)
Grohs, P.: Continuous shearlet frames and resolution of the wavefront set. Monatshefte Math. 164(4), 393–426 (2011)
Grohs, P., Kutyniok, G.: Parabolic molecules. Preprint (2012)
Guo, K., Labate, D.: Analysis and detection of surface discontinuities using the 3D continuous shearlet transform. Appl. Comput. Harmon. Anal. 30(2), 231–242 (2011)
Guo, K., Labate, D.: The construction of smooth parseval frames of shearlets. Math. Model. Nat. Phenom. 8(1), 32–55 (2013)
Hennenfent, G., Fenelon, L., Herrmann, F.J.: Nonequispaced curvelet transform for seismic data reconstruction: a sparsity-promoting approach. Geophysics 75(6), WB203–WB210 (2010)
Hennenfent, G., Herrmann, F.J.: Application of stable signal recovery to seismic interpolation. In: SEG International Exposition and 76th Annual Meeting. SEG, Tulsa (2006)
Herrmann, F.J., Hennenfent, G.: Non-parametric seismic data recovery with curvelet frames. Geophys. J. Int. 173, 233–248 (2008)
Hörmander, L.: The Analysis of Linear Partial Differential Operators. I. Classics in Mathematics. Springer, Berlin (2003). Distribution theory and Fourier analysis. Reprint of the second (1990) edition [Springer, Berlin; MR1065993 (91m:35001a)]
Jing, Z.: On the stability of wavelet and Gabor frames (Riesz bases). J. Fourier Anal. Appl. 5(1), 105–125 (1999)
King, E.J.: Wavelet and frame theory: frame bound gaps, generalized shearlets, Grassmannian fusion frames, and p-adic wavelets. Ph.D. thesis, University of Maryland, College Park (2009)
King, E.J., Kutyniok, G., Zhuang, X.: Analysis of data separation and recovery problems using clustered sparsity. In: SPIE Proceedings: Wavelets and Sparsity XIV, vol. 8138 (2011)
Kowalski, M., Torrésani, B.: Sparsity and persistence: mixed norms provide simple signal models with dependent coefficients. Signal Image Video Process. 3, 251–264 (2009)
Kutyniok, G.: Geometric separation by single pass alternating thresholding. Appl. Comput. Harmon. Anal. (to appear)
Kutyniok, G., Labate, D.: Resolution of the wavefront set using continuous shearlets. Trans. Am. Math. Soc. 361(5), 2719–2754 (2009)
Kutyniok, G., Labate, D. (eds.): Shearlets: Multiscale Analysis for Multivariate Data. Applied and Numerical Harmonic Analysis. Birkhäuser, Boston (2012)
Kutyniok, G., Lemvig, J., Lim, W.: Compactly supported shearlets. In: Approximation Theory XIII, San Antonio, TX, 2010. Springer, Berlin (2010)
Kutyniok, G., Lemvig, J., Lim, W.: Shearlets and optimally sparse approximations. In: Shearlets: Multiscale Analysis for Multivariate Data. Springer, Berlin (2012)
Kutyniok, G., Lemvig, J., Lim, W.Q.: Optimally sparse approximations of 3d functions by compactly supported shearlet frames. SIAM J. Appl. Math. 44, 2962–3017 (2012)
Kutyniok, G., Lim, W.: Compactly supported shearlets are optimally sparse. J. Approx. Theory 163, 1564–1589 (2011)
Meyer, Y.: Principe d’incertitude, bases hilbertiennes et algèbres d’opérateurs. Astérisque 145–146(4), 209–223 (1987). Séminaire Bourbaki, Vol. 1985/86
Meyer, Y.: Oscillating Patterns in Image Processing and Nonlinear Evolution Equations. University Lecture Series, vol. 22. Am. Math. Soc., Providence (2001). The fifteenth Dean Jacqueline B. Lewis memorial lectures
Nam, S., Davies, M., Elad, M., Gribonval, R.: Cosparse analysis modeling—uniqueness and algorithms. In: International Conference on Acoustics, Speech, and Signal Processing (ICASSP 2011). IEEE Press, New York (2011)
Nam, S., Davies, M.E., Elad, M., Gribonval, R.: The cosparse analysis model and algorithms. Appl. Comput. Harmon. Anal. 34(1), 30–56 (2013)
Olshausen, B.A., Field, D.J.: Sparse coding with an overcomplete basis set: a strategy employed by V1? Vis. Res. 37(23), 3311–3325 (1997)
Author information
Authors and Affiliations
Corresponding author
Additional information
Emily J. King is supported by a fellowship for postdoctoral researchers from the Alexander von Humboldt Foundation. Gitta Kutyniok would like to thank David Donoho for discussions on this and related topics. She is grateful to the Department of Statistics at Stanford University and the Department of Mathematics at Yale University for their hospitality and support during her visits. She also acknowledges support by the Einstein Foundation Berlin, by Deutsche Forschungsgemeinschaft (DFG) Heisenberg fellowship KU 1446/8, Grant SPP-1324 KU 1446/13 and DFG Grant KU 1446/14, and by the DFG Research Center Matheon “Mathematics for key technologies” in Berlin. Xiaosheng Zhuang acknowledges support by DFG Grant KU 1446/14. Finally, the authors are thankful to the anonymous referees for their comments and suggestions.
Appendix: Decay of Shearlet Coefficients Related to Line Singularity
Appendix: Decay of Shearlet Coefficients Related to Line Singularity
We present the idea of a continuous shearlet system in order to prove various auxiliary results. For ι∈{h,w}, a>0, s∈R, and t∈R 2, define

It is easy to show that \(\sigma^{\iota}_{a,s,t} = a^{-3/2}\sigma ^{\iota ,a,s}(S_{s}^{\iota}A_{a^{-1}}^{\iota}(\cdot-t))\) for some smooth function σ ι,a,s. For s=±a, we similarly define the continuous version of the “seam” elements σ a,±a,t . The discrete shearlet system \(\{\sigma^{\iota}_{j,\ell,k}\}\) is then obtained by sampling \(\sigma_{a,s,t}^{\iota}\) on the discrete set of points

To prove that the choice of Λ j offers clustered sparsity for the shearlet frame, we need some auxiliary results. The following lemma gives the decay estimate of the shearlet elements.
Note that if we define \(\langle|t|_{a,s;\iota}\rangle:= \langle |S_{s}^{\iota}A_{a^{-1}}^{\iota}t|\rangle\), then
The following lemma is needed later for estimating the decay coefficients of the shearlet aligned with the singularity.
Lemma 16
Let the line segment with respect to (a,s,t;v) be \(\mathit{Seg}(a,s,t;v) :=\{S_{s}^{v} A_{a^{-1}}^{v}(x-t_{1},-t_{2}): |x|\le\rho\}\). Then
-
1.
Given the line
$$\mathit{Line}(a,s,t;v):=\bigl\{S_{s}^v A_{a^{-1}}^v(x-t_1,-t_2): x\in\mathbf{R} \bigr\}, $$the closest point P L to the origin on this line satisfies
$$d_1^2:=\|P_L\|_2^2 = \frac{a^{-4}}{1+s^2}t_2^2. $$ -
2.
Set \(x_{0} =\frac{a^{-1}s}{1+s^{2}}t_{2}+t_{1}\). If P S is the closest point on the segment Seg(a,s,t;v) to the origin, then

Proof
Let \(L(x):=S_{s}^{v} A_{a^{-1}}^{v}(x-t_{1},-t_{2})\). Then

Solving \(\frac{d}{dx}\|L(x)\|_{2} = 2(x-t_{1})a^{-2}(1+s^{2})-2a^{-3}st_{2}=0\), we have \(x_{0} =\frac{a^{-1}s}{1+s^{2}}t_{2}+t_{1}\). It follows that

Note that P L ∈Seg(a,s,t;v) if and only if x∈[−ρ,ρ], in which case d 2=0. Otherwise,

which completes the proof. □
We need another auxiliary lemma. Note that

Lemma 17
Define \(R_{N}(x_{0},y_{0}):=\int_{y_{0}}^{\infty}\langle|(x_{0},\alpha)|\rangle ^{-N}d\alpha\) (which may be thought of as a ray integral). Then for y 0≥0,
Proof
Choose β∈(0,1). Then
If we set (1−β)N=2 and f(t)=〈|(x 0,y 0+α)|〉−N, then we obtain
Since

fixing M=2 and recalling the classic identity \(\pi= \int_{-\infty }^{\infty}(1+\alpha^{2})^{-1}d\alpha\) yield the bound
Furthermore, since y 0≥0,
This completes the proof. □
Now we can estimate the decay of the shearlet coefficients aligned with the line singularity  as follows.
as follows.
Lemma 18
Retaining the notation as above, we have

Proof
We have

where we use an affine transformation of variables to turn the anisotropic norm |(x,0)| a,s,t;v into the Euclidean norm |w|. Application of the same transformation to [−ρ,ρ]×{0} yields Seg(a,s,t;v). The integral in (22) is along a curve traversing Seg(a,s,t;v) at speed \(\nu_{1}=a^{-1}\sqrt{1+s^{2}}\). If we let Ray(a,s,t;v) denote the ray starting from P S and initially traversing Seg(a,s,t;v), then

□
Next, we estimate the decay of the shearlet coefficients associated with those shearlets not aligned with the line singularity.
Lemma 19
Let t=(t 1,t 2). We consider the following three cases:
-
(i)
t 1≠0 and t 2≠0. Then we have

when 1≤|s|<a −1

and for s=±a −1

-
(ii)
If exactly one of t 1 or t 2 is 0, then we have
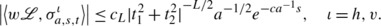
-
(iii)
t 1=t 2=0. Then we have
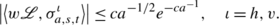
Proof
First, it is easy to show that
By definition of the line singularity  , we have
, we have

For t 1≠0 and t 2≠0, when we repeatedly apply integration by parts, we have

where
and for some function f which is sufficiently differentiable we define the multi index,
The next step is to estimate the term |h L,M (ξ 2)|.
Let Ξ a,s (ξ 2) be the support of the function
Note that for fixed a,s, the function \(\xi_{1}\mapsto\hat{w}(\xi _{1})\times \hat{\sigma}_{a,s,0}^{v}(\xi_{1},\xi_{2})\) is supported inside \([c a^{-1}|s|,\frac{1}{2}a^{-1}s)\) for a constant \(c < \frac{1}{2}\). h L,M can then be written as
We then rewrite the integrand as

Thus |h L,M (ξ 2)| is bounded by

where
Consequently, we have

Therefore,

Using the same approach, it is not difficult to show that for |s|<a −1,

and for s=±a −1

The proofs for other cases are similar with simple modifications of the above procedure. □
Rights and permissions
About this article
Cite this article
King, E.J., Kutyniok, G. & Zhuang, X. Analysis of Inpainting via Clustered Sparsity and Microlocal Analysis. J Math Imaging Vis 48, 205–234 (2014). https://doi.org/10.1007/s10851-013-0422-y
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10851-013-0422-y