Twisted Poincaré series and zeta functions on finite quotients of buildings

Abstract

In the case where $G=\hbox {SL}_{2}(F)$ for a non-archimedean local field F and $\varGamma$ is a discrete torsion-free cocompact subgroup of G, there is a known relationship between the Ihara zeta function for the quotient of the Bruhat–Tits tree of G by the action of $\varGamma$, and an alternating product of determinants of twisted Poincaré series for parabolic subgroups of the affine Weyl group of G. We show how this can be generalized to other split simple algebraic groups of rank two over F and formulate a conjecture about how this might be generalized to groups of higher rank.

1 Introduction

The classical Ihara zeta function [9] is a counting function associated with a discrete torsion-free cocompact subgroup $\varGamma$ of $G=\hbox {PGL}_2(F)$, where F is a non-archimedean local field with the discrete valuation v and q elements in its residue field, defined as follows:

$$\begin{aligned} Z(\varGamma ,u) = \prod _{[\gamma ]}\left( 1-u^{\ell ([\gamma ])}\right) ^{-1}. \end{aligned}$$

Here, $[\gamma ]$ runs through all primitive conjugacy classes in $\varGamma$ and $\ell$ is the length function defined as follows. For $\gamma \in G$ with eigenvalues $\lambda _1$ and $\lambda _2$, define

$$\begin{aligned} \ell (\gamma ) = {\max }\left\{ v\left( \frac{\lambda _1}{\lambda _2}\right) ,{v\left( \frac{\lambda _2}{\lambda _1}\right) }\right\} \quad \text{ and } \quad \ell ([\gamma ]) = \min \left\{ \ell \left( \gamma '\right) : \gamma ' \in [\gamma ]\right\} . \end{aligned}$$

Here whenever $\lambda _1,\lambda _2 \not \in F$, we set $\ell (\gamma )=1$. On the other hand, one can also regard $Z(\varGamma ,u)$ as a geometric counting function associated with the quotient of the Bruhat–Tits tree of G by the action of $\varGamma$, denoted by $\mathscr {B}_\varGamma$, such that

$$\begin{aligned} Z(\mathscr {B}_\varGamma ,u) = \prod _{c}\left( 1-u^{\ell (c)}\right) ^{-1}. \end{aligned}$$

Here, c runs through all primitive closed geodesics (which are equivalence classes of primitive closed tailless and backtrack-less walks) in $\mathscr {B}_\varGamma$ and $\ell (c)$ is the path length of c in graph theory.

Ihara showed that the zeta function is indeed a rational function given by the following formula

$$\begin{aligned} Z\left( \mathscr {B}_\varGamma ,u\right) = \frac{\left( 1-u^2\right) ^{\chi (\mathscr {B}_\varGamma )}}{\det \left( 1-\hbox {Au}+ qu^2\right) }. \end{aligned}$$

(1.1)

Here, $\chi (\mathscr {B}_\varGamma )$ is the Euler characteristic and A is the adjacency matrix of the finite graph $\mathscr {B}_\varGamma$, which is also a Hecke operator on G acting on spherical vectors of $L^2(\varGamma \backslash G)$.

Hashimoto [6] showed that there is an easy way to see the rationality of Ihara zeta function by considering the edge adjacency operator $A_E$, which is an Iwahori–Hecke operator of G acting on Iwahori spherical vectors of $L^2(\varGamma \backslash G)$. Hashimoto showed that

$$\begin{aligned} Z(\mathscr {B}_\varGamma ,u) = \frac{1}{\det (1-A_E u)}. \end{aligned}$$

(1.2)

It is natural to ask if one can generalize Ihara and Hashimoto’s result to other reductive groups. However, there is no canonical way to define Ihara zeta functions on finite quotients of higher-dimensional buildings. Thus, one must find a new interpretation of Eq. (1.1).

For example, the term ${\det (1-\hbox {Au}+ qu^2)}^{-1}$ can be regarded as the Langlands L-function associated with the unramified subrepresentation $L^2(\varGamma \backslash G)$ of G (see [12] for details). In this case, the right-hand side of Eq. (1.1) is known in general and it remains to figure out the left-hand side in terms of geometric zeta functions. For this viewpoint, see [10, 11] for the case of $\hbox {PGL}_3$, [4] for PGSP$_4$, [3] for the case of $\hbox {PGL}_n$ over the 1-adic field, and [12] for the case of rank two algebraic groups over the 1-adic field. Roughly speaking, they obtain an identity of the following form.

Zeta identity for groups of adjoint type:

$$\begin{aligned}&\text {the unramified Langlands }L\hbox {-function} \\&\quad = \text {the alternating product of geometric zeta functions of various dimensions.} \end{aligned}$$

Note that in Ihara’s original result and the above generalizations, G is always of adjoint type. On the other hand, the building of G only depends on its root system so that there are other groups having the same building as G. For instance, $\hbox {SL}_2(F)$ and $\hbox {PGL}_2(F)$ have the same associated buildings, but $\hbox {SL}_2(F)$ is simply connected instead of being of adjoint type. In this case, Hashimoto [7] gave a different way to express Ihara’s identity.

Let W be the affine Weyl group of $G=\hbox {SL}_2(F)$ with the standard generating set S consisting of elements of order two and K be the Iwahori subgroup of G. For $w \in W$, let $e_w$ be the Iwahori Hecke operator associated with w. Then, for each parabolic subgroup $W_I$ generating by $I \subset S$, one can consider its Poincaré series $W_I(\rho ,u)$ attached to a representation $\rho$ of the Iwahori Hecke algebra H(G, K) as

$$\begin{aligned} W_I(\rho ,u) = \sum _{w \in W_I} \rho (e_w)u^{\ell (w)}. \end{aligned}$$

where $\ell (\cdot )$ is the word length with respect to S. Let $\pi _\varGamma$ be the representation of H(G, K) acting on $L^2(\varGamma \backslash G / K).$ Hashimoto’s result implies that

$$\begin{aligned} Z(\mathscr {B}_\varGamma ,u) = \prod _{I \subset S} \det W_I(\pi _\varGamma ,u)^{(-1)^{|I|}}. \end{aligned}$$

(1.3)

The main goal of this paper is to generalize Ihara’s result along this direction to simple simply connected split algebraic groups of rank two. Note that the right-hand side of the above equation can be naturally defined for simple simply connected split algebraic groups of higher ranks. It remains to figure out the left-hand side. Comparing to the result of adjoint type, we expect to obtain an identity of the following form.

Zeta identity for simply connected groups:

$$\begin{aligned}&\text {the geometric zeta function of top dimension} \\&\quad = \text {the alternating product of twisted Poincar}\acute{\mathrm{e}} \text { series of parabolic subgroups.} \end{aligned}$$

Now suppose G is a simple simply connected split algebraic group of rank two. In this case, the building $\mathscr {B}$ of G and its finite quotient $\mathscr {B}_\varGamma$ are two dimensional complexes. Instead of counting closed geodesics in a finite quotient $\mathscr {B}_\varGamma$ which lift to straight lines in $\mathscr {B}$, we count closed geodesic strips in $\mathscr {B}_\varGamma$ which lift to straight strips in $\mathscr {B}$. One can define the zeta function of closed geodesic strips $Z(\mathscr {B}_\varGamma ,u)$ by the same manner as zeta function of closed geodesics (see Sect. 4.6 for details). The main theorem of the paper is the following.

Theorem 1.1

Let $\pi _\varGamma$ be the representation of the Iwahori Hecke algebra H(G, K) acting on $L^2(\varGamma \backslash G / K).$ There are two Iwahori–Hecke operators $e_{w_1}$ and $e_{w_2}$, such that

$$\begin{aligned} Z(\mathscr {B}_\varGamma ,u) = \frac{1}{\det \left( I- \pi _\varGamma (e_{w_1}) u^{\ell (w_1)}\right) \det \left( I- \pi _\varGamma (e_{w_2}) u^{\ell (w_2)}\right) }. \end{aligned}$$

(1.4)

Moreover, we also have

$$\begin{aligned} Z(\mathscr {B}_\varGamma ,u) = \prod _{I \subset S} \det W_I(\pi _\varGamma ,u)^{(-1)^{|I|+|S|}}. \end{aligned}$$

(1.5)

Here, $\pi _\varGamma (e_{w_1})$ and $\pi _\varGamma (e_{w_1})$ are indeed chamber adjacency operators which play the role of $A_E$ in Hashimoto’s formula (see Sect. 4.6 for details).

Remark

The zeta function of closed geodesic strips in this paper is indeed the geometric zeta function of top dimension (which is called chamber zeta function or gallery zeta function) occurred in the works [4, 10, 11].

When G is of rank $n >2$, one may consider the zeta function $Z(\mathscr {B}_\varGamma ,u)$ counting closed geodesic tube in $\mathscr {B}_\varGamma$ which lift to straight tubes in $\mathscr {B}$ by the same manner (however we will not define the zeta function of closed geodesic tubes in this paper). If the above two theorems still hold, then there should exist some Iwahori Hecke operators $e_{w_1},\ldots , e_{w_n}$ so that

$$\begin{aligned} Z(\mathscr {B}_\varGamma ,u)= & {} \frac{1}{\det (I- \pi _\varGamma (e_{w_1}) u^{\ell (w_1)})\cdots \det (I- \pi _\varGamma (e_{w_n}) u^{\ell (w_n)})} \\= & {} \prod _{I \subset S} \det W_I(\pi _\varGamma ,u)^{(-1)^{|I|+|S|}}. \end{aligned}$$

In the end of the paper, we verify the second part of the above identity with $\pi _\varGamma$ replaced by the trivial representation $\rho _0$. In this case, $W_I(\rho _0,u)=W_I(u)$ is the usual (un-twisted) Poincaré series and the second part of the above identity becomes the following.

$$\begin{aligned} \prod _{I \subset S} W_I(u)^{(-1)^{|I|+|S|}}=\frac{1}{\left( 1- u^{\ell (w_1)}\right) \cdots \left( 1- u^{\ell (w_n)}\right) }. \end{aligned}$$

We obtain the following result.

Theorem 1.2

Let W be the affine Coxeter group of rank $n+1$. Then the alternating product $\prod _{I \subset S} W_I(u)^{(-1)^{|I|+|S|}}$ is the reciprocal of a polynomial of the form

$$\begin{aligned} \left( 1-u^{d_1}\right) \cdots \left( 1-u^{d_n}\right) \end{aligned}$$

where $d_i$ are positive integers.

Note that for a general Coxeter group W, $\prod _{I \subset S} W_I(u)^{(-1)^{|I|+|S|}}$ is a rational function. In fact, by direct computation, one can show that for an irreducible Coxeter group with three generators, this alternating product is a reciprocal of a polynomial if and only if it is an affine Coxeter group.

The paper is organized as follows. In Sect. 2, we review the definition of Poincaré series and their twistings and state Hashimoto’s interpretation of Ihara’s formula. Especially, the result is based on a length-preserving decomposition of the affine Weyl group of $\hbox {SL}_2$. In Sect. 3, we study such decomposition for affine Weyl groups of rank three and discuss their relation with geometric zeta functions in Sect. 4. The Proof of Theorem 1.1 is given in the end of Sect. 4. In Sect. 5, we state our conjecture about higher-dimensional cases and prove Theorem 1.2.

2 Twisted Poincaré series and Ihara zeta functions

2.1 Poincaré series

Let (W, S) be a Coxeter system with a generating set S consisting of elements of order two. For $w \in W$, let $\ell (w)$ be the shortest length of a word consisting of elements of S whose product is equal to w. The Poincaré series associated with (W, S) is a power series with integer coefficients defined as

$$\begin{aligned} W(u) = \sum _{w \in W} u^{\ell (w)}. \end{aligned}$$

For a subset D of W, we also define $D(u) = \sum _{w \in D} u^{\ell (w)}.$ Especially, we are interested in the case where $D=W_I$, the subgroup generated by some subset $I \subset S$. For instance, when W is finite,

$$\begin{aligned} \sum _{I \subset S} (-1)^{|I|}\frac{W(u)}{W_I(u)} = u^{\ell (w_0)}. \end{aligned}$$

Here, $w_0$ is the unique element of maximal length. When W is infinite,

$$\begin{aligned} \sum _{I \subset S} (-1)^{|I|}\frac{W(u)}{W_I(u)} = 0, \end{aligned}$$

which implies that

$$\begin{aligned} W(u) = \left( \sum _{I \subsetneq S} \frac{(-1)^{|I|+|S|+1}}{W_I(u)} \right) ^{\text {-1}}. \end{aligned}$$

(2.1)

See [8, Sections 1.11 and 5.12] for the proof of these statements.

2.2 Hecke algebras

For a Coxeter system (W, S) and a formal parameter q, there is an associative $\mathbb {C}$-algebra $H_q(W,S)$, called a Hecke algebra, with generators $\{e_w\}_{w \in W}$. The multiplication of $H_q(W,S)$ is characterized by the following the relations:

$$\begin{aligned} (e_s+1)(e_s-q)= & {} 0, \qquad \text{ if } s \in S; \\ e_w e_{v}= & {} e_{wv}, \qquad \text{ if } \ell (wv)= \ell (w)+\ell (v). \end{aligned}$$

Especially, if we set $q=1$, then $H_q(W,S)$ is isomorphic to the group algebra $\mathbb {C}[W]$. Recall that, one can identify the (affine) Hecke algebra $H_q(W,S)$ and the Iwahori–Hecke algebra $H(G,K)$ by mapping $e_w$ to $KwK$.

2.3 Twisted Poincaré series

For a representation $(\rho ,V_\rho )$ of $H_{q}(W,S)$, consider the following power series

$$\begin{aligned} D(\rho ,u) = \sum _{w \in D} \rho (e_w) u^{\ell (w)} \in \mathrm {End}(V_\rho )[[u]], \end{aligned}$$

called the Poincaré series of D twisted by $\rho$. Note that when D contains the identity element (e.g. $D=W_I$), the constant term of $D(\rho ,u)$ is the identity operator and $D(\rho ,u)$ has an inverse in $\mathrm {End}(V_\rho )[[u]]$.

Note that $e_s \mapsto q$ for all $s \in S$ induces a one-dimensional representation $\rho _1$ of $H_q(W,S)$. In this case,

$$\begin{aligned} D(\rho _1,u) = \sum _{w \in D} \rho _1(e_w) u^{\ell (w)} = \sum _{w \in D} q^{\ell (w)} u^{\ell (w)} = D(qu). \end{aligned}$$

Therefore, one can regard the usual Poincaré series as a special case of twisted Poincaré series.

2.4 Ihara zeta functions

Let W be the affine Weyl group of $G=\hbox {SL}_2$ over a local field F with $p^{n}$ elements in its residue field. In this case, $S=\{s_1,s_2\}$ and $s_1 s_2$ has order infinity. Let the formal parameter q be equal to $p^n$, then the Hecke algebra $H_q(W,S)$ is isomorphic to the Iwahori–Hecke algebra of G. Fix a discrete torsion-free cocompact subgroup $\varGamma$ of G. Then, the quotient of the Bruhat–Tits tree $\mathscr {B}$ of G by $\varGamma$ is a bipartite finite $(q+1)$-regular graph $\mathscr {B}_\varGamma$. The Ihara zeta function of $\mathscr {B}_\varGamma$ is defined as

$$\begin{aligned} Z(\mathscr {B}_\varGamma ,u) = \prod _{c}(1-u^{\ell (c)})^{\text {-1}}\in \mathbb {Z}[[u]]. \end{aligned}$$

Here, c runs over all primitive closed geodesics in $\mathscr {B}_\varGamma$ and $\ell (c)$ is the usual length in graph theory.

Let $\pi _\varGamma$ be the complex representation of $H_q(W,S)$ on the space of Iwahori-fixed vectors of $L^2(\varGamma \backslash G)$. In this case, elements in $H_q(W,S)$ can be regarded as operators on edges of $\mathscr {B}_\varGamma$ and Hashimoto [6] showed that

Theorem 2.1

$Z(\mathscr {B}_\varGamma ,u) =\det (1- \pi _\varGamma (e_{s_2 s_1}) u^2)^{\mathrm {-1}}.$

On the other hand, one can factor the group W as a product of three subsets as follows.

$$\begin{aligned} W= \langle s_1 \rangle \times \{ (s_2 s_1)^m\}_{m=0}^\infty \times \langle s_2 \rangle . \end{aligned}$$

(2.2)

Here, for three subsets X, Y, Z of W, we say X factors into a product of Y and Z, denoted by $X=Y \times Z$, if every element of X can be written as yz for unique some $y \in Y$ and $z \in Z$. Similar notations apply to factorization involving more than two sets.

Note that all elements in the above product are reduced words. Therefore, for any representation $\rho$ of $H_q(W,S)$, we have

$$\begin{aligned} W_{\{s_1,s_2\}}(\rho ,u)&= W_{\{s_1\}}(\rho ,u) \bigg (\sum _{i=1}^\infty \rho (e_{s_2}e_{s_1})^m u^{2m} \bigg ) W_{\{s_2\}}(\rho ,u) \\&= W_{\{s_1\}}(\rho ,u) \left( I- \rho (e_{s_2}e_{s_1})u^2 \right) ^{\text {-1}}W_{\{s_2\}}(\rho ,u) \end{aligned}$$

Moreover, when $\rho$ is a finite dimensional representation over a field K, one can consider the determinant of $W_I(\rho ,u)$, which is an invertible element in the power series K[[u]] (since its constant term is equal to one). For convenience, define

$$\begin{aligned} \mathrm {Alt}(W)(u)= \prod _{I \subset S} W_I(u)^{(-1)^{|I|+|S|}} \end{aligned}$$

and

$$\begin{aligned} \det \mathrm {Alt}(W)(\rho , u)= \prod _{I \subset S} \det W_I(\rho ,u)^{(-1)^{|I|+|S|}}. \end{aligned}$$

It was pointed out in [15] that one can rewrite Hashimoto’s result as the following.

Theorem 2.2

As a power series,

$$\begin{aligned} Z(\mathscr {B}_\varGamma ,u) = \det \mathrm {Alt}(W)(\pi _\varGamma ,u). \end{aligned}$$

(2.3)

Note that the above theorem is the Eq. (1.3) in the introduction. Besides, this interpretation suggests a possible way to generalize Ihara’s theorem to higher rank cases.

3 Affine Coxeter groups of rank three

3.1 Alternating products of Poincaré series

Suppose (W, S) is an irreducible affine Coxeter system of rank three where $S=\{s_1,s_2,s_3\}$. Let $m_{ij}$ be the order of $s_i s_j$. There are three types of such Coxeter systems up to isomorphism, characterized as the following:

• Type $\tilde{A_2}$: $(m_{12},m_{23},m_{13})=(3,3,3)$.

• Type $\tilde{C_2}$: $(m_{12},m_{23},m_{13})=(4,2,4)$.

• Type $\tilde{G_2}$: $(m_{12},m_{23},m_{13})=(6,2,3)$.

Especially, every such Coxeter group is isomorphic to an affine Weyl group of some irreducible root system. To evaluate $\mathrm {Alt}(W)(u)$, note that $W_I$ is a dihedral group or a cyclic group of order two when I is a non-empty proper subset of S. In this case, $W_I(u)$ can be written down directly. On the other hand, one can apply Eq. (2.1) to compute the Poincaré series of W(u) and obtain the following results.

$$\begin{aligned} \mathrm {Alt}(W)(u)^{\text {-1}}= {\left\{ \begin{array}{ll} (1-u^3)^2, &{}\quad \text{ if } (W,S) \text{ is } \text{ of } \text{ type } \tilde{A}_2; \\ (1-u^4)(1-u^3), &{}\quad \text{ if } (W,S) \text{ is } \text{ of } \text{ type } \tilde{C}_2; \\ (1-u^5)(1-u^3), &{}\quad \text{ if } (W,S) \text{ is } \text{ of } \text{ type } \tilde{G}_2.\\ \end{array}\right. } \end{aligned}$$

We shall show that the above identities can be extended to the case of twisted Poincaré series of Hecke algebras.

3.2 Coxeter complexes

For the affine Coxeter system (W, S), fix a geometric realization of (W, S) on a real vector space V endowed with a Euclidean metric invariant under W.

The hyperplane $H_s$ fixed by an affine reflection s in W is called a wall. The set of walls gives V a simplicial structure and the resulting simplicial complex is called the Coxeter complex $\mathscr {A}$ of W. Connected components of V with all walls removed are open 2-simplices, called alcoves or chambers.

The unique chamber whose boundary is contained in $H_{s_1} \cup H_{s_2} \cup H_{s_3}$ is the fundamental chamber $\mathscr {C}$. Label the edge (1-simplex) of $\mathscr {C}$ by i if it is contained in $H_{s_i}$. Then, one can extend this labeling to a W-invariant labeling on all edges in $\mathscr {A}$ uniquely.

Besides, there is a bijection between W and chambers in $\mathscr {A}$ given by $w \mapsto w \mathscr {C}$. Moreover, if $w=s_{i_1} \cdots s_{i_n}$, then the chambers $\mathscr {C}$ and $w \mathscr {C}$ can be linked by the gallery

$$\begin{aligned} C_0= \mathscr {C}\rightarrow C_1= s_{i_1} \mathscr {C}\rightarrow C_2= s_{i_1} s_{i_2} \mathscr {C}\rightarrow \cdots \rightarrow C_n= s_{i_1} \cdots s_{i_n} \mathscr {C}\end{aligned}$$

such that the edge $\bar{C}_k \cap \bar{C}_{k+1}$ is labeled by $i_{k+1}$. In other words, starting from the fundamental chamber $\mathscr {C}$, one can cross the edges labeled by $i_1,\ldots , i_n$ sequentially to arrive at the chamber $w\mathscr {C}$.

3.3 Straight strip

Let $v_i = H_{s_{i+1}} \cap H_{s_{i+2}}$ be the vertex of the fundamental chamber $\mathscr {C}$ where the subscripts are read modulo 3. For convenience, we may assume that $v_3$ is the origin of V. Then the stabilizer of $v_3$ in W is the linear subgroup $W_0$ generated by $s_1$ and $s_2$, which is the Weyl group (this follows from our special choice of the ordering of $m_{ij}$ in the beginning of the section). For the affine transformation $w \in W$, we can uniquely write $w = w_0w_t$ where $w_0 \in W_0$ is the linear part of w and $w_t$ is a translation.

Now for $i=1,2$, removing all walls parallel to the vector $v_{i}$ from V, the connected component containing $\mathscr {C}$ in the resulting set is called the fundamental straight strip $\mathscr {T}_i$ in the direction $v_i$, which is the gray region in Figs. 1, 2, 3 and 4. For $w=w_0w_t \in W$, $w \mathscr {T}_i$ is a straight strip in the direction of $w_0 v_i$ and all such strips are called of type i.

Fig. 1

Type $\tilde{A}_2$

Fig. 2

Type $\tilde{C}_2$

Fig. 3

$\mathscr {T}_1$ in type $\tilde{G}_2$

Fig. 4

$\mathscr {T}_2$ in type $\tilde{G}_2$

3.4 Stabilizer of $\mathscr {T}_i$

Let $\mathrm {Stab}(\mathscr {T}_i)$ be the stabilizer of $\mathscr {T}_i$ consisting of elements mapping $\mathscr {T}_i$ to itself and preserving the direction $v_i$. Let $\mathscr {L}$ be the middle line of $\mathscr {T}_i$, then for $w \in \mathrm {Stab}(\mathscr {T}_i)$, w must preserve $\mathscr {L}$ and its action on $\mathscr {L}$ has to be a translation (in the direction of $v_i$ or $-v_i$). If the action of w on $\mathscr {L}$ is trivial, w fixes $\mathscr {L}$ point-wisely and it is the identity element or an affine reflection whose reflection axis is $\mathscr {L}$. On the other hand, $\mathscr {L}$ is not a wall (by the construction of $\mathscr {T}_i$) and w must therefore be the identity element in this case. Therefore, elements in $\mathrm {Stab}(\mathscr {T}_i)$ are uniquely determined by their actions on $\mathscr {L}$.

Let $w_i$ be the element in Stab$(\mathscr {T}_i)$ such that its action on $\mathscr {L}$ is the minimal translation in the direction of $v_i$. Then, we have the following theorem.

Theorem 3.1

The stabilizer $\hbox {Stab}(\mathscr {T}_i)$ is a cyclic group generated by $w_i$.

By direct computation, we obtain the following.

• 1. When (W, S) is of type $\tilde{A}_2$, we have $w_1=s_3 s_2 s_1$ and $w_2 = s_3 s_1 s_2$.

• 2. When (W, S) is of type $\tilde{C}_2$, we have $w_1= s_3 s_1 s_2 s_1$ and $w_2= s_3 s_1 s_2$.

• 3. When (W, S) is of type $\tilde{G}_2$, we have $w_1 = s_3 s_1 s_2 s_3 s_1$ and $w_2 = s_3 s_1 s_2 s_1 s_2$.

One can check case by case to see that except for $w_1$ in the case of type $\tilde{G_2}$,

• the length of $(w_i)^k$ is equal to |k| times of the length of $w_i$.

In general, an element in W satisfying the above property is called straight (the notion of straight element was first introduced by [13]).

Now, in the case of $\tilde{G_2}$, we shall replace $w_1$ by

$$\begin{aligned} w_1' = s_1 w_1 s_1 = (s_1 s_3 s_1) s_2 s_3 = (s_3 s_1 s_3 )s_2 s_3 = s_3 s_1 (s_3 s_2 s_3) = s_3 s_1 s_2. \end{aligned}$$

which is a generator of the stabilizer of $s_1 \mathscr {T}_1$. Then, $w_1'$ will be straight. To abuse the notation, we will also denote $w_1'$ by $w_1$ (in the case of the group $\tilde{G_2}$) in the rest of paper.

Let $H_i = \{ (w_i)^k \}_{k \in \mathbb {Z}_\ge 0}.$ Note that

$$\begin{aligned} H_i(u)= \sum _{i=0}^\infty u^{\ell \left( w_i^k\right) } = \sum _{i=0}^\infty u^{k \ell (w_i)} = \left( 1- u^{\ell (w_i)}\right) ^{\text {-1}}. \end{aligned}$$

Therefore, we can rewrite the result in Sect. 3.1 as

Proposition 3.2

For any affine Coxeter group (W, S) of rank three, the following holds.

$$\begin{aligned} H_1(u)H_2(u)=\mathrm {Alt}(W)(u). \end{aligned}$$

3.5 Factorization of Coxeter groups

Next, we will factor W in terms of $W_I$ and $H_i$. To do so, we need the following lemma.

Lemma 3.3

Let $D_1,\ldots , D_m$ be non-empty subsets of a Coxeter group W. If $W=D_1\times \cdots \times D_m$ and $D_1(u)\cdots D_m(u)=W(u)$, then this factorization is length-preserving, i.e. for $w_i \in D_i$, $\ell (w_1 \cdots w_m) = \ell (w_1)+ \cdots +\ell (w_m)$.

Proof

Since $\ell (w_1 \cdots w_m) \le \ell (w_1)+ \cdots +\ell (w_m)$, for any integer k we have

$$\begin{aligned} \varOmega _k:= & {} \{ (w_1,\ldots ,w_m) \in D_1 \times \cdots \times D_m: \ell (w_1)+ \cdots +\ell (w_m)\le k\} \\\subseteq & {} \{ (w_1,\ldots ,w_m) \in D_1 \times \cdots \times D_m :\ell (w_1\cdots w_m)\le k\} \\= & {} \{ w \in W : \ell (w) \le k\}=: \varOmega _k'. \end{aligned}$$

On the other hand,

$$\begin{aligned} D_1(u)\cdots D_m(u) = \prod _{i=1}^m \left( \sum _{w_i \in D_i} u^{\ell (w_i)}\right) =|\varOmega _{0}|+ \sum _{i=1}^\infty \left( |\varOmega _{i}|-|\varOmega _{i-1}|\right) u^i \end{aligned}$$

and

$$\begin{aligned} W(u) = |\varOmega _{0}'| + \sum _{i=1}^\infty \left( |\varOmega _{i}'|-|\varOmega _{i-1}'|\right) u^i \end{aligned}$$

From $D_1(u)\cdots D_m(u)=W(u)$, we conclude that $|\varOmega _{i}|= |\varOmega _{i}'|$ for all i. Therefore, $\varOmega _k = \varOmega _k'$ and $\ell (w_1 \cdots w_m) = \ell (w_1)+ \cdots +\ell (w_m)$ for $w_i \in D_i$. $\square$

Note that when $\ell (w_1 \cdots w_m) = \ell (w_1)+ \cdots +\ell (w_m)$, for any representation $\rho$ of $H_q(W,S)$, we have

$$\begin{aligned} \rho (e_{w_1 \cdots w_m}) = \rho (e_{w_1}) \cdots \rho (e_{w_m}). \end{aligned}$$

Together with the above lemma, we have

Theorem 3.4

If $W=D_1\times \cdots \times D_m$ and $D_1(u)\cdots D_m(u)=W(u)$, then for any representation $\rho$ of $H_q(W,S)$

$$\begin{aligned} W(\rho ,u) = D_1(\rho ,u) \cdots D_m(\rho ,u). \end{aligned}$$

Let us give some examples of the above theorem. For subsets $I \subset J \subset S$, define

$$\begin{aligned} W_{J/I}= & {} \{ w \in W_J: \ell (ws)> \ell (w) , \forall s \in I\} \qquad \text{ and } \qquad \\ W_{I\backslash J}= & {} \{ w \in W_J: \ell (sw)> \ell (w) , \forall s \in I\} \end{aligned}$$

which are the sets of left minimal length $W_I$-coset representatives and right minimal length $W_I$-coset representatives of $W_J$ respectively (remark: more common notations for left and right minimal length coset representative are $W_J^I$ and ${^I}W_J$. However, such notations may cause confusion when we consider the product of several such sets).

Theorem 3.5

[8, Sect. 1.11] For subsets $I \subset J \subset S$, the following hold.

• 1. $W_J = W_{J/I} \times W_I = W_I \times W_{I\backslash J}.$

• 2. $W_J(u) = W_{J/I}(u) W_I(u) = W_I(u) W_{I\backslash J}(u).$

For convenience, we also denote the set of generators $I=\{s_{i_1},\ldots ,s_{i_k}\}$ by its set of indices $\{i_1,\ldots ,i_k\}$. Next, let us prove the following theorem for affine Coxeter groups of rank three.

Theorem 3.6

Let $D_1,\ldots , D_m$ be subsets of W given by the following.

• $(D_1,\ldots ,D_5) = (W_{\{1,2\}/\{2\}},H_1,W_{\{2,3\}/\{3\}}, H_2, W_{\{1\}\backslash \{1,3\}})$ if (W, S) is of type $\tilde{A}_2$ or $\tilde{C}_2$.

• $(D_1,\ldots ,D_4) = (W_{\{2,1\}/\{1\}},H_2 H_1 W_{\{1,3\}})$ if (W, S) is of type $\tilde{G}_2$.

Then $D_1(u)\cdots D_m(u)=W(u)$ and $W=D_1 \times \cdots \times D_m$.

Proof

Note that for type $\tilde{A}_2$ or $\tilde{C}_2$, by Proposition 4.5,

$$\begin{aligned} D_1(u)\cdots D_5(u)&= W_{\{1,2\}/\{2\}}(u) H_1 (u) W_{\{2,3\}/\{3\}} (u) H_2(u) W_{\{1\}\backslash \{1,3\}}(u)\\&= \frac{ W_{\{1,2\}}(u)W_{\{2,3\}}(u)W_{\{1,3\}}(u)}{W_{\{1\}}(u)W_{\{2\}}(u)W_{\{3\}}(u)} \mathrm {Alt}(W)(u) = W(u). \end{aligned}$$

For type $\tilde{G}_2$, note that $W_{\{2,3\}}=\{e, s_2, s_3, s_2 s_3\} = W_{\{2\}} \times W_{\{3\}}.$ Therefore,

$$\begin{aligned} W_{\{2,3\}}(u)=W_{\{2\}}(u)W_{\{3\}}(u) \end{aligned}$$

and

$$\begin{aligned} D_1(u)\cdots D_4(u)&= W_{\{2,1\}/\{1\}}(u) H_2 (u) H_1(u) W_{\{1,3\}}(u)\\&= \frac{ W_{\{2,1\}}(u)W_{\{1,3\}}(u)}{W_{\{1\}}(u)} \mathrm {Alt}(W)(u)\cdot \frac{W_{\{2,3\}}(u)}{W_{\{2\}}(u)W_{\{3\}}(u)} = W(u). \end{aligned}$$

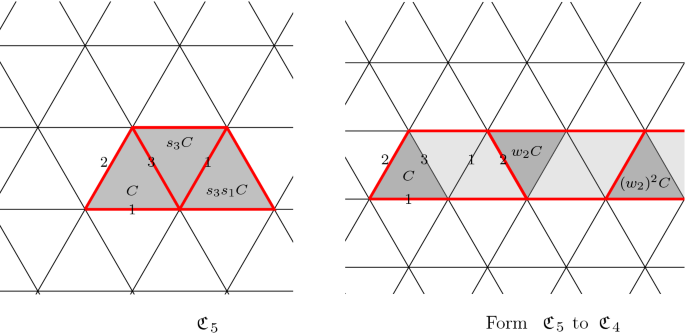
It remains to show that $W=D_1 \times \cdots \times D_m$. Our strategy is to study the geometric interpretation of this factorization. As we mentioned before, for each $w=s_{i_1}\cdots s_{i_k} \in W$, one can start from the fundamental chamber C and cross the edges labeled by $i_1,\ldots , i_n$ sequentially to arrive the chamber wC. Therefore, one can find the collections of chambers $\mathfrak {C}_{m+1}=\{C\}$, $\mathfrak {C}_m= D_m( \mathfrak {C}_{m+1})$, $\cdots , \mathfrak {C}_1 =D_1(\mathfrak {C}_{2})$ step by step.

More precisely, for the case of type $\tilde{A}_2$, we have

• 1. $\mathfrak {C}_5=D_5(C)=\{C, s_3C, s_3 s_1C\}$.

• 2. $\mathfrak {C}_4=D_4(\mathfrak {C}_5)=\{ (w_2)^i \mathfrak {C}_5, i=0 \sim \infty \}$, where $w_2=s_3s_1s_2$ is a glide reflection.

  

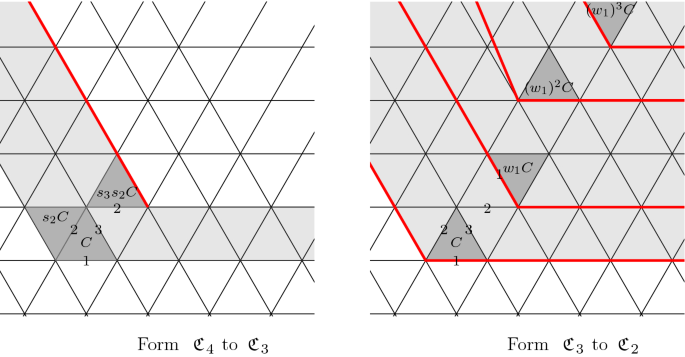
• 3. $\mathfrak {C}_3=D_3(\mathfrak {C}_4)=\{ \mathfrak {C}_4, s_2\mathfrak {C}_4, s_3 s_2 \mathfrak {C}_4\}$. Here, $s_3s_2$ is a rotation.

• 4. $\mathfrak {C}_2=D_2(\mathfrak {C}_3)=\{ (w_1)^i \mathfrak {C}_3: i=0 \sim \infty \}$, where $w_1=s_3s_2s_1$ is a glide reflection.

  

• 5. $\mathfrak {C}_1=D_1(\mathfrak {C}_2)=\{\mathfrak {C}_1, s_1 \mathfrak {C}_1, s_2 s_1 \mathfrak {C}_1\}$. $\square$

Here, at each stage, the whole gray area is the region $\mathfrak {C}_i$; connected components with red boundaries are copies of $\mathfrak {C}_{i+1}$. Moreover, the set of dark gray triangles is the image of $D_{i}(C)$. From these figures, we see that $\mathfrak {C}_1=D_1 \cdots D_m(C)$ and W(C) are bijective. We conclude that $W=D_1 \times \cdots \times D_m$.

The arguments are similar for type $\tilde{C}_2$ and $\tilde{G}_2$, so we just draw the following figures.

3.6 Type $\tilde{C}_2$

3.7 Type $\tilde{G}_2$

$\square$

Combining Theorems 3.4 and 3.6, we obtain the main result of this section.

Theorem 3.7

Let (W, S) be an affine Coxeter system of rank three and $\rho$ be a finite dimensional representation of $H_q(W,S)$. Then

$$\begin{aligned} \det H_1(\rho ,u) \det H_2(\rho ,u) = \det \mathrm {Alt}(W)(\rho ,u). \end{aligned}$$

4 Zeta functions of closed geodesic strips

In this section, we will pass the result from affine Coxeter systems in the previous section to algebraic groups.

4.1 Straight strips in the building

Let G be a simply connected connected split simple algebraic group over a local field F with q elements in its residue field, whose affine Weyl group W is a Coxeter group of rank three with the generating set S. Let $\mathscr {B}$ be the Bruhat–Tits building of G whose chambers are parametrized by the cosets $G/K$, where $K$ is the Iwahori subgroup, which is the stabilizer of a fixed choice of the fundamental chamber. We shall identify the Coxeter complex $\mathscr {A}$ of the Coxeter system (W, S) as the fundamental apartment so that the fundamental chamber $\mathscr {C}$ in $\mathscr {A}$ is represented by the Iwahori subgroup $K$. Now for $g \in G$ and the strip $\mathscr {T}_i$ defined Sect. 3.4 (which is a subset of $\mathscr {A}$) whose stabilizer is generated by $w_i$, we call $g\mathscr {T}_i$ a straight strip of type $w_i$.

Fix a discrete torsion-free cocompact subgroup $\varGamma$ of G, the quotient $\mathscr {B}_\varGamma$ is a finite complex with the fundamental group $\varGamma$. We will give a geometric interpretation of Theorem 3.7 as a zeta function of closed geodesic strips on $\mathscr {B}_\varGamma$.

4.2 Chambers in an apartment

In order to study straight strips in the building, we need a criterion to determine when a given set of chambers is contained in an apartment. Let $C_1=g_1\mathscr {C}$ and $C_2=g_2\mathscr {C}$ be two chambers in the building $\mathscr {B}$. Recall the Weyl distance of $C_1$ and $C_2$ is defined to be

$$\begin{aligned} \delta (C_1,C_2) = w \in W \end{aligned}$$

where w satisfies $g_1^{-1}g_2 \in Kw K$. Then, we have the following lemma.

Lemma 4.1

[1, Exercise 5.77] Let $\mathscr {S}$ be a collection of chambers of $\mathscr {B}$. If for any three chambers $C_1,C_2,$ and $C_3$ in $\mathscr {S}$, we have

$$\begin{aligned} \delta (C_1,C_3)=\delta (C_1,C_2)\delta (C_2,C_3). \end{aligned}$$

Then $\mathscr {S}$ is contained in an apartment in the maximal apartment system.

On the other hand, when the Iwahori subgroup is open and compact (which is always the case when F is a non-archimedean local field), the group G acts transitively on the maximal apartment systems (see [5, Sect. 17.7] for details). Together with the above lemma, we have the following useful theorem.

Theorem 4.2

If $\gamma \in KwK$ and w is straight (i.e. $\ell (w)^k = k \ell (w)$ for all k), then $\{ \gamma ^k \mathscr {C}: k \in \mathbb {Z}\}$ is contained in $g\mathscr {A}$ for some $g \in G$.

4.3 Stabilizer of straight strips

Let $\mathscr {T}:=\mathscr {T}_i$ be the fundamental straight strip in the direction of $v=v_i$ defined in Sect. 3.4. Note that for a simplicial automorphism $\sigma$ on $\mathscr {T}$, its action on the middle line $\mathscr {L}$ is either an affine reflection (which has a fixed point) or a translation by kv for some real number k. In the later case, when $k>0$, $\sigma \big |_\mathscr {L}$ is called a positive translation (with respect to v). Note that $\mathrm {Aut}_1(\mathscr {T})$ is a cyclic generated by a minimal positive translation. Now let $\mathrm {Aut}(\mathscr {T})$ be the group of simplicial automorphisms of $\mathscr {T}$ and consider the following subgroup of $\mathrm {Aut}(\mathscr {T})$.

and

Then, one can verify that $\mathrm {Aut}_1(\mathscr {T})\cap \mathrm {Aut}_2(\mathscr {T})$ is a cyclic group generated by $w=w_i$, on a case-by-case basis from Figs. 1, 2, 3 and 4 in Sect. 2.

Since G is simply connected, the action of G on the building is type-preserving. Moreover, the assumption that $\varGamma$ is discrete and torsion-free implies that no non-identity element can have a fixed point in the building. Thus, the setwise stabilizer of $\mathscr {T}$ in $\varGamma$ acts faithfully on $\mathscr {T}$ and

$$\begin{aligned} \langle \gamma _0 \rangle = \mathrm {Stab}_\varGamma ({\mathscr {T}}) \cong \mathrm {Stab}_\varGamma (\mathscr {T}) \big |_{\mathscr {T}} {\subseteq } \langle w \rangle \end{aligned}$$

for some unique $\gamma _0$ with $\gamma _0\big |_{\mathscr {L}}$ being a positive translation. A similar result is true for any other straight strip in the building $\mathscr {B}$. Thus, immediately, we have the following lemma.

Proposition 4.3

For $\gamma \in \varGamma$, if $\gamma (g\mathscr {T})=g\mathscr {T}$, then $\gamma g\mathscr {C}= g w^{k} \mathscr {C}$ for some $k \in \mathbb {Z}$. Especially, it implies that $g^{-1} \gamma g\in Kw^k K$.

Denote by $\mathrm {SConv}( \langle \gamma \rangle g\mathscr {C})$ the simplicial convex hull of $\{\gamma ^n g \mathscr {C}\}_{n \in \mathbb {Z}}$, which is the smallest simplicial convex set containing this set.

Proposition 4.4

For $\gamma \in \varGamma$ and $g\in G$, suppose that $g^{-1} \gamma g \in Kw^k K$ for some $k \in \mathbb {Z}$. Then $\mathrm {SConv}( \langle \gamma \rangle g\mathscr {C})$ is a straight strip.

Proof

Recall that $w=w_i$ is straight and so is $w^k$ (see Sect. 3.4). By Theorem 4.2, the set $\{ g^{-1}\gamma ^k g\mathscr {C}: k \in \mathbb {Z}\}$ is contained in some apartment $g'\mathscr {A}$, and so are the set $\{\gamma ^k g\mathscr {C}: k \in \mathbb {Z}\}$ and its simplicial convex hull $\mathrm {SConv}( \langle \gamma \rangle g\mathscr {C})$. Moreover, we may assume that $g'\mathscr {C}= g\mathscr {C}$ since the stabilizer of an apartment acts transitively on its chambers. Note that every chamber in the apartment $g'\mathscr {A}$ is uniquely determined by its Weyl distance to the chamber $g'\mathscr {C}$. On the other hand, we have

$$\begin{aligned} \delta \left( g'\mathscr {C}, g'w^{kn} \mathscr {C}\right) = w^{kn} = \delta \left( g\mathscr {C}, \gamma ^{n} g\mathscr {C}\right) \end{aligned}$$

for all $n \in \mathbb {Z}$. We conclude that $g \gamma ^n \mathscr {C}= g'w^{kn}\mathscr {C}$ for all n and hence

$$\begin{aligned} \mathrm {SConv}\left( \langle \gamma \rangle g\mathscr {C}\right) = g' \mathrm {SConv}\left( \langle w^k \rangle \mathscr {C}\right) = g'\mathscr {T}. \end{aligned}$$

Here, we use the fact that $\mathrm {SConv}\left( \langle w^k \rangle \mathscr {C}\right) = \mathscr {T}$ which can be checked case by case via Figs. 1, 2, 3 and 4. $\square$

4.4 Pointed closed geodesic strips

Consider the following set

endowed with an equivalence relation defined as follows: $(\gamma _1, g_1\mathscr {C}, g_1\mathscr {T}) \sim (\gamma _2, g_2\mathscr {C}, g_2\mathscr {T})$ if there exists some $\gamma \in \varGamma$, such that

$$\begin{aligned} \gamma g_1 \mathscr {T}= g_2 \mathscr {T}, \gamma g_1 \mathscr {C}= g_2 \mathscr {C}, \quad \gamma \gamma _1 g_1 \mathscr {C}=\gamma _2 g_2 \mathscr {C}. \end{aligned}$$

The equivalence class of $(\gamma , g\mathscr {C}, g\mathscr {T})$ is given by

$$\begin{aligned} \left[ \left( \gamma , g\mathscr {C}, g\mathscr {T}\right) \right] =\left\{ \left( \tilde{\gamma }\gamma \tilde{\gamma }^{-1}, \tilde{\gamma } g\mathscr {C}, \tilde{\gamma } g\mathscr {T}\right) : \quad \forall \tilde{\gamma } \in \varGamma \right\} . \end{aligned}$$

We define the notion of a “pointed closed geodesic strip of type w” in $\mathscr {B}_\varGamma$ to be an equivalence class of $\mathscr {P}$. Note that when $\gamma (g\mathscr {T}) = g\mathscr {T}$, the projection of $g\mathscr {T}$ is a closed strip in $\mathscr {B}_\varGamma$, called a closed geodesic strip of $\mathscr {B}_\varGamma$. Therefore, each pointed closed geodesic strip can be regarded as a closed geodesic strip with a fixed choice chamber in $\mathscr {B}_\varGamma$. In other words, the pointed closed strips are analogue of the closed geodesics with fixed starting vertex/directed edge in graphs.

Combing Propositions 4.3 and 4.4, when $\gamma (g\mathscr {T}) = g\mathscr {T}$, $\mathrm {SConv}( \langle \gamma \rangle g\mathscr {C})$ is a also straight strip and it must be equal to $g \mathscr {T}$. Thus we have the following proposition.

Proposition 4.5

For $(\gamma , g\mathscr {C},g\mathscr {T})\in \mathscr {P}$, $(\gamma , g\mathscr {C},g\mathscr {T})= (\gamma , g\mathscr {C}, \mathrm {SConv}( \langle \gamma \rangle g\mathscr {C})).$

Now let $g_1\mathscr {C},\ldots g_n \mathscr {C}$ be a complete list of liftings of chambers in $\mathscr {B}_\varGamma$.

Theorem 4.6

The set $\cup _{k=1}^\infty \mathscr {P}_k$ forms a set of representatives of the equivalence classes in $\mathscr {P}$, where

$$\begin{aligned} \mathscr {P}_k=\{(\gamma , g_i\mathscr {C}, \mathrm {SConv}( \langle \gamma \rangle g_i\mathscr {C}) : \gamma \in \varGamma , i\in \{1,2, \ldots n\}, g_i^{-1} \gamma g_i \in Kw^k K\}. \end{aligned}$$

Proof

For an element $p=(\gamma , g\mathscr {C}, g\mathscr {T})$ of $\mathscr {P}$, first we show that p is equivalent to some element in $\mathscr {P}_k$. Write $g\mathscr {C}= \delta g_i \mathscr {C}$ for some representative $g_i\mathscr {C}$ and $\delta \in \varGamma$. Then by Proposition 4.5,

$$\begin{aligned} p= (\gamma , g\mathscr {C}, \mathrm {SConv}( \langle \gamma \rangle g\mathscr {C}))= (\gamma , \delta g_i \mathscr {C}, \mathrm {SConv}( \langle \gamma \rangle \delta g_i \mathscr {C})) \end{aligned}$$

which is equivalent to

$$\begin{aligned} p'=( \delta ^{-1}\gamma \delta , g_i \mathscr {C}, \delta ^{-1} \mathrm {SConv}( \langle \gamma \rangle \delta g_i \mathscr {C})) = ( \gamma ', g_i \mathscr {C}, \mathrm {SConv}( \langle \gamma ' \rangle g_i \mathscr {C})) \end{aligned}$$

where $\gamma '= \delta ^{-1} \gamma \delta \in \varGamma$. Next, we show that $p'$ is indeed an element of some $\mathscr {P}_k$. Since $g\mathscr {C}= \delta g_i \mathscr {C}$ and $\gamma (g\mathscr {T})=g \mathscr {T}$, we have $g a = \delta g_i$ for some $a \in K$ and $g^{-1} \gamma g \in Kw^k K$ for some positive integer k. Therefore,

$$\begin{aligned} g_i^{-1} \gamma ' g_i = g_i^{-1} \delta ^{-1} \gamma \delta g_i = a^{-1} g^{-1} \gamma g a \in Kw^k I. \end{aligned}$$

Thus, $p' \in \mathscr {P}_k$.

To complete the proof, it remains to show that all elements in $\cup _{k=1}^\infty \mathscr {P}_k$ are not equivalent. Suppose that $(\gamma _1, g_{i_1}\mathscr {C}, \mathrm {SConv}( \langle \gamma _1 \rangle g_{i_1}\mathscr {C})$ are equivalent, $(\gamma _2, g_{i_2}\mathscr {C}, \mathrm {SConv}( \langle \gamma _2 \rangle g_{i_2}\mathscr {C}))$. Then

$$\begin{aligned} \gamma g_{i_1} \mathscr {T}= g_{i_2} \mathscr {T}, \gamma g_{i_1} \mathscr {C}= g_{i_2} \mathscr {C}, \quad \gamma \gamma _1 g_{i_1} \mathscr {C}=\gamma _2 g_{i_2} \mathscr {C}\end{aligned}$$

for some $\gamma \in \varGamma$. Since $\{g_i\mathscr {C}\}$ are representatives of $\varGamma$-orbits, we have $g=g_{i_1}=g_{i_2}$. Therefore $\gamma g \mathscr {C}= g \mathscr {C}$ which implies $\gamma \in \varGamma \cap g Kg^{-1} = \{ e\}$ (since the intersection is a discrete compact torsion-free subgroup). Thus, $\gamma$ must be the identity element. Applying the third part of the above condition,

$$\begin{aligned} \gamma \gamma _1 g_{i_1} \mathscr {C}=\gamma _2 g_{i_2} \mathscr {C}\, \Rightarrow \, \gamma _1 g \mathscr {C}=\gamma _2 g \mathscr {C}\, \Rightarrow \, \gamma _1^{-1} \gamma _2 \in \varGamma \cap g Kg^{-1} \, \Rightarrow \,\gamma _1 = \gamma _2. \end{aligned}$$

We conclude that any two equivalent elements are always the same element. $\square$

Now for a pointed closed geodesic strip p represented by some element in $\mathscr {P}_k$, we define its length $\ell (p)$ to be $k \ell (w)$ and its normalized length $\ell _0(p)$ to be k.

4.5 Counting pointed closed geodesic strips

Recall that one can identify the (affine) Hecke algebra $H_q(W,S)$ and the Iwahori–Hecke algebra $H(G,K)$ by mapping $e_w$ to $KwK$. Let $\pi _\varGamma$ be the natural representation of $H_q(W,S)$ acting on $L^2(\varGamma \backslash G/K)$ and let $A_w$ be the matrix of $\pi _\varGamma (e_w)$ with respect to the basis of characteristic functions on $\varGamma g_1 K,\ldots ,\varGamma g_n K$, denoted by $\{f_1,\ldots ,f_n\}$. Write

$$\begin{aligned} Kw^k K= \bigsqcup _{\alpha \in \varOmega _k} \alpha K, \end{aligned}$$

Then

$$\begin{aligned} (A_w^k)_{i,j} =\# \{ \alpha \in \varOmega _k: \varGamma g_i K= \varGamma g_j \alpha K\}. \end{aligned}$$

Theorem 4.7

The cardinality of $\mathscr {P}_k$ is equal to the trace of $(A_{w})^k$.

Proof

Note that when $\varGamma g_i K= \varGamma g_j \alpha K$, there exists some $\gamma \in \varGamma$, such that $\gamma g_i K= g_j \alpha K$ and such $\gamma$ is unique since if there exists $\gamma '$ satisfying the same condition, then again we have $\gamma ' \gamma ^{-1} \in \varGamma \cap g_i Kg_i^{-1}=\{e\}$. Therefore, we can rewrite the above as

$$\begin{aligned} (A_w^k)_{i,j} = \# \{ (\alpha , \gamma ) \in \varOmega _k \times \varGamma : \gamma g_i K= g_j \alpha K\}. \end{aligned}$$

On the other hand, when $\gamma g_i K= g_j \alpha K$, we have $\gamma g_i K\subset g_j Kw^k K$ and conversely, when $\gamma g_i K\subset g_j Kw^k K$ there exists a unique $\alpha \in \varOmega _k$ such that $\gamma g_i K= g_j \alpha K$. Therefore, we obtain

$$\begin{aligned} (A_w^k)_{i,j} = \# \{ \gamma \in \varGamma : \gamma g_i K\subseteq g_j Kw^k K\} =\# \{ \gamma \in \varGamma : g_j^{-1} \gamma g_i \in Kw^k K\}. \end{aligned}$$

Consequently, we have

$$\begin{aligned} \mathrm {tr}( (A_w)^k)=\# \{ (g_i K, \gamma ): i=1\sim n, \gamma \in \varGamma , g_i^{-1}\gamma g_i \in Kw^k K\} = \# \mathscr {P}_k. \end{aligned}$$

$\square$

4.6 Closed geodesic strips

We shall regard pointed closed geodesic strips as analogues of closed geodesics with a fixed starting vertex in finite graphs. In this subsection, we define the concept of closed geodesic strips, which are an analogue of closed geodesics without a fixed starting vertex in finite graphs. Set

$$\begin{aligned} \tilde{\mathscr {P}}=\{(\gamma , g \mathscr {T}): g \in G, \gamma \in \varGamma , \gamma (g \mathscr {T}) = g \mathscr {T}, \gamma \mid _{g \mathscr {L}} \text{ is } \text{ a } \text{ positive } \text{ translation }\} \end{aligned}$$

and define $(\gamma _1, g_1 \mathscr {T}) \sim (\gamma _2, g_2 \mathscr {T})$ if there exists some chambers $C_1$ and $C_2$ such that $(\gamma _1, C_1, g_1 \mathscr {T}) \sim (\gamma _2, C_2, g_2 \mathscr {T})$. Equivalence classes of $\tilde{\mathscr {P}}$ are called closed straight strips in $\mathscr {B}_\varGamma$ (of type w).

Furthermore, a closed geodesic strip is called primitive if it is not a repetition of a shorter closed geodesic strip. It is clear that every closed geodesic strip is a repetition of a unique primitive closed geodesic strip.

Theorem 4.8

The number of pointed closed geodesic strips mapped to a given closed geodesic strip is equal to the normalized length of its primitive closed geodesic strip.

Proof

Consider the canonical map $\sigma$ from $\mathscr {P}$ to $\tilde{\mathscr {P}}$ given by $\sigma ((\gamma , g\mathscr {C}, g \mathscr {T})) = (\gamma , g\mathscr {T})$. By Proposition 4.3, we have

$$\begin{aligned} \sigma ^{-1}\left( (\gamma , g\mathscr {T})\right) = \left\{ \left( \gamma , g w^k \mathscr {C}, g \mathscr {T}\right) : k \in \mathbb {Z}\right\} . \end{aligned}$$

Observe that the equivalence relation on $\tilde{\mathscr {P}}$ is induced form the equivalence relation on $\mathscr {P}$ and $\sigma$ induces a map $\tilde{\sigma }$ from $\mathscr {P}/\sim$ to $\tilde{\mathscr {P}}/\sim$, which is the map from the set of closed geodesic strips to the set of pointed closed geodesic strips by dropping pointed chambers. The size of the preimage of the equivalence class of $[(\gamma , g\mathscr {T})]$ is given by

$$\begin{aligned} \# \tilde{\sigma }^{-1}( [(\gamma , g\mathscr {T})]) = \# \left( \{(\gamma , g w^k \mathscr {C}, g \mathscr {T}): k \in \mathbb {Z}\}/\sim \right) . \end{aligned}$$

To evaluate the left-hand side of the above equation, recall that the setwise stabilizer $\mathrm {Stab}_\varGamma (g\mathscr {T})$ is a cyclic group containing $\gamma$. Let $\gamma _0$ be the unique generator of $\mathrm {Stab}_\varGamma (g\mathscr {T})$ satisfying that $\gamma |_{g\mathscr {L}}$ is a positive translation. Then, $\gamma = (\gamma _0)^m$ for some positive integer m and $\gamma _0 g \mathscr {C}= g w^{k_0} \mathscr {C}$ for some positive integer $k_0$. Moreover, the closed strip $[(\gamma , g \mathscr {T})]$ is primitive. Now we have

$$\begin{aligned} \left\{ \left( \gamma , g w^k \mathscr {C}, g \mathscr {T}\right) : k \in \mathbb {Z}\right\} /\sim =\left\{ \left( \gamma , g w^k \mathscr {C}, g \mathscr {T}\right) : k \in \mathbb {Z}\right\} / \langle \gamma _0 \rangle \end{aligned}$$

which contains exactly $k_0$ elements. $\square$

4.7 Zeta functions of closed geodesic strips

Set

$$\begin{aligned} Z_{w_i}(\mathscr {B}_\varGamma , u) = \prod _{c} (1- u^{\ell _0(c)})^{-1} = \prod _{[c]} (1+u^{\ell _0(c)}+u^{2\ell _0(c)}+\cdots ) \in \mathbb {Z}[[u]] \end{aligned}$$

where c runs through primitive closed geodesic strips of type $w_i$ and $\ell _0(c)$ is its normalized length defined in Sect. 4.4. Note that there are only finite many primitive closed strips with a given length. Therefore, the infinite product in the above definition is well-defined.

Recall that if a closed strip c of type $w_i$ has normalized length n, then its length $\ell (c)=n \ell (w_i).$ Define the zeta function of closed geodesic strips of $\mathscr {B}_\varGamma$ to be

$$\begin{aligned} Z\left( \mathscr {B}_\varGamma ,u\right) = Z_{w_1}\left( \mathscr {B}_\varGamma , u^{\ell \left( w_i\right) }\right) Z_{w_2}\left( \mathscr {B}_\varGamma , u^{\ell \left( w_2\right) }\right) . \end{aligned}$$

4.8 The Proof of Theorem 1.1

Like the case of graph zeta functions, zeta functions of straight strips also have infinite sum expression.

Theorem 4.9

As a function in the complex variable u, the zeta function $Z_{w_i}(\mathscr {B}_\varGamma , u)$ can be expressed as

$$\begin{aligned} Z_{w_i}(\mathscr {B}_\varGamma , u)= \exp \left( \sum _{n=1}^\infty \frac{N_n u^n}{n}\right) = \det \left( 1- A_{w_i} u\right) ^{-1} \end{aligned}$$

for $|u|<\Vert A_{w_i}\Vert ^{-1}$. Here, $\Vert A_{w_i}\Vert$ is the operator norm of $A_{w_i}$ and $N_n$ is the number of pointed closed geodesic strips of type $w_i$ of normalized length n.

Proof

Since $\mathrm {tr}((A_{w_i})^n) =N_n$ and the Taylor series of $\log (1-u)$ converges when $|u|<1$, we have

$$\begin{aligned} \sum _{n=1}^\infty \frac{N_n u^n}{n}= \sum _{n=1}^\infty \frac{\mathrm {tr}\left( \left( A_{w_i}\right) ^n\right) u^n}{n} = \log \left( \det \left( 1- A_{w_i} u\right) ^{-1}\right) \quad \text{ when } |u|< \Vert A_{w_i}\Vert ^{-1}. \end{aligned}$$

Let $\mathscr {P}_0$ be the set of primitive pointed closed geodesic strips of type $w_i$ and $\tilde{\mathscr {P}}_0$ be the set of primitive closed geodesic strips of type $w_i$. By Theorem 4.8, when $|u|< \Vert A_{w_i}\Vert ^{-1}$ we have

$$\begin{aligned} \sum _{n=1}^\infty \frac{N_n u^n}{n}&= \sum _{c \in \mathscr {P}} \frac{u^{\ell (c)}}{\ell (c)}= \sum _{c \in \mathscr {P}_0} \sum _{m=1}^\infty \frac{u^{m\ell (c)}}{m \ell (c)} = \sum _{c \in \tilde{\mathscr {P}}_0} \sum _{m=1}^\infty \frac{u^{m\ell (c)}}{m}\\&= \sum _{c \in \tilde{\mathscr {P}}_0} \log \left( 1- u^{\ell (c)}\right) ^{-1}\\&= \log \prod _{c \in \tilde{\mathscr {P}}_0} \left( 1- u^{\ell (c)}\right) ^{-1}. \end{aligned}$$

Here, we use the fact that $\sum _{n=1}^\infty \frac{N_n u^n}{n}$ converges absolutely when $|u|< \Vert A_{w_i}\Vert ^{-1}$ so that we can change the order of summation. $\square$

Note that $\det (1-A_{w_i}u)$ is a polynomial and $A_{w_i}$ is the matrix of $\pi _\varGamma (e_{w_i})$. Therefore, as a power series in u, we also have

$$\begin{aligned} Z\left( \mathscr {B}_\varGamma , u\right) = \det \left( 1-\pi _\varGamma \left( e_{w_1}\right) u^{\ell (w_1)}\right) ^{-1}\det \left( 1-\pi _\varGamma \left( e_{w_2}\right) u^{\ell (w_2)}\right) ^{-1} \end{aligned}$$

which proves the first part of Theorem 1.1. On the other hand, by the definition of $H_i(\rho ,u)$ in Sect. 3, we have

$$\begin{aligned} H_i(\pi _\varGamma ,u) = (I- \pi _\varGamma (e_{w_i}) u^{\ell (w_i)})^{-1}. \end{aligned}$$

Together with the above equation and Theorem 3.7, we have

$$\begin{aligned} Z(\mathscr {B}_\varGamma , u)=\det H_1(\pi _\varGamma ,u) \det H_2(\pi _\varGamma ,u) =\det \mathrm {Alt}(W)(\pi _\varGamma ,u) \end{aligned}$$

which proves the second part Theorem 1.1.

5 Alternating products of Poincaré series

Note that one can generalize the definition of straight strips to “straight tubes” in the higher rank cases in the following manner. Once again one identifies the apartment with a real vector space and the origin with a special vertex v , and then for each vertex other than v with a corresponding vector $v_i$ one may consider the connected components of the complement of the union of all the hyperplanes which are invariant under translation by the vector $v_i$. In this way, one obtains the straight tubes in the direction $v_i$ for each i, and one may study their stabilizers. We expect that there exists an analogue of Theorems 1.1 and 3.7 for higher ranks cases. More precisely, let (W, S) be an irreducible affine Coxeter group of rank $|S|=n+1$, and set

$$\begin{aligned} \mathrm {Alt}(W)(u)= \prod _{I \subset S} W_I(u)^{(-1)^{|I|+|S|}}. \end{aligned}$$

Then, we have the following conjecture.

Conjecture 5.1

There exist straight elements $w_1,\ldots , w_n \in W$ such that for $H_i=\{ w_i^k\}_{k \in \mathbb {Z}_{\ge 0}}$, the following two identities holds.

• 1. $w_i$ is a generator of the stabilizer of some straight tube.

• 2. $\mathrm {Alt}(W)(u)=H_1(u)\cdots H_n(u)$.

• 3. For any finite dimensional representation $\rho$ of $H_q(W,S)$,

  $$\begin{aligned} \prod _{i=1}^n \det H_i(\rho ,u)= \prod _{I \subset S} \det W_I(\rho ,u)^{(-1)^{|I|+|S|}}. \end{aligned}$$

Note that the above conjecture implies that

$$\begin{aligned} \mathrm {Alt}(W)(u)^{\text {-1}}= \left( 1-u^{d_1}\right) \cdots \left( 1-u^{d_n}\right) \end{aligned}$$

(5.1)

where $d_i = \ell (w_i)$ are positive integers.

In the rest of the paper, we examine Eq. (5.1) for all affine Coxeter groups.

Let R be an irreducible reduced crystallographic root system of rank n, and let $W_0$ be the Weyl group with generating set $S_0$, and let W be the affine Weyl group with generating set S. Let h be the Coxeter number of $W_0$. Denote by $[a,b]^k$ the multiset consisting integers between a and b with multiplicity k and denote it by $[a]^k$ when $a=b$. For example,

$$\begin{aligned} {[}3]^2=\{3,3\} \quad \text{ and } \quad [2,4]^3=\{2,2,2,3,3,3,4,4,4\}. \end{aligned}$$

The main result of this section is the following theorem which is the same theorem as Theorem 1.2 with the extra table of $d_i$.

Theorem 5.2

For the affine Weyl group W, its power series $\mathrm {Alt}(W)(u)^{\text {-1}}$ is indeed a polynomial of the form

$$\begin{aligned} \left( 1-u^{d_1}\right) \cdots \left( 1-u^{d_n}\right) \end{aligned}$$

where $d_i$ are integers with $n+1= d_1 \le d_2 \le \cdots \le d_n \le h$ as shown as in the following table.

Type	Coxeter number h	$\{d_1,\ldots , d_n\}$
${A_{n}}$	$n+1$	$[h]^n$
${B_{n}}$	2n	$[n+1,h]$
${C_{n}}$	2n	$[n+1,h]$
${D_{n}}$	$2n-2$	$[n+1,h]\sqcup [h]^2$
${E_{6}}$	12	$\{7, 9, 9, 11, 12, 12\}$
${E_{7}}$	18	$\{8, 10, 11, 13, 14, 17, 18\}$
${E_{8}}$	30	$\{9, 11, 13, 14, 17, 19, 23, 29\}$
${F_{4}}$	12	$\{5, 7, 8, 11\}$
${G_{2}}$	6	$\{3, 5\}$

Remark

Note that $d_n$ is always equal to h or $h-1$, and further the number of times h occurs in the set of all $d_n$ is equal to the connection index minus one. Moreover, $d_n=h-1$ only when W is of type $E_7$, $F_4$ or $G_2$. These three types of groups are the only simple algebraic groups whose simply connected and adjoint forms are the same. Besides, the multiplicity of h in the above table is equal to the number of conjugacy classes of Coxeter elements.

5.1 MacDonald’s formula

We shall prove the above theorem using MacDonald’s formula [14] for Poincaré series of affine Weyl groups in terms of positive roots. Let us recall his result. Let R be a reducible root system in a finite dimensional real vector space V. Fix a set of simple roots $B=\{\alpha _1,\ldots ,\alpha _n\}$ and let $R^+$ be the set of positive roots with respect to B. Let $S_0$ be the set of reflections corresponding to B and $W_0$ be the group generated by $S_0$, which is the Weyl group of R. In this case, $(W_0,S_0)$ forms a finite Coxeter system. For a root $\alpha = \sum c_i \alpha _i$, its height is defined as

$$\begin{aligned} {\mathrm {ht}}(\alpha )= \sum _{i=1}^n c_i. \end{aligned}$$

Theorem 5.3

(MacDonald) The following identities hold.

$$\begin{aligned} W_0(u)= \prod _{a \in R^+} \frac{1-u^{ {\mathrm {ht}}(a)+1}}{1-u^{ {\mathrm {ht}}(a)}} \end{aligned}$$

Next, let us consider the affine root system $\tilde{R} = R \times \mathbb {Z}$, whose elements $\lambda =(\alpha ,k)$ are regarded as affine functions on V

$$\begin{aligned} \lambda (x)=(\alpha ,x)+k. \end{aligned}$$

For convenience, we also denote $\lambda$ by $k+\alpha$ and regard R as a subset of $\tilde{R}$. Let $\tilde{B}=B \cup \{\alpha _0\}$, where $\alpha _0$ = $1-\rho$ and $\rho$ is the highest root. Let $\tilde{R}^+$ be the set of positive affine roots, which elements are non-negative integer linear combinations of $\tilde{B}$. Let S be the set of affine reflections corresponding to $\tilde{B}$ and W be the group generated by S, which is the affine Weyl group of R. Then, (W, S) is a Coxeter system associated with $\tilde{R}$. For $k+\alpha = \sum _{i=0}^n c_i \alpha _i \in \tilde{R}$, define its weight to be

$$\begin{aligned} {\mathrm {ht}}(k+\alpha )= \sum _{i=0}^n c_i. \end{aligned}$$

Then, we also have

$$\begin{aligned} {\mathrm {ht}}(k+\alpha ) = k {\mathrm {ht}}(1) + {\mathrm {ht}}(\alpha ) = kh + {\mathrm {ht}}(\alpha ). \end{aligned}$$

Here, h is the Coxeter number which is equal to ${\mathrm {ht}}(1)=1+ {\mathrm {ht}}(\rho ).$

Consider the set

$$\begin{aligned} P=\{\lambda \in \tilde{R}: 0< {\mathrm {ht}}(\lambda ) < h\}=R^+ \cup \{1-\alpha : \alpha \in R^+\}. \end{aligned}$$

Theorem 5.4

(MacDonald) The following identities hold.

$$\begin{aligned} W(u)= \frac{1}{\left( 1-u^h\right) ^n} \prod _{a \in P} \frac{1-u^{ {\mathrm {ht}}(a)+1}}{1-u^{ {\mathrm {ht}}(a)}}. \end{aligned}$$

5.2 A Proof of Theorem 5.2

For a subset I of S, consider the Möbius function $\mu (I) = (-1)^{|I|}$ which satisfies the property

$$\begin{aligned} \sum _{I \subset J \subset S} \mu (J) = {\left\{ \begin{array}{ll} \mu (S), &{}\quad \text{ if }\quad I=S;\\ 0,&{}\quad \text{ otherwise }. \end{array}\right. } \end{aligned}$$

Then, we can write the alternating product as:

$$\begin{aligned} \mathrm {Alt}(W)(u)= \prod _{I \subset S}W_I(u)^{(-1)^{|I|+|S|}} = \prod _{I\subset S} W_{I}(u)^{\mu (I)\mu (S)}. \end{aligned}$$

Now for a subset I of S, let $\bar{B}_I$ be the subset of $\tilde{B}$ consisting positive simple affine roots corresponding to affine reflections in I. Let $\bar{R}_I$ be the subroot system of $\tilde{R}$ with the set of simple roots $\bar{B}_I$. Then, we have $\bar{R}_I^+ \subset \bar{R}_J^+$ if $I \subset J$. Note that every proper subroot system $\bar{R}_I$ is a (finite) reducible root system so that $W_I(u)$ satisfies Theorem 5.3.

Applying Theorems 5.3 and 5.4 to the above equation, we have

$$\begin{aligned} \mathrm {Alt}(W)(u)&= W(u) \prod _{I\subsetneq S} W_{I}(u)^{\mu (I)\mu (S)}\\&= \frac{1}{(1-u^h)^n} \prod _{\lambda \in P} \left( \frac{1-u^{ {\mathrm {ht}}(\lambda )+1}}{1-u^{ {\mathrm {ht}}(\lambda )}} \right) \cdot \prod _{I\subsetneq S} \prod _{\lambda \in \bar{R}_I^+} \left( \frac{1-u^{ {\mathrm {ht}}(\lambda )+1}}{1-u^{ {\mathrm {ht}}(\lambda )}} \right) ^{\mu (I)\mu (S)}. \end{aligned}$$

To simplify the above equation, for a positive affine root $\lambda = \sum _{i=0}^n c_i \alpha _i$ with $c_i\ge 0$, define its support to be

$$\begin{aligned} {\mathrm {Supp}}(\lambda )=\left\{ \alpha _i \in \tilde{B}: c_i \ne 0\right\} . \end{aligned}$$

Then, $\lambda$ is a positive root in $\bar{R}_J$ when ${\mathrm {Supp}}(\lambda ) \subset \bar{B}_J$. Thus

$$\begin{aligned}&\prod _{I\subsetneq S} \prod _{\lambda \in \bar{R}_I^+} \left( \frac{1-u^{ {\mathrm {ht}}(\lambda )+1}}{1-u^{ {\mathrm {ht}}(\lambda )}} \right) ^{\mu (I)\mu (S)}= \prod _{\lambda \in \bar{R}^+} \prod _{I: {\mathrm {Supp}}(\lambda )\subset \bar{B}_I \subsetneq \tilde{B}} \left( \frac{1-u^{ {\mathrm {ht}}(\lambda )+1}}{1-u^{ {\mathrm {ht}}(\lambda )}} \right) ^{\mu (I)\mu (S)}. \end{aligned}$$

On the other hand, it is easy to see that every positive root in the proper subroot system with height bounded by h, which implies such root is contained in P. Therefore, we can write the alternating product as:

$$\begin{aligned} \mathrm {Alt}(\tilde{W})(u)&= \frac{1}{(1-u^h)^n} \prod _{\lambda \in P} \left( \frac{1-u^{ {\mathrm {ht}}(\lambda )+1}}{1-u^{ {\mathrm {ht}}(\lambda )}} \right) ^{\mu (S)^2}\\&\quad \cdot \prod _{\lambda \in P} \prod _{{\mathrm {Supp}}(\lambda )\subset \bar{B}_I \subsetneq \tilde{B}} \left( \frac{1-u^{ {\mathrm {ht}}(\lambda )+1}}{1-u^{ {\mathrm {ht}}(\lambda )}} \right) ^{\mu (I)\mu (S)}\\&= \frac{1}{(1-u^h)^n} \prod _{\lambda \in P} \prod _{{\mathrm {Supp}}(\lambda )\subset \bar{B}_I \subset \tilde{B}} \left( \frac{1-u^{ {\mathrm {ht}}(\lambda )+1}}{1-u^{ {\mathrm {ht}}(\lambda )}} \right) ^{\mu (I)\mu (S)}\\&= \frac{1}{(1-u^h)^n} \prod _{\lambda \in P,{\mathrm {Supp}}(\lambda )= \bar{B}} \frac{1-u^{ {\mathrm {ht}}(\lambda )+1}}{1-u^{ {\mathrm {ht}}(\lambda )}}. \end{aligned}$$

Since $P= \{\lambda \in \tilde{R}: 0< {\mathrm {ht}}(\lambda ) < h\}=R^+ \cup \{1-\alpha : \alpha \in R^+\}$ and none of element in $R^+$ satisfies ${\mathrm {Supp}}(\alpha )=\bar{B}$, we can write the above result as

$$\begin{aligned} \mathrm {Alt}(W)(u)&= \frac{1}{(1-u^h)^n} \prod _{\alpha \in R^+,{\mathrm {Supp}}(1-\alpha )= \bar{B}} \frac{1-u^{ {\mathrm {ht}}(1-a)+1}}{1-u^{ {\mathrm {ht}}(1-\alpha )}}. \end{aligned}$$

Observe that $1-\alpha = (1-\rho )+(\rho - \alpha )$. Therefore, ${\mathrm {Supp}}(1-\alpha )=\bar{B}$ if and only if ${\mathrm {Supp}}(\rho -\alpha )=B$. On the other hand, one can find the complete list positive roots $R^+$ and the highest root $\rho$ in [2]. Therefore, we can compute those elements with ${\mathrm {Supp}}(\lambda -\alpha )=B$ case-by-case.

For example, suppose R is of type $B_n$. We have

$$\begin{aligned} R^+= \left\{ \sum _{i\le k \le j} \alpha _k : 1\le i \le j \le n\right\} \bigcup \left\{ \sum _{i\le k<j} \alpha _k + 2 \sum _{j\le k \le n} \alpha _k : 1\le i < j \le n\right\} \end{aligned}$$

and

$$\begin{aligned} \rho = a_1+2 a_2 + 2 a_3+ \cdots + 2 a_n. \end{aligned}$$

Therefore, $I(1- \alpha )=B$ if and only if $\alpha$ is of the form

$$\begin{aligned} \sum _{i\le k \le j} \alpha _k , 1 < i \le j \le n. \end{aligned}$$

The set of weight of those $\alpha$ is

$$\begin{aligned} {[}1]^{n-1} \sqcup [2]^{n-2}\sqcup \cdots \sqcup [n-2]^2 \sqcup [n-1]. \end{aligned}$$

Note that the Coxeter number $h=1+ {\mathrm {ht}}(\rho )=2n$ and the set of weight of $1-\alpha$ is

$$\begin{aligned} {[}h-1]^{n-1} \sqcup [h-2]^{n-2}\sqcup \cdots \sqcup [n+2]^2 \sqcup [n+1]. \end{aligned}$$

We can also rewrite the above set of weight of as

$$\begin{aligned} {[}n+1,h-1] \sqcup [n+2,h-1] \sqcup \cdots \sqcup [h-2,h-1] \sqcup [h-1]. \end{aligned}$$

Now we have

$$\begin{aligned} \mathrm {Alt}(W)(u)&= \frac{1}{(1-u^h)^n} \prod _{\alpha \in R^+,{\mathrm {Supp}}(\rho -\alpha )= B} \frac{1-u^{ {\mathrm {ht}}(1-a)+1}}{1-u^{ {\mathrm {ht}}(1-a)}}\\&= \frac{1}{(1-u^{2n})^n} \prod _{i=n+1}^{2n-1} \prod _{j=i}^{2n-1} \frac{1-u^{j+1}}{1-u^{j}}\\&= \frac{1}{(1-u^{2n})^n} \prod _{i=n+1}^{2n-1} \frac{1-u^{2n}}{1-u^{i}}\\&= \prod _{i=n+1}^{2n} \frac{1}{1-u^{i}}. \end{aligned}$$

which proves Theorem 5.2 for type $B_n$. For the rest of cases, the computations are similar so we only record the heights of those positive root $\alpha$ with ${\mathrm {Supp}}(\rho -\alpha )=B$ in the following table.

Type	Coxeter no. h	Heights of $1-\alpha$ with ${\mathrm {Supp}}(\rho -\alpha )=B$
$A_n$	$n+1$	Empty set
$B_n$	2n	$\bigsqcup _{i}[i,h-1]$, $i \in [n+1,h-1]$
$C_n$	2n	$\bigsqcup _{i}[i,h-1]$, $i \in [n+1,h-1]$
$D_n$	$2n-2$	$\bigsqcup _{i}[i,h-1]$, $i \in [n+1,h-1]$
$E_6$	12	$\bigsqcup _{i}[i,h-1]$, $i=7,9,9,11$
$E_7$	18	$\bigsqcup _{i}[i,h-1]$, $i=8,10,11,13,14,17$
$E_8$	30	$\bigsqcup _{i}[i,h-1],$ $i=9,11,13,14,17,19,23,29$
$F_4$	12	$\bigsqcup _{i}[i,h-1],$ $i=5,7,8,11$
$G_2$	6	$\bigsqcup _{i}[i,h-1],$ $i=3,5$