Direct Measurement of Positronium HyperFine Structure: ∼ A New Horizon of Precision Spectroscopy Using Gyrotrons ∼

Abstract

Positronium is an ideal system for research on QED, especially in a bound state. A discrepancy (3.9σ) is found recently between measured HFS values and the QED prediction (including up-to O(α ³ log α ^− 1), where α is the fine-structure constant.). It might be due to a contribution of unknown new physics or common systematic problems in all the previous measurements. A new method to measure HFS directly is performed using a high power gyrotron. The transition from ortho-positronium to para-positronium has been observed with 5 σ CL, which is the first observation of M1 transition in (sub)Terahertz region. New technologies of high power gyrotrons are developed for precision spectroscopy.

1 Introduction

Positronium (Ps), the bound state of an electron and a positron, is a purely leptonic system and is a good target to study Quantum Electrodynamics (QED) precisely. The triplet ($1^{3}S_{1}$) state of Ps, ortho-positronium(o-Ps), decays slowly into three photons with the long lifetime of 142.05 nsec. On the other hand the singlet state ($1^{1}S_{0}$) of Ps, para-positronium(p-Ps), decays into two photons promptly (lifetime 125psec). The energy level of o-Ps is higher than that of p-Ps, and this difference of the energy levels is called Positronium Hyper Fine Structure (Ps-HFS). Ps-HFS is significantly large about 203 GHz, compared to hydrogen-atom (1.4 GHz).

Precise measurement of Ps-HFS gives direct information about QED, especially QED in the bound state. If an unknown light particle (like the axion or a milli-charged particle) exits, it contributes virtually to the energy levels, and makes a difference from the QED prediction calculated with only known particles. The precise measurements have been performed in 70’s and 80’s, which results are shown in Fig. 1 with the theoretical value. These results are consistent with each other, and a value combined with the most accurate two results [1, 2] is 203.388 65(67) GHz (3.3 ppm), which is shown with the green band.

Fig. 1

Historical plot of Ps-HFS values. Points with error bars show the experimental results with references. Green and red bands show the average of the measured values (the most precise and the latest results), and the theoretical value calculated up-to O(α ³ logα ^− 1), respectively. α is the fine-structure constant.

The new method to calculate higher order corrections for the bound state was established in 2000, and the 2nd and 3rd order corrections have been performed [3–5]. The QED prediction is 203.3917(6) GHz (2 ppm) shown with the red band in the same figure. A discrepancy of 3.04(79) MHz (15 ppm) is found between the measured value and the QED prediction, and this might not be a statistical fluctuation (3.9 σ). It is very important to measure Ps-HFS again with a method totally different from the previous experiments.

1.1 Possible systematic errors in the previous experiments

In all the previous measurements, the Ps-HFS transition was not observed, since 203 GHz was too high frequency to be handled. Static magnetic field causes the Zeeman mixing between the m _z  = 0 state of o-Ps and p-Ps, the resultant energy level of new m _z  = 0 state( $|+\rangle$ ) becomes higher than that of the m _z  = ±1 state. On the other hand, the m _z  = ±1 state of o-Ps does not couple to static magnetic field, and does not change the energy level. A shift of energy (Δ_mix ) between $|+\rangle$ and $|m_z=\pm1\rangle$, “the Zeeman shift”, is proportional to Ps-HFS(Δ_HFS ) as follows;

$$ \Delta_{\rm{mix}} = \frac{\Delta_{\rm{HFS}}}{2} ( \sqrt{1+\chi^2} -1 ) \, . $$

(1)

where $\chi=\frac{2g' \mu_B H}{h \Delta_{\rm{HFS}}}$, H is the static magnetic field strength, μ _B is the Bohr magneton, g’ is the g-factor of a electron, and h is the Planck constant. The Zeeman shift Δ_mix has been measured in all the previous experiments, and Δ_HFS was extracted using the formula 1.

Positron emitted from a ²² Na radioactive source stopped in gases (N ₂, Argon etc), then Ps formed. The gas was filled in a RF cavity, in which high power 2.3 GHz microwave was stored, and the static magnetic field (about 8 kGauss) was also applied. The magnetic field strength was scanned to obtain the resonance curve of the Zeeman shift. When Δ_mix became the same as the RF microwave, the transition from the m _z  = ±1 state to $|+\rangle$ increased, and the $|+\rangle$ state decayed into 2γ immediately through the p-Ps state. 2γ decay, which were tagged with back-to-back topology using NaI scintillators, increased near the resonance. Breit–Wigner resonance curve was measured by changing the static magnetic field strength, and the Δ_mix was obtained. Since Ps was produced in the gas, the produced Ps collided with the gas molecule and an electric field of the gas molecule made a shift of HFS, “the Stark effect”. About 10 ppm shift of Ps-HFS was observed for 1 atm gas [1, 2]. Ps-HFS values including the Stark effect were measured by changing gas pressures. The values obtained in the gases were extrapolated to zero pressure, and Ps-HFS in vacuum was obtained.

There are two possible uncertainties in this method and we propose a new method to overcome these problems [6].

• 1. The formed Ps was widely spread in a RF cavity (size about 20 cm in diameter) and the distribution depended on the pressure of the gases and the strength of the magnetic field. On the other hand, a size of the magnet used was limited and the non-uniformity of the magnetic field was worse than 10ppm. The complicated correction has been applied but the uncertainty of the magnetic field was still the leading systematic error. Non-uniformity of the magnetic field might be unknown systematic error.

• 2. Non-thermalized o-Ps is also a source of the uncertainty not considered in the previous experiments. The extrapolation procedure was assumed that the collision rate between Ps and gas molecule was proportional to the gas pressure. It was correct only when the average velocity of Ps is the same for the various pressured gases, i.e. Ps was well thermalized. We have already shown in the decay rate measurements [7–9] that this thermalized assumption was not satisfied, and that this extrapolation caused the serious systematic error, known as “o-Ps lifetime puzzle” in 80’s and 90’s. The non-thermal Ps would affect also on the measurement of Ps-HFS.

1.2 Direct transition using gyrotron

Direct measurement of the Ps-HFS transition without a static magnetic field is free from the systematic uncertainty of magnetic field mentioned above. Since the transition from o-Ps(S=1) to p-Ps(S=0) is the M1 transition and seriously suppressed (transition rate is 3.37 × 10^− 8 s ^− 1 [12]), this transition has not yet observed so far. A gyrotron [10] is a novel high power radiation source for (sub) THz region, and the gyrotron, FU CW V, is developed to measure the Ps-HFS transition. The first target of our experiment is to detect the Ps-HFS transition directly. Frequency of FU CW V is fixed at the peak of Breit–Wigner resonance. In the second phase, Breit–Wigner resonance curve will be measured directly using a frequency-tunable gyrotron. Tunable frequency is also big challenge of (sub) THz light source, and a new gyrotron with tunable frequency is developed using a gyro-backward-wave oscillator [11]. In this paper, results of the first phase are reported.

2 Experimental setup

2.1 Gyrotron

Figure 2a shows a schematic view of the experimental setup, and Fig. 2b shows a photograph of the developed gyrotron (Gyrotron FU CW V) which is dedicated to the first phase of the Ps-HFS direct measurement. Electrons are emitted and accelerated at a DC electron gun(lower part of the photograph), rotated as the cyclotron motion in a superconducting magnet(blue part in middle). The cyclotron frequency f _c is

$$ f_c = \frac{eB}{2\pi{}m_0\gamma}, $$

(2)

where B is the magnetic field strength, m ₀ is the electron rest mass and γ is the relativistic factor of the electron. A cavity is placed at the maximum magnetic field, whose resonance frequency is tuned to the cyclotron frequency. The electrons stimulate resonance of the cavity and produce coherent photons in the cavity. Photons are guided to an output port through a window, while electrons are dumped at a collector(top part in Fig. 2b). FU CW V, operated at f _c  = 202.9 GHz with B = 7.425 Tesla, γ ∼ 1.02, achieves power of 609 W, but is operated at 300 W stably during run time, typically 170 h. Power of gyrotrons is usually unstable, and fluctuation of power is usually about factor 2. Power is monitored, whose output is fed back to the voltage of heater of the electron gun, then stable power (stability  a few %) is obtained in FU CW V. Accumulated operation time of FU CW V is longer than 3,000 h with stable power of 300 W.

Fig. 2

(a) Schematic view of the whole experimental setup (b) Photograph of the gyrotron FU CW V.

The gyrotron power has a pulse structure. Photons are emitted during 15 msec (called “ON” status hereafter) for every 50 msec (20 Hz, duty factor 30%). The pulse is fast rising, and photons are produced continuously (CW mode) in the ON status. Another period (70%) is “OFF” status, in which photons are not emitted, and data in the OFF status can be used to estimate the background without 203 GHz radiation.

2.2 Mode converter

203 GHz mm-waves emitted from FU CW V pass through a mode converter, which is constituted with three parabolic mirrors(main parabolic, M1 and M2) and one plane mirror(M3) as shown in Fig. 2a. Cross-section of the main parabolic mirror and a step-cut waveguide of the gyrotron is shown in Fig. 3. Azimuthal-polarized wave out-going from the step-cut waveguide is converted into linear-polarized wave (bi-Gaussian shape) using the main parabolic mirror because of OPR=OP‘R’ [13]. The plane wave is converted into a Gaussian beam using the M1 and M2 parabolic mirrors, which have the long focal-distance and are set orthogonal to each other. Power distributions measured with an infrared camera are shown in Fig. 4, in which (a) and (b) are power profiles before and after the mode converter, respectively. The waveform is TE₀₃ mode, which is resonance mode used in the gyrotron, but a hole connecting to a vacuum pomp in the waveguide makes an asymmetric shape shown in Fig. 4a. Conversion efficiency(ϵ _conv) is currently about 30%, because the waveform of the gyrotron output is not perfect TE₀₃ (purity 40%) mode. We can expect ϵ _conv ∼ 80% for the pure TE₀₃ wave.

Fig. 3

Cross-section of the main parabolic mirror and the step-cut waveguide of the gyrotron: the green lines and the blue arrows show the trajectory and polarization of photon, respectively.

Fig. 4

Power profiles (a) at waveguide of the gyrotron(TE03 mode) (b) after the mode converter (Gaussian mode).

2.3 Fabry–Pérot cavity

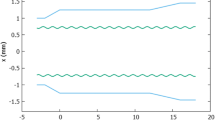
The converted photons are transported and accumulated in a Fabry–Pérot cavity to cause the Ps-HFS transition. This cavity consists of two high reflective mirrors as shown in Fig. 2a, since 203 GHz (λ = 1.475 mm) photons can be treated optically at centimeter (or larger) scale. A gold-mesh and a copper-concave mirrors are used on the input and the other side of the cavity, respectively. Figure 5 show photographs of the mesh mirror and the magnified view, the gold mesh is evaporated on the quartz. Thickness of gold is 1 μm which is much larger than the skin depth of the photon (170 nm). There are three sources of power losses in cavities; (1) diffraction loss, (2) medium loss and (3) ohmic loss. The first two losses are expected to be negligible in our cavity. The last one, ohmic loss, occurs at the mirrors, which is about 0.15% on the copper mirror and more on the mesh mirror. The ohmic loss and the coupling performance mentioned later are opposed to each other, and we optimize the best parameters of the mesh (width = 200 μm and gap = 150 μm) using the simulation [14, 15]. Reflectivity of the gold-mesh mirror is very high (99.3%) and the transmittance is reasonable (0.5%). The copper-concave mirror is mounted on a Piezo stage to shift cavity-length precisely (step 200 nm).

Fig. 5

Photographs of the mesh mirror and the magnified view.

Photons are accumulated in the cavity when the cavity is on the resonance. Photon power of the input, the transmitted(copper side) and the reflected(mesh mirror side) are monitored by pyroelectric power monitors(SPECTRUM SPC-9H). Pyroelectric monitors for the input and the reflected are located at M3 mirror of the mode converter shown in Fig. 2a. M3 is a half mirror and some part of photon is transmitted to measure the power. Figure 6a and b show outputs of the reflected and the transmitted monitors, respectively, as a function of the distance between two mirrors. The sharp resonance is observed in both. Two important characteristics of the cavity are “coupling C” and “finesse $\mathcal{F}$”. The input coupling can be estimated from decrease of the reflection power of the cavity at the resonance, and C ∼ 67% is obtained from Fig. 6a.

Fig. 6

(a) Reflection power of the cavity (b) Transmission power of the cavity.

Finesse can be written as $\mathcal{F} = 2\pi N_{\rm round} = \lambda/2\Gamma$, where N _round is a number of round-trips of photons in the cavity, λ is a wavelength of the photon, and Γ is sharpness of the resonance (FWHM). A Sharp resonance (Γ = 1.1 μm) is observed as shown in Fig. 6b. $\mathcal{F}$ is, therefore, about 650 and N _round is about 100. Gain of the cavity is estimated G = C × 2N _round = 140, and the accumulated power in the cavity is about 12.6 kW,

$$ P_{\rm acc} = P_{\rm gyro} \times \epsilon_{\rm conv} \times G = 300 [{\rm W}] \times 0.3 \times 140 = 12.6 [{\rm kW}]. $$

(3)

2.4 Ps assembly and γ-ray detectors

Figure 7 show a photograph and a schematic of the Ps assembly and γ-ray detectors. A ²² Na positron source(1MBq) is installed in a thin plastic scintillator(100 μm), and timing information of a positron emission is tagged using signal from the plastic scintillator. A positron, passing through the plastic scintillator, stops in gas and forms a positronium atom (formation efficiency is about 20%). The gas used in our experiment is mixture of nitrogen (90%) and i-C₄H₁₀(10%). I-C₄H₁₀ is mixed to quench the slow positron whose kinetic energy is too low to ionize an electron of the gas . P-Ps (25% of the formed Ps) annihilates to two γ’s (E = 511 keV) immediately as well as positron annihilation(about 80% of positron do not form Ps, just annihilation with an electron of the gas). On the other hand, o-Ps (75%) remains with the long lifetime of τ ∼ 142 ns and decays to three γ’s whose energies are continuous distributions (< 511 keV). These γ rays are detected by surrounding the detectors shown in Fig. 2a and Fig. 7. Four LaBr₃ crystal scintillators are used because of the good energy resolution (FWHM = 4% at 511 keV) and the fast response. The decay constant of scintillation pulse of LaBr₃ is significantly fast 16 nsec and the obtained time resolution is about 200 psec.

Fig. 7

Ps assembly and γ-ray detectors. (Left) Photograph (Right) Schematic view.

3 Results

Run time is 3.5 days on the resonance of Ps-HFS. A trigger of the data acquisition is as follows: at least two signals from the LaBr₃ scintillators are coincident within 20 nsec, and this coincidence timing is also required to be within −100 and 1,100 nsec of the timing of the thin plastic scintillator. The trigger rate is about 1kHz. Average accumulated power in the Fabry–Pérot cavity is about 12 kW during the data acquisition.

Figure 8 shows the time difference between the pulse of the plastic scintillator and the signals of the LaBr₃ scintillators. A sharp peak from prompt annihilation is followed by the exponential curve of o-Ps, and then the constant accidental spectrum. Fitted lifetime is 134.32 ± 0.12 nsec which is consistent with an expected value in the mixture gas (0.9 atm N ₂ and 0.1atm i-C₄H₁₀). A decayed coincidence (time window from 50 to 250 nsec) is required to select o-Ps decay events. Time information is also new progress in the Ps-HFS measurement. (Time information was not measured in the previous experiments.) There are two benefits using the delayed coincidence.

• 1. Large part of positron(∼80%) are just annihilated into 2γ’s at t = 0, and 2γ annihilated events make S/N seriously worse. 2γ annihilation background events can be removed significantly with the delayed coincidence, and S/N is improved by factor 20.

• 2. Suppress the effect of the non-thermalized Ps. The formed o-Ps atom collides with a molecule of N ₂ gas, and the kinetic energy losses gradually. O-Ps becomes thermal within the delayed time window. This solves the systematic problem (2) mentioned in Section 1.1.

Fig. 8

Time difference between the plastic scintillator(e ⁺ emission) and the coincidence signals of the LaBr₃ scintillators(γ-ray detection). Red and black spectrum are with/without 203 GHz radiation. Region labeled by “Delayed” shows the time window to select the o-Ps events.

203 GHz photons stored in the Fabry–Pérot cavity drive the stimulated transition from o-Ps to p-Ps, and p-Ps decays into two γs promptly. Figure 9a shows the energy spectrum with/without 203 GHz radiation after all event selections are applied. Power of the gyrotron is ON during 15 msec for every 50 msec (20Hz, duty factor 30%) and the pulse is fast rising enough and 203 GHz photons are accumulated in the cavity only during this period. Even in the spectrum without the radiation (OFF), a sharp peak is observed at 511 keV. This is corresponding to “pick-off annihilation”, in which o-Ps collides with a gas molecular, and a positron of o-Ps annihilates with an electron in the collided molecular. This is inevitable in gases, and is the reason why the measured lifetime is shorter than 142.05 nsec. This effect is the same both with and without 203 GHz radiation. Spectrum without the radiation is subtracted from that with radiation to draw out signals of the transition. Figure 9b shows the subtracted spectrum and a clear peak due to the transition is observed at 511 keV. Signal rate of the stimulated transition from o-Ps to p-Ps is 15.2 ± 3.0(stat.) $^{+0.6} _{-0.1}$(sys.) mHz. Systematic errors are summarized in Table 1. Main systematic error is due to the number of o-Ps in the delayed window, which is propagated from the positronium formation probability in the gas. The quadrature sum of all systematic errors is + 0.18 − − 0.02% of the transition rate, which is much smaller than the statistical error. This is the first observation of the direct HFS transition of positronium with 5σ confidence level.

Fig. 9

Energy spectra after all event selections. (a) Red and black histogram show energy spectrum with/without 203 GHz radiation (b) difference spectrum between with and without 203 GHz radiation.

Table 1 Summary of the systematic errors.

4 Summary and plan

There is a discrepancy (3.9σ) between the measured Ps-HFS values and the QED prediction (O(α ³ log(α ^− 1))). We point out the possible common systematic uncertainties(non-uniformity of magnetic field and non-thermalized Ps) in the previous experiments, and propose the new method to measure Ps-HFS precisely and directly. The stable gyrotron, the mode converter and the Fabry–Pérot cavity are developed. The gyrotron is operated stable (stability a few %) for the long period, and more than 12 kW power is accumulated in the cavity. These are useful technologies for the spectroscopy using gyrotrons. The HFS transition from ortho-positronium to para-positronium is observed with 5 σ CL, which is the first observation of M1 transition in (sub)Terahertz region. For the next step, a frequency-tunable gyrotron is developed, which is also crucial for spectroscopy.