An Overview of Modeling Cement Based Materials at Elevated Temperatures with Mechanics of Multi-Phase Porous Media

Abstract

Application of mechanics of multi-phase porous media for modeling cement based materials at high temperature is presented. The considerations are based on the mathematical model of mechanistic type, developed by the authors within recent years. The model has been previously experimentally validated and successfully applied for analyzing performance of various concrete structures at high temperature. Physical phenomena in a concrete element heated during a fire are described and analyzed, confirming multi-phase nature of concrete in these conditions. Main stages of the mathematical model development by means of hygro-thermo-mechanics of porous media are briefly presented. The mass, energy and linear momentum conservation equations at micro-scale are given and averaged in space to obtain the macroscopic form of the equations. Some main key-points in modeling cement-based materials at high temperature are discussed. Final form of the model equations and method of their numerical solution are presented. The model is validated by comparison with some published results of experimental studies. Two examples of the model application for numerical simulation of concrete structures exposed to fire conditions, including also a cooling phase, are analyzed.

1 Introduction

When concrete is exposed to high temperature a rather complex analysis is required to deal with the coupled heat and mass transfer that can occur, involving both liquid mass transfer and vapour mass transfer and related mechanical effects [1–5].

In such severe conditions in terms of temperatures and pressures, assessment of concrete performance is of great interest in nuclear engineering applications, in safety evaluation in tall buildings and in tunnels [3, 5]. In particular as far as tunnels are concerned, recent major fires in key European tunnels (Channel, Mont-Blanc, Great Belt Link, Tauern) emphasised the serious hazards they present in human and economic terms. In these accidents, in the affected sections, tunnels presented extensive damage to the concrete elements. Part of the concrete lining was almost completely removed by spalling.

Spalling is the violent or non-violent breaking off of layers or pieces of concrete from the surface of a structural element when it is exposed to high and rapidly rising temperatures. It can result in significant loss of section leading to reduction in load-bearing capacity, see Figure 1 for two examples of spalling.

Figure 1

Some examples of spalling occurred in concrete structures. a Spalling of a tunnel vault due to a fire (UPTUN project—[49]). b Corner spalling of a concrete column (HITECO project—[50])

For example, up to 75% of the concrete segment thickness was lost in multiple layered explosive spalling in the 1994 Great Belt tunnel fire. In the 1996 Channel tunnel fire, up to 100% of the segment spalled off explosively.

Spalling, which may be explosive, is mainly due to different coexisting coupled processes, such as thermal (heat transfer), chemical (dehydration of cement paste), hygral (transfer of water mass, in liquid and vapor form) and mechanical processes (release of the elastic energy stored during heating and buckling effects in the external layer).

In general, moisture transport in concrete structures during fire may include air-vapor mixture flow due to forced convection, free convection, and infiltration through cracks and pores, vapor transport by diffusion, flow of liquid water due to diffusion, capillary action, or gravity, and further complications associated with phase changes due to condensation/evaporation, ablimation/sublimation, and adsorption/desorption.

Movement of air and water through the concrete is accompanied by significant energy transfer, associated with the latent heat of water and the heats of hydration and dehydration. At temperature largely above critical point of water important chemical transformations of components of concrete take place.

These situations are much more dangerous in the case of High Performance (HPC) and Ultra High Performance (UHPC) concrete. The compressive strength of the high performance concretes used in the tunnels mentioned above exceeded 100 MPa at the time of the fire.

At ambient temperature these kinds of concrete present much better features than a normal concrete because of their lower permeability, lower porosity and higher compactness. This means greater mechanical strength, in particular as far as the compression strength is concerned, and an improved durability. At normal ambient temperatures, in fact, the cement matrix increases the strength of high performance concrete, because of its higher density and homogeneity, involving a better distribution of the stresses than a traditional concrete. At higher temperature this matrix becomes the weak point of the materials showing low mechanical strength. With the temperature increase the aggregates progressively expand as long as they are not chemically altered, while the cement matrix, after an initial expansion, is subject (over 150°C) to a progressive shrinkage. These two opposite phenomena induced a micro-cracking process which involve damaging of the material microstructure. Further, low permeability inhibits water mass transfer causing high gas pressure values, crack-opening and then an increase of intrinsic permeability.

Hence, for concrete, particularly at high temperature, one cannot predict heat transfer only from the traditional thermal properties: thermal conductivity and volumetric specific heat.

The majority of models used for the analysis of the effect of high temperature on concrete can be classified as thermo-mechanical. Most of these essentially consist of two separate thermal and mechanical models used in sequence that the temperature field obtained from the thermal model is input into the mechanical model at every time step of simulations to produce the resulting strains and stresses. Such models are capable to predict reasonably the overall deflections of beams and columns exposed to fire, although discrepancies between experiment and model appear at the lower temperatures of 100°C to 200°C because the influence of evaporable moisture cannot be properly incorporated. For such applications, the relatively simple thermo-mechanical models offer a reasonably accurate and cost effective solution of predicting, for example, fire resistance of beams and columns in terms of total deformations after one or 2 h of exposure to fire. But they are totally unreliable in spalling prediction.

To predict reliably the behavior of a concrete structure in such conditions, in particular evolutions of temperature, moisture content, gas pressure, and first of all degradation processes, rather complex and sophisticated mathematical models are required.

Several mathematical and numerical models, usually based on extensive laboratory tests, have been developed for this purpose, e.g. [1–24]. Some main features of the models are summarized in [25].

Mechanics of multi-phase porous media proved to be a theory enabling an efficient modeling of cement-based materials at high temperature. It allows for considering the porous and multiphase nature of the materials, their chemical transformations, water phase changes and different behavior of moisture below and above the critical temperature of water, mutual interactions between the thermal, hygric and degradation processes, as well as several material nonlinearities, especially those due to temperature changes, material cracking and thermo-chemical degradation.

In this paper we explain how mechanics of multi-phase porous media can be applied for modeling cement based materials at high temperature. Our considerations are based on the mathematical model developed within the recent years by the authors [9, 11, 12, 16]. This model is based on the Hybrid Mixture Theory [26–30]. It considers the deformations which are characteristic for heated concrete, i.e. load free thermal strain (LFTS) and load induced thermal strain (LITS called also ‘thermal creep’) [16], as well as cracking and thermo-chemical degradation of concrete [12] and related changes of the material properties, like for example permeability and strength properties [10, 11, 13, 14]. The model has been validated against results of several available experimental tests [12, 22, 31], showing its usefulness for better understanding and predicting concrete performance at high temperature.

The paper is organized in such a way that its’ structure follows the main stages of a mathematical model development by means of hygro-thermo-mechanics of porous media. First, physical phenomena in heated concrete and development of conservation equations at micro- and macro-scale are presented in Sects. 2 and 3. Then, main key-points in modeling cement-based materials at high temperature are discussed in Sect. 4. The final form of the model equations and their numerical solution are described in Sect. 5. Finally, the model validation and two examples of its application for analysis of a 1-D concrete structure exposed to the standard ISO-834 fire conditions and a 2-D structure during a parametric fire, including a cooling phase, are presented in Sect. 6.

2 Physical Phenomena in Heated Concrete

During fire the surface of a concrete element is heated both by a convective heat flux from the surrounding air of higher temperature and by a radiation heat flux, which can be direct (from the flames) or mutual (from other heated surfaces). The heating results in a gradual increase of the element temperature, starting from the surface zone. Due to this process the temperature gradients in the zone are high because before a further temperature increase almost all moisture must evaporate in the temperature range of 100°C to 200°C, what requires considerable amounts of heat. For this reason, even after several tens of minutes of fire duration the temperature of the inner part of wall remains almost unchanged [15].

Due to moisture evaporation, the water content in the surface zone decreases to a very low value and a sharp front, separating the moist and dry material, moves slowly inwards, see Figure 2. At this front intensive evaporation takes place, increasing considerably the vapor pressure. The maximum values of vapor and gas pressures increase initially, [32], then they remain constant as the surface temperature increases and the front moves inwards [15].

Figure 2

The four observed zones and the process for the build-up of pressure

The maximum value of gas pressure usually occurs at the position where the temperature equals ~160°C to 220°C, [15]. In the region with lower temperatures, below about 130°C, the gas pressure increase is caused mainly by a growth of the dry air pressure due to heating. In the regions with higher temperature the effects of a rapid increase of vapor pressure due to heating and temperature-dependence of the saturation vapor pressure predominate. At temperatures 160°C to 350°C the gas in the material pores consists mainly of water vapor [15]. The gradients of vapor pressure (and related gradients of vapor concentration) cause the vapor flow (due to advection and diffusion) both towards the surface and inwards. The latter mass flow results in vapor condensation when the hot vapor inflows the colder, internal layers of concrete, and in an increase of the pore saturation with liquid moisture above the initial value, usually referred as the so called “moisture clog” phenomenon, [4]. An additional increase of the liquid water volume in the pores is due to the liquid thermal dilatation, which is particularly important above the temperature of about 160°C, [11]. These effects cause a significant decrease of the gas permeability, because the space available for the gas is decreased.

Increasing temperature causes the material dilatation which in part is due to concrete dehydration (products of the thermal dissolution of concrete components have greater volume than their initial volume), in part due to the material cracking and progressive cracks opening [33], and finally due to ‘normal’ thermal dilatation of the material skeleton. The concrete cracking during heating is caused by an incompatibility of thermal dilatation of the aggregate and the cement paste, resulting in high traction stresses and development of local micro-cracks. Due to these cracks and chemical transformations of concrete (generally called dehydration), the concrete strength properties degrade gradually [12, 13].

A thermal dilatation of the external layers of a heated element is constrained by the core material which has visibly lower temperature. This causes a considerable macro-stress in the external layers of the element (traction in the direction perpendicular to the surface) and accumulation of elastic strain energy. Development of the cracks, both of thermo-chemical origin and the macro-stress induced ones, causes a considerable increase of the material intrinsic permeability [10, 13], and thereupon gas pressure decreases in the external layers where high temperatures are observed. The highest values of gas pressure usually correspond to the temperatures 170°C to 280°C [32], and this is also the range where thermal spalling of concrete occurs. Physical causes of the phenomenon, and in particular a role played by elastic strain energy of a constrained thermal dilatation accumulated in the surface layer and by a high value of gas pressure, are discussed in detail in [15].

The description presented above shows clearly that moist concrete should be modeled as a multi-phase porous material.

3 Mathematical Model Development

Development of the mathematical model proposed by the authors for analyzing concrete performance at high temperature will be presented in this section. The model is based on the mechanics of multiphase porous media [29] and considers most important mutual couplings and material nonlinearities, as well as different physical behavior of water above the critical point of water [11, 12, 15]. It was extensively validated [12, 16, 22], and its’ constitutive relationships were experimentally determined [9, 12, 13, 16]. Main stages of the model development will be presented in successive subsections.

3.1 Basic Assumptions of the Model

In modeling it is usually assumed that the material phases are in thermodynamic equilibrium state locally. In this way their thermodynamic state is described by one common set of state variables and not by separate sets for every component of the material, what reduces the number of unknowns in a mathematical model. In this way we have, for example, one common temperature for the multi-phase material, and not different temperatures for the skeleton, liquid water, vapor and dry air, etc. When fast hygro-thermal phenomena in a material at high temperature are analyzed, the assumption is debatable, but it is almost always used in modeling, giving reasonable results from the physical point of view and in part confirmed by the available experimental results. We also apply this assumption in development of the present model.

Concrete is here considered to be a multiphase medium where the voids of the solid skeleton could be filled with various combinations of liquid- and gas-phases (Figure 3). In the specific case the fluids filling pore space are the moist air (mixture of dry air and vapor), capillary water and physically adsorbed water. The chemically bound water is considered to be part of the solid skeleton until it is released on heating.

Figure 3

Schematic representation of the moist concrete as a multiphase porous material

Below the critical temperature of water, T _cr , the liquid phase consists of physically adsorbed water, which is present in the whole range of moisture content, and capillary water, which appears when degree of water saturation S _w exceeds the upper limit of the hygroscopic region, S _ssp (i.e. below S _ssp there is only physically adsorbed water). Above the temperature T _cr the liquid phase consists of the adsorbed water only. In the whole temperature range the gas phase is a mixture of dry air and water vapor (condensable constituent for T < T _cr ).

3.2 Microscopic Conservation Equations

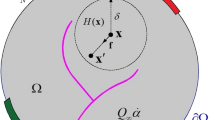
In the present approach the mathematical model is formulated by using two different scales starting from micro level, i.e. from a local form of the governing equations at the pore scale. The microscopic situation of any π phase of the considered medium is described by the classical equations of continuum mechanics. At the interfaces with other constituents, the material properties and thermodynamic quantities may present step discontinuities.

For a thermodynamic property, Ψ, the balance equation within the π phase may be written as follows,

$$ {\frac{{\partial \left( {\rho \Uppsi } \right)}}{\partial t}} + div \, \left( {\rho \Uppsi \,{\mathbf{v}}^{\pi } } \right) = div\,{\mathbf{i}}_{\Uppsi } + \, \rho {\mathbf{b}}_{\Uppsi } + \rho {\mathbf{G}}_{\Uppsi } , $$

(1)

where ${\mathbf{v}}^{\pi }$ is the local value of the velocity field of the π phase in a fixed point in space, ${\mathbf{i}}_{\Uppsi }$ is the flux vector associated with Ψ, ${\mathbf{b}}_{\Uppsi }$ the external supply of Ψ and ${\mathbf{G}}_{\Uppsi }$ is the net production of Ψ. Fluxes are positive as outflows.

Equation 1 can be interpreted that the rate of (ρΨ)-variation (including volumetric deformation) is equal to the difference between inflowing and outflowing fluxes of ${\mathbf{i}}_{\Uppsi }$, $div\,{\mathbf{i}}_{\Uppsi }$, and sum of the sources of Ψ due to its external supply, ${\mathbf{b}}_{\Uppsi }$, and net production of Ψ, ${\mathbf{G}}_{\Uppsi }$.

The thermodynamic quantity Ψ to be introduced into Equation 1 can be mass, momentum, angular momentum, energy or entropy. The relevant thermodynamic properties Ψ for the different balance equations and values assumed by ${\mathbf{i}}_{\Uppsi }$, ${\mathbf{b}}_{\Uppsi }$ and ${\mathbf{G}}_{\Uppsi }$ are listed in Table 1.

Table 1 Thermodynamic Properties for the Microscopic Mass Balance Equations

In Table 1, E is the specific intrinsic energy, λ the specific entropy, ${\mathbf{t}}_{m}$ the microscopic stress tensor, q a heat flux vector, ${\varvec{\Upphi}}$ entropy flux, g external momentum supply related to gravitational forces, h intrinsic heat source, S an intrinsic entropy source and φ denotes an increase of entropy. The constituents are assumed to be microscopically non-polar, hence the angular momentum balance equation has been omitted here. This equation shows however that the stress tensor is symmetric.

3.3 Volume Averaging Procedure and Macroscopic Conservation Equations

The final form of the macroscopic balance equations is obtained by applying appropriate space averaging operators (for the so called Representative Volume Element—RVE) to the equations at micro-level, while the constitutive laws are defined directly at the upper scale, according to the so called Hybrid Mixture Theory (HMT) originally proposed by Hassanizadeh and Gray [26–28].

The chosen procedure does not exclude the use of a numerical multi-scale approach (i.e. numerical averaging in RVE) in the formulation of the material properties, which nowadays is often used for solving problems involving multi-physics aspects in material mechanics.

For the sake of brevity, only the final form of the macroscopic conservation equations is given below. The full development of the model equations, starting from the local, microscopic balance equations with successive volume averaging, is presented in [12, 29, 34, 35].

The general form of the macroscopic, volume averaged mass conservation equation of the π-phase is, [29]:

$$ {\frac{{\mathop D\limits^{\pi } \rho_{\pi } }}{Dt}} + \rho_{\pi } {\kern 1pt} div \, {\mathbf{v}}^{\pi } = \rho_{\pi } e^{\pi } \left( \rho \right) , $$

(2)

where ρ _π is apparent density (related to the whole volume of the medium), v ^π the velocity and $\rho_{\pi } e^{\pi } \left( \rho \right)$ the volumetric mass source, super or subscript π refers to the π-phase.

This mass balance equation has the following form for the solid skeleton, [12]:

$$ {\frac{{\mathop D\limits^{s} \rho_{s} }}{Dt}} + \rho_{s} {\kern 1pt} div \, {\mathbf{v}}^{s} = - \dot{m}_{dehydr} , $$

(3)

where $\dot{m}_{{_{dehydr} }}$ is mass source of liquid water (and corresponding skeleton mass sink) related to the material dehydration process.

After application of the relation between the phase averaged density, ρ _π (averaged in the whole RVE), and the intrinsic phase averaged density, ρ ^π (averaged in the volume occupied by π phase contained in RVE), [29]:

$$ \rho_{\pi } = \eta^{\pi } \rho^{\pi } , $$

(4)

with η ^π being the volume fraction occupied by the π-phase, and after some simple transformations, Equation 3 can be rewritten as, [12]:

$$ {\frac{{\left( {1 - n} \right)}}{{\rho^{s} }}}\,{\frac{{\mathop D\limits^{s} \rho^{s} }}{Dt}} - {\frac{{\mathop D\limits^{s} n}}{Dt}} + \left( {1 - n} \right)div \, {\mathbf{v}}^{s} = - {\frac{{\dot{m}_{dehydr} }}{{\rho^{s} }}} , $$

(5)

The volume averaged mass conservation equation for liquid water (capillary and physically adsorbed) has the following form, [12]:

$$ {\frac{{\mathop D\limits^{w} {\text{ }}{\rho^{w}} }}{{Dt}}} + \rho_{w}div \,{\mathbf{v}}^{w}={\dot{m}_{dehydr}} -{\dot{m}_{vap}},$$

(6)

where $\dot{m}_{{_{vap} }}$ is the vapor mass source caused by the liquid water evaporation or desorption (for low values of the relative humidity inside the material pores). It is worth to underline that for the liquid water we have two source terms, in the whole temperature range due to dehydration process and at temperatures T < T _cr due to water phase changes.

By introducing the water relative velocity and material derivative of water density, with respect to the skeleton, and application of (4) with η ^w = nS _w , we have, [12]:

$$ \begin{gathered} {\frac{{\mathop D\limits^{s} n}}{Dt}} + {\frac{n}{{\rho^{w} }}}\,{\frac{{\mathop D\limits^{s} \rho^{w} }}{Dt}} + {\frac{n}{{S_{w} }}}\,{\frac{{\mathop D\limits^{s} S_{w} }}{Dt}} + {\frac{1}{{S_{w} \rho^{w} }}}div\left( {nS_{w} \rho^{w} {\mathbf{v}}^{ws} } \right) + n{\kern 1pt} {\kern 1pt} div{\kern 1pt} {\mathbf{v}}^{s} \hfill \\ = {\frac{{\dot{m}_{dehydr} - \dot{m}_{vap} }}{{S_{w} \rho^{w} }}} . { } \hfill \\ \end{gathered} $$

(7)

where v ^πs means the π-phase relative velocity with respect to the skeleton.

In order to eliminate the time derivative of porosity, ${\frac{{\mathop D\limits^{s} n}}{Dt}}$, from the latter equation, we sum it up with (3) and obtain the mass conservation equation of liquid water and solid skeleton as follows [12]:

$$ \begin{gathered} {\frac{{\left( {1 - n} \right)}}{{\rho^{s} }}}\,{\frac{{\mathop D\limits^{s} \rho^{s} }}{Dt}} + div \, {\mathbf{v}}^{s} + {\frac{n}{{\rho^{w} }}}\,{\frac{{\mathop D\limits^{s} \rho^{w} }}{Dt}} + {\frac{n}{{S_{w} }}}\,{\frac{{\mathop D\limits^{s} S_{w} }}{Dt}} + \hfill \\ + {\frac{1}{{S_{w} \rho^{w} }}}div\left( {nS_{w} \rho^{w} {\mathbf{v}}^{ws} } \right) = {\frac{{\dot{m}_{dehydr} - \dot{m}_{vap} }}{{S_{w} \rho^{w} }}} - {\frac{{\dot{m}_{dehydr} }}{{\rho^{s} }}} \hfill \\ \end{gathered} $$

(8)

The macroscopic volume averaged mass conservation equation of dry air, [29]:

$$ {\frac{{\mathop D\limits^{ga} \rho_{ga} }}{Dt}} + \rho_{ga} {\kern 1pt} div{\kern 1pt} {\mathbf{v}}^{ga} = 0 , $$

(9)

after introducing the material time derivative with respect to the gas phase and decomposition of the dry air velocity into the diffusional, ${\mathbf{u}}^{ga} = {\mathbf{v}}^{ga} - {\mathbf{v}}^{g}$, and advectional (i.e. related to the centre of gravity of the whole gas phase), ${\mathbf{v}}^{g}$, components, [29], can be transformed in a similar way as done for the liquid water balance (with η ^ga = nS _g ) giving the following equation, [12]:

$$ \begin{gathered} {\frac{n}{{S_{g} }}}\,{\frac{{\mathop D\limits^{s} S_{g} }}{Dt}} + {\frac{n}{{\rho^{ga} }}}\,{\frac{{\mathop D\limits^{s} \rho^{ga} }}{Dt}} + {\frac{1}{{S_{g} \rho^{ga} }}}div{\kern 1pt} {\mathbf{J}}_{d}^{ga} + {\frac{1}{{S_{g} \rho^{ga} }}}{\kern 1pt} div{\kern 1pt} {\kern 1pt} \left( {nS_{g} \rho^{ga} {\mathbf{v}}^{gs} } \right) \hfill \\ + {\frac{1 - n}{{\rho^{s} }}}\,{\frac{{\mathop D\limits^{s} \rho^{s} }}{Dt}} + div\,{\mathbf{v}}^{s} = - {\frac{{\dot{m}_{dehydr} }}{{\rho^{s} }}}. \hfill \\ \end{gathered} $$

(10)

where

$$ {\mathbf{J}}_{d}^{ga} = \rho_{ga} {\mathbf{u}}^{ga} = nS_{g} \rho^{ga} {\mathbf{u}}^{ga} $$

(11)

is the diffusive mass flux of dry air molecules in the gas phase.

The macroscopic mass balance of the water vapor, [29],

$$ {\frac{{\mathop D\limits^{gw} \rho_{gw} }}{Dt}} + \rho_{gw} {\kern 1pt} div{\kern 1pt} {\mathbf{v}}^{gw} = \dot{m}_{vap} , $$

(12)

can be presented and transformed, similarly to the equation for the dry air, resulting in the following equation, [12]:

$$ \begin{gathered} {\frac{n}{{S_{g} }}}\,{\frac{{\mathop D\limits^{s} S_{g} }}{Dt}} + {\frac{n}{{\rho^{gw} }}}\,{\frac{{\mathop D\limits^{s} \rho^{gw} }}{Dt}} + {\frac{1}{{S_{g} \rho^{gw} }}}div{\kern 1pt} {\mathbf{J}}_{d}^{gw} + {\frac{1}{{S_{g} \rho^{gw} }}}{\kern 1pt} div{\kern 1pt} {\kern 1pt} \left( {nS_{g} \rho^{gw} {\mathbf{v}}^{gs} } \right) \hfill \\ + {\frac{1 - n}{{\rho^{s} }}}\,{\frac{{\mathop D\limits^{s} \rho^{s} }}{Dt}} + div\,{\mathbf{v}}^{s} = - {\frac{{\dot{m}_{dehydr} }}{{\rho^{s} }}} + {\frac{{\dot{m}_{vap} }}{{S_{g} \rho^{gw} }}}. \hfill \\ \end{gathered} $$

(13)

where the diffusive mass flux of vapor molecules in the gas is defined as, [29],

$$ {\mathbf{J}}_{d}^{gw} = \rho_{gw} {\mathbf{u}}^{gw} = nS_{g} \rho^{gw} {\mathbf{u}}^{gw} = - {\mathbf{J}}_{d}^{ga} . $$

(14)

in which the gas phase is assumed as ideal binary gas mixture of dry air and water vapor.

We do not have any constitutive relationship for the mass source term, $\dot{m}_{vap}$, appearing in the latter equation and in (7), but we can use one of the two mass balance equations to eliminate this source term from the another one. The macroscopic, volume averaged enthalpy balance equation for the π-phase, after neglecting some terms related to viscous dissipation and mechanical work, has the following general form, [29]:

$$ \rho_{\pi } C_{p}^{\pi } {\frac{{\mathop D\limits^{\pi } T^{\pi } }}{Dt}} = \rho_{\pi } h^{\pi } - div\,{\tilde{\mathbf{q}}}^{\pi } + \rho_{\pi } R_{H}^{\pi } - \rho_{\pi } e^{\pi } \left( \rho \right)H^{\pi } , $$

(15)

where $C_{p}^{\pi }$ is the specific isobaric heat, ${\tilde{\mathbf{q}}}^{\pi }$ the heat flux, $\rho_{\pi } h^{\pi }$ the volumetric heat sources, $\rho_{\pi } R_{H}^{\pi }$ the term expressing energy exchange with the other phases, H ^π the specific enthalpy, of the π-phase. In concrete at high temperature all heat sources, except those related to phase changes and dehydration process, can be neglected.

Having assumed here that all phases of the material are locally in thermodynamic equilibrium, their temperatures are the same, T ^π = T (π = s, w, g). These temperatures may however vary throughout the domain.

Summing up the enthalpy balances for all the phases of the medium, one obtains the following enthalpy balance equation for the whole medium, [12]:

$$ \begin{gathered} \left( {\rho C_{p} } \right)_{eff} {\frac{{\mathop D\limits^{s} T}}{Dt}} + \left( {\rho_{w} C_{p}^{w} {\mathbf{v}}^{ws} + \rho_{g} C_{p}^{g} {\mathbf{v}}^{gs} } \right) grad\,T - div\,{\tilde{\mathbf{q}}} = \hfill \\ - \dot{m}_{vap} \Updelta H_{vap} - \dot{m}_{dehydr} \Updelta H_{dehydr} , \hfill \\ \end{gathered} $$

(16)

where

$$ \begin{aligned} \left( {\rho C_{p} } \right)_{eff} & = \rho_{s} C_{p}^{s} + \rho_{w} C_{p}^{w} + \rho_{g} C_{p}^{g} , \\ {\tilde{\mathbf{q}}} &= {\tilde{\mathbf{q}}}^{s} + {\tilde{\mathbf{q}}}^{w} + {\tilde{\mathbf{q}}}^{g} , \\ \Updelta H_{vap} &= H^{gw} - H^{w} , \\ \Updelta H_{dehydr} &= H^{w} - H^{ws}. \end{aligned} $$

(17)

Above, H ^w is the specific enthalpy of the capillary (or physically adsorbed) water, H ^gw the specific enthalpy of water vapor, H ^ws the specific enthalpy of the chemically bound water, ΔH _vap the specific enthalpy of evaporation and ΔH _dehydr the specific enthalpy of dehydration.

Hygro-thermal phenomena in concrete, even at high temperature, are relatively slow, hence inertial forces can be neglected. For such a case the macroscopic, volume averaged linear momentum balance equation (i.e. the mechanical equilibrium equation) for the π-phase has the following, general form, [29]:

$$ div\,{\mathbf{t}}^{\pi } + \rho_{\pi } {\mathbf{g}} + \rho_{\pi } \left[ {{\mathbf{e}}^{\pi } \left( {\rho \,{\dot{\mathbf{r}}}} \right) + \, {\hat{\mathbf{t}}}^{\pi } } \right] = 0, $$

(18)

where t ^π is the macroscopic stress tensor in the π-phase, g the acceleration of gravity, $\rho_{\pi } {\hat{\mathbf{t}}}^{\pi }$ the volumetric exchange term of linear momentum with other phases due to mechanical interaction, and $\rho_{\pi } {\mathbf{e}}^{\pi } \left( {\rho \,{\dot{\mathbf{r}}}} \right)$ that due to phase changes or chemical reactions. After summing up the macroscopic linear momentum balances for all the phases and introducing the total stress tensor, [36]:

$$ {\mathbf{t}}^{total} = {\mathbf{t}}^{s} + {\mathbf{t}}^{w} + {\mathbf{t}}^{g} , $$

(19)

one obtains, [29]:

$$ div\,{\mathbf{t}}^{total} \user1{ + }\left[ {\left( {1 - n} \right)\rho^{s} + nS_{w} \rho^{w} + n\left( {1 - S_{w} } \right)} \right]{\mathbf{g}} = {\bf{0}} , $$

(20)

where the term in the square parenthesis is the averaged apparent density of the medium.

The volume averaged angular momentum balance equation shows that for non-polar media, as moist concrete is assumed in this work, all macroscopic partial stress tensors are symmetric, [29]:

$$ {\mathbf{t}}^{\pi } = \left( {{\mathbf{t}}^{\pi } } \right)^{\text{T}} , $$

(21)

4 Key Points in Modeling Cement-Based Materials at High Temperature

Following the procedure briefly described in Sect. 3, the macroscopic balance equations can be formulated for any porous material. However, dealing with cement-based materials at high temperature introduces some additional physical and theoretical difficulties, which should be overcome to formulate a mathematical model giving reliable results for the material. These key points are discussed in the following subsections.

4.1 Choice of State Variables

A proper choice of state variables for description of materials at high temperature is of particular importance. From a practical point of view, the physical quantities used, should be possibly easy to measure during experiments, and from a theoretical point of view, they should uniquely describe the thermodynamic state of the medium. They should also assure a good numerical performance of the computer code based on the resulting mathematical model. As already mentioned in Sect. 3.1, the necessary number of the state variables may be significantly reduced if existence of local thermodynamic equilibrium at each point of the medium is assumed. In such a case physical state of different phases of water can be described by use of the same variable.

Having in mind all the aforementioned remarks, we will briefly discuss now the state variables chosen for the present model. Use of temperature (the same for all constituents of the medium because of the assumption about the local thermodynamic equilibrium state) and solid skeleton displacement vector is rather obvious, thus it needs no further explanation. As a hygrometric state variable various physical quantities, which are thermodynamically equivalent, may be used, e.g. volumetric- or mass moisture content, liquid water saturation degree, vapor pressure, relative humidity, or capillary pressure. Analyzing materials at high temperature, one must remember that at temperatures higher than the critical point of water (i.e. 374.15°C or 647.3 K) there is no capillary (or free) water present in the material pores, and there exists only the gas phase of water, i.e. vapor. Then, very different moisture contents may be encountered at the same moment in a heated cement-based materials, ranging from full saturation with liquid water (e.g. in some nuclear vessels or in so called “moisture clog” zone in a heated concrete, see [3]) up to almost completely dry material. Moreover, some quantities (e.g. saturation or moisture content) which can be chosen as primary variable are not continuous at interfaces between different materials.

For these reasons apparently it is not possible to use, in a direct way, one single variable for the whole range of moisture contents.

Hence the moisture state variable selected in the model is capillary pressure, [11], that was shown to be a thermodynamic potential of the physically adsorbed water and, with an appropriate interpretation, can be also used for description of water at pressures higher than the atmospheric one, [37]. The capillary pressure has been shown to assure good numerical performance of the computer code, [9, 11, 12, 14, 15], and is very convenient for analysis of stress state in concrete, because there is a clear relation between pressures and stresses, [36, 38].

Hence, the chosen primary state variables of the present model are the volume averaged values of: gas pressure, p ^g, capillary pressure, p ^c, temperature, T, and displacement vector of the solid matrix, u.

For temperatures lower than the critical point of water, T < T _cr , and for capillary saturation range, S _w  > S _ssp (T) (S _ssp is not only the upper limit of the hygroscopic moisture range as mentioned in Sect. 3.1, but also the lower limit of the capillary one), the capillary pressure is defined as:

$$ p^{c} = \, p^{g} - \, p^{w} $$

(22)

where p ^w denotes water pressure.

For all other situations, and in particular T ≥ T _cr when condition S _w  < S _ssp is always fulfilled (there is no capillary water in the pores), the capillary pressure only substitutes formally the water potential Ψ_c, defined as, [11]:

$$ \Uppsi_{\text{c}} = {\frac{RT}{{M_{w} }}} \ln \left( {{\frac{{p^{gw} }}{{f^{gws} }}}} \right) , $$

(23)

where M _w is the molar mass of water, R the universal gas constant and f ^gws the fugacity of water vapor in thermodynamic equilibrium with saturated film of physically adsorbed water, [11]. For physically adsorbed water at lower temperatures (S < S _ssp and T < T _cr ) the fugacity f ^gws should be substituted in the definition of the potential Ψ_c, Equation 23, by the saturated vapor pressure p ^gws. Having in mind the Kelvin equation, [39], valid for the equilibrium state of capillary water with water vapor above the curved interface (meniscus):

$$ \ln \left( {{\frac{{p^{gw} }}{{p^{gws} }}}} \right) = - {\frac{{p^{c} }}{{\rho^{w} }}}\,{\frac{{M_{w} }}{RT}} , $$

(24)

we can note, that in the situations, where (23) is valid, the capillary pressure may be treated formally as the water potential multiplied by the density of the liquid water, ρ ^w, according to the relation, [11]:

$$ p^{c} = - \Uppsi_{\text{c}} \rho^{w} . $$

(25)

Thanks to this similarity, it is possible to use “formally” during computations the capillary pressure even in the low moisture content range, when the capillary water is not present into the pores, and capillary pressure has no physical meaning.

4.2 Modeling Passing the Critical Point of Water

In a concrete structure exposed to fire conditions temperatures higher than critical point of water can be encountered in a part of the structure after a period of heating. Above this temperature the liquid water and gaseous water phase (water vapor) cannot be distinguished and only the gas phase exists. As a result, there are no phase changes of the pore water (condensation–evaporation) and capillary pressure has not any physical meaning.

Hence, after reaching in a part of moist porous material temperatures higher than the critical point of water, we deal with a kind of Stefan’s problem, where two regions, with the temperatures below and above the critical point of water, are separated by the moving interface boundary.

Gawin et al. [11] presented a method which formally allows us to avoid direct tracing of the boundary position in the space. It consists in giving formally different physical meaning to the capillary pressure (as discussed in Sect. 4.1) and using it still for description of the hygrometric state of concrete in the zone, where temperature exceeds the critical point of water. Then, a special ‘switching’ procedure is applied for a finite element, where this temperature is encountered, from the below- to the above- critical temperature description of the medium, using still the governing equations of the same form, but with different physical meaning.

4.3 Water and Material Properties at High Temperature

The density of water vapor calculated by means of the Clapeyron equation, often used in simulations at ambient temperature, differs significantly from the results of the laboratory tests for the temperatures higher than ~433.15 K (i.e. 160°C). For better coherence with the experimentally measured values, the following formula can be used in computations [11]:

$$ \rho^{v} = \rho^{v} \left( {T,p^{v} } \right) = \left[ {p^{v} \,{\frac{{M_{w} }}{RT}} + \Updelta \rho^{v} } \right], \quad for \, T_{\text{ref}} < T < T_{crit} $$

(26)

where T _ref is the reference temperature (around 160°C) and the correcting term, Δρ ^v, is exclusively function of temperature, taking into account the real behavior of water vapor in the range 160°C to 374.15°C. The first term on the RHS of (26) is related to ideal gas behavior.

The water vapor saturation pressure p ^vs in the Kelvin equation (24) depends only on temperature T and may be calculated with sufficient accuracy (for T < T _cr ) from the formula of Hyland and Wexler [40].

The state equation of liquid water should take into account a considerable, non-linear decrease of water density in temperature range close to the critical point of water. The following formula gives a reasonable coherence with experimental results and assures a good numerical performance of the computer code [11]:

$$ \begin{aligned} \rho^{w} &= \left( {b_{0} + b_{1} T + b_{2} T^{2} + b_{3} T^{3} + b_{4} T^{4} + b_{5} T^{5} } \right) \\ &+ \left( {p_{w1} - p_{wr} } \right)\left( {a_{0} + a_{1} T + a_{2} T^{2} + a_{3} T^{3} + a_{4} T^{4} + a_{5} T^{5} } \right) \\ \end{aligned} $$

(27)

where: p _w1  = 10 MPa, p _wr  = 20 MPa, a ₀ = 4.89 × 10⁻⁷, a ₁ = −1.65 × 10⁻⁹, a ₂ = 1.86 × 10⁻¹², a ₃ = 2.43 × 10⁻¹³, a ₄ = −1.60 × 10⁻¹⁵, a ₅ = 3.37 × 10⁻¹⁸, b ₀ = 1.02 × 10⁻³, b ₁ = −7.74 × 10⁻¹, b ₂ = 8.77 × 10⁻³, b ₃ = −9.21 × 10⁻⁵, b ₄ = 3.35 × 10⁻⁷, b ₅ = −4.40 × 10⁻¹⁰. In this formula it was assumed that the liquid water is incompressible.

The enthalpy of water evaporation depends upon the temperature and may be approximated by the Watson formula, [12]:

$$ \Updelta H_{vap} = 2.672 \times 10^{5} \,\left( {T - T_{cr} } \right)^{0.38} , $$

(28)

where T _cr  = 647.3 K is the critical temperature of water. Above the temperature free water can exist only as a gas, hence no phase changes and the related heat effects are physically admissible, so formally ΔH _vap  = 0.

Several physical properties of cement-based materials at high temperature, like for example thermal conductivity, thermal capacity, intrinsic permeability, Young modulus of elasticity, compressive and tensile strength etc., are dependent upon temperature, gas pressure, moisture content and damage parameter. They play a role of the constitutive relationships for the mathematical model and should be determined experimentally. The exact formulae describing them were discussed in detail elsewhere [9–12, 15] and will be not given here.

4.4 Effective Stress Principle

Cement-based materials are treated as multi-phase porous media, hence analyzing the stress state and the deformation of the material it is necessary to consider not only the action of an external load, but also the pressure exerted on the skeleton by fluids present in its voids. Hence, the total stress tensor t ^total acting in a point of the porous medium may be split into the effective stress η ^s τ ^s, which accounts for stress effects due to changes in porosity, spatial variation of porosity and the deformations of the solid matrix, and a part accounting for the solid phase pressure exerted by the pore fluids, [36, 38, 41]:

$$ {\mathbf{t}}^{total} = \eta^{s} {\varvec{\uptau}}^{s} - \alpha P^{s} {\mathbf{I}}, $$

(29)

where I is the second order unit tensor, α is the Biot coefficient and P ^s is some measure of solid pressure acting in the system, i.e. the normal force exerted on the solid surface by the surrounding fluids.

Taking into account several simplifications [36, 41], Equation 38 can be rewritten in the following manner, [38, 41]:

$$ \eta^{s} {\varvec{\uptau}}^{s} = {\mathbf{t}}^{total} + \left( {p^{g} - x_{s}^{ws} p^{c} } \right){\mathbf{I}}. $$

(30)

where $x_{s}^{ws}$ is the fraction of skeleton area in contact with the water. This form of, the so called “effective stress principle”, Equation 30, takes into account the effects of the “disjoining pressure” in the definition of the capillary pressure, [16].

4.5 Thermo-Chemical and Mechanical Degradation at High Temperature

During heating concrete structures deteriorate both due to stresses caused by mechanical load and due to thermo-chemical degradation of concrete at high temperature. These unfavorable effects can be described by means of the so called isotropic damage theory [42]. The total damage parameter D in the evolution equations accounting for the thermo-chemical and mechanical deterioration processes, is defined on the base of the following multiplicative combination, [11, 16, 43]:

$$ 1 - D = {\frac{E(T)}{{E_{o} (T_{a} )}}} = \left( {1 - d} \right) \left( {1 - V} \right), $$

(31)

where d and V are the mechanical and thermo-chemical damage components. The latter ones are identified on the basis of the experimentally determined stress–strain profiles at various temperatures as follows [11, 16, 43]:

$$ d = 1 - {\frac{E(T)}{{E_{o} (T)}}},\quad V = 1 - {\frac{{E_{o} (T)}}{{E_{o} (T_{a} )}}}, $$

(32)

where the subscript ‘o’ refers to the elastic behavior.

The Young’s modulus of a sound material at temperature T is hence given by equation: $E_{o} (T) = \left[ {1 - V\left( T \right)} \right]E_{o} (T_{a} )$ , where E _o (T _a ) is the Young’s modulus at the reference (i.e. ambient) temperature T _a , and function V(T) is determined experimentally.

We consider that only the elastic properties of the material are affected by the total damage parameter D, i.e. the material is supposed to behave elastically and to remain isotropic and that the dependence on damage is introduced through the stiffness tensor, $\varvec{\Uplambda } = \varvec{\Uplambda }\left( D \right) = (1 - D)\user1{\Uplambda }_{{\mathbf{0}}}$, [42]:

$$ \eta^{s} {\varvec{\uptau}}^{s} = \varvec{\Uplambda }\left( D \right):\varvec{\varepsilon }^{s} , $$

(33)

in which ε ^s is the strain tensor for infinitesimal deformations of the solid phase and $\user1{\Uplambda }_{{\mathbf{0}}}$ is the stiffness tensor at ambient temperature for an undamaged material.

The effective stress tensor is then given by:

$$ \eta^{s} {\varvec{\uptau}}^{s} = \varvec{\Uplambda }(D):\varvec{\varepsilon }^{s} = (1 - d)(1 - V)\user1{\Uplambda }_{{\mathbf{0}}} :\varvec{\varepsilon }^{s} . $$

(34)

Some experimental studies show that the value of intrinsic permeability of deteriorated concrete k can be related directly to the value of damage parameter D and actual values of temperature and gas pressure, [13]:

$$ k = k_{o} \times \,10^{f(T)} \left( {{\frac{{p^{g} }}{{p_{o}^{g} }}}} \right)^{{A_{p} }} \,10^{{A_{D} D}} $$

(35)

where k _o is the value of sound concrete at ambient temperature, f(T) is a function determined experimentally, A _P and A _D are material constants.

4.6 Strains of Cement-Based Materials at High Temperature

An unloaded sample of plain concrete or cement stone, exposed for the first time to heating, exhibits considerable changes of its chemical composition, inner structure of porosity and changes of sample dimensions (irreversible in part), [44, 45]. The concrete strains during first heating, called load-free thermal strains (LFTS) are usually treated as superposition of thermal and shrinkage components, and often are considered as almost inseparable. LFTS are decomposed in three main contributions [16], see Figure 4:

Figure 4

Decomposition of total strains in heated concrete (C90) [16]

• Thermal dilatation strains,

  $$ d{\varvec{\varepsilon}}_{th} = \beta_{s} \left( T \right)\,dT{\mathbf{I}}, $$

  (36)

  where $\beta_{s}$ is thermal dilatation coefficient, which for concrete can usually be approximated by a linear function of temperature,

  $$ \beta_{s} \left( T \right)\, = A_{B1} \left( {T - T_{0} } \right) + A_{B0} . $$

  (37)

• Capillary shrinkage strains,

  $$ d{\varvec{\varepsilon }}_{sh} = {\frac{\alpha }{{\tilde{K}_{T} }}}\left( {dx_{s}^{ws} p^{c} + x_{s}^{ws} dp^{c} } \right){\mathbf{I}}, $$

  (38)

  where $\tilde{K}_{T}$ is the bulk modulus of the porous medium,

• Thermo-chemical strains

  $$ d{\varvec{\varepsilon }}_{tchem} = \beta_{tchem} \left( V \right)dV{\mathbf{I}}, $$

  (39)

  where $\beta_{tchem} \left( V \right) = {\frac{{\partial \user1{\varepsilon }_{tchem} (V)}}{\partial V}}$ is obtained from experimental tests and usually it can be approximated by a linear function of thermo-chemical damage, V:

  $$ \beta_{chem} \left( V \right)\, = A_{tch} V . $$

  (40)

Shrinkage strains are modeled by means of the effective stress principle, in the form derived in Equation 30, see Figure 5. In this way the contribution of the term related to the capillary pressure in Equation 30 can be interpreted as a sort of “internal” load for the skeleton of the material. Hence, the associated shrinkage strains are not computed directly in the strain decomposition as it is usual in the classical phenomenological approaches.

Figure 5

Shrinkage strains for HPC concrete: comparison with experimental results [16]

During first heating, mechanically loaded concrete exhibits greater strains as compared to the load-free material at the same temperature. These additional deformations are referred to as load induced thermal strains (LITS), [44, 45]. Part of them originates just from the elastic deformation due to mechanical load, and it increases during heating because of thermo-chemical and mechanical degradation of the material strength properties. The time dependent part of the strains during transient thermal processes due to temperature increase is generally called thermal creep. The results of transient thermal strain tests, usually performed at constant heating rate equal to 2 K/min, for the C-90 concrete are presented and compared to numerical results in Figure 6.

Figure 6

Evolution of thermal creep strain (C90 concrete): comparison with experimental results [16]

The strains can be modeled with the formulation originally proposed by Thelandersson [46] and modified by using the effective stresses instead of total stresses [16]:

$$ d{\varvec{\varepsilon }}_{tr} = {\frac{{\bar{\beta }_{tr} (V)}}{{{\text{f}}_{\text{c}} (T_{a} )}}}{\mathbf{Q:}}\,{\frac{{\eta^{s} {\varvec{\uptau}}_{{}}^{s} }}{1 - D}} dV. $$

(41)

The normalized transient strain $\bar{\beta }_{tr} (V)$ was identified as a bi-linear function of thermo-chemical damage V, [16]:

$$ \begin{aligned} \bar{\beta }_{tr} (V) &= A_{tr1} V + \, A_{tr2} \quad {\text{for}}{\kern 1pt} {\kern 1pt} \,V \le V_{\lim } , \\ \bar{\beta }_{tr} (V) &= A_{tr3} \left( {V - V_{\lim } } \right) + \, A_{tr1} V_{\lim } + \, A_{tr2} \quad {\text{for}}{\kern 1pt} {\kern 1pt} \,V > V_{\lim } . \hfill \\ \end{aligned} $$

(42)

The value V _lim of thermo-chemical damage is dependent on the composition of a concrete, e.g. for the C-60 concrete analyzed in [16] it corresponds to the temperature at which starts decomposition of the calcareous aggregate.

Due to application of the effective stresses in Equation 41, the thermo-chemo-mechanical damage and capillary shrinkage model are coupled with the thermal creep model, [16, 41].

In Equation 41 Q is a fourth order tensor and f _c is the compressive strength of the material at 20°C.

The final decomposition of the mechanical strains, acting on the solid phase, used in the present model is the following one:

$$ \varvec{\varepsilon }^{s} = \varvec{\varepsilon }_{tot} - \varvec{\varepsilon }_{th} - \varvec{\varepsilon }_{tchem} - \varvec{\varepsilon }_{tr} , $$

(43)

in which the various components of strains are described by means of Equations 36–42.

5 Final Form of Mathematical Model Equations and their Numerical Solution

The state of cement based materials at high temperature is described by four primary state variables, i.e. gas pressure, p ^g, capillary pressure (in its generalized meaning, see Sect. 4.1), p ^c, temperature, T, and displacement vector, u, as well as three internal variables describing advancement of the dehydration and deterioration processes, i.e. degree of dehydration, Γ _dehydr , chemical damage parameter, V, and mechanical damage parameter, d.

The mathematical model describing the material performance consists of seven equations: 2 mass balances (continuity equations of water and dry air), enthalpy (energy) balance, linear momentum balance (mechanical equilibrium equation) and three evolution equations. For convenience of the Reader, the final form of the model equations, expressed in terms of the primary state variables, are listed below. The full development of the equations is presented in [12].

Mass balance equation of dry air takes into account both the diffusive (described by the term L.44.7) and advective air flow (L.44.8), the variations of the saturation degree with water (L.44.1) and air density (L.44.4), as well as the variations of porosity caused by: dehydration process (L.44.5), temperature variation (L.44.2), skeleton density changes due to dehydration (L.44.6) and by skeleton deformations (L.44.3). The mass balance has the following form:

$$ \begin{gathered} - \underbrace {{n{\frac{{D^{s} S_{w} }}{Dt}}}}_{{{\text{L}}.44.1}} - \underbrace {{\beta_{s} \left( {1 - n} \right)S_{g} \,{\frac{{D^{s} T}}{Dt}}}}_{{{\text{L}}.44.2}} + \underbrace {{\mathop {}\limits_{{}} S_{g} div\,{\mathbf{v}}^{s} }}_{{{\text{L}}.44.3}} + \underbrace {{{\frac{{S_{g} n}}{{\rho^{ga} }}}\,{\frac{{D^{s} \rho^{ga} }}{Dt}}}}_{{{\text{L}}.44.4}} - \underbrace {{{\frac{{\dot{m}_{dehydr} }}{{\rho^{s} }}}S_{g} }}_{{{\text{L}}.44.5}} \hfill \\ - \underbrace {{{\frac{{\left( {1 - n} \right)S_{g} }}{{\rho^{s} }}}\,{\frac{{\partial \rho^{s} }}{{\partial \Upgamma_{dehydr} }}}\,{\frac{{D^{s} \Upgamma_{dehydr} }}{Dt}}}}_{{{\text{L}}.44.6}} + \underbrace {{{\frac{1}{{\rho^{ga} }}}div\,{\mathbf{J}}_{g}^{ga} }}_{{{\text{L}}.44.7}} + \underbrace {{{\frac{1}{{\rho^{ga} }}}div\left( {nS_{g} \rho^{ga} {\mathbf{v}}^{gs} } \right)}}_{{{\text{L}}.44.8}} = 0 \hfill \\ \end{gathered} $$

(44)

Mass balance equation of gaseous and liquid water considers the diffusive (L.45.6) and advective flows of water vapor (L.45.7) and water (L.45.8), the mass sources related to phase changes of vapor (evaporation–condensation, physical adsorption–desorption) (the sum of those mass sources equals to zero) and dehydration (R.45.1), and the changes of porosity caused by variation of: temperature (L.45.3), dehydration process (L.45.10), variation of skeleton density due to dehydration (L.45.9) and deformations of the skeleton (L.45.2), as well as the variations of: water saturation degree (L.45.1) and the densities of vapor (L.45.4) and liquid water (L.45.5). This gives the following equation [12]:

$$ \begin{array}{l} \underbrace {{n\left( {\rho^{w} - \rho^{gw} } \right){\frac{{D^{s} S_{w} }}{Dt}}}}_{{{\text{L}}.45.1}} + \underbrace {{\mathop {}\limits_{{}} \left( {\rho^{w} S_{w} + \rho^{gw} S_{g} } \right)\alpha \,div\,{\mathbf{v}}^{s} }}_{{{\text{L}}.45.2}} - \underbrace {{\beta_{swg}^{*} {\frac{{D^{s} T}}{Dt}}}}_{{{\text{L}}.45.3}} + \underbrace {{S_{g} n{\frac{{D^{s} \rho^{gw} }}{Dt}}}}_{{{\text{L}}.45.4}} \hfill \\ + \underbrace {{S_{w} n{\frac{{D^{s} \rho^{w} }}{Dt}}}}_{{{\text{L}}.45.5}} + \underbrace {{\mathop {}\limits_{{}} div\,{\mathbf{J}}_{g}^{gw} }}_{{{\text{L}}.45.6}} + \underbrace {{\mathop {}\limits_{{}} div\,\left( {nS_{g} \rho^{gw} {\mathbf{v}}^{gs} } \right)}}_{{{\text{L}}.45.7}} + \underbrace {{\mathop {}\limits_{{}} div\,\left( {nS_{w} \rho^{w} {\mathbf{v}}^{ws} } \right)}}_{{{\text{L}}.45.8}} \hfill \\ - \underbrace {{\left( {\rho^{w} S_{w} + \rho^{gw} S_{g} } \right)\,{\frac{{\left( {1 - n} \right)}}{{\rho^{s} }}}\,{\frac{{\partial \rho^{s} }}{{\partial \Upgamma_{dehydr} }}}\,{\frac{{D^{s} \Upgamma_{dehydr} }}{Dt}}}}_{{{\text{L}}.45.9}} - \underbrace {{{\frac{{\dot{m}_{dehydr} }}{{\rho^{s} }}}\left( {\rho^{w} S_{w} + \rho^{gw} S_{g} } \right)}}_{{{\text{L}}.45.10}} = - \underbrace {{\mathop {}\limits_{{}} \dot{m}_{dehydr} }}_{{{\text{R}}.45.1}} \hfill \\ \end{array} $$

(45)

with β _swg defined by:

$$ \beta_{swg} = \beta_{s} \left( {1 - n} \right)\left( {S_{g} \rho^{gw} + S_{w} \rho^{w} } \right) + n \, \beta_{w} S_{w} \rho^{w} $$

(46)

Enthalpy balance equation of the multi-phase medium, accounting for the conductive (L.47.3) and convective (L.47.2) heat flows, the heat effects of phase changes (R.47.1) and dehydration process (R.47.2), and heat accumulation by a material (L.47.1), can be written as follows [12]:

$$ \begin{gathered} \underbrace {{\left( {\rho C_{p} } \right)_{eff} {\frac{\partial T}{\partial t}}}}_{{{\text{L}} . 4 7.1}} + \underbrace {{\mathop {}\limits_{{}} \left( {\rho_{w} C_{p}^{w} {\mathbf{v}}^{w} + \rho_{g} C_{p}^{g} {\mathbf{v}}^{g} } \right) grad\,T}}_{{{\text{L}} . 4 7.2}} - \underbrace {{\mathop {}\limits_{{}} div\left( {{\tilde{\mathbf{q}}}_{T} } \right)}}_{{{\text{L}} . 4 7.3}} = \hfill \\ = - \underbrace {{\dot{m}_{vap} \Updelta H_{vap} }}_{{{\text{R}} . 4 7.1}} + \underbrace {{\dot{m}_{dehydr} \Updelta H_{dehydr} }}_{{{\text{R}} . 4 7.2}} \hfill \\ \end{gathered} $$

(47)

where ${\tilde{\mathbf{q}}}_{T}$is the conductive thermal flux,

$$ \left( {\rho C_{p} } \right)_{eff} = \rho_{s} C_{p}^{s} + \rho_{w} C_{p}^{w} + \rho_{g} C_{p}^{g} , $$

(48)

and the vapor mass source is given by, [12]:

$$ \begin{gathered} \underbrace {{\mathop {}\limits_{{}} \dot{m}_{vap} }}_{{{\text{L}} . 4 9.1}} = - \underbrace {{\rho^{w} n{\frac{{\partial S_{w} }}{\partial t}}}}_{{{\text{R}} . 4 9.1}} - \underbrace {{\mathop {}\limits_{{}} \rho^{w} S_{w} \,\alpha \,div{\kern 1pt} {\mathbf{v}}^{s} }}_{{{\text{R}} . 4 9.2}} + \underbrace {{\beta_{sw}^{*} {\frac{\partial T}{\partial t}}}}_{{{\text{R}} . 4 9.3}} - \underbrace {{\mathop {}\limits_{{}} div\,\left( {nS_{w} \rho^{w} {\mathbf{v}}^{ws} } \right)}}_{{{\text{R}} . 4 9.4}} \hfill \\ - \underbrace {{\left( {1 - n} \right)\,{\frac{{\rho^{w} S_{w} }}{{\rho^{s} }}}\,{\frac{{\partial \rho^{s} }}{{\partial \Upgamma_{dehydr} }}}\,{\frac{{\partial \Upgamma_{dehydr} }}{\partial t}}}}_{{{\text{R}} . 4 9.5}} - \underbrace {{\dot{m}_{dehydr} \,{\frac{{\rho^{w} S_{w} }}{{\rho^{s} }}}}}_{{{\text{R}} . 4 9.6}} + \underbrace {{\mathop {}\limits_{{\mathop {}\limits_{{}} }} \dot{m}_{dehydr} }}_{{{\text{R}} . 4 9.7}} \hfill \\ \end{gathered} $$

(49)

with:

$$ \beta_{sw}^{*} = \rho^{w} S_{w} \left[ {\left( {1 - n} \right)\beta_{s} + n\beta_{w} } \right] $$

(50)

Equation 49 is obtained from the water mass conservation equation, considering the variations of water saturation degree (R.49.1), the advective flow of water (R.49.4), the mass sources related to dehydration (R.49.7) and the changes of porosity caused by: variation of temperature (R.49.3), dehydration process (R.49.6), as well as variation of skeleton density due to dehydration (R.49.5) and deformations of the skeleton (R.49.2).

The dehydrated water source is proportional to the dehydration rate, [12]:

$$ \dot{m}_{dehydr} = k_{b} \,\dot{\Upgamma }_{dehydr} $$

(51)

k _b is a material parameter related to the chemically bound water and dependent on the stoichiometry of the chemical reactions associated to dehydration process. Linear momentum conservation equation of the multi-phase medium has the following form [12]:

$$ \begin{gathered} div\underbrace {{\left[ {(1 - d)(1 - V)\user1{\Uplambda }_{{\mathbf{0}}} :\left( {\user1{\varepsilon }_{tot} - \user1{\varepsilon }_{th} - \user1{\varepsilon }_{tchem} - \user1{\varepsilon }_{tr} } \right)} \right.\mathop {}\limits_{{}} }}_{{{\text{L}} . 5 2. 1}} - {\underbrace {{\mathop {}\limits_{{}} \alpha \left( {p^{g} - x_{s}^{ws} p^{c} } \right){\mathbf{I}}}}_{{{\text{L}} . 5 2. 2}}} ] \hfill \\ \quad { + }\underbrace {{\mathop {}\limits_{{}} \left[ {\left( {1 - n} \right)\rho^{s} + n\left( {S_{g} \rho^{g} + S_{w} \rho^{w} } \right)} \right]{\kern 1pt} \,{\mathbf{g}}}}_{{{\text{L}} . 5 2. 3}} = 0. \hfill \\ \end{gathered} $$

(52)

Equation 52 was obtained by neglecting inertial forces and considering mechanical and thermo-chemical material degradation (L.52.1), stresses due to pore pressure (L.52.2) (with effective stress principle), and the gravity forces (L.52.3).

The evolution equation for dehydration process can be obtained from the results of thermo-gravimetric (TG or DTA) tests, and considering its irreversibility, has the form [12]:

$$ \Upgamma_{dehydr} \left( t \right) = \Upgamma_{dehydr} \left( {T_{max} \left( t \right)} \right), $$

(53)

where T _max (t) is the highest temperature reached by the concrete up to the time instant t. Hence the dehydration rate $\dot{\Upgamma }_{dehydr}$ is given by

$$ \begin{gathered} \dot{\Upgamma }_{dehydr} = {\frac{{\partial \Upgamma_{dehydr} \left( T \right)}}{\partial T}}\,{\frac{\partial T}{\partial t}} \quad {\text{for }}T (t )\ge T_{max} \left( t \right), \hfill \\ \dot{\Upgamma }_{dehydr} = 0 \quad {\text{ for }}T (t )< T_{max} \left( t \right). \hfill \\ \end{gathered} $$

(54)

The dehydration degree should be determined experimentally from the mass changes during concrete heating, [12]:

$$ \Upgamma_{dehydr} (T) = {\frac{{m(T_{o} ) - m(T)}}{{m(T_{o} ) - m(T_{\infty } )}}}, $$

(55)

where m(T) is mass of concrete specimen measured at temperature T during TG tests, T _o and T _∞ are temperatures when the dehydration process starts and finishes (usually T _o  = 105°C and T _∞  = 1000°C are assumed). The evolution equations for mechanical and thermo-chemical damage parameters, $d\left( t \right) = d\left( {\tilde{\varepsilon }\left( t \right)} \right)$ ($\tilde{\varepsilon }$ is the equivalent strain given by equations of the classical non-local, isotropic damage theory [42]) and $V\left( t \right) = V\left( {T_{max} \left( t \right)} \right)$, should be determined from relations (32) using the data concerning Young’s modulus changes, obtained from the “stress–strain curves” measured for concrete at ambient temperature after previous heating to different temperatures (i.e. giving so called residual properties).

5.1 Initial and Boundary Conditions

For the model closure we need the initial and boundary conditions. The initial conditions (ICs) specify the values of primary state variables at time instant t = 0 in the whole analyzed domain (and on its boundary Γ, ($\Upgamma = \Upgamma_{\pi } \cup \Upgamma_{\pi }^{q}$, π = g, c, t, u):

$$ p^{g} = p_{o}^{g} ,\; p^{c} = p_{o}^{c} ,\; T = T_{o} ,\; {\mathbf{u}} = {\mathbf{u}}_{o} ,\quad {\text{on }}\left( {\Upomega \cup \Upgamma } \right) , { } $$

(56)

The boundary conditions (BCs) describe the values of the primary state variables at time instants t > 0 (Dirichlet’s BCs) on the boundary $\Upgamma_{\pi }$:

$$ \begin{gathered} p^{g} \left( t \right) = \hat{p}^{g} \left( t \right){\text{ on }}\Upgamma_{g} , \\ p^{c} \left( t \right) = \hat{p}^{c} \left( t \right){\text{ on }}\Upgamma_{c} , \\ T\left( t \right) = \hat{T}\left( t \right){\text{ on }}\Upgamma_{t} , \\ {\mathbf{u}}\left( t \right) = {\hat{\mathbf{u}}}\left( t \right){\text{ on }}\Upgamma_{u} , \\ \end{gathered} $$

(57)

or heat and mass exchange, and mechanical equilibrium condition on the boundary $\Upgamma_{\pi }^{q}$ (the BCs of Cauchy’s type or the mixed BCs):

$$ \begin{array} {l}\left( {nS_{g} \rho^{ga} {\mathbf{v}}^{gs} + {\mathbf{J}}_{d}^{ga} } \right) {\mathbf{n}} = q^{ga} ,{\text{ on }} \Upgamma_{g}^{q} \\ \left( {nS_{w} \rho^{w} {\mathbf{v}}^{ws} + nS_{g} \rho^{gw} {\mathbf{v}}^{gs} + {\mathbf{J}}_{d}^{gw} } \right) {\mathbf{n}} = q^{gw} + q^{w} + \beta_{c} \left( {\rho^{gw} - \rho_{\infty }^{gw} } \right),{\text{ on }} \Upgamma_{c}^{q} \\ \left( {nS_{w} \rho^{w} {\mathbf{v}}^{ws} \Updelta H_{vap} + {\tilde{\mathbf{q}}}} \right) {\mathbf{n}} = q^{T} + \alpha_{c} \left( {T - T_{\infty } } \right) + e{\kern 1pt} \sigma_{o} \left( {T^{4} - T_{\infty }^{4} } \right),{\text{ on }}\Upgamma_{T}^{q} \\ \left[ {\mathbf{t}}^{total} \right] {\mathbf{n}} = {\bar{\mathbf{t}}},{\text{ on }}\Upgamma_{u}^{q} \\ \end{array} $$

(58)

where n is the unit normal vector, pointing toward the surrounding gas, q ^ga , q ^gw , q ^w and q ^T are respectively the imposed fluxes of dry air, vapor, liquid water and the imposed heat flux, and ${\bar{\mathbf{t}}}$ is the imposed traction, $\rho_{\infty }^{gw}$ and T _∞ are the mass concentration of water vapor and the temperature in the far field of undisturbed gas phase, e is emissivity of the interface, σ _o the Stefan-Boltzmann constant, while α _c and β _c are convective heat and mass exchange coefficients.

The boundary conditions, with only imposed fluxes given, are called Neumann’s BCs. The purely convective boundary conditions for heat and moisture exchange are also called Robin’s BCs.

5.2 Numerical Solution

The variational or weak form of the model equations, including the ones required to complete the model, was obtained in [12, 34, 35] by means of Galerkin’s method (weighted residuals). The governing equations of the model are then discretized in space by means of the finite element method, e.g. [47]. The unknown variables are expressed in terms of their nodal values as,

$$ \begin{aligned} p^{g} \left( t \right) &\cong {\mathbf{N}}_{p} \,{\bar{\mathbf{p}}}^{g} \left( t \right),\quad p^{c} \left( t \right) \cong {\mathbf{N}}_{p} \,{\bar{\mathbf{p}}}^{c} \left( t \right), \\ T\left( t \right) &\cong {\mathbf{N}}_{t} \,{\bar{\mathbf{T}}}\left( t \right),\quad {\mathbf{u}}\left( t \right) \cong {\mathbf{N}}_{u} \,{\bar{\mathbf{u}}}\left( t \right). \\ \end{aligned} $$

(59)

The resulting system of equations can be written in the following concise discretized matrix form,

$$ {\mathbf{C}}_{ij} \left( {{\mathbf{x}}_{j} } \right){\frac{{\partial {\bar{\mathbf{x}}}_{j} }}{\partial t}} + {\mathbf{K}}_{ij} \left( {{\mathbf{x}}_{j} } \right) {\bar{\mathbf{x}}}_{j} = \,{\mathbf{f}}_{i} \left( {{\mathbf{x}}_{j} } \right), $$

(60)

with

$$ \begin{gathered} {\mathbf{C}}_{ij} = \left[ {\begin{array}{*{20}c} {{\mathbf{C}}_{gg} } & {{\mathbf{C}}_{gc} } & {{\mathbf{C}}_{gt} } & {{\mathbf{C}}_{gu} } \\ {\mathbf{0}} & {{\mathbf{C}}_{cc} } & {{\mathbf{C}}_{ct} } & {{\mathbf{C}}_{cu} } \\ {\mathbf{0}} & {{\mathbf{C}}_{tc} } & {{\mathbf{C}}_{tt} } & {{\mathbf{C}}_{tu} } \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ \end{array} } \right],\quad {\bar{\mathbf{x}}}_{j} = \left\{ {\begin{array}{*{20}c} {{\bar{\mathbf{p}}}^{g} } \\ {{\bar{\mathbf{p}}}^{c} \,} \\ {{\bar{\mathbf{T}}}\,} \\ {{\bar{\mathbf{u}}}} \\ \end{array} } \right\}, \hfill \\ {\mathbf{K}}_{ij} = \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{gg} } & {{\mathbf{K}}_{gc} } & {{\mathbf{K}}_{gt} } & {\mathbf{0}} \\ {{\mathbf{K}}_{cg} } & {{\mathbf{K}}_{cc} } & {{\mathbf{K}}_{ct} } & {\mathbf{0}} \\ {{\mathbf{K}}_{tg} } & {{\mathbf{K}}_{tc} } & {{\mathbf{K}}_{tt} } & {\mathbf{0}} \\ {{\mathbf{K}}_{ug} } & {{\mathbf{K}}_{uc} } & {{\mathbf{K}}_{ut} } & {{\mathbf{K}}_{uu} } \\ \end{array} } \right],\quad {\mathbf{f}}_{i} = \left\{ {\begin{array}{*{20}c} {{\mathbf{f}}_{g} } \\ {{\mathbf{f}}_{c} } \\ {{\mathbf{f}}_{t} } \\ {{\mathbf{f}}_{u} } \\ \end{array} } \right\}, \hfill \\ \end{gathered} $$

(61)

where the non-linear matrix coefficients C _ij (x _j ), K _ij (x _j ) and f _i (x _j ) are defined in detail in [12].

The time discretization is accomplished through a fully implicit finite difference scheme (backward difference),

$$ {\varvec{\Uppsi}}_{i} \left( {{\bar{\mathbf{x}}}_{n + 1}^{{}} } \right) = {\mathbf{C}}_{ij} \left( {{\mathbf{x}}_{n + 1}^{{}} } \right){\frac{{{\bar{\mathbf{x}}}_{n + 1}^{{}} - {\bar{\mathbf{x}}}_{n} }}{\Updelta t}} + {\mathbf{K}}_{ij} \left( {{\mathbf{x}}_{n + 1}^{{}} } \right) {\bar{\mathbf{x}}}_{n + 1} - \,{\mathbf{f}}_{i} \left( {{\mathbf{x}}_{n + 1}^{{}} } \right) = {\mathbf{0}}, $$

(62)

where subscript i (i = g,c,t,u) denotes the state variable, n is the time step number and Δt the time step length.

The equation set (62) is solved by means of a monolithic Newton–Raphson type iterative procedure [12, 29]:

$$ {\varvec{\Uppsi}}_{i} \left( {{\bar{\mathbf{x}}}_{n + 1}^{k} } \right) = \left. { - {\frac{{\partial {\varvec{\Uppsi}}_{i} }}{{\partial {\mathbf{x}}}}}} \right|_{{{\bar{\mathbf{x}}}_{n + 1}^{k} }} \Updelta {\bar{\mathbf{x}}}_{n + 1}^{k} , \quad {\bar{\mathbf{x}}}_{n + 1}^{k + 1} = {\bar{\mathbf{x}}}_{n + 1}^{k} + \Updelta {\bar{\mathbf{x}}}_{n + 1}^{k} , $$

(63)

where k is the iteration index and ${\frac{{\partial {\varvec{\Uppsi}}_{i} }}{{\partial {\mathbf{x}}}}}$ is Jacobian matrix.

More details concerning numerical techniques used for solution of the model equations can be found in [12, 15, 16].

A two-stage solution strategy has been applied at every time step to take into account damage of concrete. First an intermediate problem, keeping the mechanical damage value constant and equal to that obtained at the previous time step, is solved. Then, the “final” solution is obtained, for all state variables and total damage parameter, by means of the modified Newton–Raphson method, using the tangential or Jacobian matrix from the last iteration of the first stage. This allowed us to avoid differentiation of the K _ij matrix with respect to the damage and to obtain a converging solution, [12, 15, 16].

Because of different physical meaning of the capillary pressure p ^c and different nature of the physical phenomena above the temperature T _cr , we have introduced a special ‘switching’ procedure (for physical explanation see Sect. 4.2), [11]. When in an element part of its nodes have temperature above T _cr , the capillary pressure is blocked at the previous value, until the temperature in all the nodes passes the critical point of water. Then equations valid for temperature range T > T _cr are applied in all nodes of this element.

6 Simulation Results

In this section three examples of application of the mathematical model, described in previous sections, for the model validation and numerical analyses concerning performance of concrete structures during fire are presented. The first example shows the experimental validation of the present numerical model and computer software based on it, called COMES-HTC, developed by the authors. The simulations concern the experiments performed by Kalifa et al. [32] who measured the temperature and gas pressure evolution in several points of a concrete slab heated from one side to three different target temperatures. The second example deals with a concrete wall exposed to the standard ISO-834 fire. The simulation results illustrate behavior of concrete structures during a fire and allow us to understand better the degradation phenomena accompanying it. The third example concerns a concrete column exposed to a parametric fire, including also a cooling phase, according to the Eurocode 1, part 1 to 2, [48]. The simulations show a typical, for 2D structures, evolution of concrete deterioration due to increase of temperature and pore pressure in the corner zone, as well as further progress of the material degradation during the cooling phase of fire.

6.1 Validation of the Model

The COMES-HTC software output was compared with the results of tests carried out by Kalifa et al. [32]. He monitored temperature and pore pressure (with respect to the atmospheric pressure) in six locations at different distances from the specimen surface. They were measured with thermocouples and pressure gauges installed during casting. The prismatic specimens (30 × 30 × 12 cm³) were made of two types of concrete, C30 and M100 HPC. Here, the results concerning the temperature and vapor pressure fields in the C30 specimens, heated to different target temperature, 450°C, 600°C or 800°C, were compared with the output from the numerical simulation. The comparison for the HPC specimens heated to 600°C is presented elsewhere [11, 22].

The thermal load was applied on one face of the specimen, whereas the lateral faces of the specimen were heat-insulated with porous ceramic blocks. Heating was provided by means of a radiant heater (up to 5 kW and the target temperature) that covered the surface of the specimen, placed 3 cm above it.

The main parameters of the C30 concrete at ambient temperature, used in our simulations, are shown in Table 2. Initial conditions are as follows: gas pressure equal to atmospheric pressure, p ^g _o  = 101325 Pa, temperature T _o  = 298.15 K (25°C) and relative humidity φ _o  = 70% RH. Considering the way of the concrete surface heating, mixed radiative-convective boundary conditions for heat exchange and purely convective conditions for mass exchange have been employed [11]. The average values for heat and mass exchange coefficients, supposed constant during simulation, have been assumed as follows: for the heated side—α _c  = 18 W/m²K and β _c  = 0.019 m/s, and for the not heated side—α _c  = 8.3 W/m²K and β _c  = 0.009 m/s. The heated surface emissivity is e = 0.9.

Table 2 Main Properties of Dry Concrete (at T = 20°C), Assumed in the Simulations

The heat flow is unidirectional, so the discretization applied, i.e. 133 eight-node elements (133 × 1) with 673 nodes, corresponds to a 1D problem. The simulations are performed for the first 6 h of the heating, using a time step Δt = 1 s.

The simulation results concerning time development of temperature and vapor pressure for the three considered cases of heating temperature are compared with experimental values, [32], in Figures 7 8, 9, 10a, 11 and 12a. Additionally, the results concerning evolutions of relative humidity in the analyzed heating temperatures are presented in Figures 10b, 11, and 12b, showing gradual specimen drying starting from the surface layers. For the heating temperature of 600°C so called ‘moisture clog’ phenomenon is visible, Figure 11b, which has not been observed for the temperatures of 450°C and 800°C, Figures 10b and 12b.

Figure 7

Evolutions of gas pressure in a concrete specimen heated according to [32] for target temperature of 450°C: (a) experimental results [32], and (b) numerical results

Figure 8

Evolutions of gas pressure in a concrete specimen heated according to [32] for target temperature of 600°C: (a) experimental results [32], and (b) numerical results

Figure 9

Evolutions of gas pressure in a concrete specimen heated according to [32] for target temperature of 800°C: (a) experimental results [32], and (b) numerical results

Figure 10

Simulation results of a concrete specimen heated according to [32] for target temperature of 450°C: (a) temperature compared to the experimental values [32] (indicated with the broken lines) and (b) relative humidity

Figure 11

Simulation results of a concrete specimen heated according to [32] for target temperature of 600°C: (a) temperature compared to the experimental values [32] (indicated with the broken lines) and (b) relative humidity

Figure 12

Simulation results of a concrete specimen heated according to [32] for target temperature of 800°C: (a) temperature compared to the experimental values [32] (indicated with the broken lines) and (b) relative humidity

The experimental results clearly show that during the tests rather high peak values of pore pressure, up to 9.3 bar at T = 450°C, Figures 7a, 18 bar at T = 600°C, Figures 8a, and 11 bar at T = 800°C, Figure 9a, have been reached. Slightly lower values of the peak pressure and similar time evolutions of gas pressure have been obtained in the numerical simulations, Figures 7b, 8, and 9b. In some cases, at advanced stages of the process analyzed, unexpected low values of pressure were registered during the tests, probably due to the localized fracturing around the pressures gauges, causing a leakage of gas. In the simulations the material cracking and its effect on the permeability is modeled by means of non-local isotropic damage theory, which is not suitable for description of localized fractures. In general, the gas pressures at advanced stages of the process, obtained from the simulations, were decreasing slower than during the tests, but their maximal values and time of its occurrence are predicted quite accurately. Then, the temperatures in the numerical simulation are slightly higher than the measured ones, Figures 10a, 11, and 12a. This is probably due to the choice of boundary conditions and the conductivity of the material, which may not be well set. However, numerical results present a good agreement with experimental ones, in terms of both temperature and pressure. This shows that the numerical model proposed can be a useful tool for analyses of performance of concrete structures during a fire.

6.2 Concrete Wall Exposed to ISO-834 Fire

In this section a 60-cm concrete wall, made of a C-80 concrete, exposed to the convective-radiative heating from both sides, is analyzed. The heating rate of surrounding air corresponds to the standard 834 ISO fire. Due to symmetry, one half of the wall is modeled by a mesh of 100 (100 × 1) isoparametric, 8-noded elements of equal size (0.3 cm × 1.0 cm), involving 503 nodes and 2515 DOFs. The initial values of relative humidity and temperature are equal to φ ₀ = 50% RH and T ₀ = 293.15 K (20°C).

The simulations are performed for the first 60 min of the fire, using a time step Δt = 1 s, which is automatically halved by the computer code when some numerical problems are encountered, like for example when temperature reaches value of about 200°C or when it is passing the critical point of water. The main material data of the C-80 concrete and the boundary conditions, used in our simulations, are given in Tables 2 and 3.

Table 3 Boundary Examples for the Simulation of a Wall During Exposed to Heating

The time histories of some the most characteristic variables describing the evolution of hygro-thermal and degradation processes in heated concrete, i.e. temperature, water saturation degree, gas and vapor pressures, total- and thermo-chemical damage parameters, obtained from the simulations performed with the model described in previous sections, are presented and briefly discussed.

The results are plotted as a function of time in four characteristic points at different distance from the heated surface: 3 mm (in a surface zone), 2.4 cm (in a zone where thermal spalling usually occurs), 6 cm (in a zone with a temperature increase of about 200 K at the end of simulations) and 10 cm (in a deeper zone, but with a temperature increase of about 80 K at the end of simulations).

After 60 min of the standard 834-ISO fire heating, the temperature reached at a surface layer about 830°C (~1100 K), at a distance of 6 cm −~200°C, while in a core zone it remained below 100°C, Figure 13. During heating, at temperatures below ~100°C, vapor condensation was observed, causing a visible increase of moisture content (ΔS _w  ≅ 0.1) in the so called ‘moisture clog’ zone. The phenomenon is followed by a rapid water evaporation in the temperature range between ~100°C and ~200°C, Figure 13. The latter process was accompanied by a gas pressure increase up to about 7 to 9 bars, Figure 14, which was induced at temperatures below 100°C mainly by heating of dry air and then, up to ~200°C, by a rapid evaporation of water what caused that up to the temperature of ~300°C the gas phase was composed mainly of vapor. During heating process concrete was exposed to a gradual thermo-chemical degradation (reaching in a surface layer value of ~90%), Figure 15, and additionally high gas pressure and compressive stress due to constrained thermal dilatation of a surface layer induced material cracking (described here as an increase of mechanical damage). As a result permeability of concrete was gradually increasing what caused a decrease of gas pressure down to the atmospheric pressure value, Figure 14.

Figure 13

A concrete wall heated according to the standard ISO 834 fire-curve—the evolutions of temperature and saturation degree at four different distances from the heated surface, obtained from simulations with the present model

Figure 14

A concrete wall heated according to the standard ISO 834 fire-curve—the evolutions of gas- and vapor pressure at four different distances from the heated surface, obtained from simulations with the present model

Figure 15

A concrete wall heated according to the standard ISO 834 fire-curve—the evolutions of total- and thermo-chemical damage parameter at four different distances from the heated surface, obtained from simulation with the present model

The presented results allow us for better understanding of physical phenomena and in particular evolution of degradation processes in the considered concrete structure during standard 834-ISO fire. One can conclude that in these conditions thermal spalling is not expected to occur in the considered structure because the phenomenon is accompanied by a rapid increase of mechanical damage parameter (as showed our previous analyses, see e.g. [15]) which is not observed here.

6.3 Concrete Column Exposed to Parametric Fire and Fast Cooling

In this section a concrete column exposed to a fire described by a parametric heating profile, following the Annex A of the Eurocode 1 [48], is analysed. The profile differs significantly from the nominal fire curves (e.g. standard 834-ISO fire curve used in Sect. 6.2) because after a heating stage formulated on experimental basis, it defines also a cooling stage.

The heating profile T _heat (t) selected for the calculation is the following:

$$ T_{heat} \left( t \right) = 293.15 + 1325 \left( {1 - 0.324 e^{ - 0. 0 0 7 7 t} - 0.204 e^{ - 0. 0 6 5 4 5 t} - 0.472 e^{ - 0. 7 3 4 5 t} } \right) $$

(64)

and that corresponds, for the chosen material, to the minimum value of the opening coefficient allowed in the European rules (i.e. 0.02 m^1/2).

The heating stage is followed by a cooling phase, corresponding to a rapid intervention of firemen (calculated for the same case as the heating one), described as follows:

$$ T_{cool} \left( t \right) = 709.532 - 20.5681 (t - 4920) $$

(65)

This is a fast cooling with the environmental temperature decrease within 20 s from the maximum value (i.e. 709.532 K reached after 80 min) down to the initial value, after a stationary stage at the maximum temperature for 2 min.

As far as the boundary conditions are concerned, mixed convective-radiative heat exchange has been assumed with the convective heat exchange coefficient α _c  = 20 W/m² K and the emissivity e = 0.9. The convective mass exchange between the surface of the concrete element and the environment is assumed, with mass exchange coefficient equal to β _c  = 0.025 m/s and constant water vapor pressure p ^gw = 1300 Pa. During heating this corresponds to a rapid decrease of the ambient relative humidity down to a value close to zero.

Due to symmetry, one-fourth of the cross section of the analysed square column under consideration (30 × 30 cm) is modelled with the FE mesh (Figure 16). The main properties of the material (C60) assumed in the simulation are listed in Table 2.

Figure 16

Cross section of the concrete column: geometry and FE mesh used in the simulations

Figure 17 shows the temperature evolution in six different points located at various depths from the heated surfaces of the column. The sharp decrease of environmental temperature, due to the cooling, leads to a rapid decrease of the temperature in these points, especially those close to the lateral sides of the cross section. The inversion of thermal fluxes has important consequences not only from the thermo-hygral point of view, but also for the mechanical behavior of the material.

Figure 17

Temperature histories in the environment (solid blue line), and in points: A, B, C, D, E and F at the depths of: 15 cm, 10 cm, 5 cm, 3 cm, 1 cm and 0.05 cm from the heated sides (see Figure 16)

In Figure 18a one can observe the distribution of temperature at t = 80 min, corresponding to the time instant of maximum heating. Figure 18b represents the temperature distribution at the end of the computation (i.e. ~100 min). The surface temperature decrease of about 200 K is observed.

Figure 18

Distributions of the temperature [K] at 80 min (a) and at the final time of simulations (b)

Vapor pressure distribution at 80 min and at the end of calculation is depicted in Figures 19a, b. In this case it is worthy to notice the influence of the damage on the pressure value: the pressure peaks are concentrated in the zones characterized by a lower value of damage parameter, see Figure 20a. The pressure is lower where the material is more damaged (i.e. close to the corner). At the end of the process the pressure is almost uniformly distributed throughout the cross section of the column and its values are no higher than 1 bar, Figure 19b.

Figure 19

Distributions of the vapor pressure [Pa] at 80 min (a) and at the final time of simulations (b)

Figure 20

Distributions of the mechanical damage d [−] (Equation 32) at 80 min (a) and at the final time of simulations (b)

Finally, in Figures 20a, b one can observe the distribution of damage parameter. Unlike temperature and other thermo-hygral quantities, the damage is continuously increasing because of an additional damaging of the material even during the cooling phase. In Figure 20b it is clearly visible that the zone of damaged concrete close the element surface is larger than the one in Figure 20b, (i.e. before the cooling stage).

7 Conclusions

Application of mechanics of multi-phase porous media for modeling cement based materials at high temperature has been presented and explained. The considerations were based on the mathematical model of mechanistic type, developed by the authors within the recent years. The model has been previously experimentally validated and successfully applied for analyzing performance of concrete structures at high temperature.

Physical phenomena in a concrete wall heated during a fire have been described and analyzed, showing clearly a multi-phase nature of concrete in these conditions. Main stages of a mathematical model development by means of hygro-thermo-mechanics of porous media have been briefly presented. First, the mass, energy and linear momentum conservation equations at micro-scale have been given and then averaged in space to obtain the macroscopic form of the equations. Some main key-points in modeling cement-based materials at high temperature have been discussed. Final form of the model equations and method of their numerical solution have been briefly summarized. The model validation and two examples of its application for numerical simulation and analysis of concrete structures exposed to fire conditions, including also a cooling phase, have been presented and analyzed. Mechanics of multi-phase porous media has proved its usefulness for better understanding and predicting concrete performance at high temperature. Obviously, due to the complexity of the model it is aimed at the analysis of single structural elements, like for example columns, beams, slabs etc. Then, it is a powerful tool for predicting thermal spalling [15] and the simulation results can be used for the development of a database, an expert system could be based on. Such an approach has been already successfully followed in the framework of UPTUN project [49]. The model validity was confirmed by comparison with some published experimental results at laboratory scale, where the model predicted the elements’ performance with reasonable accuracy which is sufficient for engineering applications. To the knowledge of the authors there are not available any experimental results suitable for the model validation at the whole structure scale thus the model accuracy at this scale could not be confirmed.