Climate change impact assessment on mild and extreme drought events using copulas over Ankara, Turkey

Abstract

Climate change, one of the major environmental challenges facing mankind, has caused intermittent droughts in many regions resulting in reduced water resources. This study investigated the impact of climate change on the characteristics (occurrence, duration, and severity) of meteorological drought across Ankara, Turkey. To this end, the observed monthly rainfall series from five meteorology stations scattered across Ankara Province as well as dynamically downscaled outputs of three global climate models that run under RCP 4.5 and RCP 8.5 scenarios was used to attain the well-known SPI series during the reference period of 1986–2018 and the future period of 2018–2050, respectively. Analyzing drought features in two time periods generally indicated the higher probability of occurrence of drought in the future period. The results showed that the duration of mild droughts may increase, and extreme droughts will occur with longer durations and larger severities. Moreover, joint return period analysis through different copula functions revealed that the return period of mild droughts will remain the same in the near future, while it declines by 12% over extreme droughts in the near future.

Introduction

Drought is a climatic disaster that heavily affects all the aspects of the ecosystem and human life. In general, drought is defined as a deficit in the amount of water, a deviation from the normal condition, while the meteorological droughts mostly depend on the decrease in the amount of the precipitation received through a long period (e.g., a season, a year, and more). Meteorological droughts have many factors that play a significant role in its occurrences such as characteristics of rainfall (i.e., duration and intensity, rainy days distribution in the growing season, onset and termination, severity and its temporal variability), temperature, low relative humidity, and hisgh winds (Mishra and Singh 2010).

The drought monitoring system is one of the fundamental essentials for drought management plans (Hao et al. 2014). One of the main tools for drought monitoring is the use of drought indices. Drought indices are used to quantify the drought phenomenon and make it easier for different users to analyze climate irregularities in terms of severity, duration, frequency, and spatial expansion. Among the several indices developed for meteorological drought analysis, the standardized precipitation index (SPI; McKee et al. 1993) is one of the most commonly used indices in the literature. The simplicity of its calculation and application to different timescales has enabled this index to analyze meteorological drought for any location (Svoboda and Fuchs 2016).

In recent years, many studies found convincing evidence that climate change impacts water resources, environment, health, and safety significantly (Danandeh Mehr and Kahya 2017; Tirado et al. 2010). Typically, one of the most common methods to evaluate the impact of future climate on different processes is using of simulations of general circulation models (GCMs) based on the representative concentration pathway (RCP) climate scenarios. The GCM-based datasets have been employed in many studies that are aimed to investigate the impact of climate change on drought events by considering a wide range of projections of precipitation or other climatic variables (Giorgetta et al. 2013).

Given that drought is a complex phenomenon in which its physical characteristics (e.g., severity and duration) are interdependent and affecting each other, multivariate analysis can provide a better description of the probabilistic characterization of droughts (Tosunoğlu and Onof 2017) in comparison with univariate drought analysis. Copula functions are useful tools that can imitate the joint behavior of physical characteristic droughts and preserve the dependence structure among them. Following this ability, copula functions have been utilized in probabilistic determination (i.e., frequency analysis) of the drought events in most recent studies (Madadgar and Moradkhani 2013; Shiau 2006).

Many studies have investigated the impact of climate change on climatic events including droughts and runoff extremes (Cheng et al. 2019; Madadgar and Moradkhani 2013), drought characteristics (Bisht et al. 2019; Nazeri Tahroudi et al. 2019), and regionalization of droughts (Adib and Marashi 2019; Mortuza et al. 2019). However, so far, there has not been a study to compare the response of the joint behavior of both mild and extreme drought with climate change, while these drought events have different impacts on various aspects of human life (Tunalıoğlu and Durdu 2012; Wang et al. 2019). The goal of this study is, therefore, to evaluate the changes in the return period of the mild and extreme meteorological droughts due to climate change using copula functions. To this end, drought characteristics in the reference period of 1984–2018 are compared with those of the near future (2018–2050) over the Ankara Province, Turkey. Future projections were attained through dynamically downscaling of three different GCMs considering the RCP 8.5 and 4.5 scenarios. To the best of the authors’ knowledge, this is the first study that explores the differences between the recurrence intervals of both mild and extreme drought under RCP scenarios, particularly across Ankara.

Materials and methods

In drought frequency analysis, important drought characteristics (e.g., duration, and average severity) are generally derived from hydro-meteorological datasets using a drought index. Given that drought characteristics are typically interrelated, it is more convenient to use bivariate or multivariate models in their frequency analysis. On the other hand, given that the drought characteristics usually follow different types of univariate distributions, it is not possible to use traditional bivariate distributions in their frequency analysis. In this study, copula functions are utilized to overcome such difficulties and provide reliable estimates of multivariate drought frequencies (Hangshing and Dabral 2018; Tosunoglu and Can 2016).

Copula functions

Based on Sklar’s theorem, copula functions link the univariate distribution functions to form multivariate distribution functions. The advantage of using copula functions in forming multivariate distribution functions is that they can model the joint dependence among different variables without being dependent on their marginal distributions (Afshar and Yilmaz 2017). Given that U and V are two dependent random variables (e.g., drought duration and severity), the bivariate joint cumulative distribution functions (CDF) of them can be obtained by using Eq. (1) as follows:

$$ \mathrm{F}\left(\mathrm{u},\mathrm{v}\right)=\mathrm{C}\left(\mathrm{F}\left(\mathrm{u}\right),\mathrm{F}\left(\mathrm{v}\right)\right) $$

(1)

where C(.) is the copula function; F(u, v) is the joint CDF of u; and v are random variables; and F(u) and F(v) are the marginal CDF of u and v, respectively. Here, F(u) and F(v) are used as inputs to copula functions to obtain F(u, v) and defined as follows:

$$ \mathrm{F}\left(\mathrm{u}\right)=\mathrm{P}\left(\mathrm{U}\le \mathrm{u}\right) $$

(2)

$$ \mathrm{F}\left(\mathrm{v}\right)=\mathrm{P}\left(\mathrm{V}\le \mathrm{v}\right) $$

(3)

where P(U ≤ u) and P(V ≤ v) are the probabilities that random variables U and V take values smaller than u and v. In Eqs. (2) and (3), the copula functions link the univariate CDF to bivariate joint CDFs (F(u, v)). Using these joint CDFs, bivariate conditional CDFs can be found by utilizing the multiplication rule:

$$ \mathrm{F}\left(\mathrm{u}|\mathrm{v}\right)=\frac{\mathrm{F}\left(\mathrm{u},\mathrm{v}\right)}{\mathrm{F}\left(\mathrm{v}\right)} $$

(4)

After the marginal distributions of each drought characteristics are defined and their CDF’s are computed, the copula functions can be applied for joint modeling of the drought characteristics. There are multiple different copula functions available for modeling the joint behavior of different dependent univariate variables, while in this study, bivariate Archimedean (i.e., Clayton, Frank, Gumbel Hougaard, and Joe) and elliptical copulas (normal, and t student) are considered (Table 1). Among different theoretical copula functions, the best function for modeling different scenarios is selected by using the root mean square error (RMSE) as a goodness of fit statistics between any fitted copula and empirical one as follows:

$$ \mathrm{RMSE}=\sqrt{\frac{\sum_{\mathrm{i}=1}^{\mathrm{n}}{\left(\mathrm{C}{\left(\mathrm{u},\mathrm{v}\right)}_{\mathrm{t}}-\mathrm{C}{\left(\mathrm{u},\mathrm{v}\right)}_{\mathrm{e}}\right)}^2}{\mathrm{n}}} $$

(5)

where C(u, v)_t and C(u, v)_e are the theoretical and empirical copula functions, respectively, that are used for modeling the joint dependence among characteristics of n drought events. In this study, the calculation of empirical copula and validation of different theoretical copula functions are done using copula package (Yan 2007) in the R environment (R Core Team 2018).

Table 1 Equations of copula functions. Here, u and ν are two dependent univariate variables, df is the degree of freedom, θ and ρ are copula dependence parameters, ∅ is the CDF of standard univariate Gaussian distribution, and t_df is the Student t distribution function

Return periods

The return period of certain drought event is associated with a specified exceedance probability. According to Shiau and Shen (2001), the return periods of drought events with univariate drought characteristics (e.g., duration and average severity) can be estimated as a function of drought inter-arrival time:

$$ {\mathrm{T}}_{\mathrm{U}\ge \mathrm{u}}=\frac{\mathrm{E}\left(\mathrm{DIT}\right)}{\mathrm{P}\left(\mathrm{U}\ge \mathrm{u}\right)} $$

(6)

where E(DIT) is the expected value of drought inter-arrival time estimated using the past observations, and T_U ≥ u is the return period of the drought event with the characteristic of U greater than or equal to u. However, since a drought event is considered mostly a bivariate event that is characterized mostly by drought duration and severity, estimation of the joint return period of these characteristics is more helpful for the assessment and management of droughts. Therefore, in this study, the estimated joint return periods has been done by using a methodology proposed by Shiau (2006) as follows:

$$ {\mathrm{T}}_{\left(\mathrm{U}\ge \mathrm{u},\kern0.5em \mathrm{V}\ge \mathrm{v}\right)}=\frac{\mathrm{E}\left(\mathrm{DIT}\right)}{\mathrm{P}\left(\mathrm{U}\ge \mathrm{u},\mathrm{V}\ge \mathrm{v}\right)} $$

(7)

$$ {\mathrm{T}}_{\left(\mathrm{U}\ge \mathrm{u}\ \mathrm{or}\ \mathrm{V}\ge \mathrm{v}\right)}=\frac{\mathrm{E}\left(\mathrm{DIT}\right)}{\mathrm{P}\left(\mathrm{U}\ge \mathrm{u}\ \mathrm{or}\ \mathrm{V}\ge \mathrm{v}\right)} $$

(8)

$$ {\mathrm{T}}_{\left(\mathrm{U}\ge \mathrm{u}\ \right|\ \mathrm{V}\ge \mathrm{v}\Big)}=\frac{\mathrm{E}\left(\mathrm{DIT}\right)}{\mathrm{P}\left(\mathrm{U}\ge \mathrm{u},|\mathrm{V}\ge \mathrm{v}\right)} $$

(9)

where P(.) values in the denominators of Eqs. (7–9) are the bivariate joint probability of drought events with characteristics of U and V varying for a combination of duration and average severity (defined below in Section 2.4) among and/or conditional cases in Eqs. (7–9), respectively. The P(.) for the conditional cases can be found by using the CDF of the used drought characteristics in them. Equations (10) and (11) are the examples of univariate and bivariate cases whereby using copula function in calculation of F_UV(u, v); the joint probabilities of drought events with characteristics of U and V for three cases of and/or conditional can be calculated via Eqs. (12–15).

$$ \mathrm{P}\left(\mathrm{U}\ge \mathrm{u}\right)=1-{\mathrm{F}}_{\mathrm{U}}\left(\mathrm{u}\right) $$

(10)

$$ \mathrm{P}\left(\mathrm{U}\ge \mathrm{u},\mathrm{V}\ge \mathrm{v}\right)=1-{\mathrm{F}}_{\mathrm{UV}}\left(\mathrm{u},\mathrm{v}\right) $$

(11)

$$ \mathrm{P}\left(\mathrm{U}\ge \mathrm{u},\mathrm{V}\ge \mathrm{v}\right)=1-{\mathrm{F}}_{\mathrm{U}}\left(\mathrm{u}\right)-{\mathrm{F}}_{\mathrm{V}}\left(\mathrm{v}\right)+\mathrm{C}\left({\mathrm{F}}_{\mathrm{U}}\left(\mathrm{u}\right),{\mathrm{F}}_{\mathrm{V}}\left(\mathrm{v}\right)\right) $$

(12)

$$ \mathrm{P}\left(\mathrm{U}\ge \mathrm{u}\ \mathrm{or}\ \mathrm{V}\ge \mathrm{v}\right)=1-\mathrm{C}\left({\mathrm{F}}_{\mathrm{U}}\left(\mathrm{u}\right),{\mathrm{F}}_{\mathrm{V}}\left(\mathrm{v}\right)\right) $$

(13)

$$ \mathrm{P}\left(\mathrm{U}\ge \mathrm{u}|\mathrm{V}\ge \mathrm{v}\right)=\frac{\mathrm{P}\left(\mathrm{U}\ge \mathrm{u},\mathrm{V}\ge \mathrm{v}\right)}{\mathrm{P}\left(\mathrm{V}\ge \mathrm{v}\right)}=\frac{1-{\mathrm{F}}_{\mathrm{U}}\left(\mathrm{u}\right)-{\mathrm{F}}_{\mathrm{V}}\left(\mathrm{v}\right)+\mathrm{C}\left({\mathrm{F}}_{\mathrm{U}}\left(\mathrm{u}\right),{\mathrm{F}}_{\mathrm{V}}\left(\mathrm{v}\right)\right)}{1-{\mathrm{F}}_{\mathrm{V}}\left(\mathrm{v}\right)} $$

(14)

The described equations above are the main drivers of the joint probability and hence joint return period analysis. By using such formulations, the joint probability of any drought event (e.g., a drought event with duration more than 7 months and average severity of 1.25) can be calculated. Once the joint probability is being calculated, by inserting joint probability information to the equations of 7 to 8, the return period of that event can be calculated with three different scenarios of and/or conditional forms.

Standard precipitation index

The SPI is one of the most commonly used drought indices which is developed based on the normalization of precipitation probabilities. Although SPI is generally calculated by using monthly precipitation data (for the different number of timescales), its values can be produced with daily or weekly precipitation data as well (WMO, 2006). Owing to the simplicity of SPI and its utilities, the World Meteorological Organization (WMO) recommends the use of SPI as the most essential meteorological drought index compulsory in all countries in monitoring drought conditions (Hayes et al. 2011).

Regardless of the time interval at which precipitation values are presented, the SPI calculation method is the same for all time intervals. Based on the definition of (McKee et al. 1993), initially, the accumulated precipitation amounts are calculated based on considered time step (here in this study, 12-month time step has been selected for further drought analysis). Later, the accumulated time series of precipitation data is fitted to the desired distribution function, and finally, the probabilities of accumulated precipitation observations are normalized with using inverse CDF of the standard normal distribution function. In this study, the SPI calculations are done by using the SPEI package (Santiago and Vicente-Serrano 2017) in the R environment. For more details about SPI and other different drought indices and their way of calculations, see (WMO, 2006).

Drought analysis

Drought events, in general, have multiple characteristics including drought duration (the length of the dry period), drought severity (summation of SPI values during the dry period), drought average severity (average of SPI values during the dry period), and drought intensity (minimum SPI value during the dry period). Among drought characteristics, the drought severity and intensity are highly associated with drought duration and average severity (the severity of drought can be determined by multiplication of drought duration and average severity, and drought intensity is highly correlated with drought average severity; Afshar et al. 2016). Hence, this study is based on two drought characteristics of drought duration and average severity, while any dry period is defined to have continuously negative SPI values and at least one SPI value below minus one. While among the SPI time series, many periods satisfy this condition; those dry periods with less than 3-month duration are not considered as drought events to avoid an enormous number of droughts and get reliable information about the total number of drought events and their dispersion over different time periods. The two important drought characteristics investigated in this study (i.e., drought duration and average severity) and the overall procedure of drought analysis conducted in this study are presented schematically in Fig. 1.

Fig. 1

The overall procedure of drought analysis conducted in this study. D#, duration of draught event; CDF, cumulative distribution function

Given that the frequency and return period analysis require long time series of drought characteristics, in this study, the drought characteristics of events occurred over different stations are bound to generate longer drought characteristic time series and hence more robust areal average analysis. Moreover, to visualize the univariate and joint cumulative probabilities, the bound drought characteristics are fitted to different univariate probability distributions to generate synthetically continuous data of different drought characteristics. Among different univariate distribution functions (i.e., gamma, log-normal, logistic, normal, and Weibull), the best distribution is selected based on the chi-squared statistics between the cumulative distribution functions of theoretical and empirical cumulative distributions function values for each join dependence and scenario separately.

Datasets

Drought events and their spatiotemporal variations are the most crucial problem to tackle over the semi and arid climatic regions like Central Anatolia (Duzenli et al. 2018) where the Ankara Province is located. The required amount of water for municipal and industrial purposes must be managed carefully where the water supply sources get critical under climate change. The datasets used in this study are elaborated below.

Station-based observations

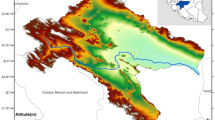
The analysis of the reference meteorological drought characteristics is performed using monthly precipitation records obtained for the period of 1984 and 2018 over the five automated meteorological stations operated by the General Directorate of Meteorology (MGM) located in Ankara Province (Fig. 2).

Fig. 2

Location of the study area (Ankara Province) and the meteorological stations located in it

GCMs

The drought analyses related to the future projections are performed using projected datasets between the years 2018 and 2050. The climate projections for this period are simulated by MGM using three different available GCMs (i.e., HadGEM2-ES, MPI-ESM-MR, GFDL-ESM2M), a single regional climate model (RCM; Reg4), and two different RCP scenarios (RCP 4.5, and RCP 8.5; Table 2) at 20-km spatial resolution. The three selected GCMs are picked up from those of Coupled Model Inter-comparison Project Phase 5 (CMIP5) experiments to closest average temperature forecasts during control runs (1971–2000) over Turkey (Demircan et al. 2017), while the remaining GCM biases for local precipitation and temperature were minimized using high-resolution observed reanalysis data from the Climate Research Unit and the University of Delaware at the reference period (Danandeh Mehr et al. 2020). For more details about the products, downscaling steps, and the implemented bias correction procedures, the interested readers are referred to Demircan et al. (2017).

Table 2 Highlight information of the GCMs used in this study

HadGEM2-ES

HadGEM2 (Hadley Center Global Environment Model version 2) is a second-generation global model developed by Hadley Center, a research organization affiliated with the UK Meteorological Service. There are various HadGEM2 models based on available atmospheric, hydrological, and oceanographic cycles (i.e., HadGEM2-A, HadGEM2-O, HadGEM2-AO, HadGEM2-CC, HadGEM2-CCS, HadGEM2-ES). These models have the same physical infrastructure containing different levels of detail. These models have an integrated atmospheric-ocean configuration with a vertical atmospheric expansion that provides optional better stratosphere modeling, and a surface system configuration with dynamic vegetation, ocean biology, and atmospheric chemistry (Collins et al. 2011).

MPI-ESM-MR

The MPI-ESM (Max-Planck-Institute Earth System Model) model, developed by the Max Planck Institute of Germany, is an integrated circulation model consisting of several sub-modules. The MPI-ESM model integrates multiple models including atmospheric ECHAM6 model (Stevens et al. 2013), MPIOM ocean model (Jungclaus et al. 2013), the ground and vegetation subsystem model JSBACH (Reick et al. 2013), ocean bio—the geochemistry model HAMMOCC5 (Ilyina et al. 2013), and the OASIS module (Valcke 2013), which allows the modules to work simultaneously. The MPI-ESM is available in three different versions of MPI-ESM-LR (Low Resolution, Dynamic Vegetation), MPI-ESM-MR (Medium Resolution, Dynamic Vegetation), and MPI-ESM-P (Low Resolution Paleo Mode).

GFDL-ESM2M

The Earth System Model (GFDL-ESM2) is a global-coupled climate-carbon model which is developed at the Geophysical Fluid Dynamics Laboratory (GFDL) of the National Oceanic and Atmospheric Administration (NOAA). There are two different versions of the GFDL model (i.e., ESM2M and ESM2G). Both ESM2m and ESM25 versions use same ocean ecology and biogeochemistry but different ocean components with this difference that in the ESM2M version, the vertical coordinate is based on depth, while in the ESM2G version, the vertical coordinate is based on density (Dunne et al. 2012).

Representative concentration pathways

In the climatic scenarios, the different RCPs are generally distinguished from each other based on the annual changes of global greenhouse gas emissions, the socio-economic and technological development assumptions, the impact of climate-affecting gas emissions, and atmospheric particle changes. RCP scenarios used in this study (i.e., RCP 8.5 and 4.5) are defined by their total radiative forcing pathway and level by 2100. Relatively, more pessimistic RCP 8.5 scenario assumes that there will be no policy change about emission reduction in the future, while increased greenhouse gas emissions will increase the concentration of greenhouse gasses in the atmosphere. On the other hand, the relatively more optimistic RCP 4.5 scenario foresees that radiative forcing will stabilize soon after 2100 with the help of global emission reduction policies (van Vuuren et al. 2011).

Results and discussion

To illustrate the impact of climate change on drought characteristics, the number of drought events at each meteorological station and overall average over Ankara Province are derived both for the reference and the projected periods using the approach described in Section 2.4. The number of drought events for the reference period and the six model-scenario combinations (three models and two scenarios) are given in Fig. 3. The comparison of the number of drought events between the reference and the near future periods indicates that on average, the number of droughts will be less in the future compared with the reference period (13 out of 30 comparisons show lower drought numbers for future periods than reference period, 10 out of 30 comparisons show higher numbers, and seven out of 30 comparisons show equal drought numbers). On average, the differences between the models are marginal, while the number of drought events for the RCP 8.5 scenario is higher than that of the RCP 4.5 scenario. This implies the increasing probability of drought events with increasing emission levels (Fig. 3).

Fig. 3

The number of drought events compared among the reference and future scenarios over stations located in Ankara Province. 4.5 = RCP 4.5; 8.5 = RCP 8.5; HG HadGEM

The accuracy statistics and the parameters of the best fitting functions for the estimation of the univariate CDF of drought characteristics are given in Table 3, while the relevant CDF and the corresponding probability density function (PDF) of drought characteristics estimated using these best-fitted distribution functions are presented in Fig. 4. The comparison of the PDF curves of reference and future projection drought characteristics shows that the future PDF curves are skewed positively, clearly showing both future drought durations and average severity decrease relative to the reference period. On average, most of the projection PDF curves of drought durations less than ~ 15 months (relatively short-living droughts) and higher than ~ 35 months (relatively long-living droughts) are located above the curve of the reference period (particularly over RCP 4.5 scenario; Fig. 4a and b), implying the probability that the probability of occurrence of such short- and long-living droughts in the future is more likely. On the other hand, the same figure also shows that PDF curves of drought durations between ~ 15 and ~ 30 months are located below the curve of the reference period, implying that there will be less medium-duration drought events (Fig. 4a). Similar to drought duration PDF curves, average severity PDF curves show that low-severity (< ~ 0.80) and high-severity (> ~ 1.20) droughts will be more likely in the future (for all scenarios) while medium-severity droughts will be less likely (Fig. 4b and f).

Table 3 The best univariate distribution and copula function that has been selected based on the comparison of chi-squared and RMSE values between theoretical and empirical cumulative probabilities. Ave. Sev., average severity; l, location; s, scale; ml, meanlog; sl, sdlog; sh, shape; r, rate; m, mean; sd, standard deviation; P, parameter

Fig. 4

CDF and PDF of different drought characteristics (duration and average severity) over Ankara Province generated by using reference and future scenario simulations

The joint behavior of drought characteristics for different occurrence probabilities simulated with different copula functions with respect to their performance in capturing the joint dependence among drought duration and average severity is given in Table 3, while the corresponding joint CDF curves over Ankara Province are presented in Fig. 5. The comparison of the relationship between drought characteristics within the reference and future projections demonstrates that over moderate droughts (i.e., drought with joint CDF of 0.5), both the duration and the average severity of droughts will be close to those of the reference period. This trend is also visible for severe droughts; however, when the occurrence probability of drought decreases (i.e., extreme droughts with joint CDF of 0.95), both duration and average severity of drought events increase (all of GCM contour lines except HadGEM 8.5 and MPI 8.5 move to the above of the reference contour lines), which implies that future extreme events will have a longer duration and larger severities than reference period. These results are consistent with the findings of other climate change studies focused over the central Anatolia region which showed that the duration of drought events in near future is higher than reference periods, while the trend in average severities varies with respect to different RCPs (Danandeh Mehr et al. 2020).

Fig. 5

The comparison of the relationship between drought characteristics by considering the same joint probability for both reference and future projections over Ankara Province

Average drought duration and severity values corresponding to various univariate return periods (5, 11, 17, 24, and 30) and joint return periods reflecting various levels of drought events are given in Table 4. These values are calculated by averaging the GCM values over 5 stations for the two emission scenarios separately, while the joint return periods are given for both “and,” “or,” and “conditional” cases. Results showed that on average every 5 years, a drought event with ~ 12 months of duration or ~ 0.76 average severity is observed, while droughts with a return period of 30 years showed to have the longer durations of 28 months and larger average severities of 1.23. On average, the joint return periods for the RCP 8.5 scenario are higher than the RCP 4.5 scenarios for the “and” case, which implies, observing a drought event with any given duration, and average severity at the same time (“and” case) for the higher emission RCP 8.5 scenario is less likely than for the lower emission scenario RCP 4.5.

Table 4 Comparison of the impact of climate change on univariate and joint return periods of droughts with different duration and average severity amounts. The reference refers to the 1986–2018 period, and RCP 4.5 and RCP8.5 are two climate projections up to 2050 (results are averaged across three GCMs and five stations within Ankara Province)

Moreover, the comparison of the return periods of drought events shows that the joint return period of mild droughts (a drought event with a return period of 5 years in case of univariate probability) does not vary much within the reference and future projection time periods (and, or, conditional columns under joint return period). In contrast, the joint return period of extreme drought (a drought with a return period of 30 years in case of univariate probability) decreases within future projection periods (e.g., joint return period decreases from 189 years to 93 and 169 years for RCP 4.5 and 8.5 scenarios, respectively, for and case) implying that extreme droughts will be more frequent within future projections while the frequency of mild droughts will remain the same.

Conclusion

Drought is one of the extreme events that has inverse effects on various sectors including agriculture and water resources. Investigation of the effects of climate change on drought is important for the planning and the management of water resources. In this study, the impact of climate change on univariate and bivariate drought characteristics (duration and average severity) is investigated using long-term station-based historical observations and climate projections (three GCMs and two emission scenarios) over Ankara Province.

The comparison of the drought characteristics shows that while over extreme droughts the average severity of drought events increases, the mild drought events will be expected to happen with longer duration and milder average severities (Fig. 5 and Table 4), which implies that projection scenarios may experience more extreme precipitation deficits compared with the reference period. However, it should be noted that these conclusions are associated with precipitation amounts recorded by meteorological stations available in Ankara Province with a warm climate and hence might not be valid for other climates with different precipitation regimes.

Results also show that the return periods of events with low and high drought characteristic (both duration and severity) values decrease (i.e., such events will occur more frequently), while the return periods of events with medium drought duration and severity increase (i.e., such events will occur less frequently). Given that events with high drought duration or severity values are more significant from the drought planning and management perspective (i.e., such events yield more significant economic/hydrological/social results), these results imply that Ankara Province will need to prepare and adapt for worse drought conditions in the future than the past.

Overall, the joint return periods determined using copula formulations for three possible probability combinations (i.e., and, or, conditional) showed that the frequency of mild drought events obtained using different GCMs will be close to those experienced in the reference period, while the return period of extreme events (i.e., drought events with return period more than 30 years) will decrease by 30%. These results imply that the extreme droughts will occur more frequently in comparison with the reference time period. The results found here should be repeated over larger regions (e.g., country scale) to make a general conclusion and determine the impacts of climate changes on mild and extreme droughts.