Medical-image-based aorta modeling with zero-stress-state estimation

Abstract

Because the medical-image-based geometries used in patient-specific arterial fluid–structure interaction computations do not come from the zero-stress state (ZSS) of the artery, we need to estimate the ZSS required in the computations. The task becomes even more challenging for arteries with complex geometries, such as the aorta. In a method we introduced earlier the estimate is based on T-spline discretization of the arterial wall and is in the form of integration-point-based ZSS (IPBZSS). The T-spline discretization enables dealing with complex arterial geometries, such as an aorta model with branches, while retaining the desirable features of isogeometric discretization. With higher-order basis functions of the isogeometric discretization, we may be able to achieve a similar level of accuracy as with the linear basis functions, but using larger-size and fewer elements. In addition, the higher-order basis functions allow representation of more complex shapes within an element. The IPBZSS is a convenient representation of the ZSS because with isogeometric discretization, especially with T-spline discretization, specifying conditions at integration points is more straightforward than imposing conditions on control points. The method has two main components. 1. An iteration technique, which starts with a calculated ZSS initial guess, is used for computing the IPBZSS such that when a given pressure load is applied, the medical-image-based target shape is matched. 2. A design procedure, which is based on the Kirchhoff–Love shell model of the artery, is used for calculating the ZSS initial guess. Here we increase the scope and robustness of the method by introducing a new design procedure for the ZSS initial guess. The new design procedure has two features. (a) An IPB shell-like coordinate system, which increases the scope of the design to general parametrization in the computational space. (b) Analytical solution of the force equilibrium in the normal direction, based on the Kirchhoff–Love shell model, which places proper constraints on the design parameters. This increases the estimation accuracy, which in turn increases the robustness of the iterations and the convergence speed. To show how the new design procedure for the ZSS initial guess performs, we first present 3D test computations with a straight tube and a Y-shaped tube. Then we present a 3D computation where the target geometry is coming from medical image of a human aorta, and we include the branches in the model.

1 Introduction

Space–time (ST) computational methods [1, 2], with all the desirable features of moving-mesh methods, have a relatively long track record in arterial fluid–structure interaction (FSI) analysis, starting with computations reported in [3,4,5,6]. These were among the earliest arterial FSI computations, and the core method was the early version of the Deforming-Spatial-Domain/Stabilized ST (DSD/SST) method [1, 2], now called “ST-SUPS.” The acronym “SUPS” indicates the stabilization components, the Streamline-Upwind/Petrov-Galerkin (SUPG) [7] and Pressure-Stabilizing/Petrov-Galerkin (PSPG) [1].

The ST computations have been a small part of the many cardiovascular fluid mechanics and FSI computations reported in the last 15 years (see, for example, [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29] for computations with other methods), with the Arbitrary Lagrangian–Eulerian (ALE) method having the largest share. Still, many ST computations were also reported in the last 15 years. In the first 8 years of that period the ST computations were for FSI of abdominal aorta [30], carotid artery [30] and cerebral aneurysms [31,32,33,34,35,36,37]. In the last 7 years, the ST computations focused on even more challenging aspects of cardiovascular fluid mechanics and FSI, including comparative studies of cerebral aneurysms [38, 39], stent treatment of cerebral aneurysms [40,41,42,43,44], heart valve flow computation [45,46,47,48,49,50], aorta flow analysis [50,51,52,53], and coronary arterial dynamics [54]. The computational challenges encountered were addressed by the advances in the core methods for moving boundaries and interfaces (MBI) and FSI (see, for example, [20, 21, 39, 45, 46, 48, 49, 55,56,57,58,59,60,61,62,63] and references therein) and in the special methods targeting cardiovascular MBI and FSI (see, for example, [20, 37, 43, 44, 47,48,49,50, 53, 64] and references therein). For an overview of the ST MBI and FSI computations in general, see [65].

A challenge specific to patient-specific arterial FSI computations is how to use the medical-image-based arterial geometry, which does not come from the zero-stress state (ZSS) of the artery. The special methods targeting cardiovascular MBI and FSI include those intended to account for that. The task becomes even more challenging for arteries with complex geometries, such as the aorta. The attempt to find a ZSS for the artery in the FSI computation was first made in a 2007 conference paper [66], where the concept of estimated zero-pressure (EZP) arterial geometry was introduced. The method introduced in [66] for calculating an EZP geometry was also included in a 2008 journal paper on ST arterial FSI methods [31], as “a rudimentary technique” for addressing the issue. It was pointed out in [31, 66] that quite often the medical-image-based geometries were used as arterial geometries corresponding to zero blood pressure, and that it would be more realistic to use the medical-image-based geometry as the arterial geometry corresponding to the time-averaged value of the blood pressure. Given the arterial geometry at the time-averaged pressure value, an estimated arterial geometry corresponding to zero blood pressure needed to be built. The special methods developed to address the issue include the newer EZP versions [20, 33, 36, 37, 64] and the prestress technique introduced in [16], which was refined in[18] and presented also in [20, 64].

A method for estimation of the element-based ZSS (EBZSS) was introduced in [67] in the context of finite element discretization of the arterial wall. The method has three main components. 1. An iteration technique, which starts with a calculated ZSS initial guess, is used for computing the EBZSS such that when a given pressure load is applied, the medical-image-based target shape is matched. 2. A technique for straight-tube segments is used for computing the EBZSS so that we match the given diameter and longitudinal stretch in the target configuration and the “opening angle.” 3. An element-based mapping between the artery and straight-tube is extracted from the mapping between the artery and straight-tube segments. This provides the mapping from the arterial configuration to the straight-tube configuration, and from the estimated EBZSS of the straight-tube configuration back to the arterial configuration, to be used as the ZSS initial guess for the iteration technique that matches the medical-image-based target shape. Test computations with the method were also presented in [67] for straight-tube configurations with single and three layers, and for a curved-tube configuration with single layer. The method was used also in [54] in coronary arterial dynamics computations with medical-image-based time-dependent anatomical models.

The version of the EBZSS estimation method with isogeometric wall discretization, using NURBS basis functions, was introduced in [68]. With isogeometric discretization, we can obtain the element-based mapping directly, instead of extracting it from the mapping between the artery and straight-tube segments. Because all we need for the element-based mapping, including the curvatures, can be obtained within an element. With NURBS basis functions, we may be able to achieve a similar level of accuracy as with the linear basis functions, but using larger-size and fewer elements, and the NURBS basis functions enable representation of more complex shapes within an element. The 2D test computations with straight-tube configurations presented in [68] showed how the EBZSS estimation method with NURBS discretization works. In [69], which is an expanded, journal version of [68], how the method can be used in a 3D computation where the target geometry is coming from medical image of a human aorta was also shown.

In the method introduced in [70], the estimate is based on T-spline discretization of the arterial wall and is in the form of integration-point-based ZSS (IPBZSS). The T-spline discretization enables dealing with complex arterial geometries, such as an aorta model with branches, while retaining the desirable features of isogeometric discretization. The IPBZSS is a convenient representation of the ZSS because with isogeometric discretization, especially with T-spline discretization, specifying conditions at integration points is more straightforward than imposing conditions on control points. The method has two main components. 1. An iteration technique, which starts with a calculated ZSS initial guess, is used for computing the IPBZSS such that when a given pressure load is applied, the medical-image-based target shape is matched. 2. A design procedure, which is based on the Kirchhoff–Love shell model of the artery, is used for calculating the ZSS initial guess.

In this article we increase the scope and robustness of the method by introducing a new design procedure for the ZSS initial guess. The new design procedure has two features. (a) An IPB shell-like coordinate system, which increases the scope of the design to general parametrization in the computational space. (b) Analytical solution of the force equilibrium in the normal direction, based on the Kirchhoff–Love shell model, which places proper constraints on the design parameters. This increases the estimation accuracy, which in turn increases the robustness of the iterations and the convergence speed. To show how the new design procedure for the ZSS initial guess performs, we first present 3D test computations with a straight tube and a Y-shaped tube. Then we present a 3D computation where the target geometry is coming from medical image of a human aorta, and we include the branches in the model.

In Sect. 2, from [70], we describe the Element-Based Total Lagrangian (EBTL) method, including the EBZSS and IPBZSS concepts. The IPB shell-like coordinate system and the related mesh generation are described in Sect. 3. The design procedure for the ZSS initial guess, based on the Kirchhoff–Love shell model, is described in Sect. 4. The numerical examples are given in Sect. 5, and the concluding remarks in Sect. 6.

2 EBTL method

We first provide, from [70], an overview of the EBTL method [67], including the EBZSS and IPBZSS concepts and the conversion between the two ZSS.

Let ${\varOmega }_0\subset \mathbb {R}^{n_{\mathrm {sd}}}$ be the material domain of a structure in the ZSS, where ${n_{\mathrm {sd}}}$ is the number of space dimensions, and let ${\varGamma }_0$ be its boundary. Let ${\varOmega }_t\subset \mathbb {R}^{n_{\mathrm {sd}}}$, $t \in (0,T)$, be the material domain of the structure in the deformed state, and let ${\varGamma }_{t}$ be its boundary. The structural mechanics equations based on the total Lagrangian formulation can be written as

$$\begin{aligned} \quad&\int _{{\varOmega }_0} \mathbf {w}\cdot \rho _0\frac{\mathrm {d}^2 \mathbf {y}}{\mathrm {d}t^2}~\mathrm {d}{\varOmega }+ \int _{{\varOmega }_0} \delta \mathbf {E}: \mathbf {S}~\mathrm {d}{\varOmega }- \int _{{\varOmega }_0} \mathbf {w}\cdot \rho _0\mathbf {f}~\mathrm {d}{\varOmega }\nonumber \\\quad &= \int _{\left( {\varGamma }_t\right) _\mathrm {h}} \mathbf {w}\cdot \mathbf {h}~\mathrm {d}{\varGamma }. \end{aligned}$$

(1)

Here, $\mathbf {y}$ is the displacement, $\mathbf {w}$ is the virtual displacement, $\delta \mathbf {E}$ is the variation of the Green–Lagrange strain tensor, $\mathbf {S}$ is the second Piola–Kirchhoff stress tensor, $\rho _0$ is the mass density in the ZSS, $\mathbf {f}$ is the body force per unit mass, and $\mathbf {h}$ is the external stress vector applied on the subset $\left( {\varGamma }_t\right) _\mathrm {h}$ of the boundary ${\varGamma }_{t}$.

2.1 EBZSS

In the EBTL method the ZSS is defined with a set of positions $\mathbf {X}_0^e$ for each element e. Positions of nodes from different elements mapping to the same node in the mesh do not have to be the same. In the reference state, $\mathbf {X}_\mathrm {REF}\in {\varOmega }_{\mathrm {REF}}$, all elements are connected by nodes, and we measure the displacement $\mathbf {y}$ from that connected state. The implementation of the method is simple. The deformation gradient tensor $\mathbf {F}$ is evaluated for each element:

$$\begin{aligned} \mathbf {F}^e&\equiv \frac{\partial \mathbf {x}}{\partial \mathbf {X}_0^e}, \end{aligned}$$

(2)

$$\begin{aligned}&= \frac{\partial \left( \mathbf {X}_\mathrm {REF}+ \mathbf {y}\right) }{\partial \mathbf {X}_0^e}, \end{aligned}$$

(3)

where $\mathbf {x}$ is the position in the deformed configuration. The deformation gradient tensors for different elements are on different states, but the terms in Eq. (1), including the second term, do not depend on the orientation. Therefore the rest of the process is the same as it is in the total Lagrangian formulation.

2.2 IPBZSS

The key idea behind the EBZSS method was that, due to the objectivity, all the quantities seen in Eq. (1) can be computed with any orientation of the ZSS. We can extend the way we see $\mathbf {X}_0^e$ to integration-point counterpart of $\mathbf {X}_0^e$. As we did with the EBZSS, we work with the reference domain. With the reference Jacobian

$$\begin{aligned} J_\mathrm {REF}&= \det \left( \frac{\partial \mathbf {X}_\mathrm {REF}}{\partial \mathbf {X}_0}\right) , \end{aligned}$$

(4)

Eq. (1) can be rearranged as

$$\begin{aligned} \quad&\int _{{\varOmega }_{\mathrm {REF}}} \mathbf {w}\cdot \rho _0\frac{\mathrm {d}^2 \mathbf {y}}{\mathrm {d}t^2}~J_\mathrm {REF}^{-1} \mathrm {d}{\varOmega }+ \int _{{\varOmega }_{\mathrm {REF}}} \delta \mathbf {E}: \mathbf {S}~J_\mathrm {REF}^{-1} \mathrm {d}{\varOmega }\nonumber \\&\quad - \int _{{\varOmega }_{\mathrm {REF}}} \mathbf {w}\cdot \rho _0\mathbf {f}~J_\mathrm {REF}^{-1} \mathrm {d}{\varOmega }= \int _{\left( {\varGamma }_t\right) _\mathrm {h}} \mathbf {w}\cdot \mathbf {h}~\mathrm {d}{\varGamma }. \end{aligned}$$

(5)

In our implementation, we use the natural coordinates, with covariant basis vectors

$$\begin{aligned} \mathbf {g}_I&= \frac{\partial \mathbf {x}}{\partial \xi ^I}, \end{aligned}$$

(6)

$$\begin{aligned} \mathbf {G}_I&= \frac{\partial \mathbf {X}}{\partial \xi ^I}, \end{aligned}$$

(7)

where $\xi ^I$ is the parametric coordinate, and $I = 1, \ldots , {n_{\mathrm {pd}}}$, with ${n_{\mathrm {pd}}}$ being the number of parametric dimensions. The contravariant basis vectors can be calculated with the metric tensor components as

$$\begin{aligned} \mathbf {g} ^I&= g^{IJ} \mathbf {g} _J , \end{aligned}$$

(8)

$$\begin{aligned} \mathbf {G} ^I&= G^{IJ} \mathbf {G}_J , \end{aligned}$$

(9)

where

$$\begin{aligned} g_{IJ}&= \mathbf {g}_I \cdot \mathbf {g}_J, \end{aligned}$$

(10)

$$\begin{aligned} G_{IJ}&= \mathbf {G}_I \cdot \mathbf {G}_J, \end{aligned}$$

(11)

$$\begin{aligned} \left[ g^{IJ} \right]&= \left[ g_{IJ} \right] ^{-1} , \end{aligned}$$

(12)

$$\begin{aligned} \left[ G^{IJ}\right]&= \left[ G_{IJ} \right] ^{-1}. \end{aligned}$$

(13)

With those vectors, we can express the deformation gradient tensor:

$$\begin{aligned} \mathbf {F}&= \mathbf {g}_I \mathbf {G}^I, \end{aligned}$$

(14)

and the Cauchy–Green deformation tensor:

$$\begin{aligned} \mathbf {C}&= \mathbf {F}^T \cdot \mathbf {F}\end{aligned}$$

(15)

$$\begin{aligned}&= \mathbf {G}^I \mathbf {g}_I \cdot \mathbf {g}_J \mathbf {G}^J \end{aligned}$$

(16)

$$\begin{aligned}&= g_{IJ} \mathbf {G}^I \mathbf {G}^J. \end{aligned}$$

(17)

The Jacobian, $J= \det \mathbf {F}$, can be expressed as

$$\begin{aligned} J^2&= \det \mathbf {C}. \end{aligned}$$

(18)

We can write $\det \mathbf {C}$ as

$$\begin{aligned} \det \mathbf {C}&= \frac{\det \left[ g_{IJ}\right] }{\det \left[ G_{IJ}\right] }, \end{aligned}$$

(19)

and from that we obtain

$$\begin{aligned} J&= \left( \frac{\det \left[ g_{IJ}\right] }{\det \left[ G_{IJ}\right] } \right) ^{\frac{1}{2}}. \end{aligned}$$

(20)

We define the covariant basis vectors corresponding to $\mathbf {X}_\mathrm {REF}$:

$$\begin{aligned} \left( \mathbf {G}_\mathrm {REF}\right) _I&= \frac{\partial \mathbf {X}_\mathrm {REF}}{\partial \xi ^I}, \end{aligned}$$

(21)

and the components of the metric tensor are

$$\begin{aligned} \left( G_\mathrm {REF}\right) _{IJ} = \left( \mathbf {G}_\mathrm {REF}\right) _I \cdot \left( \mathbf {G}_\mathrm {REF}\right) _J. \end{aligned}$$

(22)

In Eq. (20), we replace $\mathbf {g}_I$ and $\mathbf {g}_J$ with $\left( \mathbf {G}_\mathrm {REF}\right) _I$ and $\left( \mathbf {G}_\mathrm {REF}\right) _J$ and obtain an alternative to the expression given by Eq. (4):

$$\begin{aligned} J_\mathrm {REF}&= \left( \frac{\det \left[ \left( G_\mathrm {REF}\right) _{IJ}\right] }{\det \left[ G_{IJ}\right] } \right) ^{\frac{1}{2}} . \end{aligned}$$

(23)

The Green–Lagrange strain tensor,

$$\begin{aligned} \mathbf {E}&= \frac{1}{2}\left( \mathbf {C}- \mathbf {I}\right) , \end{aligned}$$

(24)

where $\mathbf {I}$ is the identity tensor, can be expressed with the contravariant basis vectors as

$$\begin{aligned} \mathbf {E}&= \frac{1}{2}\left( g_{IJ} - G_{IJ} \right) \mathbf {G}^I \mathbf {G}^J. \end{aligned}$$

(25)

The second Piola–Kirchhoff tensor can be expressed with the covariant basis vectors as

$$\begin{aligned} \mathbf {S}&= S^{IJ} \mathbf {G}_I \mathbf {G}_J, \end{aligned}$$

(26)

where $S^{IJ}$ can be expressed with the components of the metric tensors. Thus, the inner product $\delta \mathbf {E}: \mathbf {S}$, and all the other quantities, in the weak form given by Eq. (5) can be evaluated without actually using the basis vectors $\mathbf {G}_I$. This justifies using $\left( G_{IJ}\right) _k$ as the integration-point counterpart of $\mathbf {X}_0^e$, with $k=1, \ldots , n_\mathrm {int}$, where $n_\mathrm {int}$ is the number of integration points. Note that $G_{IJ}$ is symmetric, and therefore the IPBZSS representation will in 3D have $6{\times }n_\mathrm {int}$ parameters for each element.

2.3 EBZSS to IPBZSS

Converting the EBZSS representation to IPBZSS representation is straightforward. From given $\mathbf {X}_0^e$ we can calculate the covariant basis vectors at each integration point $\pmb {\xi }_k$:

$$\begin{aligned} \left( \mathbf {G}_I\right) _k&= \left. \frac{\partial \mathbf {X}_0^e}{\partial \xi ^I}\right| _{\pmb {\xi }=\pmb {\xi }_k}, \end{aligned}$$

(27)

and obtain the components of the metric tensor from Eq. (11).

2.4 IPBZSS to EBZSS

Converting the IPBZSS representation to EBZSS representation, which we might need for visualization purposes, will, in general, not be exact because the IPBZSS has more parameters than the EBZSS. Given $\left( G_{IJ}\right) _k$, we solve a steady-state element-based problem (with $\mathbf {f}=\mathbf {0}$ and $\mathbf {h}= \mathbf {0}$):

$$\begin{aligned} \int _{{\varOmega }^e_{\mathrm {REF}}} \delta \mathbf {E}: \mathbf {S}~J_\mathrm {REF}^{-1} \mathrm {d}{\varOmega }= 0, \end{aligned}$$

(28)

and the solution to that, in the form $\mathbf {X}_\mathrm {REF} + \mathbf {y}$, will be the EBZSS representation. If the stress calculated from the solution is zero, then the conversion will be exact. We note that to obtain a steady-state solution, we need to preclude translation and rigid-body rotation by imposing 6 appropriate constraints. To do that we first select three control points: A, B and C. We set all three components of $\mathbf {y}_A$ to be zero and constrain $\mathbf {y}_B$ to be in the direction $(\mathbf {X}_\mathrm {REF})_B - (\mathbf {X}_\mathrm {REF})_A$. The last constraint is $\mathbf {y}_C$ to be on the plane defined by the vector $\left( (\mathbf {X}_\mathrm {REF})_B - (\mathbf {X}_\mathrm {REF})_A\right) \times \left( (\mathbf {X}_\mathrm {REF})_C - (\mathbf {X}_\mathrm {REF})_A\right)$.

3 Coordinate systems for the artery inner surface and wall

A geometrical relationship between the ZS and reference states, for a straight tube, was described in [70]. It was based on the shell model, where it is assumed that the inner-surface elements are extruded in the normal direction. Here we increase the scope of the method to general parametrization in the computational space. For each integration point of the computational space, we use a special shell-like coordinate system specific to that integration point. We will explain that coordinate system later in this section, after first explaining how the mesh is generated.

In our notation here, $\mathbf {x}$ will now imply $\mathbf {X}_\mathrm {REF}$, which is our “target” shape, and $\mathbf {X}$ will imply $\mathbf {X}_0$. We explain the method in the context of one element across the wall. Extending the method to multiple elements is straightforward.

3.1 Mesh generation

We again start with the artery inner surface, and build the wall in some fashion. Here we first build a T-spline inner-surface mesh. Then we expand that by an estimated thickness to obtain the outer-surface mesh. After that we modify the outer-surface mesh manually by moving the control points. When the thickness is larger than the radius of curvature, parts of the outer surface overlap. This might happen near the branches. Therefore, a simple extrusion does not work. Since the outer surface cannot be obtained from medical images, the design of the outer surface has to be based on other anatomical knowledge. This is the reason why currently meshes are generated manually rather than by an automated process. After defining the outer-surface mesh, which will have a control point corresponding to every control point on the inner surface, we add two control points for each pair. We use the four control points to form a cubic Bézier element across the wall. This is the way we obtain a T-spline volume mesh.

3.2 Inner-surface coordinates in the target state

The natural coordinates is used for the surface representation as explained in [70]. With the notation $\overline{\bullet }$ indicating the inner surface, the basis vectors are

$$\begin{aligned} \overline{\mathbf {g}}_\alpha&= \frac{\partial \overline{\mathbf {x}}}{\partial \xi ^{\alpha }}, \end{aligned}$$

(29)

where $\alpha = 1, 2$. We define the unit normal vector as

$$\begin{aligned} \mathbf {n}&= \frac{ \overline{\mathbf {g}}_1 \times \overline{\mathbf {g}}_2 }{ \left\| \overline{\mathbf {g}}_1 \times \overline{\mathbf {g}}_2 \right\| } \end{aligned}$$

(30)

and the second fundamental form as

$$\begin{aligned} \overline{b}_{\alpha \beta }&= \frac{\partial \overline{\mathbf {g}}_\alpha }{\partial \xi ^{\beta }} \cdot \mathbf {n}, \end{aligned}$$

(31)

and the curvature tensor is

$$\begin{aligned} \hat{\pmb {\kappa }}&= \underbrace{- \overline{b}_{\alpha \beta } }_{\hat{\kappa }_{\alpha \beta }} \overline{\mathbf {g}}^{\alpha } \overline{\mathbf {g}}^{\beta }. \end{aligned}$$

(32)

We also define two orthonormal vectors $\mathbf {t}_1$ and $\mathbf {t}_2$, which are the principal directions of the curvature tensor:

$$\begin{aligned} \hat{\pmb {\kappa }}&= \hat{\kappa }_1 \mathbf {t}_1 \mathbf {t}_1 + \hat{\kappa }_2 \mathbf {t}_2 \mathbf {t}_2 , \end{aligned}$$

(33)

where $\hat{\kappa }_1$ and $\hat{\kappa }_2$ are the corresponding eigenvalues, and $\hat{\kappa }_1 \ge \hat{\kappa }_2$. The derivation and more details are in [70].

3.3 Inner-surface coordinates in the ZSS

Since the principal-curvature directions $\mathbf {t}_1$ and $\mathbf {t}_2$ of the target shape are orthogonal to each other, we can build the ZSS shape using those directions. The basis vectors on the inner surface in the ZSS are

$$\begin{aligned} \overline{\mathbf {G}}_\alpha&= \frac{\partial \overline{\mathbf {X}}}{\partial \xi ^{\alpha }}, \end{aligned}$$

(34)

and the unit normal vector in the thickness direction is

$$\begin{aligned} \mathbf {N}&= \frac{ \overline{\mathbf {G}}_1 \times \overline{\mathbf {G}}_2 }{ \left\| \overline{\mathbf {G}}_1 \times \overline{\mathbf {G}}_2 \right\| } . \end{aligned}$$

(35)

We assume that the two directions $\mathbf {t}_1$ and $\mathbf {t}_2$ are also the principal-stretch directions. Then the ZSS basis vectors are calculated from

$$\begin{aligned} \hat{\lambda }_1 \mathbf {t}_1&= \mathbf {F} \cdot \mathbf {t}_1, \end{aligned}$$

(36)

$$\begin{aligned} \hat{\lambda }_2 \mathbf {t}_2&= \mathbf {F} \cdot \mathbf {t}_2, \end{aligned}$$

(37)

where $\hat{\lambda }_1$ and $\hat{\lambda }_2$ are the principal stretches. Based on that we obtain the ZSS covariant basis vectors as

$$\begin{aligned} \begin{bmatrix} \overline{\mathbf {G}}_1 \\ \overline{\mathbf {G}}_2 \\ \end{bmatrix}&= \begin{bmatrix} \left( {t}_1\right) ^1&\left( {t}_1\right) ^2 \\ \left( {t}_2\right) ^1&\left( {t}_2\right) ^2 \\ \end{bmatrix}^{-1} \begin{bmatrix} \frac{1}{\hat{\lambda }_1}&0 \\ 0&\frac{1}{\hat{\lambda }_2} \\ \end{bmatrix} \begin{bmatrix} \left( {t}_1\right) ^1&\left( {t}_1\right) ^2 \\ \left( {t}_2\right) ^1&\left( {t}_2\right) ^2 \\ \end{bmatrix} \begin{bmatrix} \overline{\mathbf {g}}_1 \\ \overline{\mathbf {g}}_2 \\ \end{bmatrix} , \end{aligned}$$

(38)

where $\left( t_{\alpha }\right) ^\beta = \mathbf {t}_\alpha \cdot \mathbf {g}^\beta$. The derivation and more details are in [70].

3.4 Wall coordinates in the target state

In a target volume element, we again use the natural coordinate system. The position in the target state is $\mathbf {x}(\pmb {\xi })$, and the total differential of the position is

$$\begin{aligned} \mathrm {d}\mathbf {x}&= \mathbf {g}_I \mathrm {d}\xi ^I. \end{aligned}$$

(39)

Here we introduce a coordinate $\vartheta$ in the “normal” direction:

$$\begin{aligned} \mathrm {d}\vartheta&= \hat{\mathbf {n}} \cdot \mathbf {g}_I \mathrm {d}\xi ^I, \end{aligned}$$

(40)

where $\hat{\mathbf {n}}$ is the unit normal vector inside the wall. As we perform the integration $\int \mathrm {d}\vartheta$, the difference between the values we find as we reach the inner and outer surfaces will be our formal definition of the thickness $h_\mathrm {th}$. There are two options for defining $\hat{\mathbf {n}}$.

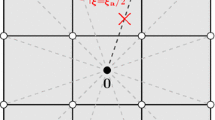
The first option is that we find the closest point $\overline{\mathbf {x}}^\bot$ on the inner surface from a given position $\mathbf {x}$:

$$\begin{aligned} \hat{\mathbf {n}}(\pmb {\xi })&= \frac{\mathbf {x}(\pmb {\xi }) - \overline{\mathbf {x}}^\bot }{\left\| \mathbf {x}(\pmb {\xi }) - \overline{\mathbf {x}}^\bot \right\| }, \end{aligned}$$

(41)

assuming a reasonable geometry for the purpose of calculating $\hat{\mathbf {n}}$. For $\Vert \mathbf {x}(\pmb {\xi })-\overline{\mathbf {x}}^\bot \Vert =0$, we get Eq. (30). Figure 1 shows the normal definition.

Fig. 1

The coordinate system with the normal based on the closest point

The second option is

$$\begin{aligned} \hat{\mathbf {n}}(\pmb {\xi })&= \frac{\mathbf {g}_1 \times \mathbf {g}_2}{\left\| \mathbf {g}_1 \times \mathbf {g}_2\right\| }, \end{aligned}$$

(42)

which naturally gives Eq. (30) at the surface. Figure 2 shows the normal definition. The other two components of the new coordinate system is represented by the vector $\hat{\pmb {\xi }} \in \mathbb {R}^{{n_{\mathrm {sd}}}-1}$, and the corresponding basis vectors are $\hat{\mathbf {g}}_\alpha$:

$$\begin{aligned} \hat{\mathbf {g}}_\alpha \left( \hat{\pmb {\xi }}(\pmb {\xi }), \vartheta (\pmb {\xi })\right)&= \left( \mathbf {I}- \hat{\mathbf {n}}(\pmb {\xi }) \hat{\mathbf {n}}(\pmb {\xi }) \right) \cdot \mathbf {g}_\alpha (\pmb {\xi }). \end{aligned}$$

(43)

For the normal-vector definition of Eq. (42), it simplifies to

$$\begin{aligned} \hat{\mathbf {g}}_\alpha \left( \hat{\pmb {\xi }}(\pmb {\xi }), \vartheta (\pmb {\xi })\right)&= \mathbf {g}_\alpha (\pmb {\xi }). \end{aligned}$$

(44)

Fig. 2

The coordinate system with the normal based on the two axis of the natural coordinates, $\mathbf {g}_1$ and $\mathbf {g}_2$

Remark 1

We note that even if $\hat{\mathbf {g}}_\alpha = \mathbf {g}_\alpha$, $\hat{\mathbf {g}}^\gamma$ and $\mathbf {g}^\gamma$ are not the same in general, because $\mathbf {g}_3$ is not perpendicular to $\mathbf {g}_1$ and $\mathbf {g}_2$ and $\mathbf {g}^\gamma$ will have an out-of-plane component.

The total differential of the position is expressed as

$$\begin{aligned} \mathrm {d}\mathbf {x}&= \hat{\mathbf {g}}_\alpha \mathrm {d}\hat{\xi }^\alpha + \hat{\mathbf {n}} \mathrm {d}\vartheta . \end{aligned}$$

(45)

Remark 2

The first normal-vector option is closer to the shell theory. The downside is that we may not always have a reasonable geometry, for example when the radius of curvature is low compared to the thickness. The second option does not suffer from that problem and gives us the possibility of coming up with an $\hat{\mathbf {n}}$ design that would make the method better. However its quality depends on the mesh, such as the smoothness of the constant-$\xi ^3$ surfaces.

At the $k\hbox {th}$ integration point we define a shell-like coordinate system:

$$\begin{aligned} \mathbf {x}(\pmb {\xi })&= \hat{\mathbf {x}}(\hat{\pmb {\xi }}(\pmb {\xi })) + \hat{\mathbf {n}}(\pmb {\xi }) \left( \vartheta - \vartheta _k\right) , \end{aligned}$$

(46)

where $\vartheta _k$ is an offset defined in such a way that ${\mathbf {x}}(\pmb {\xi }(\hat{\pmb {\xi }}, 0))$ is $\overline{\mathbf {x}}$ on the surface. To find the value, we use the following expression:

$$\begin{aligned} \vartheta _k&= \left\| \mathbf {x}(\pmb {\xi }_k) - \overline{\mathbf {x}}^\bot \right\| . \end{aligned}$$

(47)

Remark 3

In generating the ZSS, for each integration point, we calculate $h_\mathrm {th}$ as

$$\begin{aligned} h_\mathrm {th}&= \left\| \mathbf {x}^{\top } - \mathbf {x} \right\| +\left\| \mathbf {x} - \overline{\mathbf {x}}^{\bot } \right\| , \end{aligned}$$

(48)

where $\mathbf {x}^{\top }$ is the closest point on the outer surface.

By differentiating $\mathbf {x}$ from Eq. (46) with respect to $\hat{\xi }^\alpha$, we obtain the covariant basis vectors in the thickness direction:

$$\begin{aligned} \hat{\mathbf {g}}_\alpha (\hat{\pmb {\xi }}, \vartheta )&= \left. \hat{\mathbf {g}}_\alpha \right| _{\vartheta _k} + \left. \frac{\partial \hat{\mathbf {n}} }{\partial \hat{\xi }^\alpha } \right| _{\pmb {\xi }(\hat{\pmb {\xi }}, \vartheta _k)} \left( \vartheta - \vartheta _k\right) \end{aligned}$$

(49)

$$\begin{aligned}&= \left. \hat{\mathbf {g}}_\alpha \right| _{\vartheta _k} - \left. \left( \hat{b}_{\alpha \gamma } \hat{\mathbf {g}}^\gamma \right) \right| _{\vartheta _k} \left( \vartheta - \vartheta _k\right) . \end{aligned}$$

(50)

Here $\hat{b}_{\alpha \gamma }$ is the second fundamental form:

$$\begin{aligned} \hat{b}_{\alpha \gamma } (\hat{\pmb {\xi }}, \vartheta )&= \frac{\partial \hat{\mathbf {g}}_\alpha (\hat{\pmb {\xi }}, \vartheta )}{\partial \hat{\xi }^\gamma } \cdot \hat{\mathbf {n}}(\pmb {\xi }(\hat{\pmb {\xi }}, \vartheta )), \end{aligned}$$

(51)

which can be calculated by using the natural coordinates:

$$\begin{aligned} \hat{b}_{\alpha \gamma }&= \frac{\partial \mathbf {g}_I}{\partial \xi ^J} \frac{\partial \xi ^I}{\partial \hat{\xi }^\alpha } \frac{\partial \xi ^J}{\partial \hat{\xi }^\gamma } \cdot \hat{\mathbf {n}}. \end{aligned}$$

(52)

How to obtain this expression is described in Appendix A. To obtain $\frac{\partial \xi ^I}{\partial \hat{\xi }^\alpha }$, we inner-product the right-hand sides of Eqs. (39) and (45) with $\mathbf {g}^J$ and equate the two:

$$\begin{aligned} \mathrm {d}\xi ^J&= \underbrace{ \mathbf {g}^J \cdot \hat{\mathbf {g}}_\alpha }_{=\frac{\partial \xi ^J}{\partial \hat{\xi }^\alpha }} \mathrm {d}\hat{\xi }^\alpha + \mathbf {g}^J \cdot \hat{\mathbf {n}} \mathrm {d}\vartheta . \end{aligned}$$

(53)

Therefore

$$\begin{aligned} \frac{\partial \xi ^I}{\partial \hat{\xi }^\alpha }&= \mathbf {g}^I \cdot \hat{\mathbf {g}}_\alpha . \end{aligned}$$

(54)

For the normal-vector definition of Eq. (42), the expression given by Eq. (52) simplifies to

$$\begin{aligned} \hat{b}_{\alpha \gamma }&= \frac{\partial \mathbf {g}_\alpha }{\partial \xi ^\gamma } \cdot \hat{\mathbf {n}}. \end{aligned}$$

(55)

From Eqs. (50) and (51), we obtain:

$$\begin{aligned} \hat{b}_{\alpha \beta }\left( \hat{\pmb {\xi }}, \vartheta \right)&= \left. \hat{b}_{\alpha \beta } \right| _{\vartheta _k} - \left. \frac{\partial \hat{b}_{\alpha \gamma } }{\partial \hat{\xi }^\beta } \right| _{\vartheta _k} \underbrace{ \left. \hat{\mathbf {g}}^\gamma \right| _{\vartheta _k} \cdot \hat{\mathbf {n}} }_{=0} \left( \vartheta - \vartheta _k\right) \nonumber \\&\quad - \left. \hat{b}_{\alpha \gamma } \right| _{\vartheta _k} \left. \frac{\partial \hat{\mathbf {g}}^\gamma }{\partial \hat{\xi }^\beta } \right| _{\vartheta _k} \cdot \hat{\mathbf {n}} \left( \vartheta - \vartheta _k\right) \end{aligned}$$

(56)

$$\begin{aligned}&= \left. \hat{b}_{\alpha \beta } \right| _{\vartheta _k} - \left. \left( \hat{b}_{\alpha \gamma } \hat{g}^{\gamma \delta } \right) \right| _{\vartheta _k} \underbrace{ \left. \frac{\partial \hat{\mathbf {g}}_\delta }{\partial \hat{\xi }^\beta } \right| _{\vartheta _k} \cdot \hat{\mathbf {n}} }_{ \left. \hat{b}_{\delta \beta } \right| _{\vartheta _k} } \left( \vartheta - \vartheta _k\right) \end{aligned}$$

(57)

$$\begin{aligned}&= \left. \hat{b}_{\alpha \beta } \right| _{\vartheta _k} - \left. \left( \hat{b}_{\alpha \gamma } \hat{g}^{\gamma \delta } \hat{b}_{\delta \beta } \right) \right| _{\vartheta _k} \left( \vartheta - \vartheta _k\right) . \end{aligned}$$

(58)

The derivative of the contravariant basis vector needed in Eq. (56) is derived in Appendix B.

3.5 Wall coordinates in the ZSS

Once we define the shell-like coordinate system for kth integration point, we can use the corresponding ZSS coordinate system as described in [70]. From that we compute the components of the metric tensor corresponding to the natural coordinates.

Here we redescribe the method by using the notation from the earlier parts of Sect. 3. The position in the ZSS configuration is

$$\begin{aligned} \mathbf {X}(\pmb {\xi }(\hat{\pmb {\xi }}, \vartheta ))&= \overline{\mathbf {X}}(\hat{\pmb {\xi }}) + \hat{\mathbf {N}}(\hat{\pmb {\xi }}) \vartheta _0(\vartheta ), \end{aligned}$$

(59)

where $0 \le \vartheta _0 \le \left( h_\mathrm {th}\right) _0$, and $\left( h_\mathrm {th}\right) _0$ is the wall thickness in the ZSS configuration. This thickness will be expressed as $(h_\mathrm {th})_0(\hat{\pmb {\xi }})$. The position $\overline{\mathbf {X}}$ on the inner surface is an arbitrary position, and $\hat{\mathbf {N}}=\mathbf {N}$ as given in Eq. (35):

$$\begin{aligned} \hat{\mathbf {N}} = \mathbf {N} = \frac{ \overline{\mathbf {G}}_1 \times \overline{\mathbf {G}}_2 }{ \left\| \overline{\mathbf {G}}_1 \times \overline{\mathbf {G}}_2 \right\| } . \end{aligned}$$

(60)

The covariant basis vectors are

$$\begin{aligned} \hat{\mathbf {G}}_\alpha (\hat{\pmb {\xi }}, \vartheta )&= \frac{\partial \mathbf {X}}{\partial \hat{\xi }^\alpha } \end{aligned}$$

(61)

$$\begin{aligned}&= \overline{\mathbf {G}}_\alpha + \frac{\partial \hat{\mathbf {N}}}{\partial \hat{\xi }^\alpha } \vartheta _0(\vartheta ) \end{aligned}$$

(62)

$$\begin{aligned}&= \overline{\mathbf {G}}_\alpha - \hat{B}_{\alpha \gamma } \overline{\mathbf {G}}^\gamma \vartheta _0(\vartheta ), \end{aligned}$$

(63)

where $\overline{\mathbf {G}}_\alpha$ is obtained from Eq. (38) with

$$\begin{aligned} \overline{\mathbf {g}}_\alpha&= \left. \hat{\mathbf {g}}_\alpha \right| _{\vartheta _k} + \left. \left( \hat{b}_{\alpha \gamma } \hat{\mathbf {g}}^\gamma \right) \right| _{\vartheta _k} \vartheta _k , \end{aligned}$$

(64)

which is from Eq. (50) at $\vartheta =0$. The curvature tensor in the ZSS configuration is

$$\begin{aligned} \hat{\pmb {\kappa }}_0&= \left( \hat{\kappa }_0\right) _1 \mathbf {t}_1 \mathbf {t}_1 + \left( \hat{\kappa }_0\right) _2 \mathbf {t}_2 \mathbf {t}_2 , \end{aligned}$$

(65)

and the second fundamental form $\hat{B}_{\alpha \beta }$ can be obtained from that as

$$\begin{aligned} \hat{B}_{\alpha \beta }&= - \hat{\pmb {\kappa }}_0 : \overline{\mathbf {G}}_\alpha \overline{\mathbf {G}}_\beta \end{aligned}$$

(66)

$$\begin{aligned}&= - \left( \hat{\kappa }_0\right) _1 \left( \mathbf {t}_1 \cdot \overline{\mathbf {G}}_\alpha \right) \left( \mathbf {t}_1 \cdot \overline{\mathbf {G}}_\beta \right) - \left( \hat{\kappa }_0\right) _2 \left( \mathbf {t}_2 \cdot \overline{\mathbf {G}}_\alpha \right) \left( \mathbf {t}_2 \cdot \overline{\mathbf {G}}_\beta \right) . \end{aligned}$$

(67)

Typically, the curvature in the ZSS is a function of the curvature at the inner surface. The inner-surface curvature tensor can be calculated as

$$\begin{aligned} \left. \hat{\pmb {\kappa }}\right| _{\vartheta =0}&= - \left( \left. \hat{b}_{\alpha \beta } \right| _{\vartheta _k} + \left. \left( \hat{b}_{\alpha \gamma } \hat{g}^{\gamma \delta } \hat{b}_{\delta \beta } \right) \right| _{\vartheta _k} \vartheta _k \right) \overline{\mathbf {g}}^\alpha \overline{\mathbf {g}}^\beta , \end{aligned}$$

(68)

where the basis vectors are obtained from the covariant basis vectors given by Eq. (64).

The relationship $\vartheta _0(\vartheta )$ is given by

$$\begin{aligned} \frac{\mathrm {d}\vartheta _0}{\mathrm {d}\vartheta }&= \frac{1}{\lambda _3}. \end{aligned}$$

(69)

The stretch $\lambda _3$ can be obtained by the in-plane deformation and the constitutive law.

With all from the earlier parts of Sect. 3, we obtain $\mathbf {F}^{-1}$ at $\pmb {\xi }_k$:

$$\begin{aligned} \mathbf {F}^{-1}&= \hat{\mathbf {G}}_{\alpha } \hat{\mathbf {g}}^\alpha + \frac{1}{\lambda _3} \hat{\mathbf {N}} \hat{\mathbf {n}}. \end{aligned}$$

(70)

With

$$\begin{aligned} \mathbf {F}^{-1} = \mathbf {G}_I \mathbf {g}^I \end{aligned}$$

(71)

and

$$\begin{aligned} \mathbf {F}^{-T} \cdot \mathbf {F}^{-1} = G_{IJ} \mathbf {g}^I \mathbf {g}^J, \end{aligned}$$

(72)

we extract $G_{IJ}$ from

$$\begin{aligned} G_{IJ}&= \left( \mathbf {F}^{-T} \cdot \mathbf {F}^{-1}\right) : \mathbf {g}_I \mathbf {g}_J, \end{aligned}$$

(73)

while obtaining $\mathbf {F}^{-T}\cdot \mathbf {F}^{-1}$ from Eq. (70):

$$\begin{aligned} \mathbf {F}^{-T} \cdot \mathbf {F}^{-1}&= \hat{G}_{\alpha \beta } \hat{\mathbf {g}}^\alpha \hat{\mathbf {g}}^\beta + \lambda _3^{-2} \hat{\mathbf {n}} \hat{\mathbf {n}} . \end{aligned}$$

(74)

More explicitly, we can write

$$\begin{aligned} G_{IJ}&= \left( \hat{G}_{\alpha \beta } \hat{\mathbf {g}}^\alpha \hat{\mathbf {g}}^\beta + \lambda _3^{-2} \hat{\mathbf {n}} \hat{\mathbf {n}} \right) : \mathbf {g}_I \mathbf {g}_J . \end{aligned}$$

(75)

4 Analytical expression and design for the ZSS initial guess

As explained in [70], the design parameters are the principal curvatures $\left( \hat{\kappa }_0\right) _1$ and $\left( \hat{\kappa }_0\right) _2$, and the stretches $\hat{\lambda }_1$ and $\hat{\lambda }_2$ for each principal-curvature direction. However, they are not a set of independent values because there are constraints for the ZSS to give us the target shape for the given load, and we try to get close to that even for the initial guess. To that end, we use the force equilibrium in the normal direction by using a local analytical solution for each integration point. After that, we describe the design for the ZSS initial guess.

4.1 Analytical solution based on the Kirchhoff–Love shell model

We use the Kirchhoff–Love shell model with plane-stress condition to obtain the analytical solution. That is the generalized version of the solutions given in [71] for pressurized sphere and cylinder.

To deal with an arbitrary geometry, we assume the shape is given in terms of the principal curvatures. That is the reason we use only the equilibrium equation in the normal direction and focus on a small surface area $\delta \overline{{\varGamma }}$. From that surface area, we extrude in the normal direction by $h_\mathrm {th}$ to define a volume: $\delta {\varOmega }= \int _{0}^{h_\mathrm {th}} \delta {\varGamma }(\vartheta ) \mathrm {d}\vartheta$.

The force equilibrium in the normal direction is

$$\begin{aligned} -\mathbf {n}\cdot \int _{0}^{h_\mathrm {th}} \int _{\delta {\varGamma }(\vartheta )} \pmb {\nabla }\cdot \pmb {\sigma }\mathrm {d}{\varGamma }\mathrm {d}\vartheta&= p \delta \overline{{\varGamma }} , \end{aligned}$$

(76)

where $\pmb {\sigma }$ and p are the Cauchy stress tensor and pressure load. Now we express this by using the shell-coordinate system. Using the plane-stress condition, we can write

$$\begin{aligned} \pmb {\sigma }&= \hat{\sigma }^{\alpha \beta } \hat{\mathbf {g}}_\alpha \hat{\mathbf {g}}_\beta , \end{aligned}$$

(77)

and the divergence of it is

$$\begin{aligned} \pmb {\nabla }\cdot \pmb {\sigma }&= \frac{\partial \pmb {\sigma }}{\partial \hat{\xi }^\gamma } \cdot \hat{\mathbf {g}}^\gamma \end{aligned}$$

(78)

$$\begin{aligned}&=\frac{\partial \left( \hat{\sigma }^{\alpha \beta } \hat{\mathbf {g}}_\alpha \hat{\mathbf {g}}_\beta \right) }{\partial \hat{\xi }^\gamma } \cdot \hat{\mathbf {g}}^\gamma \end{aligned}$$

(79)

$$\begin{aligned}&= \frac{\partial \hat{\sigma }^{\alpha \gamma }}{\partial \hat{\xi }^\gamma } \hat{\mathbf {g}}_\alpha + \hat{\sigma }^{\alpha \gamma } \frac{\partial \hat{\mathbf {g}}_\alpha }{\partial \hat{\xi }^\gamma } + \hat{\sigma }^{\alpha \beta } \hat{\mathbf {g}}_\alpha \frac{\partial \hat{\mathbf {g}}_\beta }{\partial \hat{\xi }^\gamma } \cdot \hat{\mathbf {g}}^\gamma . \end{aligned}$$

(80)

Because $\delta {\varGamma }\rightarrow 0$, $\mathbf {n}\cdot \hat{\mathbf {g}}_\alpha \rightarrow 0$. Thus, what is left in the normal direction is

$$\begin{aligned} \mathbf {n}\cdot \left( \pmb {\nabla }\cdot \pmb {\sigma }\right)&= \hat{\sigma }^{\alpha \gamma } \mathbf {n}\cdot \frac{\partial \mathbf {g}_\alpha }{\partial \xi ^\gamma } \end{aligned}$$

(81)

$$\begin{aligned}&= \hat{\sigma }^{\alpha \gamma } \hat{b}_{\alpha \gamma }. \end{aligned}$$

(82)

The small area can be expressed as

$$\begin{aligned} \delta {\varGamma }(\vartheta )&= \hat{A}(\vartheta ) \delta \hat{\xi }^1 \delta \hat{\xi }^2, \end{aligned}$$

(83)

where

$$\begin{aligned} \hat{A}(\vartheta )&= \left\| \hat{\mathbf {g}}_1\times \hat{\mathbf {g}}_2 \right\| . \end{aligned}$$

(84)

At the inner surface, we write

$$\begin{aligned} \overline{A}&= \left\| \overline{\mathbf {g}}_1\times \overline{\mathbf {g}}_2 \right\| . \end{aligned}$$

(85)

With all above, Eq. (76) becomes

$$\begin{aligned} - \int _{0}^{h_\mathrm {th}} \hat{\sigma }^{\alpha \gamma } \hat{b}_{\alpha \gamma } \hat{A} \delta \hat{\xi }^1 \delta \hat{\xi }^2 \mathrm {d}\vartheta&= p \overline{A} \delta \hat{\xi }^1 \delta \hat{\xi }^2 . \end{aligned}$$

(86)

Thus, we obtain the relationship

$$\begin{aligned} p&= - \frac{1}{\overline{A}} \int _{0}^{h_\mathrm {th}} \hat{\sigma }^{\alpha \gamma } \hat{b}_{\alpha \gamma } \hat{A} \mathrm {d}\vartheta , \end{aligned}$$

(87)

where

$$\begin{aligned} \hat{b}_{\alpha \beta }&= \overline{b}_{\alpha \beta } - \overline{b}_{\alpha \gamma } \overline{g}^{\gamma \delta } \overline{b}_{\delta \beta } \vartheta , \end{aligned}$$

(88)

which can be obtained from Eq. (58) with $\vartheta _k=0$. To express the stress components, we need the basis vectors for all $\vartheta$, which are

$$\begin{aligned} \hat{\mathbf {g}}_\alpha&= \overline{\mathbf {g}}_\alpha - \overline{b}_{\alpha \gamma } \overline{\mathbf {g}}^\gamma \vartheta . \end{aligned}$$

(89)

The expression comes from Eq. (50) with $\vartheta _k=0$.

Now we use the orthonormal vectors corresponding to the principal curvatures to be the covariant basis vectors at the inner surface: $\overline{\mathbf {g}}_\alpha = \mathbf {t}_\alpha$, and the second fundamental form becomes diagonal: $b_{\alpha \alpha } = -\hat{\kappa }_\alpha$ (no sum). Thus, Eqs. (88) and (89) become

$$\begin{aligned} \hat{b}_{\alpha \alpha }&= - \hat{\kappa }_\alpha \left( 1 + \hat{\kappa }_\alpha \vartheta \right)&\text {(no sum)}, \end{aligned}$$

(90)

$$\begin{aligned} \hat{\mathbf {g}}_\alpha&= \left( 1 + \hat{\kappa }_\alpha \vartheta \right) \mathbf {t}_\alpha&\text {(no sum)}. \end{aligned}$$

(91)

From that, we also obtain $\overline{A}=1$,

$$\begin{aligned} \hat{A}&= \left( 1 + \hat{\kappa }_1 \vartheta \right) \left( 1 + \hat{\kappa }_2 \vartheta \right) , \end{aligned}$$

(92)

and

$$\begin{aligned} \hat{\mathbf {g}}^\alpha&= \frac{1}{1 + \hat{\kappa }_\alpha \vartheta } \mathbf {t}_\alpha&\text {(no sum)}. \end{aligned}$$

(93)

Here we introduce the components of the Cauchy stress tensor based on the orthonormal vectors:

$$\begin{aligned} \pmb {\sigma }&= \tilde{\sigma }_{\gamma \delta } \mathbf {t}_\gamma \mathbf {t}_\delta , \end{aligned}$$

(94)

and obtain

$$\begin{aligned} \hat{\sigma }^{\alpha \beta }&= \tilde{\sigma }_{\gamma \delta } \mathbf {t}_\gamma \mathbf {t}_\delta : \hat{\mathbf {g}}^\alpha \hat{\mathbf {g}}^\beta . \end{aligned}$$

(95)

That can be simplified as

$$\begin{aligned} \hat{\sigma }^{\alpha \beta }= \frac{ \tilde{\sigma }_{\alpha \beta } }{ \left( 1 + \hat{\kappa }_\alpha \vartheta \right) \left( 1 + \hat{\kappa }_\beta \vartheta \right) }\text {(no sum)} . \end{aligned}$$

(96)

Thus, Eq. (87) becomes

$$\begin{aligned} p= \int _{0}^{h_\mathrm {th}} \left( \tilde{\sigma }_{11} \hat{\kappa }_1 \left( 1+\hat{\kappa }_2\vartheta \right) + \tilde{\sigma }_{22} \hat{\kappa }_2 \left( 1+\hat{\kappa }_1\vartheta \right) \right) \mathrm {d}\vartheta \end{aligned}$$

(97)

$$\begin{aligned}&= \hat{\kappa }_1 \int _{0}^{h_\mathrm {th}} \tilde{\sigma }_{11} \mathrm {d}\vartheta + \hat{\kappa }_2 \int _{0}^{h_\mathrm {th}} \tilde{\sigma }_{22} \mathrm {d}\vartheta \nonumber \\&\quad + \hat{\kappa }_1 \hat{\kappa }_2 \int _{0}^{h_\mathrm {th}} \left( \tilde{\sigma }_{11} + \tilde{\sigma }_{22} \right) \vartheta \mathrm {d}\vartheta . \end{aligned}$$

(98)

To calculate $\tilde{\sigma }_{\alpha \beta }$, we need the ZSS. For that, we substitute $\overline{\mathbf {g}}_\alpha = \mathbf {t}_\alpha$ into Eq. (38) and obtain the covariant basis vectors of the ZSS:

$$\begin{aligned} \overline{\mathbf {G}}_\alpha&= \frac{1}{\hat{\lambda }_\alpha } \mathbf {t}_\alpha&\text {(no sum)}, \end{aligned}$$

(99)

and from $\vartheta _0(\vartheta )$, yet to be calculated, we obtain the covariant basis vectors:

$$\begin{aligned} \hat{\mathbf {G}}_\alpha&= \frac{1}{\hat{\lambda }_\alpha } \left( 1 + (\hat{\kappa }_0)_\alpha \vartheta _0(\vartheta ) \right) \mathbf {t}_\alpha&(\text {no sum}). \end{aligned}$$

(100)

From that, we obtain the contravariant basis vectors:

$$\begin{aligned} \hat{\mathbf {G}}^\alpha&= \frac{\hat{\lambda }_\alpha }{ 1 + (\hat{\kappa }_0)_\alpha \vartheta _0 (\vartheta ) } \mathbf {t}_\alpha&(\text {no sum)}. \end{aligned}$$

(101)

Because we assume that the principal stretches are also in the principal-curvature directions, we obtain the principal stretch in $\alpha$ direction as

$$\begin{aligned} \left( \lambda _\alpha \right) ^2&= \mathbf {F}^T \cdot \mathbf {F} : \mathbf {t}_\alpha \mathbf {t}_\alpha&\text {(no sum)} \end{aligned}$$

(102)

$$\begin{aligned}&= \hat{g}_{\gamma \delta } \hat{\mathbf {G}}^\gamma \hat{\mathbf {G}}^\delta : \mathbf {t}_\alpha \mathbf {t}_\alpha&\text {(no sum over }\alpha ) \end{aligned}$$

(103)

$$\begin{aligned}&= \left( 1 + \hat{\kappa }_\alpha \vartheta \right) ^2 \left( \frac{ \hat{\lambda }_\alpha }{ 1 + (\hat{\kappa }_0)_\alpha \vartheta _0 } \right) ^2&\text {(no sum)}. \end{aligned}$$

(104)

From that, we obtain

$$\begin{aligned} \lambda _\alpha&= \frac{ 1 + \hat{\kappa }_\alpha \vartheta }{ 1 + (\hat{\kappa }_0)_\alpha \vartheta _0(\vartheta ) } \hat{\lambda }_\alpha&\text {(no sum)} . \end{aligned}$$

(105)

To obtain $\vartheta _0(\vartheta )$, we start from $\vartheta =\vartheta _0=0$ and integrate by using Eq. (69). This requires numerical integration, unless the constitutive law is very simple.

4.2 The design for the ZSS initial guess

As proposed in [69, 70], the two principal directions are seen as circumferential and longitudinal directions, and $\hat{\kappa }_1$ is in the circumferential direction, giving us

$$\begin{aligned} \left( \hat{\kappa }_0\right) _1 = \frac{2 \pi - \phi }{2 \pi } \hat{\kappa }_1. \end{aligned}$$

(106)

Here $\phi$ is the opening angle, which is seen after a longitudinal cut, based on artery experimental data [72]. The wall thickness is about 8–10 % of the diameter at the target configuration. This means that $\hat{\kappa }_1 h_\mathrm {th}$ is 0.16–0.20, and $\hat{\kappa }_2 h_\mathrm {th}$ is nearly equal to zero but it could be negative.

Patient-specific geometries are more complicated than that. To classify the local shapes, we consider the quadrants of the space formed by $\hat{\kappa }_1 h_\mathrm {th}$ and $\hat{\kappa }_2 h_\mathrm {th}$. In the first quadrant, we have a balloon-like shape, which may be seen at a branch or an aneurysm. In the second and fourth quadrants, we have saddle points, which may be seen near branches. In the third quadrant, we have both curvatures negative, which may be seen also near branches. We note that because of the Kirchhoff–Love shell assumption, the following conditions (for $\alpha =1$ or 2) are out of scope:

$$\begin{aligned} \hat{\kappa }_\alpha h_\mathrm {th}< -1 \end{aligned}$$

(107)

or

$$\begin{aligned} \left( \hat{\kappa }_0\right) _\alpha (h_\mathrm {th})_0 < -1. \end{aligned}$$

(108)

5 Computations

All computations are based on the Fung’s model (see Appendix C) with $D_1 = 2.6447\,{\times }\,10^3~\mathrm {Pa}$, $D_2 = 8.365$, and the Poisson’s ratio $\nu = 0.49$. The load is $p = 92~\mathrm {mm~Hg}$. We use the normal-vector definition of Eq. (42).

5.1 Analytical solution for constant stretch on the inner surface

We assume that the stretches $\hat{\lambda }_1 = \hat{\lambda }_2 = 1.05$ and find the opening angles $\phi _1$ and $\phi _2$ in terms of $\hat{\kappa }_1 h_\mathrm {th}$ and $\hat{\kappa }_2 h_\mathrm {th}$. We define an opening angle for each direction:

$$\begin{aligned} \phi _\alpha&= 2 \pi \left( 1 - \frac{(\hat{\kappa }_0)_\alpha }{\hat{\kappa }_\alpha }\right)&\text {(no sum)}, \end{aligned}$$

(109)

where $\alpha =1, 2$.

Remark 4

We note that the stretch value 1.05 gives $\phi _1 = 410^\circ$ for a straight tube with $\hat{\kappa }_1h_\mathrm {th}= 0.16$, and $\phi _1 = 310^\circ$ with $\hat{\kappa }_1 h_\mathrm {th}= 0.20$.

Figure 3 shows $\phi _1$, which is obtained iteratively and may not be unique. The figure also gives us $\phi _2$ when we interchange $\hat{\kappa }_1 h_\mathrm {th}$ and $\hat{\kappa }_2 h_\mathrm {th}$. We note that in many regions we have symmetry with respect to $\hat{\kappa }_1 h_\mathrm {th}= \hat{\kappa }_2 h_\mathrm {th}$. We see large departure from the symmetry in regions where $\hat{\kappa }_1 \hat{\kappa }_2 < 0$, which are the saddle points.

Fig. 3

Opening angle $\phi _1$ over the space formed by $\hat{\kappa }_1 h_\mathrm {th}$ and $\hat{\kappa }_2 h_\mathrm {th}$

We use this map for generating the initial guess. When the geometry is out of scope, we set $\phi _\alpha =0$.

5.2 Straight tube

The tube has $\hat{\kappa }_1 h_\mathrm {th}= 0.20$. The meshes used in the computations are shown in Figs. 4 and 5. They are based on cubic B-splines, with 16, 8 and 1 elements in the circumferential, longitudinal and thickness directions. For the first mesh, $\mathbf {g}_3$ is in $\mathbf {n}$ direction, and for the second mesh, $\mathbf {g}_3$ is skew to $\mathbf {n}$ direction. As can be clearly seen in Fig. 5, the mesh is twisted.

Fig. 4

Straight tube. The mesh has $\mathbf {g}_3$ in $\mathbf {n}$ direction

Fig. 5

Straight tube. The mesh has $\mathbf {g}_3$ skew to $\mathbf {n}$ direction

Figures 6 and 7 show, for the mesh in Fig. 4, the stretches from the ZSS initial guess and converged ZSS. Figures 8 and 9 do the same for the mesh in Fig. 5. From all these results we see that our initial guess is very good, even for the mesh where $\mathbf {g}_3$ is skew to $\mathbf {n}$ direction.

Fig. 6

Straight tube. Maximum principal stretch for the mesh in Fig. 4. From the ZSS initial guess (left) and converged ZSS (right)

Fig. 7

Straight tube. Minimum principal stretch for the mesh in Fig. 4. From the ZSS initial guess (left) and converged ZSS (right)

Fig. 8

Straight tube. Maximum principal stretch for the mesh in Fig. 5. From the ZSS initial guess (left) and converged ZSS (right)

Fig. 9

Straight tube. Minimum principal stretch for the mesh in Fig. 5. From the ZSS initial guess (left) and converged ZSS (right)

5.3 Y-shaped tube

This geometry was motivated by branched arteries. The tube parts have $\hat{\kappa }_1 h_\mathrm {th}= 0.16$, with constant thickness. Figures 10 and 11 show the shape and $\hat{\kappa }_1 h_\mathrm {th}$ and $\hat{\kappa }_2 h_\mathrm {th}$. The geometry has two umbilical points, where $\hat{\kappa }_1=\hat{\kappa }_2$, and three saddle-point regions. The mesh is shown in Fig. 12.

Fig. 10

Y-shaped tube. $\hat{\kappa }_1 h_\mathrm {th}$

Fig. 11

Y-shaped tube. $\hat{\kappa }_2 h_\mathrm {th}$

Fig. 12

Y-shaped tube. Inner-surface mesh made of cubic and quartic T-splines. Red circles represent the control points. The parts with the quartic T-splines, obtained by order elevation [73], are around the two extraordinary points, each connected to six edges

Figure 13 shows the IPBZSS, using the EBZSS representation, from the ZSS initial guess and converged ZSS. The stretches are shown in Figs. 14 and 15. The initial guess has nearly uniform stretch on the inner surface. However, at the saddle point, the maximum stretch is higher than what we obtain from the ZSS initial guess. This affects the stretch on the outer surface too. There is less effect at the umbilical points. Figure 16 shows the stretch in $\hat{\mathbf {n}}$ direction. Again, there is less effect at the umbilical points.

Fig. 13

Y-shaped tube. The IPBZSS, shown using the EBZSS representation. From the ZSS initial guess (top) and converged ZSS (bottom)

Fig. 14

Y-shaped tube. Maximum principal stretch. From the ZSS initial guess (top) and converged ZSS (bottom)

Fig. 15

Y-shaped tube. Minimum principal stretch. From the ZSS initial guess (top) and converged ZSS (bottom)

Fig. 16

Y-shaped tube. Stretch in $\hat{\mathbf {n}}$ direction. From the ZSS initial guess (top) and converged ZSS (bottom)

5.4 Patient-specific aorta

The largest diameter is about $30~\mathrm {mm}$. Figures 17 and 18 show the shape and $\hat{\kappa }_1$ and $\hat{\kappa }_2$. The inner-surface mesh is shown in Fig. 19. We use Laplace’s equation to determine a smooth thickness distribution, setting the values at the boundaries to result in $\hat{\kappa }_1 h_\mathrm {th}= 0.20$. We then generate the volume mesh as described in Sect. 3.1, which involves modification of the outer surface and consequently the thickness. The volume mesh is shown in Fig. 20. The measured thickness is displayed on the inner-surface mesh in Fig. 21, with an average value of $\hat{\kappa }_1 h_\mathrm {th}= 0.18$.

Fig. 17

Patient-specific aorta. $\hat{\kappa }_1~(\mathrm {mm}^{-1})$. The maximum and minimum values are $1.822~\mathrm {mm}^{-1}$ and $-0.2810~\mathrm {mm}^{-1}$

Fig. 18

Patient-specific aorta. $\hat{\kappa }_2~(\mathrm {mm}^{-1})$. The maximum and minimum values are $0.1973~\mathrm {mm}^{-1}$ and $-1.543~\mathrm {mm}^{-1}$

Fig. 19

Patient-specific aorta. Inner-surface mesh, made of cubic and quartic T-splines. Red circles represent the control points. The parts with the quartic T-splines, obtained by order elevation [73], are around the two extraordinary points, each connected to six edges

Fig. 20

Patient-specific aorta. Volume mesh, made of cubic and quartic T-splines. Red circles represent the control points

Fig. 21

Patient-specific aorta. $h_\mathrm {th}~(\mathrm {mm})$

From the results of the Y-shaped tube we learned that the initial guess should have had, on the outer surface, less variation in the stretch in $\hat{\mathbf {n}}$ direction. Based on that, we improve the initial guess in parts of the region where we do not have both curvatures positive. For a straight tube with $\hat{\kappa }_1 h_\mathrm {th}= 0.18$, on the outer surface, the stretch in $\hat{\mathbf {n}}$ direction is 0.80. We target that value in improving the initial guess.

We define four cases in deciding how to do the improvement, which we go through in the order given below:

• 1. $\hat{\kappa }_1 h_\mathrm {th}< - 0.6$ or $\hat{\kappa }_2 h_\mathrm {th}< - 0.6$

• 2. $\hat{\kappa }_1 h_\mathrm {th}< - 0.4$ or $\hat{\kappa }_2 h_\mathrm {th}< - 0.4$

• 3. $\hat{\kappa }_1 h_\mathrm {th}+ \hat{\kappa }_2 h_\mathrm {th}< 0$

• 4. Elsewhere

We take the following actions for each case:

• 1. Set $\phi _1=\phi _2 = 0$ and $\hat{\lambda }_1 = \hat{\lambda _2} = 1$.

• 2. Set $\phi _1 = \phi _2 = 0$. Assume that $\hat{\lambda }_1$ and $\hat{\lambda }_2$ are the same. Determine them in such a way that, on the outer surface, the stretch in $\hat{\mathbf {n}}$ direction is 0.80.

• 3. Leave $\hat{\lambda }_1=\hat{\lambda }_2 = 1.05$ unchanged. Assume that $\phi _1$ and $\phi _2$ are the same. Determine them in such a way that, on the outer surface, the stretch in $\hat{\mathbf {n}}$ direction is 0.80.

• 4. No modification.

Figure 22 shows the IPBZSS, using the EBZSS representation, from the ZSS initial guess and converged ZSS. The stretches are shown in Figs. 23 and 24. Figure 25 shows the stretch in $\hat{\mathbf {n}}$ direction. Overall, the ZSS initial guess and converged ZSS are very similar. This indicates that reaching the ZSS design targets based on the analytical solution works well.

Fig. 22

Patient-specific aorta. The IPBZSS, shown using the EBZSS representation. From the ZSS initial guess (top) and converged ZSS (bottom)

Fig. 23

Patient-specific aorta. Maximum principal stretch. From the ZSS initial guess (top) and converged ZSS (bottom)

Fig. 24

Patient-specific aorta. Minimum principal stretch. From the ZSS initial guess (top) and converged ZSS (bottom)

Fig. 25

Patient-specific aorta. Stretch in $\hat{\mathbf {n}}$ direction. From the ZSS initial guess (top) and converged ZSS (bottom)

6 Concluding remarks

We have increased the scope and robustness of the method we introduced earlier for estimating the ZSS required in patient-specific arterial FSI computations, where the medical-image-based arterial geometries do not come from the ZSS of the artery.

The estimate is based on T-spline discretization of the arterial wall and is in the form of IPBZSS. The T-spline discretization enables dealing with complex arterial geometries, such as an aorta model with branches, while retaining the desirable features of isogeometric discretization. With higher-order basis functions of the isogeometric discretization, we may be able to achieve a similar level of accuracy as with the linear basis functions, but using larger-size and fewer elements. In addition, the higher-order basis functions allow representation of more complex shapes within an element. The IPBZSS is a convenient representation of the ZSS because with isogeometric discretization, especially with T-spline discretization, specifying conditions at integration points is more straightforward than imposing conditions on control points.

The method has two main components. 1. An iteration technique, which starts with a calculated ZSS initial guess, is used for computing the IPBZSS such that when a given pressure load is applied, the medical-image-based target shape is matched. 2. A design procedure, which is based on the Kirchhoff–Love shell model of the artery, is used for calculating the ZSS initial guess.

We increased the scope and robustness of the method by introducing a new design procedure for the ZSS initial guess. The new design procedure has two features. (a) An IPB shell-like coordinate system, which increases the scope of the design to general parametrization in the computational space. (b) Analytical solution of the force equilibrium in the normal direction, based on the Kirchhoff–Love shell model, which places proper constraints on the design parameters. This increases the estimation accuracy, which in turn increases the robustness of the iterations and the convergence speed.

To show how the new design procedure for the ZSS initial guess performs, we first presented 3D test computations with a straight tube and a Y-shaped tube. After that we presented a 3D computation where the target geometry is coming from medical image of a human aorta, and we included the branches in the model. The computations show that the new design procedure for the ZSS initial guess is reaching the design targets well.

Appendices

Appendix A: The second fundamental form in the shell-like coordinate system in terms of the natural coordinates

The covariant basis vectors for $\alpha =1, \ldots , {n_{\mathrm {sd}}}-1$ are

$$\begin{aligned} \hat{\mathbf {g}}_\alpha&=\frac{\partial \mathbf {x}(\pmb {\xi }(\hat{\pmb {\xi }}, \vartheta ))}{\partial \hat{\xi }^\alpha }, \end{aligned}$$

(110)

which can be represented by using the chain rule:

$$\begin{aligned} \hat{\mathbf {g}}_\alpha&= \frac{\partial \mathbf {x}}{\partial \xi ^I} \frac{\partial \xi ^I}{\partial \hat{\xi }^{\alpha }} , \end{aligned}$$

(111)

where $I=1, \ldots , {n_{\mathrm {sd}}}$. Differentiating that with respect to $\hat{\xi }^\beta$, we obtain

$$\begin{aligned} \frac{\partial \hat{\mathbf {g}}_\alpha }{\partial \hat{\xi }^\beta }&= \frac{\partial \hat{\mathbf {g}}_\alpha }{\partial \xi ^J} \frac{\partial \xi ^J}{\partial \hat{\xi }^{\beta }} \end{aligned}$$

(112)

$$\begin{aligned}&= \frac{\partial }{\partial \xi ^J} \left( \frac{\partial \mathbf {x}}{\partial \xi ^I} \frac{\partial \xi ^I}{\partial \hat{\xi }^{\alpha }}\right) \frac{\partial \xi ^J}{\partial \hat{\xi }^{\beta }} \end{aligned}$$

(113)

$$\begin{aligned}&= \Bigg( \frac{\partial ^2 \mathbf {x}}{\partial \xi ^I \partial \xi ^J} \frac{\partial \xi ^I}{\partial \hat{\xi }^{\alpha }}+ \frac{\partial \mathbf {x}}{\partial \xi ^I} \underbrace{ \frac{\partial ^2 \xi ^I}{\partial \hat{\xi }^{\alpha } \partial \xi ^J} }_{\frac{\partial \delta _{IJ}}{\partial \hat{\xi }^{\alpha }}=0} \Bigg) \frac{\partial \xi ^J}{\partial \hat{\xi }^{\beta }} \end{aligned}$$

(114)

$$\begin{aligned}&= \frac{\partial ^2 \mathbf {x}}{\partial \xi ^I \partial \xi ^J} \frac{\partial \xi ^I}{\partial \hat{\xi }^{\alpha }} \frac{\partial \xi ^J}{\partial \hat{\xi }^{\beta }}, \end{aligned}$$

(115)

where $\beta =1,\ldots ,{n_{\mathrm {sd}}}-1$ and $J=1,\ldots ,{n_{\mathrm {sd}}}$. Thus, the second fundamental form is

$$\begin{aligned} \hat{b}_{\alpha \beta }&= \frac{\partial ^2 \mathbf {x}}{\partial \xi ^I \partial \xi ^J} \cdot \mathbf {n}\frac{\partial \xi ^I}{\partial \hat{\xi }^{\alpha }} \frac{\partial \xi ^J}{\partial \hat{\xi }^{\beta }} . \end{aligned}$$

(116)

Appendix B: Derivative of the contravariant basis vectors

Here we show that $\frac{\partial \mathbf {g}^\gamma }{\partial \xi ^\beta }$ can be expressed as

$$\begin{aligned} \frac{\partial \mathbf {g}^\gamma }{\partial \xi ^\beta }&= \left( g^{\delta \gamma } \mathbf {n}\mathbf {n}- \mathbf {g}^\delta \mathbf {g}^\gamma \right) \cdot \frac{\partial \mathbf {g}_{\delta }}{\partial \xi ^\beta }. \end{aligned}$$

(117)

We start with the transformation from the contravariant basis vectors to the covariant basis vectors:

$$\begin{aligned} \mathbf {g}_{\alpha }&= g_{\alpha \delta } \mathbf {g}^{\delta }. \end{aligned}$$

(118)

We take the derivative of both sides:

$$\begin{aligned} \frac{\partial \mathbf {g}_{\alpha }}{\partial \xi ^\beta }&= \frac{\partial g_{\alpha \delta }}{\partial \xi ^\beta } \mathbf {g}^{\delta } + g_{\alpha \delta } \frac{\partial \mathbf {g}^{\delta }}{\partial \xi ^\beta } , \end{aligned}$$

(119)

and from that obtain

$$\begin{aligned} g_{\alpha \delta } \frac{\partial \mathbf {g}^{\delta } }{\partial \xi ^\beta }&= \frac{\partial \mathbf {g}_{\alpha } }{\partial \xi ^\beta } - \frac{\partial g_{\alpha \delta } }{\partial \xi ^\beta } \mathbf {g}^{\delta }. \end{aligned}$$

(120)

From that and using $g_{\alpha \delta } = \mathbf {g}_\alpha \cdot \mathbf {g}_\delta$, we obtain

$$\begin{aligned} g_{\alpha \delta } \frac{ \partial \mathbf {g}^{\delta } }{\partial \xi ^\beta }&= \frac{\partial \mathbf {g}_{\alpha }}{\partial \xi ^\beta } - \left( \frac{\partial \mathbf {g}_\alpha }{\partial \xi ^\beta } \cdot \mathbf {g}_{\delta } + \mathbf {g}_\alpha \cdot \frac{\partial \mathbf {g}_{\delta } }{\partial \xi ^\beta } \right) \mathbf {g}^{\delta } \end{aligned}$$

(121)

$$\begin{aligned}&= \frac{\partial \mathbf {g}_{\alpha }}{\partial \xi ^\beta } - \frac{\partial \mathbf {g}_\alpha }{\partial \xi ^\beta } \cdot \underbrace{ \mathbf {g}_{\delta } \mathbf {g}^{\delta } }_{=\mathbf {I}-\mathbf {n}\mathbf {n}} - \mathbf {g}_\alpha \cdot \frac{\partial \mathbf {g}_{\delta } }{\partial \xi ^\beta } \mathbf {g}^{\delta } \end{aligned}$$

(122)

$$\begin{aligned}&= \frac{\partial \mathbf {g}_\alpha }{\partial \xi ^\beta } \cdot \mathbf {n}\mathbf {n}- \mathbf {g}_\alpha \cdot \frac{\partial \mathbf {g}_{\delta } }{\partial \xi ^\beta } \mathbf {g}^{\delta } \end{aligned}$$

(123)

$$\begin{aligned}&= \mathbf {n}\mathbf {n}\cdot \frac{\partial \mathbf {g}_\alpha }{\partial \xi ^\beta } - \mathbf {g}_\alpha \cdot \frac{\partial \mathbf {g}_{\delta }}{\partial \xi ^\beta } \mathbf {g}^{\delta }. \end{aligned}$$

(124)

Multiplying both sides with $g^{\gamma \alpha }$, we obtain

$$\begin{aligned} \underbrace{ g^{\gamma \alpha } g_{\alpha \delta } }_{=\delta ^\gamma _\delta } \frac{\partial \mathbf {g}^{\delta } }{\partial \xi ^\beta }&= g^{\gamma \delta } \mathbf {n}\mathbf {n}\cdot \frac{\partial \mathbf {g}_\delta }{\partial \xi ^\beta } - \underbrace{ g^{\gamma \delta } \mathbf {g}_\delta }_{=\mathbf {g}^\gamma } \cdot \frac{\partial \mathbf {g}_{\delta } }{\partial \xi ^\beta } \mathbf {g}^{\delta }. \end{aligned}$$

(125)

Thus,

$$\begin{aligned} \frac{\partial \mathbf {g}^{\gamma } }{\partial \xi ^\beta }&= \left( g^{\gamma \delta } \mathbf {n}\mathbf {n}- \mathbf {g}^{\delta } \mathbf {g}^\gamma \right) \cdot \frac{\partial \mathbf {g}_{\delta } }{\partial \xi ^\beta }. \end{aligned}$$

(126)

Appendix C: Fung’s model

The elastic-energy density function for the Fung’s model is

$$\begin{aligned} \varphi _\mathrm {F} \left( \mathbf {C}\right)= {D_1}\left( {{e^{{D_2}{\rm{tr(}}{\bf{C}} - {n_{{\rm{sd}}}})}} - 1} \right) , \end{aligned}$$

(127)

where $D_1$ and $D_2$ are the coefficients of the Fung’s model. As a compressible-material model, we use the following expression:

$$\begin{aligned} \varphi _\mathrm {FR} \left( \mathbf {C}\right)&= \varphi _\mathrm {F} \left( J^{-\frac{2}{{n_{\mathrm {sd}}}}}\mathbf {C}\right) + \varphi _\mathrm {vol}\left( J\right) , \end{aligned}$$

(128)

where

$$\begin{aligned} \varphi _\mathrm {vol} \left( J\right)&=\frac{1}{2}\kappa \left( \frac{1}{2}\left( J^2-1\right) - \ln J\right) , \end{aligned}$$

(129)

and $\kappa$ is the bulk modulus. We determine the bulk modulus from the Poisson’s ratio $\nu$ as

$$\begin{aligned} \kappa = \frac{4 D_1 D_2 \left( 1 + \nu \right) }{3 \left( 1 - 2 \nu \right) }. \end{aligned}$$

(130)