1 Introduction

In recent years, non-selfadjoint operators are attracting increasing attention, both in view of applications to quantum mechanics and other branches of physics, and for the interesting mathematical challenges they present. While the theory of selfadjoint operators is mature and well established, references for the non-selfadjoint case are more sparse. Good sources for the theory and its developments are the monographs [27, 32, 41] or e.g. the more recent books [3, 15] where also physical applications may be found.

In this paper, we deal with the free Dirac operator \({\mathscr {D}}_0\) perturbed by a potential

$$\begin{aligned} {\mathscr {D}}_{V} = {\mathscr {D}}_{0} + V. \end{aligned}$$

The importance of this family of operators in quantum physics is well known: in two dimensions, the operator \({\mathscr {D}}_{V}\) is related to the quantum theory of graphene, while in the 3D case the Hamiltonian \({\mathscr {D}}_{V}\) models the dynamic of a relativistic quantum particle of spin \(\frac{1}{2}\) subject to an external electric field.

We consider the operator \({\mathscr {D}}_{V}\) acting on the Hilbert space of spinors \({\mathfrak {H}}= L^2({\mathbb {R}}^n; {\mathbb {C}}^{N} )\), where \(n\ge 2\), \(N := 2^{\lceil n/2 \rceil }\) and \({\lceil \cdot \rceil }\) is the ceiling function. The free Dirac operator \({\mathscr {D}}_{0}\) with non negative mass m is defined as

$$\begin{aligned} {\mathscr {D}}_{0} = -i c \hbar \, {\varvec{\alpha }} \cdot \nabla + m c^2 \alpha _0 = -i c \hbar \sum _{k=1}^{n} \alpha _k \frac{\partial }{\partial x_k} + m c^2 \alpha _0, \end{aligned}$$

where c is the speed of light, \(\hbar \) is the reduced Planck constant and the matrices \(\alpha _k \in {\mathbb {C}}^{N \times N}\), for \(k \in \{0,\dots ,n\}\), are elements of the Clifford algebra (see [37]) satisfying the anti-commutation relations

$$\begin{aligned} \alpha _j \alpha _k + \alpha _k \alpha _j = 2\delta _{j,k} I_{{\mathbb {C}}^N}, \quad \text {for } j,k \in \{0,\dots ,n\}, \end{aligned}$$
(1.1)

where \(\delta _{j,k}\) is the Kronecker symbol. Without loss of generality we can take

$$\begin{aligned} \alpha _0 = \begin{pmatrix} I_{{\mathbb {C}}^{N/2 \times N/2}} &{} {\varvec{0}}\\ {\varvec{0}} &{} -I_{{\mathbb {C}}^{N/2 \times N/2}} \end{pmatrix} \end{aligned}$$

and choose units so that \(c=\hbar =1\). The free Dirac operator is selfadjoint with domain

$$\begin{aligned} {{\,\mathrm{dom}\,}}({\mathscr {D}}_0) = \{ \psi \in {\mathfrak {H}}:\nabla \psi \in {\mathfrak {H}}^n \} \end{aligned}$$

and core \(C_0^\infty ({\mathbb {R}}^n; {\mathbb {C}}^N)\).

The potential \(V :{\mathbb {R}}^n \rightarrow {\mathbb {C}}^{N \times N}\) will be any complex matrix-valued function with \(|V|\in L_{\text {loc}}^2({\mathbb {R}}^n;{\mathbb {R}})\), where |V(x)| is the operator norm of the matrix V(x). With the usual slight abuse, the same symbol V will denote the multiplication operator by V on \({\mathfrak {H}}\), with initial domain \({{\,\mathrm{dom}\,}}(V)=C_0^\infty ({\mathbb {R}}^n;{\mathbb {C}}^N)\).

In the case of the non-selfadjoint Schrödinger operator \(-\Delta +V\), properties of the point spectrum \(\sigma _{p}(-\Delta +V)\) were investigated among others by Frank [22, 23], Frank and Sabin [24], Frank and Simon [25]. In particular, the eigenvalues of \(-\Delta +V\) satisfy the bound

$$\begin{aligned} |z|^{\gamma } \le D_{\gamma ,n} \int _{{\mathbb {R}}_n} |V(x)|^{\gamma +n/2}dx, \quad 0 < \gamma {\left\{ \begin{array}{ll} =\frac{1}{2}, &{}\text {if } n=1, \\ \le \frac{1}{2}, &{}\text {if } n\ge 2, \end{array}\right. } \end{aligned}$$

where the constant \(D_{\gamma ,n}>0\) is independent of z and V. This localization estimate is due to Abramov, Aslanyan and Davies [2] for \(n=1\), with sharp constant \(D_{1/2,1}=1/2\), and for larger n to Frank [22]. The proof combines the Birman–Schwinger principle with the uniform Sobolev inequalities

$$\begin{aligned} \left\Vert (-\Delta -z)^{-1}\right\Vert _{L^p \rightarrow L^{p'}} \le C |z|^{-n/2+n/p-1}, \quad \frac{2}{n+1} \le \frac{1}{p}-\frac{1}{p'} \le \frac{2}{n}, \end{aligned}$$

by Kenig et al. [33], where \(p'= p/(p-1)\) is the dual exponent of p. In [35, 39], Laptev and Safronov conjectured that the range of \(\gamma \) for \(n\ge 2\) can be extended to \(0<\gamma <n/2\), and Frank and Simon [25] proved the conjecture to be true for radial symmetric potentials.

Consider now the structure of \(\sigma _{p}({\mathscr {D}}_V)\). In the selfadjoint case there exists an extensive literature on the spectral properties of \({\mathscr {D}}_V\), see for example the monograph by Thaller [40]. In the non-selfadjoint case, the study of the spectrum of \({\mathscr {D}}_{V}\) was initiated by Cuenin et al. [10] in the 1D case, followed by [8, 11, 18]. For the higher dimensional case, we refer to the works [9, 16, 20, 38].

In the 1D paper [10], it is proved that if \(V=(V_{ij})_{i,j \in \{1,2\}}\) with \(V_{ij} \in L^1({\mathbb {R}})\) and

$$\begin{aligned} \left\Vert V\right\Vert _{L^1({\mathbb {R}})} = \int _{{\mathbb {R}}} |V(x)|dx < 1 \end{aligned}$$

then every non-embedded eigenvalue \(z\in \rho ({\mathscr {D}}_{0})\) of \({\mathscr {D}}_{V}\) lies in the union

$$\begin{aligned} z \in {\overline{B}}_{R_0}(x^-_0) \cup {\overline{B}}_{R_0}(x^+_0) \end{aligned}$$

of two disjoint closed disks, with centers and radius respectively

$$\begin{aligned} x^\pm _0 = \pm \sqrt{\frac{\left\Vert V\right\Vert _1^4-2\left\Vert V\right\Vert _1^2+2}{4(1-\left\Vert V\right\Vert _1^2)} + \frac{1}{2}}, \quad R_0 = \sqrt{\frac{\left\Vert V\right\Vert _1^4-2\left\Vert V\right\Vert _1^2+2}{4(1-\left\Vert V\right\Vert _1^2)} - \frac{1}{2}}. \end{aligned}$$

In particular, in the massless case (\(m=0\)), the spectrum of \({\mathscr {D}}_{V}\) is \({\mathbb {R}}\). Moreover, this inclusion is sharp. The proof is essentially based on the combination of the Birman–Schwinger principle with the resolvent estimate for the free Dirac operator

$$\begin{aligned} \left\Vert ({\mathscr {D}}_{0}-z)^{-1}\right\Vert _{L^1({\mathbb {R}}) \rightarrow L^\infty ({\mathbb {R}})} \le \sqrt{\frac{1}{2} +\frac{1}{4} \left|\frac{z+m}{z-m}\right|+\frac{1}{4} \left|\frac{z-m}{z+m}\right|}, \quad {z \in \rho ({\mathscr {D}}_{0})}. \end{aligned}$$

It should be remarked that, in higher dimensions \(n\ge 2\), \(L^p({\mathbb {R}}^n) \rightarrow L^{p'}({\mathbb {R}}^n)\) estimates for \(({\mathscr {D}}_0-z)^{-1}\) do not exist, as observed in the Introduction of [8]. Indeed, Cuenin points out that, due to the Stein–Thomas restriction theorem and standard estimates for Bessel potentials, the resolvent \(({\mathscr {D}}_{0}-z)^{-1} :L^p({\mathbb {R}}^n) \rightarrow L^{p'}({\mathbb {R}}^n)\) is bounded uniformly in \(|z|>1\) if and only if

$$\begin{aligned} \frac{2}{n+1} \le \frac{1}{p} + \frac{1}{p'} \le \frac{1}{n}, \end{aligned}$$

and thus we are forced to choose \(n=1\). The situation for the Schrödinger operator is better since the right-hand side of the above range is 2/n, as per the Kenig–Ruiz–Sogge estimates.

In [9], Cuenin localized the eigenvalues of the perturbed Dirac operator in terms of the \(L^p\)-norm of the potential V, but in an unbounded region of the complex plane. Indeed, Theorem 6.1.b of [9] states that, if \(n\ge 2\) and \(|V|\in L^p\), with \(p\ge n\), then any eigenvalue \(z \in \rho ({\mathscr {D}}_0)\) of \({\mathscr {D}}_V\) satisfies

$$\begin{aligned} \left|{\mathfrak {I}z}/{\mathfrak {R}z} \right|^{(n-1)/p} |\mathfrak {I}z|^{1-n/p} \le C \left\Vert V\right\Vert _{L^p({\mathbb {R}}^n)}, \end{aligned}$$

where C is a constant independent of z and V. Similar unbounded enclosing regions were obtained in [12], where Cuenin and Tretter study arbitrary non-symmetric perturbations of selfadjoint operators. In particular, for the massless Dirac operator in \({\mathbb {R}}^2\), if \(|V| \in L^p\) with \(p>2\), they obtain that

$$\begin{aligned} \sigma ({\mathscr {D}}_V) \subset \bigcap _{0<b<1} \left\{ z\in {\mathbb {C}}:|\mathfrak {I}z|^2 \le \frac{ (2\pi (p-2))^{-\frac{2}{p-2}} \left\Vert V\right\Vert _{L^p({\mathbb {R}}^2)}^{\frac{2p}{p-2}} b^{-\frac{4}{p-2}} + b^2 |\mathfrak {R}z|^2}{1-b^2} \right\} . \end{aligned}$$

Considering instead the massive Dirac operator with Coulomb-like potential in \({\mathbb {R}}^3\), the authors in [12] obtain that, if \(|V(x)|^2 \le C_1^2 + C_2^2|x|^{-2}\) for almost all \(x\in {\mathbb {R}}^3\), where \(C_1, C_2 \ge 0\) are constants such that \({C_1^2+4C_2^2m^2}<m^2\), then

$$\begin{aligned} \sigma ({\mathscr {D}}_V) \subset \left\{ z\in {\mathbb {C}}:|\mathfrak {R}z| \ge m-\sqrt{C_1^2+4C_2^2m^2}, \; |\mathfrak {I}z|^2 \le \frac{C_1^2+4C_2|\mathfrak {R}z|^2}{1-4C_2^2} \right\} . \end{aligned}$$

A different result on the localization of eigenvalues in an unbounded regions was proved by Fanelli and Krejčiřík in [20]: in 3D, if \(|V|\in L^3({\mathbb {R}}^3)\) and \(z \in \sigma _p({\mathscr {D}}_V)\), then

$$\begin{aligned} \left( 1 + \frac{(\mathfrak {R}z)^2}{(\mathfrak {R}\sqrt{m^2-z^2})^2} \right) ^{-1/2} < \left( {\pi }/{2} \right) ^{1/3} \sqrt{1+e^{-1}+2e^{-2}} \left\Vert V\right\Vert _{L^3({\mathbb {R}}^3)}. \end{aligned}$$
(1.2)

The advantage of the last result lies in the explicit condition which is easy to check in applications. However, also in this result the eigenvalues are localized in an unbounded region around the continuous spectrum \(\sigma ({\mathscr {D}}_0)=(-\infty ,-m] \cup [m,+\infty )\) of the free Dirac operator \({\mathscr {D}}_0\).

We finally mention the recent paper [7], where the authors obtain results on the absence of eigenvalues for the Schrödinger and Pauli operators with a constant magnetic field and non-Hermitian potentials, and for the purely magnetic Dirac operators. However, Dirac operators with electric perturbations can not be treated by the multiplicative techniques of [7] (recall that the square of a purely magnetic Dirac operator is a diagonal magnetic Laplacian, which allows one to use the multiplier method).

The main goal of the present paper is to generalize the results by Cuenin et al. [10] to higher dimensions, enclosing the eigenvalues of the massive (\(m>0\)) Dirac operator \({\mathscr {D}}_V\) in a compact region of the complex plane, provided the potential V satisfies a suitable smallness condition in a mixed Lebesgue norm. In the case of the massless (\(m=0\)) Dirac operator, we obtain that the point spectrum of the perturbed operator \({\mathscr {D}}_{V}\) is empty, and then \(\sigma ({\mathscr {D}}_{V})=\sigma ({\mathscr {D}}_0)={\mathbb {R}}\).

Before we formalize our results in Theorems 1 and 2 below, we introduce a few notations used throughout the paper.

Notations

We use the symbols \(\sigma (H)\), \(\sigma _p(H)\), \(\sigma _e(H)\) and \(\rho (H)\) respectively for the spectrum, the point spectrum, the essential spectrum and the resolvent of an operator H. More explicitly, we define

$$\begin{aligned} \sigma _e(H) = \{z \in {\mathbb {C}}:H-z \text { is not a Fredholm operator} \}, \end{aligned}$$

whereas the discrete spectrum is defined as

$$\begin{aligned} \sigma _d(H) = \{z \in {\mathbb {C}}:z \text { is an isolated eigenvalue of } H \text { of finite multiplicity}\}. \end{aligned}$$

Recall that for non-selfadjoint operators, the essential spectrum defined above is not the complement of the discrete spectrum, see e.g. [17]. For \(z\in \rho (H)\), we denote with \(R_H(z) := (H-z)^{-1}\) the resolvent operator of H. We recall also that

$$\begin{aligned} \sigma (-\Delta ) =\sigma _e(-\Delta ) =[0,+\infty ), \\ \sigma ({\mathscr {D}}_0) =\sigma _e({\mathscr {D}}_0) =(-\infty ,-m]\cup [m,+\infty ) . \end{aligned}$$

For \(j\in \{1,\dots ,n\}\) and \(x=(x_1,\dots ,x_n)\in {\mathbb {R}}^n\), we write

$$\begin{aligned} {{\widehat{x}}_j}&:= (x_1,\dots ,x_{j-1},x_{j+1},\dots ,x_n) \in {\mathbb {R}}^{n-1}, \\ (\overline{x},{{\widehat{x}}_j})&:= (x_1,\dots ,x_{j-1},\overline{x},x_{j+1},\dots ,x_n) \in {\mathbb {R}}^n. \end{aligned}$$

The mixed Lebesgue spaces \(L^p_{x_j}L^q_{{{\widehat{x}}_j}}({\mathbb {R}}^n)\) are the spaces of measurable functions on \({\mathbb {R}}^{n}\) with

$$\begin{aligned} \left\Vert f\right\Vert _{L^p_{x_j}L^q_{{{\widehat{x}}_j}}} := \left( \int _{{\mathbb {R}}} \left( \int _{{\mathbb {R}}^{n-1}} |f(x_j,{{\widehat{x}}_j})|^q d{{\widehat{x}}_j} \right) ^{p/q} dx_j \right) ^{1/p}<\infty . \end{aligned}$$

Obvious modifications occur for \(p=\infty \) or \(q=\infty \) (see e.g. [4] for general properties of such spaces).

For any matrix-valued function \(M :{\mathbb {R}}^n \rightarrow {\mathbb {C}}^{N\times N}\), we set

$$\begin{aligned} \left\Vert M\right\Vert _{L^p_{x_j} L^q_{{{\widehat{x}}_j}}} := \left\Vert |M|\right\Vert _{L^p_{x_j} L^q_{{{\widehat{x}}_j}}} \end{aligned}$$

where |M(x)| denotes the operator norm of the matrix M(x). Further, we write

$$\begin{aligned} {[}f *_{x_j} g](x)&:= \int _{\mathbb {R}}f(y_j,{{\widehat{x}}_j}) g(x_j-y_j,{{\widehat{x}}_j})dy_j, \\ {[}{\mathscr {F}}_{x_j} f] (\xi _j, {{\widehat{x}}_j})&:= \frac{1}{\sqrt{2\pi }} \int _{{\mathbb {R}}} e^{-i x_j \xi _j} f(x_j,{{\widehat{x}}_j}) dx_j, \\ {[}{\mathscr {F}}^{-1}_{\xi _j} f] (x_j, {{\widehat{x}}_j})&:= \frac{1}{\sqrt{2\pi }} \int _{{\mathbb {R}}} e^{i x_j \xi _j} f(\xi _j,{{\widehat{x}}_j}) d\xi _j, \end{aligned}$$

to denote the partial convolution respect to \(x_j\), the partial Fourier transform with respect to \(x_j\), and its inverse, respectively. The partial (inverse) Fourier transform with respect to \({{\widehat{x}}_j}\) and the complete (inverse) Fourier transform with respect to x are defined in a similar way. Finally, we shall need the function spaces

$$\begin{aligned} X \equiv X({\mathbb {R}}^n) := \bigcap _{j=1}^{n} L^1_{x_j} L^2_{{{\widehat{x}}_j}}({\mathbb {R}}^n), \quad Y \equiv Y({\mathbb {R}}^n) := \bigcap _{j=1}^{n} L^1_{x_j} L^\infty _{{{\widehat{x}}_j}}({\mathbb {R}}^n), \end{aligned}$$

with norms defined as follows

$$\begin{aligned} \left\Vert f\right\Vert _X = \max _{j\in \{1,\dots ,n\}} \left\Vert f \right\Vert _{L^1_{x_j} L^2_{{{\widehat{x}}_j}}}, \quad \left\Vert f\right\Vert _Y = \max _{j\in \{1,\dots ,n\}} \left\Vert f \right\Vert _{L^1_{x_j} L^\infty _{{{\widehat{x}}_j}}}. \end{aligned}$$

The dual space of X is given by

$$\begin{aligned} X^* \equiv X^*({\mathbb {R}}^n) := \sum _{j=1}^{n} L^\infty _{x_j} L^2_{{{\widehat{x}}_j}}({\mathbb {R}}^n) \end{aligned}$$

(see e.g. [5]), endowed with the norm

$$\begin{aligned} \left\Vert f\right\Vert _{X^*} := \inf \left\{ \sum _{j=1}^{n} \left\Vert f_j\right\Vert _{L^\infty _{x_j} L^2_{{{\widehat{x}}_j}}} :f=\sum _{j=1}^n f_j \right\} . \end{aligned}$$
(1.3)

We can now state our results.

Theorem 1

Let \(m>0\). There exists a constant \(C_0>0\) such that if

$$\begin{aligned} \left\Vert V\right\Vert _Y < C_0, \end{aligned}$$

then all eigenvalues \(z \in \sigma _p({\mathscr {D}}_{V})\) of \({\mathscr {D}}_{V}\) are contained in the union

$$\begin{aligned} z \in {\overline{B}}_{R_0} (x^-_0) \cup {\overline{B}}_{R_0} (x^+_0) \end{aligned}$$

of the two closed disks in \({\mathbb {C}}\) with centers in \(x_0^-,x_0^+\) and radius \(R_0\), with

$$\begin{aligned} x^\pm _0 := \pm m\,\frac{{\mathcal {V}}^2+1}{{\mathcal {V}}^2-1}, \quad R_0 := m\,\frac{2{\mathcal {V}}}{{\mathcal {V}}^2-1} \quad \text {where}\quad {\mathcal {V}}= {\mathcal {V}}(V) := \left[ \frac{(n+1)C_0}{\left\Vert V\right\Vert _Y} - n \right] ^2 > 1. \end{aligned}$$

Theorem 2

Let \(m=0\). There exists a constant \(C_0>0\) such that if

$$\begin{aligned} \left\Vert V\right\Vert _Y < C_0, \end{aligned}$$

then \({\mathscr {D}}_V\) has no eigenvalues.

In this case, we have \(\sigma ({\mathscr {D}}_{V})=\sigma _{e}({\mathscr {D}}_{V})={\mathbb {R}}\).

Remark 1.1

The crucial tool in our proof is a sharp uniform resolvent estimate for the free Dirac operator. This approach is inspired by [22], where the result by Kenig et al. [33] was used for the same purpose. In our case, we prove in Sect. 2 the following estimates, of independent interest:

$$\begin{aligned} \left\Vert R_{-\Delta }(z)\right\Vert _{X \rightarrow X^*} \le C |z|^{-1/2}, \quad \left\Vert \partial _k R_{-\Delta }(z)\right\Vert _{X \rightarrow X^*} \le C. \end{aligned}$$

and

$$\begin{aligned} \left\Vert R_{{\mathscr {D}}_{0}}(z) \right\Vert _{X \rightarrow X^*} \le C \left[ n + \left| \frac{z+m}{z-m}\right| ^{{{\,\mathrm{sgn}\,}}(\mathfrak {R}z)/2}\right] . \end{aligned}$$

These can be regarded as precised resolvent estimates of Agmon–Hörmander type. Note also that similar uniform estimates, but in non sharp norms, were proved earlier by the first and second Author in [13, 14, 19].

In Sect. 3, we combine our uniform estimates with the Birman–Schwinger principle, enabling us in Sect. 4 to complete the proof of Theorems 1 and 2.

Remark 1.2

The space Y satisfies the embedding

$$\begin{aligned} Y \hookrightarrow L^{n,1}({\mathbb {R}}^n) \hookrightarrow L^n({\mathbb {R}}^n), \end{aligned}$$
(1.4)

where \(L^{p,q}({\mathbb {R}}^n)\) denotes Lorentz spaces. Moreover, we have

$$\begin{aligned} W^{1,1}({\mathbb {R}}^n) \hookrightarrow \bigcap _{j=1}^{n} L^1_{{{\widehat{x}}_j}} L^\infty _{x_j}({\mathbb {R}}^n) \hookrightarrow L^{n/(n-1),1}({\mathbb {R}}^n), \end{aligned}$$

where \(W^{m,p}({\mathbb {R}}^n)\) is a Sobolev space. In particular, in dimension 2 we obtain

$$\begin{aligned} W^{1,1}({\mathbb {R}}^2) \hookrightarrow Y = L^1_{x_1} L^\infty _{x_2}({\mathbb {R}}^2) \cap L^1_{x_2} L^\infty _{x_1}({\mathbb {R}}^2) \hookrightarrow L^{2,1}({\mathbb {R}}^2) \hookrightarrow L^{2}({\mathbb {R}}^2). \end{aligned}$$

We refer to Fournier [21], Blei and Fournier [6] and Milman [36] for these inclusions.

Remark 1.3

According to the previous remark we have \(Y({\mathbb {R}}^3) \hookrightarrow L^3({\mathbb {R}}^3)\). Thus in the massive 3-dimensional case the assumption \(\left\Vert V\right\Vert _Y < C_0\) implies both our result, Theorem (1), and the one by Fanelli and Krejčiřík [20], i.e. the eigenvalue bound (1.2). Although our result improves the latter one for large eigenvalues, bounding them in two compact regions, it may happen that, in a neighbourhood of \(z=-m\) and \(z=m\), the bound in (1.2) improves the one stated in Theorem 1.

Indeed, it is not hard to check that, supposing \(\left\Vert V\right\Vert _Y\) sufficiently small, our disks are enclosed in the region found by Fanelli and Krejčiřík if

$$\begin{aligned}&m\frac{{\mathcal {V}}^2+1}{{\mathcal {V}}^2-1} - \sqrt{\left( m\frac{2{\mathcal {V}}}{{\mathcal {V}}^2-1}\right) ^2 - (\mathfrak {I}z)^2 }\nonumber \\&\ge \sqrt{(1-c^2\left\Vert V\right\Vert ^2_{L^3}) m^2 - \left( 1-\frac{1}{c^2 \left\Vert V\right\Vert ^2_{L^3}}\right) (\mathfrak {I}z)^2}, \end{aligned}$$
(1.5)

where

$$\begin{aligned} c = \left( {\pi }/{2} \right) ^{1/3} \sqrt{1+e^{-1}+2e^{-2}}, \quad {\mathcal {V}}= \left[ \frac{4C_0}{\left\Vert V\right\Vert _Y} - 3 \right] ^2. \end{aligned}$$

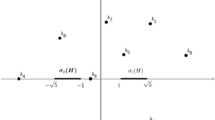
This condition may not always be satisfied and depends on the norms of the potential V in the spaces \(L^3({\mathbb {R}}^3)\) and \(Y({\mathbb {R}}^3)\). If this happens, the result in Theorem 1 and the one in [20] should be jointly taken in consideration for the eigenvalues bound. This situation is illustrated in Fig. 1.

Fig. 1
figure 1

The disks in our Theorem 1, for \(n=3\), are represented in red; the Fanelli–Krejčiřík region [20] defined by (1.2) is in blue; and the spectrum of \({\mathscr {D}}_0\) is in green. When (1.5) holds we are in situation (a) and our result implies the result in [20]; if (1.5) does not hold the two results are not entirely comparable, as shown in picture (b) (color figure online)

Full size image

2 Uniform resolvent estimates

Fix constants \(r,R,\delta >0\) such that

$$\begin{aligned} 1<r<R, \quad \sqrt{R^2-1}< \delta <1, \end{aligned}$$

and consider the open cover \({\mathcal {S}}=\{{\mathcal {S}}^+_{ j}, {\mathcal {S}}^-_{ j}, {\mathcal {S}}_\infty \}_{j\in \{1,\dots ,n\}}\) of the space \({\mathbb {R}}^n\) defined by

$$\begin{aligned} {\mathcal {S}}^\pm _{ j} = \{ \xi \in {\mathbb {R}}^n :\pm \xi _j> \delta |{\widehat{\xi }}_j|, \,\, |\xi |<R \}, \quad {\mathcal {S}}_\infty = \{ \xi \in {\mathbb {R}}^n :|\xi |>r \}. \end{aligned}$$

Let \(\{ \chi ^+_{ j}, \chi ^-_{ j} , \chi _\infty \}_{j\in \{1,\dots ,n\}}\) be a smooth partition of unity subordinate to \({\mathcal {S}}\), that is to say a family of smooth positive functions such that

$$\begin{aligned} {{\,\mathrm{supp}\,}}\chi ^\pm _{ j} \subset {\mathcal {S}}^\pm _{ j}, \quad {{\,\mathrm{supp}\,}}\chi _{\infty } \subset {\mathcal {S}}_{\infty }, \quad \chi _{\infty } + \sum _{j=1}^n [ \chi ^+_{ j} + \chi ^-_{ j} ] \equiv 1. \end{aligned}$$

From these, define the smooth partition of unity \(\chi =\{\chi _j\}_{j\in \{1,\dots ,n\}}\), with

$$\begin{aligned} \chi _j := \chi _j^+ +\chi _j^- + \frac{1}{n}\chi _{ \infty }, \end{aligned}$$
(2.1)

and correspondingly, for \(j\in \{1,\dots ,n\}\), the Fourier multipliers

$$\begin{aligned} \chi _j(|z|^{-1/2} D) f = {\mathscr {F}}^{-1}_\xi [\chi _j(|z|^{-1/2}\xi ) \, {\mathscr {F}}_x f]. \end{aligned}$$

Note in particular that

$$\begin{aligned} \sum _{j=1}^n \chi _j(|z|^{-1/2} D) f = f. \end{aligned}$$
(2.2)

The following estimates hold true.

Lemma 1

For every \(z\in \rho (-\Delta ) = {\mathbb {C}}{\setminus }[0,+\infty )\), \(f \in L_{x_j}^1 L_{{{\widehat{x}}_j}}^2\) and \(j,k \in \{1,\dots ,n\}\), we have that

$$\begin{aligned} \left\Vert \chi _j \left( |z|^{-1/2} D \right) R_{-\Delta }(z) f \right\Vert _{L_{x_j}^\infty L_{{{\widehat{x}}_j}}^2}&\le C \, |z|^{-1/2} \left\Vert f\right\Vert _{L_{x_j}^1 L_{{{\widehat{x}}_j}}^2}, \\ \left\Vert \chi _j \left( |z|^{-1/2} D \right) \partial _k R_{-\Delta }(z) f \right\Vert _{L_{x_j}^\infty L_{{{\widehat{x}}_j}}^2}&\le C \left\Vert f\right\Vert _{L_{x_j}^1 L_{{{\widehat{x}}_j}}^2}, \end{aligned}$$

where \(\{\chi _j\}_{j\in \{1,\dots ,n\}}\) are defined in (2.1) and \(C>0\) does not depend on z.

In particular, it follows that

$$\begin{aligned} \left\Vert R_{-\Delta }(z)\right\Vert _{X \rightarrow X^*} \le C |z|^{-1/2}, \quad \left\Vert \partial _k R_{-\Delta }(z)\right\Vert _{X \rightarrow X^*} \le C. \end{aligned}$$

Lemma 2

For every \(z\in \rho ({\mathscr {D}}_0) = {\mathbb {C}}{\setminus }\{\zeta \in {\mathbb {R}}:|\zeta | \ge m\}\), \(f \in L_{x_j}^1 L_{{{\widehat{x}}_j}}^2\) and \(j\in \{1,\dots ,n\}\) we have that

$$\begin{aligned} \left\Vert \chi _j \left( |z^2-m^2|^{-1/2} D \right) R_{{\mathscr {D}}_{0}}(z) f \right\Vert _{L_{x_j}^\infty L_{{{\widehat{x}}_j}}^2} \le C \left[ n + \left| \frac{z+m}{z-m}\right| ^{{{\,\mathrm{sgn}\,}}(\mathfrak {R}z)/2}\right] \left\Vert f\right\Vert _{L_{x_j}^1 L_{{{\widehat{x}}_j}}^2}, \end{aligned}$$

where \(\{\chi _j\}_{j\in \{1,\dots ,n\}}\) are defined in (2.1) and \(C>0\) is the same as in Lemma 1. In particular, it follows that

$$\begin{aligned} \left\Vert R_{{\mathscr {D}}_{0}}(z) \right\Vert _{X \rightarrow X^*} \le C \left[ n + \left| \frac{z+m}{z-m}\right| ^{{{\,\mathrm{sgn}\,}}(\mathfrak {R}z)/2}\right] . \end{aligned}$$

Remark 2.1

Before we proceed further, we give a heuristic explanation for the choice of the localization in the frequency domain via the Fourier multiplier \(\chi _j(|z|^{-1/2}D)\). Since the symbol \((|\xi |^2-z)^{-1}\) of the resolvent \(R_{-\Delta }(z)\) blows-up as \(z \rightarrow \zeta \), for every fixed \(\zeta \ge 0\), our trick is to use the norms \(L^\infty _{x_j} L^2_{{{\widehat{x}}_j}}\) for \(j\in \{1,\dots ,n\}\), which allows us to restrict the problem from the spherical surface \(\{\xi \in {\mathbb {R}}^n :|\xi |=|z|^{-1/2}\}\) to the “equator” given by \(\{ \xi \in {\mathbb {R}}^n :\xi _j=0, |{\widehat{\xi }}_j|=|z|^{-1/2} \}\). We then avoid these regions thanks to the smooth functions \(\chi _j\).

Proof of Lemma 1

The last two estimates follow trivially from the first two estimates, (2.2) and the definitions of the norms on X and \(X^*\).

For simplicity, from now on \(C>0\) will stand for a generic positive constant independent of z and which may change from line to line. Clearly, by scaling, it is sufficient to consider \(|z|=1\), \(z\ne 1\). Thus we are reduced to prove that

$$\begin{aligned} \left\Vert \chi _j(D) \partial _k^s R_{-\Delta }(z) f \right\Vert _{L_{x_j}^\infty L_{{{\widehat{x}}_j}}^2} \le C \left\Vert f\right\Vert _{L_{x_j}^1 L_{{{\widehat{x}}_j}}^2}, \end{aligned}$$

where \(|z|=1\), \(s\in \{0,1\}\), \(\partial ^0_k=1, \partial ^1_k=\partial _k\) and \(j,k\in \{1,\dots ,n\}\). This is equivalent to

$$\begin{aligned} \left\Vert {\mathscr {F}}^{-1}_{\xi } \left( \frac{\xi _k^s \, \chi _j(\xi ) }{|\xi |^2-\lambda -i\varepsilon } {\mathscr {F}}_{x}f \right) \right\Vert _{L_{x_j}^\infty L_{{{\widehat{x}}_j}}^2} \le C \left\Vert f\right\Vert _{L_{x_j}^1 L_{{{\widehat{x}}_j}}^2}, \end{aligned}$$
(2.3)

where we have written \(z=\lambda +i\varepsilon \), \(\lambda ^2+\varepsilon ^2=1\) and \(z\ne 1\). We proceed by splitting \(\chi _j\) in the functions which appear in its definition (2.1), localizing ourselves in the regions of the frequency domain near the unit sphere, i.e. \({\mathcal {S}}^\pm _j\), and far from it, i.e. \({\mathcal {S}}_\infty \).

Estimate on \({\mathcal {S}}^\pm _j\). We want to prove

$$\begin{aligned} \left\Vert {\mathscr {F}}^{-1}_{\xi } \left( \frac{\xi _k^s \chi _j^\pm (\xi )}{|\xi |^2-\lambda -i\varepsilon } {\mathscr {F}}_{x}f \right) \right\Vert _{L_{x_j}^\infty L_{{{\widehat{x}}_j}}^2} \le C \left\Vert f\right\Vert _{L^2_{{{\widehat{x}}_j}} L^1_{x_j}}. \end{aligned}$$
(2.4)

Let us define the family of operators

$$\begin{aligned} T^\pm _j :L^p_{x_j}L^2_{{{\widehat{x}}_j}} \rightarrow L^p_{x_j}L^2_{{{\widehat{x}}_j}}, \quad f \mapsto T^\pm _j f := {\mathscr {F}}_\xi ^{-1} \left( {\hat{f}} \circ \Phi \right) , \end{aligned}$$

where

$$\begin{aligned} \Phi (\xi ) := (\xi _j+\varphi ({\widehat{\xi }}_j), {\widehat{\xi }}_j), \quad \varphi ({\widehat{\xi }}_j) := \pm \sqrt{|1-|{\widehat{\xi }}_j|^2|}. \end{aligned}$$

Roughly speaking, the operator \(T^\pm _j\) flattens the upper half unit sphere in the frequency domain \(\{ \xi \in {\mathbb {R}}^n :|\xi |=1, \pm \xi _j > 0 \}\). Writing more explicitly these operators, we have

$$\begin{aligned} \begin{aligned} T^\pm _j f(x)&= \frac{1}{(2\pi )^{n/2}} \int _{{\mathbb {R}}^n} e^{i x\cdot \xi } {\hat{f}}(\xi _j+\varphi ({\widehat{\xi }}_j), {\widehat{\xi }}_j) d\xi \\&= \frac{1}{(2\pi )^{n}} \int _{{\mathbb {R}}^n} e^{i x\cdot \xi } \int _{{\mathbb {R}}^n} f(y) e^{-iy \cdot (\xi _j+\varphi ({\widehat{\xi }}_j), {\widehat{\xi }}_j)} dy d\xi \\&= \frac{1}{(2\pi )^{n}} \int _{{\mathbb {R}}^{n-1}} e^{i {{\widehat{x}}_j}\cdot {\widehat{\xi }}_j} \int _{{\mathbb {R}}^{n-1}} e^{-i y'\cdot {\widehat{\xi }}_j} \int _{{\mathbb {R}}}\int _{{\mathbb {R}}} f(y) e^{i (x_j-y_j)\xi _j -i y_j\varphi ({\widehat{\xi }}_j)} dy_j d\xi _j dy'd{\widehat{\xi }}_j \\&= \frac{1}{2\pi } {\mathscr {F}}^{-1}_{{\widehat{\xi }}_j} {\mathscr {F}}_{y'} \left( e^{-i x_j \varphi ({\widehat{\xi }}_j)} \int _{{\mathbb {R}}}\int _{{\mathbb {R}}} f(y) e^{i (x_j-y_j)\xi _j} dy_j d\xi _j \right) \\&= {\mathscr {F}}^{-1}_{{\widehat{\xi }}_j} {\mathscr {F}}_{y'} \left( e^{-i x_j \varphi ({\widehat{\xi }}_j)} f(x_j,y') \right) \end{aligned} \end{aligned}$$

where we used the substitution \(\xi _j\mapsto \xi _j-\varphi ({\widehat{\xi }}_j)\) in the fourth step. Applying the Plancherel Theorem twice, we obtain that \(T^\pm _j\) are isometries on \(L^p_{x_j}L^2_{{{\widehat{x}}_j}}\): for \(p \in [1,+\infty ]\) we have

$$\begin{aligned} \left\Vert T^\pm _j f\right\Vert _{L^p_{x_j}L^2_{{{\widehat{x}}_j}}} = \left\Vert f\right\Vert _{L^p_{x_j}L^2_{{{\widehat{x}}_j}}}. \end{aligned}$$
(2.5)

We can then write

$$\begin{aligned} \begin{aligned} \left\Vert {\mathscr {F}}^{-1}_{\xi } \left( \frac{\xi _k^s \chi _j^\pm (\xi )}{|\xi |^2-\lambda -i\varepsilon } {\mathscr {F}}_{x}f \right) \right\Vert _{L_{x_j}^\infty L_{{{\widehat{x}}_j}}^2}&= \left\Vert T^\pm _j {\mathscr {F}}^{-1}_{\xi } \left( \frac{\xi _k^s \chi _j^\pm (\xi )}{|\xi |^2-\lambda -i\varepsilon } {\mathscr {F}}_{x}f \right) \right\Vert _{L_{x_j}^\infty L_{{{\widehat{x}}_j}}^2} \\&= \left\Vert {\mathscr {F}}_\xi ^{-1} \left( \frac{ (\xi _k^s \chi _j^\pm ) \circ \Phi }{|\Phi |^2-\lambda -i\varepsilon } \, \widehat{T^\pm _j f} \right) \right\Vert _{L^\infty _{x_j}L^2_{{{\widehat{x}}_j}}} \\&= \frac{1}{\sqrt{2\pi }} \left\Vert {a_{\lambda ,\varepsilon }}(D) \psi *_{x_j} {\mathscr {F}}_{\xi _j}^{-1} \left( \frac{\widehat{T^\pm _j f} }{\xi _j-i|\varepsilon |} \right) \right\Vert _{L^\infty _{x_j}L^2_{{\widehat{\xi }}_j}} \\&\le \frac{1}{\sqrt{2\pi }} \left\Vert {a_{\lambda ,\varepsilon }}(D) \psi \right\Vert _{L^1_{x_j}L^{\infty }_{{\widehat{\xi }}_j}} \left\Vert {\mathscr {F}}_\xi ^{-1} \left( \frac{\widehat{T^\pm _j f} }{\xi _j-i|\varepsilon |} \right) \right\Vert _{L^{\infty }_{x_j}L^2_{{\widehat{\xi }}_j}} \end{aligned} \end{aligned}$$

where the last inequality follows from Young’s inequality and

$$\begin{aligned}&{a_{\lambda ,\varepsilon }}(D) \psi ={\mathscr {F}}^{-1}_{\xi _j} \left( a_{\lambda ,\varepsilon } {\mathscr {F}}_{x_j}(\psi ) \right) , \\&a_{\lambda ,\varepsilon } (\xi ) := \frac{(\xi _j-i|\varepsilon |) \, \left( \xi _k \pm \delta _{k,j}\sqrt{1-|{\widehat{\xi }}_j|^2}\right) ^s}{\xi _j \left( \xi _j \pm 2\sqrt{1-|{\widehat{\xi }}_j|^2} \right) +1-\lambda -i\varepsilon } \, \sqrt{(\chi ^\pm _j \circ \Phi )(\xi )} , \\&\psi (x_j,{\widehat{\xi }}_j) = {\mathscr {F}}_{\xi _j}^{-1} \left( \sqrt{(\chi ^\pm _j \circ \Phi )(\xi )}\right) . \end{aligned}$$

Note that we dropped the absolute value in the definition of \(\varphi \), i.e. \(\sqrt{|1-|{\widehat{\xi }}_j|^2|}=\sqrt{1-|{\widehat{\xi }}_j|^2}\), because \({{\,\mathrm{supp}\,}}\{\chi _j^\pm \circ \Phi \} \subset \{\xi \in {\mathbb {R}}^n :|{\widehat{\xi }}_j|\le 1\}\), thanks to the definition of \({\mathcal {S}}^\pm _j\) and the assumption \(\delta \ge \sqrt{R^2-1}\). It is simple to see that \({a_{\lambda ,\varepsilon }}(D) \psi \in {\mathscr {S}}\), where \({\mathscr {S}}\) is the space of Schwartz functions, since \({a_{\lambda ,\varepsilon }}(D) \psi \) is the inverse Fourier transform of a smooth compactly supported function. Moreover, we can consider \({a_{\lambda ,\varepsilon }}(D) \psi \) as a pseudodifferential operator with symbol \(a_{\lambda ,\varepsilon }\) applied to the Schwartz function \(\psi \); letting \(\lambda +i\varepsilon \rightarrow 1\) we have the pointwise convergence

$$\begin{aligned} \lim _{\lambda +i\varepsilon \rightarrow 1} a_{\lambda ,\varepsilon } (\xi ) = \frac{\left( \xi _k \pm \delta _{k,j}\sqrt{1-|{\widehat{\xi }}_j|^2}\right) ^s}{\xi _j \pm 2\sqrt{1-|{\widehat{\xi }}_j|^2}} \, \sqrt{\chi _j^\pm \left( \xi _j\pm \sqrt{1-|{\widehat{\xi }}_j|^2},{\widehat{\xi }}_j \right) } =: a(\xi ) \in {\mathscr {S}} \end{aligned}$$

and hence \({a_{\lambda ,\varepsilon }}(D)\psi \rightarrow {a}(D)\psi \) in \({\mathscr {S}}\) which implies

$$\begin{aligned} \lim _{\lambda +i\varepsilon \rightarrow 1} \left\Vert {a_{\lambda ,\varepsilon }}(D) \psi \right\Vert _{L^1_{x_j}L^\infty _{{\widehat{\xi }}_j}} = \left\Vert a(D)\psi \right\Vert _{L^1_{x_j}L^\infty _{{\widehat{\xi }}_j}} < +\infty . \end{aligned}$$

Thus, \(\left\Vert {a_{\lambda ,\varepsilon }}(D) \psi \right\Vert _{L^1_{x_j}L^\infty _{{\widehat{\xi }}_j}}\) is uniformly bounded respect to \(z\in {\mathbb {C}}\) with \(|z|=1\). We have proved

$$\begin{aligned} \left\Vert {\mathscr {F}}^{-1}_{\xi } \left( \frac{\xi _k^s \chi _j^\pm (\xi )}{|\xi |^2-\lambda -i\varepsilon } {\mathscr {F}}_{x}f \right) \right\Vert _{L_{x_j}^\infty L_{{{\widehat{x}}_j}}^2} \le C \left\Vert {\mathscr {F}}_\xi ^{-1} \left( \frac{\widehat{T^\pm _j f} }{\xi _j-i|\varepsilon |} \right) \right\Vert _{L^{\infty }_{x_j}L^2_{{\widehat{\xi }}_j}}. \end{aligned}$$
(2.6)

By Plancherel’s Theorem and Young’s inequality, and by equality (2.5), we have

$$\begin{aligned} \begin{aligned} \sqrt{2\pi } \left\Vert {\mathscr {F}}_{\xi _j}^{-1} \left( \frac{\widehat{T^\pm _j f} }{\xi _j-i|\varepsilon |} \right) \right\Vert _{L^\infty _{x_j}L^2_{{\widehat{\xi }}_j}}&= \left\Vert {\mathscr {F}}_{\xi _j}^{-1} \left( \frac{1 }{\xi _j-i|\varepsilon |}\right) *_{x_j} {\mathscr {F}}_{{{\widehat{x}}_j}} (T^\pm _j f) \right\Vert _{L^\infty _{x_j}L^2_{{\widehat{\xi }}_j}} \\&= \left\Vert i e^{-|\varepsilon | x_j } \theta *_{x_j} {\mathscr {F}}_{{{\widehat{x}}_j}} (T^\pm _j f) \right\Vert _{L^\infty _{x_j}L^2_{{\widehat{\xi }}_j}} \\&\le \left\Vert e^{-|\varepsilon | x_j } \theta *_{x_j} \left\Vert T^\pm _j f\right\Vert _{L^2_{{{\widehat{x}}_j}}} \right\Vert _{L^\infty _{x_j}} \\&\le \left\Vert e^{-|\varepsilon | x_j } \theta \right\Vert _{L^\infty _{x_j}} \left\Vert f\right\Vert _{L^1_{x_j}L^2_{{{\widehat{x}}_j}}} \\&= \left\Vert f\right\Vert _{L^1_{x_j}L^2_{{{\widehat{x}}_j}}} , \end{aligned} \end{aligned}$$

where \(\theta \equiv \theta (x_j)\) is the Heaviside function. Inserting this in (2.6) we get (2.4).

Estimate on \({\mathcal {S}}_\infty \). We shall now prove that

$$\begin{aligned} \left\Vert {\mathscr {F}}^{-1}_{\xi } \left( \frac{\xi _k^s \chi _\infty (\xi ) }{|\xi |^2-\lambda -i\varepsilon } {\mathscr {F}}_{x}f \right) \right\Vert _{L_{x_j}^\infty L_{{{\widehat{x}}_j}}^2} \le C \left\Vert f\right\Vert _{L^2_{{{\widehat{x}}_j}} L^1_{x_j}}. \end{aligned}$$
(2.7)

We consider three cases, depending on whether we are localized in the regions defined by

$$\begin{aligned} {\mathcal {C}}^{1}_{R,j}&:= \{ \xi \in {\mathbb {R}}^n :|{\widehat{\xi }}_j|>R \}, \\ {\mathcal {C}}^{2}_{R,j}&:= \{ \xi \in {\mathbb {R}}^n :|{\widehat{\xi }}_j|\le R, |\xi _j|\le 2R \}, \\ {\mathcal {C}}^{3}_{R,j}&:= \{ \xi \in {\mathbb {R}}^n :|{\widehat{\xi }}_j|\le R, |\xi _j|> 2R \}. \end{aligned}$$

We set

and observe that \(\chi _\infty = \chi ^1_\infty + \chi ^2_\infty + \chi ^3_\infty \), since \(\chi _\infty \equiv 1\) for \(|\xi |>R\), from the assumptions on the cover \({\mathcal {S}}\) and the partition \(\chi \).

By Plancherel’s Theorem and Hölder’s, Young’s and Minkowski’s integral inequalities, for \(h\in \{1,2,3\}\) we infer

$$\begin{aligned} \left\Vert {\mathscr {F}}^{-1}_{\xi } \left( \frac{\xi _k^s \chi ^h_\infty (\xi )}{|\xi |^2-\lambda -i\varepsilon } {\mathscr {F}}_{x}f \right) \right\Vert _{L_{x_j}^\infty L_{{{\widehat{x}}_j}}^2} \le {C_h} \left\Vert f\right\Vert _{L^1_{x_j} L^2_{{{\widehat{x}}_j}}} \end{aligned}$$

with

$$\begin{aligned} C_h := \frac{1}{\sqrt{2\pi }} \left\Vert {\mathscr {F}}^{-1}_{\xi _j} \left( \frac{\xi _k^s \, \chi ^h_\infty (\xi ) }{\xi _j^2 + \sigma ^2} \right) \right\Vert _{L^\infty _{x_j} L^\infty _{{\widehat{\xi }}_j}}, \quad \sigma :=\sqrt{|{\widehat{\xi }}_j|^2-\lambda -i\varepsilon }. \end{aligned}$$
(2.8)

Here and below, we always consider the principal branch of the complex square root function. Clearly, if we prove that \(C_h\) for \(h\in \{1,2,3\}\) is bounded uniformly with respect to \(\lambda \) and \(\varepsilon \), we recover (2.7).

Estimate on \({\mathcal {C}}^1_{R,j}\). Observing that \(\chi _{ \infty }^1(\xi ) \equiv \chi _{ \infty }^1({\widehat{\xi }}_j)\) and noting that

$$\begin{aligned} \mathfrak {R}\sigma&= \sqrt{ \frac{|\sigma |^2+|{\widehat{\xi }}_j|^2-\lambda }{2} } >0, \end{aligned}$$

we can explicitly compute the Fourier transforms:

  • if \(k \ne j\), then

    $$\begin{aligned} \begin{aligned} C_1 = \left\Vert \chi _\infty ^1({\widehat{\xi }}_j) \xi _k^s \frac{e^{-\sigma |x_j|}}{2\sigma } \right\Vert _{L^\infty _{x_j} L^\infty _{{\widehat{\xi }}_j}}&\le \left\Vert \chi _\infty ^1({\widehat{\xi }}_j) |{\widehat{\xi }}_j|^s \frac{e^{- \mathfrak {R}\sigma |x_j|}}{2|\sigma |} \right\Vert _{L^\infty _{x_j} L^\infty _{{\widehat{\xi }}_j}} \\&\le \sup _{|{\widehat{\xi }}_j|>R} \frac{|{\widehat{\xi }}_j|^s}{2(|{\widehat{\xi }}_j|^4-2\lambda |{\widehat{\xi }}_j|^2+1)^{1/4}} \\&\le {\left\{ \begin{array}{ll} \frac{R^s}{2\sqrt{R^2-1}} &{} \text {if } \lambda >0, \\ 1/2 &{} \text {if } \lambda \le 0; \end{array}\right. } \end{aligned} \end{aligned}$$

  • if \(s=1\), \(k = j\), then

    $$\begin{aligned} C_1 = \left\Vert \chi _\infty ^1({\widehat{\xi }}_j) \frac{i}{2} {{\,\mathrm{sgn}\,}}\{x_j\} e^{-\sigma |x_j|} \right\Vert _{L^\infty _{x_j} L^\infty _{{\widehat{\xi }}_j}} \le \frac{1}{2}. \end{aligned}$$

Estimate on \({\mathcal {C}}^2_{R,j}\). By the definition of the inverse Fourier transform in (2.8) and from the fact that \(\chi ^2_\infty (\xi ) = 0\) when \(|\xi |<r\), we see that

$$\begin{aligned} C_2 \le \frac{1}{2\pi } \left\Vert \int _{-\infty }^{+\infty } \frac{ |e^{i x_j \xi _j}| \, |\xi _k^s| \, \chi ^2_\infty (\xi )}{||\xi |^2-\lambda |} d\xi _j \right\Vert _{L^\infty _{x_j} L^\infty _{{\widehat{\xi }}_j}} \le \frac{(2R)^s}{2\pi } \left\Vert \frac{\chi ^2_\infty (\xi )}{|\xi |^2-1} \right\Vert _{L^\infty _{{\widehat{\xi }}_j} L^1_{\xi _j}} \end{aligned}$$

which is finite since \(\chi ^2_\infty \) is compactly supported due to its definition.

Estimate on \({\mathcal {C}}^3_{R,j}\). By the inverse Fourier transform in (2.8), recalling the definition of \(\chi ^3_\infty \) and exploiting the substitution \(\xi _j \mapsto {{\,\mathrm{sgn}\,}}\{x_j\}\xi _j\), we have

$$\begin{aligned} C_3&= \frac{1}{2\pi } \left\Vert (1-\chi ^1_\infty )({\widehat{\xi }}_j) \int _{|\xi _j|>R} e^{i |x_j| \xi _j} \frac{\xi _k^s }{\xi _j^2 + \sigma ^2} d\xi _j \right\Vert _{L^\infty _{x_j} L^\infty _{{\widehat{\xi }}_j}} \\&= \frac{1}{2\pi } \left\Vert \int _{|\xi _j|>R} \psi (x_j,{\widehat{\xi }}_j,\xi _j) d\xi _j \right\Vert _{L^\infty _{x_j} L^\infty _{{\widehat{\xi }}_j}} \end{aligned}$$

where, for fixed \({\widehat{\xi }}_j, x_j\), the complex function \(\psi (x_j,{\widehat{\xi }}_j,\cdot ) :{\mathbb {C}}\rightarrow {\mathbb {C}}\) is defined by

$$\begin{aligned} \psi (x_j,{\widehat{\xi }}_j,w) := \left\{ \begin{aligned}&(1-\chi ^1_\infty )({\widehat{\xi }}_j) \frac{\xi _k^s}{w^2 + \sigma ^2}e^{i |x_j| w}&\text {if } k\ne j, \\&(1-\chi ^1_\infty )({\widehat{\xi }}_j) \frac{w}{w^2 + \sigma ^2} e^{i |x_j| w}&\text {if } s=1, k=j, \end{aligned} \right. \end{aligned}$$

which is holomorphic in \({\mathbb {C}}{\setminus }\{w_-,w_+\}\), where \(w_\pm = \pm i\sigma \). Observe that \(\psi \equiv 0\) for \(|{\widehat{\xi }}_j|>R\), and if \(|{\widehat{\xi }}_j|\le R\) we have

$$\begin{aligned} |w_\pm | = |\sigma | = \root 4 \of { (|{\widehat{\xi }}_j|^2-\lambda )^2 +\varepsilon ^2 } < \sqrt{2}R . \end{aligned}$$
(2.9)

Define, for a radius \(A>0\), the half circle \( \gamma _A := \{Ae^{i\theta } :\theta \in [0,\pi ] \} \) in the upper half complex plane. Fixing \(\rho >R\), by the Residue Theorem, we get

$$\begin{aligned} \left( \int _{[-\rho ,-2R]} - \int _{\gamma _{2R}} + \int _{[2R,\rho ]} + \int _{\gamma _\rho } \right) \psi (x_j,{\widehat{\xi }}_j,w) dw = 0. \end{aligned}$$

Observing that we can consider \(x_j\ne 0\), letting \(\rho \rightarrow +\infty \) we can apply Jordan’s lemma to the integral on the curve \(\gamma _\rho \), finally getting

$$\begin{aligned} C_3&= \frac{1}{2\pi } \left\Vert \int _{\gamma _{2R}} \psi (x_j, {\widehat{\xi }}_j, w) dw \right\Vert _{L^\infty _{x_j} L^\infty _{{\widehat{\xi }}_j}} \\&\le \frac{(2R)^s}{2\pi } \left\Vert (1-\chi ^1_\infty )({\widehat{\xi }}_j) \int _{0}^{\pi } \frac{d\theta }{|4R^2e^{2i\theta } + \sigma ^2|} \right\Vert _{L^\infty _{{\widehat{\xi }}_j}} \\&\le (2R)^{s-2}, \end{aligned}$$

where we used the relation (2.9).

Summing up, we can finally recover the desired estimate (2.3), where the positive constant C does not depend on \(\lambda \) and \(\varepsilon \), but only on R and the partition \(\chi \). \(\square \)

Lemma 2 is now a straightforward corollary to Lemma 1.

Proof of Lemma 2

Again, the last estimate in the statement follows from the first one, (2.2) and the definition of the X and \(X^*\) norms.

From the anticommutation relations (1.1) we infer, for every \(z\in {\mathbb {C}}\),

$$\begin{aligned} ({\mathscr {D}}_{0} - zI_N)({\mathscr {D}}_{0} + zI_N) = (-\Delta + m^2 -z^2)I_N. \end{aligned}$$

Thus as usual, for \(z\in \rho ({\mathscr {D}}_0)\) we can write

$$\begin{aligned} R_{{\mathscr {D}}_{0}}(z) = ({\mathscr {D}}_{0} +zI_N) R_{-\Delta }(z^2-m^2)I_N. \end{aligned}$$

Write \(f_j = \chi _j(|z^2-m^2|^{-1/2}D)f\). By Lemma 1, it is easy to get

$$\begin{aligned} \begin{aligned} \left\Vert R_{{\mathscr {D}}_{0}}(z) f_j\right\Vert _{L^{\infty }_{x_j} L^2_{{\widehat{x}}_j}} \le&\, \left\Vert \sum _{k=1}^n \alpha _k \partial _k R_{-\Delta }(z^2-m^2) f_j\right\Vert _{L^{\infty }_{x_j} L^2_{{\widehat{x}}_j}} \\&+\left\Vert (m\alpha _0 + z I_{N}) R_{-\Delta }(z^2-m^2) f_j\right\Vert _{L^{\infty }_{x_j} L^2_{{\widehat{x}}_j}} \\ \le&\, \sum _{k=1}^n \left\Vert \partial _k R_{-\Delta }(z^2-m^2) f_j\right\Vert _{L^{\infty }_{x_j} L^2_{{\widehat{x}}_j}} \\&+ \max \{|z+m|, |z-m|\} \left\Vert R_{-\Delta }(z^2-m^2) f_j\right\Vert _{L^{\infty }_{x_j} L^2_{{\widehat{x}}_j}} \\ \le&\, C \left[ n + \left| \frac{z+m}{z-m}\right| ^{{{\,\mathrm{sgn}\,}}(\mathfrak {R}z)/2}\right] \left\Vert f\right\Vert _{L^{1}_{x_j} L^2_{{\widehat{x}}_j}} \end{aligned} \end{aligned}$$

as claimed. \(\square \)

3 The Birman–Schwinger principle

In this section, following the approach of Kato [31] and Konno and Kuroda [34], we define in a rigorous way the closed extension of a perturbed operator with a factorizable potential, formally defined as \(H_0+B^*A\), in order to give an abstract version of the Birman–Schwinger principle. We mention also the recent work [30] by Hansmann and Krejčiřík, where, among others, a nice and innovative approach is developed to deal with the embedded eigenvalues.

Let \({\mathfrak {H}}, {\mathfrak {H}}'\) be Hilbert spaces and consider the densely defined, closed linear operators

$$\begin{aligned} H_0 :{{\,\mathrm{dom}\,}}(H_0) \subseteq {\mathfrak {H}}\rightarrow {\mathfrak {H}}, \quad A :{{\,\mathrm{dom}\,}}(A) \subseteq {\mathfrak {H}}\rightarrow {\mathfrak {H}}', \quad B :{{\,\mathrm{dom}\,}}(B) \subseteq {\mathfrak {H}}\rightarrow {\mathfrak {H}}', \end{aligned}$$

such that \(\rho (H_0) \ne \varnothing \) and

$$\begin{aligned} {{\,\mathrm{dom}\,}}(H_0) \subseteq {{\,\mathrm{dom}\,}}(A), \quad {{\,\mathrm{dom}\,}}(H_0^*) \subseteq {{\,\mathrm{dom}\,}}(B). \end{aligned}$$

For simplicity, we assume also that \(\sigma (H_0) \subset {\mathbb {R}}\). For \(z\in \rho (H_0)\), denote by \(R_{H_0}(z)=(H_0-z)^{-1}\) the resolvent operator of \(H_0\).

The idea of the principle is easy to explain in the case of bounded operators A and B. Then \(H=H_0+B^*A\) is well defined as a sum of operators, and if \(z\in \rho (H_0)\), the Birman–Schwinger operator

$$\begin{aligned} Q(z)=A(H_0-z)^{-1}B^* \end{aligned}$$

is also a bounded operator. One checks immediately that \(z\in \sigma _p(H)\cap \rho (H_0)\) implies \(-1\in \sigma _p(Q(z))\), and so \(\left\Vert Q(z)\right\Vert _{{\mathfrak {H}}'\rightarrow {\mathfrak {H}}'} \ge 1\). Hence, a bound for the norm of Q(z) gives information on the localization of the non-embedded eigenvalues of H.

We now return to the general case of an unbounded \(B^*A\). As in [34], we assume the following set of assumptions.

Assumption 1

For some, and hence for all, \(z\in \rho (H_0)\), the operator \(AR_{H_0}(z)B^*\), densely defined on \({{\,\mathrm{dom}\,}}(B^*)\), has a closed extension Q(z) in \({\mathfrak {H}}'\),

$$\begin{aligned} Q(z) = \overline{AR_{H_0}(z)B^*}, \end{aligned}$$

which we call the Birman–Schwinger operator, with norm bounded by

$$\begin{aligned} \left\Vert Q(z)\right\Vert _{{\mathfrak {H}}'\rightarrow {\mathfrak {H}}'} \le \Lambda (z) \end{aligned}$$
(3.1)

for some function \(\Lambda :\rho (H_0) \rightarrow {\mathbb {R}}_+\).

Assumption 2

There exists \(z_0 \in \rho (H_0)\) such that \(-1 \in \rho (Q(z_0))\).

Observe that the last assumption is implied by the following one:

Assumption B’. There exists \(z_0 \in \rho (H_0)\) such that \(\Lambda (z_0)<1\).

Indeed, assuming Assumptions A and B’, we get that \(\left\Vert Q(z_0)\right\Vert _{{\mathfrak {H}}'\rightarrow {\mathfrak {H}}'} < 1\). Thus, expanding in a Neumann series, we see that \((1+Q(z_0))^{-1}\) exists and hence \(-1\in \rho (Q(z_0))\).

Let us collect some useful facts in the next lemma.

Lemma 3

Suppose Assumptions A and B and let \(z, z_1, z_2 \in \rho (H_0)\). Then the following holds true:

  1. (i)

    \(AR_{H_0}(z) \in {\mathcal {B}}({\mathfrak {H}},{\mathfrak {H}}'), \quad \overline{R_{H_0}(z)B^*} = [B(H_0^*-{\overline{z}})^{-1}]^* \in {\mathcal {B}}({\mathfrak {H}}',{\mathfrak {H}})\),

  2. (ii)

    \(\overline{R_{H_0}(z_1)B^*}-\overline{R_{H_0}(z_2)B^*} = (z_1-z_2) R_{H_0}(z_1) \overline{R_{H_0}(z_2)B^*} = (z_1-z_2) R_{H_0}(z_2) \overline{R_{H_0}(z_1)B^*}\),

  3. (iii)

    \(Q(z) = A\overline{R_{H_0}(z)B^*}\),    \(Q({\overline{z}})^* = B\overline{R_{H_0}({\overline{z}})^* A^*}\),

  4. (iv)

    \({{\,\mathrm{ran}\,}}(\overline{R_{H_0}(z)B^*}) \subseteq {{\,\mathrm{dom}\,}}(A), \quad {{\,\mathrm{ran}\,}}(\overline{R_{H_0}({\overline{z}})^* A^*}) \subseteq {{\,\mathrm{dom}\,}}(B)\),

  5. (v)

    \(Q(z_1) -Q(z_2) = (z_1-z_2) AR_{H_0}(z_1) \overline{R_{H_0}(z_2)B^*} = (z_1-z_2) AR_{H_0}(z_2) \overline{R_{H_0}(z_1)B^*}\).

Proof

See Lemma 2.2 in [29]. \(\square \)

We can construct now the extension of the perturbed operator \(H_0+B^*A\).

Lemma 4

(Extension of operators with factorizable potential) Suppose Assumptions A and B. Let \(z_0 \in \rho (H_0)\) such that \(-1\in \rho (Q(z_0))\). Then the operator

$$\begin{aligned} R_{H}(z_0) = R_{H_0}(z_0) - \overline{R_{H_0}(z_0)B^*} (1+Q(z_0))^{-1} AR_{H_0}(z_0) \end{aligned}$$
(3.2)

defines a densely defined, closed, linear operator H in \({\mathfrak {H}}\) which has \(R_{H}(z_0)\) as resolvent and which extends \(H_0 + B^*A\).

Proof

We refer to Theorem 2.3 in [29]. See also the work by Kato [31]. \(\square \)

We can finally formulate the abstract Birman–Schwinger principle.

Lemma 5

(Birman–Schwinger principle) Suppose Assumptions A and B. Let \(z_0 \in \rho (H_0)\) such that \(-1\in \rho (Q(z_0))\) and H be the extension of \(H_0+B^*A\) given by Lemma 4. Fix \(z \in \sigma _p(H)\) with eigenfunction \(0\ne \psi \in {{\,\mathrm{dom}\,}}(H)\), i.e. \(H\psi =z\psi \), and set \(\phi := A\psi \).

Then \(\phi \ne 0\), and in addition

  1. (i)

    if \(z \in \rho (H_0)\) then

    $$\begin{aligned} Q(z)\phi = -\phi \end{aligned}$$

    and in particular

    $$\begin{aligned} 1 \le \left\Vert Q(z)\right\Vert _{{\mathfrak {H}}'\rightarrow {\mathfrak {H}}'} \le \Lambda (z); \end{aligned}$$
  2. (ii)

    if \(z\in \sigma (H_0){\setminus }\sigma _p(H_0)\) and if \(H_0\) is self-adjoint, then

    $$\begin{aligned} \lim _{\varepsilon \rightarrow 0^\pm } Q(z+i\varepsilon ) \phi = -\phi \quad \text {weakly,} \end{aligned}$$

    id est

    $$\begin{aligned} \lim _{\varepsilon \rightarrow 0^\pm } (\varphi ,Q(z+i\varepsilon )\phi )_{{\mathfrak {H}}'} = -(\varphi , \phi )_{{\mathfrak {H}}'} \end{aligned}$$
    (3.3)

    for every \(\varphi \in {\mathfrak {H}}'\), where \((\cdot ,\cdot )_{{\mathfrak {H}}'}\) is the scalar product on \({\mathfrak {H}}'\). In particular

    $$\begin{aligned} 1 \le \liminf _{\varepsilon \rightarrow 0^\pm } \left\Vert Q(z+i\varepsilon )\right\Vert _{{\mathfrak {H}}'\rightarrow {\mathfrak {H}}'} \le \liminf _{\varepsilon \rightarrow 0^\pm } \Lambda (z+i\varepsilon ). \end{aligned}$$
    (3.4)

Proof

Let \(\varepsilon =0\) if \(z\in \rho (H_0)\) and \(\varepsilon \ne 0\) if \(z\in \sigma (H_0){\setminus }\sigma _p(H_0)\). In order to treat the embedded eigenvalues, we will adapt the argument of Lemma 1 in [34] together with the limiting argument from Theorem 8 in [30].

Note that \(H\psi =z \psi \) is equivalent to

$$\begin{aligned} \psi = (z-z_0) R_{H}(z_0) \psi , \end{aligned}$$
(3.5)

and hence we obtain from (3.2) that

$$\begin{aligned}&(H_0 - z -i\varepsilon ) R_{H_0}(z_0) \psi = -(z-z_0) \overline{R_{H_0}(z_0)B^*} (1+Q(z_0))^{-1} AR_{H_0}(z_0) \psi \nonumber \\&-i\varepsilon R_{H_0}(z_0) \psi . \end{aligned}$$
(3.6)

Define \({\widetilde{\psi }}=(1+Q(z_0))^{-1} AR_{H_0}(z_0)\psi \). If \({\widetilde{\psi }}=0\), by (3.6) follows \((H_0-z)R_{H_0}(z_0)\psi =0\). Since \(0\ne R_{H_0}(z_0)\psi \in {{\,\mathrm{dom}\,}}(H_0)\), we get \(z\in \sigma _p(H_0)\), which contradicts the assumption on z. Thus, we proved \({\widetilde{\psi }}\ne 0\). Moreover, we can show the identity

$$\begin{aligned} \phi = A\psi = (z-z_0) (1+Q(z_0))^{-1} AR_{H_0}(z_0)\psi = (z-z_0) {\widetilde{\psi }}, \end{aligned}$$
(3.7)

from which in particular \(\phi \ne 0\). Indeed, by (3.2) and (iii) of Lemma 3, it follows that

$$\begin{aligned} AR_{H}(z_0) = (1+Q(z_0))^{-1}AR_{H_0}(z_0) \end{aligned}$$

which combined with (3.5) gives us (3.7).

Multiplying by \((1+Q(z_0))^{-1} AR_{H_0}(z+i\varepsilon )\) both sides of (3.6), we obtain

$$\begin{aligned} \begin{aligned} {\widetilde{\psi }} =&-(z-z_0) (1+Q(z_0))^{-1} A R_{H_0}(z+i\varepsilon ) \overline{R_{H_0}(z_0)B^*} {\widetilde{\psi }} \\&- i\varepsilon (1+Q(z_0))^{-1} A R_{H_0}(z+i\varepsilon ) R_{H_0}(z_0) \psi \end{aligned} \end{aligned}$$

and so, by (v) of Lemma 3 and by the resolvent identity, we have

$$\begin{aligned} \begin{aligned} {\widetilde{\psi }} =&- \frac{z-z_0}{z-z_0+i\varepsilon } (1+Q(z_0))^{-1} [Q(z+i\varepsilon ) - Q(z_0)] {\widetilde{\psi }} \\&- \frac{i\varepsilon }{z-z_0+i\varepsilon } (1+Q(z_0))^{-1} A [R_{H_0}(z+i\varepsilon ) - R_{H_0}(z_0)] \psi \\ =&\, {\widetilde{\psi }} - \frac{z-z_0}{z-z_0+i\varepsilon } (1+Q(z_0))^{-1} (1+Q(z+i\varepsilon )){\widetilde{\psi }} \\&- \frac{i\varepsilon }{z-z_0+i\varepsilon } (1+Q(z_0))^{-1} A R_{H_0}(z+i\varepsilon )\psi , \end{aligned} \end{aligned}$$

from which, using identity (3.7), we finally arrive at

$$\begin{aligned} Q(z+i\varepsilon ) \phi = -\phi - i\varepsilon A R_{H_0}(z+i\varepsilon )\psi . \end{aligned}$$
(3.8)

If \(z\in \rho (H_0)\), then \(\varepsilon =0\) and we completely proved case (i), the “in particular” part being straightforward.

In the following, we suppose \(z\in \sigma (H_0){\setminus }\sigma _p(H_0)\) and \(H_0\) self-adjoint. Fixed \(\varphi \in {\mathfrak {H}}'\), we get from (3.8) that

$$\begin{aligned} (\varphi , Q(z+i\varepsilon ) \phi )_{{\mathfrak {H}}'}&= -(\varphi , \phi )_{{\mathfrak {H}}'} - i\varepsilon (\varphi , A R_{H_0}(z+i\varepsilon )\psi )_{{\mathfrak {H}}'} \\&=: -(\varphi , \phi )_{{\mathfrak {H}}'} + I_{\varepsilon }. \end{aligned}$$

Exploiting the Spectral Theorem and denoting the spectral measure of \(H_0\) as \(E_0\), we have

$$\begin{aligned} I_{\varepsilon } =\int _{\sigma (H_0)} f_{\varepsilon }(\lambda ) d(\varphi ,A E_0(\lambda ) \psi )_{{\mathfrak {H}}'}, \quad \text {where} \quad f_{\varepsilon }(\lambda ) := \frac{-i\varepsilon }{\lambda -z-i\varepsilon }. \end{aligned}$$

From the fact that

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0^\pm } f_{\varepsilon }(\lambda ) = \left\{ \begin{aligned}&0&\text {if } \lambda \ne z, \\&1&\text {if } \lambda = z, \end{aligned} \right. \end{aligned}$$

and \(E_0(\{z\})=0\) since \(z \not \in \sigma _p(H_0)\), we infer that \(f_{\varepsilon } \rightarrow 0\) as \(\varepsilon \rightarrow 0^{\pm }\) almost everywhere with respect to the spectral measure. Moreover

$$\begin{aligned} |f_\varepsilon (\lambda )|=\frac{|\varepsilon |}{\sqrt{(\lambda -z)^2+\varepsilon ^2}} \le 1 \quad \text {and}\quad \int _{\sigma (H_0)} d(\varphi ,AE_0(\lambda )\psi )_{{\mathfrak {H}}'} = (\varphi ,A\psi )_{{\mathfrak {H}}'}, \end{aligned}$$

hence by dominated converge theorem we conclude that \(I_{\varepsilon } \rightarrow 0\) as \(\varepsilon \rightarrow 0^\pm \), proving (3.3).

Finally, since by (3.3) we have

$$\begin{aligned} \left\Vert \phi \right\Vert _{{\mathfrak {H}}'}^2 = |(\phi , \phi )_{{\mathfrak {H}}'}| = \lim _{\varepsilon \rightarrow 0^{\pm }} |(\phi , Q(z+i\varepsilon )\phi )_{{\mathfrak {H}}'}| \le \left\Vert \phi \right\Vert _{{\mathfrak {H}}'}^2 \liminf _{\varepsilon \rightarrow 0^{\pm }} \left\Vert Q(z+i\varepsilon )\right\Vert _{{\mathfrak {H}}'\rightarrow {\mathfrak {H}}'} \end{aligned}$$

we get the first inequality in (3.4), while the second one is obvious by Assumption A. \(\square \)

4 Proof of the Theorems

We can now specialize to our problem the abstract theory developed in the last section. We choose \({\mathfrak {H}}={\mathfrak {H}}'=L^2({\mathbb {R}}^n;{\mathbb {C}}^N)\) and \(H_0\) the free Dirac operator \({\mathscr {D}}_{0}\). The factorization of V is given using the polar decomposition \(V=UW\) where \(W=(V^* V)^{1/2}\) and the unitary matrix U is a partial isometry: then we may set \(A=W^{1/2}\) and \(B=W^{1/2}U^*\). It is easy to see that Assumption A holds thanks to Lemma 2 with

$$\begin{aligned} \Lambda (z):=nC \left\Vert V\right\Vert _Y \left[ n + \left| \frac{z+m}{z-m}\right| ^{{{\,\mathrm{sgn}\,}}(\mathfrak {R}z)/2}\right] . \end{aligned}$$

Indeed, for \(\varphi \in C_0^\infty ({\mathbb {R}}^n;{\mathbb {C}}^N)\),

$$\begin{aligned} \begin{aligned} \left\Vert A R_{{\mathscr {D}}_{0}}(z) B^* \varphi \right\Vert _{{\mathfrak {H}}}&\le \sum _{j=1}^{n} \left\Vert A \, \chi _j(|z^2-m^2|^{-1/2}D) R_{{\mathscr {D}}_{0}}(z) B^* \varphi \right\Vert _{{\mathfrak {H}}} \\&\le C \left[ n + \left| \frac{z+m}{z-m}\right| ^{{{\,\mathrm{sgn}\,}}(\mathfrak {R}z)/2}\right] \sum _{j=1}^{n} \left\Vert A\right\Vert _{L^2_{x_j} L^\infty _{{\widehat{x}}_j}} \left\Vert B^* \right\Vert _{L^2_{x_j} L^\infty _{{\widehat{x}}_j}} \left\Vert \varphi \right\Vert _{{\mathfrak {H}}} \\&\le \Lambda (z) \left\Vert \varphi \right\Vert _{{\mathfrak {H}}}, \end{aligned} \end{aligned}$$

and hence by density (3.1). We used above the relation

$$\begin{aligned} \left\Vert A\right\Vert _{L^2_{x_j} L^\infty _{{\widehat{x}}_j}} = \left\Vert B^*\right\Vert _{L^2_{x_j} L^\infty _{{\widehat{x}}_j}} = \left\Vert W^{1/2}\right\Vert _{L^2_{x_j} L^\infty _{{\widehat{x}}_j}} = \left\Vert V\right\Vert ^{1/2}_{L^1_{x_j} L^\infty _{{\widehat{x}}_j}}. \end{aligned}$$

We show now that also Assumption B’ holds. To find \(z_0 \in \rho ({\mathscr {D}}_0)\) such that \(\Lambda (z_0)<1\), let us define

$$\begin{aligned} C_0=[n(n+1)C]^{-1}, \quad {\mathcal {V}}= [(n+1)C_0/\left\Vert V\right\Vert _Y - n]^2. \end{aligned}$$

Since from the hypothesis of Theorems 1, 2 we have \(\left\Vert V\right\Vert _Y < C_0\) and so \({\mathcal {V}}>1\), the condition \(1 \le \Lambda (z)\) is equivalent to \({\mathcal {V}}\le |z/z|\) if \(m=0\), and to

$$\begin{aligned} \left( \mathfrak {R}z - {{\,\mathrm{sgn}\,}}(\mathfrak {R}z) m\,\frac{{\mathcal {V}}^2+1}{{\mathcal {V}}^2-1}\right) ^2 + \mathfrak {I}z^2 \le \left( m\,\frac{2{\mathcal {V}}}{{\mathcal {V}}^2-1}\right) ^2 \end{aligned}$$
(4.1)

if \(m>0\). Then, if \(m=0\) it is sufficient to choose \(z_0\in {\mathbb {C}}{\setminus }{\mathbb {R}}\), while if \(m>0\) we take \(z_0 \in \rho ({\mathscr {D}}_0)\) outside the disks in the statement of Theorem 1.

Thus, we can apply Lemma 5, which combined with relation (4.1) and with relation \({\mathcal {V}}\le |z/z|\) proves Theorem 1 and Theorem 2 respectively.

For the final claim in Theorem 2, we will follow the argument in [10] to prove that the potential \(V \in Y = \bigcap _{j=1}^n L^1_{x_j} L^\infty _{{\widehat{x}}_j} ({\mathbb {R}}^n)\) leaves the essential spectrum invariant and that the residual spectrum of \({\mathscr {D}}_V\) is absent. To get the invariance of the essential spectrum, it is sufficient to prove that, fixed \(z \in \rho ({\mathscr {D}}_0)\) such that \(-1\in \rho (Q(z))\), the operator \(A R_{{\mathscr {D}}_0}(z)\) is a Hilbert–Schmidt operator, hence compact. Thus identity (3.2) gives

$$\begin{aligned} R_{{\mathscr {D}}_V}(z) - R_{{\mathscr {D}}_0}(z) = - \overline{R_{{\mathscr {D}}_0}(z) B^*} (1+Q(z))^{-1} A R_{{\mathscr {D}}_0}(z) \end{aligned}$$

from which it follows that \(R_{{\mathscr {D}}_V}(z) - R_{{\mathscr {D}}_0}(z)\) is compact and so, by Theorem 9.2.4 in [17],

$$\begin{aligned} \sigma _e({\mathscr {D}}_V) = \sigma _e({\mathscr {D}}_0) = (-\infty ,-m] \cup [m,\infty ). \end{aligned}$$

To see that \(A R_{{\mathscr {D}}_0}(z)\) is a Hilbert–Schmidt operator, we need to prove that its kernel \(A(x) {\mathscr {K}}(z,x-y)\) is in \(L^2({\mathbb {R}}^n\times {\mathbb {R}}^n;{\mathbb {C}}^N)\), where \({\mathscr {K}}(z,x-y)\) is the kernel of the resolvent \(({\mathscr {D}}_0-z)^{-1}\). By the Young inequality

$$\begin{aligned} \left\Vert A({\mathscr {D}}-z)^{-1}\right\Vert _{HS}^2 = \int _{{\mathbb {R}}^n} \int _{{\mathbb {R}}^n} |A(x)|^2 |{\mathscr {K}}(z,x-y)|^2 dx dy \le \left\Vert V\right\Vert _{L^p} \left\Vert {\mathscr {K}}\right\Vert _{L^{2q}}^2\nonumber \\ \end{aligned}$$
(4.2)

where \(1/p + 1/q =2\). Hence we need to find in which Lebesgue space \(L^{2q}({\mathbb {R}}^n;{\mathbb {C}}^N)\) the kernel \({\mathscr {K}}(z,x)\) lies. For \(z\in \rho (-\Delta )={\mathbb {C}}{\setminus }[0,\infty )\), it is well-known (see e.g. [26]) that the kernel \({\mathscr {K}}_0(z,x-y)\) of the resolvent operator \((-\Delta -z)^{-1}\) is given by

$$\begin{aligned} {\mathscr {K}}_0(z,x-y) = \frac{1}{(2\pi )^{n/2}} \left( \frac{\sqrt{-z}}{|x-y|}\right) ^{\frac{n}{2}-1} K_{\frac{n}{2}-1} (\sqrt{-z}|x-y|) \end{aligned}$$

where \(K_{\nu }(w)\) is the modified Bessel function of second kind and we consider the principal branch of the complex square root. Fixed now \(z\in \rho ({\mathscr {D}}_0)={\mathbb {C}}{\setminus }\{\zeta \in {\mathbb {R}}:|\zeta |\ge m\}\), from the identity

$$\begin{aligned} ({\mathscr {D}}_0-zI_N)^{-1} = ({\mathscr {D}}_0+zI_N)(-\Delta +m^2-z^2)^{-1}I_N \end{aligned}$$

and relations 9.6.26 in [1] for the derivative of the modified Bessel functions, we obtain

$$\begin{aligned} {\mathscr {K}}(z,x-y)&= \frac{1}{(2\pi )^{n/2}} \left( \frac{k(z)}{|x-y|}\right) ^{\frac{n}{2}} {\varvec{\alpha }} \cdot (x-y) K_{\frac{n}{2}}(k(z) |x-y|) \\&\quad + \frac{1}{(2\pi )^{n/2}} \left( \frac{k(z)}{|x-y|}\right) ^{\frac{n}{2}-1} (m\alpha _0+z) K_{\frac{n}{2}-1} (k(z) |x-y|) \end{aligned}$$

where for simplicity \(k(z) = \sqrt{m^2-z^2}\). From the limiting form for the modified Bessel functions

$$\begin{aligned} K_{\nu }(w)&\sim \frac{1}{2} \Gamma (\nu ) \left( \frac{w}{2}\right) ^{-\nu }&\text {for } \mathfrak {R}\nu >0 \text { and } w \rightarrow 0, \\ K_{0}(w)&\sim -\ln w&\text {for } w \rightarrow 0, \\ K_\nu (w)&\sim \sqrt{\frac{\pi }{2w}} e^{-w}&\text {for } w\rightarrow \infty \text { in } |\arg w| \le 3\pi /2-\delta , \end{aligned}$$

we obtain that

$$\begin{aligned} \left\Vert {\mathscr {K}}(z,x)\right\Vert \le C(n,m,z) \left\{ \begin{aligned}&|x|^{-(n-1)}&\text {if } |x|\le x_0(n,m,z) \\&|x|^{-(n-1)/2} e^{-\mathfrak {R}k(z) |x|}&\text {if } |x|\ge x_0(n,m,z) \end{aligned} \right. \end{aligned}$$

for some positive constants C(n, m, z), \(x_0(n,m,z)\) depending on z. Hence it is clear that \({\mathscr {K}}(z,x) \in L^{2q}({\mathbb {R}}^n; {\mathbb {C}}^N)\) for \(2q<n/(n-1)\) and, consequently, from equation (4.2) we have that \(A({\mathscr {D}}_0-z)^{-1}\) is a Hilbert–Schmidt operator if \(V \in L^p({\mathbb {R}}^n;{\mathbb {C}}^N)\) for \(p>n/2\). Since by (1.4) we have \(V \in L^n({\mathbb {R}}^n;{\mathbb {C}}^N)\), the proof of the identity \(\sigma _e({\mathscr {D}}_V)=\sigma _e({\mathscr {D}}_0)\) is complete.

Finally, to get the absence of residual spectrum, since \(\rho ({\mathscr {D}}_0)={\mathbb {C}}{\setminus }\sigma _e({\mathscr {D}}_0)\) is composed by one, or two in the massless case, connected components which intersect \(\rho ({\mathscr {D}}_V)\) in a non-empty set, by Theorem XVII.2.1 in [28] we have \( \sigma ({\mathscr {D}}_V) {\setminus } \sigma _e({\mathscr {D}}_V) = \sigma _d({\mathscr {D}}_V). \)