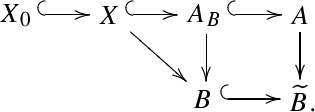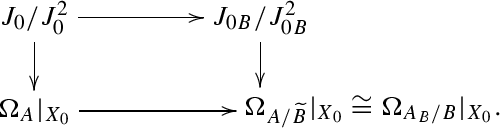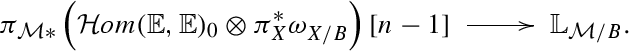Erratum to: Deformation-obstruction theory for complexes via Atiyah and Kodaira–Spencer classes

1 Erratum to: Math. Ann. (2010) 346:545–569 DOI 10.1007/s00208-009-0397-6

Fabian Langholf and Pierrick Bousseau pointed out that Lemma 2.2 in the Original publication requires $X$ and $A$ to be flat over the base $B$. For instance the sequence (2.4) in Proof of Lemma 2.2 is not in general exact without this assumption.

After inserting the assumption of flatness of $X_0,\,X$ and $A$ over $B$, Sects. 2 and 3 can be left unchanged. Applied to $B=\mathrm{Spec}\,k$ with $k$ a field, this is enough to produce virtual cycles in Sect. 4. But to prove their deformation invariance, we need to work with a relative moduli space $\mathcal M/B$ whose flatness over $B$ cannot be assumed. In fact, in the Behrend–Fantechi relative obstruction theory of Sect. 4, flatness of $X$ and $X_0$ over the base does not hold in general, so we prefer to proceed as follows.¹

• Throughout Sects. 2 and 3 we set $B=\mathrm{Spec}\,k$ with $k$ a field. All necessary flatness assumptions are then automatic. Thus, without further modifications, the paper defines the absolute, rather than relative, truncated Atiyah class $A(E_0)$ and the absolute truncated Kodaira–Spencer class $\kappa (X_0/X)$. Then Corollary 3.4 proves that their product

  $$\begin{aligned} \left( \mathrm{id}_{E_0}\otimes \kappa (X_0/X)\right) \circ A(E_0)\,\in \,\mathrm{Ext}^2_{X_0}\left( E_0,E_0\otimes I\right) \end{aligned}$$

  (1.1)

  is the obstruction to deforming a perfect complex $E_0$ from $X_0$ to its thickening $X$.

• To define relative versions of these objects we first need to define the relative truncated cotangent complex. To do this we embed $X_0\subset X$ as follows:

  

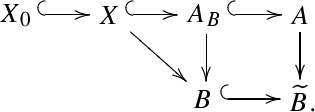
  Here $\widetilde{B}$ and $A\rightarrow \widetilde{B}$ are both smooth, and the square is Cartesian (i.e. $A_B=A\times _B\widetilde{B}$). Thus $A$ and $A_B\rightarrow B$ are also smooth. Letting $J_{0B}$ denote the ideal sheaf of $X_0\subset A_B$ we get the natural commutative diagram

  

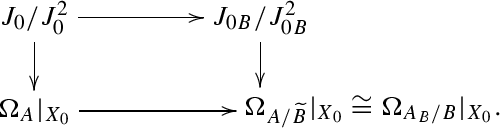
  The vertical 2-complex on the left is $\mathbb {L}_{X_0}$ and we define $\mathbb {L}_{X_0/B}$ to be the vertical 2-term complex on the right, giving the projection

  $$\begin{aligned} \mathbb {L}_{X_0}\rightarrow \mathbb {L}_{X_0/B}. \end{aligned}$$

  (1.2)

  Applied to the Atiyah class $A(E_0)\in \mathrm{Ext}^1_{X_0}(E_0,E_0\otimes \mathbb {L}_{X_0})$ this defines a relative Atiyah class $A(E_0/B)\in \mathrm{Ext}^1_{X_0}(E_0,E_0\otimes \mathbb {L}_{X_0/B})$. The natural map $J_0/J_0^2\rightarrow I$ factors through $J_{0B}/J_{0B}^2\rightarrow I$. The former defines the Kodaira–Spencer class $\kappa (X_0/X):\mathbb {L}_{X_0}\rightarrow I[1]$, so using the latter to define the relative Kodaira–Spencer class $\kappa (X_0/X/B):\mathbb {L}_{X_0/B}\rightarrow I[1]$ we see they commute with the projection (1.2). Thus the product of the relative Atiyah class and the relative Kodaira–Spencer class equals the product (1.1) of their absolute versions:

  $$\begin{aligned} \left( \mathrm{id}_{E_0}\!\otimes \!\kappa (X_0/X/B)\right) \!\circ \! A(E_0/B) \!=\!\left( \mathrm{id}_{E_0}\!\otimes \!\kappa (X_0/X)\right) \!\circ \! A(E_0) \!\in \! \mathrm{Ext}^2_{X_0}\left( E_0,E_0\!\otimes \! I\right) \!.\nonumber \\ \end{aligned}$$

  (1.3)

• Finally, in Sect. 4, we project the Atiyah class $A(\mathbb {E})\in \mathrm{Ext}^1_{X\times _B{\mathcal {M}}} (\mathbb {E},\mathbb {E}\otimes \mathbb {L}_{X\times _B{\mathcal {M}}})$ of the universal sheaf $\mathbb {E}$ by $\mathbb {L}_{X\times _B{\mathcal {M}}}\rightarrow \mathbb {L}_{X\times _B{\mathcal {M}}/X}=\pi _{\mathcal {M}}^*\mathbb {L}_{{\mathcal {M}}/B}$ to give Eq. 4.2:

  

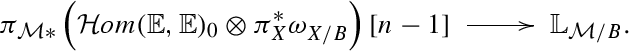
The proof that this is a perfect obstruction theory proceeds without change using the relative classes defined above. As in Eq. 4.5 we end up with an obstruction class expressed as a product of a relative truncated Atiyah class $A(\bar{f}^*\mathbb {E}/X)$ and a relative truncated Kodaira–Spencer class $\kappa (X\times _BS_0/X\times _BS/X)=\bar{\pi }^*\kappa (S_0/S/B)$.

This equals the product of the corresponding absolute classes by (1.3). By Corollary 3.4, this equals the obstruction to deforming $\bar{f}^*\mathbb {E}$ from $X\times _BS_0$ to $X\times _BS$. Since such deformations are in one-to-one correspondence with extensions from $S_0$ to $S$ of the $B$-map $f$, the proof concludes just as in Original publication.