Skip to main content
SpringerLink
Log in

Forced Convection Heat Transfer of Nanofluids in a Porous Channel

  • Published:
Transport in Porous Media Aims and scope Submit manuscript

Abstract

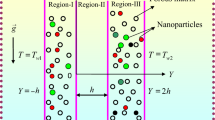
This article is concerned with the effects of flow and migration of nanoparticles on heat transfer in a straight channel occupied with a porous medium. Investigation of force convective heat transfer of nanofluids in a porous channel has not been considered completely in the literature and this challenge is generally considered to be an open research topic that may require more study. The fully developed flow and steady Darcy–Brinkman–Forchheimer equation is employed in porous channel. The thermal equilibrium model is assumed between nanofluid and solid phases. It is assumed that the nanoparticles are distributed non-uniformly inside the channel. As a result the volume fraction distribution equation is also coupled with governing equations. The effects of parameters such as Lewis number, Schmidt number, Brownian diffusion, and thermophoresis on the heat transfer are completely studied. The results show that the local Nusselt number is decreased when the Lewis number is increased. It is observed that as the Schmidt number is increased, the wall temperature gradient is decreased and as a consequence the local Nusselt number is decreased. The effects of Lewis number, Schmidt number, and modified diffusivity ratio on the volume fraction distribution are also studied and discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

x, y :

Cartesian coordinate (m)

u :

Axial velocity (ms−1)

K :

Permeability (m2)

Da :

Darcy number

P :

Pressure (Nm−2)

T :

Temperature (K)

D T :

Thermophoretic diffusion coefficient (m2 s−1)

D B :

Brownian diffusion coefficient (m2 s−1)

H :

Half length of channel

t :

Time (s)

Re :

Reynolds number

Pr :

Prandtl number

N BT :

Brownian motion parameter

k :

Thermal conductivity (Wm−1 K−1)

Le :

Lewis number

Sc :

Schmidt number

μ :

Viscosity (kg m−1 s−1)

\({\varepsilon}\) :

Porosity

ρ :

Density (kgm−3)

\({{\varphi}}\) :

Volume fraction

σ :

Thermal capacity ratio

Δ:

Inertia parameter

α :

Effective thermal diffusivity (m2 s−1)

τ :

Modified diffusivity ratio

f:

Fluid

m:

Porous media

p:

Particle

c:

Reference

*:

Dimensionless variables

References

  • Behzadmehr A., Saffar-Avval M., Galanis N.: Prediction of turbulent forced convection of a nanofluid in tube with uniform heat flux using a two phase approach. Int. J. Heat Fluid Flow 28, 211–219 (2007)

    Article  Google Scholar 

  • Bejan A.: Convective heat transfer, 3rd edn. Wiley, Hoboken (2003)

    Google Scholar 

  • Buongiorno J.: Convection transport in nanofluid. ASME J. Heat transf. 128, 240–250 (2006)

    Article  Google Scholar 

  • Choi S.U.S.: Enhancing thermal conductivity of fluid with nanoparticles. Dev. Appl Non-Newtonian Flows 66, 99–105 (1995)

    Google Scholar 

  • Duangthongsuk W., Wongwises S.: Heat transfer enhancement and pressure drop characteristics of TiO 2-water nanofluid in a double-tube counter flow heat exchangers. Int. J. Heat Mass Transf. 52, 2059–2067 (2009)

    Article  Google Scholar 

  • Epperson J.F.: An introduction to numerical methods and analysis. Wiley, Oxford (2010)

    Google Scholar 

  • Heris S.Z., Etemad S.Gh., Esfahani M.N.: Experimental investigation of oxide nanofluid laminar forced flow convective heat transfer. Int. Comm. Heat Mass Transf. 33, 529–535 (2006)

    Article  Google Scholar 

  • Heyhat, M.M., Kowsary, F.: Effect of particle migration on flow and convective heat transfer of nanofluids flowing through a circular pipe. ASME J. Heat Transf. 132, 062401 (2010)

    Google Scholar 

  • Kuznetsov A.V.: Analytical study of fluid flow and heat transfer during forced convection in a composite channel partly filled with a Brinkman–Forchheimer porous medium. Flow Turbul. Combust. 60, 173–192 (1998)

    Article  Google Scholar 

  • Kuznetsov A.V., Nield D.A.: Thermal instability in a porous medium saturated by a nanofluid: Brinkman model. Transp. Porous Media 81, 409–422 (2010a)

    Article  Google Scholar 

  • Kuznetsov A.V., Nield D.A.: Effect of local thermal non-equilibrium on the onset of convection in a porous medium layer saturated by a nanofluid. Transp. Porous Media 83, 425–436 (2010b)

    Article  Google Scholar 

  • Kuznetsov A.V., Nield D.A.: The effect of local thermal non-equilibrium on the onset of convection in a porous medium layer saturated by a nanofluid: Brinkman model. J. Porous Media 14, 285–293 (2011a)

    Article  Google Scholar 

  • Kuznetsov A.V., Nield D.A.: Double-diffusive natural convective boundary-layer flow of a nanofluid past a vertical plate. Int. J. Therm. Sci. 50, 712–717 (2011b)

    Article  Google Scholar 

  • Lee J., Mudawar I.: Assessment of the effectiveness of nanofluid for single-phase and two-phase heat transfer in micro-channels. Int. J. Heat Mass Transf. 50, 452–463 (2007)

    Article  Google Scholar 

  • Maiga S.E.B., Nguyen C.T., Galanis N., Roy G.: Heat transfer behaviors of nanofluid in a uniformly heated tube. Superlattices Microstruct. 35, 453–462 (2004)

    Article  Google Scholar 

  • Mirmasoumi S., Behzadmehr A.: Numerical study of laminar mixed convection of a nanofluid in a horizontal tube using two-phase mixture model. App. Therm. Eng. 28, 717–727 (2008)

    Article  Google Scholar 

  • Nield D.A., Kuznetsov A.V., Xiong M.: Thermally developing forced convection in a porous medium: parallel plate channel with walls atuniform temperature, with axial conduction and viscous dissipation effects. Int. J. Heat Mass Transf. 46, 643–651 (2003)

    Article  Google Scholar 

  • Nield D.A., Kuznetsov A.V.: The Cheng-Minkowycz problem for double-diffusive natural convective boundary layer flow in a porous medium saturated by a nanofluid. Int. J. Heat Mass Transf. 54, 374–378 (2011)

    Article  Google Scholar 

  • Nguyen C.T., Galanis N., Polidori G., Fohanno S., Pota C.V., Beche A.L.: An experimental study of confined and submerged impinging jet heat transfer using Al2 O3-water nanofluid. Int. J. Therm. Sci. 48, 401–411 (2009)

    Article  Google Scholar 

  • Patankar S.V.: Numerical Heat Transfer and Fluid Flow. Hemisphere, New York (1980)

    Google Scholar 

  • Santra A.K., Sen S., Chkroborty M.: Study of heat transfer due to laminar flow of copper–water nanofluid through two isothermally heated parallel plates. Int. J. Therm. Sci. 48, 391–400 (2009)

    Article  Google Scholar 

  • Shah R.K., London A.L.: Laminar Flow Forced Convection in Ducts, supplemental to advances heat transfer. Academic, New York (1978)

    Google Scholar 

  • Wang X.Q., Mujumdar A.S.: Heat transfer characteristic of nanofluid: a review. Int. J. Therm. Sci. 46, 1–9 (2007)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Ferdowsi University of Mashhad, Mashhad, Iran

    M. J. Maghrebi

  2. Department of Mechanical Engineering, Shahrood University of Technology, P.O. Box: 3619995161, Shahrood, Iran

    M. Nazari & T. Armaghani

Authors
  1. M. J. Maghrebi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Nazari
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. T. Armaghani
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. Nazari.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Maghrebi, M.J., Nazari, M. & Armaghani, T. Forced Convection Heat Transfer of Nanofluids in a Porous Channel. Transp Porous Med 93, 401–413 (2012). https://doi.org/10.1007/s11242-012-9959-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11242-012-9959-2

Keywords

Search

Navigation