Zusammenfassung
In diesem Kapitel werden die hyperreellen Zahlen eingeführt, welche die reellen Zahlen u. a. um infinite und infinitesimale Zahlen erweitern (lat. infinitus – unendlich (groß), infinitesimal – unendlich klein). Sie ermöglichen es z. B., aus einer infiniten Vergrößerung eines Funktionsgraphen seine Tangenten mit höchstens infinitesimalem Fehler zu bestimmen. Vor der Erfindung der hyperreellen Zahlen konnten Fragestellungen der Analysis exakt nur mit Hilfe des Grenzwert-Formalismus behandelt werden. Heute ist es möglich, entsprechende Aufgaben reell fehlerfrei lediglich durch Rechnen mit hyperreellen Zahlen zu lösen, weil mit diesen weit über die Grenzen der reellen Zahlen hinaus gerechnet werden kann. Ein entscheidender Vorteil dabei ist, dass der aufwendige und abstrakte Grenzwertbegriff entfällt. Hyperreelle Zahlen sind daher ein geeignetes Mittel, Funktionen zu differenzieren und zu integrieren. Deshalb dienen diese Zahlen in diesem Buch als Hilfsmittel für die Differential- und Integralrechnung.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
- 2.
Sie wird in der Nichtstandard-Analysis auch als „Monade“ oder „Halo“ bezeichnet.
- 3.
Eine entsprechende Verabredung zum Nichtschreiben von nachfolgenden Nullen gibt es nicht. Stattdessen wird die Periodenschreibweise \(...\overline{0}\) benutzt.
- 4.
Die hyperreelle Version einer reellen Zahl r wird mit
 bezeichnet und eine Standardzahl in
bezeichnet und eine Standardzahl in 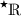 genannt, wenn Verwechslungen möglich erscheinen.
genannt, wenn Verwechslungen möglich erscheinen. - 5.
Zum Beweis der Dreiecksungleichung siehe Abschn. 2.5.1.
- 6.
Man beachte, dass infinitesimale Zahlen zu den finiten Zahlen gehören.
- 7.
Für \(f=0\) gilt \(|f|\cdot |\alpha |=|f|\cdot p=0\).
- 8.
Diverse Beispiele findet man im Abschn. 2.3.5.
- 9.
Der zugehörige Beweisteil stützt sich auf die Dezimaldarstellung hyperreeller Zahlen und wird erst dann komplett, wenn diese vollständig geklärt ist (vgl. Abschn. 2.5.3).
- 10.
Das Verfahren entspricht vollständig der sog. Polynomdivision.
- 11.
Die Sprechweise für \((b_{n}) = (n^{2})\) ist: „Folge \(b_{n}\) ist gleich Folge \(n^{2}\)“.
- 12.
lat.: alternare – abwechseln, schwanken.
- 13.
von Hermann Hankel erstmals 1867 formuliert.
- 14.
In seiner heutigen Fassung nennt man dies das Transferprinzip (vgl. Abschn. 2.5).
- 15.
Solche Folgen werden auch Cauchy-Folgen genannt.
- 16.
Die einzelnen Ergebnisse werden fortlaufend mittels (gv Nr.) gekennzeichnet und am Schluss nochmals zusammengestellt.
- 17.
Dass diese Forderungen wirklich erfüllbar sind, wird zunächst einfach vorausgesetzt. Im Abschn. 2.6 über Zahlbereichserweiterungen findet der interessierte Leser den hier fehlenden Beweis. Dort wird auch gezeigt, dass das Rechnen mit den Äquivalenzklassen unabhängig von Repräsentantenfolgen möglich ist.
- 18.
Hier könnte natürlich genauso gut die Entscheidung getroffen werden, dass die ungeraden Zahlen bereits genügend viele Indizes umfassen. Dann ergäbe sich \(a=1\) und \(b=0\).
- 19.
Der Nachweis, dass ein solches System \(\mathscr {U}\) existiert und die Forderungen sämtlich erfüllt, findet sich im Abschn. 2.6.
- 20.
Auf den unterscheidenden Stern wird verzichtet, weil die Definition 2.9 dafür sorgt, dass sämtliche Eigenschaften der bekannten Relation < erhalten bleiben.
- 21.
Die Zahl \({\varvec{\omega }}\) wird „klein Omega“ gelesen.
- 22.
Nicht zu verwechseln mit der Menge \({\mathbb {N}}^{*} = {\mathbb {N}}\setminus \{0\}\) (gesprochen „\({\mathbb {N}}\) Stern“).
- 23.
Der Stern von „
 “ wird danach wie üblich fortgelassen.
“ wird danach wie üblich fortgelassen. - 24.
Man vergleiche mit Definition 2.6.
- 25.
Der Zusatz \({\mathbb {Q}}\) an \(m_{{\mathbb {Q}}}\) dient dazu, diese Funktion von der Funktion m bei der Erweiterung von \({\mathbb {R}}\) nach
 zu unterscheiden.
zu unterscheiden. - 26.
Die Identifikation unterscheidet sich nicht von der bei der Einbettung von \({\mathbb {Q}}\) in \({\mathbb {R}}\).
- 27.
Man kann daraus ablesen, das alle Begründungen zur Herstellung hyperreeller Zahlen, die in diesem Buch zu finden sind, auf Schulniveau entfallen könnten, deren Entsprechung bei der Herstellung der reellen Zahlen in den Schulen gewöhnlich nicht thematisiert werden.
- 28.
Der Buchstabe \({\mathscr {F}}\) soll darauf hinweisen, dass solche Mengen von Teilmengen T von \({\mathbb {N}}^*\) „Filter“ genannt werden.
Literatur
Keisler, H.J.: Elementary calculus – An infinitesimal approach, 3rd edn. Dover Publications, Mineola (2012)
Keisler, H.J.: Elementary calculus – An infinitesimal approach (revised 2nd edition). http://www.math.wisc.edu/~keisler/calc.html
Robinson, A.: Non-standard analysis. North-Holland Publishing Company, Amsterdam (1966)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2019 Springer-Verlag GmbH Deutschland, ein Teil von Springer Nature
About this chapter
Cite this chapter
Baumann, P., Kirski, T. (2019). Hyperreelle Zahlen. In: Infinitesimalrechnung. Springer Spektrum, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-56792-0_2
Download citation
DOI: https://doi.org/10.1007/978-3-662-56792-0_2
Published:
Publisher Name: Springer Spektrum, Berlin, Heidelberg
Print ISBN: 978-3-662-56791-3
Online ISBN: 978-3-662-56792-0
eBook Packages: Life Science and Basic Disciplines (German Language)


 erfüllt das (klassische) archimedische Axiom nicht mehr (vgl. Fußnote
erfüllt das (klassische) archimedische Axiom nicht mehr (vgl. Fußnote  bezeichnet und eine Standardzahl in
bezeichnet und eine Standardzahl in 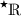 genannt, wenn Verwechslungen möglich erscheinen.
genannt, wenn Verwechslungen möglich erscheinen. “ wird danach wie üblich fortgelassen.
“ wird danach wie üblich fortgelassen. zu unterscheiden.
zu unterscheiden.