Abstract
Compiler correctness proofs for higher-order concurrent languages are difficult: they involve establishing a termination-preserving refinement between a concurrent high-level source language and an implementation that uses low-level shared memory primitives. However, existing logics for proving concurrent refinement either neglect properties such as termination, or only handle first-order state. In this paper, we address these limitations by extending Iris, a recent higher-order concurrent separation logic, with support for reasoning about termination-preserving refinements. To demonstrate the power of these extensions, we prove the correctness of an efficient implementation of a higher-order, session-typed language. To our knowledge, this is the first program logic capable of giving a compiler correctness proof for such a language. The soundness of our extensions and our compiler correctness proof have been mechanized in Coq.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Parallelism and concurrency impose great challenges on both programmers and compilers. In order to make compiled code more efficient and help programmers avoid errors, languages can provide type systems or other features to constrain the structure of programs and provide useful guarantees. The design of these kinds of concurrent languages is an active area of research. However, it is frequently difficult to prove that efficient compilers for these languages are correct, and that important properties of the source-level language are preserved under compilation.
For example, in work on session types [8, 14, 16, 38, 41], processes communicate by sending messages over channels. These channels are given a type which describes the kind of data sent over the channel, as well as the order in which each process sends and receives messages. Often, the type system in these languages ensures the absence of undesired behaviors like races and deadlocks; for instance, two threads cannot both be trying to send a message on the same channel simultaneously.
Besides preventing errors, the invariants enforced by session types also permit these language to be compiled efficiently to a shared-memory target language [39]. For example, because only one thread can be sending a message on a given channel at a time, channels can be implemented without performing locking to send and receive messages. It is particularly important to prove that such an implementation does not introduce races or deadlocks, since this would destroy the very properties that make certain session-typed languages so interesting.
In this paper, we develop a higher-order program logic for proving the correctness of such concurrent language implementations, in a way that ensures that termination is preserved. We have used this program logic to give a machine-checked proof of correctness for a lock-free implementation of a higher-order session-typed language, i.e., a language in which closures and channels can be sent over channels. To our knowledge, this is the first such proof of its kind.
As we describe below, previously developed program logics cannot be used to obtain these kinds of correctness results due to various limitations. In the remainder of the introduction, we will explain why it is so hard to prove refinements between higher-order, concurrent languages. To this end, we first have to provide some background.
Refinement for concurrent languages. To show that a compiler is correct, one typically proves that if a source expression  is well-typed, its translation
is well-typed, its translation  refines
refines  . In the sequential setting, this notion of refinement is easy to defineFootnote 1: (1) if the target program
. In the sequential setting, this notion of refinement is easy to defineFootnote 1: (1) if the target program  terminates in some value v, we expect
terminates in some value v, we expect  to also have an execution that terminates with value v, and (2) if
to also have an execution that terminates with value v, and (2) if  diverges, then
diverges, then  should also have a diverging execution.
should also have a diverging execution.
In the concurrent setting, however, we need to change this definition. In particular, the condition (2) concerning diverging executions is too weak. To see why, consider the following program, where x initially contains 0:
Here, || represents parallel composition of two threads. In every execution where the thread on the right eventually gets to run, this program will terminate. However, the program does have a diverging execution in which only the left thread runs: because x remains 0, the left thread continues to loop. Such executions are “unrealistic” in the sense that generally, we rely on schedulers to be fair and not let a thread starve. As a consequence, for purposes of compiler correctness, we do not want to consider these “unrealistic” executions which only diverge because the scheduler never lets a thread run.
Formally, an infinite execution is said to be fair [23] if every thread which does not terminate in a value takes infinitely many steps.Footnote 2 In the definition of refinement above, we change (2) to demand that if  has a fair diverging execution, then
has a fair diverging execution, then  also has a fair diverging execution. We impose no such requirement about unfair diverging executions. This leads us to fair termination-preserving refinement.
also has a fair diverging execution. We impose no such requirement about unfair diverging executions. This leads us to fair termination-preserving refinement.
Logics for proving refinement. To prove our compiler correct, we need to reason about the concurrent execution and (non)termination of the source and target programs. Rather than reason directly about all possible executions of these programs, we prefer to use a concurrent program logic in order to re-use ideas found in rely-guarantee reasoning [18] and concurrent separation logic [29]. However, although a number of concurrency logics have recently been developed for reasoning about termination and refinements, they cannot be used to prove our compiler correctness result because they either:
Although the limitations are different in each of the above papers, let us focus on the approach by Turon et al. [36] since we will build on it. That paper establishes a termination-insensitive form of refinement, i.e., a diverging program refines every program. Refinement is proven in a higher-order concurrent separation logic which, in addition to the usual points-to assertions  , also provides assertions about the source language’s state. For instance, the assertionFootnote 3
, also provides assertions about the source language’s state. For instance, the assertionFootnote 3  says thread i in the source language’s execution is running expression \(E\). A thread which “owns” this resource is allowed to modify the state of the source program by simulating steps of the execution of \(E\). Then, we can prove that \(e\) refines \(E\) by showing:
says thread i in the source language’s execution is running expression \(E\). A thread which “owns” this resource is allowed to modify the state of the source program by simulating steps of the execution of \(E\). Then, we can prove that \(e\) refines \(E\) by showing:

As usual, the triple enforces that the post-condition holds on termination of \(e\). Concretely for the triple above, the soundness theorem for the logic implies that if target expression \(e\) terminates with a value \(v\), then there is an execution of source expression \(E\) that also terminates with value \(v\). However, the Hoare triple above only expresses partial correctness. That means if \(e\) does not terminate, then the triple above is trivial, and so these triples can only be used to prove termination-insensitive refinements.
Ideally, one would like to overcome this limitation by adapting ideas from logics that deal with termination for first-order state. Notably, Liang et al. [24] have recently developed a logic for establishing fair refinements (as defined above).
However, there is a serious difficulty in trying to adapt these ideas. Semantic models of concurrency logics for higher-order state usually involve step-indexing [2, 5]. In step-indexed logics, the validity of Hoare triples is restricted to program executions of arbitrary but finite length. How can we use these to reason about fairness, a property which is inherently about infinite executions?
In this paper, we show how to overcome this difficulty: the key insight is that when the source language has only bounded non-determinism, step-indexed Hoare triples are actually sufficient to establish properties of infinite program executions. Using this observation, we extend Iris [19, 20], a recent higher-order concurrent separation logic, to support reasoning about fair termination-preserving refinement. The soundness of our extensions to Iris and our case studies have been verified in Coq.
Overview. We start by introducing the case study that we will focus on in this paper: a session-typed source language, a compiler into an ML-like language, and the compiler’s correctness property – fair, termination-preserving refinement (Sect. 2). Then we present our higher-order concurrent separation logic for establishing said refinement (Sect. 3). We follow on by explaining the key changes to Iris that were necessary to perform this kind of reasoning (Sect. 4). We then use the extended logic to prove the correctness of the compiler for our session-typed language (Sect. 5). Finally, we conclude by describing connections to related work and limitations of our approach that we hope to address in future work (Sect. 6).
2 Session-Typed Language and Compiler
This section describes the case study that we chose to demonstrate our logic: a concurrent message-passing language and a type system establishing safety and race-freedom for this language. On top of that, we explain how to implement the message-passing primitives in terms of shared-memory concurrency, i.e., we define a compiler translating the source language into an ML-like target language. Finally, we discuss the desired correctness statement for this compiler.
2.1 Source Language
The source language for our compiler is a simplified version of the language described in Gay and Vasconcelos [14]. The syntax and semantics are given in Fig. 1. It is a functional language extended with primitives for message passing and a command  for creating threads. The semantics is defined by specifying a reduction relation for a single thread, which is then lifted to a concurrent semantics on thread-pools in which at each step a thread is selected non-deterministically to take the next step.
for creating threads. The semantics is defined by specifying a reduction relation for a single thread, which is then lifted to a concurrent semantics on thread-pools in which at each step a thread is selected non-deterministically to take the next step.
Threads can communicate asynchronously with each other by sending messages over channels. For example, consider the following program (which will be a running example of the paper):

The command  creates a new channel and returns two end-points (bound to x and y in the example). An end-point consists of a channel id \(c\) and a side \(s\) (either
creates a new channel and returns two end-points (bound to x and y in the example). An end-point consists of a channel id \(c\) and a side \(s\) (either  or
or  ), and is written as \({c}_{s}\). Each channel is a pair of buffers \((b_{\rightarrow }, b_{\leftarrow }\)), which are lists of messages. Buffer \(b_{\rightarrow }\) stores messages traveling left-to-right (from x to y, in the example above), and \(b_{\leftarrow }\) is for right-to-left messages, as shown in the visualization in Fig. 1.
), and is written as \({c}_{s}\). Each channel is a pair of buffers \((b_{\rightarrow }, b_{\leftarrow }\)), which are lists of messages. Buffer \(b_{\rightarrow }\) stores messages traveling left-to-right (from x to y, in the example above), and \(b_{\leftarrow }\) is for right-to-left messages, as shown in the visualization in Fig. 1.
A thread can then use  to send a value \(V\) along the channel c, with the side \(s\) specifying which buffer is used to store the message. For instance, when \(s\) is
to send a value \(V\) along the channel c, with the side \(s\) specifying which buffer is used to store the message. For instance, when \(s\) is  , it inserts the value at the end of the first buffer (SendLeft). This value will then later be taken by a thread receiving on the right side (RecvRight). Alternatively, if the buffer is empty when receiving, recv takes an “idle” step and tries again (RecvRightIdle). (The reason send and \(\textsf {recv}\) return the end-point again will become clear when we explain the type system.)
, it inserts the value at the end of the first buffer (SendLeft). This value will then later be taken by a thread receiving on the right side (RecvRight). Alternatively, if the buffer is empty when receiving, recv takes an “idle” step and tries again (RecvRightIdle). (The reason send and \(\textsf {recv}\) return the end-point again will become clear when we explain the type system.)
In the example above, after creating a new channel, the initial thread forks off a child which will send 42 from the left end-point, x. Meanwhile, the parent thread tries to receive from the right end-point y, and returns the message it gets. If the parent thread does this recv before the child has done its send, there will be no message and the parent thread will take an idle step. Otherwise, the receiver will see the message and the program will evaluate to 42.
2.2 Session Type System
A type system for this language is shown in Fig. 1. This is a simplified version of the type system given in Gay and Vasconcelos [14].Footnote 4 In addition to base types Int and Unit, we have pair types \(\tau _1 \otimes \tau _2\), function types \(\tau _1 \multimap \tau _2\), and session types \(S\). Session types are used to type the end-points of a channel. These types describe a kind of protocol specifying what types of data will flow over the channel, and in what order messages are sent. Notice that this type system is higher-order in the sense that both closures and channel end-points are first-class values and can, in particular, be sent over channels.
Session types. The possible session types are specified by the grammar in Fig. 1. If an end-point has the session type \({! \tau .\, S}\), this means that the next use of this end-point must be to send a value of type \(\tau \) (Send). Afterward, the end-point that is returned by the send will have type \(S\). Dually, \({? \tau .\, S}\) says that the end-point can be used in a receive (Recv), in which case the message read will have type \(\tau \), and the returned end-point will have type \(S\). Notice that this is the same end-point that was passed to the command, but at a different type. The type of the end-point evolves as messages are sent and received, always representing the current state of the protocol. Finally, end is a session type for an end-point on which no further messages will be sent or received.
When calling  to create a new channel, it is important that the types of the two end-points match: whenever one side sends a message of type \(\tau \), the other side should be expecting to receive a message of the same type. This relation is called duality. Given a session type \(S\), its dual \(\overline{S}\) is the result of swapping sends and receives in \(S\). In our example (1), the end-point x is used to send a single integer, so it can be given the type
to create a new channel, it is important that the types of the two end-points match: whenever one side sends a message of type \(\tau \), the other side should be expecting to receive a message of the same type. This relation is called duality. Given a session type \(S\), its dual \(\overline{S}\) is the result of swapping sends and receives in \(S\). In our example (1), the end-point x is used to send a single integer, so it can be given the type  . Conversely, y receives a single integer, so it has the dual type
. Conversely, y receives a single integer, so it has the dual type  .
.
Affinity. The type system of the source language is affine, which means that a variable in the context can be used at most once. This can be seen, e.g., in the rule Fork: the forked-off thread  and the local continuation \(E\) are typed using the two disjoint contexts \({\varGamma }_1\) and \({\varGamma }_2\), respectively.
and the local continuation \(E\) are typed using the two disjoint contexts \({\varGamma }_1\) and \({\varGamma }_2\), respectively.
One consequence of affinity is that after using an end-point to send or receive, the variable passed to send/recv has been “used up” and cannot be used anymore. Instead, the program has to use the channel returned from send/recv, which has the new “evolved” type for the end-point.
The type system given here ensures safety and race-freedom. However, it does not guarantee termination. We discuss alternative type systems guaranteeing different properties in the conclusion.
2.3 Compilation
We now describe a simple translation from this session-typed source language to a MiniML language with references and a forking primitive like the one in the source language. We omit the details of the MiniML syntax and semantics as they are standard.
Our translation needs to handle essentially one feature: the implementation of channel communication in terms of shared memory references.
The code for the implementation of the channel primitives is shown in Fig. 2. We write  for the translation in which we replace the primitives of the source language with the corresponding implementations. Concretely, applying the translation to our running example program we get:
for the translation in which we replace the primitives of the source language with the corresponding implementations. Concretely, applying the translation to our running example program we get:

Each channel is implemented as a linked list which represents both buffers. Nodes in this list are pairs \((l, v\)), where \(l\) is a reference to the (optional) next node, and \(v\) is the message that was sent. Why is it safe to use just one list? Duality in the session types guarantees that if a thread is sending from one end-point, no thread can at the same time be sending a message on the other end-point. This ensures that at least one of the two buffers in a channel is always empty. Hence we just need one list to represent both buffers.
The implementation of  , given by heapNewch, creates a new empty linked list by allocating a new reference \(l\) which initially contains none. The function heapSend implements send by appending a node to the end (\(l'\)) of the list, and returning the new end. Meanwhile, for recv, heapRecv takes an end-point \(l\) and waits in a loop until it finds that the end-point contains a node.
, given by heapNewch, creates a new empty linked list by allocating a new reference \(l\) which initially contains none. The function heapSend implements send by appending a node to the end (\(l'\)) of the list, and returning the new end. Meanwhile, for recv, heapRecv takes an end-point \(l\) and waits in a loop until it finds that the end-point contains a node.
2.4 Refinement
Having given the implementation, let us now clarify what it means for the compiler to be correct. Intuitively, we want to show that if we take a well-typed source expression \(E\), all the behaviors of its translation  are also possible behaviors of \(E\). We say that
are also possible behaviors of \(E\). We say that  refines \(E\).
refines \(E\).
Before we come to the formal definition of refinement, we need to answer the question: which behaviors do we consider equivalent? In our case, the only observation that can be made about a whole program is its return value, so classifying “behaviors” amounts to relating return values. Formally speaking:

For integer and unit values, we expect them to be exactly equal; similarly, pairs are the same if their components are. Coming to locations/end-points and closures, we do not consider them to be interpretable by the user looking at the result of a closed program. So, we just consider all closures to be equivalent, and all heap locations to relate to all channel end-points. Of course, the proof of compiler correctness will use a more fine-grained logical relation between source and target values.
Based on this notion of equivalent observations, we define what it means for a MiniML program \(e\) to refine a source program \(E\), written \(e\sqsubseteq E\). When executing from an initial “empty” state  , the following conditions must hold:
, the following conditions must hold:
-
1.
If
 then no \(e_{i}\) is stuck in state \(\sigma \).
then no \(e_{i}\) is stuck in state \(\sigma \).In other words: the target program does not reach a stuck state.
-
2.
If
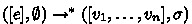 then either:
then either:-
(a)
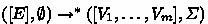 and \(v_{1} \approx V_{1}\), or
and \(v_{1} \approx V_{1}\), or -
(b)
there is an execution of
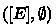 in which some thread gets stuck.
in which some thread gets stuck.
That is, if all threads of the target program terminate with a value, then either all threads of the source program terminate in some execution and the return values of the first (main) source thread and target thread are equivalent; or the source program can get stuck.
-
(a)
-
3.
If
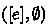 has a fair diverging execution, then
has a fair diverging execution, then  also has a fair diverging execution. Recall that an infinite execution is fair if every non-terminating thread takes infinitely many steps. This last condition makes the refinement a fair, termination-preserving refinement.
also has a fair diverging execution. Recall that an infinite execution is fair if every non-terminating thread takes infinitely many steps. This last condition makes the refinement a fair, termination-preserving refinement.
To understand why we have emphasized the importance of fair termination-preservation, suppose we had miscompiled our running example as:

That is, we removed the sender thread. We consider this to be an incorrect compilation; i.e., this program should not be considered a refinement of the source program. But imagine that we removed the word “fair” from condition (3) above: then this bad target program would be considered a refinement of the source. How is that? The program does not get stuck, so it satisfies condition (1). Condition (2) holds vacuously since the target program will never terminate; it will loop in  , forever waiting for a message. Finally, to satisfy condition (3), we have to exhibit a diverging execution in the source program. Without the fairness constraint, we can pick the (unfair) execution in which the sender source thread never gets to run.
, forever waiting for a message. Finally, to satisfy condition (3), we have to exhibit a diverging execution in the source program. Without the fairness constraint, we can pick the (unfair) execution in which the sender source thread never gets to run.
Notice that this unfair execution is very much like the example we gave in the introduction, where a thread waited forever for another one to perform a change in the shared state.
We consider such unfair executions to be unrealistic [23]; they should not give license to a compiler to entirely remove a thread from the compiled program. That’s why our notion of refinement restricts condition (3) to fair executions, i.e., executions in which all non-terminating threads take infinitely many steps.
Compiler correctness. We are now equipped to formally express the correctness statement of our compiler:
Theorem 1
For every well-typed source program \(E\), we have that:

We prove this theorem in Sect. 5. In the intervening sections, we first develop and explain a logic to help carry out this proof.
3 A Logic for Proving Refinement
Proving Theorem 1 is a challenging exercise. Both the source and the target program are written in a concurrent language with higher-order state, which is always a difficult combination to reason about. Moreover, the invariant relating the channels and buffers to their implementation as linked lists is non-trivial and relies on well-typedness of the source program.
The contribution of this paper is to provide a logic powerful enough to prove theorems like Theorem 1. In this section, we will give the reader an impression of both the logic and the proof by working through a proof of one concrete instance of our general result: we will prove that the translation of our running example is in fact a refinement of its source.
3.1 Refinement as a Hoare Logic
Our logic is an extension of Iris [19, 20], a concurrent higher-order separation logic. We use the ideas presented by Turon et al. [36] to extend this (unary) Hoare logic with reasoning principles for refinement. Finally, we add some further extensions which become necessary due to the termination-preserving nature of our refinement. We will highlight these extensions as we go.
The following grammar covers the assertions from our logic that we will need:Footnote 5

Many of these assertions are standard in separation logics, and our example proof will illustrate the non-standard ones.
Recalling the example and its translation,we want to prove:

or, for short, \(e_{\text {ex}} \sqsubseteq E_{\text {ex}}\). Following Ht-refine (Fig. 3), it is enough to prove

In other words, we “just” prove a Hoare triple for \(e_{\text {ex}}\) (the MiniML program). In order to obtain a refinement from a Hoare proof, we equip our logic with assertions talking about the source program \(E\). The assertion  states that source-level thread i is about to execute \(E\), and we have delay \(d\) left. (We will come back to delays shortly.) The assertion
states that source-level thread i is about to execute \(E\), and we have delay \(d\) left. (We will come back to delays shortly.) The assertion  says that source-level channel \(c\) currently has buffer contents \((b_{\rightarrow }, b_{\leftarrow })\). As usual in separation logic, both of these assertions furthermore assert exclusive ownership of their thread or channel. For example, in the case of
says that source-level channel \(c\) currently has buffer contents \((b_{\rightarrow }, b_{\leftarrow })\). As usual in separation logic, both of these assertions furthermore assert exclusive ownership of their thread or channel. For example, in the case of  , this means that no other thread can access the channel and we are free to mutate it (i.e., send or receive messages) – we will see later how the logic allows threads to share these resources. Put together, these two assertions let us control the complete state of the source program’s execution.
, this means that no other thread can access the channel and we are free to mutate it (i.e., send or receive messages) – we will see later how the logic allows threads to share these resources. Put together, these two assertions let us control the complete state of the source program’s execution.
So far, we have not described anything new. However, to establish termination-preserving refinement, we have to add two features to this logic: step shifts and linear assertions.
Step shifts. The rules given in Fig. 3 let us manipulate the state of the source program’s execution by taking steps in the source program. Such steps are expressed using step shifts  . Every step shift corresponds to one rule in the operational semantics (Fig. 1). For example, src-newch expresses that if we have
. Every step shift corresponds to one rule in the operational semantics (Fig. 1). For example, src-newch expresses that if we have  (which means that the source is about to create a new channel), we can “execute” that
(which means that the source is about to create a new channel), we can “execute” that  and obtain some fresh channel \(c\) and ownership of the channel (
and obtain some fresh channel \(c\) and ownership of the channel ( ). We also obtain
). We also obtain  , so we can go on executing the source thread.
, so we can go on executing the source thread.
Crucially, having  shows that in going from
shows that in going from  to
to  , the source has taken a step. We need to force the source to take steps because the refinement we show is termination-preserving. If a proof could just decide not to ever step the source program, we could end up with a MiniML program \(e\) diverging, while the corresponding source program \(E\) cannot actually diverge. That would make Ht-refine unsound. So, to avoid this, all rules that take a step in the MiniML program (Fig. 3) force us to also take a step shift.
, the source has taken a step. We need to force the source to take steps because the refinement we show is termination-preserving. If a proof could just decide not to ever step the source program, we could end up with a MiniML program \(e\) diverging, while the corresponding source program \(E\) cannot actually diverge. That would make Ht-refine unsound. So, to avoid this, all rules that take a step in the MiniML program (Fig. 3) force us to also take a step shift.
A strict implementation of this idea requires a lock-step execution of source and target program. This is too restrictive. For that reason, the source assertion does not just record the state of the source thread, but also a delay \(d\). Decrementing the delay counts as taking a step in the source (src-delay). When we take an actual source step, we get to reset the delay to some new \(d'\) – so long as \(d'\) is less than or equal to some fixed upper bound D that we use throughout the proof. There are also rules that allow executing multiple source steps when taking just a single step in the target program; we omit these rules for brevity. For the remainder of this proof, we will also gloss over the bookkeeping for the delay and just write  .
.
The assertion  expresses that a source thread can no longer take steps. As expected, this happens when the source thread reaches a value (src-stopped).
expresses that a source thread can no longer take steps. As expected, this happens when the source thread reaches a value (src-stopped).
Linearity. There is one last ingredient we have to explain before we start the actual verification: linearity. Assertions in our logic are generally linear, which means they cannot be “thrown away”, i.e.,  does not hold generically in
does not hold generically in  and
and  . As a consequence, assertions represent not only the right to perform certain actions (like modifying memory), but also the obligation to keep performing steps in the source program. This ensures that we do not “lose track” of a source thread and stop performing step shifts justifying its continued execution.
. As a consequence, assertions represent not only the right to perform certain actions (like modifying memory), but also the obligation to keep performing steps in the source program. This ensures that we do not “lose track” of a source thread and stop performing step shifts justifying its continued execution.
The modality  says that we have a proof of
says that we have a proof of  , and that this is an affine proof – so there are no obligations encoded in this assertion, and we can throw it away. Some rules are restricted to affine assertions, e.g., rules for framing around a Hoare triple or a step shift (Ht-frame and step-frame). Again, this affine requirement ensures that we do not “smuggle” a source thread around the obligation to perform steps in the source. All the base assertions, with the exception of
, and that this is an affine proof – so there are no obligations encoded in this assertion, and we can throw it away. Some rules are restricted to affine assertions, e.g., rules for framing around a Hoare triple or a step shift (Ht-frame and step-frame). Again, this affine requirement ensures that we do not “smuggle” a source thread around the obligation to perform steps in the source. All the base assertions, with the exception of  , are affine.
, are affine.
Coming back to the Hoare triple (2) above that we have to prove, the pre-condition  expresses that we start out with a source program executing
expresses that we start out with a source program executing  (and not owning any channels), and we somehow have to take steps in the source program to end up with
(and not owning any channels), and we somehow have to take steps in the source program to end up with  such that \(V\) is “equivalent” (in the sense defined in Sect. 2.4) to the return value of the target program. Intuitively, because we can only manipulate source by taking steps in the source program, and because we end up stepping from
such that \(V\) is “equivalent” (in the sense defined in Sect. 2.4) to the return value of the target program. Intuitively, because we can only manipulate source by taking steps in the source program, and because we end up stepping from  to “the same” return value as the one obtained from
to “the same” return value as the one obtained from  , proving the Hoare triple actually establishes a refinement between the two programs. Furthermore, since source is linear and we perform a step shift at every step of the MiniML program, the refinement holds even for diverging executions.
, proving the Hoare triple actually establishes a refinement between the two programs. Furthermore, since source is linear and we perform a step shift at every step of the MiniML program, the refinement holds even for diverging executions.
3.2 Proof of the Example
The rest of this section will present in great detail the proof of our example (2). The rough structure of this proof goes as follows: after a small introduction covering the allocation of the channel, we will motivate the need for state-transition systems (STS), a structured way of controlling the interaction between cooperating threads. We will define the STS used for the example and decompose the remainder of the proof into two pieces: one covering the sending thread and one for the receiving thread.
Getting started. The first statement in both source and target program is the allocation of a channel. The following Hoare triple that’s easily derived from ml-alloc summarizes the action of  : It allocates a channel in both programs.
: It allocates a channel in both programs.

Let us pause a moment to expand on that post-condition. On the source side, we have a channel c with both buffers being empty; on the target side we have a location l representing the empty buffer with none. The return value x is a pair with both components being l. Finally, the source thread changed from  in the pre-condition to
in the pre-condition to  , meaning that the
, meaning that the  has been executed and the context can now go on with its evaluation based on the pair
has been executed and the context can now go on with its evaluation based on the pair  .
.
We apply this triple for  with the appropriate evaluation context
with the appropriate evaluation context  for the source program, and the post-condition of (3) becomes our new context of current assertions. Next, we reduce the let on both sides, so we end up with
for the source program, and the post-condition of (3) becomes our new context of current assertions. Next, we reduce the let on both sides, so we end up with

where

and the remaining MiniML code is

(In the following, we will perform these pure reduction steps and the substitutions implicitly.)
As we can see, both programs are doing a fork to concurrently send and receive messages on the same channel. Usually, this would be ruled out by the exclusive nature of ownership in separation logic. To enable sharing, the logic provides a notion of protocols coordinating the interaction of multiple threads on the same shared state. The protocol governs ownership of both l (in the target) and c (in the source), and describes which thread can perform which actions on this shared state.
State-transition systems. A structured way to describe protocols is the use of state-transition systems (STS), following the ideas of Turon et al. [36]. An STS  consists of a directed graph with the nodes denoting states and the arrows denoting transitions.
consists of a directed graph with the nodes denoting states and the arrows denoting transitions.
The STS for our example is given in Fig. 4. It describes the interaction of our two threads over the shared buffer happening in three phases. In the beginning, the buffer is empty (init). Then the message is sent by the forked-off sending thread (sent). Finally, the message is received by the main thread (received).
The STS also contains two tokens. Tokens are used to represent actions that only particular threads can perform. In our example, the state sent requires the token [S]. The STS enforces that, in order to step from init to sent, a thread must provide (and give up) ownership of [S]. This is called the law of token preservation [36]: Because sent contains more tokens than init, the missing tokens have to be provided by the thread performing the transition. Similarly, [R] is needed to transition to the final state received.
To tie the abstract state of the STS to the rest of the verification, every STS comes with an interpretation  . For every state, it defines an affine assertion that has to hold at that state. In our case, we require the buffer to be initially empty, and to contain 42 in state sent. Once we reach the final state, the programs no longer perform any action on their respective buffers, so we stop keeping track.
. For every state, it defines an affine assertion that has to hold at that state. In our case, we require the buffer to be initially empty, and to contain 42 in state sent. Once we reach the final state, the programs no longer perform any action on their respective buffers, so we stop keeping track.
We need a way to track the state of the STS in our proof. To this end, the assertion  states that the STS is at least in state s, and that we own tokens T. We cannot know the exact current state of the STS because other threads may have performed further transitions in the mean time. The proof rules for STSs can be found in the appendix [34]; in the following, we will keep the reasoning about the STS on an intuitive level to smooth the exposition.
states that the STS is at least in state s, and that we own tokens T. We cannot know the exact current state of the STS because other threads may have performed further transitions in the mean time. The proof rules for STSs can be found in the appendix [34]; in the following, we will keep the reasoning about the STS on an intuitive level to smooth the exposition.
Plan for finishing the proof. Let us now come back to our example program. We already described the STS we are going to use for the verification (Fig. 4). The next step in the proof is thus to initialize said STS.
Remember our current context is (4). When allocating an STS, we get to pick its initial state – that would be init, of course. We have to provide  to initialize the STS, so we give up ownership of l and \(c\). In exchange, we obtain
to initialize the STS, so we give up ownership of l and \(c\). In exchange, we obtain  and the tokens. Our context is now
and the tokens. Our context is now

The next command executed in both programs is fork. We are thus going to apply ml-fork and prove the step shift using src-fork. The two remaining premises of ml-fork are the following two Hoare triples:


Showing these will complete the proof. The post-condition  of (6) is mandated by ml-fork; we will discuss it when verifying that Hoare triple. Note that we are splitting the
of (6) is mandated by ml-fork; we will discuss it when verifying that Hoare triple. Note that we are splitting the  to hand the two tokens that we own to two different threads.
to hand the two tokens that we own to two different threads.
Verifying the sender. To prove the sending Hoare triple (6), the context we have available is  , and the code we wish to verify is (unfolding the definition of heapSend, and performing some pure reductions):
, and the code we wish to verify is (unfolding the definition of heapSend, and performing some pure reductions):

The allocation is easily handled with ml-alloc, and it turns out we don’t even need to remember anything about the returned \(l_{new}\).
The next step is the core of this proof: showing that we can change the value stored in l. Notice that we do not own \(l \hookrightarrow \_\,\); the STS “owns” l as part of its interpretation. So we will open the STS to get access to l.
Looking at Fig. 4, we can see that doing the transition from init to sent requires the token [S], which we own – as a consequence, nobody else could perform this transition. It follows that the STS is currently in state init. We obtain  , so that we can apply ml-store with src-send-left, yielding
, so that we can apply ml-store with src-send-left, yielding

To finish up accessing the STS, we have to pick a new state and show that we actually possess the tokens to move to said state. In our case, we cannot pick received, since we do not own the token [R] necessary for that step. Instead, we will pick \(\textsc {sent}\) and give up our token. This means we have to establish  . Doing so consumes most of our context (8), leaving only
. Doing so consumes most of our context (8), leaving only  . What remains to be done? We have to establish the post-condition of our triple (6), which is
. What remains to be done? We have to establish the post-condition of our triple (6), which is  . By src-stopped, this immediately follows from the fact that we reduced the source thread to
. By src-stopped, this immediately follows from the fact that we reduced the source thread to  , which is a value.
, which is a value.
Notice that this last step was important: We showed that when the MiniML thread terminates, so does the source thread. The original fork rule for Iris allows picking any post-condition for the forked-off thread, because nothing happens any more with this thread once it terminates. However, we wish to establish that if all MiniML threads terminate, then so do all source threads – and for this reason, ml-fork forces us to prove  , which asserts that all the threads we keep track of have reduced to a value. This finishes the proof of the sender.
, which asserts that all the threads we keep track of have reduced to a value. This finishes the proof of the sender.
Verifying the receiver. The next (and last) step in establishing the refinement (2) is to prove the Hoare triple for the receiving thread (7). This is the target code to verify:

Since heapRecv is a recursive function, we use ml-rec, which says that we can assume that recursive occurrences of heapRecv have already been proven correct. It may be surprising to see this rule – after all, rules like ml-rec are usually justified by saying that all we do is partial correctness. Notice, however, that we are not showing that  terminates. All we show is that, if
terminates. All we show is that, if  diverges, then so does
diverges, then so does  . That is, we are establishing termination-preservation, not termination.
. That is, we are establishing termination-preservation, not termination.
In continuing the proof, we thus get to assume correctness of the recursive call. Our current context is

and the code we are verifying is

with post-condition  .
.
The first command of this program is \(! l\). To access l, we have to again open the STS. Since we own [R], we can rule out being in state received. We perform a case distinction over the remaining two states.
-
If we are in init, we get
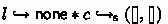 from the STS’s
from the STS’s  . We use ml-load with src-recv-right-miss. Notice how we use
. We use ml-load with src-recv-right-miss. Notice how we use 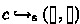 to justify performing an “idle” step in the source. This is crucial – after all, we are potentially looping indefinitely in the target, reading l over and over; we have to exhibit a corresponding diverging execution in the source.
to justify performing an “idle” step in the source. This is crucial – after all, we are potentially looping indefinitely in the target, reading l over and over; we have to exhibit a corresponding diverging execution in the source.Since we did not change any state, we close the invariant again in the init state. Next, the program executes the none arm of the match: heapRecv l. Here, we use our assumption that the recursive call is correct to finish the proof.
-
Otherwise, the current state is sent, and we obtain
 . We use ml-load with src-recv-right-hit; this time we know that the recv in the source will succeed. We also know that we are loading \((\_, 42)\) from l. We pick received as the next state (giving up our STS token), and trivially establish
. We use ml-load with src-recv-right-hit; this time we know that the recv in the source will succeed. We also know that we are loading \((\_, 42)\) from l. We pick received as the next state (giving up our STS token), and trivially establish  . We can now throw away ownership of l and \(c\) as well as
. We can now throw away ownership of l and \(c\) as well as 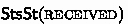 since we no longer need them – we can do this because all these assertions are affine.
since we no longer need them – we can do this because all these assertions are affine.All that remains is the source thread:

Next, the target program will execute the some branch of the match. To finish, we need to justify the post-condition:
 . We already established that the second component of the value loaded from l is 42, and the source thread is easily reduced to 42 as well.
. We already established that the second component of the value loaded from l is 42, and the source thread is easily reduced to 42 as well.
This finishes the proof of (7) and therefore of (2): we proved that  .
.
4 Soundness of the Logic
We have seen how to use our logic to establish a refinement for a particular simple instance of our translation. We now need to show that this logic is sound.
As already mentioned, our logic is an extension of Iris, so we need to adapt the soundness proof of Iris [19]. The two extensions that were described in Sect. 3.1 are:
-
1.
We add a notion of a step shift, which is used to simulate source program threads.
-
2.
We move from an affine logic to a linear logic. This is needed to capture the idea that some resources (like
 ) represent obligations that cannot be thrown away.
) represent obligations that cannot be thrown away.
In this section we describe how we adapt the semantic model of Iris to handle these changes. Although our extensions sound simple, the modification of the model requires some care. Many of the features we used in Sect. 3, such as STSs [20] and reasoning about the source language, are derived constructions that are not “baked-in” to the logic. As we change the model, we need to ensure that all of these features can still be encoded. We also strive to keep our extensions as general as possible so as to not unnecessarily restrict the flexibility of Iris.
Brief review of the Iris model. We start by recalling some aspects of the Iris model [19] that we modify in our extensions. A key concept is the notion of a resource. Resources describe the physical state of the program as well as additional ghost state that is added for the purpose of verification and used, e.g., to interpret STSs or the assertions talking about source programs. Resources are instances of a partial commutative monoid-like algebraic structure; in particular, two resources  ,
,  can be composed to
can be composed to  . This operation is used to combine resources held by different threads. When the composition
. This operation is used to combine resources held by different threads. When the composition  is defined, the elements
is defined, the elements  and
and  are said to be compatible. Iris always ensures that the resources held by different threads are compatible. This guarantees that, e.g., different threads cannot own the same channel or the same STS token. The operation also gives rise to a pre-order on resources, defined as
are said to be compatible. Iris always ensures that the resources held by different threads are compatible. This guarantees that, e.g., different threads cannot own the same channel or the same STS token. The operation also gives rise to a pre-order on resources, defined as  , i.e.,
, i.e.,  is included in
is included in  if the former can be extended to the latter by adding some additional resource
if the former can be extended to the latter by adding some additional resource  .
.
Ideally, we would just interpret an assertion  as a set of resources. For technical reasons (that we will mostly gloss over), Iris needs an additional component: the step-index n. An assertion is thus interpreted as a set of pairs
as a set of resources. For technical reasons (that we will mostly gloss over), Iris needs an additional component: the step-index n. An assertion is thus interpreted as a set of pairs  of step-indices and resources. We write
of step-indices and resources. We write  to indicate that
to indicate that  , and read this as saying that
, and read this as saying that  satisfies
satisfies  for n steps of the target program’s execution.
for n steps of the target program’s execution.
Iris furthermore demands that assertions (interpreted as sets) satisfy two closure properties: They must be closed under larger resources and smaller step-indices. Formally:
-
1.
If
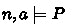 and
and  , then
, then  .
. -
2.
If
 and \(n' \le n\), then
and \(n' \le n\), then  .
.
The first point above makes Iris an affine as opposed to a linear logic: we can always “add-on” more resources and continue to satisfy an assertion. Put differently, there is no way to state an upper bound on our resources. The second point says that if  holds for n steps, then it also holds for fewer than n steps.
holds for n steps, then it also holds for fewer than n steps.
To give a model to assertions like \(l\hookrightarrow v\), we need a function  describing, as a resource, a heap which maps location \(l\) to v. We then define:
describing, as a resource, a heap which maps location \(l\) to v. We then define:

Notice the use of  , ensuring that the closure property (1) holds.
, ensuring that the closure property (1) holds.
Equipping Iris with linear assertions. In order to move to a linear setting with minimal disruption to the existing features of Iris, we replace the judgment  with
with  . That is, assertions are now sets of triples: a step-index and two resources. The downward closure condition on n and the upward closure condition on
. That is, assertions are now sets of triples: a step-index and two resources. The downward closure condition on n and the upward closure condition on  still apply, but we do not impose such a condition on
still apply, but we do not impose such a condition on  : this second resource will represent the “linear piece” of an assertion. Crucially, whereas affine assertions like \(l\hookrightarrow v\) continue to “live” in the a piece, the linear
: this second resource will represent the “linear piece” of an assertion. Crucially, whereas affine assertions like \(l\hookrightarrow v\) continue to “live” in the a piece, the linear  resides in
resides in  :
:

where  is the unit of the monoid. We assume
is the unit of the monoid. We assume  to define, as a resource, a source thread i executing
to define, as a resource, a source thread i executing  with \(d\) delay steps left.
with \(d\) delay steps left.
As we can see,  describes the exact linear resources
describes the exact linear resources  that we own, whereas \(\hookrightarrow \) merely states a lower bound on the affine resources
that we own, whereas \(\hookrightarrow \) merely states a lower bound on the affine resources  (due to the upwards closure on
(due to the upwards closure on  ). Notice that
). Notice that  and
and  are both elements of the same set of resources; it is just their treatment in the closure properties of assertions which makes one affine and the other linear. Because there is no upward closure condition on the second monoid element, the resulting logic is not affine: if
are both elements of the same set of resources; it is just their treatment in the closure properties of assertions which makes one affine and the other linear. Because there is no upward closure condition on the second monoid element, the resulting logic is not affine: if  , then it is not necessarily the case that
, then it is not necessarily the case that  .
.
We define the affine modality by:

This says that in addition to satisfying  ,
,  should equal the unit of the monoid. That is, the linear part is “empty”; there are no obligations encoded in
should equal the unit of the monoid. That is, the linear part is “empty”; there are no obligations encoded in  . That makes it sound to throw away
. That makes it sound to throw away  or to frame it.
or to frame it.
The advantage of this “two world” model is that it does not require us to change many of the encodings already present in Iris, like STSs.
Step Shifts. We are now ready to explain the ideas behind the step shift. Remember the goal here is to account for the steps taken in the source program, in a way that we can prove refinements by proving Hoare triples (Ht-refine). This is subtle because by the definition of refinement (Sect. 2.4), we need to make statements even about infinite executions, i.e., executions that never have to satisfy the post-condition.
The key idea is to equip the resources of Iris with a relation that represents a notion of taking a (resource) step. We write  , and say that
, and say that  steps to
steps to  . We will then pick the resources in such a way as to represent the status of a source program,Footnote 6 and we define the resource step to be taking a step in the source program. All the other components of the resource, like STSs, will not be changed by resource steps.
. We will then pick the resources in such a way as to represent the status of a source program,Footnote 6 and we define the resource step to be taking a step in the source program. All the other components of the resource, like STSs, will not be changed by resource steps.
Recall that the resources owned by different threads always need to be compatible. To ensure this, we define a relation that performs a step while maintaining compatibility with the resources owned by other threads. Formally, a frame-preserving step-update  holds if
holds if  and for all
and for all  such that
such that  is defined, so is
is defined, so is  . The intuition is that, if a thread owns some resources
. The intuition is that, if a thread owns some resources  and
and  , that restricts the ownership of other threads to frames
, that restricts the ownership of other threads to frames  that are compatible with
that are compatible with  and
and  . Since
. Since  and
and  are also compatible with the frame, the step is guaranteed not to interfere with resources owned by other threads.
are also compatible with the frame, the step is guaranteed not to interfere with resources owned by other threads.
These frame-preserving step-updates are reflected into the logic through the step shift assertions:  holds if, whenever some resources satisfy
holds if, whenever some resources satisfy  , it is possible to perform a frame-preserving step-update to resources satisfying
, it is possible to perform a frame-preserving step-update to resources satisfying  .
.
We then connect Hoare triples to these resource steps. To this end, we change the definition of Hoare triples so that whenever a target thread takes a step, we have to also take a step on our resources. This gives rise to the proof rules in Fig. 3, which force the user of the logic to perform a step shift alongside every step of the MiniML program. We also enforce that forked-off threads must have a post-condition of  , ensuring that target language threads cannot stop executing while source language threads are still running.
, ensuring that target language threads cannot stop executing while source language threads are still running.
Soundness of the refinement. Having extended the definition of Hoare triples in this way, we can prove our refinement theorem. Recall that the definition of refinement had three parts. For each of these parts, we proved an adequacy theorem for our extensions relating Hoare triples to properties of program executions. These theorems are parameterized by the kind of resource picked by the user, and in particular the kind of resource step. Below, we show these theorems specialized to the case where resource steps correspond to source language steps.
The first refinement condition, which says that the target program must not get stuck, follows from a “safety” theorem that was already present in the original Iris:
Lemma 2
If  holds and we have
holds and we have  , then each
, then each  is either a value or it can take a step in state \(\sigma \).
is either a value or it can take a step in state \(\sigma \).
The second refinement condition says that if the execution of  terminates, then there should be a related terminating execution in the source. Remember that the definition of the Hoare triple requires us to take a step in the source whenever the target steps (modulo a finite number of delays). Hence a proof of such a triple must have “built-up” the desired source execution:
terminates, then there should be a related terminating execution in the source. Remember that the definition of the Hoare triple requires us to take a step in the source whenever the target steps (modulo a finite number of delays). Hence a proof of such a triple must have “built-up” the desired source execution:
Lemma 3
If  holds and we have
holds and we have  , then there exists \(V_1\),
, then there exists \(V_1\),  , \(\dots \),
, \(\dots \),  , \(\varSigma \) s.t.
, \(\varSigma \) s.t.  . Moreover, each
. Moreover, each  is either stuck or a value, and \(v_1 \approx V_1\).
is either stuck or a value, and \(v_1 \approx V_1\).
Here, we are already making crucial use of both linearity of  and the fact that forked-off threads must have post-condition
and the fact that forked-off threads must have post-condition  : if it were not for these requirements, even when all target threads terminated with a value \(v_i\), we could not rule out the existence of source threads that can go on executing.
: if it were not for these requirements, even when all target threads terminated with a value \(v_i\), we could not rule out the existence of source threads that can go on executing.
Finally, we come to the third condition, which says fair diverging executions of the target should correspond to fair diverging executions of the source:
Lemma 4
If  holds and
holds and  has a diverging execution, then
has a diverging execution, then  has a diverging execution as well. Moreover, if the diverging target execution is fair, then the source execution is too.
has a diverging execution as well. Moreover, if the diverging target execution is fair, then the source execution is too.
This is the hardest part of the soundness proof. We would like to start by arguing that, just as for the finite case, if the target program took an infinite number of steps, then the proof of the refinement triple must give a corresponding infinite number of steps in the source program. Unfortunately, this argument is not so simple because of step-indexing.
In Iris, Hoare triples are themselves step-indexed sets. We write  to say that the triple holds at step-index n. Then, when we say we have proved a Hoare triple, we mean the triple holds for all step-indices n and all resources satisfying the precondition. As is usual with step-indexing, when a triple
to say that the triple holds at step-index n. Then, when we say we have proved a Hoare triple, we mean the triple holds for all step-indices n and all resources satisfying the precondition. As is usual with step-indexing, when a triple  holds for step-index n, that means when the precondition is satisfied, execution of
holds for step-index n, that means when the precondition is satisfied, execution of  is safe for up-to n steps, and if it terminates within those n steps, the post-condition holds. In our case, it also means that each step of the target program gives a step of the source program, for up to n target steps.
is safe for up-to n steps, and if it terminates within those n steps, the post-condition holds. In our case, it also means that each step of the target program gives a step of the source program, for up to n target steps.
This restriction to only hold “up to n steps” arises due to the way Hoare triples are defined in the model: when proving the Hoare triple at step-index n, if  steps to
steps to  , we are only required to show
, we are only required to show  for some
for some  .
.
The restriction to a finite number of steps did not bother us for Lemmas 2 and 3. Since they only deal with finite executions, and the Hoare triple holds for all starting indices n, we can simply pick n to be greater than the finite execution we are considering. But we cannot do this when we want to prove something about a diverging execution of the target. Whatever n we start with, it is not big enough to get the infinite source execution we need.
Bounded non-determinism, infinite executions, and step-indexing. Our insight is that when the source language has only bounded non-determinism, we can set up a more careful inductive argument. By bounded non-determinism, we mean that each configuration  only has finitely many possible successor configurations. The key result is the following quantifier inversion lemma:
only has finitely many possible successor configurations. The key result is the following quantifier inversion lemma:
Lemma 5
Let  be a step-indexed predicate on a finite set X. Then:
be a step-indexed predicate on a finite set X. Then:

Proof
By assumption, for each n, there exists \(x_n \in X\) such that  . Since X is finite, by the pigeon-hole principle, there must be some \(x \in X\) such that
. Since X is finite, by the pigeon-hole principle, there must be some \(x \in X\) such that  for infinitely many values of m. Now, given arbitrary n, this means there exists \(m > n\) such that
for infinitely many values of m. Now, given arbitrary n, this means there exists \(m > n\) such that  . Since step-indexed predicates are downward-closed,
. Since step-indexed predicates are downward-closed,  . Hence
. Hence  .
.
Ignoring delay steps for the moment, we apply this lemma to our setting to get:
Lemma 6
Suppose  steps to
steps to  and
and  . Then,
. Then,  such that
such that  steps to
steps to  and
and  .
.
Proof
Let X by the set of  that
that  can step to, which we know to be finite.Footnote 7 Consider the step-indexed predicate
can step to, which we know to be finite.Footnote 7 Consider the step-indexed predicate  on X defined by
on X defined by  . By assumption, for each \(n > 0\),
. By assumption, for each \(n > 0\),  for some
for some  . The definition of Hoare triples implies that there exists some
. The definition of Hoare triples implies that there exists some  such that
such that  . Thus,
. Thus,  , so we can apply Lemma 5 to get the desired result.
, so we can apply Lemma 5 to get the desired result.
Notice that in the conclusion of Lemma 6, if  takes another step, we can apply Lemma 6 again to the triples for
takes another step, we can apply Lemma 6 again to the triples for  . So, given some initial triple
. So, given some initial triple  and a diverging execution of
and a diverging execution of  , by induction we can repeatedly apply Lemma 6 to construct an infinite execution of the source program. Finally, we prove that if the execution of
, by induction we can repeatedly apply Lemma 6 to construct an infinite execution of the source program. Finally, we prove that if the execution of  was fair, this source execution will be fair as well, giving us Lemma 4. Of course, for the full mechanized proof we have to take into account the delay steps and consider the case where the target thread owns multiple source threads. But all of these are finite additional possibilities, they do not fundamentally change the argument sketched above.
was fair, this source execution will be fair as well, giving us Lemma 4. Of course, for the full mechanized proof we have to take into account the delay steps and consider the case where the target thread owns multiple source threads. But all of these are finite additional possibilities, they do not fundamentally change the argument sketched above.
5 Proof of Compiler Correctness
We now give a brief overview of our proof of Theorem 1. Recall that we want to show that if E is a well-typed source expression, then  .
.
Our proof is a binary logical relations argument. We interpret each type \(\tau \) as a relation on values from the target and source language, writing  to say that \(v\) and \(V\) are related at type \(\tau \). However, following the example of [21, 22], these are relations in our refinement logic, which means we can use all of the constructs of the logic to describe the meaning of types. We then prove a fundamental lemma showing that well-typed expressions are logically related to their translation. Next, we show that our logical relation implies the triple used in Ht-refine. Theorem 1 is then a direct consequence of these two lemmas.
to say that \(v\) and \(V\) are related at type \(\tau \). However, following the example of [21, 22], these are relations in our refinement logic, which means we can use all of the constructs of the logic to describe the meaning of types. We then prove a fundamental lemma showing that well-typed expressions are logically related to their translation. Next, we show that our logical relation implies the triple used in Ht-refine. Theorem 1 is then a direct consequence of these two lemmas.
Details of these proofs can be found in the appendix [34]; here we focus on the definition of the logical relation itself. For most types, the interpretation is straight-forward and fairly standard. For instance,  holds exactly when \(v= V= n\), for some integer n. The important exception, of course, is the interpretation of session types, in which we need to relate the encoding of channels as linked-lists to the source language’s primitive buffers.
holds exactly when \(v= V= n\), for some integer n. The important exception, of course, is the interpretation of session types, in which we need to relate the encoding of channels as linked-lists to the source language’s primitive buffers.
Sessions as an STS. To interpret session types, we generalize the state transition system from the example in Sect. 3 to handle the more complicated “protocols” that session types represent.
What should the states of this STS be? In the STS used in Sect. 3, we had three states: init, in which the message had not been sent; sent, where a message had been sent from the left end-point, but not received; and received, where the message had now been received at the right end-point. In the general case, we will have more than one message, so our states need to track how many messages have been sent/received on each end-point. We also need to know the “current” type of the end-points, but notice that if we know the starting type of an end-point, and how many messages have been sent/received on it, we can always recover these current types. We write \({S}^{n}\) for the type after n messages have been sent/received starting from \(S\).
We also need to know which heap locations  and
and  currently represent the end-points of the channel. All together then, the states will be tuples
currently represent the end-points of the channel. All together then, the states will be tuples  describing how many messages have been sent/received on each end-point, and the corresponding heap locations.
describing how many messages have been sent/received on each end-point, and the corresponding heap locations.
Remember that we also need to define the tokens and transitions associated with each state of our STS. The transitions are simple: we can either advance the left end-point, incrementing  and updating
and updating  , and similarly for the right end-point. For the tokens, recall that in our example proof, we had [S] and [R] tokens used by each thread to advance the state when they had interacted with their respective end-points. In general, the threads will now use the end-points multiple times, so we need a token for each of these uses on both sides. Concretely, we will have two kinds of tokens,
, and similarly for the right end-point. For the tokens, recall that in our example proof, we had [S] and [R] tokens used by each thread to advance the state when they had interacted with their respective end-points. In general, the threads will now use the end-points multiple times, so we need a token for each of these uses on both sides. Concretely, we will have two kinds of tokens,  and
and  , which are used when advancing the left and right end-point counter to n, respectively.
, which are used when advancing the left and right end-point counter to n, respectively.
To complete the description of the STS, we have to talk about the interpretation of the states. This interpretation has to relate the messages in the source channel’s current buffers to the nodes in the linked list on the target heap. The individual messages should, of course, be related by our logical relation ( ). We lift this relation to lists of messages (
). We lift this relation to lists of messages ( ) as follows:
) as follows:

For now, ignore the  symbol. The left rule says that two empty lists are equivalent at any session type. The right rule says two lists are related at a receive type \({? \tau .\, S}\), if their heads are related under \(\tau \), and the remainders of each list are related at \(S\). It is important that this is a receive type: if the current type of the end-point is a send type, then there should not be any messages in its receive buffer, so the rule for empty lists is the only one that applies.
symbol. The left rule says that two empty lists are equivalent at any session type. The right rule says two lists are related at a receive type \({? \tau .\, S}\), if their heads are related under \(\tau \), and the remainders of each list are related at \(S\). It is important that this is a receive type: if the current type of the end-point is a send type, then there should not be any messages in its receive buffer, so the rule for empty lists is the only one that applies.
We can now give our state interpretation,  , which is parameterized by (a) the starting type \(S\) of the left end-point (the right end-point’s starting type is by necessity dual so there is no need to track it), and (b) the name c of the channel:
, which is parameterized by (a) the starting type \(S\) of the left end-point (the right end-point’s starting type is by necessity dual so there is no need to track it), and (b) the name c of the channel:


Let us explain this piece by piece. To start, we have that there exists a list of source values  and a list of target values
and a list of target values  , representing the messages that are stored in the buffer right now. We then distinguish between two cases: either the first buffer is empty or the second buffer is empty. We omit the second case (corresponding to the second disjunct) because it is symmetric. In the first case, the channel’s first buffer contains
, representing the messages that are stored in the buffer right now. We then distinguish between two cases: either the first buffer is empty or the second buffer is empty. We omit the second case (corresponding to the second disjunct) because it is symmetric. In the first case, the channel’s first buffer contains  and the second buffer is empty (10, left). On the target side, the buffer is represented as a linked list from
and the second buffer is empty (10, left). On the target side, the buffer is represented as a linked list from  to
to  containing the values
containing the values  (10, right). Of course, the lists of values need to be related according to the end-point’s current type
(10, right). Of course, the lists of values need to be related according to the end-point’s current type  (11, left). Finally, the number of messages sent/received through the left end-point, plus the number of messages still in the buffer, should equal the total number of messages sent/received through the right end-point (11, right). Therefore, when these remaining messages are received by the left end-point, the two types will again be dual.
(11, left). Finally, the number of messages sent/received through the left end-point, plus the number of messages still in the buffer, should equal the total number of messages sent/received through the right end-point (11, right). Therefore, when these remaining messages are received by the left end-point, the two types will again be dual.
Informally then, the value relation at session types \({l} \mathrel {\simeq ^{\mathcal {V}}_{}} {{c}_{s}} : {S}\) says that there exists an appropriate STS and tokens for the session S which relates \(l\) and \({c}_{s}\). We can then prove Hoare triples for the message-passing primitives that manipulate this STS. For instance, for heapRecv we have (omitting delay steps):

This triple closely corresponds to the typing rule Recv (Fig. 1): typing judgments in the premise become value relations in the pre-condition, and the conclusion is analogously transformed into the postcondition. Indeed, the proof of the fundamental lemma for the logical relation essentially just appeals to these triples.
There is something we have glossed over: when we defined the logical relation, we used the STS, but the STS interpretation used the logical relation! This circularity is the reason for the  symbol guarding the recursive occurrence of (
symbol guarding the recursive occurrence of ( ) in L-cons. The details are spelled out in the appendix.
) in L-cons. The details are spelled out in the appendix.
6 Conclusion and Related Work
We have presented a logic for establishing fair, termination-preserving refinement of higher-order, concurrent languages. To our knowledge, this is the first logic combining higher-order reasoning (and in particular, step-indexing) with reasoning for termination-sensitive concurrent refinement. Moreover, we applied this logic to verify the correctness of a compiler that translates a session-typed source language with channels into an ML-like language with a shared heap.
All of these results have been fully mechanized in Coq. Our mechanization builds on the Coq development described in Jung et al. [19] and the proof-mode from Krebbers et al. [21]. The proofs use the axioms of excluded middle and indefinite description. The proof scripts can be found online [1].
Second Case Study. Our logic is not tied to this source language and translation: we have used it to mechanize a proof that the Craig-Landin-Hagersten queue lock [9, 27] refines a ticket lock. Further details can be found in the appendix [34].
Linearity. Linearity has been used in separation logics to verify the absence of memory leaks: if heap assertions like \(l \hookrightarrow v\) are linear, and the only way to “dispose” of them is by freeing the location l, then post conditions must mention all memory that persists after a command completes [17]. Our treatment of linearity has limitations that make it unsuitable for tracking resources like the heap. First, in our logic, only affine assertions can be framed (see Ht-frame), because framing could hide the obligation to perform steps on source threads. Of course, for resources like the heap this would be irrelevant, and this rule could be generalized. Second, linear resources cannot be put in STS interpretations, so they cannot be shared between threads. Since STSs are implemented in terms of a more primitive feature in Iris called invariants, which are affine, allowing linear resources to be put inside would circumvent the precise accounting that motivates linearity in the first place. Thus, we would need to extend Iris with a useful form of “linear” shared invariants, which we leave to future work.
Session Types. Starting from the seminal work of Honda [16], a number of session-type systems have been presented with different features [8, 14, 35, 38, 41] (among many others). The language presented here is a simplified version of the one in Gay and Vasconcelos [14]. Wadler [38] has shown that a restricted subset of the language in [14] does enjoy a deadlock freedom property. This property holds only when the type system is linear, like the original in [14]. Pérez et al. [30] and Caires et al. [7] give logical relations for session-typed languages, which they use to prove strong normalization and contextual equivalence results. Their logical relation is defined “directly”, instead of translating into an intermediary logic. Early versions of another session-typed system [39] used a ring-buffer to represent channels instead of linked lists, which would be interesting to verify.
Logics for Concurrency, Termination, and Refinement. There is a vast literature on program logics for concurrency [6, 10,11,12,13, 15, 19, 20, 24,25,26, 28, 29, 31, 32, 36, 37]. Indeed, the reason for constructing a logical relation on top of a program logic, as in Krogh-Jespersen et al. [22], is so that we can take advantage of the many ideas that have proliferated in this community.
Focusing on logics for refinement and termination properties: Benton [3] pioneered the use of a relational Hoare logic for showing the correctness of compiler transformations in the sequential setting. Yang [40] generalized this to relational separation logic. We have already described [36], which developed a higher-order concurrent separation logic for termination-insensitive refinement. Liang et al. [25] also allow non-terminating programs to refine terminating ones. This was extended in [26] for a termination-preserving refinement, but this deals with termination-preservation without fairness. Most recently Liang and Feng [24] addressed fair termination-preserving refinement. In their logic, threads can explicitly reason about how their actions may or may not further delay other threads, which is more general than our approach and may be needed for verifying some of the examples they consider. It would be interesting to adapt this more explicit fairness reasoning to the higher-order setting.
Hoffmann et al. [15] features a concurrent separation logic for total correctness. Threads own resources called “tokens”, which must be “used up” every time a thread repeats a while loop. This “using up” of tokens inspired our step shifts. Later, da Rocha Pinto et al. [31] generalized this by using ordinals instead of tokens: threads decrease the ordinal they own as they repeat a loop. This is useful for languages with unbounded non-determinism. Our technique for coping with step-indexing in Sect. 4 relied on bounded non-determinism. It may be possible to remove this limitation by using transfinite step-indexing [4, 33] instead.
Notes
- 1.
Setting aside issues of IO behavior.
- 2.
This definition is simpler than the version found in Lehmann et al. [23], because there threads can be temporarily disabled, i.e., blocked and unable to take a step. In the languages we consider, threads can always take a step unless they have finished executing or have “gone wrong”.
- 3.
The notation in Turon et al. [36] is different.
- 4.
For the reader familiar with that work: we leave out subtyping and choice types. Also, we present an affine type system instead of a linear one.
- 5.
- 6.
Iris is designed to be parametric in the choice of resources, so we can pick a particular resource for this source language and still use most of the general Iris machinery.
- 7.
To be precise we ought to mention the initial states \(\sigma \) and \(\varSigma \) that
 and
and  run in and assume they satisfy the precondition of the triple.
run in and assume they satisfy the precondition of the triple.
References
Website with Coq development (2016). http://www.cs.cmu.edu/~jtassaro/papers/iris-refinement
Appel, A., McAllester, D.: An indexed model of recursive types for foundational proof-carrying code. TOPLAS 23(5), 657–683 (2001)
Benton, N.: Simple relational correctness proofs for static analyses and program transformations. In: POPL (2004)
Birkedal, L., Bizjak, A., Schwinghammer, J.: Step-indexed relational reasoning for countable nondeterminism. Logical Methods Comput. Sci. 9(4), 1–22 (2013)
Birkedal, L., Støvring, K., Thamsborg, J.: The category-theoretic solution of recursive metric-space equations. Theor. Comput. Sci. 411(47), 4102–4122 (2010)
Brookes, S.D.: Variables as resource for shared-memory programs: semantics and soundness. Electr. Notes Theor. Comput. Sci. 158, 123–150 (2006)
Caires, L., Pérez, J.A., Pfenning, F., Toninho, B.: Behavioral polymorphism and parametricity in session-based communication. In: Felleisen, M., Gardner, P. (eds.) ESOP 2013. LNCS, vol. 7792, pp. 330–349. Springer, Heidelberg (2013). doi:10.1007/978-3-642-37036-6_19
Caires, L., Pfenning, F.: Session types as intuitionistic linear propositions. In: Gastin, P., Laroussinie, F. (eds.) CONCUR 2010. LNCS, vol. 6269, pp. 222–236. Springer, Heidelberg (2010). doi:10.1007/978-3-642-15375-4_16
Craig, T.S.: Building fifo and priority-queueing spin locks from atomic swap. Technical report 93-02-02, Computer Science Department, University of Washington (1993)
da Rocha Pinto, P., Dinsdale-Young, T., Gardner, P.: TaDA: a logic for time and data abstraction. In: Jones, R. (ed.) ECOOP 2014. LNCS, vol. 8586, pp. 207–231. Springer, Heidelberg (2014). doi:10.1007/978-3-662-44202-9_9
Dinsdale-Young, T., Dodds, M., Gardner, P., Parkinson, M.J., Vafeiadis, V.: Concurrent abstract predicates. In: D’Hondt, T. (ed.) ECOOP 2010. LNCS, vol. 6183, pp. 504–528. Springer, Heidelberg (2010). doi:10.1007/978-3-642-14107-2_24
Dinsdale-Young, T., Birkedal, L., Gardner, P., Parkinson, M.J., Yang, H.: Views: compositional reasoning for concurrent programs. In: POPL (2013)
Feng, X.: Local rely-guarantee reasoning. In: POPL, pp. 315–327 (2009)
Gay, S.J., Vasconcelos, V.T.: Linear type theory for asynchronous session types. J. Funct. Program. 20(1), 19–50 (2010)
Hoffmann, J., Marmar, M., Shao, Z.: Quantitative reasoning for proving lock-freedom. In: LICS, pp. 124–133 (2013)
Honda, K.: Types for dyadic interaction. In: Best, E. (ed.) CONCUR 1993. LNCS, vol. 715, pp. 509–523. Springer, Heidelberg (1993). doi:10.1007/3-540-57208-2_35
Ishtiaq, S.S., O’Hearn, P.W.: BI as an assertion language for mutable data structures. In: POPL, pp. 14–26 (2001)
Jones, C.B.: Tentative steps toward a development method for interfering programs. TOPLAS 5(4), 596–619 (1983)
Jung, R., Krebbers, R., Birkedal, L., Dreyer, D.: Higher-order ghost state. In: ICFP, pp. 256–269 (2016, to appear)
Jung, R., Swasey, D., Sieczkowski, F., Svendsen, K., Turon, A., Birkedal, L., Dreyer, D.: Iris: monoids and invariants as an orthogonal basis for concurrent reasoning. In: POPL, pp. 637–650 (2015)
Krebbers, R., Timany, A., Birkedal, L.: Interactive proofs in higher-order concurrent separation logic. In: POPL, pp. 205–217 (2017, to appear)
Krogh-Jespersen, M., Svendsen, K., Birkedal, L.: A relational model of types-and-effects in higher-order concurrent separation logic. In: POPL, pp. 218–231 (2017, to appear)
Lehmann, D., Pnueli, A., Stavi, J.: Impartiality, justice and fairness: the ethics of concurrent termination. In: Even, S., Kariv, O. (eds.) ICALP 1981. LNCS, vol. 115, pp. 264–277. Springer, Heidelberg (1981). doi:10.1007/3-540-10843-2_22
Liang, H., Feng, X.: A program logic for concurrent objects under fair scheduling. In: POPL, pp. 385–399 (2016)
Liang, H., Feng, X., Fu, M.: Rely-guarantee-based simulation for compositional verification of concurrent program transformations. ACM Trans. Program. Lang. Syst. 36(1), 3 (2014)
Liang, H., Feng, X., Shao, Z.: Compositional verification of termination-preserving refinement of concurrent programs. In: CSL-LICS, pp. 65:1–65:10 (2014)
Magnusson, P.S., Landin, A., Hagersten, E.: Queue locks on cache coherent multiprocessors. In: International Symposium on Parallel Processing, pp. 165–171 (1994)
Nanevski, A., Ley-Wild, R., Sergey, I., Delbianco, G.A.: Communicating state transition systems for fine-grained concurrent resources. In: Shao, Z. (ed.) ESOP 2014. LNCS, vol. 8410, pp. 290–310. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54833-8_16
O’Hearn, P.: Resources, concurrency, and local reasoning. TCS 375(1), 271–307 (2007)
Pérez, J.A., Caires, L., Pfenning, F., Toninho, B.: Linear logical relations for session-based concurrency. In: Seidl, H. (ed.) ESOP 2012. LNCS, vol. 7211, pp. 539–558. Springer, Heidelberg (2012). doi:10.1007/978-3-642-28869-2_27
da Rocha Pinto, P., Dinsdale-Young, T., Gardner, P., Sutherland, J.: Modular termination verification for non-blocking concurrency. In: Thiemann, P. (ed.) ESOP 2016. LNCS, vol. 9632, pp. 176–201. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49498-1_8
Svendsen, K., Birkedal, L.: Impredicative concurrent abstract predicates. In: Shao, Z. (ed.) ESOP 2014. LNCS, vol. 8410, pp. 149–168. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54833-8_9
Svendsen, K., Sieczkowski, F., Birkedal, L.: Transfinite step-indexing: decoupling concrete and logical steps. In: Thiemann, P. (ed.) ESOP 2016. LNCS, vol. 9632, pp. 727–751. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49498-1_28
Tassarotti, J., Jung, R., Harper, R.: A higher-order logic for concurrent termination-preserving refinement. Available as arXiv:1701.05888 [cs.PL] (2017). http://iris-project.org/pdfs/2017-esop-refinement-final.pdf. Extended version with appendices
Toninho, B., Caires, L., Pfenning, F.: Higher-order processes, functions, and sessions: a monadic integration. In: Felleisen, M., Gardner, P. (eds.) ESOP 2013. LNCS, vol. 7792, pp. 350–369. Springer, Heidelberg (2013). doi:10.1007/978-3-642-37036-6_20
Turon, A., Dreyer, D., Birkedal, L.: Unifying refinement and Hoare-style reasoning in a logic for higher-order concurrency. In: ICFP, pp. 377–390 (2013)
Vafeiadis, V., Parkinson, M.: A marriage of rely/guarantee and separation logic. In: Caires, L., Vasconcelos, V.T. (eds.) CONCUR 2007. LNCS, vol. 4703, pp. 256–271. Springer, Heidelberg (2007). doi:10.1007/978-3-540-74407-8_18
Wadler, P.: Propositions as sessions. J. Funct. Program. 24(2–3), 384–418 (2014)
Willsey, M., Prabhu, R., Pfenning, F.: Design and implementation of concurrent C0. In: Linearity (2016)
Yang, H.: Relational separation logic. TCS 375(1–3), 308–334 (2007)
Yoshida, N., Vasconcelos, V.T.: Language primitives and type discipline for structured communication-based programming revisited: Two systems for higher-order session communication. Electr. Notes Theor. Comput. Sci. 171(4), 73–93 (2007)
Acknowledgments
The authors thank Robbert Krebbers, Jeehoon Kang, Max Willsey, Frank Pfenning, Derek Dreyer, Lars Birkedal, and Jan Hoffmann for helpful discussions and feedback. This research was conducted with U.S. Government support under and awarded by DoD, Air Force Office of Scientific Research, National Defense Science and Engineering Graduate (NDSEG) Fellowship, 32 CFR 168a; and with support by a European Research Council (ERC) Consolidator Grant for the project “RustBelt”, funded under the European Union’s Horizon 2020 Framework Programme (grant agreement no. 683289). Any opinions, findings and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of these funding agencies.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer-Verlag GmbH Germany
About this paper
Cite this paper
Tassarotti, J., Jung, R., Harper, R. (2017). A Higher-Order Logic for Concurrent Termination-Preserving Refinement. In: Yang, H. (eds) Programming Languages and Systems. ESOP 2017. Lecture Notes in Computer Science(), vol 10201. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-54434-1_34
Download citation
DOI: https://doi.org/10.1007/978-3-662-54434-1_34
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-54433-4
Online ISBN: 978-3-662-54434-1
eBook Packages: Computer ScienceComputer Science (R0)







 then no
then no 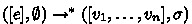 then either:
then either: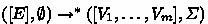 and
and  in which some thread gets stuck.
in which some thread gets stuck. has a fair diverging execution, then
has a fair diverging execution, then  also has a fair diverging execution. Recall that an infinite execution is fair if every non-terminating thread takes infinitely many steps. This last condition makes the refinement a fair, termination-preserving refinement.
also has a fair diverging execution. Recall that an infinite execution is fair if every non-terminating thread takes infinitely many steps. This last condition makes the refinement a fair, termination-preserving refinement.

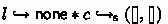 from the STS’s
from the STS’s  . We use
. We use 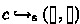 to justify performing an “idle” step in the source. This is crucial – after all, we are potentially looping indefinitely in the target, reading l over and over; we have to exhibit a corresponding diverging execution in the source.
to justify performing an “idle” step in the source. This is crucial – after all, we are potentially looping indefinitely in the target, reading l over and over; we have to exhibit a corresponding diverging execution in the source. . We use
. We use  . We can now throw away ownership of l and
. We can now throw away ownership of l and 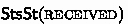 since we no longer need them – we can do this because all these assertions are affine.
since we no longer need them – we can do this because all these assertions are affine.
 . We already established that the second component of the value loaded from l is 42, and the source thread is easily reduced to 42 as well.
. We already established that the second component of the value loaded from l is 42, and the source thread is easily reduced to 42 as well. ) represent obligations that cannot be thrown away.
) represent obligations that cannot be thrown away.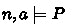 and
and  , then
, then  .
. and
and  .
. and
and  run in and assume they satisfy the precondition of the triple.
run in and assume they satisfy the precondition of the triple.