Abstract
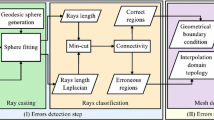
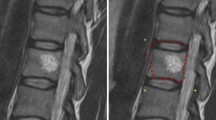
Volumetric image segmentation methods often produce delineations of anatomical structures and pathologies that require user modifications. We present a new method for the correction of segmentation errors. Given an initial geometrical mesh, our method semi automatically identifies the mesh vertices in erroneous regions with min-cut segmentation. It then deforms the mesh by correcting its vertex coordinates with Laplace deformation based on local geometrical properties. The key advantages of our method are that: 1) it supports fast user interaction on a single surface rendered 2D view; 2) its parameters values are fixed to the same value for all cases; 3) it is independent of the initial segmentation method, and; 4) it is applicable to a variety of anatomical structures and pathologies. Experimental evaluation on 44 initial segmentations of kidney and kidney vessels from CT scans show an improvement of 83% and 75% in the average surface distance and the volume overlap error between the initial and the corrected segmentations with respect to the ground-truth.
Chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
References
Boykov, Y.Y., Jolly, M.P.: Interactive graph cuts for optimal boundary & region segmentation of objects in nd images. In: Proceedings of the Eighth IEEE International Conference on Computer Vision, ICCV 2001, vol. 1, pp. 105–112. IEEE (2001)
Grady, L., Funka-Lea, G.: An energy minimization approach to the data driven editing of presegmented images/Volumes. In: Larsen, R., Nielsen, M., Sporring, J. (eds.) MICCAI 2006. LNCS, vol. 4191, pp. 888–895. Springer, Heidelberg (2006)
Heckel, F., Braunewell, S., Soza, G., Tietjen, C., Hahn, H.K.: Sketch-based image-independent editing of 3D tumor segmentations using variational interpolation. In: Eurographics Workshop on Visual Computing for Biology and Medicine, pp. 73–80. The Eurographics Association (2012)
Meyer, M., Desbrun, M., Schröder, P., Barr, A.H.: Discrete differential-geometry operators for triangulated 2-manifolds. Visualization and Mathematics 3(7), 34–57 (2002)
Boykov, Y., Funka-Lea, G.: Graph Cuts and Efficient N-D Image Segmentation. Int. J. of Comp. Vis. 70(2), 109–131 (2006)
Reuter, M., Biasotti, S., Giorgi, D., Patanč, G., Spagnuolo, M.: Discrete laplace-beltrami operators for shape analysis and segmentation. Computers & Graphics 33(3), 381–390 (2009)
Davis, T.A.: Algorithm 832: Umfpack v4. 3—an unsymmetric-pattern multifrontal method. ACM Transactions on Mathematical Software (TOMS) 30(2), 196–199 (2004)
Yushkevich, P.A., Piven, J., Cody, H., Ho, S., Gee, J.C., Gerig, G.: User-guided level set segmentation of anatomical structures with itk-snap. Insight Journal, Special Issue on ISC/NA-MIC/MICCAI Workshop on Open-Source Software (2005)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Kronman, A., Joskowicz, L. (2013). Image Segmentation Errors Correction by Mesh Segmentation and Deformation. In: Mori, K., Sakuma, I., Sato, Y., Barillot, C., Navab, N. (eds) Medical Image Computing and Computer-Assisted Intervention – MICCAI 2013. MICCAI 2013. Lecture Notes in Computer Science, vol 8150. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-40763-5_26
Download citation
DOI: https://doi.org/10.1007/978-3-642-40763-5_26
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-40762-8
Online ISBN: 978-3-642-40763-5
eBook Packages: Computer ScienceComputer Science (R0)