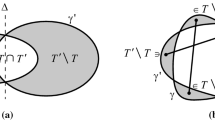
Abstract
The family of separating circles of two finite sets S 1 and S 2 in the plane consists of all the circles that enclose S 1 but exclude S 2. We prove that the maximum and minimum distance between a point p and any separating circle in this family can be found by examining only a finite subset of circles, although the family itself is infinite. In addition, we introduce the concept of elementary circular separations to clarify some of the properties of separating circles.
Chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
References
Chazelle, B.: An optimal convex hull algorithm in any fixed dimension. Discrete and Computational Geometry 10, 377–409 (1993)
Clarkson, K.L., Shor, P.: Applications of random sampling in computational geometry, II. Discrete Computational Geometry 4, 387–421 (1989)
Coeurjolly, D., Gerard, Y., Reveilles, J.-P., Tougne, L.: An elementary algorithm for digital arc segmentation. Discrete Applied Mathematics 139, 31–50 (2004)
Damaschke, P.: The linear time recognition of digital arcs. Pattern Recognition Letters 16, 543–548 (1995)
Fisk, S.: Separating points sets by circles, and the recognition of digital disks. IEEE Transactions on Pattern Analysis and Machine Intelligence 8, 554–556 (1986)
Kim, C.E., Anderson, T.A.: Digital disks and a digital compactness measure. In: Annual ACM Symposium on Theory of Computing, pp. 117–124 (1984)
O’Rourke, J., Koraraju, S.R., Meggido, N.: Computing circular separability. Discrete and Combinatorial Geometry 1, 105–113 (1986)
Roussillon, T., Tougne, L., Sivignon, I.: On three constrained versions of the digital circular arc recognition problem. In: Brlek, S., Reutenauer, C., Provençal, X. (eds.) DGCI 2009. LNCS, vol. 5810, pp. 34–45. Springer, Heidelberg (2009)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2011 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Veelaert, P. (2011). Distance between Separating Circles and Points. In: Debled-Rennesson, I., Domenjoud, E., Kerautret, B., Even, P. (eds) Discrete Geometry for Computer Imagery. DGCI 2011. Lecture Notes in Computer Science, vol 6607. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-19867-0_29
Download citation
DOI: https://doi.org/10.1007/978-3-642-19867-0_29
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-19866-3
Online ISBN: 978-3-642-19867-0
eBook Packages: Computer ScienceComputer Science (R0)