Abstract
Parallel snapshot isolation (PSI) is a standard transactional consistency model used in databases and distributed systems. We argue that PSI is also a useful formal model for software transactional memory (STM) as it has certain advantages over other consistency models. However, the formal PSI definition is given declaratively by acyclicity axioms, which most programmers find hard to understand and reason about.
To address this, we develop a simple lock-based reference implementation for PSI built on top of the release-acquire memory model, a well-behaved subset of the C/C++11 memory model. We prove that our implementation is sound and complete against its higher-level declarative specification.
We further consider an extension of PSI allowing transactional and non-transactional code to interact, and provide a sound and complete reference implementation for the more general setting. Supporting this interaction is necessary for adopting a transactional model in programming languages.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Software Transactional Memory (STM)
- Declarative Specification
- Lockean Version
- Weak Memory Models
- Execution Graph
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Following the widespread use of transactions in databases, software transactional memory (STM) [19, 35] has been proposed as a programming language abstraction that can radically simplify the task of writing correct and efficient concurrent programs. It provides the illusion of blocks of code, called transactions, executing atomically and in isolation from any other such concurrent blocks.
In theory, STM is great for programmers as it allows them to concentrate on the high-level algorithmic steps of solving a problem and relieves them of such concerns as the low-level details of enforcing mutual exclusion. In practice, however, the situation is far from ideal as the semantics of transactions in the context of non-transactional code is not at all settled. Recent years have seen a plethora of different STM implementations [1,2,3, 6, 17, 20], each providing a slightly different—and often unspecified—semantics to the programmer.
Simple models in the literature are lock-based, such as global lock atomicity (GLA) [28] (where a transaction must acquire a global lock prior to execution and release it afterwards) and disjoint lock atomicity (DLA) [28] (where a transaction must acquire all locks associated with the locations it accesses prior to execution and release them afterwards), which provide serialisable transactions. That is, all transactions appear to have executed atomically one after another in some total order. The problem with these models is largely their implementation cost, as they impose too much synchronisation between transactions.
The database community has long recognised this performance problem and has developed weaker transactional models that do not guarantee serialisability. The most widely used such model is snapshot isolation (SI) [10], implemented by major databases, both centralised (e.g. Oracle and MS SQL Server) and distributed [16, 30, 33], as well as in STM [1, 11, 25, 26]. In this article, we focus on a closely related model, parallel snapshot isolation (PSI) [36], which is known to provide better scalability and availability in large-scale geo-replicated systems. SI and PSI allow conflicting transactions to execute concurrently and to commit successfully, so long as they do not have a write-write conflict. This in effect allows reads of SI/PSI transactions to read from an earlier memory snapshot than the one affected by their writes, and permits outcomes such as the following:

The above is also known as the write skew anomaly in the database literature [14]. Such outcomes are analogous to those allowed by weak memory models, such as x86-TSO [29, 34] and C11 [9], for non-transactional programs. In this article, we consider—to the best of our knowledge for the first time—PSI as a possible model for STM, especially in the context of a concurrent language such as C/C++ with a weak memory model. In such contexts, programmers are already familiar with weak behaviours such as that exhibited by SB+txs above.
A key reason why PSI is more suitable for a programming language than SI (or other stronger models) is performance. This is analogous to why C/C++ adopted non-multi-copy-atomicity (allowing two different threads to observe a write by a third thread at different times) as part of their concurrency model. Consider the following “IRIW” (independent reads of independent writes) litmus test:

In the annotated behaviour, transactions T2 and T3 disagree on the relative order of transactions T1 and T4. Under PSI, this behaviour (called the long fork anomaly) is allowed, as T1 and T4 are not ordered—they commit in parallel—but it is disallowed under SI. This intuitively means that SI must impose ordering guarantees even on transactions that do not access a common location, and can be rather costly in the context of a weakly consistent system.
A second reason why PSI is much more suitable than SI is that it has better properties. A key intuitive property a programmer might expect of transactions is monotonicity. Suppose, in the (SB+txs) program we split the two transactions into four smaller ones as follows:

One might expect that if the annotated behaviour is allowed in (SB+txs), it should also be allowed in (SB+txs+chop). This indeed is the case for PSI, but not for SI! In fact, in the extreme case where every transaction contains a single access, SI provides serialisability. Nevertheless, PSI currently has two significant drawbacks, preventing its widespread adoption. We aim to address these here.
The first PSI drawback is that its formal semantics can be rather daunting for the uninitiated as it is defined declaratively in terms of acyclicity constraints. What is missing is perhaps a simple lock-based reference implementation of PSI, similar to the lock-based implementations of GLA and DLA, that the programmers can readily understand and reason about. As an added benefit, such an implementation can be viewed as an operational model, forming the basis for developing program logics for reasoning about PSI programs.
Although Cerone et al. [15] proved their declarative PSI specification equivalent to an implementation strategy of PSI in a distributed system with replicated storage over causal consistency, their implementation is not suitable for reasoning about shared-memory programs. In particular, it cannot help the programmers determine how transactional and non-transactional accesses may interact.
As our first contribution, in Sect. 4 we address this PSI drawback by providing a simple lock-based reference implementation that we prove equivalent to its declarative specification. Typically, one proves that an implementation is sound with respect to a declarative specification—i.e. every behaviour observable in the implementation is accounted for in the declarative specification. Here, we also want the other direction, known as completeness, namely that every behaviour allowed by the specification is actually possible in the implementation. Having a (simple) complete implementation is very useful for programmers, as it may be easier to understand and experiment with than the declarative specification.
Our reference implementation is built in the release-acquire fragment of the C/C++ memory model [8, 9, 21], using sequence locks [13, 18, 23, 32] to achieve the correct transactional semantics.
The second PSI drawback is that its study so far has not accounted for the subtle effects of non-transactional accesses and how they interact with transactional accesses. While this scenario does not arise in ‘closed world’ systems such as databases, it is crucially important in languages such as C/C++ and Java, where one cannot afford the implementation cost of making every access transactional so that it is “strongly isolated” from other concurrent transactions.
Therefore, as our second contribution, in Sect. 5 we extend our basic reference implementation to make it robust under uninstrumented non-transactional accesses, and characterise declaratively the semantics we obtain. We call this extended model RPSI (for “robust PSI”) and show that it gives reasonable semantics even under scenarios where transactional and non-transactional accesses are mixed.
Outline. The remainder of this article is organised as follows. In Sect. 2 we present an overview of our contributions and the necessary background information. In Sect. 3 we provide the formal model of the C11 release/acquire fragment and describe how we extend it to specify the behaviour of STM programs. In Sect. 4 we present our PSI reference implementation (without non-transactional accesses), demonstrating its soundness and completeness against the declarative PSI specification. In Sect. 5 we formulate a declarative specification for RPSI as an extension of PSI accounting for non-transactional accesses. We then present our RPSI reference implementation, demonstrating its soundness and completeness against our proposed declarative specification. We conclude and discuss future work in Sect. 6.
2 Background and Main Ideas
One of the main differences between the specification of database transactions and those of STM is that STM specifications must additionally account for the interactions between mixed-mode (both transactional and non-transactional) accesses to the same locations. To characterise such interactions, Blundell et al. [12, 27] proposed the notions of weak and strong atomicity, often referred to as weak and strong isolation. Weak isolation guarantees isolation only amongst transactions: the intermediate state of a transaction cannot affect or be affected by other transactions, but no such isolation is guaranteed with respect to non-transactional code (e.g. the accesses of a transaction may be interleaved by those of non-transactional code.). By contrast, strong isolation additionally guarantees full isolation from non-transactional code. Informally, each non-transactional access is considered as a transaction with a single access. In what follows, we explore the design choices for implementing STMs under each isolation model (Sect. 2.1), provide an intuitive account of the PSI model (Sect. 2.2), and describe the key requirements for implementing PSI and how we meet them (Sect. 2.3).
2.1 Implementing Software Transactional Memory
Implementing STMs under either strong or weak isolation models comes with a number of challenges. Implementing strongly isolated STMs requires a conflict detection/avoidance mechanism between transactional and non-transactional code. That is, unless non-transactional accesses are instrumented to adhere to the same access policies, conflicts involving non-transactional code cannot be detected. For instance, in order to guarantee strong isolation under the GLA model [28] discussed earlier, non-transactional code must be modified to acquire the global lock prior to each shared access and release it afterwards.
Implementing weakly-isolated STMs requires a careful handling of aborting transactions as their intermediate state may be observed by non-transactional code. Ideally, the STM implementation must ensure that the intermediate state of aborting transactions is not leaked to non-transactional code. A transaction may abort either because it failed to commit (e.g. due to a conflict), or because it encountered an explicit abort instruction in the transactional code. In the former case, leaks to non-transactional code can be avoided by pessimistic concurrency control (e.g. locks), pre-empting conflicts. In the latter case, leaks can be prevented either by lazy version management (where transactional updates are stored locally and propagated to memory only upon committing), or by disallowing explicit abort instructions altogether – an approach taken by the (weakly isolated) relaxed transactions of the C++ memory model [6].
As mentioned earlier, our aim in this work is to build an STM with PSI guarantees in the RA fragment of C11. As such, instrumenting non-transactional accesses is not feasible and thus our STM guarantees weak isolation. For simplicity, throughout our development we make a few simplifying assumptions: (i) transactions are not nested; (ii) the transactional code is without explicit abort instructions (as with the weakly-isolated transactions of C++ [6]); and (iii) the locations accessed by a transaction can be statically determined. For the latter, of course, a static over-approximation of the locations accessed suffices for the soundness of our implementations.
2.2 Parallel Snapshot Isolation (PSI)
The initial model of PSI introduced in [36] is described informally in terms of a multi-version concurrent algorithm as follows. A transaction \( \texttt {T} \) at a replica r proceeds by taking an initial snapshot S of the shared objects in r. The execution of \( \texttt {T} \) is then carried out locally: read operations query S and write operations similarly update S. Once the execution of \( \texttt {T} \) is completed, it attempts to commit its changes to r and it succeeds only if it is not write-conflicted. Transaction \( \texttt {T} \) is write-conflicted if another committed transaction \( \texttt {T} '\) has written to a location in r also written to by \( \texttt {T} \), since it recorded its snapshot S. If \( \texttt {T} \) fails the conflict check it aborts and may restart the transaction; otherwise, it commits its changes to r, at which point its changes become visible to all other transactions that take a snapshot of replica r thereafter. These committed changes are later propagated to other replicas asynchronously.
The main difference between SI and PSI is in the way the committed changes at a replica r are propagated to other sites in the system. Under the SI model, committed transactions are globally ordered and the changes at each replica are propagated to others in this global order. This ensures that all concurrent transactions are observed in the same order by all replicas. By contrast, PSI does not enforce a global order on committed transactions: transactional effects are propagated between replicas in causal order. This ensures that, if replica \(r_1\) commits a message m which is later read at replica \(r_2\), and \(r_2\) posts a response \(m'\), no replica can see \(m'\) without having seen the original message m. However, causal propagation allows two replicas to observe concurrent events as if occurring in different orders: if \(r_1\) and \(r_2\) concurrently commit messages m and \(m'\), then replica \(r_3\) may initially see m but not \(m'\), and \(r_4\) may see \(m'\) but not m. This is best illustrated by the (IRIW+txs) example in Sect. 1.
2.3 Towards a Lock-Based Reference Implementation for PSI
While the description of PSI above is suitable for understanding PSI, it is not very useful for integrating the PSI model in languages such as C, C++ or Java. From a programmer’s perspective, in such languages the various threads directly access the shared memory; they do not access their own replicas, which are loosely related to the replicas of other threads. What we would therefore like is an equivalent description of PSI in terms of unreplicated accesses to shared memory and a synchronisation mechanism such as locks.
In effect, we want a definition similar in spirit to global lock atomicity (GLA) [28], which is arguably the simplest TM model, and models committed transactions as acquiring a global mutual exclusion lock, then accessing and updating the data in place, and finally releasing the global lock. Naturally, however, the implementation of PSI cannot be that simple.
A first observation is that PSI cannot be simply implemented over sequentially consistent (SC) shared memory.Footnote 1 To see this, consider the IRIW+txs program from the introduction. Although PSI allows the annotated behaviour, SC forbids it for the corresponding program without transactions. The point is that under SC, either the \(x:=1\) or the \(y:=1\) write first reaches memory. Suppose, without loss of generality, that \(x:=1\) is written to memory before \(y:=1\). Then, the possible atomic snapshots of memory are \(x=y=0\), \(x=1\wedge y=0\), and \(x=y=1\). In particular, the snapshot read by T3 is impossible.
To implement PSI we therefore resort to a weaker memory model. Among weak memory models, the “multi-copy-atomic” ones, such as x86-TSO [29, 34], SPARC PSO [37, 38] and ARMv8-Flat [31], also forbid the weak outcome of (IRIW+txs) in the same way as SC, and so are unsuitable for our purpose. We thus consider release-acquire consistency (RA) [8, 9, 21], a simple and well-behaved non-multi-copy-atomic model. It is readily available as a subset of the C/C++11 memory model [9] with verified compilation schemes to all major architectures.
RA provides a crucial property that is relied upon in the earlier description of PSI, namely causality. In terms of RA, this means that if thread A observes a write w of thread B, then it also observes all the previous writes of thread B as well as any other writes B observed before performing w.
A second observation is that using a single lock to enforce mutual exclusion does not work as we need to allow transactions that access disjoint sets of locations to complete in parallel. An obvious solution is to use multiple locks—one per location—as in the disjoint lock atomicity (DLA) model [28]. The question remaining is how to implement taking a snapshot at the beginning of a transaction.
A naive attempt is to use reader/writer locks, which allow multiple readers (taking the snapshots) to run in parallel, as long as no writer has acquired the lock. In more detail, the idea is to acquire reader locks for all locations read by a transaction, read the locations and store their values locally, and then release the reader locks. However, as we describe shortly, this approach does not work. Consider the (IRIW+txs) example in Sect. 1. For T2 to get the annotated outcome, it must release its reader lock for y before T4 acquires it. Likewise, since T3 observes \(y=1\), it must acquire its reader lock for y after T4 releases it. By this point, however, it is transitively after the release of the y lock by T2, and so, because of causality, it must have observed all the writes observed by T2 by that point—namely, the \(x:=1\) write. In essence, the problem is that reader-writer locks over-synchronise. When two threads acquire the same reader lock, they synchronise, whereas two read-only transactions should never synchronise in PSI.
To resolve this problem, we use sequence locks [13, 18, 23, 32]. Under the sequence locking protocol, each location x is associated with a sequence (version) number vx, initialised to zero. Each write to x increments vx before and after its update, provided that vx is even upon the first increment. Each read from x checks vx before and after reading x. If both values are the same and even, then there cannot have been any concurrent increments, and the reader must have seen a consistent value. That is, \( \texttt {read(x)} \triangleq \texttt {do\{v:= \texttt {vx} ;\,s:=x\}\, while(is-odd(v)\,||\, \texttt {vx} !=v)} \). Under SC, sequence locks are equivalent to reader-writer locks; however, under RA, they are weaker exactly because readers do not synchronise.
Handling Non-transactional Accesses. Let us consider what happens if some of the data accessed by a transaction is modified concurrently by an atomic non-transactional write. Since non-transactional accesses do not acquire any locks, the snapshots taken can include values written by non-transactional accesses. The result of the snapshot then depends on the order in which the variables are read. Consider for example the following litmus test:

In our implementation, if the transaction’s snapshot reads y before x, then the annotated weak behaviour is not possible, because the underlying model (RA) disallows the weak “message passing” behaviour. If, however, x is read before y by the snapshot, then the weak behaviour is possible. In essence, this means that the PSI implementation described so far is of little use, when there are races between transactional and non-transactional code.
Another problem is the lack of monotonicity. A programmer might expect that wrapping some code in a transaction block will never yield additional behaviours not possible in the program without transactions. Yet, in this example, removing the T block and unwrapping its code gets rid of the annotated weak behaviour!
To get monotonicity, it seems that snapshots must read the variables in the same order they are accessed by the transactions. How can this be achieved for transactions that say read x, then y, and then x again? Or transactions that depending on some complex condition, access first x and then y or vice versa? The key to solving this conundrum is surprisingly simple: read each variable twice. In more detail, one takes two snapshots of the locations read by the transaction, and checks that both snapshots return the same values for each location. This ensures that every location is read both before and after every other location in the transaction, and hence all the high-level happens-before orderings in executions of the transactional program are also respected by its implementation.
There is however one caveat: since equality of values is used to determine whether the two snapshots are the same, we will miss cases where different non-transactional writes to a variable write the same value. In our formal development (see Sect. 5), we thus assume that if multiple non-transactional writes write the same value to the same location, they cannot race with the same transaction. This assumption is necessary for the soundness of our implementation and cannot be lifted without instrumenting non-transactional accesses.
3 The Release-Acquire Memory Model for STM
We present the notational conventions used in the remainder of this article and proceed with the declarative model of the release-acquire (RA) fragment [21] of the C11 memory model [9], in which we implement our STM. In Sect. 3.1 we describe how we extend this formal model to specify the behaviour of STM programs.
Notation. Given a relation  on a set A, we write
on a set A, we write  ,
,  and
and  for the reflexive, transitive and reflexive-transitive closure of
for the reflexive, transitive and reflexive-transitive closure of  , respectively. We write
, respectively. We write  for the inverse of
for the inverse of  ;
;  for
for  ; [A] for the identity relation on A, i.e. \( \left\{ \begin{array}{@{} l @{} | @{} l @{}} \begin{array}{@{} l @{}} (a, a) \end{array}&\begin{array}{@{} l @{}} a \in A \end{array} \end{array} \right\} \); \( \textsf {irreflexive} (r)\) for \(\lnot \exists a.\; (a, a) \in r\); and
; [A] for the identity relation on A, i.e. \( \left\{ \begin{array}{@{} l @{} | @{} l @{}} \begin{array}{@{} l @{}} (a, a) \end{array}&\begin{array}{@{} l @{}} a \in A \end{array} \end{array} \right\} \); \( \textsf {irreflexive} (r)\) for \(\lnot \exists a.\; (a, a) \in r\); and  for
for  . Given two relations
. Given two relations  and
and  , we write
, we write  for their (left) relational composition, i.e.
for their (left) relational composition, i.e.  . Lastly, when
. Lastly, when  is a strict partial order, we write
is a strict partial order, we write  for the immediate edges in
for the immediate edges in  :
:  .
.
The RA model is given by the fragment of the C11 memory model, where all read accesses are acquire (\({\mathtt {acq}}\)) reads, all writes are release (\({\mathtt {rel}}\)) writes, and all atomic updates (i.e. RMWs) are acquire-release (\({\mathtt {acqrel}}\)) updates. The semantics of a program under RA is defined as a set of consistent executions.
Definition 1
(Executions in RA). Assume a finite set of locations  ; a finite set of values
; a finite set of values  ; and a finite set of thread identifiers
; and a finite set of thread identifiers  . Let x, y, z range over locations, v over values and \(\tau \) over thread identifiers. An RA execution graph of an STM implementation, \( G \), is a tuple of the form
. Let x, y, z range over locations, v over values and \(\tau \) over thread identifiers. An RA execution graph of an STM implementation, \( G \), is a tuple of the form  with its nodes given by \( \textit{E} \) and its edges given by the
with its nodes given by \( \textit{E} \) and its edges given by the  and
and  relations such that:
relations such that:
-
\( \textit{E} \subset {\mathbb {N}}\) is a finite set of events, and is accompanied with the functions
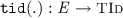 and
and 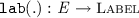 , returning the thread identifier and the label of an event, respectively. We typically use a, b, and e to range over events. The label of an event is a tuple of one of the following three forms: (i) \({\mathtt {R}}( x, v) \) for read events; (ii) \({\mathtt {W}}(x, v) \) for write events; or (iii) \({\mathtt {U}}(x, v, v') \) for update events. The \({\mathtt {lab}}({.})\) function induces the functions \({\mathtt {typ}}(.)\), \({\mathtt {loc}}({.})\), \({\mathtt {val_r}}({.})\) and \({\mathtt {val_w}}({.})\) that respectively project the type (\({\mathtt {R}}\), \({\mathtt {W}}\) or \({\mathtt {U}}\)), location, and read/written values of an event, where applicable. The set of read events is denoted by \({\mathcal {R}}\triangleq \left\{ \begin{array}{@{} l @{} | @{} l @{}} \begin{array}{@{} l @{}} e \in \textit{E} \end{array}&\begin{array}{@{} l @{}} {\mathtt {typ}}(e) \in \{{\mathtt {R}},{\mathtt {U}}\} \end{array} \end{array} \right\} \); similarly, the set of write events is denoted by \({\mathcal {W}}\triangleq \left\{ \begin{array}{@{} l @{} | @{} l @{}} \begin{array}{@{} l @{}} e \in \textit{E} \end{array}&\begin{array}{@{} l @{}} {\mathtt {typ}}(e) \in \{{\mathtt {W}},{\mathtt {U}}\} \end{array} \end{array} \right\} \) and the set of update events is denoted by \({\mathcal {U}}\triangleq {\mathcal {R}}\cap {\mathcal {W}}\).
, returning the thread identifier and the label of an event, respectively. We typically use a, b, and e to range over events. The label of an event is a tuple of one of the following three forms: (i) \({\mathtt {R}}( x, v) \) for read events; (ii) \({\mathtt {W}}(x, v) \) for write events; or (iii) \({\mathtt {U}}(x, v, v') \) for update events. The \({\mathtt {lab}}({.})\) function induces the functions \({\mathtt {typ}}(.)\), \({\mathtt {loc}}({.})\), \({\mathtt {val_r}}({.})\) and \({\mathtt {val_w}}({.})\) that respectively project the type (\({\mathtt {R}}\), \({\mathtt {W}}\) or \({\mathtt {U}}\)), location, and read/written values of an event, where applicable. The set of read events is denoted by \({\mathcal {R}}\triangleq \left\{ \begin{array}{@{} l @{} | @{} l @{}} \begin{array}{@{} l @{}} e \in \textit{E} \end{array}&\begin{array}{@{} l @{}} {\mathtt {typ}}(e) \in \{{\mathtt {R}},{\mathtt {U}}\} \end{array} \end{array} \right\} \); similarly, the set of write events is denoted by \({\mathcal {W}}\triangleq \left\{ \begin{array}{@{} l @{} | @{} l @{}} \begin{array}{@{} l @{}} e \in \textit{E} \end{array}&\begin{array}{@{} l @{}} {\mathtt {typ}}(e) \in \{{\mathtt {W}},{\mathtt {U}}\} \end{array} \end{array} \right\} \) and the set of update events is denoted by \({\mathcal {U}}\triangleq {\mathcal {R}}\cap {\mathcal {W}}\).We further assume that \( \textit{E} \) always contains a set \( \textit{E} _0\) of initialisation events consisting of a write event with label \({\mathtt {W}}(x, 0) \) for every
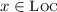 .
. -
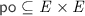 denotes the ‘program-order’ relation, defined as a disjoint union of strict total orders, each orders the events of one thread, together with \( \textit{E} _0\times ( \textit{E} \setminus \textit{E} _0)\) that places the initialisation events before any other event.
denotes the ‘program-order’ relation, defined as a disjoint union of strict total orders, each orders the events of one thread, together with \( \textit{E} _0\times ( \textit{E} \setminus \textit{E} _0)\) that places the initialisation events before any other event. -
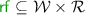 denotes the ‘reads-from’ relation, defined as a relation between write and read events of the same location and value; it is total and functional on reads, i.e. every read event is related to exactly one write event;
denotes the ‘reads-from’ relation, defined as a relation between write and read events of the same location and value; it is total and functional on reads, i.e. every read event is related to exactly one write event; -
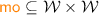 denotes the ‘modification-order’ relation, defined as a disjoint union of strict orders, each of which totally orders the write events to one location.
denotes the ‘modification-order’ relation, defined as a disjoint union of strict orders, each of which totally orders the write events to one location.
We often use “\( G .\)” as a prefix to project the various components of \( G \) (e.g. \( G . \textit{E} \)). Given a relation  , we write
, we write  for
for  . Analogously, given a set \(A \subseteq \textit{E} \), we write \(A_{x}\) for \(A \cap \left\{ \begin{array}{@{} l @{} | @{} l @{}} \begin{array}{@{} l @{}} a \end{array}&\begin{array}{@{} l @{}} {\mathtt {loc}}({a}) = x \end{array} \end{array} \right\} \). Lastly, given the
. Analogously, given a set \(A \subseteq \textit{E} \), we write \(A_{x}\) for \(A \cap \left\{ \begin{array}{@{} l @{} | @{} l @{}} \begin{array}{@{} l @{}} a \end{array}&\begin{array}{@{} l @{}} {\mathtt {loc}}({a}) = x \end{array} \end{array} \right\} \). Lastly, given the  and
and  relations, we define the ‘reads-before’ relation
relations, we define the ‘reads-before’ relation  .
.
An RA-consistent execution of a transaction-free variant of (IRIW+txs) in Sect. 1, with program outcome \(a=c=1\) and \(b=d=0\).
Executions of a given program represent traces of shared memory accesses generated by the program. We only consider “partitioned” programs of the form  , where \(\parallel \) denotes parallel composition, and each \(c_i\) is a sequential program. The set of executions associated with a given program is then defined by induction over the structure of sequential programs. We do not define this construction formally as it depends on the syntax of the implementation programming language. Each execution of a program P has a particular program outcome, prescribing the final values of local variables in each thread (see example in Fig. 1).
, where \(\parallel \) denotes parallel composition, and each \(c_i\) is a sequential program. The set of executions associated with a given program is then defined by induction over the structure of sequential programs. We do not define this construction formally as it depends on the syntax of the implementation programming language. Each execution of a program P has a particular program outcome, prescribing the final values of local variables in each thread (see example in Fig. 1).
In this initial stage, the execution outcomes are unrestricted in that there are no constraints on the  and
and  relations. These restrictions and thus the permitted outcomes of a program are determined by the set of consistent executions:
relations. These restrictions and thus the permitted outcomes of a program are determined by the set of consistent executions:
Definition 2
(RA-consistency). A program execution \( G \) is RA-consistent, written \( \textsf {RA\hbox {-}consistent} ( G )\), if  holds, where
holds, where  denotes the ‘RA-happens-before’ relation.
denotes the ‘RA-happens-before’ relation.
Among all executions of a given program P, only the RA-consistent ones define the allowed outcomes of P.
3.1 Software Transactional Memory in RA: Specification
Our goal in this section is to develop a declarative framework that allows us to specify the behaviour of mixed-mode STM programs under weak isolation guarantees. Whilst the behaviour of transactional code is dictated by the particular isolation model considered (e.g. PSI), the behaviour of non-transactional code and its interaction with transactions is guided by the underlying memory model. As we build our STM in the RA fragment of C11, we assume the behaviour of non-transactional code to conform to the RA memory model. More concretely, we build our specification of a program P such that (i) in the absence of transactional code, the behaviour of P is as defined by the RA model; (ii) in the absence of non-transactional code, the behaviour of P is as defined by the PSI model.
Definition 3
(Specification Executions). Assume a finite set of transaction identifiers  . An execution graph of an STM specification, \(\varGamma \), is a tuple of the form
. An execution graph of an STM specification, \(\varGamma \), is a tuple of the form  \({\mathcal {T}})\) where:
\({\mathcal {T}})\) where:
-
\( \textit{E} \triangleq {\mathcal {R}}\cup {\mathcal {W}}\cup {\mathcal {B}}\cup {\mathcal {E}}\), denotes the set of events with \({\mathcal {R}}\) and \({\mathcal {W}}\) defined as the sets of read and write events as described above; and the \({\mathcal {B}}\) and \({\mathcal {E}}\) respectively denote the set of events marking the beginning and end of transactions. For each event \(a \in {\mathcal {B}}\cup {\mathcal {E}}\), the \({\mathtt {lab}}({.})\) function is extended to return \( \texttt {B} \) when \(a \in {\mathcal {B}}\), and \( \texttt {E} \) when \(a \in {\mathcal {E}}\). The \({\mathtt {typ}}(.)\) function is accordingly extended to return a type in \( \left\{ \begin{array}{@{} l @{}} {\mathtt {R}}, {\mathtt {W}}, {\mathtt {U}}, \texttt {B} , \texttt {E} \end{array} \right\} \), whilst the remaining functions are extended to return default (dummy) values for events in \({\mathcal {B}}\cup {\mathcal {E}}\).
-
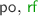 and
and  denote the ‘program-order’, ‘reads-from’ and ‘modification-order’ relations as described above;
denote the ‘program-order’, ‘reads-from’ and ‘modification-order’ relations as described above; -
\({\mathcal {T}}\subseteq \textit{E} \) denotes the set of transactional events with \({\mathcal {B}}\cup {\mathcal {E}}\subseteq {\mathcal {T}}\). For transactional events in \({\mathcal {T}}\), event labels are extended to carry an additional component, namely the associated transaction identifier. As such, a specification graph is additionally accompanied with the function
 , returning the transaction identifier of transactional events. The derived ‘same-transaction’ relation,
, returning the transaction identifier of transactional events. The derived ‘same-transaction’ relation, 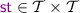 , is the equivalence relation given by
, is the equivalence relation given by 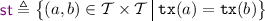 .
.
We write  for the set of equivalence classes of \({\mathcal {T}}\) induced by
for the set of equivalence classes of \({\mathcal {T}}\) induced by  ;
;  for the equivalence class that contains a; and \({\mathcal {T}}_\xi \) for the equivalence class of transaction
for the equivalence class that contains a; and \({\mathcal {T}}_\xi \) for the equivalence class of transaction  : \({\mathcal {T}}_\xi \triangleq \left\{ \begin{array}{@{} l @{} | @{} l @{}} \begin{array}{@{} l @{}} a \end{array}&\begin{array}{@{} l @{}} \texttt {tx} ({a}) {=} \xi \end{array} \end{array} \right\} \). We write \({{\mathcal {N}}}{{\mathcal {T}}}\) for non-transactional events: \({{\mathcal {N}}}{{\mathcal {T}}}\triangleq \textit{E} \setminus {\mathcal {T}}\). We often use “\(\varGamma .\)” as a prefix to project the \(\varGamma \) components.
: \({\mathcal {T}}_\xi \triangleq \left\{ \begin{array}{@{} l @{} | @{} l @{}} \begin{array}{@{} l @{}} a \end{array}&\begin{array}{@{} l @{}} \texttt {tx} ({a}) {=} \xi \end{array} \end{array} \right\} \). We write \({{\mathcal {N}}}{{\mathcal {T}}}\) for non-transactional events: \({{\mathcal {N}}}{{\mathcal {T}}}\triangleq \textit{E} \setminus {\mathcal {T}}\). We often use “\(\varGamma .\)” as a prefix to project the \(\varGamma \) components.
Specification Consistency. The consistency of specification graphs is model-specific in that it is dictated by the guarantees provided by the underlying model. In the upcoming sections, we present two consistency definitions of PSI in terms of our specification graphs that lack cycles of certain shapes. In doing so, we often write  for lifting a relation
for lifting a relation  to transaction classes:
to transaction classes:  . Analogously, we write
. Analogously, we write  to restrict
to restrict  to the internal events of a transaction:
to the internal events of a transaction:  .
.
Comparison to Dependency Graphs. Adya et al. proposed dependency graphs for declarative specification of transactional consistency models [5, 7]. Dependency graphs are similar to our specification graphs in that they are constructed from a set of nodes and a set of edges (relations) capturing certain dependencies. However, unlike our specification graphs, the nodes in dependency graphs denote entire transactions and not individual events. In particular, Adya et al. propose three types of dependency edges: (i) a read dependency edge,  , denotes that transaction \(T_2\) reads a value written by \(T_1\); (ii) a write dependency edge
, denotes that transaction \(T_2\) reads a value written by \(T_1\); (ii) a write dependency edge  denotes that \(T_2\) overwrites a value written by \(T_1\); and (iii) an anti-dependency edge
denotes that \(T_2\) overwrites a value written by \(T_1\); and (iii) an anti-dependency edge  denotes that \(T_2\) overwrites a value read by \(T_1\). Adya’s formalism does not allow for non-transactional accesses and it thus suffices to define the dependencies of an execution as edges between transactional classes. In our specification graphs however, we account for both transactional and non-transactional accesses and thus define our relational dependencies between individual events of an execution. However, when we need to relate an entire transaction to another with relation
denotes that \(T_2\) overwrites a value read by \(T_1\). Adya’s formalism does not allow for non-transactional accesses and it thus suffices to define the dependencies of an execution as edges between transactional classes. In our specification graphs however, we account for both transactional and non-transactional accesses and thus define our relational dependencies between individual events of an execution. However, when we need to relate an entire transaction to another with relation  , we use the transactional lift (
, we use the transactional lift ( ) defined above. In particular, Adya’s dependency edges correspond to ours as follows. Informally, the
) defined above. In particular, Adya’s dependency edges correspond to ours as follows. Informally, the  corresponds to our
corresponds to our  ; the
; the  corresponds to our
corresponds to our  ; and the
; and the  corresponds to our
corresponds to our  . Adya’s dependency graphs have been used to develop declarative specifications of the PSI consistency model [14]. In Sect. 4, we revisit this model, redefine it as specification graphs in our setting, and develop a reference lock-based implementation that is sound and complete with respect to this abstract specification. The model in [14] does not account for non-transactional accesses. To remedy this, later in Sect. 5, we develop a declarative specification of PSI that allows for both transactional and non-transactional accesses. We then develop a reference lock-based implementation that is sound and complete with respect to our proposed model.
. Adya’s dependency graphs have been used to develop declarative specifications of the PSI consistency model [14]. In Sect. 4, we revisit this model, redefine it as specification graphs in our setting, and develop a reference lock-based implementation that is sound and complete with respect to this abstract specification. The model in [14] does not account for non-transactional accesses. To remedy this, later in Sect. 5, we develop a declarative specification of PSI that allows for both transactional and non-transactional accesses. We then develop a reference lock-based implementation that is sound and complete with respect to our proposed model.
4 Parallel Snapshot Isolation (PSI)
We present a declarative specification of PSI (Sect. 4.1), and develop a lock-based reference implementation of PSI in the RA fragment (Sect. 4.2). We then demonstrate that our implementation is both sound (Sect. 4.3) and complete (Sect. 4.4) with respect to the PSI specification. Note that the PSI model in this section accounts for transactional code only; that is, throughout this section we assume that \(\varGamma . \textit{E} =\varGamma .{\mathcal {T}}\). We lift this assumption later in Sect. 5.
4.1 A Declarative Specification of PSI STMs in RA
In order to formally characterise the weak behaviour and anomalies admitted by PSI, Cerone and Gotsman [14, 15] formulated a declarative PSI specification. (In fact, they provide two equivalent specifications: one using dependency graphs proposed by Adya et al. [5, 7]; and the other using abstract executions.) As is standard, they characterise the set of executions admitted under PSI as graphs that lack certain cycles. We present an equivalent declarative formulation of PSI, adapted to use our notation as discussed in Sect. 3. It is straightforward to verify that our definition coincides with the dependency graph specification in [15]. As with [14, 15], throughout this section, we take PSI execution graphs to be those in which \( \textit{E} = {\mathcal {T}}\subseteq ({\mathcal {R}}\cup {\mathcal {W}}) \setminus {\mathcal {U}}\). That is, the PSI model handles transactional code only, consisting solely of read and write events (excluding updates).
PSI Consistency. A PSI execution graph  is consistent, written \( \textsf {psi\hbox {-}consistent} (\varGamma )\), if the following hold:
is consistent, written \( \textsf {psi\hbox {-}consistent} (\varGamma )\), if the following hold:

Informally, int ensures the consistency of each transaction internally, while ext provides the synchronisation guarantees among transactions. In particular, we note that the two conditions together ensure that if two read events in the same transaction read from the same location x, and no write to x is  -between them, then they must read from the same write (known as ‘internal read consistency’).
-between them, then they must read from the same write (known as ‘internal read consistency’).
Next, we provide an alternative formulation of PSI-consistency that is closer in form to RA-consistency. This formulation is the basis of our extension in Sect. 5 with non-transactional accesses.
Lemma 1
A PSI execution graph  is consistent if and only if
is consistent if and only if  holds, where
holds, where  denotes the ‘PSI-happens-before’ relation, defined as
denotes the ‘PSI-happens-before’ relation, defined as  .
.
Proof
The full proof is provided in the technical appendix [4].
Note that this acyclicity condition is rather close to that of RA-consistency definition presented in Sect. 3, with the sole difference being the definition of ‘happens-before’ relation by replacing  with
with  . The relation
. The relation  is a strict extension of
is a strict extension of  with
with  , which captures additional synchronisation guarantees resulting from transaction orderings, as described shortly. As in RA-consistency, the
, which captures additional synchronisation guarantees resulting from transaction orderings, as described shortly. As in RA-consistency, the  and
and  are included in the ‘PSI-happens-before’ relation
are included in the ‘PSI-happens-before’ relation  . Additionally, the
. Additionally, the  and
and  also contribute to
also contribute to  .
.
Intuitively, the  corresponds to synchronisation due to causality between transactions. A transaction \( \texttt {T} _1\) is causally-ordered before transaction \( \texttt {T} _2\), if \( \texttt {T} _1\) writes to x and \( \texttt {T} _2\) later (in ‘happens-before’ order) reads x. The inclusion of
corresponds to synchronisation due to causality between transactions. A transaction \( \texttt {T} _1\) is causally-ordered before transaction \( \texttt {T} _2\), if \( \texttt {T} _1\) writes to x and \( \texttt {T} _2\) later (in ‘happens-before’ order) reads x. The inclusion of  ensures that \( \texttt {T} _2\) cannot read from \( \texttt {T} _1\) without observing its entire effect. This in turn ensures that transactions exhibit an atomic ‘all-or-nothing’ behaviour. In particular, transactions cannot mix-and-match the values they read. For instance, if \( \texttt {T} _1\) writes to both x and y, transaction \( \texttt {T} _2\) may not read the value of x from \( \texttt {T} _1\) but read the value of y from an earlier (in ‘happens-before’ order) transaction \( \texttt {T} _0\).
ensures that \( \texttt {T} _2\) cannot read from \( \texttt {T} _1\) without observing its entire effect. This in turn ensures that transactions exhibit an atomic ‘all-or-nothing’ behaviour. In particular, transactions cannot mix-and-match the values they read. For instance, if \( \texttt {T} _1\) writes to both x and y, transaction \( \texttt {T} _2\) may not read the value of x from \( \texttt {T} _1\) but read the value of y from an earlier (in ‘happens-before’ order) transaction \( \texttt {T} _0\).
The  corresponds to synchronisation due to conflicts between transactions. Its inclusion enforces the write-conflict-freedom of PSI transactions. In other words, if two transactions \( \texttt {T} _1\) and \( \texttt {T} _2\) both write to the same location x via events \(w_1\) and \(w_2\) such that
corresponds to synchronisation due to conflicts between transactions. Its inclusion enforces the write-conflict-freedom of PSI transactions. In other words, if two transactions \( \texttt {T} _1\) and \( \texttt {T} _2\) both write to the same location x via events \(w_1\) and \(w_2\) such that  , then \( \texttt {T} _1\) must commit before \( \texttt {T} _2\), and thus the entire effect of \( \texttt {T} _1\) must be visible to \( \texttt {T} _2\).
, then \( \texttt {T} _1\) must commit before \( \texttt {T} _2\), and thus the entire effect of \( \texttt {T} _1\) must be visible to \( \texttt {T} _2\).
PSI implementation of transaction T given RS, WS; the RPSI implementation (Sect. 5) is obtained by replacing valid on line 7 with \( \texttt {valid} _{\mathrm {RPSI}}\).
4.2 A Lock-Based PSI Implementation in RA
We present an operational model of PSI that is both sound and complete with respect to the declarative semantics in Sect. 4.1. To this end, in Fig. 2 we develop a pessimistic (lock-based) reference implementation of PSI using sequence locks [13, 18, 23, 32], referred to as version locks in our implementation. In order to avoid taking a snapshot of the entire memory and thus decrease the locking overhead, we assume that a transaction \( \texttt {T} \) is supplied with its read set, \( \texttt {RS} \), containing those locations that are read by \( \texttt {T} \). Similarly, we assume \( \texttt {T} \) to be supplied with its write set, \( \texttt {WS} \), containing the locations updated by \( \texttt {T} \).Footnote 2
The implementation of \( \texttt {T} \) proceeds by exclusively acquiring the version locks on all locations in its write set (line 0). It then obtains a snapshot of the locations in its read set by inspecting their version locks, as described shortly, and subsequently recording their values in a thread-local array s (lines 1–7). Once a snapshot is recorded, the execution of T proceeds locally (via \(\llbracket { \texttt {T} }\rrbracket \) on line 8) as follows. Each read operation consults the local snapshot in \( \texttt {s} \); each write operation updates the memory eagerly (in-place) and subsequently updates its local snapshot to ensure correct lookup for future reads. Once the execution of \( \texttt {T} \) is concluded, the version locks on the write set are released (line 9). Observe that as the writer locks are acquired pessimistically, we do not need to check for write-conflicts in the implementation.
To facilitate our locking implementation, we assume that each location x is associated with a version lock at address \( \texttt {x} {+} 1\), written \( \texttt {vx} \). The value held by a version lock \( \texttt {vx} \) may be in one of two categories: (i) an even number, denoting that the lock is free; or (ii) an odd number, denoting that the lock is exclusively held by a writer. For a transaction to write to a location x in its write set WS, the x version lock (vx) must be acquired exclusively by calling lock vx . Each call to lock vx reads the value of vx and stores it in v[x], where v is a thread-local array. It then checks if the value read is even (vx is free) and if so it atomically increments it by 1 (with a ‘compare-and-swap’ operation), thus changing the value of vx to an odd number and acquiring it exclusively; otherwise it repeats this process until the version lock is successfully acquired. Conversely, each call to unlock vx updates the value of vx to v[x]+2, restoring the value of vx to an even number and thus releasing it. Note that deadlocks can be avoided by imposing an ordering on locks and ensuring their in-order acquisition by all transactions. For simplicity however, we have elided this step as we are not concerned with progress or performance issues here and our main objective is a reference implementation of PSI in RA.
Analogously, for a transaction to read from the locations in its read set RS, it must record a snapshot of their values (lines 1–7). To obtain a snapshot of location x, the transaction must ensure that x is not currently being written to by another transaction. It thus proceeds by reading the value of vx and recording it in v[x]. If vx is free (the value read is even) or x is in its write set WS, the value of x can be freely read and tentatively stored in s[x]. In the latter case, the transaction has already acquired the exclusive lock on vx and is thus safe in the knowledge that no other transaction is currently updating x. Once a tentative snapshot of all locations is obtained (lines 1–5), the transaction must validate it by ensuring that it reflects the values of the read set at a single point in time (lines 6–7). To do this, it revisits the version locks, inspecting whether their values have changed (by checking them against v) since it recorded its snapshot. If so, then an intermediate update has intervened, potentially invalidating the obtained snapshot; the transaction thus restarts the snapshot process. Otherwise, the snapshot is successfully validated and returned in s.
4.3 Implementation Soundness
The PSI implementation in Fig. 2 is sound: for each RA-consistent implementation graph \( G \), a corresponding specification graph \(\varGamma \) can be constructed such that \( \textsf {psi\hbox {-}consistent} (\varGamma )\) holds. In what follows we state our soundness theorem and briefly describe our construction of consistent specification graphs. We refer the reader to the technical appendix [4] for the full soundness proof.
Theorem 1
(Soundness). For all RA-consistent implementation graphs \( G \) of the implementation in Fig. 2, there exists a PSI-consistent specification graph \(\varGamma \) of the corresponding transactional program that has the same program outcome.
Constructing Consistent Specification Graphs. Observe that given an execution of our implementation with t transactions, the trace of each transaction \(i \in \{1 \cdots t\}\) is of the form  , where \( Ls _i\), \( FS _i\), \( S _i\), \( Ts _i\) and \( Us _i\) respectively denote the sequence of events acquiring the version locks, attempting but failing to obtain a valid snapshot, recording a valid snapshot, performing the transactional operations, and releasing the version locks. For each transactional trace \(\theta _i\) of our implementation, we thus construct a corresponding trace of the specification as
, where \( Ls _i\), \( FS _i\), \( S _i\), \( Ts _i\) and \( Us _i\) respectively denote the sequence of events acquiring the version locks, attempting but failing to obtain a valid snapshot, recording a valid snapshot, performing the transactional operations, and releasing the version locks. For each transactional trace \(\theta _i\) of our implementation, we thus construct a corresponding trace of the specification as  , where \(B_i\) and \(E_i\) denote the transaction begin and end events (\({\mathtt {lab}}({B_i}) {=} \texttt {B} \) and \({\mathtt {lab}}({E_i}) {=} \texttt {E} \)). When \( Ts _i\) is of the form
, where \(B_i\) and \(E_i\) denote the transaction begin and end events (\({\mathtt {lab}}({B_i}) {=} \texttt {B} \) and \({\mathtt {lab}}({E_i}) {=} \texttt {E} \)). When \( Ts _i\) is of the form  , we construct \( Ts '_i\) as
, we construct \( Ts '_i\) as  with each \(t'_j\) defined either as \(t'_j \triangleq {\mathtt {R}}( \texttt {x} , v) \) when \(t_j = {\mathtt {R}}( \texttt {s[x]} , v) \) (i.e. the corresponding implementation event is a read event); or as \(t'_j \triangleq {\mathtt {W}}( \texttt {x} , v) \) when
with each \(t'_j\) defined either as \(t'_j \triangleq {\mathtt {R}}( \texttt {x} , v) \) when \(t_j = {\mathtt {R}}( \texttt {s[x]} , v) \) (i.e. the corresponding implementation event is a read event); or as \(t'_j \triangleq {\mathtt {W}}( \texttt {x} , v) \) when  .
.
For each specification trace \(\theta '_i\) we construct the ‘reads-from’ relation as:

That is, we construct our graph such that each read event \(t'_j\) from location x in \( Ts '_i\) either (i) is preceded by a write event w to x in \( Ts '_i\) without an intermediate write in between them and thus ‘reads-from’ w (lines two and three); or (ii) is not preceded by a write event in \( Ts '_i\) and thus ‘reads-from’ the write event w from which the initial snapshot read \(r'\) in \(S_i\) obtained the value of x (last two lines).
Given a consistent implementation graph  , we construct a consistent specification graph
, we construct a consistent specification graph  such that:
such that:
-
\(\varGamma . \textit{E} \triangleq \bigcup _{i \in \{1 \cdots t\}} \theta '_i. \textit{E} \) – the events of \(\varGamma . \textit{E} \) is the union of events in each transaction trace \(\theta '_i\) of the specification constructed as above;
-
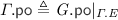 – the
– the 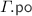 is that of
is that of 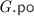 limited to the events in \(\varGamma . \textit{E} \);
limited to the events in \(\varGamma . \textit{E} \); -
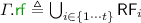 – the
– the 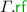 is the union of
is the union of 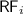 relations defined above;
relations defined above; -
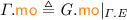 – the
– the 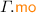 is that of
is that of 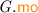 limited to the events in \(\varGamma . \textit{E} \);
limited to the events in \(\varGamma . \textit{E} \); -
\(\varGamma .{\mathcal {T}}\triangleq \varGamma . \textit{E} \), where for each \(e \in \varGamma .{\mathcal {T}}\), we define \( \texttt {tx} ({e}) = i\) when \(e \in \theta '_i\).
4.4 Implementation Completeness
The PSI implementation in Fig. 2 is complete: for each consistent specification graph \(\varGamma \) a corresponding implementation graph \( G \) can be constructed such that \( \textsf {RA\hbox {-}consistent} ( G )\) holds. We next state our completeness theorem and describe our construction of consistent implementation graphs. We refer the reader to the technical appendix [4] for the full completeness proof.
Theorem 2
(Completeness). For all PSI-consistent specification graphs \(\varGamma \) of a transactional program, there exists an RA-consistent execution graph \( G \) of the implementation in Fig. 2 that has the same program outcome.
Constructing Consistent Implementation Graphs. In order to construct an execution graph of the implementation \( G \) from the specification \(\varGamma \), we follow similar steps as those in the soundness construction, in reverse order. More concretely, given each trace \(\theta '_i\) of the specification, we construct an analogous trace of the implementation by inserting the appropriate events for acquiring and inspecting the version locks, as well as obtaining a snapshot. For each transaction class  , we must first determine its read and write sets and subsequently decide the order in which the version locks are acquired (for locations in the write set) and inspected (for locations in the read set). This then enables us to construct the ‘reads-from’ and ‘modification-order’ relations for the events associated with version locks.
, we must first determine its read and write sets and subsequently decide the order in which the version locks are acquired (for locations in the write set) and inspected (for locations in the read set). This then enables us to construct the ‘reads-from’ and ‘modification-order’ relations for the events associated with version locks.
Given a consistent execution graph of the specification  , and a transaction class
, and a transaction class  , we write \( \texttt {WS} _{{\mathcal {T}}_i}\) for the set of locations written to by \({\mathcal {T}}_i\). That is, \( \texttt {WS} _{{\mathcal {T}}_i} \triangleq \bigcup _{e \in {\mathcal {T}}_i \cap {\mathcal {W}}} {\mathtt {loc}}({e})\). Similarly, we write \( \texttt {RS} _{{\mathcal {T}}_i}\) for the set of locations read from by \({\mathcal {T}}_i\), prior to being written to by \({\mathcal {T}}_i\). For each location \( \texttt {x} \) read from by \({\mathcal {T}}_i\), we additionally record the first read event in \({\mathcal {T}}_i\) that retrieved the value of x. That is,
, we write \( \texttt {WS} _{{\mathcal {T}}_i}\) for the set of locations written to by \({\mathcal {T}}_i\). That is, \( \texttt {WS} _{{\mathcal {T}}_i} \triangleq \bigcup _{e \in {\mathcal {T}}_i \cap {\mathcal {W}}} {\mathtt {loc}}({e})\). Similarly, we write \( \texttt {RS} _{{\mathcal {T}}_i}\) for the set of locations read from by \({\mathcal {T}}_i\), prior to being written to by \({\mathcal {T}}_i\). For each location \( \texttt {x} \) read from by \({\mathcal {T}}_i\), we additionally record the first read event in \({\mathcal {T}}_i\) that retrieved the value of x. That is,

Note that transaction \({\mathcal {T}}_i\) may contain several read events reading from x, prior to subsequently updating it. However, the internal-read-consistency property ensures that all such read events read from the same write event. As such, as part of the read set of \({\mathcal {T}}_i\) we record the first such read event (in program-order).
Determining the ordering of lock events hinges on the following observation. Given a consistent execution graph of the specification  , let for each location x the total order
, let for each location x the total order  be given as:
be given as:  . Observe that this order can be broken into adjacent segments where the events of each segment belong to the same transaction. That is, given the transaction classes
. Observe that this order can be broken into adjacent segments where the events of each segment belong to the same transaction. That is, given the transaction classes  , the order above is of the following form where
, the order above is of the following form where  and for each such \({\mathcal {T}}_i\) we have \( \texttt {x} \in \texttt {WS} _{{\mathcal {T}}_i}\) and \(w_{(i, 1)} \cdots w_{(i, n_i)} \in {\mathcal {T}}_i\):
and for each such \({\mathcal {T}}_i\) we have \( \texttt {x} \in \texttt {WS} _{{\mathcal {T}}_i}\) and \(w_{(i, 1)} \cdots w_{(i, n_i)} \in {\mathcal {T}}_i\):

Were this not the case and we had  such that \(w_1, w_2 \in {\mathcal {T}}_i\) and \(w \in {\mathcal {T}}_j \ne {\mathcal {T}}_i\), we would consequently have
such that \(w_1, w_2 \in {\mathcal {T}}_i\) and \(w \in {\mathcal {T}}_j \ne {\mathcal {T}}_i\), we would consequently have  , contradicting the assumption that \(\varGamma \) is consistent. Given the above order, let us then define
, contradicting the assumption that \(\varGamma \) is consistent. Given the above order, let us then define  . We write
. We write  for the ith item of
for the ith item of  . As we describe shortly, we use
. As we describe shortly, we use  to determine the order of lock events.
to determine the order of lock events.
Note that the execution trace for each transaction  is of the form
is of the form  , where \( B _i\) is a transaction-begin (\( \texttt {B} \)) event, \( E _i\) is a transaction-end (\( \texttt {E} \)) event, and
, where \( B _i\) is a transaction-begin (\( \texttt {B} \)) event, \( E _i\) is a transaction-end (\( \texttt {E} \)) event, and  for some n, where each \( t '_j\) is either a read or a write event. As such, we have
for some n, where each \( t '_j\) is either a read or a write event. As such, we have  .
.
For each trace \(\theta '_i\) of the specification, we construct a corresponding trace of our implementation \(\theta _i\) as follows. Let \( \texttt {RS} _{{\mathcal {T}}_i} = \{( \texttt {x} _1, r_1) \cdots ( \texttt {x} _p, r_p)\}\) and \( \texttt {WS} _{{\mathcal {T}}_i} = \{ \texttt {y} _1 \cdots \texttt {y} _q\}\). We then construct  , where
, where
-
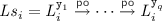 and
and 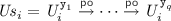 denote the sequence of events acquiring and releasing the version locks, respectively. Each \( L _i^{ \texttt {y} _j}\) and \( U _i^{ \texttt {y} _j}\) are defined as follows, the first event \(L_i^{ \texttt {y} _1}\) has the same identifier as that of \(B_i\), the last event \(U_i^{ \texttt {y} _q}\) has the same identifier as that of \(E_i\), and the identifiers of the remaining events are picked fresh:
denote the sequence of events acquiring and releasing the version locks, respectively. Each \( L _i^{ \texttt {y} _j}\) and \( U _i^{ \texttt {y} _j}\) are defined as follows, the first event \(L_i^{ \texttt {y} _1}\) has the same identifier as that of \(B_i\), the last event \(U_i^{ \texttt {y} _q}\) has the same identifier as that of \(E_i\), and the identifiers of the remaining events are picked fresh: 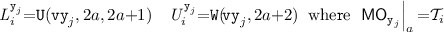
We then define the
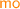 relation for version locks such that if transaction \({\mathcal {T}}_i\) writes to y immediately after \({\mathcal {T}}_j\) (i.e. \({\mathcal {T}}_i\) is
relation for version locks such that if transaction \({\mathcal {T}}_i\) writes to y immediately after \({\mathcal {T}}_j\) (i.e. \({\mathcal {T}}_i\) is 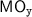 -ordered immediately after \({\mathcal {T}}_j\)), then \({\mathcal {T}}_i\) acquires the vy version lock immediately after \({\mathcal {T}}_j\) has released it. On the other hand, if \({\mathcal {T}}_i\) is the first transaction to write to \( \texttt {y} \), then it acquires vy immediately after the event initialising the value of vy, written \( init _{ \texttt {vy} }\). Moreover, each \( \texttt {vy} \) release event of \({\mathcal {T}}_i\) is
-ordered immediately after \({\mathcal {T}}_j\)), then \({\mathcal {T}}_i\) acquires the vy version lock immediately after \({\mathcal {T}}_j\) has released it. On the other hand, if \({\mathcal {T}}_i\) is the first transaction to write to \( \texttt {y} \), then it acquires vy immediately after the event initialising the value of vy, written \( init _{ \texttt {vy} }\). Moreover, each \( \texttt {vy} \) release event of \({\mathcal {T}}_i\) is  -ordered immediately after the corresponding \( \texttt {vy} \) acquisition event in \({\mathcal {T}}_i\):
-ordered immediately after the corresponding \( \texttt {vy} \) acquisition event in \({\mathcal {T}}_i\): 
This partial
 order on lock events of \({\mathcal {T}}_i\) also determines the
order on lock events of \({\mathcal {T}}_i\) also determines the  relation for its lock acquisition events:
relation for its lock acquisition events: 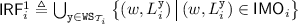 .
. -
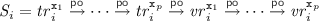 denotes the sequence of events obtaining a tentative snapshot (\( tr _i^{ \texttt {x} _j}\)) and subsequently validating it (\( vr _i^{ \texttt {x} _j}\)). Each \( tr _i^{ \texttt {x} _j}\) sequence is defined as
denotes the sequence of events obtaining a tentative snapshot (\( tr _i^{ \texttt {x} _j}\)) and subsequently validating it (\( vr _i^{ \texttt {x} _j}\)). Each \( tr _i^{ \texttt {x} _j}\) sequence is defined as 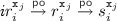 (reading the version lock \( \texttt {vx} _j\), reading \( \texttt {x} _j\) and recoding it in s), with \( ir _{i}^{ \texttt {x} _j}\), \(r_{i}^{ \texttt {x} _j}\), \(s_i^{ \texttt {x} _j}\) and \( vr _{i}^{ \texttt {x} _j}\) events defined as follows (with fresh identifiers). We then define the
(reading the version lock \( \texttt {vx} _j\), reading \( \texttt {x} _j\) and recoding it in s), with \( ir _{i}^{ \texttt {x} _j}\), \(r_{i}^{ \texttt {x} _j}\), \(s_i^{ \texttt {x} _j}\) and \( vr _{i}^{ \texttt {x} _j}\) events defined as follows (with fresh identifiers). We then define the  relation for each of these read events in \(S_i\). For each \(( \texttt {x} , r) \in \texttt {RS} _{{\mathcal {T}}_i}\), when r (i.e. the read event in the specification class \({\mathcal {T}}_i\) that reads the value of \( \texttt {x} \)) reads from an event w in the specification graph
relation for each of these read events in \(S_i\). For each \(( \texttt {x} , r) \in \texttt {RS} _{{\mathcal {T}}_i}\), when r (i.e. the read event in the specification class \({\mathcal {T}}_i\) that reads the value of \( \texttt {x} \)) reads from an event w in the specification graph 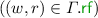 , we add \((w, r_i^{ \texttt {x} })\) to the
, we add \((w, r_i^{ \texttt {x} })\) to the 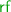 relation of \( G \) (the first line of
relation of \( G \) (the first line of  below). For version locks, if transaction \({\mathcal {T}}_i\) also writes to \( \texttt {x} _j\), then \( ir _{i}^{ \texttt {x} _j}\) and \( vr _i^{ \texttt {x} _j}\) events (reading and validating the value of version lock \( \texttt {vx} _j\)), read from the lock event in \({\mathcal {T}}_i\) that acquired \( \texttt {vx} _j\), namely \(L_i^{ \texttt {x} _j}\). On the other hand, if transaction \({\mathcal {T}}_i\) does not write to \( \texttt {x} _j\) and it reads the value of \( \texttt {x} _j\) written by \({\mathcal {T}}_j\), then \( ir _{i}^{ \texttt {x} _j}\) and \( vr _i^{ \texttt {x} _j}\) read the value written to \( \texttt {vx} _j\) by \({\mathcal {T}}_j\) when releasing it (\( U _j^{ \texttt {x} }\)). Lastly, if \({\mathcal {T}}_i\) does not write to \( \texttt {x} _j\) and it reads the value of \( \texttt {x} _j\) written by the initial write, \( init _{ \texttt {x} }\), then \( ir _{i}^{ \texttt {x} _j}\) and \( vr _i^{ \texttt {x} _j}\) read the value written to \( \texttt {vx} _j\) by the initial write to vx, \( init _{ \texttt {vx} }\).
below). For version locks, if transaction \({\mathcal {T}}_i\) also writes to \( \texttt {x} _j\), then \( ir _{i}^{ \texttt {x} _j}\) and \( vr _i^{ \texttt {x} _j}\) events (reading and validating the value of version lock \( \texttt {vx} _j\)), read from the lock event in \({\mathcal {T}}_i\) that acquired \( \texttt {vx} _j\), namely \(L_i^{ \texttt {x} _j}\). On the other hand, if transaction \({\mathcal {T}}_i\) does not write to \( \texttt {x} _j\) and it reads the value of \( \texttt {x} _j\) written by \({\mathcal {T}}_j\), then \( ir _{i}^{ \texttt {x} _j}\) and \( vr _i^{ \texttt {x} _j}\) read the value written to \( \texttt {vx} _j\) by \({\mathcal {T}}_j\) when releasing it (\( U _j^{ \texttt {x} }\)). Lastly, if \({\mathcal {T}}_i\) does not write to \( \texttt {x} _j\) and it reads the value of \( \texttt {x} _j\) written by the initial write, \( init _{ \texttt {x} }\), then \( ir _{i}^{ \texttt {x} _j}\) and \( vr _i^{ \texttt {x} _j}\) read the value written to \( \texttt {vx} _j\) by the initial write to vx, \( init _{ \texttt {vx} }\). 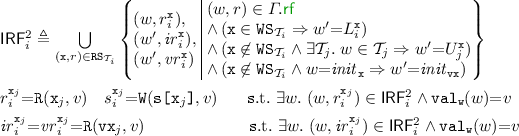
-
 (when
(when  ), with \( t _j\) defined as follows:
), with \( t _j\) defined as follows: 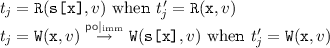
When \( t '_j\) is a read event, the \( t _j\) has the same identifier as that of \( t '_j\). When \( t '_j\) is a write event, the first event in \( t _j\) has the same identifier as that of \( t _j\) and the identifier of the second event is picked fresh.
We are now in a position to construct our implementation graph. Given a consistent execution graph \(\varGamma \) of the specification, we construct an execution graph  of the implementation as follows.
of the implementation as follows.
-
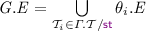 – note that \( G . \textit{E} \) is an extension of \(\varGamma . \textit{E} \): \(\varGamma . \textit{E} \subseteq G . \textit{E} \).
– note that \( G . \textit{E} \) is an extension of \(\varGamma . \textit{E} \): \(\varGamma . \textit{E} \subseteq G . \textit{E} \). -
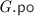 is defined as
is defined as 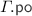 extended by the
extended by the 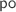 for the additional events of \( G \), given by the \(\theta _i\) traces defined above.
for the additional events of \( G \), given by the \(\theta _i\) traces defined above. -
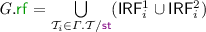
-
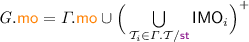
5 Robust Parallel Snapshot Isolation (RPSI)
In the previous section we adapted the PSI semantics in [14] to STM settings, in the absence of non-transactional code. However, a reasonable STM should account for mixed-mode code where shared data is accessed by both transactional and non-transactional code. To remedy this, we explore the semantics of PSI STMs in the presence of non-transactional code with weak isolation guarantees (see Sect. 2.1). We refer to the weakly isolated behaviour of such PSI STMs as robust parallel snapshot isolation (RPSI), due to its ability to provide PSI guarantees between transactions even in the presence of non-transactional code.
In Sect. 5.1 we propose the first declarative specification of RPSI STM programs. Later in Sect. 5.2 we develop a lock-based reference implementation of our RPSI specification in the RA fragment. We then demonstrate that our implementation is both sound (Sect. 5.3) and complete (Sect. 5.4) with respect to our proposed specification.
5.1 A Declarative Specification of RPSI STMs in RA
We formulate a declarative specification of RPSI semantics by adapting the PSI semantics presented in Sect. 4.1 to account for non-transactional accesses. As with the PSI specification in Sect. 4.1, throughout this section, we take RPSI execution graphs to be those in which \({\mathcal {T}}\subseteq ({\mathcal {R}}\cup {\mathcal {W}}) \setminus {\mathcal {U}}\). That is, RPSI transactions consist solely of read and write events (excluding updates). As before, we characterise the set of executions admitted by RPSI as graphs that lack cycles of certain shapes. More concretely, as with the PSI specification, we consider an RPSI execution graph to be consistent if  holds, where
holds, where  denotes the ‘RPSI-happens-before’ relation, extended from that of PSI
denotes the ‘RPSI-happens-before’ relation, extended from that of PSI  .
.
Definition 4
(RPSI consistency). An RPSI execution graph  is consistent, written \( \textsf {rpsi\hbox {-}consistent} (\varGamma )\), if
is consistent, written \( \textsf {rpsi\hbox {-}consistent} (\varGamma )\), if  holds, where
holds, where  denotes the ‘RPSI-happens-before’ relation, defined as the smallest relation that satisfies the following conditions:
denotes the ‘RPSI-happens-before’ relation, defined as the smallest relation that satisfies the following conditions:

The trans and psi-hb ensure that  is transitive and that it includes
is transitive and that it includes  and
and  as with its PSI counterpart. The nt-rf ensures that if a value written by a non-transactional write w is observed (read from) by a read event r in a transaction T, then its effect is observed by all events in T. That is, the w happens-before all events in \( \texttt {T} \) and not just r. This allows us to rule out executions such as the one depicted in Fig. 3a, which we argue must be disallowed by RPSI.
as with its PSI counterpart. The nt-rf ensures that if a value written by a non-transactional write w is observed (read from) by a read event r in a transaction T, then its effect is observed by all events in T. That is, the w happens-before all events in \( \texttt {T} \) and not just r. This allows us to rule out executions such as the one depicted in Fig. 3a, which we argue must be disallowed by RPSI.
Consider the execution graph of Fig. 3a, where transaction \( \texttt {T} _1\) is denoted by the dashed box labelled \( \texttt {T} _1\), comprising the read events \(r_1\) and \(r_2\). Note that as \(r_1\) and \(r_2\) are transactional reads without prior writes by the transaction, they constitute a snapshot of the memory at the time \( \texttt {T} _1\) started. That is, the values read by \(r_1\) and \(r_2\) must reflect a valid snapshot of the memory at the time it was taken. As such, since we have  , any event preceding \(w_2\) by the ‘happens-before’ relation must also be observed by (synchronise with) \( \texttt {T} _1\). In particular, as \(w_1\) happens-before \(w_2\)
, any event preceding \(w_2\) by the ‘happens-before’ relation must also be observed by (synchronise with) \( \texttt {T} _1\). In particular, as \(w_1\) happens-before \(w_2\)  , the \(w_1\) write must also be observed by \( \texttt {T} _1\). The nt-rf thus ensures that a non-transactional write read from by a transaction (i.e. a snapshot read) synchronises with the entire transaction.
, the \(w_1\) write must also be observed by \( \texttt {T} _1\). The nt-rf thus ensures that a non-transactional write read from by a transaction (i.e. a snapshot read) synchronises with the entire transaction.
Recall from Sect. 4.1 that the PSI  relation includes
relation includes  which has not yet been included in
which has not yet been included in  through the first three conditions described. As we describe shortly, the t-rf is indeed a strengthening of
through the first three conditions described. As we describe shortly, the t-rf is indeed a strengthening of  to account for the presence of non-transactional events. In particular, note that
to account for the presence of non-transactional events. In particular, note that  is included in the left-hand side of t-rf: when
is included in the left-hand side of t-rf: when  in
in  is replaced with
is replaced with  , the left-hand side yields
, the left-hand side yields  . As such, in the absence of non-transactional events, the definitions of
. As such, in the absence of non-transactional events, the definitions of  and
and  coincide.
coincide.
Recall that inclusion of  in
in  ensured transactional synchronisation due to causal ordering: if \( \texttt {T} _1\) writes to x and \( \texttt {T} _2\) later (in
ensured transactional synchronisation due to causal ordering: if \( \texttt {T} _1\) writes to x and \( \texttt {T} _2\) later (in  order) reads x, then \( \texttt {T} _1\) must synchronise with \( \texttt {T} _2\). This was achieved in PSI because either (i) \( \texttt {T} _2\) reads x directly from \( \texttt {T} _1\) in which case \( \texttt {T} _1\) synchronises with \( \texttt {T} _2\) via
order) reads x, then \( \texttt {T} _1\) must synchronise with \( \texttt {T} _2\). This was achieved in PSI because either (i) \( \texttt {T} _2\) reads x directly from \( \texttt {T} _1\) in which case \( \texttt {T} _1\) synchronises with \( \texttt {T} _2\) via  ; or (ii) \( \texttt {T} _2\) reads x from another later (
; or (ii) \( \texttt {T} _2\) reads x from another later ( -ordered) transactional write in \( \texttt {T} _3\), in which case \( \texttt {T} _1\) synchronises with \( \texttt {T} _3\) via
-ordered) transactional write in \( \texttt {T} _3\), in which case \( \texttt {T} _1\) synchronises with \( \texttt {T} _3\) via  , \( \texttt {T} _3\) synchronises with \( \texttt {T} _2\) via
, \( \texttt {T} _3\) synchronises with \( \texttt {T} _2\) via  , and thus \( \texttt {T} _1\) synchronises with \( \texttt {T} _2\) via
, and thus \( \texttt {T} _1\) synchronises with \( \texttt {T} _2\) via  . How are we then to extend
. How are we then to extend  to guarantee transactional synchronisation due to causal ordering in the presence of non-transactional events?
to guarantee transactional synchronisation due to causal ordering in the presence of non-transactional events?
To justify t-rf, we present an execution graph that does not guarantee synchronisation between causally ordered transactions and is nonetheless deemed RPSI-consistent without the t-rf condition on  . We thus argue that this execution must be precluded by RPSI, justifying the need for t-rf. Consider the execution in Fig. 3b. Observe that as transaction \( \texttt {T} _1\) writes to x via \(w_1\), transaction \( \texttt {T} _2\) reads x via \(r_2\), and
. We thus argue that this execution must be precluded by RPSI, justifying the need for t-rf. Consider the execution in Fig. 3b. Observe that as transaction \( \texttt {T} _1\) writes to x via \(w_1\), transaction \( \texttt {T} _2\) reads x via \(r_2\), and  (
( ), \( \texttt {T} _1\) is causally ordered before \( \texttt {T} _2\) and hence \( \texttt {T} _1\) must synchronise with \( \texttt {T} _2\). As such, the \(r_3\) in \( \texttt {T} _2\) must observe \(w_2\) in \( \texttt {T} _1\): we must have
), \( \texttt {T} _1\) is causally ordered before \( \texttt {T} _2\) and hence \( \texttt {T} _1\) must synchronise with \( \texttt {T} _2\). As such, the \(r_3\) in \( \texttt {T} _2\) must observe \(w_2\) in \( \texttt {T} _1\): we must have  , rendering the above execution RPSI-inconsistent. To enforce the
, rendering the above execution RPSI-inconsistent. To enforce the  relation between such causally ordered transactions with intermediate non-transactional events, t-rf stipulates that if a transaction \( \texttt {T} _1\) writes to a location (e.g. x via \(w_1\) above), another transaction \( \texttt {T} _2\) reads from the same location (\(r_2\)), and the two events are related by ‘RPSI-happens-before’
relation between such causally ordered transactions with intermediate non-transactional events, t-rf stipulates that if a transaction \( \texttt {T} _1\) writes to a location (e.g. x via \(w_1\) above), another transaction \( \texttt {T} _2\) reads from the same location (\(r_2\)), and the two events are related by ‘RPSI-happens-before’  , then \( \texttt {T} _1\) must synchronise with \( \texttt {T} _2\). That is, all events in \( \texttt {T} _1\) must ‘RPSI-happen-before’ those in \( \texttt {T} _2\). Effectively, this allows us to transitively close the causal ordering between transactions, spanning transactional and non-transactional events in between.
, then \( \texttt {T} _1\) must synchronise with \( \texttt {T} _2\). That is, all events in \( \texttt {T} _1\) must ‘RPSI-happen-before’ those in \( \texttt {T} _2\). Effectively, this allows us to transitively close the causal ordering between transactions, spanning transactional and non-transactional events in between.
5.2 A Lock-Based RPSI Implementation in RA
We present a lock-based reference implementation of RPSI in the RA fragment (Fig. 2) by using sequence locks [13, 18, 23, 32]. Our implementation is both sound and complete with respect to our declarative RPSI specification in Sect. 5.1.
The RPSI implementation in Fig. 2 is rather similar to its PSI counterpart. The main difference between the two is in how they validate the tentative snapshot recorded in s. As before, in order to ensure that no intermediate transactional writes have intervened since s was recorded, for each location x in RS, the validation phase revisits vx, inspecting whether its value has changed from that recorded in v[x]. If this is the case, the snapshot is deemed invalid and the process is restarted. However, checking against intermediate transactional writes alone is not sufficient as it does not preclude the intervention of non-transactional writes. This is because unlike transactional writes, non-transactional writes do not update the version locks and as such their updates may go unnoticed. In order to rule out the possibility of intermediate non-transactional writes, for each location x the implementation checks the value of x against that recorded in s[x]. If the values do not agree, an intermediate non-transactional write has been detected: the snapshot fails validation and the process is restarted. Otherwise, the snapshot is successfully validated and returned in s. Observe that checking the value of x against s[x] does not entirely preclude the presence of non-transactional writes, in cases where the same value is written (non-transactionally) to x twice.
To understand this, consider the mixed-mode program on the left of Fig. 4 comprising a transaction in the left-hand thread and a non-transactional program in the right-hand thread writing the same value (1) to z twice. Note that the annotated behaviour is disallowed under RPSI: all execution graphs of the program with the annotated behaviour yield RPSI-inconsistent execution graphs. Intuitively, this is because the values read by the transaction (x : 0, y : 0, z : 1) do not constitute a valid snapshot: at no point during the execution of this program, are the values of x, y and z as annotated.
Nevertheless, it is possible to find an RA-consistent execution of the RPSI implementation in Fig. 2 that reads the annotated values as its snapshot. Consider the execution graph on the right-hand side of Fig. 4, depicting a particular execution of the RPSI implementation (Fig. 2) of the program on the left. The rx, ry and rz denote the events reading the initial snapshot of x, y and z and recording them in s (line 5), respectively. Similarly, the \(rx'\), \(ry'\) and \(rz'\) denote the events validating the snapshots recorded in s (line 7). As T is the only transaction in the program, the version numbers \( \texttt {vx} \), \( \texttt {vy} \) and \( \texttt {vz} \) remain unchanged throughout the execution and we have thus omitted the events reading (line 2) and validating (line 7) their values from the execution graph. Note that this execution graph is RA-consistent even though we cannot find a corresponding RPSI-consistent execution with the same outcome. To ensure the soundness of our implementation, we must thus rule out such scenarios.
To do this, we assume that if multiple non-transactional writes write the same value to the same location, they cannot race with the same transaction. More concretely, we assume that every RPSI-consistent execution graph of a given program satisfies the following condition:

That is, given a transactional read r from location x, and any two distinct non-transactional writes w, \(w'\) of the same value to x, either (i) at least one of the writes RPSI-happen-after r; or (ii) they both RPSI-happen-before r.
Observe that this does not hold of the program in Fig. 2. Note that this stipulation does not prevent two transactions to write the same value to a location x. As such, in the absence of non-transactional writes, our RPSI implementation is equivalent to that of PSI in Sect. 4.2.
5.3 Implementation Soundness
The RPSI implementation in Fig. 2 is sound: for each consistent implementation graph \( G \), a corresponding specification graph \(\varGamma \) can be constructed such that \( \textsf {rpsi\hbox {-}consistent} (\varGamma )\) holds. In what follows we state our soundness theorem and briefly describe our construction of consistent specification graphs. We refer the reader to the technical appendix [4] for the full soundness proof.
Theorem 3
(Soundness). Let P be a program that possibly mixes transactional and non-transactional code. If every RPSI-consistent execution graph of P satisfies the condition in (\(*\)), then for all RA-consistent implementation graphs \( G \) of the implementation in Fig. 2, there exists an RPSI-consistent specification graph \(\varGamma \) of the corresponding transactional program with the same program outcome.
Constructing Consistent Specification Graphs. Constructing an RPSI-consistent specification graph from the implementation graph is similar to the corresponding PSI construction described in Sect. 4.3. More concretely, the events associated with non-transactional events remain unchanged and are simply added to the specification graph. On the other hand, the events associated with transactional events are adapted in a similar way to those of PSI in Sect. 4.3. In particular, observe that given an execution of the RPSI implementation with t transactions, as with the PSI implementation, the trace of each transaction \(i \in \{1 \cdots t\}\) is of the form  , with \( Ls _i\), \( FS _i\), \( S _i\), \( Ts _i\) and \( Us _i\) denoting analogous sequences of events to those of PSI. The difference between an RPSI trace \(\theta _i\) and a PSI one is in the \( FS _i \) and \( S _i\) sequences, obtaining the snapshot. In particular, the validation phases of \( FS _i\) and \( S _i\) in RPSI include an additional read for each location to rule out intermediate non-transactional writes. As in the PSI construction, for each transactional trace \(\theta _i\) of our implementation, we construct a corresponding trace of the specification as
, with \( Ls _i\), \( FS _i\), \( S _i\), \( Ts _i\) and \( Us _i\) denoting analogous sequences of events to those of PSI. The difference between an RPSI trace \(\theta _i\) and a PSI one is in the \( FS _i \) and \( S _i\) sequences, obtaining the snapshot. In particular, the validation phases of \( FS _i\) and \( S _i\) in RPSI include an additional read for each location to rule out intermediate non-transactional writes. As in the PSI construction, for each transactional trace \(\theta _i\) of our implementation, we construct a corresponding trace of the specification as  , with \(B_i\), \(E_i\) and \( Ts '_i\) as defined in Sect. 4.3.
, with \(B_i\), \(E_i\) and \( Ts '_i\) as defined in Sect. 4.3.
Given a consistent RPSI implementation graph  , let \( G .{{\mathcal {N}}}{{\mathcal {T}}}\triangleq G . \textit{E} \setminus \bigcup _{i \in \{1 \cdots t\}} \theta . \textit{E} \) denote the non-transactional events of \( G \). We construct a consistent RPSI specification graph
, let \( G .{{\mathcal {N}}}{{\mathcal {T}}}\triangleq G . \textit{E} \setminus \bigcup _{i \in \{1 \cdots t\}} \theta . \textit{E} \) denote the non-transactional events of \( G \). We construct a consistent RPSI specification graph  such that:
such that:
-
\(\varGamma . \textit{E} \triangleq G .{{\mathcal {N}}}{{\mathcal {T}}}\cup \bigcup _{i \in \{1 \cdots t\}} \theta '_i. \textit{E} \) – the \(\varGamma . \textit{E} \) events comprise the non-transactional events in \( G \) and the events in each transactional trace \(\theta '_i\) of the specification;
-
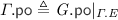 – the
– the  is that of
is that of 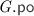 restricted to the events in \(\varGamma . \textit{E} \);
restricted to the events in \(\varGamma . \textit{E} \); -
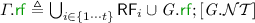 – the
– the  is the union of
is the union of  relations for transactional reads as defined in Sect. 4.3, together with the
relations for transactional reads as defined in Sect. 4.3, together with the  relation for non-transactional reads;
relation for non-transactional reads; -
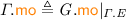 – the
– the 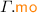 is that of
is that of  restricted to the events in \(\varGamma . \textit{E} \);
restricted to the events in \(\varGamma . \textit{E} \); -
\(\varGamma .{\mathcal {T}}\triangleq \bigcup _{i \in \{1 \cdots t\}} \theta '_i. \textit{E} \), where for each \(e \in \theta '_i. \textit{E} \), we define \( \texttt {tx} ({e}) = i\).
We refer the reader to the technical appendix [4] for the full proof demonstrating that the above construction of \(\varGamma \) yields a consistent specification graph.
5.4 Implementation Completeness
The RPSI implementation in Fig. 2 is complete: for each consistent specification graph \(\varGamma \) a corresponding implementation graph \( G \) can be constructed such that \( \textsf {RA\hbox {-}consistent} ( G )\) holds. We next state our completeness theorem and describe our construction of consistent implementation graphs. We refer the reader to the technical appendix [4] for the full completeness proof.
Theorem 4
(Completeness). For all RPSI-consistent specification graphs \(\varGamma \) of a program, there exists an RA-consistent execution graph \( G \) of the implementation in Fig. 2 that has the same program outcome.
Constructing Consistent Implementation Graphs. In order to construct an execution graph of the implementation \( G \) from the specification \(\varGamma \), we follow similar steps as those in the corresponding PSI construction in Sect. 4.4. More concretely, the events associated with non-transactional events are unchanged and simply added to the implementation graph. For transactional events, given each trace \(\theta '_i\) of a transaction in the specification, as before we construct an analogous trace of the implementation by inserting the appropriate events for acquiring and inspecting the version locks, as well as obtaining a snapshot. For each transaction class  , we first determine its read and write sets as before and subsequently decide the order in which the version locks are acquired and inspected. This then enables us to construct the ‘reads-from’ and ‘modification-order’ relations for the events associated with version locks.
, we first determine its read and write sets as before and subsequently decide the order in which the version locks are acquired and inspected. This then enables us to construct the ‘reads-from’ and ‘modification-order’ relations for the events associated with version locks.
Given a consistent execution graph of the specification  , and a transaction class
, and a transaction class  , we define \( \texttt {WS} _{{\mathcal {T}}_i}\) and \( \texttt {RS} _{{\mathcal {T}}_i}\) as described in Sect. 4.4. Determining the ordering of lock events hinges on a similar observation as that in the PSI construction. Given a consistent execution graph of the specification
, we define \( \texttt {WS} _{{\mathcal {T}}_i}\) and \( \texttt {RS} _{{\mathcal {T}}_i}\) as described in Sect. 4.4. Determining the ordering of lock events hinges on a similar observation as that in the PSI construction. Given a consistent execution graph of the specification  , let for each location x the total order
, let for each location x the total order  be given as:
be given as:  . This order can be broken into adjacent segments where the events of each segment are either non-transactional writes or belong to the same transaction. That is, given the transaction classes
. This order can be broken into adjacent segments where the events of each segment are either non-transactional writes or belong to the same transaction. That is, given the transaction classes  , the order above is of the following form where
, the order above is of the following form where  and for each such \({\mathcal {T}}_i\) we have \( \texttt {x} \in \texttt {WS} _{{\mathcal {T}}_i}\) and \(w_{(i, 1)} \cdots w_{(i, n_i)} \in {\mathcal {T}}_i\):
and for each such \({\mathcal {T}}_i\) we have \( \texttt {x} \in \texttt {WS} _{{\mathcal {T}}_i}\) and \(w_{(i, 1)} \cdots w_{(i, n_i)} \in {\mathcal {T}}_i\):

Were this not the case and we had  such that \(w_1, w_2 \in {\mathcal {T}}_i\) and \(w \in {\mathcal {T}}_j \ne {\mathcal {T}}_i\), we would consequently have
such that \(w_1, w_2 \in {\mathcal {T}}_i\) and \(w \in {\mathcal {T}}_j \ne {\mathcal {T}}_i\), we would consequently have  , contradicting the assumption that \(\varGamma \) is consistent. We thus define
, contradicting the assumption that \(\varGamma \) is consistent. We thus define  .
.
Note that each transactional execution trace of the specification is of the form  , with \( B _i\), \( E _i\) and \( Ts '_i\) as described in Sect. 4.4. For each such \(\theta '_i\), we construct a corresponding trace of our implementation as
, with \( B _i\), \( E _i\) and \( Ts '_i\) as described in Sect. 4.4. For each such \(\theta '_i\), we construct a corresponding trace of our implementation as  , where \( Ls _i\), \( Ts _i\) and \( Us _i\) are as defined in Sect. 4.4, and
, where \( Ls _i\), \( Ts _i\) and \( Us _i\) are as defined in Sect. 4.4, and  denotes the sequence of events obtaining a tentative snapshot (\( tr _i^{ \texttt {x} _j}\)) and subsequently validating it (\( vr _i^{ \texttt {x} _j}\)). Each \( tr _i^{ \texttt {x} _j}\) sequence is of the form
denotes the sequence of events obtaining a tentative snapshot (\( tr _i^{ \texttt {x} _j}\)) and subsequently validating it (\( vr _i^{ \texttt {x} _j}\)). Each \( tr _i^{ \texttt {x} _j}\) sequence is of the form  , with \( ivr _{i}^{ \texttt {x} _j}\), \( ir _{i}^{ \texttt {x} _j}\) and \(s_i^{ \texttt {x} _j}\) defined below (with fresh identifiers). Similarly, each \( vr _{i}^{ \texttt {x} _j}\) sequence is of the form
, with \( ivr _{i}^{ \texttt {x} _j}\), \( ir _{i}^{ \texttt {x} _j}\) and \(s_i^{ \texttt {x} _j}\) defined below (with fresh identifiers). Similarly, each \( vr _{i}^{ \texttt {x} _j}\) sequence is of the form  , with \( fr _{i}^{ \texttt {x} _j}\) and \( fvr _{i}^{ \texttt {x} _j}\) defined as follows (with fresh identifiers). We then define the
, with \( fr _{i}^{ \texttt {x} _j}\) and \( fvr _{i}^{ \texttt {x} _j}\) defined as follows (with fresh identifiers). We then define the  relation for each of these read events in \(S_i\) in a similar way.
relation for each of these read events in \(S_i\) in a similar way.
For each \(( \texttt {x} , r) \in \texttt {RS} _{{\mathcal {T}}_i}\), when r (the event in the specification class \({\mathcal {T}}_i\) that reads the value of \( \texttt {x} \)) reads from w in the specification graph  , we add \((w, ir _i^{ \texttt {x} })\) and \((w, fr _i^{ \texttt {x} })\) to the
, we add \((w, ir _i^{ \texttt {x} })\) and \((w, fr _i^{ \texttt {x} })\) to the  of \( G \) (the first line of
of \( G \) (the first line of  below). For version locks, as before if transaction \({\mathcal {T}}_i\) also writes to \( \texttt {x} _j\), then \( ivr _{i}^{ \texttt {x} _j}\) and \( fvr _i^{ \texttt {x} _j}\) events (reading and validating \( \texttt {vx} _j\)), read from the lock event in \({\mathcal {T}}_i\) that acquired \( \texttt {vx} _j\), namely \(L_i^{ \texttt {x} _j}\). Similarly, if \({\mathcal {T}}_i\) does not write to \( \texttt {x} _j\) and it reads the value of \( \texttt {x} _j\) written by the initial write, \( init _{ \texttt {x} }\), then \( ivr _{i}^{ \texttt {x} _j}\) and \( fvr _i^{ \texttt {x} _j}\) read the value written to \( \texttt {vx} _j\) by the initial write to vx, \( init _{ \texttt {vx} }\). Lastly, if transaction \({\mathcal {T}}_i\) does not write to \( \texttt {x} _j\) and it reads \( \texttt {x} _j\) from a write other than \( init _{ \texttt {x} }\), then \( ir _{i}^{ \texttt {x} _j}\) and \( vr _i^{ \texttt {x} _j}\) read from the unlock event of a transaction \({\mathcal {T}}_j\) (i.e. \(U_j^{ \texttt {x} }\)), who has x in its write set and whose write to x, \(w_{ \texttt {x} }\), maximally ‘RPSI-happens-before’ r. That is, for all other such writes that ‘RPSI-happen-before’ r, then \(w_{ \texttt {x} }\) ‘RPSI-happens-after’ them.
below). For version locks, as before if transaction \({\mathcal {T}}_i\) also writes to \( \texttt {x} _j\), then \( ivr _{i}^{ \texttt {x} _j}\) and \( fvr _i^{ \texttt {x} _j}\) events (reading and validating \( \texttt {vx} _j\)), read from the lock event in \({\mathcal {T}}_i\) that acquired \( \texttt {vx} _j\), namely \(L_i^{ \texttt {x} _j}\). Similarly, if \({\mathcal {T}}_i\) does not write to \( \texttt {x} _j\) and it reads the value of \( \texttt {x} _j\) written by the initial write, \( init _{ \texttt {x} }\), then \( ivr _{i}^{ \texttt {x} _j}\) and \( fvr _i^{ \texttt {x} _j}\) read the value written to \( \texttt {vx} _j\) by the initial write to vx, \( init _{ \texttt {vx} }\). Lastly, if transaction \({\mathcal {T}}_i\) does not write to \( \texttt {x} _j\) and it reads \( \texttt {x} _j\) from a write other than \( init _{ \texttt {x} }\), then \( ir _{i}^{ \texttt {x} _j}\) and \( vr _i^{ \texttt {x} _j}\) read from the unlock event of a transaction \({\mathcal {T}}_j\) (i.e. \(U_j^{ \texttt {x} }\)), who has x in its write set and whose write to x, \(w_{ \texttt {x} }\), maximally ‘RPSI-happens-before’ r. That is, for all other such writes that ‘RPSI-happen-before’ r, then \(w_{ \texttt {x} }\) ‘RPSI-happens-after’ them.

We are now in a position to construct our implementation graph. Given a consistent execution graph \(\varGamma \) of the specification, we construct an execution graph of the implementation,  , such that:
, such that:
6 Conclusions and Future Work
We studied PSI, for the first time to our knowledge, as a consistency model for STMs as it has several advantages over other consistency models, thanks to its performance and monotonic behaviour. We addressed two significant drawbacks of PSI which prevent its widespread adoption. First, the absence of a simple lock-based reference implementation to allow the programmers to readily understand and reason about PSI programs. To address this, we developed a lock-based reference implementation of PSI in the RA fragment of C11 (using sequence locks), that is both sound and complete with respect to its declarative specification. Second, the absence of a formal PSI model in the presence of mixed-mode accesses. To this end, we formulated a declarative specification of RPSI (robust PSI) accounting for both transactional and non-transactional accesses. Our RPSI specification is an extension of PSI in that in the absence of non-transactional accesses it coincides with PSI. To provide a more intuitive account of RPSI, we developed a simple lock-based RPSI reference implementation by adjusting our PSI implementation. We established the soundness and completeness of our RPSI implementation against its declarative specification.
As directions of future work, we plan to build on top of the work presented here in three ways. First, we plan to explore possible lock-based reference implementations for PSI and RPSI in the context of other weak memory models, such as the full C11 memory models [9]. Second, we plan to study other weak transactional consistency models, such as SI [10], ALA (asymmetric lock atomicity), ELA (encounter-time lock atomicity) [28], and those of ANSI SQL, including RU (read-uncommitted), RC (read-committed) and RR (repeatable reads), in the STM context. We aim to investigate possible lock-based reference implementations for these models that would allow the programmers to understand and reason about STM programs with such weak guarantees. Third, taking advantage of the operational models provided by our simple lock-based reference implementations (those presented in this article as well as those in future work), we plan to develop reasoning techniques that would allow us to verify properties of STM programs. This can be achieved by either extending existing program logics for weak memory, or developing new program logics for currently unsupported models. In particular, we can reason about the PSI models presented here by developing custom proof rules in the existing program logics for RA such as [22, 39].
Notes
- 1.
Sequential consistency (SC) [24] is the standard model for shared memory concurrency and defines the behaviours of a multi-threaded program as those arising by executing sequentially some interleaving of the accesses of its constituent threads.
- 2.
A conservative estimate of \( \texttt {RS} \) and \( \texttt {WS} \) can be obtained by simple syntactic analysis.
References
The Clojure Language: Refs and Transactions. http://clojure.org/refs
Haskell STM. http://hackage.haskell.org/package/stm-2.2.0.1/docs/Control-Concurrent-STM.html
Software transactional memory (Scala). https://doc.akka.io/docs/akka/1.2/scala/stm.html
Technical appendix for this paper. http://plv.mpi-sws.org/transactions/
Generalized isolation level definitions. In: Proceedings of the 16th International Conference on Data Engineering (2000)
Technical specification for C++ extensions for transactional memory (2015). http://www.open-std.org/jtc1/sc22/wg21/docs/papers/2015/n4514.pdf
Adya, A.: Weak consistency: a generalized theory and optimistic implementations for distributed transactions. Ph.D. thesis, MIT (1999)
Alglave, J., Maranget, L., Tautschnig, M.: Herding cats: modelling, simulation, testing, and data mining for weak memory. ACM Trans. Program. Lang. Syst. 36(2), 7:1–7:74 (2014)
Batty, M., Owens, S., Sarkar, S., Sewell, P., Weber, T.: Mathematizing C++ concurrency. In: Proceedings of the 38th Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, pp. 55–66 (2011)
Berenson, H., Bernstein, P., Gray, J., Melton, J., O’Neil, E., O’Neil, P.: A critique of ANSI SQL isolation levels. In: Proceedings of the 1995 ACM SIGMOD International Conference on Management of Data, pp. 1–10 (1995)
Bieniusa, A., Fuhrmann, T.: Consistency in hindsight: a fully decentralized STM algorithm. In: Proceedings of the 2010 IEEE International Symposium on Parallel and Distributed Processing, IPDPS 2010, pp. 1–12 (2010)
Blundell, C., Lewis, E.C., Martin, M.M.K.: Deconstructing transactions: the subtleties of atomicity. In: 4th Annual Workshop on Duplicating, Deconstructing, and Debunking (2005)
Boehm, H.J.: Can seqlocks get along with programming language memory models? In: Proceedings of the 2012 ACM SIGPLAN Workshop on Memory Systems Performance and Correctness, pp. 12–20 (2012)
Cerone, A., Gotsman, A.: Analysing snapshot isolation. In: Proceedings of the 2016 ACM Symposium on Principles of Distributed Computing, pp. 55–64 (2016)
Cerone, A., Gotsman, A., Yang, H.: Transaction chopping for parallel snapshot isolation. In: Moses, Y. (ed.) DISC 2015. LNCS, vol. 9363, pp. 388–404. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48653-5_26
Daudjee, K., Salem, K.: Lazy database replication with snapshot isolation. In: Proceedings of the 32nd International Conference on Very Large Data Bases, pp. 715–726 (2006)
Harris, T., Marlow, S., Peyton-Jones, S., Herlihy, M.: Composable memory transactions. In: Proceedings of the Tenth ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, pp. 48–60 (2005)
Hemminger, S.: Fast reader/writer lock for gettimeofday 2.5.30. http://lwn.net/Articles/7388/
Herlihy, M., Moss, J.E.B.: Transactional memory: architectural support for lock-free data structures. In: Proceedings of the 20th Annual International Symposium on Computer Architecture, pp. 289–300 (1993)
Hickey, R.: The Clojure programming language. In: Proceedings of the 2008 Symposium on Dynamic Languages, p. 1:1 (2008)
Lahav, O., Giannarakis, N., Vafeiadis, V.: Taming release-acquire consistency. In: Proceedings of the 43rd Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, pp. 649–662 (2016)
Lahav, O., Vafeiadis, V.: Owicki-Gries reasoning for weak memory models. In: Halldórsson, M.M., Iwama, K., Kobayashi, N., Speckmann, B. (eds.) ICALP 2015, Part II. LNCS, vol. 9135, pp. 311–323. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47666-6_25
Lameter, C.: Effective synchronization on Linux/NUMA systems (2005). http://www.lameter.com/gelato2005.pdf
Lamport, L.: How to make a multiprocessor computer that correctly executes multiprocess programs. IEEE Trans. Comput. 28(9), 690–691 (1979)
Litz, H., Cheriton, D., Firoozshahian, A., Azizi, O., Stevenson, J.P.: SI-TM: reducing transactional memory abort rates through snapshot isolation. SIGPLAN Not. 42(1), 383–398 (2014)
Litz, H., Dias, R.J., Cheriton, D.R.: Efficient correction of anomalies in snapshot isolation transactions. ACM Trans. Archit. Code Optim. 11(4), 65:1–65:24 (2015)
Martin, M., Blundell, C., Lewis, E.: Subtleties of transactional memory atomicity semantics. IEEE Comput. Archit. Lett. 5(2), 17 (2006)
Menon, V., Balensiefer, S., Shpeisman, T., Adl-Tabatabai, A.R., Hudson, R.L., Saha, B., Welc, A.: Single global lock semantics in a weakly atomic STM. SIGPLAN Not. 43(5), 15–26 (2008)
Owens, S., Sarkar, S., Sewell, P.: A better x86 memory model: x86-TSO. In: Proceedings of the 22nd International Conference on Theorem Proving in Higher Order Logics, pp. 391–407 (2009)
Peng, D., Dabek, F.: Large-scale incremental processing using distributed transactions and notifications. In: Proceedings of the 9th USENIX Conference on Operating Systems Design and Implementation, pp. 251–264 (2010)
Pulte, C., Flur, S., Deacon, W., French, J., Sarkar, S., Sewell, P.: Simplifying ARM concurrency: multicopy-atomic axiomatic and operational models for ARMv8. Proc. ACM Program. Lang. 2(POPL), 19:1–19:29 (2017). http://doi.acm.org/10.1145/3158107
Rajwar, R., Goodman, J.R.: Speculative lock elision: enabling highly concurrent multithreaded execution. In: Proceedings of the 34th Annual ACM/IEEE International Symposium on Microarchitecture, pp. 294–305 (2001)
Serrano, D., Patino-Martinez, M., Jimenez-Peris, R., Kemme, B.: Boosting database replication scalability through partial replication and 1-copy-snapshot-isolation. In: Proceedings of the 13th Pacific Rim International Symposium on Dependable Computing, pp. 290–297 (2007)
Sewell, P., Sarkar, S., Owens, S., Zappa Nardelli, F., Myreen, M.O.: x86-TSO: a rigorous and usable programmer’s model for x86 multiprocessors. Commun. ACM 53(7), 89–97 (2010)
Shavit, N., Touitou, D.: Software transactional memory. In: Proceedings of the Fourteenth Annual ACM Symposium on Principles of Distributed Computing, pp. 204–213 (1995)
Sovran, Y., Power, R., Aguilera, M.K., Li, J.: Transactional storage for geo-replicated systems. In: Proceedings of the Twenty-Third ACM Symposium on Operating Systems Principles, pp. 385–400 (2011)
CORPORATE SPARC International Inc.: The SPARC Architecture Manual: Version 8 (1992)
CORPORATE SPARC International Inc.: The SPARC Architecture Manual (Version 9) (1994)
Vafeiadis, V., Narayan, C.: Relaxed separation logic: a program logic for c11 concurrency. In: Proceedings of the 2013 ACM SIGPLAN International Conference on Object Oriented Programming Systems Languages and Applications, pp. 867–884 (2013)
Acknowledgments
We thank the ESOP 2018 reviewers for their constructive feedback. This research was supported in part by a European Research Council (ERC) Consolidator Grant for the project “RustBelt”, under the European Union’s Horizon 2020 Framework Programme (grant agreement no. 683289). The second author was additionally partly supported by Len Blavatnik and the Blavatnik Family foundation.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made. The images or other third party material in this book are included in the book's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the book's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Raad, A., Lahav, O., Vafeiadis, V. (2018). On Parallel Snapshot Isolation and Release/Acquire Consistency. In: Ahmed, A. (eds) Programming Languages and Systems. ESOP 2018. Lecture Notes in Computer Science(), vol 10801. Springer, Cham. https://doi.org/10.1007/978-3-319-89884-1_33
Download citation
DOI: https://doi.org/10.1007/978-3-319-89884-1_33
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-89883-4
Online ISBN: 978-3-319-89884-1
eBook Packages: Computer ScienceComputer Science (R0)





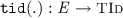 and
and 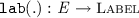 , returning the thread identifier and the label of an event, respectively. We typically use a, b, and e to range over events. The label of an event is a tuple of one of the following three forms: (i)
, returning the thread identifier and the label of an event, respectively. We typically use a, b, and e to range over events. The label of an event is a tuple of one of the following three forms: (i) 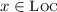 .
.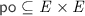 denotes the ‘program-order’ relation, defined as a disjoint union of strict total orders, each orders the events of one thread, together with
denotes the ‘program-order’ relation, defined as a disjoint union of strict total orders, each orders the events of one thread, together with 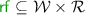 denotes the ‘reads-from’ relation, defined as a relation between write and read events of the same location and value; it is total and functional on reads, i.e. every read event is related to exactly one write event;
denotes the ‘reads-from’ relation, defined as a relation between write and read events of the same location and value; it is total and functional on reads, i.e. every read event is related to exactly one write event;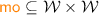 denotes the ‘modification-order’ relation, defined as a disjoint union of strict orders, each of which totally orders the write events to one location.
denotes the ‘modification-order’ relation, defined as a disjoint union of strict orders, each of which totally orders the write events to one location.
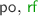 and
and 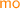 denote the ‘program-order’, ‘reads-from’ and ‘modification-order’ relations as described above;
denote the ‘program-order’, ‘reads-from’ and ‘modification-order’ relations as described above; , returning the transaction identifier of transactional events. The derived ‘same-transaction’ relation,
, returning the transaction identifier of transactional events. The derived ‘same-transaction’ relation, 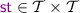 , is the equivalence relation given by
, is the equivalence relation given by 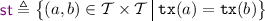 .
.
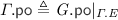 – the
– the  is that of
is that of  limited to the events in
limited to the events in 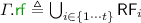 – the
– the 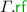 is the union of
is the union of 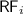 relations defined above;
relations defined above; – the
– the  is that of
is that of  limited to the events in
limited to the events in 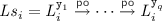 and
and 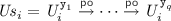 denote the sequence of events acquiring and releasing the version locks, respectively. Each
denote the sequence of events acquiring and releasing the version locks, respectively. Each 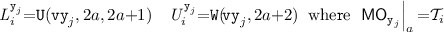
 relation for version locks such that if transaction
relation for version locks such that if transaction  -ordered immediately after
-ordered immediately after  -ordered immediately after the corresponding
-ordered immediately after the corresponding 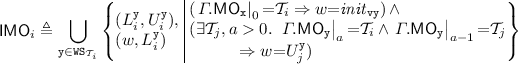
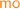 order on lock events of
order on lock events of  relation for its lock acquisition events:
relation for its lock acquisition events:  .
.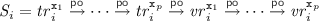 denotes the sequence of events obtaining a tentative snapshot (
denotes the sequence of events obtaining a tentative snapshot (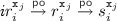 (reading the version lock
(reading the version lock  relation for each of these read events in
relation for each of these read events in  , we add
, we add 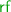 relation of
relation of  below). For version locks, if transaction
below). For version locks, if transaction 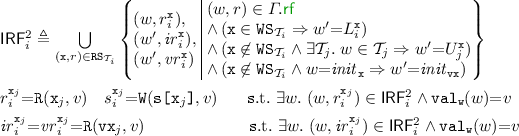
 (when
(when  ), with
), with 
 – note that
– note that  is defined as
is defined as  extended by the
extended by the  for the additional events of
for the additional events of 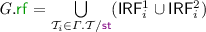
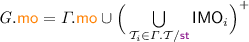


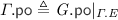 – the
– the  is that of
is that of  restricted to the events in
restricted to the events in 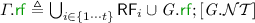 – the
– the  is the union of
is the union of 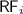 relations for transactional reads as defined in Sect.
relations for transactional reads as defined in Sect.  relation for non-transactional reads;
relation for non-transactional reads; – the
– the  is that of
is that of  restricted to the events in
restricted to the events in  ;
; is defined as
is defined as  extended by the
extended by the  for the additional events of
for the additional events of  , with
, with  as in Sect.
as in Sect.  defined above;
defined above; , with
, with  as defined in Sect.
as defined in Sect.