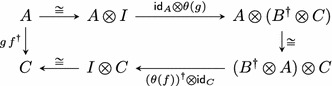Abstract
Notions of guardedness serve to delineate the admissibility of cycles, e.g. in recursion, corecursion, iteration, or tracing. We introduce an abstract notion of guardedness structure on a symmetric monoidal category, along with a corresponding notion of guarded traces, which are defined only if the cycles they induce are guarded. We relate structural guardedness, determined by propagating guardedness along the operations of the category, to geometric guardedness phrased in terms of a diagrammatic language. In our setup, the Cartesian case (recursion) and the co-Cartesian case (iteration) become completely dual, and we show that in these cases, guarded tracedness is equivalent to presence of a guarded Conway operator, in analogy to an observation on total traces by Hasegawa and Hyland. Moreover, we relate guarded traces to unguarded categorical uniform fixpoint operators in the style of Simpson and Plotkin. Finally, we show that partial traces based on Hilbert-Schmidt operators in the category of Hilbert spaces are an instance of guarded traces.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
In models of computation, various notions of guardedness serve to control cyclic behaviour by allowing only guarded cycles, with the aim to ensure properties such as solvability of recursive equations or productivity. Typical examples are guarded process algebra specifications [6, 29], coalgebraic guarded (co-)recursion [27, 33], finite delay in online Turing machines [9], and productive definitions in intensional type theory [1, 30], but also contractive maps in (ultra-)metric spaces [24].
A highly general model for unrestricted cyclic computations, on the other hand, are traced monoidal categories [22]; besides recursion and iteration, they cover further kinds of cyclic behaviour, e.g. in Girard’s Geometry of Interaction [4, 14] and quantum programming [3, 34]. In the present paper we parametrize the framework of traced symmetric monoidal categories with a notion of guardedness, arriving at (abstractly) guarded traced categories, which effectively vary between two extreme cases: symmetric monoidal categories (nothing is guarded) and traced symmetric monoidal categories (everything is guarded). In terms of the standard diagrammatic language for traced monoidal categories, we decorate input and output gates of boxes to indicate guardedness; the diagram governing trace formation would then have the general form depicted in Fig. 1 – that is, we can only form traces connecting guarded (black) output gates to input gates that are unguarded (black), i.e. not assumed to be already guarded.
We provide basic structural results on our notion of abstract guardedness, and identify a wide array of examples. Specifically, we establish a geometric characterization of guardedness in terms of paths in diagrams; we identify a notion of guarded ideal, along with a construction of guardedness structures from guarded ideals and simplifications of this construction for the (co-)Cartesian and the Cartesian closed case; and we describe ‘vacuous’ guardedness structures where traces do not actually generate proper diagrammatic cycles. In terms of examples, we begin with the case where the monoidal structure is either product (Cartesian), corresponding to guarded recursion, or coproduct (co-Cartesian), for guarded iteration; the axioms for guardedness allow for a basic duality that indeed makes these two cases precisely dual. For total traces in Cartesian categories, Hasegawa and Hyland observed that trace operators are in one-to-one correspondence with Conway fixpoint operators [18, 19]; we extend this correspondence to the guarded case, showing that guarded trace operators on a Cartesian category are in one-to-one correspondence with guarded Conway operators. In a more specific setting, we relate guarded traces in Cartesian categories to unguarded categorical uniform fixpoints as studied by Crole and Pitts [11] and by Simpson and Plotkin [37, 38]. Concluding with a case where the monoidal structure is a proper tensor product, we show that the partial trace operation on (infinite-dimensional) Hilbert spaces is an instance of vacuous guardedness; this result relates to work by Abramsky, Blute, and Panangaden on traces over nuclear ideals, in this case over Hilbert-Schmidt operators [2].
Related Work. Abstract guardedness serves to determine definedness of a guarded trace operation, and thus relates to work on partial traces. We discuss work on nuclear ideals [2] in Sect. 6. In partial traced categories [17, 26], traces are governed by a partial equational version (consisting of both strong and directed equations) of the Joyal-Street-Verity axioms; morphisms for which trace is defined are called trace class. A key difference to the approach via guardedness is that being trace class applies only to morphisms with inputs and outputs of matching types while guardedness applies to arbitrary morphisms, allowing for compositional propagation. Also, the axiomatizations are incomparable: Unlike for trace class morphisms [17, Remark 2.2], we require guardedness to be closed under composition with arbitrary morphisms (thus covering contractivity but not, e.g., monotonicity as in the modal \(\mu \)-calculus); on the other hand, as noted by Jeffrey [21], guarded traces, e.g. of contractions, need not satisfy Vanishing II as a Kleene equality as assumed in partial traced categories. Some approaches treat traces as partial over objects [8, 20]. In concrete algebraic categories, partial traces can be seen as induced by total traces in an ambient category of relations [5]. We discuss work on guardedness via endofunctors in Remark 23.
2 Preliminaries
We recall requisite categorical notions; see [25] for a comprehensive introduction.
Symmetric Monoidal Categories. A symmetric monoidal category \((\mathbf {C}, \mathbin {\otimes }, I)\) consists of a category \(\mathbf {C}\) (with object class \(|\mathbf {C}|\)), a bifunctor \(\mathbin {\otimes }\) (tensor product), and a (tensor) unit \(I\in |\mathbf {C}|\), and coherent isomorphisms witnessing that \(\mathbin {\otimes }\) is, up to isomorphism, a commutative monoid structure with unit I. For the latter, we reserve the notation \(\alpha _{A,B,C}:(A\mathbin {\otimes }B)\mathbin {\otimes }C\cong A\mathbin {\otimes }(B\mathbin {\otimes }C)\) (associator), \(\gamma _{A,B}: A\mathbin {\otimes }B\cong B\mathbin {\otimes }A\) (symmetry), and \(\upsilon _A:I\mathbin {\otimes }A\cong A\) (left unitor); the right unitor \(\hat{\upsilon }_A:A\mathbin {\otimes }I\cong A\) is expressible via the symmetry. A symmetric monoidal category is Cartesian if the monoidal structure is finite product (i.e. \(\mathbin {\otimes }=\times \), and \(I=1\) is a terminal object), and, dually, co-Cartesian if the monoidal structure is finite coproduct (i.e. \(\mathbin {\otimes }=+\), and  is an initial object). Coproduct injections are written
is an initial object). Coproduct injections are written  (\(i=1,2\)), and product projections
(\(i=1,2\)), and product projections  . Various notions of algebraic tensor products also induce symmetric monoidal structures; see Sect. 6 for the case of Hilbert spaces. One has an obvious expression language for objects and morphisms in symmetric monoidal categories [36], the former obtained by postulating basic objects and closing under I and \(\mathbin {\otimes }\), and the latter by postulating basic morphisms of given profile and closing under \(\mathbin {\otimes }\), I, composition, identities, and the monoidal isomorphisms, subject to the evident notion of well-typedness. Morphism expressions are conveniently represented as diagrams consisting of boxes representing the basic morphisms, with input and output gates corresponding to the given profile. Tensoring is represented by putting boxes on top of each other, and composition by wires connecting outputs to inputs [36]. In a traced symmetric monoidal category one has an additional operation (trace) that essentially enables the formation of loops in diagrams, as in Fig. 1 (but without decorations).
. Various notions of algebraic tensor products also induce symmetric monoidal structures; see Sect. 6 for the case of Hilbert spaces. One has an obvious expression language for objects and morphisms in symmetric monoidal categories [36], the former obtained by postulating basic objects and closing under I and \(\mathbin {\otimes }\), and the latter by postulating basic morphisms of given profile and closing under \(\mathbin {\otimes }\), I, composition, identities, and the monoidal isomorphisms, subject to the evident notion of well-typedness. Morphism expressions are conveniently represented as diagrams consisting of boxes representing the basic morphisms, with input and output gates corresponding to the given profile. Tensoring is represented by putting boxes on top of each other, and composition by wires connecting outputs to inputs [36]. In a traced symmetric monoidal category one has an additional operation (trace) that essentially enables the formation of loops in diagrams, as in Fig. 1 (but without decorations).
Monads and (Co-)algebras. A(n F)-coalgebra for a functor \(F:\mathbf {C}\rightarrow \mathbf {C}\) is a pair \((X,f:X\rightarrow FX)\) where \(X\in |\mathbf {C}|\), thought of as modelling states and generalized transitions [33]. A final coalgebra is a final object in the category of coalgebras (with \(\mathbf {C}\)-morphisms \(h:X\rightarrow Y\) such that \((Fh) f = g h\) as morphisms \((X,f)\rightarrow (Y,g)\)), denoted \((\nu F,\mathsf {out}:\nu F\rightarrow F\nu F)\) if it exists. Dually, an F-algebra has the form \((X,f:FX\rightarrow X)\). A monad \(\mathbb {T}=(T,\mu ,\eta )\) on a category \(\mathbf {C}\) consists of an endofunctor T on \(\mathbf {C}\) and natural transformations \(\eta :{\text {Id}}\rightarrow T\) (unit) and \(\mu :T^2\rightarrow T\) (multiplication) subject to standard equations [25]. As observed by Moggi [31], monads can be seen as capturing computational effects of programs, with TX read as a type of computations with side effects from T and results in X. In this view, the Kleisli category \(\mathbf {C}_\mathbb {T}\) of \(\mathbb {T}\), which has the same objects as \(\mathbf {C}\) and \(\mathsf {Hom}_{\mathbf {C}_\mathbb {T}}(X,Y)= \mathsf {Hom}_{\mathbf {C}}(X,TY)\), is a category of side-effecting programs. A monad is strong if it is equipped with a strength, i.e. a natural transformation \(X\times TY\rightarrow T(X\times Y)\) satisfying evident coherence conditions (e.g. [31]). A T-algebra \((A,a)\) is an (Eilenberg-Moore) \(\mathbb {T}\)-algebra (for the monad \(\mathbb {T}\)) if additionally \(a\eta =\mathsf {id}\) and \(a(Ta) = a\mu _A\); the category of \(\mathbb {T}\)-algebras is denoted \(\mathbf {C}^{\mathbb {T}}\).
3 Guarded Categories
We now introduce our notion of guarded structure. A standard example of guardedness are guarded definitions in process algebra. E.g. in the definition \(P = a.P\), the right hand occurrence of P is guarded, ensuring unique solvability (by a process that keeps outputting a). A further example is contractivity of maps between complete metric spaces. We formulate abstract closure properties for partial guardedness where only some of the inputs and outputs of a morphism are guarded. Specifically, we distinguish guarded outputs and guarded inputs (D and B, respectively, in the following definition), with the intended reading that guarded outputs yield guarded data provided guarded data is already provided at guarded inputs, while unguarded inputs may be fed arbitrarily.
Definition 1
(Guarded category). An (abstractly) guarded category is a symmetric monoidal category \((\mathbf {C}, \mathbin {\otimes }, I)\) equipped with distinguished subsets \(\mathsf {Hom}^{\bullet }(A\mathbin {\otimes }B,C\mathbin {\otimes }D)\subseteq \mathsf {Hom}({A\mathbin {\otimes }B},C\mathbin {\otimes }D)\) of partially guarded morphisms for \(A,B,C,D\in |\mathbf {C}|\), satisfying the following conditions:
- (uni\({}_{\mathbin {\otimes }}\)):
-
\(\gamma _{I,A}\in \mathsf {Hom}^{\bullet }(I\mathbin {\otimes }A, A\mathbin {\otimes }I)\);
- (vac\({}_{\mathbin {\otimes }}\)):
-
\(f\mathbin {\otimes }g\in \mathsf {Hom}^{\bullet }(A\mathbin {\otimes }B, C\mathbin {\otimes }D)\) for all \(f:A\rightarrow C\), \(g:B\rightarrow D\);
- (cmp\({}_{\mathbin {\otimes }}\)):
-
\(g\in \mathsf {Hom}^{\bullet }(A\mathbin {\otimes }B, E\mathbin {\otimes }F)\) and \(f\in \mathsf {Hom}^{\bullet }(E\mathbin {\otimes }F, C\mathbin {\otimes }D)\) imply \(fg\in \mathsf {Hom}^{\bullet }(A\mathbin {\otimes }B, C\mathbin {\otimes }D)\);
- (par\({}_{\mathbin {\otimes }}\)):
-
for \(f\in \mathsf {Hom}^{\bullet }(A\mathbin {\otimes }B, C\mathbin {\otimes }D)\), \(g\in \mathsf {Hom}^{\bullet }(A'\mathbin {\otimes }B', C'\mathbin {\otimes }D')\), the evident transpose of \(f\mathbin {\otimes }g\) is in \(\mathsf {Hom}^{\bullet }((A\mathbin {\otimes }A')\mathbin {\otimes }(B\mathbin {\otimes }B'), (C\mathbin {\otimes }C')\mathbin {\otimes }(D\mathbin {\otimes }D'))\).
We emphasize that \(\mathsf {Hom}^{\bullet }(A\mathbin {\otimes }B,C\mathbin {\otimes }D)\) is meant to depend individually on A, B, C, D and not just on \(A\mathbin {\otimes }B\) and \(C\mathbin {\otimes }D\).
One easily derives a weakening rule stating that if \(f\in \mathsf {Hom}^{\bullet }((A\mathbin {\otimes }A')\mathbin {\otimes }B,C\mathbin {\otimes }(D'\mathbin {\otimes }D))\), then the obvious transpose of f is in \(\mathsf {Hom}^{\bullet }(A\mathbin {\otimes }(A'\mathbin {\otimes }B),(C\mathbin {\otimes }D')\mathbin {\otimes }D)\).

We extend the standard diagram language for symmetric monoidal categories (Sect. 2), representing morphisms \(f\in \mathsf {Hom}^{\bullet }(A\mathbin {\otimes }B,C\mathbin {\otimes }D)\) by decorated boxes as shown on the right, with black bars marking the unguarded input gates A and the guarded output gates D. Weakening then corresponds to shrinking the black bars of decorated boxes. Figure 2 depicts the above axioms in this language. Solid boxes represent the assumptions, while dashed boxes represent the conclusions. The latter only occur in the derivation process and do not form part of the actual diagrams representing concrete morphisms. We silently identify object expressions and sets of gates in diagrams. Given a (well-typed) morphism expression e, a judgement \(e\in \mathsf {Hom}^{\bullet }(A\mathbin {\otimes }B,C\mathbin {\otimes }D)\), called a guardedness typing of e, is derivable if it can be derived from the assumed guardedness typing of the constituent basic boxes of e using the rules in Definition 1. We have an obvious notion of (directed) paths in diagrams; a path is guarded if it passes some basic box f through an unguarded input gate and a guarded output gate (intuitively, guardedness is then introduced along the path as the passage through f will guarantee guarded output without assuming guarded input). We then have the following geometric characterization of guardedness typing:
Theorem 2
For a well-typed morphism expression \(e\in \mathsf {Hom}(A\mathbin {\otimes }B,C\mathbin {\otimes }D)\), the guardedness typing \(e\in \mathsf {Hom}^{\bullet }(A\mathbin {\otimes }B,C\mathbin {\otimes }D)\) is derivable iff in the diagram of e, every path from an input gate in A to an output gate in D is guarded.
Every symmetric monoidal category has both a largest (\(\mathsf {Hom}^{\bullet }(A\mathbin {\otimes }B,C\mathbin {\otimes }D)=\mathsf {Hom}(A\mathbin {\otimes }B,C\mathbin {\otimes }D)\)) and a least guarded structure:
Lemma and Definition 3
(Vacuous guardedness). Every symmetric monoidal category is guarded under taking \(f\in \mathsf {Hom}^{\bullet }(A\mathbin {\otimes }B,C\mathbin {\otimes }D)\) iff f factors as
(eliding associativity) with \(g:B\rightarrow E\mathbin {\otimes }D\), \(h:A \mathbin {\otimes }E\rightarrow C\). This is the least guarded structure on \(\mathbf {C}\), the vacuous guarded structure.
E.g. the natural guarded structure on Hilbert spaces (Sect. 6) is vacuous.
Remark 4
(Duality). The rules and axioms in Fig. 2 are stable under \(180^\circ \)-rotation, that is, under reversing arrows and applying the monoidal symmetry on both sides (this motivates decorating the unguarded inputs). Consequently, if \(\mathbf {C}\) is guarded, then so is the dual category \(\mathbf {C}^{op}\), with guardedness given by \(f\in \mathsf {Hom}^{\bullet }_{\mathbf {C}^{op}}(A\mathbin {\otimes }B, C\mathbin {\otimes }D)\) iff the obvious transpose of f is in \(\mathsf {Hom}^{\bullet }_{\mathbf {C}}(D\mathbin {\otimes }C,B\mathbin {\otimes }A)\).
In case \(\mathbin {\otimes }\) is coproduct, we can simplify the description of partial guardedness:
Proposition 5
Partial guardedness in a co-Cartesian category  is equivalently determined by distinguished subsets \(\mathsf {Hom}_{\sigma }(X,Y)\subseteq \mathsf {Hom}(X,Y)\) with \(\sigma \) ranging over coproduct injections \(Y_2\rightarrow Y_1+Y_2\cong Y\), subject to the rules on the right hand side of Fig. 3, where \(f:X\rightarrow _\sigma Y\) denotes \(f\in \mathsf {Hom}_\sigma (X,Y)\), with \(f\in \mathsf {Hom}^{\bullet }(X_1+X_2,Y_1+Y_2)\) iff
is equivalently determined by distinguished subsets \(\mathsf {Hom}_{\sigma }(X,Y)\subseteq \mathsf {Hom}(X,Y)\) with \(\sigma \) ranging over coproduct injections \(Y_2\rightarrow Y_1+Y_2\cong Y\), subject to the rules on the right hand side of Fig. 3, where \(f:X\rightarrow _\sigma Y\) denotes \(f\in \mathsf {Hom}_\sigma (X,Y)\), with \(f\in \mathsf {Hom}^{\bullet }(X_1+X_2,Y_1+Y_2)\) iff  .
.
We have used the mentioned rules for \(\rightarrow _\sigma \) in previous work on guarded iteration [16] (with (vac\({}_{\times }\)) called (trv), and together with weakening, which as indicated above turns out to be derivable). By duality (Remark 4), we immediately have a corresponding description for the Cartesian case:
Corollary 6
Partial guardedness in a Cartesian category \((\mathbf {C},\times ,1)\) is equivalently determined by distinguished subsets \(\mathsf {Hom}^{\sigma }(X,Y)\subseteq \mathsf {Hom}(X,Y)\) with \(\sigma \) ranging over product projections \(X\cong X_1\times X_2 \rightarrow X_1\), subject to the rules on the left hand side of Fig. 3, where \(f:X\rightarrow ^\sigma Y\) denotes \(f\in \mathsf {Hom}^\sigma (X,Y)\), with \(f\in \mathsf {Hom}^{\bullet }(X_1\times X_2, Y_1\times Y_2)\) iff \(\mathsf {pr}_2 f\in \mathsf {Hom}^{\mathsf {pr}_1}(X_1\times X_2 ,Y_2)\).
Remark 7
In a co-Cartesian category, vacuous guardedness (Lemma 3) can equivalently be described by \(f\in \mathsf {Hom}^{\bullet }(A+B,C+D)\) iff f decomposes as  (uniquely provided that
(uniquely provided that  is monic), or in terms of the description from Proposition 5,
is monic), or in terms of the description from Proposition 5,  iff u factors through
iff u factors through  . Of course, the dual situation obtains in Cartesian categories.
. Of course, the dual situation obtains in Cartesian categories.
Example 8
(Process algebra). Fix a monad \(\mathbb {T}\) on  and an endofunctor \(\varSigma :\mathbf {C}\rightarrow \mathbf {C}\) such that the generalized coalgebraic resumption transform
and an endofunctor \(\varSigma :\mathbf {C}\rightarrow \mathbf {C}\) such that the generalized coalgebraic resumption transform  exists; we think of \(T_\varSigma X\) as a type of processes that have side-effects in \(\mathbb {T}\) and perform communication actions from \(\varSigma \), seen as a generalized signature. The Kleisli category \(\mathbf {C}_{\mathbb {T}_{\varSigma }}\) of \(\mathbb {T}_{\varSigma }\) is again co-Cartesian. Putting
exists; we think of \(T_\varSigma X\) as a type of processes that have side-effects in \(\mathbb {T}\) and perform communication actions from \(\varSigma \), seen as a generalized signature. The Kleisli category \(\mathbf {C}_{\mathbb {T}_{\varSigma }}\) of \(\mathbb {T}_{\varSigma }\) is again co-Cartesian. Putting

(cf. Sect. 2 for notation), we make \(\mathbf {C}_{\mathbb {T}_{\varSigma }}\) into a guarded category [16]. The standard motivating example of finitely nondeterministic processes is obtained by taking \(\mathbb {T}={\mathcal P}_{\omega }\) (finite powerset monad) and \(\varSigma = A\times {-}\) (action prefixing).
Example 9
(Metric spaces). Let \(\mathbf {C}\) be the Cartesian category of metric spaces and non-expansive maps. Taking \(f:X\times Y\rightarrow ^{\mathsf {pr}_2} Z\) iff \(\lambda y.\, f(x,y)\) is contractive for every \(x\in X\) makes \(\mathbf {C}\) into a guarded Cartesian category.
4 Guardedness via Guarded Ideals
Most of the time, the structure of a guarded category is determined by morphisms with only unguarded inputs and guarded outputs, which form an ideal:
Definition 10
(Guarded morphisms). A morphism \(f:X\rightarrow Y\) in a guarded category is guarded (as opposed to only partially guarded) if  ; we write
; we write  for the set of guarded morphisms \(f:X\rightarrow Y\).
for the set of guarded morphisms \(f:X\rightarrow Y\).
Definition 11
(Guarded ideal). A family G of subsets \(G(X,Y)\subseteq \mathsf {Hom}(X,Y)\) (\(X,Y\in |\mathbf {C}|\)) in a monoidal category \((\mathbf {C},\mathbin {\otimes },I)\) is a guarded ideal if it is closed under \(\mathbin {\otimes }\) and under composition with arbitrary \(\mathbf {C}\)-morphisms on both sides, and \(G(I,I)=\mathsf {Hom}(I,I)\).
There is always a least guarded ideal, \(G(X,Y) = \{gf\mid f:X\rightarrow I, g:I\rightarrow Y\}\). Moreover, as indicated above:
Lemma and Definition 12
In a guarded category, the sets  form a guarded ideal, the guarded ideal induced by the guarded structure.
form a guarded ideal, the guarded ideal induced by the guarded structure.
Conversely, it is clear that every guarded ideal generates a guarded structure by just closing under the rules of Definition 1.
Definition 13
(Ideally guarded category). A guarded category is ideal or ideally guarded (over G) if it is generated by some guarded ideal (G).
We give a more concrete description:
Theorem 14
Let \((\mathbf {C},\mathbin {\otimes },I)\) be ideally guarded over G. Then \(\mathsf {Hom}^{\bullet }(A\mathbin {\otimes }B,C\mathbin {\otimes }D)\) consists of the morphisms of the form

for \(g_i\) in G and arbitrary p, q, \(f_i\), \(h_i\).
The transitions between guarded ideals and guarded structures are not in general mutually inverse: The guarded structure generated the guarded ideal induced by a guarded structure may be smaller than the original one (Example 21), and the guarded ideal induced by the guarded structure generated by a guarded ideal G may be larger than G (Remark 16). We proceed to analyse details.
Proposition 15
On every symmetric monoidal category, the least guarded structure (Lemma 3) is ideal.
Remark 16
Vacuously guarded categories need not induce the least guarded ideal (although by the next results, this does hold in the Cartesian and the co-Cartesian case). In fact, by Lemma 3, the guarded ideal induced by the vacuous guarded structure consists of the morphisms of the form \((h\mathbin {\otimes }\mathsf {id}_D)(\mathsf {id}_A\mathbin {\otimes }g)\) (eliding associativity and the unitor) where \(g:I\rightarrow E\mathbin {\otimes }D\), \(h:A \mathbin {\otimes }E\rightarrow I\):

This ideal will resurface in the discussion of Hilbert spaces (Sect. 6).
The situation is simpler in the Cartesian and, dually, in the co-Cartesian case.
Lemma 17
Let \(\mathbf {C}\) be ideally guarded over G, and suppose that every  factors through \(\hat{f}\mathbin {\otimes }\mathsf {id}:X\mathbin {\otimes }Y\rightarrow V\mathbin {\otimes }Y\) for some \(\hat{f}\in G(X,V)\). Then the guardedness structure of \(\mathbf {C}\) induces G.
factors through \(\hat{f}\mathbin {\otimes }\mathsf {id}:X\mathbin {\otimes }Y\rightarrow V\mathbin {\otimes }Y\) for some \(\hat{f}\in G(X,V)\). Then the guardedness structure of \(\mathbf {C}\) induces G.
If \(\mathbin {\otimes }=+\), the premise of the lemma is automatic, since \(f\in G(X+Y,Z)\) can be represented as  where
where  by the closure properties of guarded ideals. Hence, we obtain
by the closure properties of guarded ideals. Hence, we obtain
Theorem 18
The guarded structure generated by a guarded ideal G on a co-Cartesian category is equivalently described by  , and hence induces G.
, and hence induces G.
Corollary 19
The guarded structure generated by a guarded ideal G on a Cartesian category is equivalently described by  , and hence induces G.
, and hence induces G.
The description can be further simplified in the Cartesian closed case.
Corollary 20
Given a guarded ideal G on a Cartesian closed category, put \(f:X\times Y\rightarrow ^{\mathsf {pr}_1} Z\) iff \(\mathsf {curry}~ f\in G(X,Z^Y)\). This describes the guarded structure induced by G iff G is exponential, i.e. \(f\in G(X,Y)\) implies \(f^V\in G(X^V,Y^V)\).
(We leave it as an open question whether a similar characterization holds in the monoidal closed case.) Natural examples of both ideal and non-ideal guardedness are found in metric spaces:
Example 21
(Metric spaces). The guarded structure on metric spaces from Example 9 fails to be ideal: It induces the guarded ideal of contractive maps, which however generates the (ideal) guarded structure described by  iff f(x, y) is uniformly contractive in y, i.e. there is \(c<1\) such that for every x, \(\lambda y.\,f(x,y)\) is contractive with contraction factor c.
iff f(x, y) is uniformly contractive in y, i.e. there is \(c<1\) such that for every x, \(\lambda y.\,f(x,y)\) is contractive with contraction factor c.
A large class of ideally guarded structures arises as follows.
Proposition 22
Let \(\mathbf {C}\) be a Cartesian category equipped with an endofunctor \({\blacktriangleright }:\mathbf {C}\rightarrow \mathbf {C}\) and a natural transformation \(\mathsf {next}:{\text {Id}}\rightarrow {\blacktriangleright }\). Then the following definition yields a guarded ideal in \(\mathbf {C}\): \(G(X,Y) = \{f~\mathsf {next}\mid f:{\blacktriangleright }X\rightarrow Y\}\). The arising guarded structure is  . If moreover \(\mathsf {next}:X\times Y\rightarrow {\blacktriangleright }(X\times Y)\) factors through \(\mathsf {next}\times \mathsf {id}:X\times Y\rightarrow {\blacktriangleright }X\times Y\), then \(\mathsf {Hom}^{{\mathsf {pr}_1}}(X\times Y,Z) = \{f(\mathsf {next}\times \mathsf {id})\mid f:{\blacktriangleright }X\times Y\rightarrow Z\}\).
. If moreover \(\mathsf {next}:X\times Y\rightarrow {\blacktriangleright }(X\times Y)\) factors through \(\mathsf {next}\times \mathsf {id}:X\times Y\rightarrow {\blacktriangleright }X\times Y\), then \(\mathsf {Hom}^{{\mathsf {pr}_1}}(X\times Y,Z) = \{f(\mathsf {next}\times \mathsf {id})\mid f:{\blacktriangleright }X\times Y\rightarrow Z\}\).
Remark 23
Proposition 22 connects our approach to previous work based precisely on the assumptions of the proposition [28] (in fact, the term guarded traced category is already used there, with different meaning). A limitation of the approach via a functor \({\blacktriangleright }\) arises from the need to fix \({\blacktriangleright }\) globally, so that, e.g., the ideal guarded structure on metric spaces (Example 21) is not covered – capturing contractivity via \({\blacktriangleright }\) requires fixing a single global contraction factor.
The following instance of Proposition 22 has received extensive recent interest in programming semantics:
Example 24
(Topos of Trees). Let \(\mathbf {C}\) be the topos of trees [7], i.e. the presheaf category \(\mathbf {Set}^{\omega ^{op}}\) where \(\omega \) is the preorder of natural numbers (starting from 1) ordered by inclusion. An object X of \(\mathbf {C}\) is thus a family \((X(n))_{n=1,2\ldots }\) of sets with restriction maps \(r_n:X(n+1)\rightarrow X(n)\). The later-endofunctor \({\blacktriangleright }:\mathbf {C}\rightarrow \mathbf {C}\) is defined by \({\blacktriangleright }X(1) = \{\star \}\) and \({\blacktriangleright }X(n+1) = X(n)\), and the natural transformation \(\mathsf {next}_X:X\rightarrow \,{\blacktriangleright }X\) by \(\mathsf {next}_X (1)={\text {!}}:X(1)\rightarrow \{\star \}\), \(\mathsf {next}_X (n+1)=r_{n+1}:X{(n+1})\rightarrow X(n)\). Guarded morphisms according to Proposition 22 are called contractive, generalizing the metric setup. Contractive morphisms form an exponential ideal, so partial guardedness is described as in Corollary 20, and hence agrees with contractivity in part of the input as in [7, Definition 2.2].
5 Guarded Traces
As indicated previously, the main purpose of our notion of abstract guardedness is to enable fine-grained control over the formation of feedback loops, viz, traces.
Definition 25
(Guarded traced category). We call a guarded category \((\mathbf {C},\mathbin {\otimes },I)\) guarded traced if it is equipped with a guarded trace operator
visually corresponding to the diagram formation rule in Fig. 1, so that the adaptation of the Joyal-Street-Verity axiomatization of traced symmetric monoidal categories [22] shown in Fig. 4 is satisfied.
Remark 26
The versions of the sliding axiom in Fig. 4 differ in the way the loop is guarded. They are in line with duality (Remark 4): Sliding II arises from Sliding I by \(180^\circ \) rotation, and Sliding III is symmetric under \(180^\circ \) rotation.
We proceed to investigate the geometric properties of guarded traced categories, partly extending Theorem 2. The syntactic setting extends the one for guarded categories by additionally closing morphism expressions under the trace operator (interpreted diagrammatically as in Fig. 1), obtaining traced morphism expressions. Term formation thus becomes mutually recursive with guardedness typing: if e is a traced morphism expression such that \(e\in \mathsf {Hom}^{\bullet }((A\mathbin {\otimes }U)\mathbin {\otimes }B,C\mathbin {\otimes }(D\mathbin {\otimes }U))\) is derivable, then \(\mathsf {tr}_{A,B,C,D}(e)\) is a traced morphism expression, and \(\mathsf {tr}_{A,B,C,D}(e)\in \mathsf {Hom}^{\bullet }(A\mathbin {\otimes }B,C\mathbin {\otimes }D)\) is derivable. Traced diagrams consists of finitely many (decorated) basic boxes and wires connecting output gates of basic boxes to input gates, with each gate attached to at most one wire; open gates are regarded as inputs or outputs, respectively, of the whole diagram. Of course, acyclicity is not required. We first note that the easy direction of Theorem 2 adapts straightforwardly to the setting with traces:
Proposition 27
Let e be a traced morphism expression such that \(e\in \mathsf {Hom}^{\bullet }(A\mathbin {\otimes }B,C\mathbin {\otimes }D)\) is derivable. Then in the diagram of e, all loops and all paths from input gates in A to output gates in D are guarded (p. 4).
Remarkably, the converse of Proposition 27 in general fails in several ways:
Example 28
The left diagram below

shows that guardedness typing is not closed under equality of traced morphism expressions: Write e for the expression inducing the dashed box. By Proposition 27, e, and hence \(\mathsf {tr}(e)\), fail to type as indicated. However, \(\mathsf {tr}(e)=gf\), for which the overall guardedness typing indicated is easily derivable.
Moreover, the diagram on the right above satisfies the necessary condition from Proposition 27 but is not induced by an expression for which the indicated guardedness typing is derivable, essentially because both ways of cutting the loop violate the necessary condition from Proposition 27.
However, if \(\mathbf {C}\) is ideally guarded over a guarded ideal G, we do have a converse to Proposition 27: By Theorem 14, we can then restrict basic boxes in diagrams to be either guarded, i.e. have only black gates, or unguarded, i.e. have only white gates. We call the correspondingly restricted diagrams ideally guarded. (We emphasize that the guardedness typing of composite ideally guarded diagrams still needs to mix guarded and unguarded inputs and outputs.) A path in an ideally guarded diagram is guarded iff it passes through a guarded basic box.
The left-hand diagram in (2) is in fact ideally guarded, so guardedness typing fails to be closed under equality also in the ideally guarded case. However, for ideally guarded diagrams we have the following converse of Proposition 27.
Theorem 29
Let \(\varDelta \) be an ideally guarded diagram, with sets of input and output gates disjointly decomposed as  and
and  , respectively. If every loop in \(\varDelta \) and every path from a gate in A to a gate in D is guarded, then \(\varDelta \) is induced by a traced morphism expression e such that \(e\in \mathsf {Hom}^{\bullet }(A\mathbin {\otimes }B,C\mathbin {\otimes }D)\) is derivable.
, respectively. If every loop in \(\varDelta \) and every path from a gate in A to a gate in D is guarded, then \(\varDelta \) is induced by a traced morphism expression e such that \(e\in \mathsf {Hom}^{\bullet }(A\mathbin {\otimes }B,C\mathbin {\otimes }D)\) is derivable.
We next take a look at the Cartesian and co-Cartesian cases. Recall that by Proposition 5, the definition of guarded category can be simplified if \(\mathbin {\otimes }=+\) (and dually if \(\mathbin {\otimes }=\times \)). This simplification extends to guarded traced categories by generalizing Hyland-Hasegawa’s equivalence between Cartesian trace operators and Conway fixpoint operators [18, 19].
Definition 30
(Guarded Conway operators). Let \(\mathbf {C}\) be a guarded co-Cartesian category. We call an operator \(({-})^\dagger \) of profile
a guarded iteration operator if it satisfies
-
fixpoint: \(f^{\dagger } = [\mathsf {id},f^\dagger ]f\) for
 ;
;
and a Conway iteration operator if it additionally satisfies
-
naturality: \(gf^{\dagger } = ((g+\mathsf {id}) f)^{\dagger }\) for
 , \(g : Y \rightarrow Z\);
, \(g : Y \rightarrow Z\); -
dinaturality:
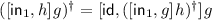 for
for 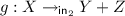 and \(h:Z\rightarrow Y+X\) or \(g : X \rightarrow Y + Z\) and
and \(h:Z\rightarrow Y+X\) or \(g : X \rightarrow Y + Z\) and  ;
; -
(co)diagonal:
 for
for  .
.
Furthermore, we distinguish the following principles:
-
squaring [12]:
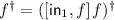 for
for 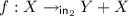 ;
; -
uniformity w.r.t. a subcategory \(\mathbf {S}\) of \(\mathbf {C}\): \((\mathsf {id}+ h)f = gh\) implies \(f^{\dagger } = g^{\dagger }h\) for all
 ,
,  and \(h: Y\rightarrow X\) from \(\mathbf {S}\);
and \(h: Y\rightarrow X\) from \(\mathbf {S}\);
and call \(({-})^\dagger \) squarable or uniform if it satisfies squaring or uniformity, respectively.
Guarded (Conway) recursion operators \(({-})_{\dagger }\) on guarded Cartesian categories are defined dually in a straightforward manner. We collect the following facts about guarded iteration operators for further reference.
Lemma 31
Let \(({-})^\dagger \) be a guarded iteration operator on  .
.
-
1.
If \(({-})^\dagger \) is uniform w.r.t. some co-Cartesian subcategory of \(\mathbf {C}\) and satisfies the codiagonal identity then it is squarable.
-
2.
If \(({-})^\dagger \) is squarable and uniform w.r.t. coproduct injections then it is dinatural.
-
3.
If \(({-})^\dagger \) is Conway then it is uniform w.r.t. coproduct injections.
Proposition 32
A guarded co-Cartesian category \(\mathbf {C}\) is traced iff it is equipped with a guarded Conway iteration operator \(({-})^\dagger \), with mutual conversions like in the total case [18, 19].
Example 33
(Guarded Conway operators). We list some examples of guarded Conway iteration/recursion operators. In all cases except 2, Conwayness follows from uniqueness of fixpoints [16, Theorem 17].
-
1.
In a vacuously guarded co-Cartesian category (Remark 7),
 iff
iff  for some \(g:X\rightarrow Y\). If coproduct injections are monic, then g is uniquely determined, and \(f^\dagger = g\) defines a guarded Conway operator.
for some \(g:X\rightarrow Y\). If coproduct injections are monic, then g is uniquely determined, and \(f^\dagger = g\) defines a guarded Conway operator. -
2.
Every Cartesian category \(\mathbf {C}\) is guarded under \(\mathsf {Hom}^{\pi }(X,Y) = \mathsf {Hom}(X,Y)\) (making every morphism guarded). Then \(\mathbf {C}\) has a guarded Conway recursion operator iff \(\mathbf {C}\) is a Conway category [13], i.e. models standard total recursion.
-
3.
The guarded Cartesian category of complete metric spaces as in Example 9 is traced: For \(f:X\times Y\rightarrow ^{\mathsf {pr}_2} Y\), define \(f^\dagger (x)\) as the unique fixpoint of \(\lambda y.\,f(x,y)\) according to Banach’s fixpoint theorem.
-
4.
Similarly, the topos of trees, ideally guarded as in Example 24, has a guarded Conway recursion operator obtained by taking unique fixpoints [7, Theorem 2.4].
-
5.
The guarded co-Cartesian category \(\mathbf {C}_{\mathbb {T}_{\varSigma }}\) of side-effecting processes (Example 8) has a guarded Conway iteration operator obtained by taking unique fixpoints, thanks to the universal property of the final coalgebra \(T_{\varSigma }X\) [32].
Guarded vs. Unguarded Recursion. We proceed to present a class of examples relating guarded and unguarded recursion. For motivation, consider the category \((\mathbf {Cpo},\times ,1)\) of complete partial orders (cpos) and continuous maps. This category nearly supports recursion via least fixpoints, except that, e.g., \(\mathsf {id}:X\rightarrow X\) only has a least fixpoint if X has a bottom. The following equivalent approaches involve the lifting monad \(({-})_{\bot }\), which adjoins a fresh bottom \(\bot \) to a given \(X\in |\mathbf {Cpo}|\).
-
Classical approach [38, 39]: Define a total recursion operator \((-)_\ddagger \) on the category \(\mathbf {Cpo}_{\bot }\) of pointed cpos and continuous maps, using least fixpoints.
-
Guarded approach (cf. [28]): Extend \(\mathbf {Cpo}\) to a guarded category:
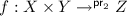 iff \(f\in \{g(\mathsf {id}\times \eta )\mid g:X\times Y_{\bot }\rightarrow Z\}\) (see Proposition 22), and define a guarded recursion operator sending
iff \(f\in \{g(\mathsf {id}\times \eta )\mid g:X\times Y_{\bot }\rightarrow Z\}\) (see Proposition 22), and define a guarded recursion operator sending 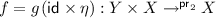 to \(f_{\dagger } = g\langle \mathsf {id},\hat{f}\rangle :Y\rightarrow X\) with \(\hat{f}(y)\in X_{\bot }\) calculated as the least fixpoint of \(\lambda z.\, \eta g(y, z)\).
to \(f_{\dagger } = g\langle \mathsf {id},\hat{f}\rangle :Y\rightarrow X\) with \(\hat{f}(y)\in X_{\bot }\) calculated as the least fixpoint of \(\lambda z.\, \eta g(y, z)\).
Pointed cpos happen to be always of the form \(X_{\bot }\) with \(X\in |\mathbf {Cpo}|\), which indicates that \(({-})_{\ddagger }\) is a special case of \(({-})_{\dagger }\). This is no longer true in more general cases when the connection between \(({-})_{\ddagger }\) and \(({-})_{\dagger }\) is more intricate. We show that \(({-})_{\ddagger }\) and \(({-})_{\dagger }\) are nevertheless equivalent under reasonable assumptions.
Definition 34
([11]). A let-ccc with a fixpoint object is a tuple \((\mathbf {C}, \mathbb {T}, \varOmega , \omega )\), consisting of a Cartesian closed category \(\mathbf {C}\), a strong monad \(\mathbb {T}\) on it, an initial T-algebra \((\varOmega ,\mathsf {in})\) and an equalizer \(\omega :1\rightarrow \varOmega \) of \(\mathsf {in}\ \eta :\varOmega \rightarrow \varOmega \) and \(\mathsf {id}:\varOmega \rightarrow \varOmega \).
The key requirement is the last one, satisfied, e.g., for \(\mathbf {Cpo}\) and the lifting monad. Given a monad \(\mathbb {T}\) on \(\mathbf {C}\), \(\mathbf {C}^{\mathbb {T}}_{\star }\) denotes the category of \(\mathbb {T}\)-algebras and \(\mathbf {C}\)-morphisms (instead of \(\mathbb {T}\)-algebra homomorphisms).
Proposition 35
([37, Theorem 4.6]). Let \((\mathbf {C}, \mathbb {T}, \varOmega , \omega )\) be a let-ccc with a fixpoint object. Then \(\mathbf {C}^{\mathbb {T}}_{\star }\) has a unique \(\mathbf {C}^{\mathbb {T}}\)-uniform recursion operator \(({-})_{\ddagger }\).
By [38, Theorem 4], the operator \(({-})_{\ddagger }\) in Proposition 35 is Conway, in particular, by Lemma 31, squarable, if \(\mathbf {C}\) has a natural numbers object and \(\mathbb {T}\) is an equational lifting monad [10], such as \((-)_\bot \). There are however further squarable operators obtained via Proposition 35, e.g. for the partial state monad \(TX = {(X\times S)^S_{\bot }}\) [11]. By Lemma 31, the following result applies in particular in the setup of Proposition 35 under the additional assumption of squarability.
Theorem 36
Let \(\mathbb {T}\) be a strong monad on a Cartesian category \(\mathbf {C}\). The following gives a bijective correspondence between squarable dinatural recursive operators \(({-})_{\ddagger }\) on \(\mathbf {C}^\mathbb {T}_\star \) and squarable dinatural guarded recursive operators \(({-})_{\dagger }\) on \(\mathbf {C}\) ideally guarded over  :
:

(in (5) we call on a slight extension of \(({-})_{\ddagger }\); the right hand side of (4) is defined because \(\eta f(\mathsf {id}\times a)\) factors as \(\eta f(\mathsf {id}\times a(Ta)\eta )\)). Moreover, \(({-})_\dagger \) is Conway iff so is \(({-})_\ddagger \).
6 Vacuous Guardedness and Nuclear Ideals
We proceed to discuss traces in vacuously guarded categories (Lemma 3), and show that the partial trace operation in the category of (possibly infinite-dimensional) Hilbert spaces [2] in fact lives over the vacuous guarded structure. We first note that vacuous guarded structures are traced as soon as a simple rewiring operation satisfies a suitable well-definedness condition (similar to one defining traced nuclear ideals [2, Definition 8.14]):
Proposition 37
Let \((\mathbf {C},\mathbin {\otimes },I)\) be vacuously guarded. If for  with factorization \(f=(h\mathbin {\otimes }\mathsf {id}_{D\mathbin {\otimes }U})(\mathsf {id}_{A\mathbin {\otimes }U}\mathbin {\otimes }g)\) (eliding associativity), \(g:B\rightarrow E\mathbin {\otimes }D\mathbin {\otimes }U\), \(h:A \mathbin {\otimes }U\mathbin {\otimes }E\rightarrow C\) as per Lemma 3, the composite
with factorization \(f=(h\mathbin {\otimes }\mathsf {id}_{D\mathbin {\otimes }U})(\mathsf {id}_{A\mathbin {\otimes }U}\mathbin {\otimes }g)\) (eliding associativity), \(g:B\rightarrow E\mathbin {\otimes }D\mathbin {\otimes }U\), \(h:A \mathbin {\otimes }U\mathbin {\otimes }E\rightarrow C\) as per Lemma 3, the composite
depends only on f, then \(\mathbf {C}\) is guarded traced, with \(\mathsf {tr}^U_{A,B,C,D}(f)\) defined as (6).
Diagrammatically, the trace in a vacuously guarded category is thus given by

We proceed to instantiate the above to Hilbert spaces. On a more abstract level, a dagger symmetric monoidal category [35] (or tensored \(*\)-category [2]) is a symmetric monoidal category \((\mathbf {C},\mathbin {\otimes },I)\) equipped with an identity-on-objects strictly involutive functor \(({-})^\dagger :\mathbf {C}\rightarrow \mathbf {C}^{op}\) coherently preserving the symmetric monoidal structure. The main motivation for dagger symmetric monoidal categories is to capture categories that are similar to (dagger) compact closed categories in that they admit a canonical trace construction for certain morphisms, but fail to be closed, much less compact closed. The “compact closed part” of a dagger symmetric monoidal category is axiomatized as follows.
Definition 38
(Nuclear Ideal, [2]). A nuclear ideal \(\mathsf {N}\) in a dagger symmetric monoidal category \((\mathbf {C},\mathbin {\otimes }, I, ({-})^\dagger )\) is a family of subsets \(\mathsf {N}(X,Y)\subseteq \mathsf {Hom}_{\mathbf {C}}(X,Y)\), \(X,Y\in |\mathbf {C}|\), satisfying the following conditions:
-
1.
\(\mathsf {N}\) is closed under \(\mathbin {\otimes }\), \(({-})^\dagger \), and composition with arbitrary morphisms on both sides;
-
2.
There is a bijection \(\theta :\mathsf {N}(X,Y)\rightarrow \mathsf {Hom}_{\mathbf {C}}(I,X^\dagger \mathbin {\otimes }Y)\), natural in X and Y, coherently preserving the dagger symmetric monoidal structure.
-
3.
(Compactness) For \(f\in \mathsf {N}(B,A)\) and \(g\in \mathsf {N}(B,C)\), the following diagram commutes:
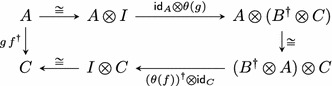
The above definition is slightly simplified in that we elide a covariant involutive functor \(\overline{({-})}:\mathbf {C}\rightarrow \mathbf {C}\), capturing, e.g. complex conjugation; i.e., we essentially restrict to spaces over the reals.
We proceed to present a representative example of a nuclear ideal in the category of Hilbert spaces. Recall that a Hilbert space [23] H over the field \(\varvec{\mathsf {R}}\) of reals is a vector space with an inner product \(\langle {-},{-}\rangle :H\times H\rightarrow \varvec{\mathsf {R}}\) that is complete as a normed space under the induced norm  . Let \(\mathbf {Hilb}\) be the category of Hilbert spaces and bounded linear operators.
. Let \(\mathbf {Hilb}\) be the category of Hilbert spaces and bounded linear operators.
Clearly, \(\varvec{\mathsf {R}}\) itself is a Hilbert space; linear operators \(X\rightarrow \varvec{\mathsf {R}}\) are conventionally called functionals. More generally, we consider (multi-)linear functionals \(X_1\times \ldots \times X_n\rightarrow \varvec{\mathsf {R}}\), i.e. maps that are linear in every argument. Such a functional is bounded if  for some constant \(c\in \varvec{\mathsf {R}}\). We can move between bounded linear operators and bounded linear functionals, similarly as we can move between relations and functions to the Booleans:
for some constant \(c\in \varvec{\mathsf {R}}\). We can move between bounded linear operators and bounded linear functionals, similarly as we can move between relations and functions to the Booleans:
Proposition 39
([23, Theorem 2.4.1]). Given a bounded linear operator \(f:X\rightarrow Y\), \(f^\circ (x,y) = \langle fx, y\rangle \) defines a bounded linear functional \(f^\circ \), and every bounded linear functional \(X\times Y\rightarrow \varvec{\mathsf {R}}\) arises in this way.
Definition 40
(Hilbert-Schmidt operators/functionals). A bounded linear functional \(f:X_1\times \ldots \times X_n\rightarrow \varvec{\mathsf {R}}\) is Hilbert-Schmidt if the sum
is finite for some, and then any, orthonormal bases \(B_1,\ldots ,B_n\) of \(X_1,\ldots ,X_n\), respectively. A bounded linear operator \(f:X\rightarrow Y\) is Hilbert-Schmidt if the induced functional \(f^\circ \) (Proposition 39) is Hilbert-Schmidt, equivalently if  is finite for some, and then any, orthonormal basis B of X. We denote by \(\mathsf {HS}(X,Y)\) the space of all Hilbert-Schmidt operators from X to Y.
is finite for some, and then any, orthonormal basis B of X. We denote by \(\mathsf {HS}(X,Y)\) the space of all Hilbert-Schmidt operators from X to Y.
For \(X,Y\in |\mathbf {Hilb}|\), the space of Hilbert-Schmidt functionals \(X\times Y\rightarrow \varvec{\mathsf {R}}\) is itself a Hilbert space, denoted \(X\mathbin {\otimes }Y\), with the pointwise vector space structure and the inner product \(\langle f,g\rangle = \sum \nolimits _{x\in B}\sum \nolimits _{y\in B'} f(x, y)g(x, y)\) where B and \(B'\) are orthonormal bases of X and Y, respectively. By virtue of the equivalence between f and \(f^\circ \), this induces a Hilbert space structure on \(\mathsf {HS}(X,Y)\), with induced norm \({{\Vert f\Vert }_2} =\sqrt{\sum \nolimits _{x\in B} {\Vert fx\Vert ^2}}\). The operator \(\mathbin {\otimes }\) forms part of a dagger symmetric monoidal structure on \(\mathbf {Hilb}\), with unit \(\varvec{\mathsf {R}}\). For a bounded linear operator \(f:X\rightarrow Y\), \(f^\dagger :Y\rightarrow X\) is the adjoint operator uniquely determined by equation \(\langle x, f^\dagger y\rangle = \langle fx, y\rangle \). The tensor product of \(f:A\rightarrow B\) and \(g:C\rightarrow D\) is the functional sending \(h:A\times C\rightarrow \varvec{\mathsf {R}}\) to \(h(f^\dagger \times g^\dagger ):B\times D\rightarrow \varvec{\mathsf {R}}\). Given \(a\in A\) and \(c\in C\), let us denote by  the functional \((a',c')\mapsto \langle a,a'\rangle \langle c,c'\rangle \), and so, with the above f and g, \((f\mathbin {\otimes }g)(a\mathbin {\otimes }c) = f(a)\mathbin {\otimes }g(c)\).
the functional \((a',c')\mapsto \langle a,a'\rangle \langle c,c'\rangle \), and so, with the above f and g, \((f\mathbin {\otimes }g)(a\mathbin {\otimes }c) = f(a)\mathbin {\otimes }g(c)\).
Proposition 41
([2]). The Hilbert-Schmidt operators form a nuclear ideal in \(\mathbf {Hilb}\) with \(\theta :\mathsf {HS}(X,Y)\cong \mathsf {Hom}(\varvec{\mathsf {R}},X^\dagger \mathbin {\otimes }Y)\) defined by
A crucial fact underlying the proof of Proposition 41 is that \(\mathsf {HS}(X,Y)\) is isomorphic to \(X^\dagger \mathbin {\otimes }Y\), naturally in X and Y. We emphasize that what makes the case of \(\mathbf {Hilb}\) significant is that we do not restrict to finite-dimensional Hilbert spaces. In that case all bounded linear operators would be Hilbert-Schmidt and the corresponding category would be (dagger) compact closed [35]. In the infinite-dimensional case, identities need not be Hilbert-Schmidt, so \(\mathsf {HS}\) is indeed only an ideal and not a subcategory.
Let \(\mathsf {N}^2(X,Y) = \{g^\dagger h:X\rightarrow Y\mid h\in \mathsf {N}(X,Z), g\in \mathsf {N}(Y,Z)\}\) for any nuclear ideal \(\mathsf {N}\). The main theorem of the section now can be stated as follows.
Theorem 42
-
1.
The guarded ideal induced by the vacuous guarded structure on \(\mathbf {Hilb}\) (see (1)) is precisely \(\mathsf {HS}^2\), and \(\mathbf {Hilb}\) is guarded traced over \(\mathsf {HS}^2\).
-
2.
Guarded traces in \(\mathbf {Hilb}\) commute with \((-)^\dagger \) in the sense that if \(f\in \mathsf {Hom}^{\bullet }((A\mathbin {\otimes }U)\mathbin {\otimes }B,C\mathbin {\otimes }(D\mathbin {\otimes }U))\), then \(\gamma _{B,A\mathbin {\otimes }U} f^\dagger \gamma _{D\mathbin {\otimes }U,C}\in \mathsf {Hom}^{\bullet }((D\mathbin {\otimes }U)\mathbin {\otimes }C,B\mathbin {\otimes }(A\mathbin {\otimes }U))\) and \(\mathsf {tr}^U_{D,C,B,A}(\gamma _{B,A\mathbin {\otimes }U} f^\dagger \gamma _{D\mathbin {\otimes }U,C}) = \gamma _{A,B}(\mathsf {tr}_{A,B,C,D}^U(f))^\dagger \gamma _{C,D}\).
Clause 1 is a generalization of the result in [2, Theorem 8.16] to parametrized traces. Specifically, we obtain agreement with the conventional mathematical definition of trace: given \(f\in \mathsf {HS}^2(X,X)\), \(\mathsf {tr}(f) = \sum _i \langle f(e_i), e_i\rangle \) for any choice of an orthonormal basis \((e_i)_i\), and \(\mathsf {HS}^2(X,X)\) contains precisely those f for which this sum is absolutely convergent independently of the basis.
7 Conclusions and Further Work
We have presented and investigated a notion of abstract guardedness and guarded traces, focusing on foundational results and important classes of examples. We have distinguished a more specific notion of ideal guardedness, which in many respects appears to be better behaved than the unrestricted one, in particular ensures closer agreement between structural and geometric guardedness. An unexpectedly prominent role is played by ‘vacuous’ guardedness, characterized by the absence of paths connecting unguarded inputs to guarded outputs; e.g., partial traces in Hilbert spaces [2] turn out to be based on this form of guardedness. Further research will concern a coherence theorem for guarded traced categories generalizing the well-known unguarded case [22, 34], and a generalization of the Int-construction [22], which would relate guarded traced categories to a suitable guarded version of compact closed categories. Also, we plan to investigate guarded traced categories as a basis for generalized Hoare logics, extending and unifying previous work [5, 15].
References
Abel, A., Pientka, B.: Wellfounded recursion with copatterns: a unified approach to termination and productivity. In: International Conference on Functional Programming, ICFP 2013, pp. 185–196. ACM (2013)
Abramsky, S., Blute, R., Panangaden, P.: Nuclear and trace ideals in tensored*-categories. J. Pure Appl. Algebra 143, 3–47 (1999)
Abramsky, S., Coecke, B.: A categorical semantics of quantum protocols. In: Logic in Computer Science, LICS 2004, pp. 415–425. IEEE Computer Society (2004)
Abramsky, S., Haghverdi, E., Scott, P.: Geometry of interaction and linear combinatory algebras. Math. Struct. Comput. Sci. 12(5), 625–665 (2002)
Arthan, R., Martin, U., Mathiesen, E., Oliva, P.: A general framework for sound and complete Floyd-Hoare logics. ACM Trans. Comput. Log. 11, 7:1–7:31 (2009)
Baeten, J., Basten, T., Reniers, M.: Process Algebra: Equational Theories of Communicating Processes. Cambridge University Press, Cambridge (2010)
Birkedal, L., Møgelberg, R., Schwinghammer, J., Støvring, K.: First steps in synthetic guarded domain theory: step-indexing in the topos of trees. Log. Methods Comput. Sci. 8(4:1), 1–45 (2012)
Blute, R., Cockett, R., Seely, R.: Feedback for linearly distributive categories: traces and fixpoints. J. Pure Appl. Algebra 154, 27–69 (2000)
Book, R., Greibach, S.: Quasi-realtime languages. Math. Syst. Theory 4(2), 97–111 (1970)
Bucalo, A., Führmann, C., Simpson, A.: An equational notion of lifting monad. Theoret. Comput. Sci. 294, 31–60 (2003)
Crole, R., Pitts, A.: New foundations for fixpoint computations. In: Logic in Computer Science, LICS 1990, pp. 489–497. IEEE Computer Society (1990)
Ésik, Z.: Axiomatizing iteration categories. Acta Cybern. 14(1), 65–82 (1999)
Ésik, Z.: Equational properties of fixed point operations in Cartesian categories: an overview. In: Italiano, G.F., Pighizzini, G., Sannella, D.T. (eds.) MFCS 2015. LNCS, vol. 9234, pp. 18–37. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48057-1_2
Girard, J.-Y.: Towards a geometry of interaction. Contemp. Math. 92(69–108), 6 (1989)
Goncharov, S., Schröder, L.: A relatively complete generic Hoare logic for order-enriched effects. In: Proceedings of 28th Annual Symposium on Logic in Computer Science (LICS 2013), pp. 273–282. IEEE (2013)
Goncharov, S., Schröder, L., Rauch, C., Piróg, M.: Unifying guarded and unguarded iteration. In: Esparza, J., Murawski, A.S. (eds.) FoSSaCS 2017. LNCS, vol. 10203, pp. 517–533. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54458-7_30
Haghverdi, E., Scott, P.: Towards a typed geometry of interaction. Math. Struct. Comput. Sci. 20, 473–521 (2010)
Hasegawa, M.: Recursion from cyclic sharing: traced monoidal categories and models of cyclic lambda calculi. In: de Groote, P., Roger Hindley, J. (eds.) TLCA 1997. LNCS, vol. 1210, pp. 196–213. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-62688-3_37
Hasegawa, M.: Models of Sharing Graphs: A Categorical Semantics of let and letrec. Distinguished Dissertations. Springer, London (1999). https://doi.org/10.1007/978-1-4471-0865-8
Jeffrey, A.: Premonoidal categories and flow graphs. In: Higher-Order Operational Techniques in Semantics, HOOTS 1997, vol. 10 of ENTCS, p. 51. Elsevier (1997)
Jeffrey, A.: LTL types FRP: linear-time temporal logic propositions as types, proofs as functional reactive programs. In: Programming Languages Meets Program Verification, PLPV 2012, pp. 49–60. ACM (2012)
Joyal, A., Street, R., Verity, D.: Traced monoidal categories. Math. Proc. Camb. Philos. Soc. 119, 447–468 (1996)
Kadison, R., Ringrose, J.: Fundamentals of the Theory of Operator Algebras: Advanced Theory, vol. 2. AMS (1997)
Krishnaswami, N., Benton, N.: Ultrametric semantics of reactive programs. In: Logic in Computer Science, LICS 2011, pp. 257–266. IEEE Computer Society (2011)
MacLane, S.: Categories for the Working Mathematician. Springer, New York (1971). https://doi.org/10.1007/978-1-4612-9839-7
Malherbe, O., Scott, P.J., Selinger, P.: Partially traced categories. J. Pure Appl. Algebra 216, 2563–2585 (2012)
Milius, S.: Completely iterative algebras and completely iterative monads. Inf. Comput. 196, 1–41 (2005)
Milius, S., Litak, T.: Guard your daggers and traces: properties of guarded (co-)recursion. Fund. Inf. 150, 407–449 (2017)
Milner, R.: Communication and Concurrency. Prentice-Hall Inc., Upper Saddle River (1989)
Møgelberg, R.: A type theory for productive coprogramming via guarded recursion. In: Computer Science Logic/Logic in Computer Science, CSL-LICS 2014, pp. 71:1–71:10. ACM (2014)
Moggi, E.: Notions of computation and monads. Inf. Comput. 93, 55–92 (1991)
Piróg, M., Gibbons, J.: The coinductive resumption monad. In: Mathematical Foundations of Programming Semantics, MFPS 2014. ENTCS, vol. 308, pp. 273–288 (2014)
Rutten, J.: Universal coalgebra: a theory of systems. Theoret. Comput. Sci. 249, 3–80 (2000)
Selinger, P.: Towards a quantum programming language. Math. Struct. Comput. Sci. 14, 527–586 (2004)
Selinger, P.: Dagger compact closed categories and completely positive maps. In: Quantum Programming Languages, QPL 2005. ENTCS, vol. 170, pp. 139–163. Elsevier (2007)
Selinger, P.: A survey of graphical languages for monoidal categories. In: Coecke, B. (ed.) New Structures for Physics. Lecture Notes in Physics, vol. 813, pp. 289–355. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-12821-9_4
Simpson, A.: Recursive types in Kleisli categories. Technical report, University of Edinburgh (1992)
Simpson, A., Plotkin, G.: Complete axioms for categorical fixed-point operators. In: Logic in Computer Science, LICS 2000, pp. 30–41 (2000)
Winskel, G.: The Formal Semantics of Programming Languages. MIT Press, Cambridge (1993)
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made. The images or other third party material in this book are included in the book's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the book's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Goncharov, S., Schröder, L. (2018). Guarded Traced Categories. In: Baier, C., Dal Lago, U. (eds) Foundations of Software Science and Computation Structures. FoSSaCS 2018. Lecture Notes in Computer Science(), vol 10803. Springer, Cham. https://doi.org/10.1007/978-3-319-89366-2_17
Download citation
DOI: https://doi.org/10.1007/978-3-319-89366-2_17
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-89365-5
Online ISBN: 978-3-319-89366-2
eBook Packages: Computer ScienceComputer Science (R0)









 ;
; ,
, 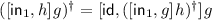 for
for 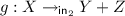 and
and  ;
; for
for  .
.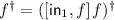 for
for 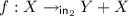 ;
; ,
,  and
and  iff
iff  for some
for some 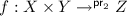 iff
iff 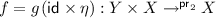 to
to