Keywords

1 Introduction

Texture analysis has playing a preponderant role in computer vision since the birth of this research field. Although a texture image does not have a unique definition, it is an attribute easily perceived by humans. In general words, textures are images composed of sub-patterns, which can be pixels, regions or visual attributes (shape, color etc.) [1]. Obviously, such concept does not address a vast range of natural textures, such as images of smoke, mammography, bark, water etc., which present a persistent stochastic pattern [2].

Throughout the years, increasingly accurate methods have been proposed for extracting signatures from texture images. As a consequence, these methods have also been applied successfully in several domains, providing expert systems for many human activities. In the medicine field, for instance, we can cite: the paper [3] performed a combination of texture measures for meningioma classification, the papers [4, 5] applied several LBP variants to classify a database of images from the cervix (pap-smear dataset [6]); in the biology field: the paper [7] applied Gabor wavelets to analyze texture images of leaf surfaces; and in industry area: the paper [8] proposed to apply a texture extraction method based on LBP and GLCM to classify tea leaves in order to improve real-time controls of tea production lines.

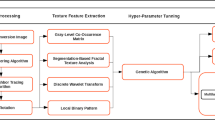
This paper aims to apply a recent and powerful texture analysis method to the analysis of images of titanium alloys, which is a very relevant problem of metallography. For this purpose, this work is organized as follows: Sect. 2 briefly describes what is metallography and the study of titanium alloys; Sect. 3 describes the randomized neural network based signature used for classifying the titanium alloy images; Sect. 4 shows all the details of the performed experiments; Sect. 5 presents the obtained results and a discussion on them; and, finally, Sect. 6 establishes some remarks about this work.

2 Metalography and Titanium Alloy

Metallography can be defined as the study of the physical properties of metals based on the inspection of their constituents. This inspection can be performed by naked eye, or, more accurately, by using optical or electron microscopes, which allow us to examine the metal microstructures [9]. In the context of this work, we focus on the microstructures of an important category of metal called “titanium alloy Ti-6Al-4V”, which has been used, for instance, in aerospace industry and medical prostheses. This type of alloy presents two phases, called “alpha” and “beta”, which are hexagonal and cubic structures, respectively, and determine the physical properties of the metal.

Fig. 1.
figure 1

(images provided by the authors of the paper [9]).

Samples of titanium alloy Ti-6Al-4V: (a) - class Alpha and Beta; (b) - class Alpha + Beta

Full size image

When titanium alloys Ti-6Al-4V are subjected to Friction Stir Welding (FSW) [10], which is a solid-state joining technique, the resulting product presents microstructure zones that can be grouped into two classes. The first class, called here “alpha and beta”, is composed of noise-like microstructures, which presents grains of alpha and beta. The second class, called here “alpha + beta”, is composed of crystal-like microstructures presented in the deformed weld zones [9]. Because these two categories of microstructures have different physical properties, classifying them correctly is an important problem in metallography. Figure 1 shows one example for each class.

3 Texture Analysis Using Randomized Neural Network

3.1 Random Neural Network

A randomized neural network [11,12,13,14] is a type of neural network with only two layers (hidden and output) and a very fast learning algorithm when compared to the traditional backpropagation approach. Basically, the weights of the hidden neurons are randomly determined according to a uniform or a Gaussian distribution, and the weights of the output neurons are calculated using a least-squares solution. Next, a variant of this neural network, which was used in [15], is briefly explained.

Let \(X=\left[ {{\varvec{x}}_\mathbf{1}}, {{\varvec{x}}_\mathbf{2}}, \dots , {{\varvec{x}}_{{\varvec{N}}}}\right] \) (each \({{\varvec{x}}_{{\varvec{i}}}}\) has a constant \(x_{i0}=-1\) to connect it to the biases of the neurons) be a matrix containing N feature vectors used for training and \(D=\left[ {{\varvec{d}}_\mathbf{1}}, {{\varvec{d}}_\mathbf{2}}, \dots , {{\varvec{d}}_{{\varvec{N}}}}\right] \) be a matrix with their respective label vectors. First, it is necessary to assign random values (uniform or Gaussian) to the weights of the hidden layer. These weights can be arranged in a matrix W, where each line represents the weights of a determined hidden neuron \(q \in \{1,2,\ldots ,Q\}\) (the weights \(w_{q0}\) of the first column are the biases of each hidden neuron and Q is the number of hidden neurons).

$$\begin{aligned} W=\left( \begin{array}{ccccc} w_{10} &{} w_{11} &{} \ldots &{} w_{1p} \\ w_{20} &{} w_{21} &{} \ldots &{} w_{2p} \\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ w_{Q0} &{} w_{Q1} &{} \ldots &{} w_{Qp} \\ \end{array} \right) \end{aligned}$$
(1)

The next step is to calculate \(Z=\phi (WX)\) (\(\phi \) is the activation function, which can be, for instance, the tangential or hyperbolic function) in order to obtain the output of the hidden neurons for each feature vector \({{\varvec{x}}_{{\varvec{i}}}}\). This new matrix \(Z=\left[ {{\varvec{z}}_\mathbf{1}}, {{\varvec{z}}_\mathbf{2}}, \dots , {{\varvec{z}}_{{\varvec{N}}}}\right] \), where each \({{\varvec{z}}_{{\varvec{i}}}}\) corresponds to each \({{\varvec{x}}_{{\varvec{i}}}}\), can be used for obtaining the weights of the output neurons. For this purpose, a constant \(-1\) is again added to each vector \({{\varvec{z}}_{{\varvec{i}}}}\) to connect it to the biases of the output neurons. Next, the weights of the output neurons are arranged in a matrix M, where each line is the weights of a specific output neuron. Finally, the weights of the output layer (arranged in a matrix M) can be computed by the following equation

$$\begin{aligned} M=DZ^{T}(ZZ^{T})^{-1}. \end{aligned}$$
(2)

3.2 Randomized Neural Network Based Signature

To use the weights of the output neurons as an image signature, the first step is to divide the image into windows \(K\times K\) (K is odd) and consider the central pixel as a label vector \({{\varvec{d}}_{{\varvec{i}}}}\) and the neighboring pixels as the feature vector \({{\varvec{x}}_{{\varvec{i}}}}\). For this purpose, the paper [15] adopted \(K=\{3,5,7\}\), which determined a circular neighborhood composed of pixels with distance less than or equal to \(\sqrt{2}, \sqrt{8}\) and \(\sqrt{13}\), respectively.

In order to make the method robust to rotation, a specific fixed mask is multiplied by every rotation of the neighboring pixels, thus resulting in several linear combinations (for instance, eight linear combinations for neighborhood \(\sqrt{2}\)). Thus, the linear combination with the minimum value determines the order of the pixels in the feature vector \({{\varvec{x}}_{{\varvec{i}}}}\). The paper [15] proposes the masks \(\left[ 2^{1.0}, 2^{2.0}, 2^{3.0}, \ldots , 2^{8.0}\right] , \left[ 2^{1.0}, 2^{1.6}, 2^{2.2}\ldots , 2^{7.6}\right] \), and \(\left[ 2^{1.0}, 2^{1.4}, 2^{1.8}\ldots , 2^{7.0}\right] \) for the windows \(3\times 3, 5\times 5\) and \(7\times 7\), respectively.

The next step of the algorithm is to assign values to the matrix W. In every training phase of a randomized neural network, different random values are assigned to the weights of the hidden layer, so that the outputs of the neural network are not necessary the same for the same input vectors. In an image such effect is undesirable because a texture analysis method must provide the same signature for the same input image. Thus, the paper [15] used the classical linear congruent generator (LCG) [16, 17] with fixed values of “seed” and “adjustment parameters” to generate pseudorandom uniform numbers for the matrix W. Lastly, all the weights of the matrix W and each line of the matrix X are normalized to zero mean and unit variance.

Taking into account all the presented procedures, the feature vector is obtained by the equation \({\varvec{f}}=DZ^{T}(ZZ^{T})^{-1}\). Based on this feature vector, it is possible to construct two image signatures. The first is

$$\begin{aligned} \varvec{\varTheta }(Q)_{K_1, K_2, \ldots , K_n}=\left[ {\varvec{f}}_{K_1}, {\varvec{f}}_{K_2}, \ldots , {\varvec{f}}_{K_n}\right] , \end{aligned}$$
(3)

where K is the window size used to divide the image.

The second signature can be expressed as the concatenation of the previous signature for different numbers of hidden neurons, that is,

$$\begin{aligned} \varvec{\varPsi }_{Q_1,Q_2,\ldots ,Q_m}=\left[ \varvec{\varTheta }(Q_1)_{K_1,\ldots , K_n}, \varvec{\varTheta }(Q_2)_{K_1, \ldots , K_n}, \ldots , \varvec{\varTheta }(Q_m)_{K_1, \ldots , K_n} \right] . \end{aligned}$$
(4)

More details on this algorithm can be found in the paper [15].

4 Experiments

Our database was kindly provided by the authors of the paper [9] and consists of 30 images \(1079 \times 816\) pixel size equally divided into two classes (“alpha and beta” and “alpha + beta”). To construct a new database for our experiments, we followed the same procedure of the paper [9], that is, we divided each image into a grid of \(13\, \times \, 10\) windows \(80 \times 80\) pixel size and discarded the residual pixels of the borders. Also, we converted the images into grayscale. Thus, each class contains 1950 images \(80 \,\times \, 80\) pixel size. Figure 2 shows some samples of both classes.

Fig. 2.
figure 2

(images provided by the authors of the paper [9]).

Samples \(80 \times 80\) pixel size of titanium alloy Ti-6Al-4V: first line - class Alpha and Beta; second line - class Alpha + Beta

Full size image

In the experiments, we used the algorithm proposed by Sá Junior and Backes [15] with the same parameter values (\(K=\{3,5,7\}, W\) determined by LCG and \(Q=\{19,39\}\) for the second type of signature, that is, \(\varvec{\varPsi }_{19,39}\)). We also compared the method with other very important grayscale texture analysis methods, which are:

  • Gabor wavelets: we used the same parameter values adopted in the paper [18], that is, 6 rotations, 4 scales, and minimum and maximum frequencies of 0.05 and 0.4, respectively. The paper [18] proposes a mathematical rule to obtain \(\sigma _x\) and \(\sigma _y\) of the Gabor filters according to the parameters above. The feature vector is constructed using the mean and standard deviation of the magnitude of the transform coefficients, thus resulting in a signature with 48 attributes.

  • Co-occurrence matrices: this is a classical algorithm that computes the “co-occurrence” of pairs of pixels at determined orientation and distance [19]. For the experiments, we used the most common distances (\(d=1\) and \(d=2\)) and orientations (\(0^{\circ }, -45^{\circ }, 90^{\circ }\) and \(135^{\circ }\)) and non-symmetric matrices. The descriptors extracted were energy and entropy, totaling 16 attributes.

  • Tourist walk [20, 21]: this method considers each image pixel as a city. A tourist starting at determined city must visit the neighboring cities according to a deterministic rule of going to the nearest or farthest city not visited in the last \(\mu \) time steps. Because of this, the tourist’s path has two elements: a transient time t (new cities are visited) and a cycle of period p (the tourist is trapped in a cycle and, therefore, visits the same cities). The next step is to construct a joint distribution map of transient times p and periods p for a determined memory \(\mu \). To obtain the feature vector, we adopted the strategy of concatenation of histograms presented in the paper [20] using \(m=4\) and memories \(\mu =\{0,1,2,\ldots ,5\}\) for the rule of going to the nearest and farthest city. The resulting signature has 48 attributes.

  • Wavelet descriptors [22, 23]: we used the multilevel 2D wavelet and performed three dyadic decompositions using Daubechies 4. Next, we computed energy and entropy from each vertical, horizontal and diagonal details, totaling a feature vector of 18 attributes.

For the classification, we used a linear discriminant analysis (LDA) with a leave-one-out cross validation strategy [24]. We also performed a comparison “similar” to that of the paper [9] by using a radial basis SVM as classifier and the precision as performance measure. For this purpose, we used the LIBSVM [25], which is a public library for SVM. We adopted as SVM parameters the default values of C and \(\gamma \) of this library (the paper [9] adopted \(C=1\) and \(\gamma =1\), which give the best results). The validation strategy adopted was the holdout (50% of the samples for training and the remainder for testing) with 100 repetitions, according to the paper [9].

Unfortunately, it was not possible to recover the same database used in the experiment of the paper [9] (the authors used 20 images - 10 images per class - from an original database with more than 150 images \(1079 \times 816\) pixel size to construct a database of 2600 images \(80 \times 80\) pixel size). However, we believe that our imperfect comparison can still confirm the high performance of the randomized neural network method.

5 Results and Discussion

Table 1 shows the comparison of the randomized neural network based signature against all the compared texture analysis methods proposed in this paper. The results clearly confirm the high performance of the randomized neural network method, since it surpassed the second best method (Gabor wavelets) in 2.28% of samples correctly classified, that is, 89 more images. When we consider the remainder methods, the difference of accuracy becomes absolutely evident. For instance, the tourist walk method, which presents a state-of-the-art approach, obtained only 86.00% of accuracy, that is, 12.84% (501 images) less than the randomized neural network based signature.

Table 1. Comparison results of different methods applied to the titanium alloy Ti-6Al-4V database - LDA classifier with leave-one-out cross validation.
Full size table

The only apparent drawback of the randomized neural network based signature is its high number of features (180) when compared to the other methods. It happens because the same parameter values of the paper [15] were adopted in order to avoid tuning the parameters of the randomized neural network, which would result in an unfair comparison with the other approaches. However, if we use the signature \(\varvec{\varPsi }_{19}\), which contains only 60 features, the obtained accuracy is 98.00%, that is, a result almost equal to that obtained by the signature \(\varvec{\varPsi }_{19,39}\) and equally overcoming all the compared methods.

When we performed the experiment “similar” to that of the paper [9], the results were: accuracy of 98.64%, precision of 99.11% for “alpha and beta”, and precision of 98.09% for “alpha + beta”. Our results of precision were superior to the best values presented in the paper [9], which obtained approximately 84.00% of precision for “alpha and beta” and almost 95.00% for “alpha + beta”. This performance demonstrates that the randomized neural network based signature is very suitable for classifying samples of titanium alloy Ti-6Al-4V, and, therefore, can be a useful tool for metallography.

6 Conclusion

This paper presented an application of a very discriminative state-of-the-art texture analysis method to an important problem of metallography. The results obtained are very promising, surpassing several compared methods as well as the results of a recent work that addresses the same problem. Thus, the obtained performance suggests that the randomized neural network based signature can be a valuable tool for other relevant problems of metallography.