New Key Recovery Attacks on Minimal Two-Round Even-Mansour Ciphers

Abstract

We propose new key recovery attacks on the two minimal two-round n-bit Even-Mansour ciphers that are secure up to $2^{2n/3}$ queries against distinguishing attacks proved by Chen et al. Our attacks are based on the meet-in-the-middle technique which can significantly reduce the data complexity. In particular, we introduce novel matching techniques which enable us to compute one of the two permutations without knowing a part of the key information. Moreover, we present two improvements of the proposed attack: one significantly reduces the data complexity and the other reduces the time complexity. Compared with the previously known attacks, our attack first breaks the birthday barrier on the data complexity although it requires chosen plaintexts. When the block size is 64 bits, our attack reduces the required data from $2^{45}$ known plaintexts to $2^{26}$ chosen plaintexts with keeping the time complexity required by the previous attacks. Furthermore, by increasing the time complexity up to $2^{62}$, the required data is further reduced to $2^{8}$, and $DT = 2^{70}$, where DT is the product of data and time complexities. We show that our low-data attack on the minimal n-bit two-round Even-Mansour ciphers requires $DT = 2^{n+6}$ in general cases. Since the proved lower bound on the required DT for the one-round n-bit Even-Mansour ciphers is $2^n$, our results imply that adding one round to the one-round Even-Mansour ciphers does not sufficiently improve the security against key recovery attacks.

1 Introduction

1.1 Even-Mansour Cipher

The Even-Mansour cipher consisting of two direct key XORs separated by one public permutation was proposed in 1991 [9, 10]. Since then, it has been considered as one of the simplest block cipher design. Indeed, its description is rather simple:

$$\begin{aligned} E_{K_0,K_1}(x)=P(x\oplus K_0)\oplus K_1, \end{aligned}$$

where P is an n-bit fixed and public permutation with two n-bit secret keys $K_0$ and $K_1$.

Bogdanov et al. generalized it as the multiple-round Even-Mansour constructions, and presented the first security bounds against distinguishing attacks for them [1]. As opposed to the original Even-Mansour cipher, the multiple-round Even-Mansour construction can comprise t independent public permutations on n-bit words separated by n-bit independent key additions:

$$\begin{aligned} E^{(t)}(x) = E_{K_{0},\ldots , K_{t}}(x) = P_t(\cdots (P_2(P_1(x \oplus K_0) \oplus K_1) \oplus K_{2}) \cdots ) \oplus K_{t}. \end{aligned}$$

There has been a series of results towards the provable security of the iterated Even-Mansour ciphers with independently and randomly drawn permutations since then. The aforementioned work [1] proves that at least $2^{\frac{2n}{3}}$ queries are required to distinguish $E^{(t)}$ with $t\ge 2$ from a random permutation and conjectures that the bound is roughly $2^{\frac{t}{t+1}n}$. Steinberger [16] improves this result by proving that the bound of $2^{\frac{3}{4}n}$ holds for $t\ge 3$. Lampe et al. [14] prove a security of $2^{\frac{t}{t+2}n}$ for all even values of t, which is slightly lower than conjectured. Chen and Steinberger [4] have managed to prove the conjectured $2^{\frac{t}{t+1}n}$ bound on the number of queries required for a distinguishing attack, and then Hoang and Tessaro proved the exact bound of it [12].

1.2 Minimal Construction

The original Even-Mansour cipher, which only consists of a single permutation surrounded by key XORs, ensures security up to $2^{n/2}$ queries of the adversary who has access to the encryption function $E_{K}$ and the internal permutation P [9, 10]. Even and Mansour proved an information-theoretic bound that any attack on the scheme must satisfy the equation of $DT = \varOmega (2^n)$, where D and T are the data and time complexities, i.e. the number of queries to the encryption function $E_{K}$ and the permutation P, respectively. The case of $(D, T) =(2^{n/2}, 2^{n/2})$ satisfies the bound of $2^{n/2}$ queries. Shortly after the introduction of the scheme, Daemen [5] presented a key recovery attack matching the bound DT = $O(2^n)$ in the chosen-plaintext model. Dunkelman et al. [8] proposed the slidex attack and its application to close the gap between the upper and lower bounds on the security of the Even-Mansour scheme for a variety of tradeoff points. Moreover, they specifically consider the minimalistic single-key Even-Mansour, with $K_0=K_1$, which provides exactly the same security. As pointed out by Dunkelman et al. [8], this construction is minimal in the sense that if one removes any component, i.e. either the addition of one of the keys, or the permutation P, the construction becomes trivially breakable.

Chen et al. [3] proved that two variants of two-round Even-Mansour ciphers are secure up to $2^{2n/3}$ queries against distinguishing attacks, while the one-round Even-Mansour cipher guarantees security up to birthday bound, namely $2^{n/2}$. One consists of two independent n-bit permutations $P_1$ and $P_2$, and a single n-bit key K:

$$\begin{aligned} \mathbf{(2EM }\text {-}\mathbf{1) } \qquad E^{(2)}_{K}(x)=P_2(P_1(x\oplus K)\oplus K)\oplus K. \end{aligned}$$

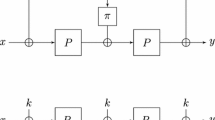
The other consists of a single n-bit permutation P, and a single n-bit key K with a simple key scheduling function $\pi$,

$$\begin{aligned} \mathbf{(2EM }\text {-}\mathbf{2) } \qquad E'^{(2)}_{K}(x)=P(P(x\oplus K)\oplus \pi (K))\oplus K, \end{aligned}$$

where $\pi$ is any linear orthomorphism of $\mathbb {F}_2^n$. Hereafter we refer to $E^{(2)}_K$ and $E'^{(2)}_K$ as 2EM-1 and 2EM-2, respectively. These constructions can be considered as minimal two-round Even-Mansour ciphers delivering security beyond the birthday bound, since they have no redundant component for the security. The proved lower bounds of 2EM-1 and 2EM-2 for distinguishing attacks by Chen et al. [3] are captured in Fig. 1. Regarding tightness of their security bounds for distinguishing attacks, Gazi proposed a generic distinguishing attack with the time complexity of $2^{n-1/2\ \mathrm{log}_2 D}$ for any D [11], i.e. $DT^2 = 2^{2n}$. The attack matches the proved bound only in the specific case $(D, T) =(2^{2n/3}, 2^{2n/3})$.

Along with the distinguishing attacks, several key recovery attacks on 2EM-1 construction have been presented [7, 15]. Unlike the one-round Even-Mansour construction, for the two-round Even-Mansour ciphers, a dedicated information-theoretic bound on D and T for any attack including key recovery attacks has not been known. At least, D and T required for key recovery attacks on the two-round constructions must satisfy $DT = \varOmega (2^n)$ which is the bound for the one-round construction. Moreover, since a distinguishing attack is directly derived from a key recovery attack, D and T for the key recovery attacks must follow the lower bounds for distinguishing attacks on 2EM-1 and 2EM-2 given by Chen et al. [3]. For $n=64$, Nikolić et al. proposed the first key recovery attacks on 2EM-1 requiring the time complexity of $2^{61}$ with $2^{59}$ known plaintexts [15]. Dinur et al. generalized it and reduced the data requirements to $2^{45}$, while keeping the time complexity [7]. Therefore, the published best upper bound on DT is estimated as $2^{105}$ for $n=64$. Since it is much larger than the lower bound for the one-round Even-Mansour ($DT = 2^{64}$), the two-round Even-Mansour cipher seems more secure against key recovery attacks than the one-round Even-Mansour cipher. However, due to the gap between the proved lower bound and the presented upper bound, the accurate security of the two-round construction is still unknown and it is an important open problem in the field of symmetric cryptography.

Table 1. Summary of our results for 2-round Even-Mansour ciphers.

Fig. 1.

Comparison of the previous results and our results when $n=64$. The blue solid line is the lower bound of the one-round Even-Mansour cipher, i.e. $DT = \varOmega (2^n)$ [9, 10]. The blue dashed and dot lines are the lower bound for distinguishing attacks on 2EM-1 and 2EM-2 by Chen et al. [3], respectively. The black solid line is the upper bound for distinguishing attacks on 2EM-1 and 2EM-2 by Gazi [11] (Color figure online).

Table 2. Comparison of the previous results and our results for key recovery attacks on 2-round Even-Mansour ciphers when $n=64$.

1.3 Our Contributions

In this paper, we propose new key recovery attacks on the two minimal two-round Even-Mansour ciphers 2EM-1 and 2EM-2. First, we present a basic attack on 2EM-1 by using the advanced meet-in-the-middle technique which potentially reduces the data complexity. In particular, we introduce novel matching techniques called partial invariable pair and matching with input-restricted public permutation, which enable us to compute one of the two permutations without knowing a part of the key information. Then, we improve the basic attack: one significantly reduces data complexity (low-data attack) and the other reduces time complexity (time-optimized attack) by dynamically finding partial invariable pairs. Our results are summarized in Table 1. In our attacks, there are some tradeoff points of data and time complexities by choosing the parameters of a, b and d under the conditions. We emphasize that all of our attacks do not contain any operation over $2^n$, and can be regarded as exponential-advantage attacks as with the previous attack [7, 15].

Figure 1 and Table 2 show the comparative results with the previous attacks when $n = 64$. Our attacks can drastically reduce the required data from $2^{45}$ to $2^{26}$ with keeping the time complexity of the previous attacks [7, 15], although our attacks require chosen plaintexts. By increasing time complexity up to $2^{62}$, the required data is further reduced to $2^{8}$. Since the previous attacks are based on multi collisions of the n-bit state, they cannot break the birthday barrier of data and time complexity. On the other hand, our attacks essentially exploit multi collisions of one part of the state, which we call partial invariable pairs in this paper. The required time and data complexity for finding such invariable pairs are much less than those required for finding multi collisions of the whole state. Therefore, our attacks are feasible even if the required data is restricted to be less than $2^{n/2}$. In the time-optimized attacks, we can reduce the computation cost of the internal permutation to $2^{53}$, but it requires $2^{62}$ memory accesses. Basically, it is hard to fairly compare the costs of one encryption and one memory access, because these costs strongly depend on the execution environments, the size of the table, and the underlying permutation. Thus, we do not claim that our time-optimized attacks sufficiently reduce the time complexity required for the previously known key recovery attacks. However, obviously the cost of encryptions is non trivially reduced. We believe that it is an interesting tradeoff to know the concrete security of the minimal two-round Even-Mansour construction. Finally, we show that all of our attacks on 2EM-1 can be applied to the other minimal variant 2EM-2.

The minimum value of DT for $n = 64$ is estimated as $2^{70}$, which is close to the proved lower bound for the single Even-Mansour cipher $DT= 2^{64}$ and Chen et al.’s lower bounds for distinguishing attacks on the two-round Even-Mansour ciphers as shown in Fig. 1. Table 1 shows that our low-data attack requires $DT = 2^{2(n-a)-d}$ and $DT^{2} = 2^{3(n-a)-d}$ for any n as long as $a \cdot 2^{a} + d \le n-a$. When choosing $a=2$, the maximum d is $d = n - 10$, and thus DT and $DT^{2}$ are estimated as $DT = 2^{n+6}$ and $DT^{2} = 2^{2n+4}$ for any n, respectively. These results reveal that adding one round does not sufficiently improve the key recovery security with respect to the product of D and T, while there has not been attacks with time complexity less than the birthday bound unlike the single Even-Mansour cipher.

1.4 Outline of the Paper

The remainder of the paper is organized as follows. In Sect. 2, we introduce the specification of Even-Mansour ciphers and review previous work. In Sect. 3, we explain a basic attack on 2EM-1. Then Sects. 4 and 5 present the improved attacks on 2EM-1 with respect to data and time complexities, respectively. In Sect. 6, we show that our attacks on 2EM-1 are applicable to 2EM-2. Section 7 is the conclusion.

2 Even-Mansour Ciphers

In this section, we introduce the two minimal two-round Even-Mansour ciphers we focus on this paper, and review the previous results on the ciphers.

2.1 Two-Round Even-Mansour Ciphers

Let $P_1,\ldots , P_{t}$: $\{0,1\}^{n} \rightarrow \{0,1\}^{n}$ be independent public permutations and let $K_0,\ldots , K_{t} \in \{0,1\}^{n}$ be round keys. The t-round Even-Mansour cipher $E^{(t)}$: $\{0,1\}^{n} \times \{0,1\}^{n(t+1)} \rightarrow \{0,1\}^{n}$ consists of t public permutations and $(t+1)$ key injections is defined as follows [1]:

$$\begin{aligned} E^{(t)}(x) = E_{K_{0},\ldots , K_{t}}(x) = P_t(\cdots (P_2(P_1(x \oplus K_0) \oplus K_1) \oplus K_{2}) \cdots ) \oplus K_{t}, \end{aligned}$$

where x is an n-bit input of $E^{(t)}$.

In this paper, we focus on the following two variants of two-round Even-Mansour ciphers $(t=2)$, which are provably secure up to $2^{2n/3}$ queries of the encryption function and the internal permutation(s) [3]:

$$\begin{aligned} \mathbf{(2EM }\text {-}\mathbf{1) }&\qquad E^{(2)}_{K}(x) = P_2(P_1(x\oplus K)\oplus K)\oplus K,\\ \mathbf{(2EM }\text {-}\mathbf{2) }&\qquad E'^{(2)}_{K}(x) = P(P(x\oplus K)\oplus \pi (K))\oplus K, \end{aligned}$$

where $P_1$, $P_2$ and P are independent n-bit permutations, K is n-bit key, and $\pi$ is any linear orthomorphism of $\mathbb {F}_2^n$. As examples of orthomorphism, a simple rotation, Feistel-like construction (e.g. $\pi$: $(x,y) \mapsto (y, x \oplus y)$), field multiplication (e.g. $\pi$: $(x) \mapsto (x \times c)$, where $c \ne 0, 1$) are well known. Figure 2 illustrates these constructions. These constructions are regarded as minimal Even-Mansour ciphers delivering security beyond the birthday bound, since removing any component causes security to drop back to $O(2^{n/2})$ queries.

Fig. 2.

Minimal two-round Even-Mansour ciphers, 2EM-1 and 2EM-2.

2.2 Previous Key Recovery Attacks on 2EM-1

Along with results on provable security of 2EM-1 [1, 3, 4, 11, 14, 16], several key recovery attacks on the construction have been published [7, 15].

Nikolić et al. proposed the first key recovery attacks on 2EM-1 [15]. They considered the graph of the function $P'(x) = x \oplus P(x)$ and showed that vertices with a large in-degree in this graph can be exploited to bypass an additional round of 2EM-1. Specifically, they define a keyed function inside of $E^{(2)}_{K}(x)$ as $Q(K,x) = K\oplus P(x \oplus K)$. Since the same key K is XORed before and after the first permutation P, the relation of $x \oplus Q(K, x) = (x \oplus K) \oplus P(x \oplus K)$ holds for any key K. If some output values of $P'$ appear more than the average, then we can predict the value of Q(K, x) with a higher probability than expected even when K is unknown. Then, K can be recovered by using the relation of $K = Q(K, x) \oplus E^{(2)}_{K}(x)$. In this attack, they exploit t-way multi collisions on the value $P'(x) = x \oplus P(x)$, namely $x_1, x_2,\ldots , x_t$ such that $x_1 \oplus P(x_1) = x_2 \oplus P(x_2) =,\ldots , = x_t \oplus P(x_t) = v$ for some value of v. Using it, Q(K, x) can be guessed with a probability which is t times higher than the expected $2^{-n}$ without knowing K. For $n=64$, their attack can recover the key of $E^{(2)}_{K}(x)$ with time complexity of $2^{61}$ and $2^{59}$ known plaintexts [15]. After that, Dinur et al. generalized their attack using concepts from graph theory [7]. In particular, they estimated the highest expected in-degree in the bipartite graph of $P'(x) = x \oplus P(x)$ depending on the number of input size. By considering all the vertices with an in-degree of at least 8, they reduced the data requirements to $2^{45}$, while keeping the time complexity. Therefore, the published upper bound of DT is estimated as $2^{105} (= 2^{60} \times 2^{45})$ for $n=64$. Since it is significantly larger than the bound of one-round Even-Mansour ($DT = 2^{64}$), two-round Even-Mansour cipher seems to sufficiently improve the key recovery security of the one-round Even-Mansour cipher. However, due to the gap between the proved lower bound [3, 9, 10] and the presented upper bound [7, 15], the accurate security of the two-round construction is still unknown and it is an important open problem.

3 Basic Attacks on 2EM-1

This section presents a basic attack on 2EM-1, $E^{(2)}_{K}$ consisting of two public permutations $P_{1}$ and $P_{2}$ interleaved with three identical key injections by K. Our attack is based on the meet-in-the-middle (MitM) framework [2, 13], i.e., two functions f and g from $E^{(2)}_{K}$ are independently computable while the previous attacks [6] use a multi-collision technique.

In our attack, we introduce a novel matching technique called matching with input-restricted public permutation, which enables us to compute one of two permutations without knowing a part of the key information. Our new matching technique is based on partial invariable pairs, which is used for constructing an input restricted table for any permutation.

3.1 Definitions of Invariable Pair

Let f be an n-bit keyed function using a k-bit key, namely $f_{K}$: $\{0,1\}^{n} \rightarrow \{0,1\}^{n}$, where $K \in \{0,1\}^{k}$. We use the following two notations for an input-output pair.

Definition 1

(Invariable Pair [13]). If there exists an input-output pair (x, y) of f such that $f_{K}(x) = y$ for any K, such an input-output pair (x, y) is defined by an invariable input-output pair of f.

Definition 2

((Target) Partial Invariable Pair). If there exists a pair of a fixed input and a b-bit partial output $(x, y')$ of f such that $tr_{b}(f_{K}(x)) = y'$ for any K, such a pair $(x, y')$ is defined by a partial b-bit invariable input-output pair of f, where $y' \in \{0,1\}^{b}$ ($b \le n$) and $tr_{b}(y)$ represents a b-bit truncation of an n-bit output y.

If the value of b bits to be fixed is predetermined, it is called a target partial b-bit invariable input-output pair.

3.2 How to Find Partial Invariable Pair

Assuming that an a-bit key is involved in f, the procedure for finding a b-bit partial invariable input-output pair is given as follows:

Step 1::

Set an n-bit input x randomly.

Step 2::

Compute $y_{1} = f_{K}(x)$ with a key K from the set of $2^{a}$ keys.

Step 3::

Store b bits of $y_{1}$ $(b \le n)$ as $y' (= tr_{b}(y_{1}))$.

Step 4::

Compute $y_{2} = f_{K'}(x)$ with another key $K'$ from the set of $2^{a}$ keys, where $K' \ne K$.

Step 5::

Check whether b bits of $y_{2}$ are equal to $y'$ at the same position. If so, repeat Steps 4 and 5. Then, if all possible $K'$ are checked, output $(x, y')$ as a b-bit partial invariable input-output pair of f. Otherwise, go back to Step 1 and restart with a different x.

The probability of the matching in Step 5 is $2^{-b}$ assuming that f is a sufficiently random function. Thus, the complexity of finding a b-bit partial invariable pair is estimated as $1/(2^{-b})^{2^a - 1}$. If b bits of $y_{1}$ are predetermined, which is called target partial b-bit invariable input-output pair, the required complexity of finding such a pair is estimated as $1/(2^{-b})^{2^a}$.

Fig. 3.

Attack overview of 2EM-1.

3.3 Attack Overview

As illustrated in Fig. 3, we first divide the n-bit key K into an a-bit $k_{0}$ and the remaining $(n-a)$-bit $k_{1}$. Then, we introduce a function f that consists of $P_{1}$ and two key injections by $k_{0}$, and a function g that consists of an initial key injection by $k_{1}$ and a final key injection by $k_{1}$. Note that f and g are independently computed with $k_{0}$ and $k_{1}$, respectively. An output of f and an input of g are represented as $(x_{0}|x_{1})$ and $(y_{0}|y_{1})$, also an input and an output of $P_{2}$ are denoted as $(v_{0}|v_{1})$ and $(z_{0}|z_{1})$, respectively, where $x_{0}, v_{0}, k_{0}, z_{0}, y_{0} \in \{0,1\}^{a}$, $x_{1}, v_{1}, k_{1}, z_{1}, y_{1} \in \{0,1\}^{n-a}$.

At first glance, it seems to be difficult to do the matching between f and g, because f and g need $k_{1}$ and $k_{0}$ to compute the matching state around $P_{2}$, respectively. Thus, if the underlying permutation has sufficiently good diffusion property such as AES-128 with a fixed-key, it seems infeasible to construct the matching. To overcome this problem, we introduce a novel matching technique called matching with input-restricted public permutation.

Matching with Input-Restricted Public Permutation. The idea behind our new technique is to construct the input-restricted table of $P_{2}$ to find the corresponding n-bit value $(v_0|v_1)$ from only an $(n-a)$-bit value $y_1(= z_1)$ without knowing $k_0$ while computing g. In a straightforward way, given a value of $y_1(= z_1)$, $2^a (= 2^n/2^{n-a})$ candidates of $(v_0|v_1)$ are found with $2^a$ $P_2$ computations. Since all $k_0$ values are tested in the function g, it totally requires $2^n (= 2^{n-a} \times 2^a)$ $P_2$ computations. Thus, two functions f and g from $E^{(2)}_{K}$ are not independently computed.

In order to get rid of this problem, b bits of inputs $(v_0|v_1)$ are fixed, then the precomputation table of $P_{2}$, indexed by values of $(n-a)$-bit $y_{1}$, is constructed with less than $2^{n}$ $P_{2}$ computations, namely $2^{n-b}$. Given an $(n-a)$-bit $y_{1}$, $2^{n-b}/2^{n-a} = 2^{a - b}$ candidates of $(v_0|v_1)$ are found with only one memory access of the precomputation table without the knowledge of $k_0$. If $a = b$, it is expected that one candidate is left. If $a \le b$, it is expected that less than one candidate is left.

Since a partial invariable pair in function f allows us to fix b bits of inputs $(v_0|v_1)$ during the MitM procedure, the combination use of two techniques, the partial invariable pair and the matching with precomputation, enables us to mount a MitM attack on 2EM-1.

In summary, we mount the attack on $E_{K}^{(2)}$ by using partial invariable pair to the permutation $P_{1}$ in conjunction with the matching with the input-restricted public permutation technique to the permutation $P_{2}$.

3.4 Attack Procedure

The attack consists of an offline and an online phase. In the offline phase, a b-bit partial invariable pair of f is found, then an input-restricted precomputation table of $P_{2}$ is constructed. In the online phase, the MitM attack is mounted by using the precomputation table and querying the encryption oracle $E_{K}^{(2)}$.

In this attack, more than a bits of input of $P_2$ are not fixed by $k_0$, because an $(n-a)$-bit $k_1$ is used between f and $P_2$. Thus we consider the case where a is equal to b, which is optimal with respect to the time complexity.

Offline Phase

Step 1::

Find an a-bit partial invariable pair of f, $(S, x_{0})$ such that $tr_{a}(f_{k_{0}}(S)) = x_{0}$ for any a-bit $k_{0}$.

Step 2::

For all a-bit $k_{0}$, compute the remaining data of the invariable pair, and make a table of $(k_{0}^{(i)}, x_{1}^{(i)})$ such that $f_{k_{0}^{(i)}}(S) = (x_{0} | x_{1}^{(i)})$, where $1 \le i \le 2^{a}$.

Step 3::

For all $(n-a)$-bit $v_{1}$, compute $(n-a)$-bit value $z_{1}$ by $P_{2}$, then make a table of $(v_{1}^{(j)}, z_{1}^{(j)})$, where $v_{0} = x_{0}$, $P_{2}(v_{0} | v_{1}^{(j)}) = (z_{0}^{(j)} | z_{1}^{(j)})$ and $1 \le j \le 2^{n-a}$.

Online Phase

Step 1::

Guess an $(n-a)$-bit $k_{1}$ and compute the corresponding plaintext P from the start state S and $k_{1}$.

Step 2::

Send P to the encryption oracle $E_{K}^{(2)}$, then obtain the corresponding ciphertext C.

Step 3::

Compute an $(n-a)$-bit $y_{1}$ from C and $k_{1}$.

Step 4::

Look for an index d in the table of $(v_{1}^{(j)}, z_{1}^{(j)})$ such that $z_{1}^{(d)} = y_{1}$. If there is no such index, go back to Step 1.

Step 5::

Compute $x'_{1} = v_{1}^{(d)} \oplus k_{1}$, and check if there exists an index e in the table of $(k_{0}^{(i)}, x_{1}^{(i)})$ satisfying $x'_{1} = x_{1}^{(e)}$. If there is no such index, go back to Step 1.

Step 6::

Check if $P_{2}(v_{0}|v_{1}^{(d)}) = (z'_{0} | z_{1}^{(d)})$ holds, where $z'_{0}$ is computed from C and $k_{0}^{(e)}$. If so, $K' = (k_{0}^{(e)}|k_{1})$ is regarded as the correct key. Otherwise, go back to Step 1.

3.5 Evaluation

Here, we evaluate the cost required in each phase.

Table 3. Summary of computational costs for the basic attack on 2EM-1.

Offline Phase. In Steps 1 and 2, the time complexity required for finding an a-bit partial invariable pair is $(2^{a})^{2^{a} - 1}$ $P_{1}$ computations and the required memory is $2^{a}$ blocks. In Step 3, the required time complexity is $2^{n - a}$ $P_{2}$ computations and the required memory is $2^{n-a}$ blocks.

-Time complexity::

($(2^{a})^{2^a - 1} + 2^{n - a}$) $\mathcal {P}$ computations, where $\mathcal {P}$ denotes $P_{1}$ or $P_{2}$,

-Memory::

$2^{a}$ and $2^{n-a}$ blocks.

For simplicity, hereafter computation costs for $P_{1}$ and $P_{2}$ are assumed to be the same and it denotes $\mathcal {P}$ computations. In addition, the cost of one encryption call is approximately estimated as two $\mathcal {P}$ computations.

Online Phase. Steps 1 to 4 are performed $2^{n - a}$ times. These steps include two XOR operations in Steps 1 and 3 and one memory access in Step 4. Note that, in Step 4, about one candidate is expected to be found due to the relation of $a = b$, if $P_{2}$ is a sufficiently good permutation. Step 5 is performed $2^{n-a}$ times with one XOR operation and one memory access. It is expected that $2^{a}/2^{n-a} = 2^{-n+2a}$ candidates will survive in Step 5.

We assume that the cost of one memory access in step 4 is sufficiently larger than one XOR operation and memory access in step 5, because the size of table in step 4 for the matching with input-restricted public permutation is much larger than one in step 5. Then, the time complexity of Steps 1 to 5 is approximately estimated as ($2^{n -a}$) memory accesses (MA). Step 6 is mounted only $2^{-n + 2a} \times 2^{n - a} = 2^{a}$ times with $\mathcal {P}$ computations. Step 2 requires $2^{n-a}$ data, since a bits of state S are fixed when computing the function g with each $k_1$.

-Time complexity::

$2^{a}$ $\mathcal {P}$ computations + ($2^{n -a}$) MA,

-Data complexity::

$2^{n-a}$ chosen plaintexts.

Summary. The computational costs of offline and online phases for the basic attacks on the 2EM-1 are estimated as Table 3, where we choose a so that time complexity is minimized. Specifically, we freely choose a as long as it holds the condition of $(2^{a})^{2^a - 1} \le 2^{n}$. If $(2^{a})^{2^a - 1}$ is less than $2^{n-a}$, time complexity is estimated as $2^{n-a}$ $\mathcal {P}$ computations ($2^{n-a-1}$ encryptions) in the offline phase and $2^{n-a}$ memory accesses in the online phase. Thus, maximizing a is optimal with respect to time complexity. Assuming the cost of memory access is sufficiently smaller than that of the encryption¹, DT is expressed as $DT = 2^{n-a}/2 \times 2^{n-a} = 2^{2(n-a-1)}$ under the condition of $(2^{a})^{2^a - 1} \le 2^{n-a}$.

4 Low-Data Attacks on 2EM-1

In this section, we introduce low-data attacks on 2EM-1 based on the attack in Sect. 3. The low-data attacks aim to reduce data requirement (i.e. access to encryption oracle $E^{(2)}_{K}$) by fixing parts of plaintexts while keeping lower time complexity than that of the brute force attack. In our attacks, the $(n-a)$-bit $k_1$ is further divided into a d-bit $k_{1L}$ and an $(n-(a + d))$-bit $k_{1R}$. A start state S and a plaintext P are represented as $S = (s_{0}|s_{1L}|s_{1R})$ and $P = (p_{0}|p_{1L}|p_{1R})$, respectively, where $s_{0},p_{0} \in \{0,1\}^{a}$, $s_{1L},p_{1L} \in \{0,1\}^{d}$ and $s_{1R},p_{1R} \in \{0,1\}^{n-(a+d)}$.

The main idea is to control $s_{1L}$ depending on $k_{1L}$ so that the d bits of $(s_{1L} \oplus k_{1L})$ are always fixed. If $s_{0}$ is also fixed, $(a + d)$ bits of a plaintext are always fixed, i.e., the required data is reduced to $2^{n- (a +d)}$. To be more specific, given a value $k_{1L}$, a b-bit target partial invariable pair of f, $(S, x_0)$ is dynamically found in the online phase, where $s_{0}$ is fixed and $s_{1L}$ is chosen such that $(s_{1L}\,\oplus \,k_{1L})$ is fixed (Fig. 4).

Fig. 4.

Attack overview of low-data attacks on 2EM-1.

4.1 Attack Procedure

In the offline phase, a b-bit input-restricted precomputation table of $P_{2}$ is constructed, where b is assumed to be equal to a. In the online phase, the MitM attack is mounted by dynamically finding a b-bit target partial invariable pair of f by the precomputation table.

Offline Phase

Step 1::

Fix a-bit $v_0$ and $(a + d)$-bit of plaintext to $p_{0}| p_{1L}$.

Step 2::

For all $(n-a)$-bit $v_{1}$, compute an $(n-a)$-bit value $z_{1}$ by $P_{2}$, then make a table of $(v_{1}^{(j)}, z_{1}^{(j)})$, where $P_{2}(v_{0} | v_{1}^{(j)}) = (z_{0}^{(j)} | z_{1}^{(j)})$ and $1 \le j \le 2^{n-b}$.

Online Phase

Step 1: :

Guess a d-bit $k_{1L}$, and compute the c-bit $s_{1L}$ as $s_{1L}$ = $k_{1L} \oplus p_{1L}$.

Step 2: :

Find a a-bit target partial invariable pair of f, $tr_b(f_{k_0}(S)) = (x_0)$ where $s_{0}$ and $s_{1L}$ are fixed. Then make a table of ($k_0^{i}, x_{1}^{i}$) for all a-bit $k_0$, where $1 \le i \le 2^a$.

Step 3::

Guess $k_{1R}$ and compute the corresponding plaintext P from the start state S and $k_1$.

Step 4::

Send P to the encryption oracle $E^{2}_K$, then obtain the corresponding ciphertext C.

Step 5::

Compute $(n-a)$-bit $y_1$ from $k_1$ and C.

Step 6::

Look for an index d in the table of $(v_{1}^{(j)}, z_{1}^{(j)})$ such that $z_{1}^{(d)} = y_1$. If there is no such index, go back to Step 3.

Step 7::

Compute $x'_{1} = v_{1}^{(j)} \oplus k_{1}$, and check if there exists an index e in the table of ($k_0^{(i)}, x_{1}^{(i)}$) satisfying $x'_{1} = x_{1}^{(e)}$. If there is no such index, go back to Step 3.

Step 8::

Check if $P_{2}(v_{0} | v_{1}^{(d)}) = (z'_{0} | z_{1}^{(d)})$ holds, where $z'_0$ is computed from C and $k_{1}^{e}$. If so, $K' = (k_0^{(e)} | k_1)$ is regarded as the correct key. Otherwise go back to Step 3.

Step 9::

For all d-bit $k_{1L}$, repeat Steps 1 to 8.

4.2 Evaluation

This section gives estimations of the cost required for our low-data attacks on 2EM-1.

Offline Phase. Step 2 in the offline phase requires $2^{n - a}$ $\mathcal {P}$ computations and $2^{n-a}$ blocks memory.

-Time complexity::

($2^{n - a}$) $\mathcal {P}$ computations,

-Memory::

$2^{n-a}$ blocks.

Online Phase. Step 2 requires $(2^{a})^{2^a}$ $\mathcal {P}$ computations to find a-bit target partial invariable pair of f by changing $n-(a +d)$-bit $s_{1R}$. Thus, it should hold the equation of $(2^{a})^{2^a} < 2^{n-(a + d)}$, namely ${a} \times {2^a} < {n-(a + d)}$. Step 2 is performed $2^d$ times with $(2^{a})^{2^a}$ $\mathcal {P}$ computations and $2^a$ memory. Steps 3 to 6 are performed $2^{n - a}$ times. These steps include two XOR operations in Steps 3 and Step 5, one memory access in Step 6. Note that Step 4 is performed under the chosen-plaintext setting. Step 7 is performed $2^{a-a} \times 2^{n -a} = 2^{n-a}$ times with one XOR and one memory access. The required time complexity of Steps 3 to 7 is approximately estimated as ($2^{n -a}$) memory accesses because the size of table in step 6 for the matching with input-restricted public permutation is assumed to be much larger than one in step 7. Step 8 is mounted only $2^{-n + 2a} \times 2^{n -a} = 2^a$ times with $\mathcal {P}$ computations. The $2^{n-(a + d)}$ data is required in Step 4.

-Time complexity::

($(2^{a})^{2^a} \cdot 2^d$ + $2^{a}$) $\mathcal {P}$ computations + ($2^{n -a}$) MA,

-Memory::

$2^{a}$ blocks,

-Data::

$2^{n-(a + d)}$ chosen plaintexts.

Summary. The computational costs for the low-data attack on 2EM-1 are estimated as Table 4. For $n = 64$, 128, 256, data complexity is drastically reduced compared to the basic attack and previous attacks [7, 15] while keeping the time complexity of basic attacks. Moreover, by increasing time complexity, i.e. choosing small a, the required data can be reduced to $2^{8}$, where it does not include any $2^{n}$ operations. Assuming the cost of memory access is sufficiently smaller than that of the encryption, DT is expressed as $DT = 2^{n-a} \times 2^{n-(a +d)} = 2^{2(n-a) - d}$ under the condition of $(2^{a})^{2^a} \cdot 2^d \le 2^{n-a}$. Once n and a are determined, the maximal d is easily obtained from the condition. The minimal value of DT of $n = 64, 128$, and 256 are $2^{70} (= 2^{62} \times 2^8)$, $2^{134} (= 2^{126} \times 2^8)$, and $2^{262} (= 2^{254} \times 2^8)$, respectively. These are very close to the bound for single Even-Mansour cipher, i.e. $2^{64}$, $2^{128}$, and $2^{256}$.

The bounds by low-data attacks can be generalized for any n as follows: when choosing $a = 2$, the maximum d is $d = n - a - 8$, and then DT is estimated as $DT = 2^{n + 6}$ for any value of n, respectively.

Table 4. Summary of computational costs for the low-data attack on the 2-round Even-Mansour cipher.

5 Time-Optimized Attacks on 2EM-1

In this section, we try to reduce the cost of $\mathcal {P}$ computations (i.e. access to the internal permutation oracle) of the basic attacks presented in Sect. 3. In this attack, an $(n- a)$-bit $k_1$ is further divided into a c-bit $k_{1L}$ and an $(n-(a + c))$-bit $k_{1R}$. Similarly, $x_{1}$ and $v_{1}$ are represented as $x_{1} = (x_{1L}|x_{1R})$ and $v_{1} = (v_{1L}|v_{1R})$, respectively, where $x_{1L},v_{1L} \in \{0,1\}^{c}$ and $x_{1R},v_{1R} \in \{0,1\}^{n-(a+c)}$ (see Fig. 5).

The cost for $\mathcal {P}$ computations is dominated by the cost for constructing an input-restricted public permutation table in the offline phase, whose cost is estimated as $2^{n-a}$ $\mathcal {P}$ computations and $2^{n-a}$ memory. If additional c bits of the input of $P_2$ can also be fixed, it is reduced to $2^{n-(a + c)}$ $\mathcal {P}$ computations and memory. However, the additional c bits are not fixed in the online phase even if a c-bit $x_{1L}$ is fixed in f, since such a c-bit input of $\mathcal {P}$ depends on $k_{1L}$ between f and $P_2$, and all values of $k_{1L}$ are tested during the MitM procedure. To solve this problem, we control $x_{1L}$ depending on $k_{1L}$ so that the c bits of $x_{1L} \oplus k_{1L}$ are always fixed in order to reduce the computational cost. In particular, given a value $k_{1L}$ in the online phase, a $b (= a + c)$-bit target partial invariable pair of f is dynamically found.

Fig. 5.

Attack overview of time-optimized attacks on 2EM-1.

5.1 Attack Procedure

In the offline phase, a $b (= a + c)$-bit input-restricted precomputation table of $P_{2}$ is constructed. In the online phase, the MitM attack is mounted by dynamically finding a b-bit target partial invariable pair of f by using the precomputation table.

Offline Phase

Step 1::

Fix an a-bit $v_0$ and a c-bit $v_{1L}$.

Step 2::

For all $(n-b)$-bit $v_{1R}$, compute $(n-a)$-bit values $z_{1}$ by $P_{2}$, then make a table of $(v_{1R}^{(j)}, z_{1}^{(j)})$, where $P_{2}(v_{0} | v_{1L} | v_{1R}^{(j)}) = (z_{0}^{(j)} | z_{1}^{(j)})$ and $1 \le j \le 2^{n-b}$

Online Phase

Step 1::

Guess a c-bit $k_{1L}$, and choose a c-bit $x_{1L}$ as $x_{1L}$ = $k_{1L} \oplus v_{1L}$.

Step 2::

Find a b-bit target partial invariable pair of f, $tr_b(f_{k_0}(S)) = (x_0|x_{1L})$ where b-bit $x_0|x_{1L}$ is fixed as $v_0 |(k_{1L} \oplus v_{1L})$, and make a table of ($k_0^{i}, x_{1R}^{i}$) for all a-bit $k_0$, where $1 \le i \le 2^a$.

Step 3::

Guess $k_{1R}$ and compute the corresponding plaintext P from the start state S and $k_1$.

Step 4::

Send P to the encryption oracle $E^{2}_K$, then obtain the corresponding ciphertext C.

Step 5::

Compute an $(n-a)$-bit $y_1$ from $k_1$ and C.

Step 6::

Look for an index d in the table of $(v_{1R}^{(j)}, z_{1}^{(j)})$ such that $z_{1}^{(d)} = y_1$. If there is no such index, go back to Step 3.

Step 7::

Compute $x'_{1R} = v_{1R}^{(j)} \oplus k_{1R}$, and check if there exists an index e in the table of ($k_0^{(i)}, x_{1R}^{(i)}$) satisfying $x'_{1R} = x_{1R}^{(e)}$. If there is no such index, go back to Step 3.

Step 8::

Check if $P_{2}(v_{0} | v_{1L} | v_{1R}^{(d)}) = (z'_{0} | z_{1}^{(d)})$ holds, where $z'_0$ is computed from C and $k_{1R}^{(e)}$. If so, $K' = (k_0^{(e)} | k_1)$ is regarded as the correct key. Otherwise go back to Step 3.

Step 9::

For all c-bit $k_{1L}$, repeat Steps 1 to 8.

5.2 Evaluation

We evaluate each cost of our time-optimized attack on 2EM-1.

Offline Phase. Step 2 requires $2^{n - b}$ $\mathcal {P}$ computations and $2^{n-b}$ blocks memory.

-Time complexity::

($2^{n - b}$) $\mathcal {P}$ computations,

-Memory::

$2^{n-b}$ blocks.

Online Phase. Step 2 is performed $2^c$ times with $(2^{b})^{2^a}$ $\mathcal {P}$ computations and $2^a$ memory. Steps 3 to 6 are performed $2^{n - a}$ times. These steps include two XOR operations in Steps 3 and 5 and one memory access in Step 6. Note that, in Step 6, it is expected that there exist $2^{a - b} (= 2^{n-b}/2^{n-a})$ desired pairs, if $P_{2}$ is a sufficiently good permutation. Step 7 is performed $2^{a-b} \times 2^{n -a} = 2^{n-b}$ times with one XOR operation and one memory access. The required time complexity of Steps 3 to 7 is approximately estimated as ($2^{n -a}$) memory accesses, assuming $2^{n -a}$ is sufficiently larger than $2^{n -b}$. Step 8 is mounted only $2^{-n + 2a} \times 2^{n -a} = 2^a$ times with $\mathcal {P}$ computations. Step 4 requires $2^{n-a}$ data, since a bits of state S are fixed when computing the g function with each $k_1$.

-Time complexity::

($(2^{b})^{2^a} \cdot 2^c+ 2^{a}$) $\mathcal {P}$ computations + ($2^{n -a}$) MA,

-Memory::

$2^{a}$ blocks,

-Data::

$2^{n-a}$ chosen plaintexts.

Summary. The computational costs for the time-optimized attack on the 2EM-1 are estimated as Table 5. For $n = 64$, 128, 256, time complexity is reduced by properly choosing the values of b, although number of memory access is unchanged. Basically, it is very hard to compare the cost of encryption and memory access because it strongly depend on the execution environments, the size of table and the underlying permutation. Thus, we do not claim that time complexity is sufficiently improved by this algorithm. However, obviously the cost of encryptions are significantly reduced. We believe that it is an interesting tradeoff.

Table 5. Summary of computational costs for the time-optimized attack on the 2-round Even-Mansour cipher.

6 Application to 2EM-2

Our key recovery attacks on 2EM-1 are applicable to the other minimized construction 2EM-2:

$$\begin{aligned} E'^{(2)}_{K}(x)=P(P(x\oplus K)\oplus \pi (K))\oplus K, \end{aligned}$$

where $\pi$ is any linear orthomorphism of $\mathbb {F}_2^n$. In this section, we consider the 2EM-2 whose $\pi$ is Feistel-like construction ($\pi$: $(x,y) \mapsto (x \oplus y, x)$) as an example. The same idea is naturally applied to another candidate of $\pi$.

Recall that the point of our attacks is to find (target) partial invariable pairs to mount the matching with input-restricted public permutations in the line of the meet-in-the-middle attack. To take care of the key scheduling function $\pi$, we further divide the $(n-a)$-bit $k_1$ into an $(n/2 - a)$-bit $k_{1L}$ and an (n / 2)-bit $k_{1R}$ in the basic attack on 2EM-1. Then, $\pi (K)$ is expressed as $(k_{1R} \oplus (k_{1L}||k_0))||(k_{1L}||k_0)$, and 2EM-2 is illustrated as shown in Fig. 6. Here, a-bit $k_0$, which is for partial invariable pairs, is used twice after the first permutation P. Since the bottom a-bit input of the second permutation P is affected by only the value of $k_0$ after the first permutation, i.e. $k_{1L}$ and $k_{1R}$ does not affect the a-bit input of the second permutation, we can use partial invariable pairs of a-bit $k_0$ to fix a bits of inputs of second permutation. Using it, we can mount basic attacks on 2EM-2 in the same manner of 2EM-1. For low-data attacks or time-optimized attacks, by dynamically finding invariable pairs of $k_0$ in the online phase to fix the part of the plaintext or inputs of the second permutation, we can mount the same attacks of 2EM-1 to 2EM-2.

In the case of different linear orthomorphism functions as a key scheduling function, our attacks are feasible as long as we can find partial invariable pairs that fix the part of inputs of the second permutation. In the other examples such as a simple rotation and a field multiplication (e.g. $\pi$: $(x) \mapsto (x \times c)$, where $c \ne 0, 1$), there exist such invariable pairs of a-bit $k_0$ that is able to fix a-bit of inputs of the second permutation, because these orthomorphism functions are not full diffusion function in which an input bit affect any bit of the output.

Fig. 6.

Application to 2EM-2.

7 Conclusion

In this paper, we proposed new key recovery attacks on the two minimal two-round Even-Mansour ciphers. Our attacks are based on the advanced meet-in-the-middle technique combined with our novel matching approach called partial invariable pair and the matching with the input-restricted public permutation. We presented the first attack that the data complexity is less than the birthday barrier, i.e. $2^{n/2}$, on the minimal two-round n-bit Even-Mansour ciphers, although in the chosen-plaintext setting. Then, by dynamically finding partial invariable pairs, the further improvements on the attacks that require the less data or the less time complexity were shown. We emphasize that our low-data attack on the two-round 64-bit Even-Mansour ciphers requires only $2^{8}$ chosen plaintexts. In this case, the minimum value of the product of time and data complexity is $2^{70}$ which is close to the proved lower bound on the product of time and data complexity for the one-round Even-Mansour ciphers ($2^{64}$). Our results revealed that adding one round to the one-round Even-Mansour ciphers does not sufficiently improve the security against the key recovery attacks.