Power Control in D2D Network Based on Game Theory

Abstract

This paper considers power control problem based on Nash equilibrium (NE) to eliminate interference in multi-cell device-to-device (D2D) network. The power control problem is modeled as a non-cooperative game model, and a user residual energy factor is introduced in the formulation. Based on the proof of the existence and uniqueness of Nash equilibrium, a distributed iterative game algorithm is proposed to realize power control. Simulation results show that the proposed algorithm can converge to Nash equilibrium quickly, and obtain a better equilibrium income by adjusting the residual energy factor.

1 Introduction

With the requirement for high speed and efficiency of data transmission, the limited spectrum resource brings great challenges for mobile network communication. D2D communication is a new wireless technology, where two devices can communicate with each other without exchanging information from base station, so that it cannot only reduce the burden of base station, but also improve communication quality of cellular users [1]. However, the D2D users will be suffered from interference of other users in cellular system. Therefore, the interference elimination has been investigated in recent years [2].

In [3], the authors studied that the D2D users and the cellular users use the same channel resources by multiplexed mode. Although it can improve spectrum utilization, it will introduce a new kind of interference. The authors in [4] investigated a power control method for single cellular system containing one cellular link and one D2D link. The algorithm can reduce the interference significantly between D2D users and cellular users. In [5], the authors studied the interference elimination problem of multi-cell D2D network, where the cellular users are communicated by base station schedule and the D2D link communication is guaranteed by power control.

The previous work mainly focused on the centralized power control method for D2D network, while the distributed implementation is less concerned. Therefore, we studied distributed power control method in this paper by use of game theory. We first establish a static game model in hybrid multi-cell D2D network, and then prove the existence and uniqueness of the Nash equilibrium. Finally, the distributed power control method is iteratively implemented to obtain the optimal state of Nash equilibrium. Simulation results show that the game model designed in this paper can converge quickly to Nash equilibrium, and the system can get better balance by adjusting the residual energy factor.

2 System Model

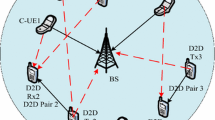
The system model of D2D network is shown in Fig. 1. We consider a multi-cell system containing D2D links, and the adjacent cells use the same frequency band for multiplexing communication. Assume there are $N$ cellular and D2D links in the system to use the same frequency resource. To eliminate the co-channel interference among the different cellular links and the interference between the cellular links and the D2D links, we propose a power control method based on game theory with pricing mechanism.

Fig. 1.

D2D network system model

According to game theory, there are three elements should be considered, which include the player, the strategy and the utility function. We define the power control model as $G = [N,P,U]$ in multi-cell D2D network, and introduce the three elements:

• (1) Player: Assume each cellular link and D2D link are the participants making decision of the game. We denote $N = \{ 1,2,\, \ldots ,\,N\}$ to be the participant set and each element represents one communication link.

• (2) Strategy: Assume one communication link is denoted by $j \in N$, where the transmit power is $p_{j} \in P_{j}$. Here $P_{j}$ is the available transmit power region of the link $j$, i.e. the strategy space of the game player. All the strategies constitute $P = \left( {p_{1} ,p_{2} ,\, \ldots ,\,p_{N} } \right)$, and all the strategy space combinations can be expressed by $P = \times_{i \in N} P_{i}$. Besides, $P_{ - j} \in \times_{i \in N,\,i \ne j} P_{i}$ represents all the left users’ strategy space combination except the link $j$. Let $P_{j} = \left[ {0,p_{\hbox{max} } } \right]$ and $p_{ \hbox{max} }$ is the maximum available transmit power for the user.

• (3) Utility function: Define $u_{j} \left( {p_{j} ,p_{ - j} } \right) = \log |1 + \frac{{\varepsilon_{j} h_{j} p_{j} }}{{\sigma^{2} + \sum\limits_{k = 1,\;k \ne j}^{N} {h_{k} p_{k} } }}| - \varepsilon_{j} h_{j} p_{j}^{2}$, where $u_{j}$ is the utility function of user $j$ and it represents the payoff obtained by the game players after making decision. $h_{j}$ is the channel gain of the link $j$ and $\sigma^{2}$ is the variance of the additive white Gaussian noise. Unlike [6], we introduce a user residual energy factor $\varepsilon$ in the utility function, which is defined as

$$ \varepsilon = E_{j}^{\hbox{max} } /\Delta E_{j} $$

(1)

where $\Delta E_{j}$ is the residual energy transmitted by link $j$, and its maximum valve is $E_{j}^{\hbox{max} }$. The energy factor $\varepsilon$ describes a price law. On one hand, when the supply exceeds the demand, the payment for the price of energy consumption is low and the user can consume more energy to obtain better performance. On the other hand, when the demand exceeds supply, the energy consumption should pay more prices. Therefore, adjusting $\varepsilon$ can make the performance and energy consumption in a reasonable trade-off state. Note that $\varepsilon$ is regarded as a control factor in the simulation.

Here we formulate the problem to establish a non-cooperative power control game model with pricing mechanism, which is

$$ \mathop { \hbox{max} }\limits_{{p_{j} \, \in \,P_{j} }} u_{j} \left( {p_{j} ,p_{ - j} } \right),j \in N $$

(2)

In this paper, we use Nash equilibrium to solve the problem. We define the policy combination $p^{*} = \left( {p_{1}^{*} ,p_{2}^{*} , \ldots ,p_{N}^{*} } \right) \in p$ as a Nash equilibrium, and establish the below expression

$$ u_{j} (p_{j}^{*} ,p_{ - j}^{*} ) \ge u_{j} (p_{j} ,p_{ - j}^{*} ),\forall p_{j} \in P_{j} ,j \in N $$

(3)

If the game players adopt the strategy combination $p^{*}$, they cannot leave and change the strategy combination, so that the Nash equilibrium will be the optimal solution.

3 Non-cooperative Power Control Game Analysis

According to the model in Eq. (2), we prove the existence and uniqueness of Nash equilibrium in this section. After that, we use a distributed iterative power algorithm to solve the Nash equilibrium point.

3.1 Existence

Theorem 1:

Nash equilibrium exists in the power control game model $G = [N,P,U]$.

Proof:

Power strategy space is a non-empty, closed, and bounded convex set in Euclidean space. The utility function $u_{j}$ is continuous for the strategy combination $p$, so that we obtain

$$ \frac{{\partial^{2} u_{j} (p_{j} ,p_{ - j} )}}{{\partial p_{j}^{2} }} = \frac{{ - \varepsilon_{j}^{2} h_{j}^{2} }}{{\left( {\sigma^{2} + \sum\limits_{k = 1,\;k \ne j}^{N} {h_{k} p_{k} + \varepsilon_{j} h_{j} p_{j} } } \right)^{2} }} - 2\varepsilon_{j} h_{j} < 0 $$

(4)

Therefore, $u_{j} (p_{j} ,p_{ - j} )$ is quasi-concave for $p_{j}$ of the $j$ th player [7]. According to the game existence theorem in [8], the game $G$ has Nash equilibrium.

3.2 Uniqueness

Theorem 2:

The iterative game algorithm can converge to the unique equilibrium point.

Proof:

If we want to prove there is Nash equilibrium point in the game, the iterative function should meet the positive $r\left( p \right) \ge 0$, monotonic $r\left( p \right) \le r\left( {p^{{\prime }} } \right)$, and expandability $r\left( {Tp} \right) > \frac{1}{T}r\left( p \right)$, where $r\left( p \right)$ is the optimal response strategy set.

Given the strategies $p_{ - j}$, the optimal response strategy set of game players is

$$ r_{j} \left( {p_{ - j} } \right) = \left( {p_{j}^{*} |p_{j}^{*} = \arg \mathop {\hbox{max} }\limits_{{p_{j} }} u_{j} \left( {p_{j} ,p_{ - j} } \right)} \right) $$

(5)

All the players $r_{j} \left( {p_{ - j} } \right)$ form the vector as

$$ r\left( p \right) = \left( {r_{1} \left( {p_{ - 1} } \right),r_{2} \left( {p_{ - 2} } \right), \cdots ,r_{j} \left( {p_{ - j} } \right), \cdots ,r_{N} \left( {p_{ - N} } \right)} \right) $$

(6)

According to the concave of utility function, we have $\arg \mathop {\hbox{max} }\limits_{{p_{j} }} u_{j} u_{j} \left( {p_{j} ,p_{ - j} } \right) = \hbox{min} \left( {\tilde{p}_{j} ,p_{\hbox{max} } } \right)$.

Let

$$ \frac{{\partial u_{j} \left( {p_{j} ,p_{ - j} } \right)}}{{\partial p_{j} }} = \frac{{\varepsilon_{j} h_{j} }}{{\sigma^{2} + \sum\limits_{k = 1,\;k \ne j}^{N} {h_{k} p_{k} + \varepsilon_{j} h_{j} p_{j} } }} - 2\varepsilon_{j} p_{j} h_{j} = 0 $$

(7)

and we obtain

$$ \begin{array}{*{20}l} {\tilde{p}_{j} = \tilde{p}_{j} \left( {p_{ - j} } \right) = \frac{{ - \left( {\sigma^{2} + \sum\limits_{k = 1,\;k \ne j}^{N} {h_{k} p_{k} } } \right) + \sqrt {\left( {\sigma^{2} + \sum\limits_{k = 1,\;k \ne j}^{N} {h_{k} p_{k} } } \right)^{2} + 2\varepsilon_{j} h_{j} } }}{{2\varepsilon_{j} h_{j} }}} \hfill \\ {\left( {{\text{Negative}}\,{\text{solution}}} \right)} \hfill \\ \end{array} $$

(8)

Therefore, the optimal response strategy is

$$ p_{j}^{*} = p_{j}^{*} \left( {p_{ - j} } \right) = \hbox{min} \left( {\tilde{p}_{j} ,p_{\hbox{max} } } \right) $$

(9)

The optimal response strategy vector is

$$ r\left( p \right) = \left( {p_{1}^{*} \left( {p_{ - 1} } \right),p_{2}^{*} \left( {p_{ - 2} } \right), \cdots ,p_{N}^{*} \left( {p_{ - N} } \right)} \right) $$

(10)

• (1) Positive: If $p \ge 0$, then $r\left( p \right) \ge 0$. If all the elements of a vector are not less than the corresponding elements of another vector, the former one will be greater than or equal to the latter vector.

• (2) Monotonicity: If $p \ge p^{{\prime }}$, then $r\left( p \right) \le r\left( {p^{{\prime }} } \right)$.

Proof:

If $p \ge p^{{\prime }}$, then

$$ \sigma^{2} + \sum\limits_{k = 1,\;k \ne j}^{N} {h_{k} p_{k} } \ge \sigma^{2} + \sum\limits_{k = 1,\;k \ne j}^{N} {h_{k} p_{k}^{{\prime }} } $$

(11)

Let $x = \sigma^{2} + \sum\limits_{k = 1,\;k \ne j}^{N} {h_{k} p_{k} }$, we have

$$ f(x) = \frac{{ - x + \sqrt {x^{2} + 2\varepsilon_{j} h_{j} } }}{{2\varepsilon_{j} h_{j} }} $$

(12)

and obtain

$$ \frac{df(x)}{dx} = - \frac{1}{{2\varepsilon_{j} h_{j} }} + \frac{1}{{2\varepsilon_{j} h_{j} }}\frac{x}{{\sqrt {x^{2} } + 2\varepsilon_{j} h_{j} }} < 0 $$

(13)

The function is a monotonically decreasing function, i.e. $r\left( p \right) \le r\left( {p^{{\prime }} } \right)$, so that the optimal response strategy vector satisfies the monotonicity.

• (3) Extensibility: If $\forall T > 1$, then $r\left( {Tp} \right) > \frac{1}{T}r\left( p \right)$.

Proof:

We have

$$ p_{j} \left( {\tilde{T}p_{ - j} } \right) = \frac{{ - \left( {\sigma^{2} + T\sum\limits_{k = 1,\;k \ne j}^{N} {h_{k} p_{k} } } \right) + \sqrt {\left( {\sigma^{2} + T\sum\limits_{k = 1,\;k \ne j}^{N} {h_{k} p_{k} } } \right)^{2} + 2\varepsilon_{j} h_{j} } }}{{2\varepsilon_{j} h_{j} }} $$

(14)

$$ \frac{1}{T}\tilde{p}_{j} \left( {p_{ - j} } \right) = \frac{1}{T}\frac{{ - \left( {\sigma^{2} + \sum\limits_{k = 1,\;k \ne j}^{N} {h_{k} p_{k} } } \right) + \sqrt {\left( {\sigma^{2} + \sum\limits_{k = 1,\;k \ne j}^{N} {h_{k} p_{k} } } \right)^{2} + 2\varepsilon_{j} h_{j} } }}{{2\varepsilon_{j} h_{j} }} $$

(15)

so that

$$ \begin{aligned} \frac{{\tilde{p}_{j} \left( {Tp_{ - j} } \right)}}{{\frac{1}{T}\tilde{p}_{ - j} \left( {p_{ - j} } \right)}} & = T\frac{{ - \left( {\sigma^{2} + T\sum\limits_{k = 1,\;k \ne j}^{N} {h_{k} p_{k} } } \right) + \sqrt {\left( {\sigma^{2} + T\sum\limits_{k = 1,\;k \ne j}^{N} {h_{k} p_{k} } } \right)^{2} + 2\varepsilon_{j} h_{j} } }}{{ - \left( {\sigma^{2} + \sum\limits_{k = 1,\;k \ne j}^{N} {h_{k} p_{k} } } \right) + \sqrt {\left( {\sigma^{2} + \sum\limits_{k = 1,\;k \ne j}^{N} {h_{k} p_{k} } } \right)^{2} + 2\varepsilon_{j} h_{j} } }} \\ & = T\frac{{\left( {\sigma^{2} + \sum\limits_{k = 1,\;k \ne j}^{N} {h_{k} p_{k} } } \right) + \sqrt {\left( {\sigma^{2} + \sum\limits_{k = 1,\;k \ne j}^{N} {h_{k} p_{k} } } \right)^{2} + 2\varepsilon_{j} h_{j} } }}{{\left( {\sigma^{2} + T\sum\limits_{k = 1,\;k \ne j}^{N} {h_{k} p_{k} } } \right) + \sqrt {\left( {\sigma^{2} + T\sum\limits_{k = 1,\;k \ne j}^{N} {h_{k} p_{k} } } \right)^{2} + 2\varepsilon_{j} h_{j} } }} > 1 \\ \end{aligned} $$

(16)

and we obtain

$$ r\left( {Tp} \right) > \frac{1}{T}r\left( p \right) $$

(17)

It means that the optimal response strategy vector can be extended.

According to the Ref. [9], we can conclude that the non-cooperative power control game has a unique Nash equilibrium point, which can be simply expressed by

$$ p = \left( {p_{1}^{*} \left( {p_{ - 1} } \right),\;p_{2}^{*} \left( {p_{ - 2} } \right), \cdots ,p_{N}^{*} \left( {p_{ - N} } \right)} \right) $$

(18)

3.3 Distributed Iterative Game Algorithm

Based on the proofs in Sect. 3.2, we present a distributed iterative algorithm to solve the Nash equilibrium. The realization is summarized below.

• Step 1: Define the number of iteration $M$, and the stop criteria $U$.

  Set $m = 0$.

  Set the initial value of the strategy combination $p^{(0)} = 0$;

• Step 2: Set $m = m + 1$.

  Update the strategy via Eq. (9) to obtain new strategy $p^{(m)}$ by use of $p^{(m - 1)}$.

• Step 3: Repeat step 2 until $p^{(m)} - p^{(m - 1)} \le U$, and the algorithm ends. The output of Nash equilibrium point strategy is $p^{(m)}$.

Note that the players only know their own channel gain $h_{j}$ and the corresponding energy factor $\varepsilon_{j}$ when the Nash equilibrium point is calculated, so that the algorithm is implemented by distributed way.

4 Simulation Results

In this section, we perform the proposed non-cooperative power control game algorithm in D2D network by matlab simulation. The wireless system in simulation composes four cells c ₁–c ₄, and each cell has single cellular link and single D2D link, so that $N = 8$. The game player set is expressed as $N = \{ 1,2,\, \ldots ,\,8\}$. Assume all the links use the same frequency band. The link gains $h_{j}$ of the four cellular links are assumed to be 0.5, 0.7, 0.9, 1.1, and the other four D2D links gains are 1.2, 1.6, 2.0, 2. The variance of additive white Gaussian noise is unit. The maximum transmit power $p_{\hbox{max} }$ of the D2D link and the cellular link is also unit. The compared algorithm comes from Ref. [9].

Figure 2 shows the valves of utility function varied with the iteration number. The control factor is set to be 2. Note the control factor in Ref. [9] represents power coefficient. From the simulation, it can be seen that our algorithm converges to the stable state within six times, while the compared algorithm in Ref. [9] needs eight times. Therefore, our method can converge more quickly than the compared one. Besides, we find that the valve of utility function of our method is bigger than the compared method, which means our method is more stable.

Fig. 2.

Utility function value comparison for two algorithms

Figure 3 gives the bar chart of the iteration number varied with the control factor. It shows that our algorithm has smaller iteration number when the control factor is bigger than 1, which means the algorithm is more efficient.

Fig. 3.

Comparison of iteration number for two algorithms

Figure 4 gives the transmit power results for all of users in Nash equilibrium state. It observed that all of transmit power of users tend to be stable. Hence the proposed price function can make the system achieve the equilibrium stable state.

Fig. 4.

Transmit power of each user in Nash equilibrium

From the simulations, we conclude that the power control algorithm based on pricing mechanism can effectively improve the performance of the system if pricing factor is adjusted reasonably.

5 Conclusion

In this paper, we investigate the power control problem in D2D network. A non-cooperative game model based on pricing mechanism is established to eliminate the interference in complex environment. We design a price function and prove its existence and uniqueness, and then propose a distributed iterative algorithm which can converge to Nash Equilibrium point. From the simulation, it can be observed that our algorithm improve the system performance compared with the conventional method.