Generating Checking Sequences for User Defined Fault Models

Abstract

In this paper, we investigate how a checking sequence can be generated from a Finite State Machine, with respect to a user-defined set of faults, modeled as a nondeterministic FSM, called Mutation Machine (MM). We propose an algorithm for generating a checking sequence in this scenario and demonstrate its correctness.

1 Introduction

Generation of checking sequence (CS) from a Finite State Machine (FSM) is a relevant problem, when the implementation may not be reset or when reset operation it prohibitively costly. There are methods which, given a distinguishing sequence, can generate a checking sequence in polynomial time [2, 3]. Other methods generate checking sequence from characterization sets instead of a distinguishing sequence [1], since the former is available for any minimal machine, while the latter may not exist. Those methods, however, rely on the repetition of the sequences in the characterization sets, resulting in an exponentially long sequence. These methods also consider the classical fault domain where the implementation may have arbitrary faults, except extra states.

In this paper, we investigate how a CS can be generated from an FSM, with respect to a subset of faults. The faults of interest are modeled as a nondeterministic FSM, called Mutation Machine (MM), such that any implementation is assumed to be a deterministic submachine of the MM. We propose an algorithm for generating a CS in this scenario. After demonstrating the correctness of the algorithm, we illustrate its application on a simple example.

2 Checking Sequence Construction

An FSM is a tuple M = (S, S ₀, X, O, h), where S is the set of states, $S_{0} \, \subseteq \,S$ is the set of initial states, X is the set of inputs, O is the set of outputs, which satisfy the condition $I\, \cap \,O =$ $\varnothing$, and $h\, \subseteq \,\left( {S \times X \times O \times S} \right)$ is the set of transitions. For state s and input x, let h(s, x) be the set of transitions from state s with input x. The FSM M is initialized if |S ₀| = 1 and is deterministic if for each (s, x) $\in$ $S \times X,\,\,\left| {h\left( {s,x} \right)} \right| \le 1$. For an initialized FSM, where |S ₀| = 1, write s ₀, instead of {s ₀}.

The machine M is completely specified (complete FSM) if |h(s, x)| ≥ 1 for each $\left( {s,x} \right) \in S \times X;$ otherwise, it is partially specified (partial FSM).

A path of the FSM M = (S, S ₀, X, O, h) from state s $\in$ S is a sequence of transitions (s ₁, x ₁, o ₁, s ₂) (s ₂, x ₂, o ₂, s ₃) … (s _k , x _k , o _k , s _k+1), such that (s _i , x _i , o _i , s _i+1) $\in$ h, for $1 \le i \le k$. Notice that we also allow a path to be empty, represented by $\varepsilon$. The machine is strongly connected, if it has a path from each state to any other state. The input projection (output projection) of the path is x ₁ x ₂ … x _k (o ₁ o ₂ … o _k ). Input sequence $\upbeta \in {I^*}$ is a defined input sequence in state s of M if it is an input projection of a path from state s. We use $\Upomega \left( s \right)$ to denote the set of all input sequences defined in state s and $\Upomega \left( M \right)$ for the states in S ₀, i.e., for M. $\Upomega \left( M \right)$ = X* holds for any complete machine M, while for a partial FSM $\Upomega \left( M \right)$ $\subset X^{*}$.

Given a path p, let trav(p) be the set of transitions of M which appear in p. For state s and input x, let trans(p, (s, x)) be the set of transitions from state s with input x in trav(p), i.e., $trans\left( {p,\,\left( {s,x} \right)} \right) = trav\left( p \right) \cap h\left( {s,x} \right)$. For the FSM M = (S, S ₀, X, O, h), given a set of states $S^{\prime } \, \subseteq \,S$ and an input sequence $\upalpha$, let $path\left( {S^{\prime } ,\upalpha} \right)$ be the set of paths of M from states of $S^{\prime }$ with input projection $\upalpha$. We denote $path\left( {S_{0} ,\upalpha} \right)$ by $path_{M} \left(\upalpha \right)$. Let $\lambda \left( {S^{\prime } ,\upalpha} \right)$ be the set of output projections of the paths in $Path\left( {S^{\prime } ,\upalpha} \right)$; we denote $\lambda \left( {S_{0} ,\upalpha} \right)$ by $\lambda_{M} \left(\upalpha \right)$. Unless stated otherwise, paths are assumed to be from an initial state.

Given states $s,\,t \in S$ of the deterministic FSM M = (S, S ₀, X, O, h), t is quasi-equivalent to s, if $\Upomega \left( t \right) \supseteq \Upomega \left( s \right)\,{\rm{and}}\,\lambda \left( {t,\upalpha } \right) = \lambda \left( {s,\upalpha } \right)\,{\rm{for}}\,{\rm{all}}\,\upalpha \in \Upomega \left( s \right)$; moreover, in case $\Upomega \left( t \right) \supseteq \Upomega \left( s \right)\,$, states are equivalent. States s, $t \in S$ are distinguishable, if $\lambda \left( {t,\upalpha} \right) \ne \lambda \left( {s,\upalpha} \right)$ for some $\alpha \in \Upomega \left( t \right) \cap \,\Upomega \left( s \right)$. The machine is reduced, if any two states are distinguishable. The quasi-equivalence (equivalence) of two deterministic FSMs is the corresponding relation of their initial states.

Spec = (S, s ₀, X, O, h) is an initialized deterministic FSM specification. We assume that it is strongly-connected machine, not necessarily complete and reduced.

Given an FSM M = (S, s ₀, X, O, h) and $s \in S$, let M/s be the FSM (S, s, X, O, h), i.e., M initialized in state s. We let s-after-α denote the set of states reached by input sequence α from state s; if α is applied to the initial state of M then we write M-after-α instead of s ₀-after-α; for deterministic machines, we write s-after-$\upalpha$ = $s^{\prime }$ instead of s-after-$\upalpha$  = $\left\{ {s^{\prime } } \right\}$.

We use a so-called mutation machine MM = $\left( {S^{\prime } ,S_{0}^{\prime } ,X,O,h^{\prime } } \right)$ which is a completely specified possibly nondeterministic FSM.

FSM M = (S, s ₀, X, O, h) is a submachine of MM = $\left( {S^{\prime } ,S_{0}^{\prime } ,X,O,h^{\prime } } \right)$ iff $S\, \subseteq \,S^{\prime }$, $s_{0} \in S_{0}^{\prime } \,{\text{and}}\,h\, \subseteq \,h^{\prime }$. Any complete deterministic submachine of MM is one of the mutants of Spec. The number of mutants is $\left| {S_{0}^{\prime } } \right|\prod\nolimits_{{\left( {s,x} \right) \in S \times X}} {\left| {h^{\prime } \left( {s,x} \right)} \right|}$. For the sets of states S, inputs X and outputs O, we define the machine Chaos(S, X, O) = $\left( {S,s_{0} ,X,O,\left( {S \times X \times O \times S} \right)} \right)$ representing the universe of all FSMs with |S| states.

Let Prod be the product of Spec and MM = $\left( {S^{\prime } ,S_{0}^{\prime } ,X,O,h^{\prime } } \right)$; the states of Prod is a subset of $\left( {S \cup \left\{ \Delta \right\}} \right) \times S^{\prime }$. A state $\left( {\Delta ,s} \right)$ is a $\Delta$-state. The product Prod = (P, P ₀, X, O, H), where $P_{0} = \left\{ {\left( {s_{0} ,\,s^{\prime } } \right)\left| {s^{\prime } \in S_{0}^{{^{\prime } }} } \right.} \right\}$ is such that P and H are the smallest sets satisfying the following rules:

• 1. If $\left( {s,s^{\prime } } \right) \in P,\left( {s,\,x,\,o,\,t} \right) \in h,\left( {s^{\prime } ,\,x,\,o^{\prime } ,\,t^{\prime } } \right) \in h^{\prime } ,\,{\text{and}}\,o = o^{\prime }$, then $\left( {t,t^{\prime } } \right) \in P\,{\text{and}}\,\left( {\left( {s,s^{\prime } } \right),x,o,\left( {t,t^{\prime } } \right)} \right) \in H.$

• 2. If $\left( {s,s^{\prime } } \right) \in P,\left( {s,\,x,\,o,\,t} \right) \in h,\left( {s^{\prime } ,\,x,\,o^{\prime } ,\,t^{\prime } } \right) \in h^{\prime } ,\,{\text{and}}\,o \ne o^{\prime }$, then $\left( {\Delta ,t^{\prime } } \right) \in P\,{\text{and}}\,\left( {\left( {s,s^{\prime } } \right),x,o^{\prime } ,\left( {\Delta ,t^{\prime } } \right)} \right) \in H.$

Notice that $\Delta$-states are sink states. If the product has no $\Delta$-states, then any mutant of MM is quasi-equivalent to Spec.

An input sequence $\upomega = \Upomega \left( {Spec} \right)$ is a checking sequence for Spec w.r.t. MM, if for each deterministic submachine N of MM, if $\lambda_{N} \left(\upomega \right) = \lambda_{Spec} \left(\upomega \right)$, then N is quasi-equivalent to Spec/s, where $s \in S$.

Given a path p = ((s ₁, m ₁), x ₁, o ₁, (s ₂, m ₂)) ((s ₂, m ₂), x ₂, o ₂, (s ₃, m ₃)) … ((s _k , m _k ), x _k , o _k , (s _k+1, m _k+1)) of the product Prod of Spec and MM, let p _↓MM be the corresponding path in MM, i.e., $p_{ \downarrow MM}$ = (m ₁, x ₁, o ₁, m ₂) (m ₂, x ₂, o ₂, m ₃) … (m _k , x _k , o _k , m _k+1).

A path of the product Prod is deterministic (w.r.t. MM) if for every state s and input x, |trans(p _↓MM , (s, x))| $\le$ 1. Given a set of paths Q of Prod, let det(Q) be the set of paths of Q which are deterministic (w.r.t. MM) and $\Delta$(Q) be the set of deterministic paths which leads to a $\Delta$-state.

Lemma 1.

Let $\upomega$ be an input sequence such that for each input sequence $\upalpha$, we have that Δ(det(path _MM ($\upomega \upalpha$))) = $\varnothing$. Then, $\upomega$ is a checking sequence for Spec w.r.t. MM.

Proof. Assume that ω is not a checking sequence for Spec w.r.t. MM, but for each input sequence $\upalpha$, we have that Δ(det(path _MM ($\upomega \upalpha$))) = $\varnothing$.

Thus, there exists a deterministic submachine N of MM, such that $\lambda_{N} \left(\upomega \right) = \lambda_{Spec} \left(\upomega \right)$, and for each $s \in S$, we have that N is not quasi-equivalent to Spec/s. This implies that state N-after-$\upomega$ is not quasi-equivalent to any state Spec/s-after-$\upomega$. Then for each $s \in S$, there exists an input sequence $\upbeta \in \Upomega \left( s \right)$ such that $\lambda_{{N /N{\text{ - after - }}\omega }} \ne \lambda_{{Spec/s{\text{ - after - }}\omega }} \left(\upbeta \right)$.

Let p _ωβ be the path in N which has ωβ as the input projection. It follows that $p_{{\upomega \upbeta }} \in \Delta \left( {det\left( {path_{MM} \left( {\upomega \upbeta } \right)} \right)} \right)$, since N is deterministic; moreover, it leads to a $\Delta$-state, since $\lambda_{{N /N{\text{ - after - }}\upomega}} \left(\upbeta \right) \ne \lambda_{{Spec/s{\text{ - after - }}\upomega}} \left(\upbeta \right)$, thus, $\Delta \left( {det\left( {pat{h_{MM}}\left( {\omega \beta } \right)} \right)} \right) \ne \varnothing$, a contradiction. □

Thus, by Lemma 1, if the algorithm stops, the resulting sequence $\upomega$ is indeed a checking sequence. It remains to show that it will always stop for any specification and mutation machine.

Lemma 2.

After a finite number of steps, the algorithm terminates.

Proof. First, notice that for a given deterministic submachine of MM, there is exactly one deterministic path with a given input sequence projection (many submachines can share the same path). Thus, the number of paths in $det\left( {path_{MM} \left(\upomega \right)} \right)$ is limited by the number of deterministic submachines of MM; as there are finitely many such submachines, there are finitely many paths in $det\left( {path_{MM} \left(\upomega \right)} \right)$. Let Sub _ω be the set of deterministic submachines for which correspond the paths in $det\left( {path_{MM} \left(\upomega \right)} \right)$. At least one path in $det\left( {path_{MM} \left(\upomega \right)} \right)$ leads to a $\Delta$-state, since the algorithm updated $\upomega$ in the previous iteration to $\upomega \upalpha$ and $\Delta \left( {det\left( {path_{MM} \left( {\upomega \upalpha } \right)} \right)} \right) \ne$ $\varnothing$.

Let $\upalpha$ be a nonempty input sequence, such that $\Delta \left( {det\left( {path_{MM} \left( {\upomega \upalpha } \right)} \right)} \right) \ne$ $\varnothing$. Let $Sub_{{\upomega \upalpha }}$ be the set of deterministic submachines each which has a path in $det\left( {path_{MM} \left( {\upomega \upalpha } \right)} \right)$. As $\Delta$-states are sink states, any submachine in $Sub_{\upomega}$ with a path to a $\Delta$-state is not in $Sub_{{\upomega \upalpha }}$. Thus, there exists at least one submachine which is in $Sub_{\upomega}$ but not in Sub _ωα. The set of submachines with paths in $det\left( {path_{MM} \left(\upomega \right)} \right)$ is thus reduced each time ω is updated by the algorithm. As the set of submachines is finite, eventually after a finite number of steps the set $Sub_{\upomega}$ has no more machines distinguishable from the specification machine Spec, which means that for any input sequence $\upalpha$, it holds that $\Delta \left( {det\left( {path_{MM} \left( {\upomega \upalpha } \right)} \right)} \right) \ne$ $\varnothing$, and the algorithm terminates. □

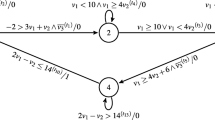
We now illustrate the application of the algorithm. Consider the FSM in Fig. 1a. Observe first that it has no distinguishing sequence. In Fig. 1b, we include a mutation machine for which we will generate a checking sequence.

Fig. 1.

(a) Specification FSM. (b) The Mutation Machine MM

Notice that there are twelve deterministic complete submachines of MM. One possibility to obtain a checking sequence for Spec is to use any of the applicable methods [2, 3], ignoring MM. However, the resulting checking sequence would be unnecessarily long.

The algorithm starts by building the product of Spec and MM, as well as initializing ω with the empty sequence. The nonempty input sequence α = aa is such that ωα reaches a $\Delta$-state in the product, since $det\left( {path_{MM} \left( {\upomega \upalpha } \right)} \right)$ = {((1, a, 0, 2), (2, a, 1, 3)), ((1, a, 0, 2) (2, a, 0, $\Delta$)), ((1, a, 0, 2), (2, a, 1, 2))}, i.e.,$\Delta \left( {det\left( {path_{MM} \left( {\upomega \upalpha } \right)} \right)} \right) \ne$ $\varnothing$. We append α to $\omega$, so that now $\upomega$ = aa. In the next iteration, the nonempty input sequence α = ba is selected, since $det\left( {path_{MM} \left( {\upomega \upalpha } \right)} \right)$ = {((1, a, 0, 2), (2, a, 1, 3), (3, b, 1, 2), (2, a, 1, 3)), ((1, a, 0, 2), (2, a, 1, 2), (2, b, 1, 1), (1, a, 0, Δ)), ((1, a, 0, 2), (2, a, 1, 2), (2, b, 1, 3), (3, a, 1, 3)), ((1, a, 0, 2), (2, a, 1, 2), (2, b, 1, 3), (3, a, 1, 2))}, i.e., $\Delta \left( {det\left( {path_{MM} \left( {\upomega \upalpha } \right)} \right)} \right) \ne$ $\varnothing$. We append α to $\upomega$, so that now$\upomega$ = aaba. In the next iteration, the nonempty input sequence α = aba is selected, since $det\left( {path_{MM} \left( {\upomega \upalpha } \right)} \right)$ = {((1, a, 0, 2), (2, a, 1, 3), (3, b, 1, 2), (2, a, 1, 3), (3, a, 1, 3), (3, b, 1, 2), (2, a, 1, 3)), ((1, a, 0, 2), (2, a, 1, 3), (3, b, 1, 2), (2, a, 1, 3), (3, a, 1, 2), (2, b, 1, 1), (1, a, 0, Δ)), ((1, a, 0, 2), (2, a, 1, 3), (3, b, 1, 2), (2, a, 1, 3), (3, a, 1, 2), (2, b, 1, 3), (3, a, 1, 2)), ((1, a, 0, 2), (2, a, 1, 2), (2, b, 1, 3), (3, a, 1, 3), (3, a, 1, 3), (3, b, 1, 2), (2, a, 1, 2)), ((1, a, 0, 2), (2, a, 1, 2), (2, b, 1, 3), (3, a, 1, 2), (2, a, 1, 2), (2, b, 1, 3), (3, a, 1, 2))}, i.e., $\Delta \left( {det\left( {path_{MM} \left( {\upomega \upalpha } \right)} \right)} \right) \ne$ $\varnothing$. We append α to $\upomega$, so that now $\upomega$ = aabaaba. In the next iteration, the nonempty input sequence α = bba is selected, since $det\left( {path_{MM} \left( {\upomega \upalpha } \right)} \right)$ = {((1, a, 0, 2), (2, a, 1, 3), (3, b, 1, 2), (2, a, 1, 3), (3, a, 1, 3), (3, b, 1, 2), (2, a, 1, 3), (3, b, 1, 2), (2, b, 1, 1), (1, a, 0, 2)), ((1, a, 0, 2), (2, a, 1, 3), (3, b, 1, 2), (2, a, 1, 3), (3, a, 1, 3), (3, b, 1, 2), (2, a, 1, 3), (3, b, 1, 2), (2, b, 1, 3), (3, a, 1, Δ)), ((1, a, 0, 2), (2, a, 1, 3), (3, b, 1, 2), (2, a, 1, 3), (3, a, 1, 2), (2, b, 1, 3), (3, a, 1, 2), (2, b, 1, 3), (3, b, 1, 2), (2, a, 1, $\Delta$)), ((1, a, 0, 2), (2, a, 1, 2), (2, b, 1, 3), (3, a, 1, 3), (3, a, 1, 3), (3, b, 1, 2), (2, a, 1, 2), (2, b, 1, 3), (3, b, 1, 2), (2, a, 1, Δ)), ((1, a, 0, 2), (2, a, 1, 2), (2, b, 1, 3), (3, a, 1, 2), (2, a, 1, 2), (2, b, 1, 3), (3, a, 1, 2), (2, b, 1, 3), (3, b, 1, 2), (2, a, 1, $\Delta$))}, i.e., $\Delta \left( {det\left( {path_{MM} \left( {\upomega \upalpha } \right)} \right)} \right) \ne$ $\varnothing$. We append α to ω, so that ω = aabaababba. There is no nonempty input sequence such that $\Delta \left( {det\left( {path_{MM} \left( {\upomega \upalpha } \right)} \right)} \right) \ne$ $\varnothing$. Thus, by Lemma 1, aabaababba is a checking sequence for Spec with respect to MM.

Consider now the Spec in Fig. 1(a) and the corresponding Chaos(S, X, O) which represents a traditional fault domain, the universe of all FSMs with up to three states. The algorithm we propose in this paper generates the checking sequence aaaabaabababbababbabbbba, of length 24. On the other hand, the algorithm proposed in [1], generates a checking sequence of length 130.

3 Experimental Results

In this section we present some preliminary experimental results on the length of the checking sequence obtained for various size of a mutation machine. The experiments are set up as follows. For each run, a random complete deterministic FSM Spec with 5 states, 2 inputs and 2 outputs is generated, as proposed in [4]. Then, increasingly bigger mutation machines are generated from Spec by adding transitions to it. The size of the mutation machine is the number of its transitions; the smallest mutation machine is the specification itself, which the biggest one is the Chaos machine with that a given number of states, inputs and outputs. We executed 30 runs and collected the length of the obtained checking sequence. Figure 2 shows the result of the experiments. We note that, as expected, the length of the checking sequence increases with the size of the mutation machine. However, the increment tends to be smaller, as the number of transitions approaches the maximum.

Fig. 2.

Variation of the length of the checking sequence with respect to the number of transitions in the mutation machine.

4 Conclusion

In this paper, we proposed an algorithm for generating a checking sequence with respect to a user-defined fault model. In the forthcoming steps of this research, we plan to characterize scenarios when the algorithm can be effectively applied as well as its scalability.