Abstract
Extended regular expressions (with complement and intersection) are used in many applications due to their succinctness. In particular, regular expressions extended with intersection only (also called semi-extended) can already be exponentially smaller than standard regular expressions or equivalent nondeterministic finite automata (NFA). For practical purposes it is important to study the average behaviour of conversions between these models. In this paper, we focus on the conversion of regular expressions with intersection to nondeterministic finite automata, using partial derivatives and the notion of support. First, we give a tight upper bound of \(2^{O(n)}\) for the worst-case number of states of the resulting partial derivative automaton, where n is the size of the expression. Using the framework of analytic combinatorics, we then establish an upper bound of \((1.056 +o(1))^n\) for its asymptotic average-state complexity, which is significantly smaller than the one for the worst case.
This work was partially supported by CMUP (UID/MAT/00144/2013), which is funded by FCT (Portugal) with national (MEC) and european structural funds through the programs FEDER, under the partnership agreement PT2020.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Regular expressions with additional operators are used in applications such as programming languages [12], XML processing [23], or runtime verification [22]. Most of these operators do not increase their language expressive power but lead to gains in the succinctness of the representation. This is the case for intersection. For regular expressions with intersection (\(\textsf {RE}_\cap \)) (or semi-extended), several computational complexity decision problems, such as membership, equivalence and emptiness, were studied by various authors. Petersen [21] has shown that the membership problem is LOGCFL-complete, while for standard regular expressions (RE) it is NL-complete [19]. Fürer [14] has proved that inequivalence and non-empty complement are EXPSPACE-complete, which contrasts with the PSPACE-completeness of these problems for RE. The complexity of the conversions from regular expressions with intersection to standard regular expressions, and to finite automata, were recently studied by Gelade and Neven [16], Gruber and Holzer [18], and Gelade [15]. The conversion from \(\textsf {RE}_\cap \) to \(\textsf {RE} \) or to nondeterministic finite automata (NFA) is exponential and it is double exponential to deterministic finite automata (DFA). The conversion from \(\alpha \in \textsf {RE}_\cap \) to a DFA can be accomplished using Brzozowski’s derivatives [8]. From \(\textsf {RE} \) to \(\textsf {NFA} \) a standard algorithm is the partial derivative automaton construction (\(\mathcal {A}_{pd}\)) introduced by Antimirov [1], which coincides with the resolution of systems of equations by Mirkin [20]. The average complexity of these conversions was recently studied using the framework of analytic combinatorics [4, 5], and also their extension to regular expressions with shuffle [7]. For these studies, Mirkin’s construction is essential as it provides inductive definitions that can be used to obtain generating functions.
Caron et al. [9] extended the \(\mathcal {A}_{pd}\) to regular expressions with both intersection and complement (extended regular expressions)Footnote 1. In their approach a partial derivative is a set of sets of expressions (akin a disjunctive normal form), whereas here it is simply a set of expressions. In the worst-case, their approach also leads to \(\textsf {NFAs} \) that can be exponentially larger than the original expressions. Moreover, considering sets of sets of expressions would turn the analytic combinatoric analysis much harder.
In this paper we show that for \(\textsf {RE}_\cap \), Mirkin’s construction can lead to automata not initially connected and thus larger than the ones built by Antimirov’s construction. However, the two constructions can produce identical \(\textsf {NFAs} \). We present an exponential worst-case upper bound which is tight for both. Using the framework of analytic combinatorics, we give an upper bound for the asymptotic average-state complexity for the Mirkin’s construction, which turns out to be much smaller than the worst-case bound. This also means that Antimirov’s construction is asymptotically and on average much smaller than the worst-case upper bound.
2 Regular Expressions with Intersection
Let \(\varSigma =\{a_1,\ldots ,a_k\}\) be an alphabet of size k. A word over \(\varSigma \) is a finite sequence of symbols of \(\varSigma \). The empty word is denoted by \(\varepsilon \). The set \(\varSigma ^\star \) is the set of all words over \(\varSigma \). A language over \(\varSigma \) is a subset of \(\varSigma ^\star \). The set \(\textsf {RE}_\cap \) of regular expressions with intersection over \(\varSigma \) contains the expression \(\emptyset \) and all terms generated by the following grammar:
where the operator \(\cdot \) (concatenation) is often omitted. Parenthesis can also be omitted considering the following precedences for the operators: \(\star> \cdot> \cap > +\). The size of a regular expression \(\alpha \in \textsf {RE}_\cap \) is denoted by \(|\!|\alpha |\!|\) and defined as the number of occurrences of symbols (parenthesis not counted) in \(\alpha \). Similarly, \(|\alpha |_\varSigma \) denotes the number of occurrences of alphabet symbols in \(\alpha \), and \(|\alpha |_\cap \) the number of occurrences of the binary operator \(\cap \). The language \(\mathcal {L}(\alpha )\) for \(\alpha \in \textsf {RE}_\cap \) is defined as usual, with \(\mathcal {L}(\alpha \cap \beta ) = \mathcal {L}(\alpha ) \cap \mathcal {L}(\beta )\). We say that two regular expressions \(\alpha , \beta \in \textsf {RE}_\cap \) are equivalent, if \(\mathcal {L}(\alpha ) = \mathcal {L}(\beta )\), and write \(\alpha \doteq \beta \) in this case. For a set \(S \subseteq \textsf {RE}_\cap \), the language of S is defined as \(\mathcal {L}(S) = \bigcup _{\alpha \in S} \mathcal {L}(\alpha )\). The notion of equivalence extends naturally to sets of regular expressions. The left-quotient of a language \(\mathcal {L}\) w.r.t. a word \(w \in \varSigma ^\star \) is defined as \(w^{-1} \mathcal {L}= \{\; x \mid wx \in \mathcal {L}\;\}\). The algebraic structure \((\textsf {RE}_\cap , +, \cdot , \emptyset , \varepsilon )\) constitutes an idempotent semiring, that with the unary operator \(\star \) is a Kleene algebra. Antimirov and Mosses [2] presented a complete and sound axiomatization for \(\textsf {RE}_\cap \), where the binary operator \(\cap \) is idempotent, commutative, associative, distributes over \(+\), and also satisfies the following axioms, where \(a_i, a_j \in \varSigma \):
With the usual abuse of notation, define the function \(\varepsilon :\textsf {RE}_\cap \rightarrow \{\emptyset , \varepsilon \}\) by \(\varepsilon (\alpha ) = \varepsilon \) if \(\varepsilon \in \mathcal {L}(\alpha )\), and \(\varepsilon (\alpha ) = \emptyset \) otherwise. The methods developed in Sects. 3 and 4 are syntactical and aim at building automata equivalent to a given regular expression. To ensure the finiteness of the constructions it is not necessary to consider regular expressions modulo any of the above propertiesFootnote 2. However, in some examples, for the sake of succinctness, we also consider regular expressions modulo the identities of \(\cdot \) and \(+\). Note that this does not affect the upper bounds of the number of states, both in the worst and in the average case.
3 Automata and Systems of Equations
We first recall the definition of a nondeterministic finite automaton (NFA) as a tuple \(\mathcal {A}= \langle S, \varSigma , S_0, \delta , F \rangle \), where S is a finite set of states, \(\varSigma \) is a finite alphabet, \(S_0 \subseteq S\) a set of initial states, \(\delta : S \times \varSigma \rightarrow 2^S\) the transition function, and \(F \subseteq S\) a set of final states. The language of \(\mathcal {A}\) is \(\mathcal {L}(\mathcal {A})=\{w\in \varSigma ^\star \mid \delta (S_0, w) \cap F \ne \emptyset \}\). The right language of a state s, denoted by \(\mathcal {L}_s\), is the language accepted by \(\mathcal {A}\) if we take \(S_0 = \{s\}\). It is well known that, for each n-state \(\textsf {NFA} \) \(\mathcal {A}\), over \(\varSigma = \{a_1, \ldots , a_k\}\), having right languages \(\mathcal {L}_1, \ldots , \mathcal {L}_n\), it is possible to associate a system of linear language equations
where \(\mathcal {L}_{ji}={\bigcup _{l\in \delta (i,a_j)}{\mathcal {L}_l}}\) and \(\mathcal {L}(\mathcal {A})=\bigcup _{i\in S_0}\mathcal {L}_i\). In the same way, it is possible to associate to each regular expression a system of equations. We here extend Mirkin’s contruction to regular expressions with intersection.
Definition 1
Consider \(\alpha _0 \in \textsf {RE}_\cap \) over \(\varSigma = \{a_1, \ldots , a_k\}\). A support of \(\alpha _0\) is a set \(\{\alpha _1, \ldots , \alpha _n\}\) of regular expressions with intersection that satisfies a system of equations
for some \(\alpha _{1i}, \ldots , \alpha _{ki}\), where each \(\alpha _{j,i}\) is a (possibly empty) sum of elements in \(\{\alpha _1, \ldots , \alpha _n\}\).
It is clear that the existence of a support of \(\alpha \) implies the existence of an \(\textsf {NFA} \) that accepts the language of \(\alpha \).
A support for a regular expression \(\alpha \in \textsf {RE}_\cap \) can be computed using the function \(\pi : \textsf {RE}_\cap \rightarrow 2^\textsf {RE}_\cap \) defined below. First, we define some operations on sets of regular expressions. Given \(S,T \subseteq \textsf {RE}_\cap \) and \(\beta \in \textsf {RE}_\cap \),  and
and  . Note, in particular, that
. Note, in particular, that  .
.
Definition 2
Given \(\alpha \in \textsf {RE}_\cap \), the set \(\pi (\alpha )\) is inductively defined by:

Proposition 3
If \(\alpha \in \textsf {RE}_\cap \), then \(\pi (\alpha )\) is a support of \(\alpha \).
Proof
We will proceed by induction on the structure of \(\alpha \). The proof for all cases, excluding \(\alpha \cap \beta \), can be found in [4, 11, 20]. Let \(\pi (\alpha _0) = \{\alpha _1, \ldots , \alpha _n\}\) and \(\pi (\beta _0) = \{\beta _1, \ldots , \beta _m\}\) be a support of \(\alpha _0\) and \(\beta _0\), respectively. Thus,
and
where, for all \(l=1,\ldots ,k\), \(\alpha _{li}\) and \(\beta _{lj}\) are linear combinations of elements of \(\pi (\alpha _0)\) and \(\pi (\beta _0)\), respectively. We want to prove that \(\pi (\alpha _0 \cap \beta _0)\) is a support for \(\alpha _0 \cap \beta _0\). For \(i=0,\ldots ,n\) and \(j=0,\ldots ,m\), and using the axioms for \(\cap \), we have
For each \(l = 1, \ldots , k\), we know that \(\alpha _{li} = \displaystyle \sum _{i'\in I_{li}} \alpha _{i'}\) and \(\beta _{lj} = \displaystyle \sum _{j'\in J_{lj}} \beta _{j'}\), for \(I_{li}\subseteq \{1, \ldots , n\}\) and \(J_{lj} \subseteq \{1,\ldots , m\}\). And, since
we conclude that  is a support for \(\alpha _0\cap \beta _0\). \(\square \)
is a support for \(\alpha _0\cap \beta _0\). \(\square \)
Example 4
Given the regular expression \(\alpha _1 = (b + ab + aab + abab) \cap (ab)^\star \), \(\pi (\alpha _1) = \{bab \cap b(ab)^\star ,\ ab \cap b(ab)^\star ,\ b \cap b(ab)^\star ,\ \varepsilon \cap b(ab)^\star ,\ bab \cap (ab)^\star ,\ ab \cap (ab)^\star ,\ b \cap (ab)^\star ,\ \varepsilon \cap (ab)^\star \}\).
The next proposition provides an upper bound on the cardinality of the support of a regular expression.
Proposition 5
For all \(\alpha \in \textsf {RE}_\cap \), the inequality \(|\pi (\alpha )| \le 2^{|\alpha |_\varSigma - |\alpha |_\cap -1}\) holds.
Proof
We proceed by induction on the structure of the regular expression \(\alpha \). It is easily proved that the statement holds for the base cases \(\varepsilon \), \(\emptyset \) and \(a \in \varSigma \). Assume that the result holds for some \(\alpha , \beta \in \textsf {RE}_\cap \). We will make use of the fact that \(2^m + 2^n \le 2^{m+n+1}\), for any \(m,n\ge 0\). For \(\alpha + \beta \), one has
The case for \(\alpha \beta \) is analogous. For \(\alpha ^\star \), one has
Finally, for \(\alpha \cap \beta \), one has

\(\square \)
The next examples present families of regular expressions that witnesses the tightness of the upper bound established in Proposition 5.
Example 6
Let the regular expression \(r_n \in \textsf {RE}_\cap \) over \(\varSigma =\{a,b\}\) be inductively defined by \(r_0= a^\star b^\star \), \(r_1 = b^\star a\) and \(r_n = r_{n-2} \cap r_{n-1}^\star \), for \(n\ge 2\). Using the definition of support it is straightforward that \(|\pi (r_0)|=|\{a^\star b^\star ,b^\star \}|= 2^1\), \(|\pi (r_1)|=|\{b^\star a,\varepsilon \}|=2^1\), and \(|\pi (r_n)| = |\pi (r_{n-2})| \cdot |\pi (r_{n-1})|\), for \(n \ge 2\). Thus, we obtain \(|\pi (r_n)| = 2^{\mathsf {fib}(n)}\), for \(n \ge 0\), and where \(\mathsf {fib}(n)\) is the Fibonacci sequence. Also, \(|r_0|_\varSigma - |r_0|_\cap -1 = 2-0-1 = 1\), \(|r_1|_\varSigma - |r_1|_\cap -1 = 2-0-1 = 1\), and \(|r_n|_\varSigma - |r_n|_\cap -1 = |r_{n-2}|_\varSigma + |r_{n-1}|_\varSigma - |r_{n-2}|_\cap - |r_{n-1}|_\varSigma - 1 -1 = (|r_{n-2}|_\varSigma - |r_{n-2}|_\cap -1) + (|r_{n-1}|_\varSigma - |r_{n-1}|_\cap -1)\), for \(n \ge 2\). Consequently, \(|r_n|_\varSigma - |r_n|_\cap -1 = \mathsf {fib}(n)\), for \(n \ge 0\). We conclude that \(|\pi (r_n)| = 2^{|r_n|_\varSigma - |r_n|_\cap -1}\), for \(n \ge 0\).
Example 7
Let the regular expression \(r_n \in \textsf {RE}_\cap \) over \(\{a\}\), be defined inductively by \(r_0=a^\star a\) and \(r_n = r_{n-1} \cap a^\star a\), for \(n\ge 1\). We have \(\pi (r_0) = \pi (a^\star a) =\{a^\star a, \varepsilon \}\), and for \(n\ge 1\),

Thus \(|\pi (r_0)| = 2\) and \(|\pi (r_n)| = |\pi (r_0)|^{n+1} = 2^{n+1}\). Note that \(|r_n|_\varSigma = 2n + 2\) and \(|r_n|_\cap = n\). Therefore \(|\pi (r_n)|= 2^{n+1} = 2^{2n+2 - n -1} = 2^{|r_n|_\varSigma - |r_n|_\cap -1}\).
4 Partial Derivatives
The notions of partial derivatives and partial derivative automata were introduced by Antimirov [1] for standard regular expressions. We now consider the Antimirov construction from \(\textsf {RE}_\cap \) expressions to \(\textsf {NFAs} \).
Definition 8
For a regular expression \(\alpha \in \textsf {RE}_\cap \) and a symbol \(a \in \varSigma \), the set \(\partial _a(\alpha )\) of partial derivatives of \(\alpha \) w.r.t. a is defined by:

This definition is extended to words \(w \in \varSigma ^\star \) by \(\partial _\varepsilon (\alpha ) = \{\alpha \}\), \(\partial _{wa}(\alpha ) = \bigcup _{\alpha _i\in \partial _w(\alpha )}\partial _a(\alpha _i)\), and \(\partial _w(R) = \bigcup _{\alpha _i \in R} \partial _w(\alpha _i)\), where \(R \subseteq \textsf {RE}_\cap \). It follows easily that \(\mathcal {L}(\partial _w(\alpha )) = w^{-1} \mathcal {L}(\alpha )\). The set of partial derivatives of an expression \(\alpha \) is \(\partial (\alpha ) = \bigcup _{w \in \varSigma ^\star } \partial _w(\alpha )\). We also define \(\partial ^+(\alpha ) = \bigcup _{w \in \varSigma ^+} \partial _w(\alpha )\).
As for standard regular expressions, the partial derivative automaton of an expression \(\alpha \in \textsf {RE}_\cap \) is defined by \(\mathcal {A}_{pd}(\alpha ) = \langle \partial (\alpha ), \varSigma , \{\alpha \}, \delta _\alpha , F_\alpha \rangle ,\) where \(F_\alpha =\{\; \gamma \in \partial (\alpha ) \mid \varepsilon (\gamma ) =\varepsilon \;\}\) and \(\delta _\alpha (\gamma , a) = \partial _a(\gamma )\). It follows that \(\mathcal {L}(\mathcal {A}_{pd}(\alpha ))\) is exactly \(\mathcal {L}(\alpha )\). Mirkin’s and Antimirov’s constructions coincide for standard regular expressions. We will see that this is not true for regular expressions with intersection.
The following lemmas present some properties of the function \(\partial _w\), used to prove Proposition 11 and are easy to prove.
Lemma 9
For all \(S, S' \subseteq \textsf {RE}_\cap \) and \( a\in \varSigma \), the following property holds

Let \({{\mathrm{suff}}}(w)\) be the set of all non-empty suffixes of w, being defined as \({{\mathrm{suff}}}(w) = \{\; v \in \varSigma ^+ \mid \exists u \in \varSigma ^\star : uv = w \;\}\). Except for the second case, the following lemma was shown by Antimirov.
Lemma 10
For every regular expressions \(\alpha , \beta \in \textsf {RE}_\cap \) and word \(w \in \varSigma ^+\), \(\partial _w\) satisfies the following:

Proposition 11
For every regular expressions \(\alpha , \beta \in \textsf {RE}_\cap \), the following holds.

Proof
First note that, given a set \(E\subseteq \textsf {RE}_\cap \) and a regular expression \(\alpha \in \textsf {RE}_\cap \), if, for all \(w \in \varSigma ^+\), we have that \(\partial _w(\alpha ) \subseteq E\), then we have \(\bigcup _{w\in \varSigma ^+} \partial _w(\alpha ) \subseteq E\) and thus \(\partial ^+(\alpha ) \subseteq E\). Moreover, we know that for every \(w \in \varSigma ^+\), \(\partial _w(\alpha ) \subseteq \partial ^+(\alpha )\), since \(\partial ^+(\alpha ) = \bigcup _{w\in \varSigma ^+} \partial _w(\alpha )\). Let \(\alpha , \beta \in \textsf {RE}_\cap \) be regular expressions over \(\varSigma \). In order to prove the inclusions above, the facts mentioned above are used. The proof of each inclusion is given, respectively, by the following four proofs:
-
1.
From Eq. (3), for all \(w \in \varSigma ^+\), the following holds:
$$\begin{aligned} \partial _w(\alpha + \beta ) = \partial _w(\alpha ) \cup \partial _w(\beta ) \subseteq \partial ^+(\alpha ) \cup \partial ^+(\beta ). \end{aligned}$$And thus, we can conclude that \(\partial ^+(\alpha + \beta ) \subseteq \partial ^+(\alpha ) \cup \partial ^+(\beta )\).
-
2.
In the same way, from Eq. (4), for all \(w \in \varSigma ^+\), the following holds:
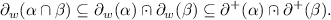
And then,
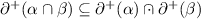 .
. -
3.
From Eq. (5), for all \(w \in \varSigma ^+\), the following holds:
$$\begin{aligned} \partial _w(\alpha \beta )&\subseteq \partial _w(\alpha )\beta \cup \bigcup _{v \in {{\mathrm{suff}}}(w)} \partial _v(\beta ) \subseteq \partial ^+(\alpha )\beta \cup \partial ^+(\beta ). \end{aligned}$$Thus, \(\partial ^+(\alpha \beta ) \subseteq \partial ^+(\alpha )\beta \cup \partial ^+(\beta )\).
-
4.
Finally, from Eq. (6), for all \(w \in \varSigma ^+\), the following holds:
$$\begin{aligned} \partial _w(\alpha ^\star ) \subseteq \bigcup _{v \in {{\mathrm{suff}}}(w)} \partial _v(\alpha )\alpha ^\star \subseteq \partial ^+(\alpha )\alpha ^\star . \end{aligned}$$Therefore, we have that \(\partial ^+(\alpha ) \subseteq \partial ^+(\alpha )\alpha ^\star \). \(\square \)
Example 12
Consider again \(\alpha _1= (b + ab + aab + abab) \cap (ab)^\star \). We have \(\partial ^+(\alpha _1) = \{ bab \cap b(ab)^\star ,\ ab \cap b(ab)^\star ,\ b \cap b(ab)^\star ,\ ab \cap (ab)^\star ,\ \varepsilon \cap (ab)^\star \}\). Now, with \(\beta = (b + ab + aab + abab)\), one has

Thus, we conclude that  .
.
The following proposition relates the function \(\partial ^+\) and the support \(\pi \).
Proposition 13
Given \(\alpha \in \textsf {RE}_\cap \), \(\partial ^+(\alpha ) \subseteq \pi (\alpha )\).
Proof
The proof proceeds by induction on the structure of \(\alpha \). It is trivial that \(\partial ^+(\emptyset ) = \pi (\emptyset )\), \(\partial ^+(\varepsilon ) = \pi (\varepsilon )\) and \(\partial ^+(a) = \pi (a)\), for a symbol \(a \in \varSigma \). Assume that \(\partial ^+(\alpha ) \subseteq \pi (\alpha )\) and \(\partial ^+(\beta ) \subseteq \pi (\beta )\) holds, for \(\alpha , \beta \in \textsf {RE}_\cap \). For \(\alpha + \beta \), we have \(\partial ^+(\alpha + \beta ) \subseteq \partial ^+(\alpha ) \cup \partial ^+(\beta ) \subseteq \pi (\alpha ) \cup \pi (\beta ).\) For \(\alpha \cap \beta \), there is  For \(\alpha \beta \), we have \(\partial ^+(\alpha \beta ) \subseteq \partial ^+(\alpha )\beta \cup \partial ^+(\beta ) \subseteq \pi (\alpha )\beta \cup \pi (\beta )\). Finally, for \(\alpha ^\star \), \(\partial ^+(\alpha ^\star ) \subseteq \partial ^+(\alpha )\alpha ^\star \subseteq \pi (\alpha )\alpha ^\star .\) \(\square \)
For \(\alpha \beta \), we have \(\partial ^+(\alpha \beta ) \subseteq \partial ^+(\alpha )\beta \cup \partial ^+(\beta ) \subseteq \pi (\alpha )\beta \cup \pi (\beta )\). Finally, for \(\alpha ^\star \), \(\partial ^+(\alpha ^\star ) \subseteq \partial ^+(\alpha )\alpha ^\star \subseteq \pi (\alpha )\alpha ^\star .\) \(\square \)
Since, for every regular expression \(\alpha \in \textsf {RE}_\cap \), the set \(\pi (\alpha )\) is finite, Proposition 13 also proves that the set \(\partial ^+(\alpha )\) is finite. For regular expressions without intersection it is known that \(\pi \) and \(\partial ^+\) coincide [11]. Examples 4 and 12 show that there exists \(\alpha \in \textsf {RE}_\cap \) such that \(\pi (\alpha ) \not = \partial ^+(\alpha )\). The following lemmas establish some conditions for the equality of \(\pi (\alpha \cap \beta )\) and \(\partial ^+(\alpha \cap \beta )\) to hold for \(\alpha , \beta \in \textsf {RE}_\cap \), and will be used in Proposition 16.
Lemma 14
Given \(\alpha , \beta \in \textsf {RE}_\cap \), one has \(\pi (\alpha \cap \beta ) = \partial ^+(\alpha \cap \beta )\) if and only if \(\pi (\alpha ) = \partial ^+(\alpha )\), \(\pi (\beta ) = \partial ^+(\beta )\) and  .
.
Proof
\((\Rightarrow )\) We have that  . From Proposition 13 follows that \(\partial ^+(\alpha ) \subseteq \pi (\alpha )\) and \(\partial ^+(\beta ) \subseteq \pi (\beta )\). Suppose by contradiction that \(\partial ^+(\alpha ) \subset \pi (\alpha )\) or \(\partial ^+(\beta ) \subset \pi (\beta )\). Then
. From Proposition 13 follows that \(\partial ^+(\alpha ) \subseteq \pi (\alpha )\) and \(\partial ^+(\beta ) \subseteq \pi (\beta )\). Suppose by contradiction that \(\partial ^+(\alpha ) \subset \pi (\alpha )\) or \(\partial ^+(\beta ) \subset \pi (\beta )\). Then  , a contradiction since \(\pi (\alpha \cap \beta ) = \partial ^+(\alpha \cap \beta )\). Thus, we conclude that \(\pi (\alpha ) = \partial ^+(\alpha )\) and \(\pi (\beta ) = \partial ^+(\beta )\). Consequently,
, a contradiction since \(\pi (\alpha \cap \beta ) = \partial ^+(\alpha \cap \beta )\). Thus, we conclude that \(\pi (\alpha ) = \partial ^+(\alpha )\) and \(\pi (\beta ) = \partial ^+(\beta )\). Consequently,  .
.
\((\Leftarrow )\) This follows trivially from the definition of support, i.e.,  , since \(\pi (\alpha ) = \partial ^+(\alpha )\) and \(\pi (\beta ) = \partial ^+(\beta )\). \(\square \)
, since \(\pi (\alpha ) = \partial ^+(\alpha )\) and \(\pi (\beta ) = \partial ^+(\beta )\). \(\square \)
Lemma 15
Given \(\alpha , \beta \in \textsf {RE}_\cap \), such that \(\partial _w(\alpha ) = \pi (\alpha )\) or \(\partial _w(\beta ) = \pi (\beta )\) holds for all \(w\in \varSigma ^+\), then  .
.
Proof
First, note that if \(\gamma \in \textsf {RE}_\cap \) and \(\partial _w(\gamma ) = \pi (\gamma )\) for every \(w \in \varSigma ^+\), then \(\partial ^+(\gamma ) = \bigcup _{w \in \varSigma ^+} \partial _w(\gamma ) = \pi (\gamma )\). Given \(\alpha , \beta \in \textsf {RE}_\cap \), there are three possible cases to prove. First, suppose that, for all \(w \in \varSigma ^+\), we have \(\partial _w(\alpha ) = \pi (\alpha )\) and \(\partial _w(\beta ) = \pi (\beta )\). Then

It remains to prove the cases that either \(\partial _w(\alpha ) = \pi (\alpha )\) or \(\partial _w(\beta ) = \pi (\beta )\), for all \(w \in \varSigma ^+\). The proof is the same for both cases. So, we will only present the proof for the first case. Suppose that, for all \(w \in \varSigma ^+\), \(\partial _w(\alpha ) = \pi (\alpha )\), it holds that

\(\square \)
By Proposition 13, \(|\pi (\alpha )|\) is an upper bound for the cardinality of \(\partial ^+(\alpha )\). This upper bound can be achieved, as shown by the following proposition.
Proposition 16
For any \(n\in \mathbb {N}\) there exists a regular expression \(r_n \in \textsf {RE}_\cap \) of size O(n) such that \(|\partial ^+(r_n)| = 2^{|r_n|_\varSigma - |r_n|_\cap -1}\).
Proof
Consider the regular expressions \(r_n \in \textsf {RE}_\cap \) from Example 7. We prove that \(\pi (r_n)=\partial ^+(r_n)\). The proof proceeds by induction on n. For \(n=0\) and for all \(w\in \varSigma ^+\), we have \(\partial _w(a^\star a) = \{a^\star a, \epsilon \} = \partial ^+(a^\star a)=\pi (a^\star a)\). Let us assume, by induction, that \(\pi (r_n) = \partial ^+(r_n)\), for \(n \ge 1\). It follows from Lemma 15 that  . Since \(\pi (a^\star a) = \partial ^+(a^\star a)\), \(\pi (r_n) = \partial ^+(r_n)\), and
. Since \(\pi (a^\star a) = \partial ^+(a^\star a)\), \(\pi (r_n) = \partial ^+(r_n)\), and  , we conclude, from Lemma 14, that \(\pi (r_{n+1}) = \pi (r_n \cap a^\star a) = \partial ^+(r_n \cap a^\star a)= \partial ^+(r_{n+1})\). \(\square \)
, we conclude, from Lemma 14, that \(\pi (r_{n+1}) = \pi (r_n \cap a^\star a) = \partial ^+(r_n \cap a^\star a)= \partial ^+(r_{n+1})\). \(\square \)
The next example provides another non-trivial family of regular expressions for which the set of partial derivatives and the support coincide.
Example 17
For \(n\ge 0\) let the regular expression \(s_n \in \textsf {RE}_\cap \) be inductively defined by \(s_0 = (a+b)^\star b (a+b)^\star \) and \(s_n = ((a+b) s_{n-1} (a+b)) \cap ((a+b)^\star (a+b))\), for \(n\ge 1\). The alphabetic length of \(s_n\) is \(|s_n|_\varSigma = 5 + 8n\) and \(|s_n|_\cap =n\). The cardinality of the support of \(s_n\) is given by: \(|\pi (s_0)| = 2 \), \(|\pi (s_1)| = 6\) and \(|\pi (s_n)| = \sum _{i=2}^{n} 2^i + 3\cdot 2^n \text{, } \text{ for }~n\ge 2\) Thus, for \(n\ge 2\) we have \(|\pi (s_n)|=O(2^n)\). Let \(m=|s_n|_\varSigma - |s_n|_\cap -1=5+7n-1\), i.e. \(n = (m-4)/7\). Then, \(|\pi (s_n)| = O(2^{\frac{1}{7}m})=O(1.105^m)\), which is much smaller than the upper bound \(2^m\). For all \(n\ge 0\), \(\pi (s_n)=\partial ^+(s_n)\).
5 Average Complexity Results
We know that the number of states in the partial derivative automaton of an expression \(\alpha \) has \(|\pi (\alpha )|\) as its tight upper bound. In this section we estimate an upper bound for the asymptotic average size of \(\pi (\alpha )\). This is done using standard methods of analytic combinatorics as expounded by Flajolet and Sedgewick [13], which apply to generating functions \(f(z)=\sum _n a_nz^n\) associated with combinatorial classes. Given some measure of the objects of a combinatorial class \(\mathcal {A}\), the coefficient \(a_n\) represents the sum of the values of this measure for all objects of size n. We will use the notation \([z^n]f(z)\) for \(a_n\). For an introduction to this approach applied to formal languages, we refer to Broda et al. [6].
Although the methods here used are the standard ones from the Analytic Combinatorics (and Complex Analysis), each application of these techniques is always a challenge, as one cannot foresee the analytic difficulties that one can incur into when conducting the study of the generation function. The generating function f can be seen as a complex analytic function, and the study of its behaviour near its dominant singularity \(\eta \) (in case there is only one, as it happens with the functions here considered) gives us access to the asymptotic form of its coefficients. In particular, if f(z) is analytic in some appropriate neighbourhood of 0 containing \(\eta \), then one has the following [6, 13]:
Proposition 18
If \(f(z)=a-b\sqrt{1-z/\rho }+o\left( \sqrt{1-z/\rho }\right) \), with \(a,b\in \mathbb {R}\), \(b\not =0\), then
If \(f(z)=\frac{a}{\sqrt{1-z/\rho }}+o\left( \frac{1}{\sqrt{1-z/\rho }}\right) \), with \(a\in \mathbb {R}\), and \(a\not =0\), then
5.1 Number of Expressions and Letters and \(\cap \) Symbols
The study of the combinatorial behaviour of the \(\textsf {RE}_\cap \)-expressions, both in terms of the number of expressions and the number of letters in them, is identical to the study of any other regular expressions with 3 binary operators and a single unary operator. Thus the results presented in Broda et al. [7] are valid for the case here studied. Denoting by \(R_k(z)\) the generating function for the number of \(\textsf {RE}_\cap \)-expressions without \(\emptyset \) over a k letters alphabet, and by \(L_k(z)\) the generating function for the number of letters in the expressions, one has:
where \(c_k = \frac{\root 4 \of {3+3k}}{6\sqrt{\pi }}\) and \(\rho _k=\frac{-1+2\sqrt{3+3k}}{11+12k}\).
The average number of letters in an expression of size n is given by
Using Eqs. (7) and (8), one obtains, asymptotically,
The number of intersections in the \(\textsf {RE}_\cap \)-expressions under consideration can be computed as follows. Consider the bivariate generating function
where \(\iota _{mn}\) is the number of \(\textsf {RE}_\cap \)-expressions with m intersection symbols and size n. From (1), and using the symbolic method, we can write
Solving this for \(\mathcal {I}_k(u,z)\), differentiating the result w.r.t. u, and making \(u=1\), we obtain an expression for the generating function for the cumulative number of intersection symbols in all \(\textsf {RE}_\cap \)-expressions of size n:
where \(q_k(z) = 1-2z-(11+12k)z^2\), from which one obtains, using the same methods,
The average number of symbols \(\cap \) in an expression of size n is given by
Using Eqs. (7) and (11), one obtains, asymptotically,
5.2 Average Size of \(\pi \)
Let \(P_k(z)\) denote the generating function for the size of \(\pi (\alpha )\) for expressions without \(\emptyset \). From Definition 2 it follows that, given an expression \(\alpha \), an upper bound, \(p(\alpha )\), for the number of elementsFootnote 3 in the set \(\pi (\alpha )\) satisfies:
From this, we directly get
from which we obtain the following closed expression
where
One now needs to determine the dominant singularity of \(P_k(z)\) which can either be a root of \(q_k(z)\) or a root of \(r_k(z)= p_k(z)+4(1-z)\sqrt{q_k(z)}.\) We need to know which of the two expressions \(r_k(z)\) or \(q_k(z)\) has the smallest positive zero. Because this is not trivial (note that one needs to decide this for all k), one will do it indirectly using the method expounded in the following paragraphs.
Observing that \(r_k(0)=9\) is positive and
by Bolzano theorem, \(r_k(z)\) must have a positive zero smaller than \(\rho _k\). This conclusion could be achieved, directly, from the fact that the absolute value of the negative zero of \(q_k(z)\) is smaller than its positive zero, and thus, by Pringsheim theorem [13], another smaller positive singularity of \(P_k(z)\) necessarily exists that can only be due to \(r_k(z)\). Letting
and observing that
one concludes that \(r_k(z)\) has necessarily two real zeros in its domain, \([\bar{\rho }_k, \rho _k]\). Analogously, \(s_k(z)= p_k(z)-4(1-z)\sqrt{q_k(z)}\) has also two real zeros in the same interval, and since \(r_k(z)s_k(z)\) is a fourth degree polynomial, it follows that \(r_k(z)\) has exactly two zeros, \(\eta _k\) and \(\eta '_k\), which are real. Since \(s_k(0)=1 < r_k(0)=9\), and \(r_k(x)=s_k(x)\) only at the end points of \([\bar{\rho }_k,\rho _k]\) it follows that \(s_k(x)< r_k(x)\) in \(]\bar{\rho }_k,\rho _k[\). Considering the four real zeros of the polynomial \(r_k(z)s_k(z)\), given what we just said, we conclude that the two more distant zeros from the origin are the roots of \(r_k(z)\). In fact, we can obtain an explicit expression for the zeros of \(r_k(z)s_k(z)\) by noticing that
and thus, solving the equations resulting of nulling those factors, we obtain the four zeros of \(r_k(z)s_k(z)\):
It is possible to verify that \(\eta _k\) and \(\eta '_k\) are the roots of \(r_k(z)\) and the other two the roots from \(s_k(z)\). Therefore, one has
From (13) one has
and we split the study of the coefficients of the series of \(P_k(z)\) into the study of the coefficients of \(1-z-\sqrt{r_k(z)}\) and of \(2\sqrt{q_k(z)}\). For the first one, we use that
and the fact that given a complex function f, defined in a neighbourhood of \(\eta \) such that \(\lim _{z\rightarrow \eta }f(z)=a\), one has, for all \(r\in \mathbb {R}\), \(f(z)(1-z/\eta )^r=a(1-z/\eta )^r+o((1-z/\eta )^r)\), together with Proposition 18, to obtain
where
For the last summand one has, similarly,
from which it follows, \( [z^n]2\sqrt{q_k(z)}\sim -\mu _k\rho _k^{-n}n^{-\frac{3}{2}}\), where
Summing up, we get that
In order to see what this result entails for the average case when compared with the worst case result, expressed in Proposition 5, attend to the following.
Setting \(\gamma _k = \frac{\rho _k}{\eta _k}\), this means that, on average,
One has \(\gamma _2\sim 1.01655\), \(\gamma _{10}\sim 1.04137\), \(\gamma _{100}\sim 1.05294\), and
Proposition 19
For large values of k and n an upper bound for the average number of states of \(\mathcal {A}_{pd}\) is \((1.056+o(1))^n\).
Considering the estimates given in (9) and (12), the worst-case upper bound \(2^{|\alpha |_\varSigma - |\alpha |_\cap -1}\) from Proposition 5 leads to an upper bound for the average case roughly of \(\root 3 \of {2}^{|\!|\alpha |\!|}\), for \(\alpha \) large enough. As \(\root 3 \of {2}\sim 1.25992\), the result just obtained shows that the upper bound for the average complexity is significantly smaller than the one for the worst case.
6 Conclusions
The conversion of a regular expression with intersection \(\alpha \) to NFA is in the worst-case \(2^{\Omega (|\!|\alpha |\!|)}\) [15, 17, 18]. This fact leads to the assumption that, although succinct, these expressions are not useful in practical applications. Here we show that, asymptotically, an upper bound for the average-state complexity of \(\mathcal {A}_{pd}(\alpha )\) is exponential but with a base only slightly above 1. Actually, experimental results using a uniform distribution suggest that the average-state complexity of \(\mathcal {A}_{pd}(\alpha )\) may even be polynomial [3].
Notes
- 1.
And a more general framework is also reported in [10].
- 2.
As is the case, for instance, for Brzozowski DFA or Caron et al. approach.
- 3.
This upper bound corresponds to the case where all unions in \(\pi (\alpha )\) are disjoint.
References
Antimirov, V.: Partial derivatives of regular expressions and finite automaton constructions. Theoret. Comput. Sci. 155(2), 291–319 (1996)
Antimirov, V.M., Mosses, P.D.: Rewriting extended regular expressions. In: Rozenberg, G., Salomaa, A. (eds.) 1st DLT. pp. 195–209. World Scientific (1994)
Bastos, R.: Manipulation of Extended Regular Expressions with Derivatives. Master’s thesis, Faculdade de Ciências da Universidade do Porto (2015)
Broda, S., Machiavelo, A., Moreira, N., Reis, R.: On the average state complexity of partial derivative automata. Int. J. Found. Comput. Sci. 22(7), 1593–1606 (2011)
Broda, S., Machiavelo, A., Moreira, N., Reis, R.: On the average size of Glushkov and partial derivative automata. Int. J. Found. Comput. Sci. 23(5), 969–984 (2012)
Broda, S., Machiavelo, A., Moreira, N., Reis, R.: A Hitchhiker’s guide to descriptional complexity through analytic combinatorics. Theoret. Comput. Sci. 528, 85–100 (2014)
Broda, S., Machiavelo, A., Moreira, N., Reis, R.: Partial derivative automaton for regular expressions with shuffle. In: Shallit, J., Okhotin, A. (eds.) DCFS 2015. LNCS, vol. 9118, pp. 21–32. Springer, Heidelberg (2015)
Brzozowski, J.A.: Derivatives of regular expressions. JACM 11(4), 481–494 (1964)
Caron, P., Champarnaud, J.-M., Mignot, L.: Partial derivatives of an extended regular expression. In: Dediu, A.-H., Inenaga, S., Martín-Vide, C. (eds.) LATA 2011. LNCS, vol. 6638, pp. 179–191. Springer, Heidelberg (2011)
Caron, P., Champarnaud, J., Mignot, L.: A general framework for the derivation of regular expressions. RAIRO - Theor. Inf. Appl. 48(3), 281–305 (2014)
Champarnaud, J.M., Ziadi, D.: From Mirkin’s prebases to Antimirov’s word partial derivatives. Fundam. Inform. 45(3), 195–205 (2001)
Christiansen, T., Foy, B.D., Wall, L., Orwant, J.: Programming Perl, 4th edn. O’Reilly Media, Sebastopol (2012)
Flajolet, P., Sedgewick, R.: Analytic Combinatorics. CUP, Cambridge (2008)
Fürer, M.: The complexity of the inequivalence problem for regular expressions with intersection. In: de Bakker, J.W., van Leeuwen, J. (eds.) ICALP 1980. LNCS, vol. 85, pp. 234–245. Springer, Heidelberg (1980)
Gelade, W.: Succinctness of regular expressions with interleaving, intersection and counting. Theoret. Comput. Sci. 411(31–33), 2987–2998 (2010)
Gelade, W., Neven, F.: Succinctness of the complement and intersection of regular expressions. In: Albers, S., Weil, P. (eds.) 25th STACS. LIPIcs, vol. 1, pp. 325–336. Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik, Germany (2008)
Gruber, H.: On the descriptional and algorithmic complexity of regular languages. Ph.D. thesis, Justus Liebig University Giessen (2010)
Gruber, H., Holzer, M.: Finite automata, digraph connectivity, and regular expression size. In: Aceto, L., Damgård, I., Goldberg, L.A., Halldórsson, M.M., Ingólfsdóttir, A., Walukiewicz, I. (eds.) ICALP 2008, Part II. LNCS, vol. 5126, pp. 39–50. Springer, Heidelberg (2008)
Jiang, T., Ravikumar, B.: A note on the space complexity of some decision problems for finite automata. Inf. Process. Lett. 40(1), 25–31 (1991)
Mirkin, B.G.: An algorithm for constructing a base in a language of regular expressions. Eng. Cybern. 5, 51–57 (1966)
Petersen, H.: The membership problem for regular expressions with intersection is complete in LOGCFL. In: Alt, H., Ferreira, A. (eds.) STACS 2002. LNCS, vol. 2285, pp. 513–522. Springer, Heidelberg (2002)
Sen, K., Rosu, G.: Generating optimal monitors for extended regular expressions. Electr. Notes Theor. Comput. Sci. 89, 231–250 (2003)
van der Vlist, E.: RELAX NG. O’Reilly Media, Cambridge (2003)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 IFIP International Federation for Information Processing
About this paper
Cite this paper
Bastos, R., Broda, S., Machiavelo, A., Moreira, N., Reis, R. (2016). On the State Complexity of Partial Derivative Automata For Regular Expressions with Intersection. In: Câmpeanu, C., Manea, F., Shallit, J. (eds) Descriptional Complexity of Formal Systems. DCFS 2016. Lecture Notes in Computer Science(), vol 9777. Springer, Cham. https://doi.org/10.1007/978-3-319-41114-9_4
Download citation
DOI: https://doi.org/10.1007/978-3-319-41114-9_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-41113-2
Online ISBN: 978-3-319-41114-9
eBook Packages: Computer ScienceComputer Science (R0)





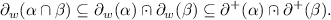
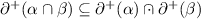 .
.