Robust Computations of Reeb Graphs in 2-D Binary Images

Abstract

In this article, we present a novel approach devoted to robustly compute the Reeb graph of a digital binary image, possibly altered by noise. We first employ a skeletonization algorithm, named DECS (Discrete Euclidean Connected Skeleton), to calculate a discrete structure centered within the object. By means of an iterative process, valid with respect to Morse theory, we finally obtain the Reeb graph of the input object. Our various experiments show that our methodology is capable of computing the Reeb graph of images with a high impact of noise, and is applicable in concrete contexts related to medical image analysis.

1 Introduction

The Reeb graph [15] is a compact discrete structure representing the topology of a graphical object by associating edges to its branches and vertices to their junctions. This graph is calculated on any compact manifold in two or in three dimensions (2-D or 3-D respectively) thanks to the definition of a given function h, in the sense of Morse theory [8, 14]. The critical points of this h function (extrema and saddle points) are related to the vertices of the graph. As a natural consequence, Reeb graphs have been extensively explored by optimizing algorithms for its construction, and especially for 3-D meshes [4, 9, 19]. For this construction, one of the keys is the definition of h. A classic viewpoint is to consider a one-directional function as Morse induced (also named height function, e.g. along one space axis X, Y or Z), but it could also be defined as a geodesic distance in 2-D or in 3-D [10, 19]. The first option, illustrated in Fig. 1(a), can be justified since the topology of many objects may be represented along an axis (statues, animals, persons, etc.), but it is generally not sufficient to model the topology of every kinds of complex objects, requiring geodesic-like functions (see Fig. 1(b)). More generally, in pattern recognition, the Reeb graph has been employed to model 2-D and 3-D shapes for many applications, e.g. object retrieval [2, 20], character recognition in license plates [18], noisy contour vectorization [22], implicit curve tracing [21] and image segmentation [12, 23].

Skeletons, medial axes and their extensions [1, 3, 5, 13] are other digital structures capable of capturing some topological features of the processed shapes. As a consequence, a natural strategy is to compute a skeleton or a medial axis of an object to obtain its Reeb graph [10, 16] and vice-versa [7]. However, in practice, these structures cannot be linked directly to Reeb graphs since they are very sensible to image noise. Generally, they produce extra branches or other unwanted data that do not belong to the Reeb graph, and the specific treatment of these artefacts is a difficult task. The closest and most recent related work (to the best of our knowlegde) following this strategy is presented in [10], wherein the authors use a classic skeletonization scheme and local binary patterns to obtain the Reeb graph of the input binary image.

Fig. 1.

From a skeleton computed in 2-D binary shapes, we can obtain a valid Reeb graph, by adopting h as a height function, along Y axis for instance, in (a), or by respecting shape’s geometry with a geodesic distance (b). Skeleton edge pixels are colored depending on their h function values (see palette below), and colored squares represent the set of these pixels having the same value

Our paper focuses on the computation of the Reeb graph of 2-D binary shapes, by employing a robust skeletonization scheme [13] (Fig. 1). Thanks to an iterative process, we can build the Reeb graph of complex and possibly very noisy objects by respecting a given height function, but also by considering other functions (by following a centrifugal force for example). The reminder of our article is the following: in Sect. 2, we recall the robust skeletonization algorithm introduced in a previous work, so that we can obtain a valid Reeb graph in Sect. 3. We propose in Sect. 4 experiments showing the robustness of our approach, and its application in our context of medical image analysis.

2 Skeleton Extraction

Througout our article, we will use the following notations. From any image I, we denote a pixel by $\mathbf{p}\in \mathbb {Z}^2$ belonging to I with its X- and Y-coordinates x and y respectively. To access randomly a pixel in I, we also use the notation I(x, y).

In this section, we remind the robust skeletonization algorithm introduced in [13] named Discrete Euclidean Connected Skeleton (DECS for short). Algorithm 1 summarizes the workflow of DECS, first calculating the sparse reduced discrete medial axis (RDMA) from [5] of the foreground object E in the input binary image I, as a part of the union of maximal balls:

$$\begin{aligned} E=\bigcup _{1 \le k\le K} B\big (\mathbf{p}_k,\delta (\mathbf{p}_k)\big ), \text {where}\,\,B\,(\mathbf{p},r)=\big \{\mathbf{q}\in \mathbb {Z}^2\ :\ d_E(\mathbf{p},\mathbf{q})<r\big \}. \end{aligned}$$

(1)

E represents the union of K balls $(\mathbf{p}_k,\delta (\mathbf{p}_k))\in {\mathbb Z}^2\times {\mathbb N}$, $\delta (\mathbf{p}_k)$ is the radius of the maximal ball centered in $\mathbf{p}_k$, and $d_E$ is the classic Euclidean distance. These radii are obtained thanks to the computation of the Euclidean distance transform of I ($EDT_I$) by any algorithm of the literature [6]. The RDMA removes the balls which are not maximal in E, and is generally illustrated by the set of balls’ centers $\{\mathbf{p}_k\}_{k=1,K}$.

With the map $EDT_I$, we also define the ridgeness map $RDG_I$ of I as

$$\begin{aligned} RDG_I(x,y)=\frac{1}{\pi \sigma ^4}\left( 1-\frac{x^2+y^2}{2\sigma ^2}\right) \exp {\left( -\frac{x^2+y^2}{2\sigma ^2}\right) }\times EDT_I(x,y). \end{aligned}$$

(2)

In [13], the authors suggest to set $\sigma =1$. This map is indeed obtained by applying the Laplacian of Gaussian operator on $EDT_I$, and represents the ridges wherein main branches of the input object are located. A simple thresholding operation on $RDG_I$ is not sufficient to obtain a valid skeleton, and a more relevant process has to be designed for this purpose.

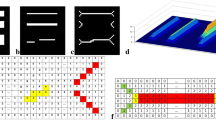
In this way, by combining both $RDMA_I$ and $RDG_I$, the DECS algorithm then leads to a coarse and thick skeleton $S_I$ of the image I, which is then pruned and thinned to obtain the final skeleton $S^*_I$. It should be noted that (1) the complexity of this algorithm has been proved to be linear with respect to the size of I in [13]; (2) the few parameters of this method can be set once for a wide range of images, always leading to a robust skeletonization. Every phases of DECS are illustrated in Fig. 2.

Fig. 2.

Example of the application of DECS algorithm on a sample binary image I (for notations, refer to Algorithm 1)

3 Reeb Graph Computation

3.1 Reeb Graph Definition

The goal of this section is to show that the calculation of a valid Reeb graph of any binary image I can be carried out using the robust skeleton obtained by DECS. We first need definitions related to topological spaces (Definition 1 below). Suppose we have an equivalence relation $\sim$ defined on a topological space M. Let ${M}_{\sim }$ be the set of equivalence classes and let $\psi : {M}\rightarrow {M}_{\sim }$ map each point $\mathbf{p}$ to its equivalence class (also called the quotient map).

Definition 1

(Quotient topology and space). The quotient topology of ${M}_{\sim }$ consists of all subsets $U\subseteq {M}_{\sim }$ whose preimages, $\psi ^{-1}(U)$ are open in M. The set ${M}_{\sim }$ together with the quotient topology is the quotient space defined by ${\sim }$.

Then, we can present the definition of the Reeb graph in the continuous case as:

Definition 2

(Reeb graph). Let h be a continuous function defined on a compact variety M, $h: {M}\rightarrow \mathbb {R}$. The Reeb graph of M, denoted by G(h), is the quotient space defined by the equivalence relation $\mathbf{p}\sim \mathbf{q} \Leftrightarrow (\mathbf{p},h(\mathbf{p})) \sim (\mathbf{q},h(\mathbf{q}))$ such that:

$$\begin{aligned} \left\{ \begin{array}{l} h(\mathbf{p})=h(\mathbf{q}), \\ \mathbf{p}\,\,\text {and}\,\,\mathbf{q}\,\,\text {belongs to the same connected component of}\,\,h^{-1}(h(\mathbf{p})). \end{array} \right. \end{aligned}$$

(3)

From this definition, we can extract the following properties of Reeb graphs.

Fig. 3.

Notations of G(h) for an illustrative continuous shape

By construction, G(h) is defined by considering the level-sets of the function h, and by associating points belonging to the same connected component (equivalence relation $\sim$), for every level-sets of h. If we consider h as a height function along an axis, as in Fig. 3, G(h) is built by considering increasing values of h along this axis. This shows that Reeb graphs bring together topology (as it is equivalent to a topological quotient space) and geometry (by the expression of the function h over the shape of M). As a consequence, the definition of h upon the geometry of M is a key for the Reeb graph computation.

Once a h function is decided, the construction of the Reeb graph $G(h)=(V,E)$ is composed of edges in E associated to the shape’s branches, i.e. the points belonging to the same connected component for any h value. In G(h), vertices of V represent the critical points of the h function (see Fig. 3) as: begin for the minimal h values and end for maximal h values, both having a degree of one; merge and split for saddle values, with higher degrees. These points are defined according to the construction of edges by merging or splitting them respectively.

All previous notions hold in the discrete case. The consequence of our observations is that algorithms designed in the construction of G(h) employ an iterative propagation process, througout a finite number of level-sets of h, calculating vertices and edges of the graph of the input digital object. To obtain those elements, our strategy is to use the robust skeletonization process presented in the previous section so that we compute a valid Reeb graph even for altered binary images.

3.2 Robust Reeb Graph Computation with DECS

The construction of the Reeb graph based on the DECS is described in Algorithm 2. Once a starting point $\mathbf{p}_S$ is selected, a breadth-first search for vertices and edges of the Reeb graph is launched. During this process, the function h is calculated in a discrete way by attributing increasing values to scanned points of the graph (line 14). Vertices are added in V by associating the correct label, with respect to the h function’s critical points, in line 10 (see also Fig. 3).

Proposition 1

For any binary image I, Algorithm 2 computes the Reeb graph of the foreground object $G_I(h)$.

We propose to justify this proposition with two axes: (1) the DECS skeleton is able to represent the medial topological branches of the input foreground object; (2) the rest of Algorithm 2 actually calculates its Reeb graph with its edges, vertices and the associated h function.

Fig. 4.

Illustration of the location of Reeb graph vertices points with respect to $RDG_I$ map

The medial axis $RDMA_I$, used in the DECS algorithm, is able to capture the topology of the foreground object in I [17]. As illustrated in Fig. 2, this is a sparse and disconnected representation, but it is also able to reconstruct the whole geometry of the input shape by calculating the union of maximal balls expressed in Eq. 1. This minimal set of the maximal balls included in the object is a relevant basis for the DECS algorithm, since this is an incomplete but sufficient representation of its branches, from a topological point of view. Conversely, the ridgeness map $RDG_I$ (see Fig. 2 again) of the input image is a dense and complete model which smoothly locates main branches by ridges for each image pixel.

Thanks to the combination of $RDMA_I$ and $RDG_I$, the DECS skeleton leads to the complete branches, stored in the edges of the Reeb graph $G_I(h)$ and, at their junctions, the vertices of $G_I(h)$. Definition 2 shows that this graph co-exists with a function defined on the input compact variety. In our case, the values of this function are calculated during the breadth-first scanning of the object; the starting point of our process is associated to zero (and is a begin critical point), then scanned points are assigned with an increasing value. They can be saddle critical points of h (merge, split) or maximal points (end).

Figure 4 shows the location of the Reeb graph vertices (black circles) with respect to the $RDG_I$ map (see Eq. 2 for its formulation) plotted as an elevation map, for each input image pixel. This figure illustrates that the Reeb graph vertices correspond to the highest $RDG_I$ values, and so located on the most relevant branches of the input shape.

As a validation of our contribution, the next section is devoted to the experimental evaluation of our robust Reeb graph computation algorithm thanks to synthetic and real images.

4 Experimental Evaluation

We first propose to build the DECS skeleton and the Reeb graph of noisy images, generated from the synthetic examples given in Fig. 1. For this purpose, we use a noise generation model close to the one proposed by Kanungo et al. [11], iterated several times to increase its impact. This alters the contour of the input object by switching the values of pixels belonging to the foreground object border. Figure 5 groups the results of our algorithm with noise generated once, then 5, 10, 50 and 100 times on the same image. We can observe that the $S_I^*$ skeleton obtained by the DECS algorithm is very robust, and enables to extract the Reeb graph of the foreground object, which stays stable despite of the increasing noise. For the simple one-hole object, we select the lowest skeleton point as the starting point of the Reeb graph construction; for the spiral object, this is the most external one. We can consider an h function along an axis (first case) or defined in a geodesic way to respect the geometry of the input shape (spiral object).

To numerically represent the topology of the processed objects, we can calculate the Euler number $\chi$ from the Reeb graph $G_I(h)=(V,E)$, thanks to this formulation [15]:

$$\begin{aligned} \chi = \sum _{n\in V, n=begin \vee n=end}deg(n) - \sum _{n\in V, n=split \vee n=merge} deg(n)-2. \end{aligned}$$

(4)

For the first one-hole object, we always obtain an Euler number $\chi =0$, meaning that it is homeomorpheous to a torus; for the spiral shape, we obtain $\chi =2$, the same number as a point. We also remind that the Euler number can be also calculated as $\chi =2-2\times \#holes$, which confirms the values we obtain. This numerical analysis will be further useful for the comparison of our contribution with other computations of Reeb graphs based on skeletonization schemes.

Fig. 5.

Extraction of DECS and Reeb graph for more and more noisy synthetic images, with an increasing number of iterations $n_{it}$. The value of h function is depicted with the palette used in Fig. 1

Fig. 6.

Extraction of Reeb graph in a liver histological image, enhanced and segmented to extract hepatocytes (a). In (b), we show that the graph can be computed by considering a one-directional height function h, from top-left to bottom-right (left), or a centrifugal function (right). Graph edge pixels are colored depending on their h function values (see palette below), and colored squares represent the set of these pixels having the same value. (c): Obtained Reeb graph superimposed on the segmented and original images (color figure online)

In Fig. 6, we propose to test our algorithm in a concrete application about analysis of histological image of liver cells. In (a), we first enhance specific colors of the complex input image of size 1280$\times$1024 pixels¹, to highlight then hepatocytes (cell centers) by applying a double thresolding operation. Then, we calculate the DECS of the image by considering the hepatocytes as background objects (and the rest obviously as foreground). By using this structure, we can then select different starting points to construct the Reeb graph (b). For example, we can select the most upper left point of the skeleton, meaning that the graph is built along a diagonal axis (from top-left to bottom-right). We can also choose the central DECS point, leading to a breadth-first scanning following a centrifugal direction. In this experiment, we have selected one starting point as in Algorithm 2, i.e. $G_I(h)$ contains only one begin node, and we could select multiple starting points as an extension. In this case, we would have to handle several breadth-first constructions of separated graphs, and merge them into a single graph. We show in Fig. 6(c) the Reeb graph we obtain, whatever the starting point chosen, superimposed on the segmented image and on the original image.

By using Eq. 4 expressed earlier, we can determine the number of holes within the processed binary object thanks to the Euler number. In our case, we have obtained $\chi =-812$, leading to 407 holes in the image (and so 407 cell centers); this number can be verified with the original segmented image, depicted in Fig. 6(a), by counting the number of connected components. Besides this numerical evaluation, the Reeb graph brings obviously more information about the shape and organization of hepatocytes in the histological image. Indeed, the graph calculated as we propose would be of high interest to analyse further the structure of the liver, since homogeneous and regular cells arranged around the central vein imply that the liver is healthy, contrary to a cirrhotic one wherein cells have irregular shapes and are disrupted around the vein.

We finally propose in Fig. 7 to compute the Reeb graph of the liver vessels represented within a sample angiogram. The input image² is first segmented by considering a simple thresholding process based on angiogram intensities, similar to the one we used in the previous experiment. This binary object is then treated by our algorithm, to obtain the vascular structure with the Reeb graph in Fig. 7(b). The starting point of our process has been selected at the entrance of the vein (most right-bottom point in DECS), which permits to have the complete path of blood inside the liver, from this entrance to the finest veins.

Fig. 7.

Reeb graph computation in an angiogram of liver vessels

5 Conclusion and Future Works

In this article, we have proposed a novel approach able to compute robustly the Reeb graph of a 2-D shape contained in a binary image. Our algorithm is capable of constructing this graph, by considering a relevant h function depending on the shape of the input object. We have shown the performance of our approach throughout two main experiments involving synthetic and real images. In the first case, we have confirmed that our contribution can compute the Reeb graph despite of a very strong contour-based noise model. We have then illustrated the application of our algorithm in a concrete context of medical image analysis.

A first future direction of our research concerns, still in the 2-D case, the validation of our approach in a medical context as shown in Sect. 4. We would like to test its performance on a large database of vascular images, requiring that we extract finely the vessel structures and their bifurcations. Moreover, we would like to compare our pipeline with other skeletonization algorithms, to ensure that DECS is the most robust way to obtain a valid Reeb graph. To do so, we can use a numerical evaluation by using the Euler number together with a structural comparison by using graph matching techniques as graph edit distance for example. Another important future work is to extend our approach to 3-D. As explained in Sect. 2, the DECS computation is based on several stages that can be adapted rather easily to higher dimensions. Then, the Reeb graph construction employs a breadth-first search-like strategy, which could be adapted to n-D. This work could also be highlighted in a medical context, to analyze the vessels in 3-D volumes acquired from CT-scans or MRI for example. Finally, we aim at designing matching algorithms for (2-D and then in higher dimensions) patterns or objects based on Reeb graphs.