Abstract
We formalize the security notions of non-malleability under selective opening attacks (NM-SO security) in two approaches: the indistinguishability-based approach and the simulation-based approach. We explore the relations between NM-SO security notions and the known selective opening security notions, and the relations between NM-SO security notions and the standard non-malleability notions.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Non-malleability. The basic goal of public-key encryption (PKE) schemes is to guarantee the privacy of messages. The universally accepted formalization for this is semantic security proposed in [9], which requires that it be infeasible to learn any useful information of the message from the ciphertext. However, some cryptographic applications in a complex setting suggest that non-malleability is necessary. Non-malleability (NM), introduced by Dolev, Dwork and Naor [8] in 1991, requires that given a challenge ciphertext, it be infeasible to generate ciphertexts whose decryptions are related to the decryption of the challenge ciphertext. Nowadays, two main kinds of formalizations (indistinguishability-based [5] and simulation-based [8]) of non-malleability are widely accepted, especially the first one. (Actually, there is another formalization of non-malleability, comparison-based non-malleability [1, 5]). Similar to semantic security, the formal security definitions of indistinguishability-based non-malleability (IND-NM) and simulation-based non-malleability (SIM-NM) consider all the three kinds of standard attacks: chosen-plaintext attacks (CPA), non-adaptive chosen-ciphertext attacks (CCA1) [16] and adaptive chosen-ciphertext attacks (CCA2) [8, 18]. The combination of SIM-NM, IND-NM and CPA, CCA1, CCA2 gives six specific security notions (e.g., IND-NM-CPA security). The relations among these six security notions were figured out in [5, 17].
Selective Opening Security (Under Sender Corruptions). In Eurocrypt 2009, Bellare et al. [4] introduced the notion of selective opening security (SOA security) under sender corruptions. Roughly speaking, selective opening attack (for sender corruptions) is as follows: n senders encrypt their own messages with the public key of a single receiver. The adversary can corrupt some of these senders, by opening their ciphertexts, i.e., obtaining their messages and the random coins which were used during the encryption. The goal of SOA security is to guarantee the privacy of the unopened messages. In [4], Bellare et al. presented two SOA security notions, the indistinguishability-based one (IND-SO) and the simulation-based one (SIM-SO). Later, Hemenway et al. [12] introduced the notions of IND-SO-CCA1/CCA2 security and SIM-SO-CCA1/CCA2 security. Over the years, several PKE schemes were proposed and proved to possess SOA security [10–13]. The relations between IND-SO-CPA security and SIM-SO-CPA security were clarified by Böhl et al. [3]. Bellare et al. [2] separated IND-CPA (even IND-CCA2) and SIM-SO-CPA security. Recently, Hofheinz and Rupp [15] showed a separation between IND-CCA2 and IND-SO-CCA2 security, and a “partial” equivalence between IND-CPA and IND-SO-CPA security.
To the best of our knowledge, how to formalize non-malleability under selective opening attacks remains elusive. Very recently, Hofheinz and Rupp referred to “NM-SO-CPA security” in [15]. But they did not present any formal definition.
Our Contributions. This paper focuses on security notions and their relations. We first formalize the notion of simulation-based non-malleability under selective opening attacks (SIM-NM-SO), and the notion of indistinguishability-based non-malleability under selective opening attacks (IND-NM-SO). We figure out the relations among SIM-NM-SO-CPA(/CCA1/CCA2) security, IND-NM-SO-CPA(/CCA1/CCA2) security, SIM/IND-SO-CPA(/CCA1/CCA2) security and non-malleability security SIM/IND-NM-CPA(/CCA1/CCA2). Specifically, our results are as follows (see Fig. 1). Below, we use \(\textsf {SEC1}\Rightarrow \textsf {SEC2}\) to indicate that SEC1 implies SEC2, and \(\textsf {SEC1}\nRightarrow \textsf {SEC2}\) to indicate the existence of some PKE scheme achieving SEC1 but not SEC2, for any two security notions SEC1 and SEC2.
-
1.
NM-SO versus SO:
-
(a)
Simulation-based (Sect. 4):
-
i.
“SIM-NM-SO-ATK
 SIM-SO-ATK”, for any \(\text {ATK}\in \{\text {CPA}, \text {CCA1}, \text {CCA2}\}\).
SIM-SO-ATK”, for any \(\text {ATK}\in \{\text {CPA}, \text {CCA1}, \text {CCA2}\}\). -
ii.
For those PKE schemes having an invertible decryption algorithm (Definition 8), if the range of its decryption algorithm is recognizable, “SIM-SO-CCA2 \(\Leftrightarrow \) SIM-NM-SO-CCA2”.
-
i.
-
(b)
Indistinguishability-based (Sect. 5):
-
i.
“IND-NM-SO-CPA
 IND-SO-CCA1”.
IND-SO-CCA1”. -
ii.
“IND-NM-SO-CCA1/CPA
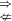 IND-SO-CCA1/CPA”, but “IND-NM-SO-CCA2 \(\Leftrightarrow \) IND-SO-CCA2”.
IND-SO-CCA1/CPA”, but “IND-NM-SO-CCA2 \(\Leftrightarrow \) IND-SO-CCA2”.
-
i.
-
(a)
-
2.
NM-SO versus NM:
-
(a)
Simulation-based (Sect. 6):
-
i.
“SIM-NM-SO-ATK
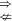 SIM-NM-ATK”, for any \(\text {ATK}\in \{\text {CPA}, \text {CCA1}, \text {CCA2}\}\). In fact, we have a stronger result: “SIM-NM-CCA2 \(\nRightarrow \) SIM-NM-SO-CPA”, which suggests “\(\text {SIM-NM-ATK}' \nRightarrow \text {SIM-NM-SO-ATK}''\)”, for any \(\text {ATK}', \text {ATK}''\in \{\text {CPA}, \text {CCA1}, \text {CCA2}\}\).
SIM-NM-ATK”, for any \(\text {ATK}\in \{\text {CPA}, \text {CCA1}, \text {CCA2}\}\). In fact, we have a stronger result: “SIM-NM-CCA2 \(\nRightarrow \) SIM-NM-SO-CPA”, which suggests “\(\text {SIM-NM-ATK}' \nRightarrow \text {SIM-NM-SO-ATK}''\)”, for any \(\text {ATK}', \text {ATK}''\in \{\text {CPA}, \text {CCA1}, \text {CCA2}\}\).
-
i.
-
(b)
Indistinguishability-based (Sect. 7):
-
i.
“IND-NM-SO-ATK \(\Rightarrow \) IND-NM-ATK”, for any \(\text {ATK}\in \{\text {CPA}, \text {CCA1}, \text {CCA2}\}\).
-
ii.
“IND-NM-CCA2 \(\nRightarrow \) IND-NM-SO-CCA2”, and “IND-NM-SO-CPA \(\nRightarrow \) IND-NM-CCA1”.
-
i.
-
(a)
-
3.
SIM-NM-SO versus IND-NM-SO (Sect. 8):
“IND-NM-SO-ATK \(\nRightarrow \) SIM-NM-SO-ATK”, for any \(\text {ATK}\in \{\text {CCA1}, \text {CCA2}\}\). In fact, we have a stronger result: “IND-NM-SO-CCA2 \(\nRightarrow \) SIM-NM-SO-CCA1”.
Based on the relations that we obtained, (in Sect. 9) we conclude that some known PKE schemes have already obtained SIM-NM-SO-CCA2 or IND-NM-SO-CCA2 security. More specifically, the NC-CCA2 secure encryption scheme proposed by Fehr et al. [10] is SIM-NM-SO-CCA2 secure; Any IND-SO-CCA2 secure encryption scheme (e.g., [11, 12]) is IND-NM-SO-CCA2 secure.
Techniques for the Implications. For two main non-trivial implication results, we provide their high-level descriptions of the reasonings here.
-
For our contribution 1. (a).ii., the key point is how to construct a SIM-NM-SO-CCA2 simulator \(S_{NS}\) from a SIM-SO-CCA2 simulator S. Given S’s output \(out_S\), if it is a valid message, \(S_{NS}\) can simply generate a ciphertext by encrypting it, such that the decryption of \(S_{NS}\)’s output equals \(out_S\). The barrier is that when \(out_S\) is not a valid message, this method doesn’t work. To overcome this issue, we apply the idea from [17], assuming that there is an algorithm \(\textsf {{F}}\) recovering ciphertexts from decrypted messages. Under this assumption, \(S_{NS}\) can use \(\textsf {{F}}\) to recover a ciphertext from \(out_S\), if \(out_S\) falls into the range of decrypted messages. However, this method fails if \(out_S\) does not belong to the range of the decryption algorithm Dec. This problem can be solved by assuming that the range of the decryption algorithm Dec is recognizable. With the recognizable property of Dec, SIM-SO-CCA2 security ensures that S’s output \(out_{S}\) is almost always in the range of Dec as long as the SIM-SO-CCA2 adversary’s final output is in the range.
-
For our contribution 2. (a).i., the key point is constructing a SIM-NM-ATK simulator \(S_{N}\) from a SIM-NM-SO-ATK simulator \(S_{NS}\). Note that \(S_{NS}\) has the ability, which \(S_N\) doesn’t, to ask an opening query. To overcome this issue, we consider a special “half-uniform” message distribution, which consists of two independent distributions and the second is a uniform one. Correspondingly, the challenge message vector generated from this specific distribution also consists of two parts. If \(S_{NS}\) outputs a “half-uniform” distribution and asks to open the uniform part, \(S_N\) can always answer it on its own by returning a uniformly chosen message vector. However, \(S_N\) still cannot deal with a misbehaved \(S_{NS}\) which outputs other distributions or it does not open the uniform part. To solve this problem, we construct a behaved SIM-NM-SO-ATK adversary \(A_{NS}\), which always outputs a half-uniform distribution and asks to open the uniform part, and then SIM-NM-SO-ATK security guarantees \(S_{NS}\) is behaved, except with negligible probability.
Observations for the Separations. Some of our separation results can be seen as extensions of [1, 17]. Most of these separations are based on the following observations. Let’s look at the SIM-based notions first. A SIM-NM security notion requires that the decryptions of both of the adversary’s and the simulator’s outputs be indistinguishable. Note that a non-NM security notion only requires that their outputs be indistinguishable. We can provide a uniformly distributed string, which leads to a special ciphertext (e.g., decrypted to sk), to the adversary through the decryption oracle. It is hard for any SIM-NM simulator to generate such a ciphertext, since it has no access to the decryption oracle. This feature can be used to separate some SIM-based NM and non-NM security notions (in a SOA or non-SOA setting). For the IND-based notions, note that even under CPA attacks, an IND-NM adversary can make a one-time parallel decryption query after receiving the challenge ciphertext. This feature can be used to separate some IND-based NM and non-NM security notions (in a SOA or non-SOA setting).
Open Question. The primary open question is to figure out the relations between SIM-NM-SO and IND-NM-SO security notions. The barriers we encounter are as follows. For NM security notions, there is always a parallel decryption process after the adversary receiving the challenge ciphertext. This fact makes the relation between these two notions (even under CPA attacks) similar to that between SIM-SO-CCA2 and IND-SO-CCA2 security. Besides that, we also need to deal with the aforementioned issue, i.e., the SIM-NM-SO simulator’s output always contains a ciphertext vector.
2 Preliminaries
Notations. Throughout this paper, we use \(\kappa \) as the security parameter, and \(\epsilon \) as the empty string. For \(n\in \mathbb {N}^+\), let [n] denote the set \(\{1,2,\cdots , n\}\). For a finite set \(\mathcal {S}\), let \(s\leftarrow \mathcal {S}\) denote the process of sampling an element s uniformly at random from \(\mathcal {S}\). For a probabilistic algorithm A, let \(\mathcal {R}_A\) denote the randomness space of A. We let \(y\leftarrow A(x;R)\) denote the process of running A on input x and inner randomness \(R\in \mathcal {R}_A\), and outputting y. We write \(y\leftarrow A(x)\) for \(y\leftarrow A(x;R)\) with uniformly chosen \(R\in \mathcal {R}_A\). If A’s running time is polynomial in \(\kappa \), we say that A is a probabilistic polynomial-time (PPT) algorithm. For two sequences of random variables \(X=\{X_\kappa \}_{\kappa \in \mathbb {N}}\) and \(Y=\{Y_\kappa \}_{\kappa \in \mathbb {N}}\), if for any PPT algorithm D, \(|\text {Pr}[D(X_\kappa , 1^\kappa )=1]-\text {Pr}[D(Y_\kappa , 1^\kappa )=1]|\) is negligible in \(\kappa \), we say that X and Y are computationally indistinguishable (denoted by \(X\overset{c}{\approx }Y\)).
We use boldface letters for vectors. For a vector \(\mathbf m \) (resp. a finite set \(\mathcal {S}\)), we let \(|\mathbf m |\) (resp. \(|\mathcal {S}|\)) denote the length of the vector (resp. the size of the set). For a set \(I=\{i_1, i_2,\cdots ,i_{|I|}\}\subseteq [|\mathbf m |]\), let \(\mathbf m [I]=(\mathbf m [i_1], \mathbf m [i_2],\cdots , \mathbf m [i_{|I|}])\). We write \(m\in \mathbf m \) to denote \(m\in \{\mathbf{m}[i]|i\in [|\mathbf{m}|]\}\), extending the set membership notation to vectors.
Decryption Oracles. For simplicity, we will use the notations \(\mathcal {O}_1(\cdot )\) and \(\mathcal {O}_2(\cdot )\) in all the security notions throughout the paper. In a chosen-plaintext attack (CPA), both the oracles \(\mathcal {O}_1(\cdot )\) and \(\mathcal {O}_2(\cdot )\) always return \(\epsilon \). In a non-adaptive chosen-ciphertext attack (CCA1), \(\mathcal {O}_1(\cdot )=\textsf {{Dec}}(sk, \cdot )\), and \(\mathcal {O}_2(\cdot )\) still returns \(\epsilon \) whatever it is queried. In an adaptive chosen-ciphertext attack (CCA2), both \(\mathcal {O}_1(\cdot )\) and \(\mathcal {O}_2(\cdot )\) are \(\textsf {{Dec}}(sk, \cdot )\), with the only exception that \(\mathcal {O}_2(\cdot )\) returns \(\epsilon \) when queried on a ciphertext appeared in the challenge ciphertext vector.
Non-malleability for Encryption. The first definition of non-malleability for encryption was proposed by Dolev, Dwork and Naor [8] in 1991. Their definition is simulation-based. Several years later, comparison-based and indistinguishability-based definitions of non-malleability were proposed [1, 5], and their relations were explored in [5, 17]. We recall the simulation/indistinguishability-based definitions in [17] as follows.
Definition 1
(SIM-NM Security). A public-key encryption scheme \(\textsf {{PKE}} = (\textsf {{Gen}}, \textsf {{Enc}}, \textsf {{Dec}})\) is SIM-NM-ATK secure, if for any stateful PPT adversary \(A=(A_1, A_2)\), there is a stateful PPT simulator \(S=(S_1, S_2)\), such that
where \(\text {ATK}\in \{\text {CPA, CCA1, CCA2}\}\), experiments \(\textsf {{Exp}}_{\textsf {{PKE}}, A}^{\text {SIM-NM-ATK-Real}}(\kappa )\) and \(\textsf {{Exp}}_{\textsf {{PKE}}, S}^{\text {SIM-NM-ATK-Ideal}}(\kappa )\) are defined in Table 1.
Definition 2
(IND-NM Security). A public-key encryption scheme \(\textsf {{PKE}} = (\textsf {{Gen}}, \textsf {{Enc}}, \textsf {{Dec}})\) is IND-NM-ATK secure, if for any stateful PPT adversary \(A=(A_1, A_2, A_3)\), its advantage \(\mathbf {Adv} _{\textsf {{PKE}}, A}^{\text {IND-NM-ATK}}(\kappa )\) is negligible, where \(\text {ATK}\in \{\text {CPA, CCA1, CCA2}\}\). Here
where experiment \(\textsf {{Exp}}_{\textsf {{PKE}}, A}^{\text {IND-NM-ATK-}b}(\kappa )\) (\(b\in \{0,1\}\)) is defined in Table 1, and we require that in the experiment, \(|\mathbf {m} _0|=|\mathbf {m} _1|\), and \(|\mathbf {m} _0[i]|=|\mathbf {m} _1[i]|\) for any \(i\in [|\mathbf {m} _0|]\).
Remark 1
Note that in Definitions 1 and 2, the ciphertexts contained in \(\mathbf y \) may be invalid (i.e., \(\bot \in \mathbf x \)). According to [17], these two definitions are stronger than the versions which require that \(\mathbf y \) must be valid ciphertexts.
Selective Opening Security for Encryption. Selective opening security notions were presented by Bellare et al. [4] in Eurocrypt 2009. We follow [3, 4, 12] for the definitions.
Definition 3
(SIM-SO Security [3]). A public-key encryption scheme \(\textsf {{PKE}} = (\textsf {{Gen}}, \textsf {{Enc}}, \textsf {{Dec}})\) is SIM-SO-ATK secure, if for any stateful PPT adversary \(A=(A_1, A_2, A_3)\), there is a stateful PPT simulator \(S=(S_1, S_2, S_3)\), such that
where \(\text {ATK}\in \{\text {CPA, CCA1, CCA2}\}\), experiments \(\textsf {{Exp}}_{\textsf {{PKE}}, A}^{\text {SIM-SO-ATK-Real}}(\kappa )\) and \(\textsf {{Exp}}_{\textsf {{PKE}}, S}^{\text {SIM-SO-ATK-Ideal}}(\kappa )\) are defined in Table 1.
For indistinguishability-based selective opening (IND-SO) security notion, we restrict message distributions to be efficiently re-samplable. In [3], this kind of security notion is called “weak” IND-SO security.
Definition 4
(Efficiently Re-samplable). A message distribution \(\mathcal {M}\) is efficiently re-samplable, if there is a PPT algorithm \(\textsf {{Resamp}}_{\mathcal {M}}\), such that for any \(\mathbf {m} \) sampled from \(\mathcal {M}\) and any subset \(I\subseteq [|\mathbf {m} |]\), \(\textsf {{Resamp}}_{\mathcal {M}}(I,\mathbf {m} [I])\) samples from \(\mathcal {M}|_{I,\mathbf {m} [I]}\), i.e., \(\mathbf {m} '\leftarrow \textsf {{Resamp}}_{\mathcal {M}}(I,\mathbf {m} [I])\) is sampled from the distribution \(\mathcal {M}\), conditioned on \(\mathbf {m} '[I]=\mathbf {m} [I]\).
Definition 5
(IND-SO Security). A public-key encryption scheme \(\textsf {{PKE}} = (\textsf {{Gen}}, \textsf {{Enc}}, \textsf {{Dec}})\) is IND-SO-ATK secure, if for any stateful PPT adversary \(A=(A_1, A_2, A_3)\), its advantage \(\mathbf {Adv} _{\textsf {{PKE}}, A}^{\text {IND-SO-ATK}}(\kappa )\) is negligible, where \(\text {ATK}\in \{\text {CPA, CCA1, CCA2}\}\). Here
where experiment \(\textsf {{Exp}}_{\textsf {{PKE}}, A}^{\text {IND-SO-ATK-}b}(\kappa )\) (\(b\in \{0,1\}\)) is defined in Table 1.
3 Non-malleability Under Selective Opening Attack
In this section, we formalize non-malleability under selective opening attacks for PKE. We consider simulation-based and indistinguishability-based formalizations of this security, which we call SIM-NM-SO security and IND-NM-SO security, respectively.
Simulation-Based Selective Opening Non-malleability. The simulation-based notion of non-malleability under selective opening attacks combines SIM-NM security and SIM-SO security. Informally, a SIM-NM-SO-ATK adversary is a SIM-NM-ATK adversary being allowed to make an additional selective opening query. Similarly, the related simulator is also allowed to make an opening query. The formal definition is as follows.
Definition 6
(SIM-NM-SO Security). A public-key encryption scheme \(\textsf {{PKE}} = (\textsf {{Gen}}, \textsf {{Enc}}, \textsf {{Dec}})\) is SIM-NM-SO-ATK secure, if for any stateful PPT adversary \(A=(A_1, A_2, A_3)\), there is a stateful PPT simulator \(S=(S_1, S_2, S_3)\), such that
where \(\text {ATK}\in \{\text {CPA, CCA1, CCA2}\}\), experiments \(\textsf {{Exp}}_{\textsf {{PKE}}, A}^{\text {SIM-NM-SO-ATK-Real}}(\kappa )\) and \(\textsf {{Exp}}_{\textsf {{PKE}}, S}^{\text {SIM-NM-SO-ATK-Ideal}}(\kappa )\) are defined as follows:

Indistinguishability-Based Selective Opening Non-malleability. The indistinguishability-based notion of non-malleability under selective opening attacks is also a combination of IND-NM security and IND-SO security. However, there are some subtleties in this combination. First, as the notion of IND-SO security, we require that every message distribution outputted by the adversary should be efficiently re-samplable. Second, in this combination, an adversary should be allowed to make two special oracle queries, a selective opening query and a parallel decryption query. In the following formal definition, we allow the adversary to decide the order of these two oracle queries. More specifically, the adversary can make these two queries at any time after receiving the vector of challenge ciphertexts, but only once for each oracle. Note that we require the adversary has to make these two oracle queries, since the “challenge bit” b is given through the opening oracle \(\textsf {Open }_{b,\mathcal {M}, \mathbf {m} _0,\mathbf {r} }(\cdot )\). The formal definition is as follows.
Definition 7
(IND-NM-SO Security). A public-key encryption scheme \(\textsf {{PKE}} = (\textsf {{Gen}}, \textsf {{Enc}}, \textsf {{Dec}})\) is IND-NM-SO-ATK secure, if for any stateful PPT adversary \(A=(A_1, A_2)\), its advantage \(\mathbf {Adv} _{\textsf {{PKE}}, A}^{\text {IND-NM-SO-ATK}}(\kappa )\) is negligible, where \(\text {ATK}\in \{\text {CPA, CCA1, CCA2}\}\). Here
where experiment \(\textsf {{Exp}}_{\textsf {{PKE}}, A}^{\text {IND-NM-SO-ATK-}b}(\kappa )\) (\(b\in \{0,1\}\)) and the related oracles are defined as follows. In experiment \(\textsf {{Exp}}_{\textsf {{PKE}}, A}^{\text {IND-NM-SO-ATK-}b}(\kappa )\), we require that adversary \(A_2\) access to both oracles \(\textsf {Open}_{b,\mathcal {M}, \mathbf {m} _0,\mathbf {r} }(\cdot )\) and \(\textsf {P}_{sk,\mathbf {c} }(\cdot )\) just once respectively.

Remark 2
In [3, 10], the notions of traditional selective opening security were generalized to a new version, where the adversary is allowed to make multiple opening queries adaptively. SIM-NM-SO security and IND-NM-SO security can also be naturally generalized to the similar notions. In this paper, for simplicity, when we talk about selective opening attack (i.e., SIM/IND-SO security or SIM/IND-NM-SO security), we just consider the adversaries making one round of opening query. However, all the results investigated in this paper can be extended to the generalized notions.
4 Relations Between SIM-NM-SO Securities and SIM-SO Securities
In this section, we explore the relations between SIM-NM-SO securities and SIM-SO securities.
SIM-NM-SO-ATK \(\Rightarrow \) SIM-SO-ATK. We provide a high-level description of the reasoning here.
Given any SIM-SO-ATK adversary \(A=(A_1, A_2, A_3)\) for an encryption scheme PKE, we construct a SIM-NM-SO-ATK adversary \(A'\) (in Table 2). If \(\textsf {{Exp}}_{\textsf {{PKE}},A'}^{\text {SIM-NM-SO-ATK-Real}}(\kappa ):=(\mathcal {M}, \mathbf {m} , I, \mathbf {x} ,\) \(\sigma )\), then \(\textsf {{Exp}}_{\textsf {{PKE}},A}^{\text {SIM-SO-ATK-Real}}(\kappa )\) \(=(\mathcal {M}, \mathbf {m} , I, \sigma )\). SIM-NM-SO-ATK security guarantees that there is a simulator \(S'\) with respect to \(A'\), such that \(\textsf {{Exp}}_{\textsf {{PKE}}, S'}^{\text {SIM-NM-SO-ATK-Ideal}}(\kappa )\overset{c}{\approx }\textsf {{Exp}}_{\textsf {{PKE}}, A'}^{\text {SIM-NM-SO-ATK-Real}}(\kappa )\), i.e., \((\mathcal {M}_{S'}, \mathbf {m} _{S'}, I_{S'}, \mathbf {x} _{S'}, \sigma _{S'}) \overset{c}{\approx } (\mathcal {M}, \mathbf {m} , I, \mathbf {x} , \sigma )\). Hence, \((\mathcal {M}_{S'}, \mathbf {m} _{S'}, I_{S'}, \sigma _{S'})\overset{c}{\approx }(\mathcal {M}, \mathbf {m} , I, \sigma )\). Based on \(S'\), we can construct a SIM-SO-ATK simulator S (in Table 2), such that \(\textsf {{Exp}}_{\textsf {{PKE}},S}^{\text {SIM-SO-ATK-Ideal}}(\kappa )\) \(:=(\mathcal {M}_{S'}, \mathbf {m} _{S'}, I_{S'}, \sigma _{S'})\). Hence, we have the following theorem.
Theorem 1
(SIM-NM-SO-ATK \(\Rightarrow \) SIM-SO-ATK). For any \(\text {ATK}\in \{\text {CPA, CCA1, CCA2}\}\), SIM-NM-SO-ATK security implies SIM-SO-ATK security.
SIM-SO-ATK \(\nRightarrow \) SIM-NM-SO-ATK. Now we show that SIM-SO security is strictly weaker than SIM-NM-SO-ATK security. Formally, we have the following theorem.
Theorem 2
(SIM-SO-ATK \(\nRightarrow \) SIM-NM-SO-ATK). For any \(\text {ATK}\in \{\text {CPA, CCA1, CCA2}\}\), there is a SIM-SO-ATK secure PKE scheme, which is not SIM-NM-SO-ATK secure.
We prove this theorem with two counterexamples.
In the case of \(\text {ATK}=\text {CPA}\), we consider the Goldwasser-Micali probabilistic encryption scheme (the GM scheme) [9]. In [4], Bellare et al. pointed out that the GM scheme is SIM-SO-CPA secure. We claim that the GM scheme is not SIM-NM-SO-CPA secure because of its homomorphic property. Roughly speaking, let the challenge ciphertext vector \(\mathbf {c} \) be generated from a random message vector \(\mathbf {m} \). We can construct an adversary A who encrypts bit 0 to obtain a ciphertext \(y'\), and then outputs\(\mathbf {y} :=(y'\cdot \mathbf {c} [i])_{i\in [n]}\ne \mathbf {c} \). Obviously, the decryption of \(\mathbf {y} \) is \(\mathbf {x} :=(0\oplus \mathbf {m} [i])_{i\in [n]}=\mathbf {m} \). However, no PPT simulator S can output a ciphertext vector \(\mathbf {y} \) satisfying \(\mathbf {x} =\mathbf {m} \), since \(\mathbf {m} \) was uniformly chosen and no information about \(\mathbf {m} \) is leaked to S except the opened messages.
In the case of \(\text {ATK}\in \{\text {CCA1, CCA2}\}\), we show a counterexample as follows. The main idea of our counterexample is similar to that in [17]. Let \(\textsf {{PKE}} = (\textsf {{Gen}}, \textsf {{Enc}}, \textsf {{Dec}})\) be an encryption scheme. We construct a new scheme \(\widetilde{\textsf {{PKE}}} = (\widetilde{\textsf {{Gen}}}, \widetilde{\textsf {{Enc}}}, \widetilde{\textsf {{Dec}}})\) in Table 3.
To prove that \(\widetilde{\textsf {{PKE}}}\) is not SIM-NM-SO-CCA1/CCA2 secure, consider the adversary A: A obtains \(\theta \) by querying the decryption oracle on input \((c,0,1^\kappa )\), and outputs a ciphertext whose decryption is \(\bot \). Notice that any PPT simulator S has no information about the uniformly chosen \(\theta \), since it cannot access to the decryption oracle. So the probability that the simulator outputs a ciphertext whose decryption is \(\bot \) is negligible. Consider the distinguisher D: On input \((\mathcal {M}, \mathbf {m} , I, \mathbf {x} , \sigma )\), return 1 if and only if \(\bot \in \mathbf {x} \). Then D can distinguish \(\textsf {{Exp}}_{\widetilde{\textsf {{PKE}}}, A}^{\text {SIM-NM-SO-CCA1/CCA2-Real}}(\kappa )\) and \(\textsf {{Exp}}_{\widetilde{\textsf {{PKE}}}, S}^{\text {SIM-NM-SO-CCA1/CCA2-Ideal}}(\kappa )\). Hence, \(\widetilde{\textsf {{PKE}}}\) is not SIM-NM-SO-CCA1/CCA2 secure. Now, what remains is to prove the SIM-SO-CCA1/CCA2 security of \(\widetilde{\textsf {{PKE}}}\), which is guaranteed by \(\textsf {{PKE}}\)’s SIM-SO-CCA1/CCA2 security. Due to space limitations, the formal proof will be given in the full version of this paper.
Remark 3
The aforementioned analysis actually shows that \(\widetilde{\textsf {{PKE}}}\) is not SIM-NM-SO-CCA1 secure, even if \(\textsf {{PKE}}\) is SIM-SO-CCA2 secure. So we have a stronger conclusion: “SIM-SO-CCA2 \(\nRightarrow \) SIM-NM-SO-CCA1”, and a similar analysis gives “SIM-SO-CCA2 \(\nRightarrow \) SIM-NM-CCA1”.
A Note on SIM-NM-SO-CCA2. In [17], Pass et al. specified a special condition (i.e., the message space and the range of the decryption algorithm are identical), under which IND-NM-CCA1/CCA2 security and SIM-NM-CCA1/CCA2 security are equivalent. Interestingly, we find that under this condition, if the range of the decryption algorithm is recognizable (i.e., roughly speaking, there is a polynomial-time algorithm, which can determine whether an element is in the range of the decryption algorithm), then SIM-SO-CCA2 security implies SIM-NM-SO-CCA2 security (i.e., these two security notions are equivalent). Below we recall the special condition proposed in [17], which we name “invertible decryption”.
Definition 8
(Invertible Decryption). Let \(\textsf {{PKE}} = (\textsf {{Gen}}, \textsf {{Enc}}, \textsf {{Dec}})\) be a PKE scheme. \(\textsf {{Dec}}\) is invertible if there exists a PPT algorithm \(\textsf {{F}}\), such that for any ciphertext c, \(\textsf {{Dec}}(sk, \textsf {{F}}(pk, \textsf {{Dec}}(sk,c)))\) \(=\textsf {{Dec}}(sk,c)\), where \((pk,sk)\leftarrow \textsf {{Gen}}(1^\kappa )\).
Theorem 3
If a SIM-SO-CCA2 secure PKE scheme has an invertible decryption algorithm, and the range of the decryption algorithm is recognizable in polynomial time, then the scheme is also SIM-NM-SO-CCA2 secure.
Proof
Let \(\textsf {{PKE}}=(\textsf {{Gen}},\textsf {{Enc}},\textsf {{Dec}})\) be a SIM-SO-CCA2 secure encryption scheme, such that it has an inverting algorithm \(\textsf {{F}}\), and the range of Dec is recognizable. Now we prove \(\textsf {{PKE}}\) is SIM-NM-SO-CCA2 secure.
For any PPT adversary \(A=(A_1,A_2, A_3)\) attacking \(\textsf {{PKE}}\) in the sense of SIM-NM-SO-CCA2, we construct a PPT adversary \(A'=(A'_1,A'_2,A'_3)\) attacking \(\textsf {{PKE}}\) in the sense of SIM-SO-CCA2 as follows.
Receiving a public key pk, \(A'_1\) runs \(A_1\) on the input of pk. For any decryption query \(c'\) asked by \(A_1\), \(A'_1\) sends \(c'\) to its own decryption oracle, and then returns the answer to \(A_1\). At some point, \(A_1\) returns a message distribution \(\mathcal {M}\). Then, \(A'_1\) outputs \(\mathcal {M}\) to the challenger.
On the other side, the challenger samples \(\mathbf {m} \leftarrow \mathcal {M}\) and \(\mathbf {r} \leftarrow (\mathcal {R}_{\textsf {{Enc}}})^{|\mathbf {m} |}\), and generates \(\mathbf {c} ^*\leftarrow \textsf {{Enc}}(pk, \mathbf {m} ; \mathbf {r} )\).
Receiving \(\mathbf {c} ^*\) from the challenger, \(A'_2\) runs \(A_2\) on the input of \(\mathbf {c} ^*\). For any decryption query \(c'\) asked by \(A_2\), \(A'_2\) answers it with its own decryption oracle as before (of course, both \(A_2\) and \(A'_2\) are not allowed to query \(c'\in \mathbf {c} ^*\)). At some point, \(A_2\) returns a subset \(I\subset [|\mathbf {c} ^*|]\). Then, \(A'_2\) outputs I to the challenger.
Receiving \(\mathbf {m} [I]\) and \(\mathbf {r} [I]\), \(A'_3\) runs \(A_3\) on the input of \(\mathbf {m} [I]\) and \(\mathbf {r} [I]\). For any decryption query \(c'\) asked by \(A_3\), \(A'_3\) answers it as before. At last, \(A_3\) returns its final output \((\mathbf {y} , \sigma )\). Then, \(A'_3\) generates \(\mathbf {x} \) (where \(|\mathbf {x} |=|\mathbf {y} |\)) as follows: For \(i=1,2,\cdots ,|\mathbf {y} |\), if \(\mathbf {y} [i]\notin \mathbf {c} ^*\), submit \(\mathbf {y} [i]\) to \(A'\)’s decryption oracle and denote the decryption by \(\mathbf {x} [i]\); if \(\mathbf {y} [i]\in \mathbf {c} ^*\), set that \(\mathbf {x} [i]:=\text {COPY}\). Finally, \(A'_3\) outputs \(out_{A'}:=(\mathbf {x} ,\sigma )\).
Notice that \(A'\) perfectly simulates experiment \(\textsf {{Exp}}_{\textsf {{PKE}}, A}^{\text {SIM-NM-SO-ATK-Real}}(\kappa )\) for A. Hence,
Since PKE is SIM-SO-CCA2 secure, there is a PPT simulator \(S'=(S'_1,S'_2,S'_3)\) such that
Now, based on \(S'\), we construct a simulator \(S=(S_1, S_2, S_3)\) in the sense of SIM-NM-SO-CCA2.
Receiving a public key pk, \(S_1\) runs \(S'_1\) on the input of \(1^{\kappa }\). Then \(S_1\) outputs the \(\mathcal {M}_{S'}\) returned by \(S'_1\).
On the other side, the challenger samples \(\mathbf {m} _{S'}\leftarrow \mathcal {M}_{S'}\), without returning anything to S.
Later, \(S'_2\) outputs a subset \(I_{S'}\). \(S_2\) outputs \(I_{S'}\) to the challenger.
Upon receiving \(\mathbf {m} _{S'}[I_{S'}]\), \(S_3\) runs \(S'_3\) on the input of \(\mathbf {m} _{S'}[I_{S'}]\), obtaining \(S'_3\)’s final output \(out_{S'}\). After parsing \(out_{S'}=(\mathbf {x} _{S'},\sigma _{S'})\), \(S_3\) checks whether there is some \(i_0\in [|\mathbf {x} _{S'}|]\) such that \(\mathbf {x} _{S'}[i_0]\ne \text {COPY}\) and meanwhile \(\mathbf {x} _{S'}[i_0]\) is not in the range of \(\textsf {{Dec}}\). It is feasible to check that in polynomial time since the range of \(\textsf {{Dec}}\) is recognizable. If there is such an \(i_0\), then \(S_3\) aborts by outputting a random string. Otherwise, \(S_3\) generates \(\mathbf {y} _S\) (where \(|\mathbf {y} _S|=|\mathbf {x} _{S'}|\)) as follows: For \(i=1,2,\cdots ,|\mathbf {y} _S|\), if \(\mathbf {x} _{S'}[i]=\text {COPY}\), then set \(\mathbf {y} _S[i]=\text {COPY}\); otherwise, generate \(\mathbf {y} _S[i]\leftarrow \textsf {{F}}(pk,\mathbf {x} _{S'}[i])\). Finally, \(S_3\) outputs \((\mathbf {y} _S, \sigma _{S'})\).
Let bad denote the event that S aborts. If bad does not occur, then for any \(j\in [|\mathbf {x} _{S'}|]\) such that \(\mathbf {x} _{S'}[j]\ne \text {COPY}\), there is some ciphertext \(\widehat{c}_j\) (not has to be valid), such that \(\textsf {{Dec}}(sk, \widehat{c}_j)=\mathbf {x} _{S'}[j]\). We have \(\textsf {{Dec}}(sk, \mathbf {y} _S[j])=\textsf {{Dec}}(sk, \textsf {{F}}(pk,\textsf {{Dec}}(sk, \widehat{c}_j)))=\textsf {{Dec}}(sk, \widehat{c}_j)=\mathbf {x} _{S'}[j]\). In this case,
So for any PPT algorithm D,
Notice that if \(\text {Pr}[\textsf {{bad}}]\) is negligible, then we have
Combining Eqs. (1), (2) and (3) gives
Hence, what remains is to prove that \(\text {Pr}[\textsf {{bad}}]\) is negligible. We consider the following distinguisher \(D'\):

It is obvious that \(\text {Pr}[D'(\textsf {{Exp}}_{\textsf {{PKE}}, A'}^{\text {SIM-SO-CCA2-Real}}(\kappa ))=1]=0\), and that \(\text {Pr}[D'(\textsf {{Exp}}_{\textsf {{PKE}}, S'}^{\text {SIM-SO-CCA2-Ideal}}(\kappa ))=1]=\text {Pr}[\textsf {{bad}}]\). In other words,
Hence, Eq. (2) guarantees that \(\text {Pr}[\textsf {{bad}}]\) is negligible. \(\square \)
5 Relations Between IND-NM-SO Securities and IND-SO Securities
In this section, we explore the relations between IND-NM-SO securities and IND-SO securities. First of all, for any \(\text {ATK}\in \{\text {CPA, CCA1, CCA2}\}\), an IND-NM-SO-ATK adversary is more powerful than an IND-SO-ATK adversary in that it can make an additional query to oracle \(\textsf {P }_{sk}(\cdot )\). Intuitively, IND-NM-SO-ATK security implies IND-SO-ATK security. Further more, any IND-SO-CCA2 adversary A is able to access to the decryption oracle after receiving the challenge ciphertext vector. So providing A the ability to make a parallel decryption query yields no additional power. The above analysis results in the following theorem.
Theorem 4
(IND-NM-SO-ATK \(\Rightarrow \) IND-SO-ATK, IND-NM-SO-CCA2 \(\Leftrightarrow \) IND-SO-CCA2). For any \(\text {ATK}\in \{\text {CPA, CCA1, CCA2}\}\), IND-NM-SO-ATK security implies IND-SO-ATK security. Further more, if \(\text {ATK}=\text {CCA2}\), these two securities are equivalent.
IND-NM-SO-CPA  IND-SO-CCA1. Formally, we have the following theorem. This is an direct extension of the conclusion in [1]. So we just provide a high-level description of the reasoning here.
IND-SO-CCA1. Formally, we have the following theorem. This is an direct extension of the conclusion in [1]. So we just provide a high-level description of the reasoning here.
Theorem 5
(IND-NM-SO-CPA  IND-SO-CCA1). There is an IND-SO-CCA1 secure PKE scheme, which is not IND-NM-SO-CPA secure; vice verse.
IND-SO-CCA1). There is an IND-SO-CCA1 secure PKE scheme, which is not IND-NM-SO-CPA secure; vice verse.
The Direction  . Note that after receiving the challenge ciphertext, the IND-SO-CCA1 adversary cannot access to the decryption oracle, but the IND-NM-SO-CPA adversary still can make a parallel decryption query. Based on this observation, any PKE scheme, achieving IND-SO-CCA1 but not IND-SO-CCA2 security, might be used as a counterexample. The following scheme \(\textsf {{PKE}}'\) (in Table 4), with message space \(\{0,1\}^\kappa \), is from [1]. If the basic scheme \(\textsf {{PKE}} = (\textsf {{Gen}}, \textsf {{Enc}}, \textsf {{Dec}})\) is IND-SO-CCA1 secure, then we can prove that \(\textsf {{PKE}}'\) is IND-SO-CCA1 secure but not IND-NM-SO-CPA secure. The formal proof will be given in the full version of this paper.
. Note that after receiving the challenge ciphertext, the IND-SO-CCA1 adversary cannot access to the decryption oracle, but the IND-NM-SO-CPA adversary still can make a parallel decryption query. Based on this observation, any PKE scheme, achieving IND-SO-CCA1 but not IND-SO-CCA2 security, might be used as a counterexample. The following scheme \(\textsf {{PKE}}'\) (in Table 4), with message space \(\{0,1\}^\kappa \), is from [1]. If the basic scheme \(\textsf {{PKE}} = (\textsf {{Gen}}, \textsf {{Enc}}, \textsf {{Dec}})\) is IND-SO-CCA1 secure, then we can prove that \(\textsf {{PKE}}'\) is IND-SO-CCA1 secure but not IND-NM-SO-CPA secure. The formal proof will be given in the full version of this paper.
The Direction \({\nRightarrow }\) . Note that an IND-NM-SO-CPA adversary can make just a one-time decryption query (although it is parallel), but an IND-SO-CCA1 adversary can query the decryption oracle polynomial times. Based on this observation, we provide a PKE scheme \(\textsf {{PKE}}''\), which is identical to the scheme \(\widetilde{\textsf {{PKE}}}\) in Sect. 4, except that during the decryption, roughly, the decryption algorithm returns the original secret key sk instead of the special symbol \(\bot \), in the case of “\(b=0\) and \(\vartheta =\theta \)”. The analysis is similar to that in Sect. 4. The IND-SO-CCA1 adversary can obtain \(\theta \) by querying the decryption oracle on input \((c,0,1^\kappa )\), so it can obtain the original sk by querying on \((c,0,\theta )\). Hence, \(\textsf {{PKE}}''\) is not IND-SO-CCA1 secure. However, the IND-NM-SO-CPA adversary cannot make any other decryption query after the parallel decryption query. Notice that \(\theta \) is uniformly chosen, so \(\textsf {{PKE}}''\) can be proved IND-NM-SO-CPA secure. The formal proof will be given in the full version of this paper.
Remark 4
Since IND-SO-CCA1 (resp. IND-NM-SO-CCA1) security implies IND-SO-CPA (resp. IND-NM-SO-CPA) security, we have the following corollary.
Corollary 1
(IND-SO-CPA/CCA1 \(\nRightarrow \) IND-NM-SO-CPA/CCA1). IND-SO-CPA/CCA1 security is strictly weaker than IND-NM-SO-CPA/ CCA1 security.
6 Relations Between SIM-NM-SO Securities and SIM-NM Securities
SIM-NM-SO-ATK \(\Rightarrow \) SIM-NM-ATK. Compared with the conclusion that “SIM-NM-SO-ATK \(\Rightarrow \) SIM-SO-ATK”, this conclusion is not that obvious. That is because, compared with the SIM-NM-SO-ATK adversary, although the SIM-NM-ATK adversary is less powerful (i.e., not allowed to make any opening query), the corresponding simulator also has less information (i.e., not allowed to make any opening query) about the message vector. Formally, we have the following theorem. Due to space limitations, its formal proof will be given in the full version of this paper.
Theorem 6
(SIM-NM-SO-ATK \(\Rightarrow \) SIM-NM-ATK). For any \(\text {ATK} \in \{\text {CPA, CCA1, CCA2}\}\), SIM-NM-SO-ATK security implies SIM-NM-ATK security.
Remark 5
We can also prove Theorem 6 by simply constructing a “non-opening” SIM-NM-SO-ATK adversary, which is a copy of the SIM-NM-ATK adversary. Hence, our proof, the overview of which has been provided in the Introduction, actually shows that even considering constrained SIM-NM-SO-ATK adversary (i.e., “opening” adversary), Theorem 6 still holds.
SIM-NM-ATK \(\nRightarrow \) SIM-NM-SO-ATK. We will show that the IND-CCA2 secure Cramer-Shoup scheme [6, 7] (the CS scheme) is SIM-NM-CCA2 secure. But the CS scheme is not SIM-SO-CPA secure [2]. According to Theorem 1, it is not SIM-NM-SO-CPA secure either. Consequently, “\(\text {SIM-NM-ATK}' \nRightarrow \text {SIM-NM-SO-ATK}''\)”, for any \(\text {ATK}', \text {ATK}''\in \{\text {CPA},\text {CCA1},\text {CCA2}\}\).
To show that the CS scheme is SIM-NM-CCA2 secure, we use the following two facts: (1) For any PKE scheme having an invertible decryption algorithm, it is IND-NM-CCA2 secure iff it is SIM-NM-CCA2 secure [17, Theorem 6]. (2) IND-CCA2 security is equivalent to IND-NM-CCA2 security, since the parallel decryption query provides no additional ability to the adversary in the case of CCA2. So what remains is to show that the CS scheme has an invertible decryption algorithm. Let \((\textsf {{Enc}},\textsf {{Dec}})\) denote the corresponding encryption/decryption algorithms. Following the notations of [7], any valid ciphertext \(\psi \) of the CS scheme has the form \(\psi :=(a, \hat{a}, c, d)\in G^4\), the message space is G, and the range of \(\textsf {{Dec}}\) is \(G\bigcup \{\textsf {{reject}}\}\), where G is a group of prime order q (see [7]). We construct an inverting algorithm \(\textsf {F}\) as follows: On input \((pk, \textsf {{Dec}}(sk,\psi ))\), if \(\textsf {{Dec}}(sk,\psi )\in G\), then \(\textsf {{F}}\) runs \(\textsf {{Enc}}(pk, \textsf {{Dec}}(sk,\psi ))\) and returns the generated ciphertext; If \(\textsf {{Dec}}(sk,\psi )=\textsf {{reject}}\), then \(\textsf {{F}}\) returns an arbitrary ciphertext not in \(G^4\).
7 Relations Between IND-NM-SO Securities and IND-NM Securities
Theorem 7
(IND-NM-CCA2 \(\nRightarrow \) IND-NM-SO-CCA2). There is an IND-NM-CCA2 secure PKE scheme, which is not IND-NM-SO-CCA2 secure.
Theorem 8
(IND-NM-SO-ATK \(\Rightarrow \) IND-NM-ATK). For any \(\text {ATK}\) \(\in \{\text {CPA, CCA1, CCA2}\}\), IND-NM-SO-ATK security implies IND-NM-ATK security.
Notice that IND-NM-CCA2 (resp. IND-NM-SO-CCA2) security is equivalent to IND-CCA2 (resp. IND-SO-CCA2) security, so Theorem 7 is directly from [15], which separated IND-CCA2 security and IND-SO-CCA2 security. The conclusion of Theorem 8 is not surprising at all. One subtlety here is that the ways that message vectors are sampled in these two notions are different. Due to space limitations, the proof of Theorem 8 will be given in the full version of this paper.
Remark 6
In Sect. 5, we have showed that scheme \(\textsf {{PKE}}''\) is IND-NM-SO-CPA secure. It is easy to see that \(\textsf {{PKE}}''\) is not IND-NM-CCA1 secure. So we conclude that “IND-NM-SO-CPA \(\nRightarrow \) IND-NM-CCA1”.
8 Relations Between SIM-NM-SO Securities and IND-NM-SO Securities
For the relations between SIM-NM-SO securities and IND-NM-SO securities, we have the following conclusion. Its proof is similar to that of Theorem 2 and [17, Theorem 4], so we just provide a sketch here.
Theorem 9
(IND-NM-SO-CCA1/CCA2 \(\nRightarrow \) SIM-NM-SO-CCA1/CCA2). For any \(\text {ATK}\in \{\text {CCA1}, \text {CCA2}\}\), there is an IND-NM-SO-ATK secure PKE scheme, which is not SIM-NM-SO-ATK secure.
Proof
(Sketch) Let \(\textsf {{PKE}} = (\textsf {{Gen}}, \textsf {{Enc}}, \textsf {{Dec}})\) be an IND-NM-SO-CCA1/CCA2 secure encryption scheme. We construct the scheme \(\widetilde{\textsf {{PKE}}} = (\widetilde{\textsf {{Gen}}}, \widetilde{\textsf {{Enc}}}, \widetilde{\textsf {{Dec}}})\) described in Table 3. Note that in Sect. 4, we have shown that \(\widetilde{\textsf {{PKE}}}\) is not SIM-NM-SO-CCA1/CCA2 secure, and the reasoning there does not involve the security of the basic scheme \(\textsf {{PKE}}\). So here we just need to prove that \(\widetilde{\textsf {{PKE}}}\) achieves IND-NM-SO-CCA1/CCA2 security.
For any PPT adversary \(\widetilde{A}\) attacking \(\widetilde{\textsf {{PKE}}}\) in the sense of IND-NM-SO-CCA1/CCA2 with non-negligible advantage, roughly speaking, we construct a PPT adversary A attacking \(\textsf {{PKE}}\) (in the sense of IND-NM-SO-CCA1/CCA2) as follows: Receiving the public key, A chooses \(\theta \leftarrow \{0,1\}^\kappa \), and uses this \(\theta \) and its own decryption oracle to answer \(\widetilde{A}\)’s decryption queries. A outputs the same message distribution \(\mathcal {M}\) as \(\widetilde{A}\) does, transforms any component \(\mathbf {c} [i]\) of its own challenge ciphertext vector into \((\mathbf {c} [i], 1, 0^\kappa )\) to get a modified challenge ciphertext vector and passes the modified one to \(\widetilde{A}\). A uses its own opening oracle to answer \(\widetilde{A}\)’s opening query. Finally, A returns \(\widetilde{A}\)’s final output. Notice that A perfectly simulates the IND-NM-SO-CCA1/CCA2 experiment (about \(\widetilde{\textsf {{PKE}}}\)) for \(\widetilde{A}\). So A’s advantage is also non-negligible, contradicting the assumption. \(\square \)
Remark 7
Note that \(\widetilde{\textsf {{PKE}}}\) is not SIM-NM-SO-CCA1 secure, even if \(\textsf {{PKE}}\) is IND-NM-SO-CCA2 secure. So we actually have a stronger conclusion: “IND-NM-SO-CCA2 \(\nRightarrow \) SIM-NM-SO-CCA1”.
9 Constructions
Fortunately, there are some known selective opening secure PKE schemes achieving SIM/IND-NM-SO securities. Details are as follows.
SIM-NM-SO-CCA2 Secure Construction. The Fehr-Hofheinz-Kiltz-Wee encryption scheme (the FHKW scheme) is SIM-SO-CCA2 secure [10, 13, 14]. We claim that the decryption algorithm of the FHKW scheme is invertible, and the range of the decryption algorithm is recognizable. Hence, according to Theorem 3, the FHKW scheme is SIM-NM-SO-CCA2 secure. Our claim is justified as follows.
According to [10], any valid ciphertext of the FHKW scheme has the form \((X_1,\cdots ,X_L, T)\), and the message space is \(\{0,1\}^{L}\). For any ciphertext of the form \((X_1,\cdots ,X_L, T)\), where \(X_i\in \mathcal {X}\) and \(T\in \mathcal {XT}\), its decryption is an L-bit string. Since \(\mathcal {X}\) and \(\mathcal {XT}\) are both efficiently recognizable, any invalid ciphertext \((X_1,\cdots ,X_L, T)\) (i.e., \(X_i\notin \mathcal {X}\) for some i, or \(T\notin \mathcal {XT}\)) will be decrypted to \(\bot \). In other words, the range of the decryption algorithm is \(\{0,1\}^{L}\bigcup \{\bot \}\), which is recognizable. As to the special inverting algorithm \(\textsf {{F}}\), we construct it as follows: Let \((\textsf {{Enc}},\textsf {{Dec}})\) denote the encryption/decryption algorithms of the FHKW scheme. For any ciphertext c, we have that \(\textsf {{Dec}}(sk,c)\in \{0,1\}^{L}\bigcup \{\bot \}\). If \(\textsf {{Dec}}(sk,c)\in \{0,1\}^{L}\), \(\textsf {{F}}\) runs \(\textsf {{Enc}}(pk, \textsf {{Dec}}(sk,c))\) and returns the generated ciphertext; If \(\textsf {{Dec}}(sk,c)=\bot \), \(\textsf {{F}}\) returns an arbitrary ciphertext \((X_1,\cdots ,X_L, T)\) where \(X_i\notin \mathcal {X}\) or \(T\notin \mathcal {XT}\).
IND-NM-SO-CCA2 Secure Construction. According to Theorem 4, IND-NM-SO-CCA2 security is equivalent to IND-SO-CCA2 security. So any IND-SO-CCA2 secure encryption scheme (e.g. the PKE scheme constructed from all-but-many lossy trapdoor functions [11]) meets IND-NM-SO-CCA2 security.
References
Bellare, M., Desai, A., Pointcheval, D., Rogaway, P.: Relations among notions of security for public-key encryption schemes. In: Krawczyk, H. (ed.) CRYPTO 1998. LNCS, vol. 1462, pp. 26–45. Springer, Heidelberg (1998)
Bellare, M., Dowsley, R., Waters, B., Yilek, S.: Standard security does not imply security against selective-opening. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 645–662. Springer, Heidelberg (2012)
Böhl, F., Hofheinz, D., Kraschewski, D.: On definitions of selective opening security. In: Fischlin, M., Buchmann, J., Manulis, M. (eds.) PKC 2012. LNCS, vol. 7293, pp. 522–539. Springer, Heidelberg (2012)
Bellare, M., Hofheinz, D., Yilek, S.: Possibility and impossibility results for encryption and commitment secure under selective opening. In: Joux, A. (ed.) EUROCRYPT 2009. LNCS, vol. 5479, pp. 1–35. Springer, Heidelberg (2009)
Bellare, M., Sahai, A.: Non-malleable encryption: equivalence between two notions, and an indistinguishability-based characterization. In: Wiener, M. (ed.) CRYPTO 1999. LNCS, vol. 1666, pp. 519–536. Springer, Heidelberg (1999)
Cramer, R., Shoup, V.: A practical public key cryptosystem provably secure against adaptive chosen ciphertext attack. In: Krawczyk, H. (ed.) CRYPTO 1998. LNCS, vol. 1462, pp. 13–25. Springer, Heidelberg (1998)
Cramer, R., Shoup, V.: Design and analysis of practical public-key encryption schemes secure against adaptive chosen ciphertext attack. SIAM J. Comput. 33(1), 167–226 (2003)
Dolev, D., Dwork, C., Naor, M.: Non-malleable cryptography. SIAM J. Comput. 30(2), 391–437 (2000)
Goldwasser, S., Micali, S.: Probabilistic encryption. J. Comput. Syst. Sci. 28(2), 270–299 (1984)
Fehr, S., Hofheinz, D., Kiltz, E., Wee, H.: Encryption schemes secure against chosen-ciphertext selective opening attacks. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 381–402. Springer, Heidelberg (2010)
Hofheinz, D.: All-but-many lossy trapdoor functions. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 209–227. Springer, Heidelberg (2012)
Hemenway, B., Libert, B., Ostrovsky, R., Vergnaud, D.: Lossy Encryption: constructions from general assumptions and efficient selective opening chosen ciphertext security. In: Wang, X., Lee, D.H. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 70–88. Springer, Heidelberg (2011)
Huang, Z., Liu, S., Qin, B.: Sender-equivocable encryption schemes secure against chosen-ciphertext attacks revisited. In: Kurosawa, K., Hanaoka, G. (eds.) PKC 2013. LNCS, vol. 7778, pp. 369–385. Springer, Heidelberg (2013)
Huang, Z., Liu, S., Qin, B., Chen, K.: Fixing the sender-equivocable encryption scheme in eurocrypt 2010. In: 2013 5th International Conference on Intelligent Networking and Collaborative Systems (INCoS), pp. 366–372. IEEE (2013)
Hofheinz, D., Rupp, A.: Standard versus selective opening security: separation and equivalence results. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 591–615. Springer, Heidelberg (2014)
Naor, M., Yung, M.: Public-key cryptosystems provably secure against chosen ciphertext attacks. In: Proceedings of the Twenty-Second Annual ACM Symposium on Theory of Computing, pp. 427–437. ACM (1990)
Pass, R., Shelat, A., Vaikuntanathan, V.: Relations among notions of non-malleability for encryption. In: Kurosawa, K. (ed.) ASIACRYPT 2007. LNCS, vol. 4833, pp. 519–535. Springer, Heidelberg (2007)
Rackoff, C., Simon, D.R.: Non-interactive zero-knowledge proof of knowledge and chosen ciphertext attack. In: Feigenbaum, J. (ed.) CRYPTO 1991. LNCS, vol. 576, pp. 433–444. Springer, Heidelberg (1992)
Acknowledgments
We would like to thank the anonymous reviewers for their helpful comments. This work is funded by the Specialized Research Fund for the Doctoral Program of Higher Education under Grant 20110073110016, the Scientific Innovation Projects of Shanghai Education Committee under Grant 12ZZ021, and the National Natural Science Foundation of China under Grants 61170229, 61373153, 61133014 and 61472114.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this paper
Cite this paper
Huang, Z., Liu, S., Mao, X., Chen, K. (2015). Non-malleability Under Selective Opening Attacks: Implication and Separation. In: Malkin, T., Kolesnikov, V., Lewko, A., Polychronakis, M. (eds) Applied Cryptography and Network Security. ACNS 2015. Lecture Notes in Computer Science(), vol 9092. Springer, Cham. https://doi.org/10.1007/978-3-319-28166-7_5
Download citation
DOI: https://doi.org/10.1007/978-3-319-28166-7_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-28165-0
Online ISBN: 978-3-319-28166-7
eBook Packages: Computer ScienceComputer Science (R0)





 SIM-SO-ATK”, for any
SIM-SO-ATK”, for any  IND-SO-CCA1”.
IND-SO-CCA1”.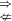 IND-SO-CCA1/CPA”, but “IND-NM-SO-CCA2
IND-SO-CCA1/CPA”, but “IND-NM-SO-CCA2 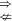 SIM-NM-ATK”, for any
SIM-NM-ATK”, for any 