Interval Arithmetic and Self Similarity Based Subthreshold Leakage Optimization in RTL Datapaths

Abstract

We propose top-down and bottom-up interval propagation techniques for identifying low leakage input vectors at primary inputs of an RTL datapath. Empirically, we observed self-similarity in the leakage distribution of adder/multiplier modules i.e., leakage distribution at the sub-space level is similar to that at the entire input space. We exploit this property to quickly search low leakage vectors. The proposed module library leakage characterization is scalable and is demonstrated on adders/multipliers. Given an RTL datapath, interval propagation is carried out with the low leakage intervals of the module instances with primary inputs. The reduced interval set is further processed with simulated annealing, to arrive at the best low leakage vector set at the primary inputs. Experimental results for various DSP filters simulated in 16 nm CMOS technology with top-down and bottom-up approaches yield leakage savings of 93.6 % and 89.2 % respectively with no area, timing, or control overheads.

1 Introduction and Motivation

Excessive subthreshold leakage power consumption is a serious concern in deep-submicron technology nodes [1]. Input vector control technique is widely used for subthreshold leakage optimization due to its low latency overhead. However, determination of minimum leakage vector (MLV) for large circuits is a difficult problem by itself as it requires excessive simulation time [2]. An MLV is an input vector that puts the circuit in lowest leakage state possible i.e., it is an optimal vector. We refer to sub-optimal MLVs as low leakage vectors (LLVs) that put the circuit with leakage close to the optimal leakage.

For a given datapath, applying MLV to each RTL module incurs significant area and control overhead. The additional area stems from input multiplexers needed to apply the minimum leakage vector. Control overhead is incurred from the select lines of these multiplexers. As data values propagate through RTL modules, we have proposed [3] to identify a set of input vectors such that they not only put the module instances at primary inputs (PIs) into low leakage, but also result in low leakage input vectors at internal module instances. In [4] (conference version of this chapter), we leverage self-similarity of module-level leakage distributions. In this book chapter, we further extend the idea by experimenting with bottom up interval propagation. We experimented with five DSP filters and obtained average leakage savings of 93 % with top down approach and 89.2 % with bottom up approach. In both cases, we did not require any internal control points for any design, thus the proposed approaches incur no overhead in terms of area, control, or delay.

The overall optimization flow is as follows: First, we characterize the module library to gather low leakage vector intervals with two-phase Monte-Carlo simulation. Next, we propagate interval sets of module instances at primary inputs through the datapath. We have two choices: top-down or bottom-up. In top-down interval sets at PIs are propagated to primary outputs (POs) and in case of bottom-up, interval sets at POs are propagated back to PIs. The interval propagation yields a reduced set of low leakage intervals at the PIs. A simulated annealing algorithm is devised to find the best input vector set from the reduced interval set. Next, we briefly describe the self-similarity based scalable module leakage characterization for bit-sliced adder/multipliers.

As the search space grows exponentially with the module bit-width, finding low leakage vectors by exhaustive simulation is infeasible. In order to make the problem tractable, we exploit the self-similarity property of leakage distribution of a given functional unit. Briefly, given a stochastic distribution, it is said to be self-similar [5, 6], if any arbitrary sub-distribution (built by choosing contiguous samples) is similar to the original distribution. Hurst parameter is a commonly used metric to determine self-similarity of a distribution. For two module types, adder and multiplier, we empirically observe that their leakage distributions are self-similar. Given a confidence level ($\alpha$) and an error tolerance ($\beta$), Halter and Najm [7] derived a formula to determine the minimum number of random vectors needed to find a LLV that is no worse than $\beta$ % of vectors with $\alpha$ % confidence, provided the leakage distribution is normal. While the goal of any MLV heuristic is to find one vector, our goal is to find as many LLVs as possible so that we can expand them into LLV data intervals. For adder and multiplier, we also empirically observe that their leakage distributions are normal. This normal leakage distribution along with self-similarity of a module enables us to partition the input space into small sub-spaces and then randomly sample each subspace with fixed number of vectors.

The chapter organization as follows: Section 2 presents background, related work, and terminology. Section 3 describes the module library characterization. Section 4 presents the proposed top-down and bottom-up interval propagation approaches followed by simulated annealing. Section 5 reports experimental results. Finally, Section 6 draws conclusions.

2 Background, Related Work, and Terminology

We first review input vector control techniques from the literature. We then provide a brief overview of fractal theory and self-similarity. Lastly, we present an overview of interval arithmetic.

2.1 Input Vector Control Techniques

As the leakage depends only on the current input vector, during the idle mode, we can apply the minimum leakage vector (MLV). Thus, MLV needs to be determined $a\,priori$ and incorporated into the circuit. This technique is known as the Input Vector Control (IVC). For an n-input module, as the input space grows exponentially ($2^{n}$), MLV determination heuristics have been proposed [2, 8]. For an IVC technique, the area penalty occurs due to additional hardware needed to incorporate MLV into the circuit. Delay penalty is incurred if this additional hardware is in the critical path of the circuit.

To the best of our knowledge, all the proposed IVC techniques are at the logic level. Abdollahi, Fallah, and Pedram [2] propose gate-level leakage reduction with two techniques. The first technique is an input vector control wherein SAT based formulation is employed to find the minimum leakage vector. The second technique involves adding nMOS and pMOS transistors to the gate in order to increase the controllability of the internal signals. The additional transistors increase the stacking effect leading to leakage current reduction. The authors report over 70 % leakage reduction with up to 15 % delay penalty. Gao and Hayes [9] present integer linear programming (ILP) and mixed integer linear programming (MILP) approaches, wherein MILP performs better than ILP and is thirteen times faster. Average leakage current is about 25 % larger than minimum leakage current. IVC technique does not work effectively for circuits with large logic depth. Yuan and Qu [8] have proposed a technique to replace the gates of worst leakage state with other gates in active mode. A divide-and-conquer approach is presented that integrates gate replacement, an optimal MLV searching algorithm for tree circuits, and a genetic algorithm to connect the tree circuits. Compared with the leakage achieved by optimal MLV in small circuits, the gate replacement heuristic and the divide-and-conquer approach can reduce on average 13 % and 17 % leakage, respectively.

2.2 Fractals and Self Similarity

Fractals are shapes made of parts similar to the whole [5]. Property of scaling is exhibited by fractals, which means the degree of irregularity in them tends to be identical at all scales [5, 6]. Many examples of fractal behaviors are observed in nature. Figure 1 shows a romanesco broccoli in which we can observe the self similar property of its shape. In VLSI structures, H-tree based clock signal network, employed for zero-skew, exhibits fractal behavior (Fig. 2).

The main classifications of fractals are time or space, self-similar or self-affine, and deterministic or stochastic. Space fractals are structures exhibiting the fractal property in the space domain. While time fractals are those exhibiting in time domain. Self-similar fractals have symmetry over entire scale, which is identical to recursion, i.e., a pattern inside another pattern. The details spread across finer and finer scales with certain constant measurements. Hurst parameter (0 $< H <$ 1), is a measure of the correlation or long range dependence in the data which leads to the fractal behavior of the data set [10]. A random process has H value equal to 0.5. If H is less than 0.5 then the process exhibits anti-persistence. If H value is between 0.5 and 1, then the process has long term persistence [5]. A stochastic process can be said to exhibit fractal behavior [11] if the H value is between 0.5 and 1. Methods to estimate Hurst parameter are described in [10]. In this work, we employed the R/S plot method.

Fig. 1.

Romanesco broccoli - an example of self-similar behavior occurring in nature. Photo credit [12].

Fig. 2.

H tree - an example of a VLSI structure exhibiting self-similar behavior. Photo credit [13].

Self similarity has been leveraged in estimation and optimization problems in diverse fields. We give three examples. Premarathne et al. [14] employ self-similarity to detect anamalous events in network traffic by showing that traffic’s self-similarity property is temporarily disturbed in the event of an attack. Radjassamy and Carothers [10] proposed a vector compaction technique to generate a compact vector set representative of original vector set such that it mimics power-determining behavior of the latter. Such vector compaction can speed up power estimation of circuits. Qian and Rasheed [15] proposed Hurst parameter based financial market analysis wherein series with high H are predicted more accurately than those with H close to 0.5. For more examples, interested reader is referred to [16].

2.3 Interval Arithmetic

Interval arithmetic (IA) [17] is concerned with arithmetic operations such as addition and subtraction on intervals. The intervals can be either discrete or continuous. IA has been extensively applied in error bound analysis arising in numerical analysis.

In this work, we are concerned with integer arithmetic therefore we restrict our discussion to integer intervals. An interval I = [a, b] represents all integers $a \le i \le b$. Further, the above interval is a closed interval as it includes both extremal values. We can have an open interval, such as I = (a, b) where $a < i < b$. The width of an interval is the difference between the extremal values $| b - a |$. If the interval width is zero, then the interval is referred to as a degenerate interval (for example [1, 1]). We can represent a given integer, say a, as a degenerate interval [a, a].

Given two intervals $U = [a, b]$ and $V = [c, d]$,the following equations hold:

$$\begin{aligned} U + V= & {} [a + c, b + d] \end{aligned}$$

(1)

$$\begin{aligned} U - V= & {} [a - d, b - c] \end{aligned}$$

(2)

$$\begin{aligned} U * V= & {} [min(a * c, a * d, b * c, b * d), max(a * c, a * d, b * c, b * d)]\end{aligned}$$

(3)

$$\begin{aligned} U \div V= & {} [min(a \div c, a \div d, b \div c, b \div d), max(a \div c, a \div d, b \div c, b \div d)] \end{aligned}$$

(4)

2.4 Notation and Problem Formulation

• A DFG, G(V, E), is a directed graph such that $v_i \in V$ represents an operation and $e = (v_i, v_j) \in E$ represents a data transfer from operation $v_i$ to $v_j$.

• A low leakage interval set, $\mathcal {L}(t, w)$, is the set of all low leakage intervals of a given module of type t and w.

• A low leakage output interval set, $\mathcal {LO}(t, w)$, is the set of corresponding outputs of all low leakage input intervals of a given module of type t and w.

• $\mathcal {P}(V, t, w)$ is the leakage power function which calculates the total leakage of the filter.

• Problem Formulation: Given the following inputs: (1) a data flow graph G(V, E); (2) set of low leakage interval sets, $\bigcup _{t,w} \mathcal {L}(t,w)$, and (3) $\bigcup _{t,w} \mathcal {LO}(t,w)$, for all distinct operations of type t and width w, we need to identify best low leakage vector on primary inputs and a set of control points $\mathcal {C}$ such that the objective functions, $\sum _{v_{i} \in V} \mathcal {P}(\mathcal {V}, \mathcal {T}(v_{i}), \mathcal {W}(v_{i}))$ and $\mathcal {C}$, are minimized, where $\mathcal {C}$ is the set of control points.

3 Self Similarity Based Monte Carlo Characterization for Low Leakage Intervals

In this Section, we first study the leakage profiles of adder and multiplier modules. Then we introduce a Monte Carlo leakage characterization technique based on self-similarity to extract low leakage interval set of a functional unit.

3.1 Leakage Profile and Scope for Optimization

Figure 3 shows the leakage current distribution of an 8 bit ripple carry adder based on simulation with all possible (exhaustive) vectors and 1000 vectors. Similarly, Fig. 4 shows the leakage current distributions of an 8 bit parallel multiplier for exhaustive and 1000 vectors respectively. The data has been generated by Synopsys Nanosim simulations of the CMOS layouts in 16 nm technology node with PTM spice models [18–20]. Similar normal leakage distribution plots were obtained for 16 bit adder and 16  bit multiplier with 1000 random vectors as shown in Figs. 5 and 6 respectively. We observed that even with increased bit width, the leakage distribution is normal for both adder and multiplier. Several prior works in literature for eg., [21, 22] report similar nomal power distributions. Based on this empirical evidence, we assume that the leakage distribution of adder and multiplier modules with any bit width is normal.

Fig. 3.

Leakage current distribution for 8 bit adder.

Fig. 4.

Leakage current distribution for 8 bit parallel multiplier.

Fig. 5.

Leakage current distribution for 16 bit adder (1000 random vectors).

Fig. 6.

Leakage current distribution for 16 bit parallel multiplier (1000 random vectors).

Consider the exhaustive simulation of 8 bit adder and multiplier. The leakage current ranges are [0.084 $\upmu$A, 4.3 $\upmu$A] and [1.4 $\upmu$A, 56 $\upmu$A] respectively. Thus, the approximate max-to-min leakage current ratio for 8b adder and 8b multiplier are 51 and 40 respectively. For 10 % tolerance ($\varepsilon$=0.1), the number of distinct LLVs for the adder is 119. Thus, the percentage of input space that puts the adder in a low-leakage state is (119/($2^8 \times 2^8$))$\times$100 = 0.18 %. These vectors can be merged into 80 low leakage intervals. Similarly, for multiplier, number of low leakage vectors is 490 and the size of the interval set is 329. The percentage of input space that puts the multiplier in a low-leakage state for $\varepsilon$=0.1, is (490/($2^8 \times 2^8$))$\times$100 = 0.74 %. Based on these numbers, we can see only a small percentage of input space can result in significant leakage reduction. Our next challenge is to locate all these low leakage intervals in the entire input space.

3.2 Self Similarity of Leakage Distributions in n Bit Adders and Multipliers

We empirically observed that the sub-threshold leakage distributions of adders and multipliers exhibit self similarity property. For example, in Fig. 7 for an 8 bit adder we show the Hurst values for various sub spaces obtained by partitioning the input space in three different ways. Recall that a distribution is self similar if Hurst value is between 0.5 and 1. For each partitioning scheme, we see that the leakage distribution of each sub space is self similar to the parent distribution. Similar results have been obtained in the case of 8 bit multiplier, 16 bit adder, and 16 bit multiplier. Due to limited space, we do not include these plots. Based on these empirical results, we assume in general that the leakage distribution of a n bit adder or multiplier is self-similar. The concept of self similarity enables us to develop a scalable methodology to identify low leakage intervals for a given module.

Fig. 7.

Eight bit adder - Measured H values of leakage distributions at sub-space level with: (a) vertical partitioning into 4 sub-spaces; (b) horizontal and vertical partitioning into four sub-spaces; and (c) sixteen sub-spaces. Note that in each partition H value satisfies the self-similarity condition (0.5 $< H <$ 1).

3.3 Monte Carlo Based Low Leakage Interval Search

We propose a two-stage Monte Carlo (MC) approach to deal with large input space. Typically, an MC based approach has four steps: (a) input space determination; (b) input sampling based on a probability distribution; (c) computation of property of interest; and (d) result aggregation.

Given a confidence level ($\alpha$) and error tolerance ($\beta$) and assuming a normal leakage distribution, Halter and Najm [7] derived a formula (Eq. 5) to determine the minimum number of random vectors needed to guarantee with (100$\times \alpha$) % confidence that the number of vectors with leakage lower than the lowest leakage found is (100$\times \beta$) %. For example, if $\alpha$=0.99 and $\beta$=0.01, then 460 random vectors are sufficient to give us 99 % confidence that only 1 % of vectors will have better leakage than the observed.

$$\begin{aligned} n = \log _{e}(1 - \alpha ) / \log _{e}(1 - \beta ) \end{aligned}$$

(5)

In Sects. 3.1 and 3.2 we empirically observed that the leakage distributions of n bit adders/multipliers are normal and self-similar. Consequently, we can now partition a module instance’s input space into sub-spaces and then sample each sub-space with a fixed number of vectors as determined by Eq. 5 for user specified confidence and error tolerance levels.

Given the SPICE-level model of an n bit module instance, we perform two successive MC runs. The property of interest is the leakage power.

Stage I - Coarse grained MC run: The input space under consideration is the entire space, i.e., $2^{2n}$ input vectors, which is partitioned into equal sized sub-spaces (as illustrated in Fig. 7). Let us assume $\alpha$=0.99 and $\beta$=0.01. Then, we uniformly sample each sub-space to identify 460 random vectors and then simulate with the vectors. For result aggregation in this stage, from each sub-space, we collect 5 % of the vectors that yield low leakage for further consideration in Stage II.

Stage II - Fine grained MC run: From the leakage profiles of the functional units, we also observed that low leakage values are clustered. Hence, the sampling in this stage is biased in the neighborhood of low leakage vectors identified in previous stage. The result aggregation involves merging input vectors to create set of low leakage intervals.

Run Time Complexity. We would like to estimate the run time complexity of the characterization for a module of size n.

Stage I: The total run time of Stage I is $S \times K \times T(n)$, where S is the number of sub-spaces resulting from partitioning the entire input space, K is the minimum number of vectors required for user-given confidence ($\alpha$) and error tolerance ($\beta$) levels, and T(n) is the simulation time for one vector. Note that K is a constant for fixed $\alpha$ and $\beta$ values. The user can keep the number of sub-spaces fixed i.e., S is a constant. T(n) is proportional to the gate complexity. In case of ripple carry adder, T(n) = O(n) as gate complexity grows linearly with bit width, while for parallel multiplier, T(n) = O($n^2$). Therefore, the complexity of Stage I is O(n) and O($n^2$) for adder and multiplier respectively. If the user chooses to linearly scale the number of sub-spaces with the module complexity (i.e., S = O(n)), then the run time complexity increases to O($n^2$) and O($n^3$) for adder and multiplier respectively.

Stage II: We perform two steps: (1) local search around the vectors found in Stage I; and (2) then merge the low leakage vectors into low leakage intervals. The run-time complexity of first step is same as that of stage I, as we sample fixed number of vectors in the neighborhood of each vector from Stage I. The worst-case run time complexity of step 2 is same as that of a two-key sorting algorithm, O(nlogn), since, we sort all input vectors and then merge immediate neighbors into intervals. Therefore, the complexity of Stage II in case of an adder is O(n) + O(nlogn) = O(nlogn), while for multiplier it is O($n^2$) + O(nlogn) = O($n^2$).

Since the two stages are performed sequentially, the overall runtime complexity of MC based leakage interval characterization procedure is O(nlogn) and O($n^2$) for n bit adder and multiplier respectively.

4 Proposed Approach

For low leakage interval propagation, we propose two variants: top down and bottom up approaches. The motivation to propose the two variants is to compare the amount of leakage savings possible by starting at PIs and at POs.

• In top down approach, we carry out the propagation in two iterations. In first iteration, we start with a raw set of low leakage intervals at PIs and propagate them to the POs i.e., forward propagation. The raw low leakage intervals at PIs are obtained through characterization presented in detail in Sect. 3. In second iteration, these output intervals are propagated backwards reducing the input interval set at each intermediate node and thus ending up with a sparser set of low leakage intervals at PIs. This sparser interval set is further processed with simulated annealing to identify the best LLV.

• In bottom up approach, we start with raw set of low leakage output intervals at POs and propagate them all the way to the PIs where we end up with a minimized interval set. This minimized set is again processed with simulated annealing to arrive at the best LLV.

We present two motivating examples illustrating top down and bottom up approaches.

4.1 Motivating Examples

Example 1: Top Down Approach. In Fig. 8, we show an example DFG with two adders (A1, A2) and one multiplier (M1). Let us say the low leakage vector sets are: $\mathcal {L}(+, 8)$ = {([2, 4], [6, 8]), ([8, 12], [8, 12]), ([14, 20], [14, 24])} and $\mathcal {L}(*, 8)$ = {([3, 4], [5, 6]), ([9, 10], [5, 6]), ([13, 24], [5, 6])}.

Fig. 8.

Example 1: Top down approach - forward propagation of interval sets.

Fig. 9.

Example 1: Top down approach - backward propagation of interval sets.

We start applying low leakage vector interval sets for A1 and A2 i.e., {[2, 4], [8, 12], [14, 20]} on the first input and {[6, 8], [8, 12], [14, 24]} on the second input. Using Eq. (1) of interval arithmetic, we compute A1’s and A2’s output range to be {[8, 12], [16, 24], [28, 44]}. As we want to apply low leakage vector to M1, we need to reduce the interval sets generated by A1 and A2 to those identified as LLVs for M1. Thus, the interval set of M1 for input 1 is {[8, 12], [16, 24], [28, 44]} $\cap \,\{[3, 4], [9, 10], [13, 24]\}$ = {[9, 10], [16, 24]} and for input 2 is {[8, 12], [16, 24], [28, 44]} $\cap \, \{[5, 6]\}$= $\varnothing$. In Fig. 8, for sake of clarity, we show the intervals corresponding to multiplier in bold font, while those for adders in regular font. At the second input of M1 as we obtained an empty set, we will introduce a control point to put M1 in low leakage mode. The control point consists of a multiplexer that can be used to force a low leakage vector in idle state. Generally speaking, if the interval intersection results in an empty set, we will insert a control point and start with an entire low leakage vector set from that point.

To determine the LLV at PIs, a backward propagation of minimized interval sets is implemented. Figure 9 illustrates this step for this example. The intervals available at input 1 of M1 are fed as outputs to A1 and these intervals are propagated to the inputs of A1. This gives a minimized interval set on which simulated annealing algorithm is applied to find the best LLV.

Example 2: Bottom Up Approach. Now consider the same DFG for bottom up approach, however with output low leakage vector sets: $\mathcal {L}(+, 8)$ = {[2, 8]} and $\mathcal {L}(*, 8)$ = {[16, 24]}. For a given output low leakage set {[16, 24]} to M1, the corresponding input leakage set is {([2, 4], [8, 8])}. Similarly, for an adder’s output set {[2, 4]}, input sets are {([1, 2], [2, 2])} and {[8, 8]}, the corresponding input sets are {([2, 2], [4, 4])}. We apply output low leakage vector interval sets on primary outputs (Fig. 10).

Fig. 10.

Example 2: Bottom up approach - backward propagation of output intervals.

We start applying output low leakage vector set for M1 i.e., {[16, 24]} at output. It propagates corresponding input vectors {[2, 4]} to input 1 and {[8, 8]} to input 2 and M1 is set to low leakage mode. The input intervals at M1 are intersected with $\mathcal {L}(+, 8)$ and $\mathcal {L}(*, 8)$. For the resulting output intervals {[2, 4]} and {[8, 8]} the corresponding input intervals of A1 and A2 are {([1, 2], [2, 2])} and {([2, 2], [4, 4])}, respectively. The best LLV is found by processing the reduced set with simulated annealing algorithm described in Sect. 4.2.

4.2 Low Leakage Vector Determination

Figure 11 shows the pseudo-code of the proposed heuristic for low leakage vector determination. It accepts an input DFG (directed acyclic graph) and low leakage vector sets for distinct types and operations obtained from the characterization procedure as described in Sect. 3. Breadth First Search is used to cover all the nodes of the graph. Flag is used to determine the direction of propagation (top down or bottom up).

Fig. 11.

Algorithm to determine low leakage vector.

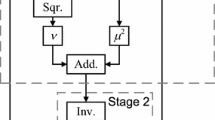
First, the graph is topologically sorted (line 5) to yield a sorted list L. A set $\mathcal {C}$ that collects the control points, is initialized (line 6). The for loop in lines 8–27 visits each node in the order specified by L. If a node is a PI node (i.e., both inputs to the node are primary), then the intervals on both inputs are intialized to the appropriate low leakage vector sets (line 13). Both inputs are added to the set $\mathcal {C}$ (line 14). On line 16, we call a function Interval_Propagate() that accepts an ordered interval pair and the operation type of the node (i.e., $\mathcal {T}(v_{i})$). Interval_Propagate() implements the interval arithmetic equations as mentioned in Sect. 2.3 and returns an appropriate output interval $I_{c}$. In line 21, we invoke Interval_Intersection() that checks if the computed interval is contained in low leakage vector set of the successor $v_{j}$. If the check succeeds, then we move onto to the next node in the list. If the check fails, then a new control point is inserted by resetting the inputs of node $v_{j}$ to its low leakage vector set (lines 22–26) and adding the inputs of $v_{j}$ to control point set. On line 28, Back_Propagate() further reduces interval set at primary outputs, $\mathcal {LO}$ reduced $\mathcal (t, w)$, by performing similar propagation in backward direction to primary inputs as shown in Fig. 12. Back_Propagate() function (line 30) performs backward propagation on the complete low leakage output interval set, $\mathcal {LO}(t, w)$, to obtain reduced interval set at primary inputs. The algorithm is similar to find_LLV(), therefore we do not elaborate in detail.

Fig. 12.

Interval back propagation algorithm.

On line 32 of find_LLV(), we invoke Simulated_Annealing_Leakage() (Fig. 13) to find the best LLV from the reduced LLV set. The initial temperature value Temp is set to 100 and cooling coefficient $\gamma$ to 0.99 on lines 5 and 6 respectively. The number of iterations at each temperature is equal to (500 x Temp) (line 11). An LLV is initially chosen at random (line 7) from the reduced interval set. In each iteration, a new LLV is chosen (line 12) from the neighborhood of the current LLV. The neighborhood window size is equal to the current temperature (Temp). $Est\_Leakage()$ function (line 26) calculates the leakage of the DFG for any given input vector. $output\_llv$ is the best LLV found by the algorithm.

Fig. 13.

Simulated annealing algorithm to find the best LLV.

In the find_LLV() algorithm, we assume only one successor for each node. This assumption is made to simplify the presentation of the algorithm. It is straightforward to extend the algorithm to multiple successors.

Run Time Complexity. In the first step of find_LLV(), topological sort has a time complexity of O(|V| + |E|). The maximum number of edges in a DAG is $(|V|)(|V| - 1)/2$. Hence the time complexity of topological sort is O($|V|^2$). The for loop (lines 8–27) runs |V| times. If the node is PI, initial interval set is initialized at the node. This initialization takes a constant time. We also have the Interval_Propagate() and Interval_Intersection() which take time proportional to $I^2$, where I is the number of low leakage intervals. The number of intervals I is a constant obtained from characterization as described in Subsect. 3.3. Back_Propagate() function on lines 28 and 31 has the same complexity as that of the code on lines 8–27. Finally, simulated annealing algorithm takes a constant time based on the quality of solution desired. Hence, the run time complexity of the algorithm is O($|V|^2$).

5 Experimental Results

We report the experiment results obtained by applying the best LLV from top down and bottom up approaches on five datapath-intensive benchmarks, namely, IIR, FIR, Elliptic, Lattice, and Differential Equation Solver. Only functional unit sharing (resource optimization technique during high level synthesis) is assumed. As described in Sect. 3 the library is characterized a priori and the low leakage vectors sets saved. Top down and bottom up techniques process these low leakage vector sets to obtain a reduced set. The best LLV is further obtained by applying simulated annealing algorithm on the reduced set. The leakage power values are measured at the layout level using Synopsys Nanosim. We employ the Predictive Technology Models for 16 nm technology node generated by the online model generation tool available on the ASU PTM website [18]. The simulations were carried out on a SunOS workstation (16 CPUs, 96 GB RAM).

To obtain the experimental results, we initially vary the value of $\varepsilon$ and determine the optimum (lowest) value for maximum leakage savings (i.e., leakage increase in any module up to $\varepsilon$ % is tolerated). Figures 14 and 15 show the variation of leakage savings with tolerance in different designs for top down and bottom up approaches, respectively. From Fig. 14, it can be observed that the optimum tolerance value for top down approach is 10 % (i.e., leakage increase in any module up to 10 % is tolerated). The low leakage vector is captured within 10 % tolerance itself. Even if the tolerance is increased above 10 %, it is observed that leakage savings do not increase any further. From Fig. 15, the optimum tolerance value for bottom up approach is observed to be 15 %.

Fig. 14.

Leakage vs. tolerance - top down approach.

Fig. 15.

Leakage vs. tolerance - bottom up approach.

Table 1. Power savings - top down approach.

Table 2. Power savings - bottom up approach.

Table 3. Speed up with interval propagation.

Table 4. Simulated Annealing (SA) Only vs. interval propagation + SA.

Tables 1 and 2 report the results for top down and bottom up approaches respectively. Column 3 presents the leakage value obtained from interval propagation with simulated annealing. We can see a significant improvement compared to the random case in Column 2. Column 4 reports leakage savings. The top down approach achieved average leakage savings of 93.6 % for 10 % tolerance with no area overhead. On the other hand, bottom up approach achieved 89.2 % average leakage savings for 15 % tolerance with no area overhead.

We conducted an experiment to compare the proposed interval arithimetic followed by pure SA based approach. Table 3 reports the simulation speed up obtained when we use simulated annealing on reduced set of intervals from top down propagation as opposed to pure simulated annealing. Columns 2 and 4 present the leakage values. Execution time is reported in columns 3 and 5 in Table 3. It shows that simulated annealing with top down propagation is much faster than simulated annealing alone to obtain a similar solution quality. The difference in solution quality is also presented in column 6 of Table 3. For EWF benchmark, a solution that is much better than pure simulated annealing solution is obtained with interval propagation and simulated annealing combined. For the rest of the benchmarks, the difference between solutions is small. Column 7 reports speed up resulting from IA with as much as 124X in case of FIR filter. The results of this experiment demonstrate that Interval Arithmetic greatly helps in finding a good low leakage vector quickly.

Table 4 compares the solution quality obtained by pure simulated annealing(SA) for 10 min, 1 h, 2 h, and 3 h with that by top down approach with simulated annealing (an average of 10 min). Columns 2–5 report the leakage obtained by pure SA. Column 6 reports the leakage obtained from top down approach. It is observed that the leakage found by interval propagation with SA in 10 min is better than the solution found by pure SA in 3 h. These results reiterate the efficacy of interval propagation based approach.

6 Conclusion

We have formulated the low leakage vector identification technique based on interval propagation and successfully demonstrated that significant subthreshold leakage savings can be obtained with no area overhead (i.e., no internal control points). We also proposed a self similarity based module characterization procedure that is scalable with module complexity. Both top down and bottom up approaches are equally effective (although in case of the benchmarks tested in this work, top down performs slightly better than bottom up approach).