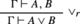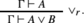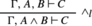Abstract
The aim of this work is to show that no group of opposition can be built for constructive logics like intuitionistic or linear logics. Moreover, the attempt to apply the square of opposition to linear logic shows that the lack of subcontrariety and the asymmetry of contradiction are not equivalent properties. The former property, not the latter, is the general reason why there can be no group of opposition for constructive logics.
The author would like to thank Élisabeth Schwartz, Emmanuel Cattin, Camille and Baptiste Debrabant, Marion Duquerroy, Sébastien Gandon, Jean-Baptiste Joinet, Nicolas Mascot and Fabien Schang.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
The classical “multiplicative” rule
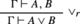
can not be used, and has to be replaced by the “additive” rule
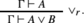
But the issue is not symmetrical: the classical multiplicative rule
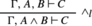
can be maintained in intuitionistic logic.
- 2.
Girard [4] calls “essentialism” the assumption that truth is eternal, and can be duplicated at will; in linear logic, a “truth” can not be used an infinite number of times without the help of exponentials.
References
Gentzen, G.: Untersuchungen über das logische Schließen. I. Math. Z. 39(1), 176–210 (1935)
Gentzen, G.: Untersuchungen über das logische Schließen. II. Math. Z. 39(1), 405–431 (1935)
Gödel, K.: Eine Interpretation des intuitionistischen Aussagenkalküls. Ergeb. Math. Kolloqu. 4, 39–40 (1933). English translation: An interpretation of the intuitionistic propositional logic. Reprinted in: Béziau, J.-Y. (ed.) Universal Logic: An Anthology, pp. 89–90. Springer, Basel (2012)
Girard, J.-Y.: Du pourquoi au comment: la théorie de la démonstration de 1950 à nos jours. In: Pier, J.-P. (ed.) Les mathématiques 1950–2000, pp. 515–545. Birkhäuser, Basel (2000)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
Appendix A: Rules for Classical Linear Logic (CLL)
Axiom and Cut
Structural Rules
Rules for Logical Connectives
Exponentials
Mix (in LL+mix)
Appendix B: Proofs for MLL±mix and MELL
Subalternation
Contradiction
Subcontrariety
Appendix C: Proofs for MALL and Quantified MALL
Subalternation
Contradiction
Rights and permissions
Copyright information
© 2012 Springer Basel
About this chapter
Cite this chapter
Mélès, B. (2012). No Group of Opposition for Constructive Logics: The Intuitionistic and Linear Cases. In: Béziau, JY., Jacquette, D. (eds) Around and Beyond the Square of Opposition. Studies in Universal Logic. Springer, Basel. https://doi.org/10.1007/978-3-0348-0379-3_14
Download citation
DOI: https://doi.org/10.1007/978-3-0348-0379-3_14
Publisher Name: Springer, Basel
Print ISBN: 978-3-0348-0378-6
Online ISBN: 978-3-0348-0379-3
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)