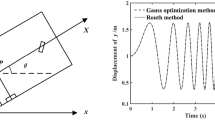
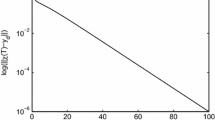
Abstract
This paper proposes an optimization method for motion of non-holonomic mechanical systems. In such system, the number of degrees of freedom is less than the number of independent generalized coordinates, so the number of independent velocities (also the number of independent accelerations) is less than the number of independent coordinates. This makes it difficult to determine the boundary conditions for the system of motion equations. In this paper, the principle of compatibility and the method of transformation matrix are used to directly build the equations of motion of the constrained dynamics system in the form of ordinary differential equations (ODEs) avoiding the use of Lagrange multipliers and then the Pontryagin’s maximum principle is used to solve the optimization of dynamics problem. A selection of boundary condition for Hamiltonian costate variables is also proposed. For illustration, the optimal control for the steering motion of an automobile while satisfying the non-holonomic constraints is carried out.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Chettibi, T., Lehtihet, H.E., Haddad, M., Hanchi, S.: Minimum cost trajectory planning for industrial robots. Eur. J. Mech. A/Solids 23, 703–715 (2004)
Jeremic, B., Radulovic, R., Obradovic, A.: Analysis of the brachistochronic motion of a variable mass nonholonomic mechanical system. Theoret. Appl. Mech. 43(1), 19–32 (2016)
Unda, J., Garcia de Jalon, J., Losantos, F., Emparantza, R.: A comparative study on some different formulations of the dynamic equations of constrained mechanical system. In: ASME Mechanisms Conference, Columbus, OH (1986)
Sanh, D.: On the principle of compatibility and equations of motion of constrained. In: Mechanical Systems ZAMM, Berlin, vol. 60, pp. 210–212 (1980)
Sanh, D.: On the motion of controlled mechanical systems. In: Advances in Mechanics, Varsawa, t.7, V. 2, pp. 3–24 (1984)
Sanh, D.: On the motion of constrained mechanisms, Thesis of Doctorate in Science, Hanoi University of Science and Technology, Vietnam (1984)
Kovecses, J., Piedboeuf, J., Lange, C.: Dynamics modeling and simulation of constrained robotic systems. IEEE/ASME Trans. Mechatron. 8(2), 165–177 (2003)
Le, N.N., Phong, D.V., Sanh, D.: On numerical methods for constrained mechanical systems. In: Iutam Symposium on Recent Developments in Nonlinear Oscillations of Mechanical Systems. IUTAM Kluwer Academic Publishers (1999)
Do, S., Do, K.D.: Method of transmission matrix applying for investigation of motion of planar mechanism. Mach. Dyn. Res. 34(40), 5–22 (2010)
Sanh, D., Phong, D.V., Khoa, D.D., Duc, T.: A method for solving the motion of constrained systems. In: Proceedings of the 16th Asian Pacific Vibration Conference, Hanoi, Vietnam, pp. 803–811 (2015)
Pontryagin, L.S., et al.: The mathematical theory of optimal processes. In: Triogoff, K. (ed.) Interscience Publishers, John Wiley and Sons. Inc, New York (1962)
Lewis, F.L., Vrabie, D., Syrmos, V.L.: Optimal Control, 3rd edn. Wiley, Hoboken (2012)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Khoa, D.D., Kien, T.S., Phong, P.D., Sanh, D. (2022). An Optimization Method for Dynamics of Non-holonomic Systems. In: Khang, N.V., Hoang, N.Q., Ceccarelli, M. (eds) Advances in Asian Mechanism and Machine Science. ASIAN MMS 2021. Mechanisms and Machine Science, vol 113. Springer, Cham. https://doi.org/10.1007/978-3-030-91892-7_12
Download citation
DOI: https://doi.org/10.1007/978-3-030-91892-7_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-91891-0
Online ISBN: 978-3-030-91892-7
eBook Packages: EngineeringEngineering (R0)