Abstract
We show how to combine a fully-homomorphic encryption scheme with linear decryption and a linearly-homomorphic encryption schemes to obtain constructions with new properties. Specifically, we present the following new results.
-
(1)
Rate-1 Fully-Homomorphic Encryption: We construct the first scheme with message-to-ciphertext length ratio (i.e., rate) \(1-\sigma \) for \(\sigma = o(1)\). Our scheme is based on the hardness of the Learning with Errors (LWE) problem and \(\sigma \) is proportional to the noise-to-modulus ratio of the assumption. Our building block is a construction of a new high-rate linearly-homomorphic encryption.
One application of this result is the first general-purpose secure function evaluation protocol in the preprocessing model where the communication complexity is within additive factor of the optimal insecure protocol.
-
(2)
Fully-Homomorphic Time-Lock Puzzles: We construct the first time-lock puzzle where one can evaluate any function over a set of puzzles without solving them, from standard assumptions. Prior work required the existence of sub-exponentially hard indistinguishability obfuscation.
The full version of this work can be found in https://eprint.iacr.org/2019/720.pdf.
Z. Brakerski—Supported by the Israel Science Foundation (Grant No. 468/14), Binational Science Foundation (Grants No. 2016726, 2014276) and European Union Horizon 2020 Research and Innovation Program via ERC Project REACT (Grant 756482) and via Project PROMETHEUS (Grant 780701).
S. Garg—Supported in part from DARPA/ARL SAFEWARE Award W911NF15C0210, AFOSR Award FA9550-15-1-0274, AFOSR Award FA9550-19-1-0200, AFOSR YIP Award, NSF CNS Award 1936826, DARPA and SPAWAR under contract N66001-15-C-4065, a Hellman Award and research grants by the Okawa Foundation, Visa Inc., and Center for Long-Term Cybersecurity (CLTC, UC Berkeley). The views expressed are those of the author and do not reflect the official policy or position of the funding agencies.
G. Malavolta—Part of the work done while at Carnegie Mellon University.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Fully-homomorphic encryption (FHE) allows one to evaluate any function over encrypted data. Since the breakthrough result of Gentry [15], the development of FHE schemes has seen a rapid surge [1, 6,7,8, 19, 32] and by now FHE has become a well-established cryptographic primitive. An FHE scheme gives an elegant solution to the problem of secure function evaluation: One party publishes the encryption of its input under its own public key \(\mathsf {Enc}(\mathsf {pk}, x)\) while the other evaluates some function f homomorphically, returning \(c = \mathsf {Enc}(\mathsf {pk}, f(x))\). The first party can recover the output by simply decrypting c. The crucial property of this approach is that its communication complexity is proportional to the size of the input and of the output, but does not otherwise depend on the size of f. This distinguishing feature is essential for certain applications, such as private information retrieval [10], and has motivated a large body of work on understanding FHE and related notions [2, 29].
Unfortunately, our understanding in secure computation protocol with optimal communication complexity is much more limited. Typically, FHE schemes introduce a polynomial blowup factor (in the security parameter) to the cipheretext size, thereby affecting the overall communication rate of the protocol. Given the current state-of-the-art FHE schemes, the only class of functions we can evaluate without communication blowup are linear functions [12]. An FHE scheme with optimal rate, i.e., with a message-to-ciphertext ratio approaching 1, would immediately give us a general-purpose tool to securely evaluate any function (with sufficiently large inputs and outputs) with asymptotically optimal communication complexity. Motivated by this objective, this work seeks to answer the following question:

We also consider the related problem of constructing fully-homomorphic time-lock puzzles (FH-TLP), a primitive recently introduced in [22] to address the computational burden of classical time-lock puzzles [31]. Time-lock puzzles encapsulate secrets for a pre-determined amount of time, and FH-TLP allow one to evaluate functions over independently generated puzzles. The key feature of FH-TLPs is that after a function has been homomorphically evaluated on a (possibly large) number of input TLPs, only a single output TLP has to be solved to recover the function result. Consequently, FH-TLP can be used in the very same way as TLPs, but the solver is spared from solving a large number of TLPs (in parallel) and only needs to solve a single TLP which encapsulates the function result.
FH-TLP have been shown to be a very versatile tool and have several applications, ranging from coin-flipping to fair contract signing [22]. In [22] FH-TLPs were constructed from probabilistic iO [9] and scheme from standard assumptions were limited to restricted classes of functions (e.g., linear functions). Motivated by this gap, the second question that we ask is:

1.1 Our Results
In this work, we answer both questions in the affirmative. Specifically, we present the following new results:
-
(1)
Our main result is the construction of an FHE which allows compressing many ciphertexts into a compressed ciphertext which has rate \(1 - 1/\lambda \). In fact, we show that for any a-priori block size
 , we can construct a scheme where the ciphertext length is at most \(\ell + \tau (\lambda )\), where \(\tau \) is a fixed polynomial (which does not depend on \(\ell \)). Setting \(\ell = \lambda \cdot \tau (\lambda )\), the rate claim follows.
, we can construct a scheme where the ciphertext length is at most \(\ell + \tau (\lambda )\), where \(\tau \) is a fixed polynomial (which does not depend on \(\ell \)). Setting \(\ell = \lambda \cdot \tau (\lambda )\), the rate claim follows.To prove security of this scheme, we only need to assume the hardness of the Learning With Errors (LWE) [30] problem with polynomial modulus-to-noise ratio.Footnote 1
-
(2)
We provide a construction of a fully-homomorphic time-lock puzzle from multi-key FHE and linearly homomorphic time-lock puzzles. The security of the former can be based on the hardness of LWE with superpolynomial modulus-to-noise ratio, whereas the latter can be constructed from the sequential squaring assumption [31] in groups of unknown order.
On a technical level, both of our main results are tied together by the common idea of combining an FHE with a linear decryption algorithm with a linearly-homomorphic encryption (time-lock puzzle, respectively) of optimal rate. The hybrid scheme inherits the best of both worlds and gives us a rate-optimal FHE scheme or an FH-TLP from standard assumptions, depending on the building block that we use. Our techniques are reminiscent of the chimeric scheme of Gentry and Halevi [16], with a new twist to how to encode information without inflating the size of the ciphertexts. Somewhat interestingly, our construction of rate-1 linearly homomorphic encryption from LWE leverages ideas which were originally conceived in the context spooky FHE [13], homomorphic secret sharing [3] and private-information retrieval [14].
Concurrent Work. In a concurrent work, Gentry and Halevi [17] constructed rate-1 FHE schemes using similar ideas as in our work. While the goal of their work is realizing practically efficient high-rate private information retrieval protocols, our constructions are more general and designed to achieve the best possible asymptotic rate.
1.2 Applications
We outline a few interesting implications of our results. We stress that the tools that we develop in this work are of general purpose and we expect them to find more (possibly indirect) applications in the near future.
-
(1)
Secure Function Evaluation: FHE yields a very natural protocol for secure function evaluation (SFE) where one party encrypts its input and the other computes the function homomorphically. Given that the input and the output are sufficiently large, rate-1 FHE yields a (semi-honest) SFE scheme where the communication complexity is within additive factor from that of the best possible insecure protocol.
-
(2)
Encrypted Databases with Updates: Using rate-1 FHE, it is possible to outsource an encrypted database to an untrusted (semi-honest) cloud provider, without suffering additional storage overhead due to ciphertext expansion. While FHE hybrid encryption (using a non-rate-1 FHE) allows to store a static database without additional storage requirements, as soon as database entries are homomorphically updated they become FHE-ciphertexts and consequently their size grows substantially. Keeping the database encrypted under a rate-1 FHE scheme enables the cloud provider to perform updates on the database, while not increasing the size of the encrypted data.
-
(3)
Malicious Circuit Privacy: Instantiating the generic compiler of Ostrovsky et al. [25] with our rate-1 FHE scheme gives the first maliciously circuit-private FHE scheme with rate-1. A maliciously circuit-private scheme does not leak any information to the decrypter about the homomorphically evaluated functions (beyond the function output) for any choice of the public parameters. Among others, a rate-1 scheme implies a maliciously statistically sender-private oblivious transfer [4] with the same rate. Previous works [14] were able to achieve rate 1 only for oblivious transfer and only in the semi-honest setting. The prior best known rate in the malicious setting was \({\le }1/2\).
-
(4)
Sealed Bid Auctions: One of the motivating applications of time-lock puzzles is to construct fair sealed bid auctions, where each bid is encrypted in a time-lock puzzle whose opening can be forced by the auctioneer in case the bidder refuses to disclose it. This however involves a computational effort proportional to the number of unopened bids, which can be used as a vector for denial-of-service attacks. Homomorphic time-lock puzzles solve this problem by allowing the auctioneer to homomorphically compute the winner of the auction and only solve a single puzzle. Since this computation cannot be expressed as a linear function, our work provides the first solution from standard assumptions.
1.3 Technical Outline
We present a detailed technical outline of our results in the following. As far as rate-1 FHE is concerned, our focus is on techniques to compress post-evaluation ciphertexts. Compressed ciphertexts can be further expanded (and homomorphically evaluated) via standard bootstrapping techniques.
Schematically, our method for achieving rate-1 FHE is as follows. We consider the “batched-Regev” LWE based encryption scheme (which appears explicitly in the literature, e.g., in [5, 28]). This scheme has much better rate than “plain” Regev, but the rate is still asymptotically 0 (i.e., o(1)). It can be shown that it is possible to convert plain-Regev ciphertexts into batched-Regev, essentially using the key-switching technique that is frequently used in the FHE literature (see, e.g., [7]). We then show that batched-Regev ciphertexts can be compressed in a way that increases the rate to \(1-o(1)\), but maintains (perfect) decryptability. We do this by combining rounding techniques that appeared previously in the literature [3, 13, 14] with new techniques that we develop and allow to maintain high rate, perfect correctness, and modest LWE modulus simultaneously. We note that in order to apply key-switching, we need to use batched-Regev in its non-compressed form, and only apply the compression after the switching is complete. This transformation, maintains decryptability but homomorphic capabilities are lost. As mentioned above, these can be restored using bootstrapping in a generic way.
Leveraging Linear Decryption. Our starting point is the observation that, for essentially any FHE construction in literature, decryption (or rather noisy decryption) is a linear function in the secret key. More specifically, we can write the decryption operation as a function \(L_{\mathsf {c}}(\mathbf {s})\), which is linear in \(\mathbf {s}\), the secret key. Typically things are set up in a way such that it holds for correctly formed ciphertexts \(\mathsf {c}\) that \(L_{\mathsf {c}}(\mathbf {s}) = \frac{q}{2} \cdot \mathsf {m}+ e\), where \(\mathsf {m}\) is the plaintext and e is a small noise term. We can then recover \(\mathsf {m}\) from \(L_\mathsf {c}(\mathbf {s})\) via rounding.
For many FHE schemes, the choice of the factor q/2 is not hardwired into the scheme, but can be provided as an explicit input to the decryption function. More specifically, it holds that
where \(L_{\alpha ,\mathsf {c}}(\cdot )\) is a linear function and e is a small noise term. Assume in the following that \(|e| < B\) for some bound B. We refer to this operation as linear decrypt-and-multiply. In fact, Micciancio [23] observed that any FHE scheme with linear decryption can be transformed into a scheme which supports linear decrypt-and-multiply.
Equipped with a linear decrypt-and-multiply FHE, our main idea to construct a rate-1 FHE scheme is to run the linear decrypt-and-multiply operation of the FHE scheme inside a high rate linearly homomorphic scheme. Consider an FHE scheme whose secret keys are vectors over  , and a rate-1 linearly homomorphic scheme \(\mathsf {HE}\) with plaintext space
, and a rate-1 linearly homomorphic scheme \(\mathsf {HE}\) with plaintext space  . Assume we are given as “compression key” the encryption \(\mathsf {ck}= \mathsf {Enc}(\mathsf {pk},\mathbf {s})\) of the FHE secret key \(\mathbf {s}\) under the linearly homomorphic scheme \(\mathsf {HE}\). Given an FHE ciphertext \(\mathsf {c}\) encrypting a message \(\mathsf {m}\in \{0,1\}\), we can transform \(\mathsf {c}\) into an encryption of \(\mathsf {m}\) under the linearly homomorphic scheme by homomorphically evaluating the linear function \(L_{\alpha ,\mathsf {c}}(\cdot )\) on \(\mathsf {ck}\), i.e. we compute \(\mathsf {HE}.\mathsf {Eval}(L_{\alpha ,\mathsf {c}}(\cdot ),\mathsf {ck})\). By homomorphic correctness, this results in an encryption of \(\alpha \cdot \mathsf {m}+ e\) under the linearly homomorphic scheme \(\mathsf {HE}\).
. Assume we are given as “compression key” the encryption \(\mathsf {ck}= \mathsf {Enc}(\mathsf {pk},\mathbf {s})\) of the FHE secret key \(\mathbf {s}\) under the linearly homomorphic scheme \(\mathsf {HE}\). Given an FHE ciphertext \(\mathsf {c}\) encrypting a message \(\mathsf {m}\in \{0,1\}\), we can transform \(\mathsf {c}\) into an encryption of \(\mathsf {m}\) under the linearly homomorphic scheme by homomorphically evaluating the linear function \(L_{\alpha ,\mathsf {c}}(\cdot )\) on \(\mathsf {ck}\), i.e. we compute \(\mathsf {HE}.\mathsf {Eval}(L_{\alpha ,\mathsf {c}}(\cdot ),\mathsf {ck})\). By homomorphic correctness, this results in an encryption of \(\alpha \cdot \mathsf {m}+ e\) under the linearly homomorphic scheme \(\mathsf {HE}\).
So far, we have not gained anything in terms of rate, as we still have a large ciphertext encrypting only a single bit \(\mathsf {m}\). However, we have not yet taken advantage of the fact that we can choose \(\alpha \) freely and that the scheme \(\mathsf {HE}\) has rate 1. Our idea to increase the rate is to pack many FHE ciphertexts \((\mathsf {c}_1,\dots ,\mathsf {c}_\ell )\), each encrypting a single bit \(\mathsf {m}_i\), into a single ciphertext of the high-rate linearly homomorphic scheme \(\mathsf {HE}\). More specifically, for given FHE ciphertexts \((\mathsf {c}_1,\dots ,\mathsf {c}_\ell )\) and a parameter t, consider the function \(L^*(x)\) defined as
Note that, although we define \(L^*\) as a sum of functions, this is not how we compute it. Since \(L^*\) is a linear function, we can obtain a matrix-representation of it by, e.g., evaluating it on a basis and then later use the matrix representation to compute the function. By correctness of the FHE scheme it holds that
where \(e = \sum _{i = 1}^\ell e_i\) is an \(\ell B\)-bounded noise term. Consequently, by homomorphically evaluating \(L^*\) on \(\mathsf {ck}\), we obtain an encryption \(\tilde{\mathsf {c}}\) of \(\sum _{i = 1}^\ell 2^{t + i} \cdot \mathsf {m}_i + e\) under the high-rate scheme \(\mathsf {HE}\). Given that \(2^t > \ell B\), the noise e does not interfer with the encodings of the message bits \(\mathsf {m}_i\) and they can be recovered during decryption.
The main effect that works in our favor here is that we can distribute the message bits \(\mathsf {m}_i\) into the high order bits by multiplying them with appropriate powers of 2, whereas the decryption noise piles up in the low order bits. Consequently, the noise occupies only the lower \(\approx \log (\ell ) + \log (B)\) bits, whereas the remaining bits of the message space can be packed with message bits. Choosing q as \(q \approx (\ell B)^{1/\epsilon }\) for a parameter \(\epsilon > 0\) we achieve an encoding rate of \(\frac{\log (q) - \log (\ell B)}{\log (q)} = 1 - \epsilon \). Given that the linearly homomorphic encryption scheme has a similarly high rate, we obtain an overall rate of \(1 - O(\epsilon )\). Consequently, this construction yields an FHE scheme with rate \(1 - O(1/\lambda )\) using, e.g., the Damgård-Jurik cryptosystem or a variant of Regev encryption as linearly homomorphic scheme, where the LWE modulus-to-noise ratio is with (sub-)exponential [28].
Towards a Scheme from Standard LWE. Our next goal is to achieve the same (asymptotic) rate assuming only LWE with polynomial modulus-to-noise ratio. Recall that our packing strategy consisted in encoding the message vector \(\mathbf {\mathsf {m}} = (\mathsf {m}_1,\dots ,\mathsf {m}_\ell )\) into the high-order bits of a \(\mathbb {Z}_q\)-element by homomorphically computing \(\mathbf {t}^\top \cdot \mathbf {\mathsf {m}}\), where \(\mathbf {t}^\top = (2^{t+1},\dots ,2^{t+\ell })\). However, this is not the only possible strategy. More generally, linear decrypt-and-multiply enables us to homomorphically pack messages \((\mathsf {m}_1,\dots ,\mathsf {m}_\ell )\) into an encoded vector \(\mathbf {T} \cdot \mathbf {\mathsf {m}}\) for some packing matrix  . Since linear decryption is inherently noisy, we will require some error correcting properties from such an encoding, i.e., we need to be able to reconstruct \(\mathbf {\mathsf {m}}\) from \(\mathbf {T} \cdot \mathbf {\mathsf {m}} + \mathbf {e}\), for short noise terms \(\mathbf {e}\). With this observation in mind, our next step will be to construct an ad-hoc high-rate linearly homomorphic encryption and pair it with an appropriate packing strategy.
. Since linear decryption is inherently noisy, we will require some error correcting properties from such an encoding, i.e., we need to be able to reconstruct \(\mathbf {\mathsf {m}}\) from \(\mathbf {T} \cdot \mathbf {\mathsf {m}} + \mathbf {e}\), for short noise terms \(\mathbf {e}\). With this observation in mind, our next step will be to construct an ad-hoc high-rate linearly homomorphic encryption and pair it with an appropriate packing strategy.
Linearly Homomorphic Encryption with Ciphertext Shrinking. We now discuss new constructions of linearly homomorphic encryption schemes from LWE which allow asymptotically optimal ciphertext sizes. To avoid confusion with our FHE ciphertext compression technique, we will refer to this technique as ciphertext shrinking. Our starting point is Regev encryption and its variants. Let q be a modulus. In Regev encryption a ciphertext \(\mathsf {c}\) consists of two parts, a vector  and a scalar
and a scalar  . The secret key is a vector
. The secret key is a vector  . Decryption for this scheme is linear, and it holds that
. Decryption for this scheme is linear, and it holds that
where e with \(|e| < B\) for some bound B is a decryption noise term. We obtain the plaintext \(\mathsf {m}\) by rounding \(\hat{\mathsf {m}}\), i.e., by computing
given that \(q > 4 B\). We first show how to shrink the component \(\mathsf {c}_2\) of the ciphertext into a single bit at the expense of including an additional ring element  in the ciphertext. Although this procedure does not actually shrink the ciphertext (in fact it increases its size by one
in the ciphertext. Although this procedure does not actually shrink the ciphertext (in fact it increases its size by one  element), we will later amortize the cost of r across multiple components. The main idea is to delegate a part of the rounding operation from the decrypter to a public operation \(\mathsf {Shrink}\) and it is inspired by recent works on spooky encryption [13], homomorphic secret sharing [3], and private-information retrieval [14].
element), we will later amortize the cost of r across multiple components. The main idea is to delegate a part of the rounding operation from the decrypter to a public operation \(\mathsf {Shrink}\) and it is inspired by recent works on spooky encryption [13], homomorphic secret sharing [3], and private-information retrieval [14].
The algorithm \(\mathsf {Shrink}\) takes as input the ciphertext \(\mathsf {c}= (\mathbf {\mathsf {c}}_1,\mathsf {c}_2)\) where  and proceeds as follows. It first chooses an
and proceeds as follows. It first chooses an  such that \(\mathsf {c}_2 + r \notin [q/4 - B,q/4 + B] \cup [3/4 \cdot q - B,3/4 \cdot q + B]\), then it computes \(w = \lceil \mathsf {c}_2 + r \rfloor _2\) and outputs a compressed ciphertext \(\tilde{\mathsf {c}} = (\mathbf {\mathsf {c}}_1,r,w)\). Given a shrunk ciphertext \(\tilde{\mathsf {c}} = (\mathbf {\mathsf {c}}_1,r,w)\) and the secret key \(\mathbf {s}\), the decrypter computes
such that \(\mathsf {c}_2 + r \notin [q/4 - B,q/4 + B] \cup [3/4 \cdot q - B,3/4 \cdot q + B]\), then it computes \(w = \lceil \mathsf {c}_2 + r \rfloor _2\) and outputs a compressed ciphertext \(\tilde{\mathsf {c}} = (\mathbf {\mathsf {c}}_1,r,w)\). Given a shrunk ciphertext \(\tilde{\mathsf {c}} = (\mathbf {\mathsf {c}}_1,r,w)\) and the secret key \(\mathbf {s}\), the decrypter computes
We claim that \(\mathsf {m}'\) is identical to \(\mathsf {Dec}(\mathbf {\mathsf {s}},\mathsf {c}) = \lceil \mathsf {c}_2 - \mathbf {s}^\top \cdot \mathbf {\mathsf {c}}_1 \rfloor _2\). To see this, note that since \(\mathsf {c}_2 - \mathbf {s}^\top \cdot \mathbf {\mathsf {c}}_1 = \frac{q}{2} \mathsf {m}+ e\), we can write
Now, since r is chosen such that \(\mathsf {c}_2 + r \notin [q/4 - B,q/4 + B] \cup [3/4 \cdot q - B,3/4 \cdot q + B]\) and \(e \in [-B,B]\), it holds that
Using the above this implies that
It follows that \(\mathsf {m}= (w - \lceil \mathbf {s}^\top \mathbf {\mathsf {c}}_1 + r \rfloor _2) \mod 2\). Note that after shrinking ciphertexts, we can no longer perform homomorphic operations (unless one is willing to run a bootstrapped ciphertext expansion). As a consequence, in our applications we will only perform the shrinking operation after all homomorphic operations have been computed.
What is left to be shown is how to amortize the cost of including r by shrinking many \(\mathsf {c}_2\) components for the same \(\mathsf {c}_1\). To achieve this, instead of using basic Regev encryption, we use batched Regev encryption. In batched Regev encryption, ciphertexts consist of a vector  and ring elements
and ring elements  for \(i \in [\ell ]\). To decrypt the i-th message component \(\mathsf {m}_i\), we compute
for \(i \in [\ell ]\). To decrypt the i-th message component \(\mathsf {m}_i\), we compute
where \(\mathbf {s}_i\) is the secret key for the i-th component. Consequently, we can use the same shrinking strategy as above for every \(\mathsf {c}_{2,i}\). However, now each \(\mathsf {c}_{2,i}\) imposes a constraint on r, namely that \(\mathsf {c}_{2,i} + r \notin [q/4 - B,q/4 + B] \cup [3/4 \cdot q - B,3/4 \cdot q + B]\).
Fortunately, given that q is sufficiently large, namely \(q > 4 \ell B\), there exists an r which fulfills all constraints simultaneously. To find such an r, we compute a union of all forbidden intervals modulo q, and pick an r outside of this set. Notice that this procedure can be efficiently implemented even if q is super-polynomially large. The rate of the resulting scheme is
For \(q \approx 4 \ell B\) and a sufficiently large  , we achieve rate \(1 - O(1/\lambda )\).
, we achieve rate \(1 - O(1/\lambda )\).
Notice that while basic Regev encryption is only additively homomorphic, we need a scheme that supports homomorphic evaluation of linear functions. Fortunately, this can be achieved by a very simple modification. Instead of encrypting a message \(\mathsf {m}\), encrypt the messages \(2^i \cdot \mathsf {m}\) for all \(i \in [\log (q)]\). Further details are deferred to the main body (Sect. 3.3).
Back to Rate-1 FHE. Returning to our main objective of rate-1 FHE, if we instantiate our generic construction from above with the packed Regev scheme that allows ciphertext shrinking, note that there is a slight mismatch. Recall that our rate 1 FHE construction assumed a linearly homomorphic encryption scheme with plaintext space  or
or  , whereas our Regev scheme with shrinking has a plaintext space \(\{0,1\}^\ell \).
, whereas our Regev scheme with shrinking has a plaintext space \(\{0,1\}^\ell \).
Towards resolving this issue, it is instructive to consider Regev encryption without message encoding and decryption without rounding. That is, we consider only the linear part of decryption where a ciphertext \(\mathsf {c}= (\mathbf {\mathsf {c}}_1,\mathsf {c}_2)\) decrypts to
where \(\mathbf {s}\) is the secret key and the message \(\mathsf {m}^*\) is an element of  . The important observation is that in the construction above the message \(\mathsf {m}^*\) is the result of a linear decrypt-and-multiply operation. This means that \(\mathsf {m}^*\) already contains a certain amount of decryption noise and the actual message contained in \(\mathsf {m}^*\) has already been encoded by the linear decrypt-and-multiply operation.
. The important observation is that in the construction above the message \(\mathsf {m}^*\) is the result of a linear decrypt-and-multiply operation. This means that \(\mathsf {m}^*\) already contains a certain amount of decryption noise and the actual message contained in \(\mathsf {m}^*\) has already been encoded by the linear decrypt-and-multiply operation.
Assuming for simplicity that \(\mathsf {m}^*= L_{\frac{q}{2},\mathsf {c}^*}(\mathbf {s}^*)\), where \(\mathsf {c}^*\) is an FHE ciphertext encrypting a message \(\mathsf {m}\) and \(\mathbf {s}^*\) the corresponding FHE secret key, we have that
where \(e''\) is a small noise term which is introduced by the inner FHE decryption. Note that above we only had to deal with noise \(e''\) coming from the inner FHE decryption, whereas now we have an additional noise term \(e'\) coming from the decryption of the linearly homomorphic scheme. Given that the compound noise \(e = e' + e''\) is sufficiently small, our shrinking technique for the ciphertext \((\mathbf {\mathsf {c}}_1,\mathsf {c}_2)\) still works. The only condition we need for the shrinking technique to work is that \(\mathsf {c}_2 - \mathbf {s}^\top \cdot \mathbf {\mathsf {c}}_1\) is of the form \(\frac{q}{2} \cdot \mathsf {m}+ e\) for a B-bounded error e.
To sum things up, all we need to ensure is that the encrypted message is well-formed before ciphertext shrinking via the \(\mathsf {Shrink}\) procedure. To stay with the notation from above, for this scheme the packing matrix \(\mathbf {T}\) which is used to encode plaintexts during the homomorphic decrypt-and-multiply step will be \(\frac{q}{2} \cdot \mathbf {I}\), where \(\mathbf {I}\) is the identity matrix.
Fully Homomorphic Time-Lock Puzzles. We finally show how ideas from our rate-1 FHE construction can be used to obtain fully homomorphic time-lock puzzles (FH-TLP) from standard assumptions. Very recently, Malavolta and Thyargarajan [22] introduced the notion of homomorphic time-lock puzzles and proposed an efficient construction of linearly homomorphic timelock puzzles (LH-TLP) from the sequential squaring assumption [31]. An LH-TLP allows for evaluations of linear functions on messages encrypted in time-lock puzzles. A key aspect here is that the time-lock puzzles may be independently generated by different players.
The basic idea underlying our construction of FH-TLP is to replace the linearly homomorphic encryption scheme in our rate-1 FHE construction above by an LH-TLP. More concretely, fix an LH-TLP scheme where the message-space is  and an FHE scheme for which the secret keys are
and an FHE scheme for which the secret keys are  vectors. We will describe how to generate a puzzle for a message \(\mathsf {m}\) and time parameter T. First, generate an FHE public key \(\mathsf {pk}\) together with a secret key
vectors. We will describe how to generate a puzzle for a message \(\mathsf {m}\) and time parameter T. First, generate an FHE public key \(\mathsf {pk}\) together with a secret key  . Next, create a puzzle \(\mathsf {Z}\) with time parameter T for the LH-TLP scheme encrypting the FHE secret key \(\mathbf {s}\). Finally, encrypt the message \(\mathsf {m}\) under the FHE public key \(\mathsf {pk}\) obtaining a ciphertext \(\mathsf {c}\). The time-lock puzzle consists of \((\mathsf {pk},\mathsf {c},\mathsf {Z})\) and can be solved by recovering the secret key \(\mathbf {s}\) and then decrypting the message \(\mathsf {m}\).
. Next, create a puzzle \(\mathsf {Z}\) with time parameter T for the LH-TLP scheme encrypting the FHE secret key \(\mathbf {s}\). Finally, encrypt the message \(\mathsf {m}\) under the FHE public key \(\mathsf {pk}\) obtaining a ciphertext \(\mathsf {c}\). The time-lock puzzle consists of \((\mathsf {pk},\mathsf {c},\mathsf {Z})\) and can be solved by recovering the secret key \(\mathbf {s}\) and then decrypting the message \(\mathsf {m}\).
While this simple idea allows us to perform homomorphic computations on a single message \(\mathsf {m}\), it fails at our actual goal of allowing homomorphic computations on puzzles generated by different puzzle generators. The reason being that every time we generate a new puzzle, we generate a fresh FHE key, and generally homomorphic computations across different keys are not possible. To overcome this issue, we instead use a multi-key FHE scheme, which enables homomorphic computations across different public keys. More specifically, given \(\ell \) puzzles \((\mathsf {pk}_1,\mathsf {c}_1,\mathsf {Z}_1),\dots ,(\mathsf {pk}_\ell ,\mathsf {c}_\ell ,\mathsf {Z}_\ell )\), encrypting messages \((m_1, \dots , m_\ell )\), and an \(\ell \) input function f, we can homomorpically compute a ciphertext \(\mathsf {c}^*= \mathsf {Eval}(\mathsf {pk}_1,\dots ,\mathsf {pk}_\ell ,f,(\mathsf {c}_1,\dots ,\mathsf {c}_\ell ))\) which encrypts the message \(\mathsf {m}^*= f(\mathsf {m}_1,\dots ,\mathsf {m}_\ell )\).
We have, however, still not solved the main problem. In order to recover \(f(\mathsf {m}_1,\dots ,\mathsf {m}_\ell )\) from \(\mathsf {c}^*\), we first have to recover all secret keys \((\mathbf {s}_1,\dots ,\mathbf {s}_\ell )\) from the LH-TLPs \((\mathsf {Z}_1,\dots ,\mathsf {Z}_\ell )\). Thus, the workload is proportional to that of solving \(\ell \) time-lock puzzles, which is identical to the trivial construction. The final idea is to use a multi-key FHE scheme with linear decryption: If \(\mathsf {c}^*\) is a (homomorphically evaluated) ciphertext which encrypts a message \(\mathsf {m}^*\) under public keys \(\mathsf {pk}_1,\dots ,\mathsf {pk}_\ell \), we can decrypt \(\mathsf {c}^*\) using a function \(L_{\mathsf {c}^*}(\mathbf {s}_1,\dots ,\mathbf {s}_\ell )\) which is linear in the secret keys \(\mathbf {s}_1,\dots ,\mathbf {s}_\ell \). As before, this decryption operation is noisy, i.e.,
where e with \(|e| < B\) is a small noise term. This allows us to homomorphically evaluate the linear function \(L_{\mathsf {c}^*}\) over the time-lock puzzles \((\mathsf {Z}_1,\dots ,\mathsf {Z}_\ell )\) (recall the \(\mathsf {Z}_i\) encrypts the secret key \(\mathbf {s}_i\)) and obtain a time-lock puzzle \(\mathsf {Z}^*= \mathsf {Eval}(L_{\mathsf {c}^*},(\mathsf {Z}_1,\dots ,\mathsf {Z}_\ell ))\) encrypting \(L_{\mathsf {c}^*}(\mathbf {s}_1,\dots ,\mathbf {s}_\ell ) = \frac{q}{2} \cdot \mathsf {m}^*+ e\). To recover the computation result \(\mathsf {m}^*\) we only have to solve \(\mathsf {Z}^*\). Note that the final puzzle \(\mathsf {Z}^*\) is a single compact puzzle for the LH-TLP scheme, thus the overhead to solve this puzzle is that of solving a single LH-TLP and therefore independent of \(\ell \).
We remark that both multi-key FHE from standard assumptions [11, 24] and LH-TLP from standard assumptions [22] need a setup. Consequently, our FH-TLP construction inherits this property. Finally, techniques that we develop to construct rate-1 FHE also apply to our FH-TLP construction.
2 Preliminaries
We denote by \(\lambda \in \mathbb {N}\) the security parameter. We say that a function  is negligible if it vanishes faster than any polynomial. Given a set S, we denote by
is negligible if it vanishes faster than any polynomial. Given a set S, we denote by  the uniform sampling from S. We say that an algorithm is PPT if it can be implemented by a probabilistic machine running in time
the uniform sampling from S. We say that an algorithm is PPT if it can be implemented by a probabilistic machine running in time  . We abbreviate the set \(\{1, \dots , n\}\) as [n]. Matrices are denoted by \(\mathbf {M}\) and vectors are denoted by \(\mathbf {v}\). We use the infinity norm of a vector \(\Vert \mathbf {v} \Vert _\infty \), since it behaves conveniently with rounding. For a given modulus q, we define the rounding function \(\lceil x \rfloor _2 = \lceil x \cdot 2/q\rfloor \mod 2\).
. We abbreviate the set \(\{1, \dots , n\}\) as [n]. Matrices are denoted by \(\mathbf {M}\) and vectors are denoted by \(\mathbf {v}\). We use the infinity norm of a vector \(\Vert \mathbf {v} \Vert _\infty \), since it behaves conveniently with rounding. For a given modulus q, we define the rounding function \(\lceil x \rfloor _2 = \lceil x \cdot 2/q\rfloor \mod 2\).
2.1 Learning with Errors
The (decisional) learning with errors (LWE) problem was introduced by Regev [30]. The LWE problem is parametrized by a modulus q, positive integers n, m and an error distribution \(\chi \). An adversary is either given \((\mathbf {A},\mathbf {s}^\top \cdot \mathbf {A} + \mathbf {e})\) or \((\mathbf {A},\mathbf {u})\) and has to decide which is the case. Here, \(\mathbf {A}\) is chosen uniformly from  , \(\mathbf {s}\) is chosen uniformly from
, \(\mathbf {s}\) is chosen uniformly from  , \(\mathbf {u}\) is chosen uniformly from
, \(\mathbf {u}\) is chosen uniformly from  and \(\mathbf {e}\) is chosen from \(\chi ^m\). The matrix version of this problem asks to distinguish \((\mathbf {A},\mathbf {S} \cdot \mathbf {A} + \mathbf {E})\) from \((\mathbf {A},\mathbf {U})\), where the dimensions are accordingly. It follows from a simple hybrid argument that the matrix version is as hard as the standard version.
and \(\mathbf {e}\) is chosen from \(\chi ^m\). The matrix version of this problem asks to distinguish \((\mathbf {A},\mathbf {S} \cdot \mathbf {A} + \mathbf {E})\) from \((\mathbf {A},\mathbf {U})\), where the dimensions are accordingly. It follows from a simple hybrid argument that the matrix version is as hard as the standard version.
As shown in [27, 30], for any sufficiently large modulus q the LWE problem where \(\chi \) is a discrete Gaussian distribution with parameter \(\sigma = \alpha q \ge 2 \sqrt{n}\) (i.e. the distribution over  where the probability of x is proportional to \(e^{-\pi (|x|/\sigma )^2}\)), is at least as hard as approximating the shortest independent vector problem (SIVP) to within a factor of \(\gamma = \tilde{O}({n}/\alpha )\) in worst case dimension n lattices. We refer to \(\alpha = \sigma / q\) as the modulus-to-noise ratio, and by the above this quantity controls the hardness of the LWE instantiation. Hereby, LWE with polynomial \(\alpha \) is (presumably) harder than LWE with super-polynomial or sub-exponential \(\alpha \). We can truncate the discrete gaussian distribution \(\chi \) to \(\sigma \cdot \omega (\sqrt{\log (\lambda )})\) while only introducing a negligible error. Consequently, we omit the actual distribution \(\chi \) but only use the fact that it can be bounded by a (small) value B.
where the probability of x is proportional to \(e^{-\pi (|x|/\sigma )^2}\)), is at least as hard as approximating the shortest independent vector problem (SIVP) to within a factor of \(\gamma = \tilde{O}({n}/\alpha )\) in worst case dimension n lattices. We refer to \(\alpha = \sigma / q\) as the modulus-to-noise ratio, and by the above this quantity controls the hardness of the LWE instantiation. Hereby, LWE with polynomial \(\alpha \) is (presumably) harder than LWE with super-polynomial or sub-exponential \(\alpha \). We can truncate the discrete gaussian distribution \(\chi \) to \(\sigma \cdot \omega (\sqrt{\log (\lambda )})\) while only introducing a negligible error. Consequently, we omit the actual distribution \(\chi \) but only use the fact that it can be bounded by a (small) value B.
2.2 Homomorphic Encryption
We recall the definition of homomorphic encryption in the following.
Definition 1 (Homomorphic Encryption)
A homomorphic encryption scheme consists of the following efficient algorithms.
-
\(\mathsf {KeyGen}(1^\lambda ) :\) On input the security parameter \(1^\lambda \), the key generation algorithm returns a key pair \((\mathsf {sk}, \mathsf {pk})\).
-
\(\mathsf {Enc}(\mathsf {pk}, \mathsf {m}) :\) On input a public key \(\mathsf {pk}\) and a message \(\mathsf {m}\), the encryption algorithm returns a ciphertext \(\mathsf {c}\).
-
\(\mathsf {Eval}(\mathsf {pk}, f, (\mathsf {c}_1, \dots , \mathsf {c}_\ell )) :\) On input the public key \(\mathsf {pk}\), an \(\ell \)-argument function f, and a vector of ciphertexts \((\mathsf {c}_1, \dots , \mathsf {c}_\ell )\), the evaluation algorithm returns an evaluated ciphertext \(\mathsf {c}\).
-
\(\mathsf {Dec}(\mathsf {sk}, \mathsf {c}) :\) On input the secret key \(\mathsf {sk}\) and a ciphertext \(\mathsf {c}\), the decryption algorithm returns a message \(\mathsf {m}\).
We say that a scheme is fully-homomorphic (FHE) if it is homomorphic for all polynomial-size circuits. We also consider a restricted class of homomorphism that supports linear functions and we refer to such a scheme as linearly-homomorphic encryption. We characterize correctness of a single function evaluation. This can be extended to the more general notion of multi-hop correctness [18] if the condition specified below is required to hold for arbitrary compositions of functions.
Definition 2 (Correctness)
A homomorphic encryption scheme \((\mathsf {KeyGen},\) \(\mathsf {Enc}, \mathsf {Eval},\mathsf {Dec})\) is correct if for all  , all \(\ell \)-argument functions f in the supported family, all inputs \((\mathsf {m}_1, \dots , \mathsf {m}_\ell )\), all \((\mathsf {sk}, \mathsf {pk})\) in the support of \(\mathsf {KeyGen}(1^\lambda )\), and all \(\mathsf {c}_i\) in the support of \(\mathsf {Enc}(\mathsf {pk}, \mathsf {m}_i)\) there exists a negligible function
, all \(\ell \)-argument functions f in the supported family, all inputs \((\mathsf {m}_1, \dots , \mathsf {m}_\ell )\), all \((\mathsf {sk}, \mathsf {pk})\) in the support of \(\mathsf {KeyGen}(1^\lambda )\), and all \(\mathsf {c}_i\) in the support of \(\mathsf {Enc}(\mathsf {pk}, \mathsf {m}_i)\) there exists a negligible function  such that
such that

We require a scheme to be compact in the sense that the size of the ciphertext should not grow with the size of the evaluated function.
Definition 3 (Compactness)
A homomorphic encryption scheme \((\mathsf {KeyGen},\) \(\mathsf {Enc}, \mathsf {Eval}, \mathsf {Dec})\) is compact if there exists a polynomial  such that for all
such that for all  , all \(\ell \)-argument functions f in the supported family, all inputs \((\mathsf {m}_1, \dots , \mathsf {m}_\ell )\), all \((\mathsf {sk}, \mathsf {pk})\) in the support of \(\mathsf {KeyGen}(1^\lambda )\), and all \(\mathsf {c}_i\) in the support of \(\mathsf {Enc}(\mathsf {pk}, \mathsf {m}_i)\) it holds that
, all \(\ell \)-argument functions f in the supported family, all inputs \((\mathsf {m}_1, \dots , \mathsf {m}_\ell )\), all \((\mathsf {sk}, \mathsf {pk})\) in the support of \(\mathsf {KeyGen}(1^\lambda )\), and all \(\mathsf {c}_i\) in the support of \(\mathsf {Enc}(\mathsf {pk}, \mathsf {m}_i)\) it holds that

The notion of security is standard for public-key encryption [20].
Definition 4 (Semantic Security)
A homomorphic encryption scheme \((\mathsf {KeyGen},\) \(\mathsf {Enc}, \mathsf {Eval}, \mathsf {Dec})\) is semantically secure if for all  and for all PPT adversaries
and for all PPT adversaries  there exists a negligible function
there exists a negligible function  such that
such that

Finally we define the rate of an encryption scheme as the asymptotic message-to-ciphertext size ratio.
Definition 5 (Rate)
We say that a homomorphic encryption scheme \((\mathsf {KeyGen}, \mathsf {Enc}, \mathsf {Eval}, \mathsf {Dec})\) has rate \(\rho = \rho (\lambda )\), if it holds for all \(\mathsf {pk}\) in the support of  , all supported functions f with sufficiently large output size, all messages \((\mathsf {m}_1, \dots , \mathsf {m}_\ell )\) in the message space, and all \(\mathsf {c}_i\) in the support of
, all supported functions f with sufficiently large output size, all messages \((\mathsf {m}_1, \dots , \mathsf {m}_\ell )\) in the message space, and all \(\mathsf {c}_i\) in the support of  that
that
We also say that a scheme has rate 1, if it holds that
Note that in Definition 5 we need to restrict ourselves to a class of supported functions for which the output size \(|f(\mathsf {m}_1, \dots , \mathsf {m}_\ell )|\) is sufficiently large. E.g., if a function output \(f(\mathsf {m}_1, \dots , \mathsf {m}_\ell )\) is just one bit, we cannot hope to achieve a good rate. Consequently we will only consider functions with a large output domain.
2.3 Multi-key Homomorphic Encryption
A multi-key homomorphic encryption supports the evaluation of functions over ciphertexts computed under different (possibly independently sampled) keys. The result of the computation can then be decrypted using all of the corresponding secret keys. Formally, this introduces a few syntactical modifications. Most notably and in contrast with the single-key variant, multi-key schemes might need a setup which generates public parameters shared across all users.
Definition 6 (Multi-Key Homomorphic Encryption)
A multi-key homomorphic encryption scheme consists of the following efficient algorithms.
-
\(\mathsf {Setup}(1^\lambda ):\) On input the security parameter \(1^\lambda \), the setup algorithm returns the public parameters \(\mathsf {pp}\).
-
\(\mathsf {KeyGen}(\mathsf {pp}) :\) On input the public parameters \(\mathsf {pp}\), the key generation algorithm returns a key pair \((\mathsf {sk}, \mathsf {pk})\).
-
\(\mathsf {Enc}(\mathsf {pk}, \mathsf {m}) :\) On input a public key \(\mathsf {pk}\) and a message \(\mathsf {m}\), the encryption algorithm returns a ciphertext \(\mathsf {c}\).
-
\(\mathsf {Eval}((\mathsf {pk}_1, \dots , \mathsf {pk}_\ell ), f, (\mathsf {c}_1, \dots , \mathsf {c}_\ell )) :\) On input a vector of public keys \((\mathsf {pk}_1, \dots , \mathsf {pk}_\ell )\), an \(\ell \)-argument function f, and a vector of ciphertexts \((\mathsf {c}_1, \dots , \mathsf {c}_\ell )\), the evaluation algorithm returns an evaluated ciphertext \(\mathsf {c}\).
-
\(\mathsf {Dec}((\mathsf {sk}_1, \dots , \mathsf {sk}_\ell ), \mathsf {c}) :\) On input a vector of secret keys \((\mathsf {sk}_1, \dots , \mathsf {sk}_\ell )\) and a ciphertext \(\mathsf {c}\), the decryption algorithm returns a message \(\mathsf {m}\).
As before, we say that the scheme is fully-homomorphic (MK-FHE) if it is homomorphic for P/poly. The definition of correctness is adapted to the multi-key settings.
Definition 7 (Multi-Key Correctness)
A multi-key homomorphic encryption scheme \((\mathsf {Setup}, \mathsf {KeyGen}, \mathsf {Enc}, \mathsf {Eval}, \mathsf {Dec})\) is correct if for all  , all \(\ell \) polynomial in \(\lambda \), all \(\ell \)-argument functions f in the supported family, all inputs \((\mathsf {m}_1, \dots , \mathsf {m}_\ell )\), all \(\mathsf {pp}\) in the support of \(\mathsf {Setup}\), all \((\mathsf {sk}_i, \mathsf {pk}_i)\) in the support of \(\mathsf {KeyGen}(\mathsf {pp})\), and all \(\mathsf {c}_i\) in the support of \(\mathsf {Enc}(\mathsf {pk}_i, \mathsf {m}_i)\) there exists a negligible function
, all \(\ell \) polynomial in \(\lambda \), all \(\ell \)-argument functions f in the supported family, all inputs \((\mathsf {m}_1, \dots , \mathsf {m}_\ell )\), all \(\mathsf {pp}\) in the support of \(\mathsf {Setup}\), all \((\mathsf {sk}_i, \mathsf {pk}_i)\) in the support of \(\mathsf {KeyGen}(\mathsf {pp})\), and all \(\mathsf {c}_i\) in the support of \(\mathsf {Enc}(\mathsf {pk}_i, \mathsf {m}_i)\) there exists a negligible function  such that
such that

Compactness is unchanged except that the ciphertext may grow with the number of keys.
Definition 8 (Multi-Key Compactness)
A multi-key homomorphic encryption scheme \((\mathsf {Setup}, \mathsf {KeyGen}, \mathsf {Enc}, \mathsf {Eval}, \mathsf {Dec})\) is compact if there exists a polynomial  such that for all
such that for all  , all \(\ell \) polynomial in \(\lambda \), all \(\ell \)-argument functions f in the supported family, all inputs \((\mathsf {m}_1, \dots , \mathsf {m}_\ell )\), all \((\mathsf {sk}_i, \mathsf {pk}_i)\) in the support of \(\mathsf {KeyGen}(1^\lambda )\), and all \(\mathsf {c}_i\) in the support of \(\mathsf {Enc}(\mathsf {pk}_i, \mathsf {m}_i)\) it holds that
, all \(\ell \) polynomial in \(\lambda \), all \(\ell \)-argument functions f in the supported family, all inputs \((\mathsf {m}_1, \dots , \mathsf {m}_\ell )\), all \((\mathsf {sk}_i, \mathsf {pk}_i)\) in the support of \(\mathsf {KeyGen}(1^\lambda )\), and all \(\mathsf {c}_i\) in the support of \(\mathsf {Enc}(\mathsf {pk}_i, \mathsf {m}_i)\) it holds that

The definition of semantic security is identical to that of single-key schemes.
2.4 Linear Decrypt-and-Multiply
To construct our schemes we will need FHE schemes with a more fine-grained correctness property. More specifically, we will require an FHE scheme where for which decryption is a linear function in the secret key. Furthermore, we require that this linear decryption function outputs a the product of the plaintext with a constant \(\omega \) (which is provided as input to the decryption algorithm). We will refer to such schemes as linear decrypt-and-multiply schemes.
The output of this function may contain some (short) noise, thus we also need an upper bound on amount of noise linear decrypt-and-multiply introduces. This property was explicitly characterized in an oral presentation of Micciancio [23] where he showed that schemes from the literature already satisfy this notion [1, 19] and discussed some applications. A formal definition is given in the following.
Definition 9 (Decrypt-and-Multiply)
We call a homomorphic encryption scheme \((\mathsf {KeyGen}, \mathsf {Enc}, \mathsf {Eval}, \mathsf {Dec})\) a decrypt-and-multiply scheme, if there exists bounds \(B = B(\lambda )\) and \(Q = Q(\lambda )\) and an algorithm \( \mathsf {Dec{ \& }Mult}\) such that the following holds. For every \(q \ge Q\), all \((\mathsf {sk}, \mathsf {pk})\) in the support of \(\mathsf {KeyGen}(1^\lambda ,q)\), every \(\ell \)-argument functions f (in the class supported by the scheme), all inputs \((\mathsf {m}_1, \dots , \mathsf {m}_\ell )\), all \(\mathsf {c}_i\) in the support of \(\mathsf {Enc}(\mathsf {pk}, \mathsf {m}_i)\) and every \(\omega \in \mathbb {Z}_q\) that
where \( \mathsf {Dec{ \& }Mult}\) is a linear function in \(\mathsf {sk}\) over  and \(|e| \le B\) with all but negligible probability.
and \(|e| \le B\) with all but negligible probability.
We also consider decrypt-and-multiply for multi-key schemes and we extend the definition below. We note that schemes with such a property were previously considered in the context of Spooky Encryption [13].
Definition 10 (Multi-Key Decrypt-and-Multiply)
We call a multi-key homomorphic encryption scheme \((\mathsf {Setup}, \mathsf {KeyGen}, \mathsf {Enc}, \mathsf {Eval}, \mathsf {Dec})\) a decrypt-and-multiply scheme, if there exists bounds \(B = B(\lambda )\) and \(Q = Q(\lambda )\) and an algorithm \( \mathsf {Dec{ \& }Mult}\) such that the following holds. For every \(q \ge Q\), all \(\mathsf {pp}\) in the support of \(\mathsf {Setup}(1^\lambda ; q)\), all \((\mathsf {sk}_i, \mathsf {pk}_i)\) in the support of \(\mathsf {KeyGen}(1^\lambda )\), every \(\ell \)-argument functions f (in the class supported by the scheme), all inputs \((\mathsf {m}_1, \dots , \mathsf {m}_\ell )\), all \(\mathsf {c}_i\) in the support of \(\mathsf {Enc}(\mathsf {pk}_i, \mathsf {m}_i)\) and every \(\omega \in \mathbb {Z}_q\) that
where \( \mathsf {Dec{ \& }Mult}\) is a linear function in the vector \((\mathsf {sk}_1, \dots , \mathsf {sk}_\ell )\) over  and \(|e| \le B\) with all but negligible probability.
and \(|e| \le B\) with all but negligible probability.
An aspect we have omitted so far is to specify over which domain we require decryption to be linear. For essentially all FHE schemes in the literature, decryption is a linear function over a ring  , which also requires that secret keys are vectors over
, which also requires that secret keys are vectors over  . As mentioned before, the main idea behind our constructions will be to perform linear decrypt-and-multiply under a linearly homomorphic encryption scheme. Consequently, we need to match the plaintext space of the linearly homomorphic scheme with the secret key-space of the fully homomorphic scheme. As for some linearly homomorphic schemes we consider, we will need a way to connect the two. Luckily, for essentially all FHE schemes in the literature, the modulus q does not depend on any secret but depends only on the security parameter. Moreover, LWE-based FHE schemes can be instantiated with any (sufficiently large) modulus q without affecting the worst-case hardness of the underlying LWE problem [27].
. As mentioned before, the main idea behind our constructions will be to perform linear decrypt-and-multiply under a linearly homomorphic encryption scheme. Consequently, we need to match the plaintext space of the linearly homomorphic scheme with the secret key-space of the fully homomorphic scheme. As for some linearly homomorphic schemes we consider, we will need a way to connect the two. Luckily, for essentially all FHE schemes in the literature, the modulus q does not depend on any secret but depends only on the security parameter. Moreover, LWE-based FHE schemes can be instantiated with any (sufficiently large) modulus q without affecting the worst-case hardness of the underlying LWE problem [27].
Consequently, we can consider the modulus q as a system parameter for the underlying FHE scheme. In abuse of notation, we will provide the modulus q as an explicit input to the FHE key generation algorithm.
Schemes with Linear Decrypt-and-Multiply. Micciancio [23] has recently shown that any FHE scheme with linear decryption always admits an efficient linear decrypt-and-multiply algorithm. Notable examples of constructions that support linear decrypt-and-multiply right away are GSW-based schemes [19], e.g., [1, 8, 11, 13, 24].
In these schemes, ciphertexts are of the form \(\mathbf {C} = \mathbf {A}\cdot \mathbf {R} + \mathsf {m}\cdot \mathbf {G}\), where  is a matrix specified in the public key, \(\mathbf {R}\) is a matrix with small entries and \(\mathbf {G}\) is the so-called gadget matrix. The secret key is a vector \(\mathbf {s}\), for which the last component \(s_n = 1\), which has the property that \(\mathbf {s}^\top \cdot \mathbf {A} = \mathbf {e}^\top \), for a vector \(\mathbf {e}^\top \) with small entries. For a vector \(\mathbf {v}\) let \(\mathbf {G}^{-1}(\mathbf {v})\) be a binary vector with the property that \(\mathbf {G} \cdot \mathbf {G}^{-1}(\mathbf {v}) = \mathbf {v}\) (\(\mathbf {G}^{-1}(\cdot )\) is a non-linear function). For an
is a matrix specified in the public key, \(\mathbf {R}\) is a matrix with small entries and \(\mathbf {G}\) is the so-called gadget matrix. The secret key is a vector \(\mathbf {s}\), for which the last component \(s_n = 1\), which has the property that \(\mathbf {s}^\top \cdot \mathbf {A} = \mathbf {e}^\top \), for a vector \(\mathbf {e}^\top \) with small entries. For a vector \(\mathbf {v}\) let \(\mathbf {G}^{-1}(\mathbf {v})\) be a binary vector with the property that \(\mathbf {G} \cdot \mathbf {G}^{-1}(\mathbf {v}) = \mathbf {v}\) (\(\mathbf {G}^{-1}(\cdot )\) is a non-linear function). For an  let
let  be a vector which is 0 everywhere but \(\omega \) in the last component. We can perform the linear decrypt-and-multiply operation by computing
be a vector which is 0 everywhere but \(\omega \) in the last component. We can perform the linear decrypt-and-multiply operation by computing
where \(e' = \mathbf {e}^\top \cdot \mathbf {R} \cdot \mathbf {G}^{-1}(\varvec{\omega })\) is a short noise vector. The second equality holds as \(\mathbf {s}^\top \cdot \mathbf {A} = \mathbf {e}^\top \), and the third one holds as \(\mathbf {s}^\top \cdot \varvec{\omega } = \omega \). We remark that the scheme of Brakerski and Vaikunthanatan [8] satisfies these constraints with a polynomial modulus-to-noise ratio, by exploiting the asymmetric noise growth in the GSW scheme and a specific way to homomorphically evaluate functions.
Since we need a multi-key FHE scheme in our construction of fully homomorphic time-lock puzzles, we briefly discuss a linear decrypt-and-multiply procedure for the MK-FHE construction of Mukherjee and Wichs [24], which in turn is a simplified version of the scheme from Clear and McGoldrick [11]. Recall that the scheme shown in [11, 24] is secure against the Learning with Errors problem (with super-polynomial modulo-to-noise ratio) and satisfies the following properties:
-
(1)
The construction is in the common random string model and all parties have access to a uniform matrix
 .
. -
(2)
For any fixed depth parameter d, the scheme supports multi-key evaluation of depth-d circuits using public keys of size
 , while secret keys are vectors
, while secret keys are vectors  , regardless of the depth parameter. More concretely, there exists an efficient algorithm \(\mathsf {MK}\text {-}\mathsf {FHE}.\mathsf {Eval}\) that is given as input:
, regardless of the depth parameter. More concretely, there exists an efficient algorithm \(\mathsf {MK}\text {-}\mathsf {FHE}.\mathsf {Eval}\) that is given as input: -
(a)
Parameters
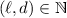 , where \(\ell \) is the number of public keys that perform depth-d computation.
, where \(\ell \) is the number of public keys that perform depth-d computation. -
(b)
A depth-d circuit that computes an \(\ell \)-argument Boolean function \(f: \{0,1\}^*\rightarrow \{0,1\}\).
-
(c)
A vector of public keys \((\mathsf {pk}_1, \dots , \mathsf {pk}_\ell )\) and a fresh (bit-by-bit) encryption of each argument \(x_i\) under \(\mathsf {pk}_i\), denoted by \(\mathsf {c}_i \leftarrow \mathsf {MK}\text {-}\mathsf {FHE}.\mathsf {Enc}(\mathsf {pk}_i, x_i)\).
Then \(\mathsf {MK}\text {-}\mathsf {FHE}.\mathsf {Eval}\) outputs a matrix \(\mathbf {C}\in \mathbb {Z}_q^{n\ell \times m\ell }\) such that
$$ \tilde{\mathbf {s}}\cdot \mathbf {C}\cdot \mathbf {G}^{-1}\left( \varvec{\omega }\right) = \omega \cdot f(x_1, \dots , x_\ell ) + e ~(\text {mod }q) $$where \(\tilde{\mathbf {s}}\) is the row concatenation of \((\mathbf {s}_1, \dots , \mathbf {s}_\ell )\), \(\varvec{\omega }\) is the vector \((0, \dots , 0, \omega )\in \mathbb {Z}_q^{n\ell }\), and \(\mathbf {G}^{-1}\) is the bit-decomposition operator. Furthermore, it holds that
$$\begin{aligned} |e| \le \beta \cdot (m^4+m)(m \ell + 1)^d = \beta \cdot 2^{O(d\cdot \log (\lambda ))} \end{aligned}$$where \(\beta \) is a bound on the absolute value of the noise of fresh ciphertexts.
-
(a)
-
(3)
By further making a circular-security assumption, \(\mathsf {MK}\text {-}\mathsf {FHE}.\mathsf {Eval}\) supports the evaluation of circuits of any depth without increasing the size of the public keys. In this case the bound on the noise is \(|e| \le \beta \cdot 2^{O(d_{\mathsf {Dec}}\cdot \log (\lambda ))}\), where \(d_{\mathsf {Dec}}\) is the depth of the decryption circuit, which is poly-logarithmic in \(\lambda \).
Note that that by setting \(\ell = 1\) we recover the FHE scheme of [19] except that for the latter we can give a slightly better bound for the noise, namely \(|e|\le \beta \cdot m^2(m + 1)^d\). The important observation here is that \(\mathbf {C}\cdot \mathbf {G}^{-1}\left( \varvec{\omega }\right) \) does not depend on the secret key and therefore defining
gives a syntactically correct linear decrypt-and-multiply algorithm and \(B = |e|\) is the corresponding noise bound. Finally we remark that the MK-FHE scheme does not impose any restriction on the choice of q (except for its size) so we can freely adjust it to match the modulus of the companion time-lock puzzle.
2.5 Homomorphic Time-Lock Puzzles
Homomorphic time-lock puzzles generalize the classical notion of time-lock puzzles [31] by allowing one to publicly manipulate puzzles to evaluate functions over the secrets. They were introduced in a recent work [22] and we recall the definition in the following.
Definition 11 (Homomorphic Time-Lock Puzzles)
A homomorphic time-lock puzzle consists of the following efficient algorithms.
-
\(\mathsf {Setup}(1^\lambda , T) :\) On input the security parameter \(1^\lambda \) and a time parameter T, the setup algorithm returns the public parameters \(\mathsf {pp}\).
-
\(\mathsf {PuzGen}(\mathsf {pp}, \mathsf {s}) :\) On input the public parameters \(\mathsf {pp}\) and a secret \(\mathsf {s}\), the puzzle generation algorithm returns a puzzle \(\mathsf {Z}\).
-
\(\mathsf {Eval}(\mathsf {pp}, f, (\mathsf {Z}_1, \dots , \mathsf {Z}_\ell )) :\) On input the public parameters \(\mathsf {pp}\), an \(\ell \)-argument function f, and a vector of puzzles \((\mathsf {Z}_1, \dots , \mathsf {Z}_\ell )\), the evaluation algorithm returns an evaluated puzzle \(\mathsf {Z}\).
-
\(\mathsf {Solve}(\mathsf {pp}, \mathsf {Z}) :\) On input the public parameters \(\mathsf {pp}\) and a puzzle \(\mathsf {Z}\), the solving algorithm returns a secret \(\mathsf {s}\).
By convention, we refer to a puzzle as fully-homomorphic (FHTLP) if it is homomorphic for all circuits. We now give the definition of (single-hop) correctness.
Definition 12 (Correctness)
A homomorphic time-lock puzzle \((\mathsf {Setup},\) \(\mathsf {PuzGen}, \mathsf {Eval}, \mathsf {Solve})\) is correct if for all  , all
, all  , all \(\ell \)-argument functions f in the supported family, all inputs \((\mathsf {s}_1, \dots , \mathsf {s}_\ell )\), all \(\mathsf {pp}\) in the support of \(\mathsf {Setup}(1^\lambda , T)\), and all \(\mathsf {Z}_i\) in the support of \(\mathsf {PuzGen}(\mathsf {pp}, \mathsf {s}_i)\) the following two conditions are satisfied:
, all \(\ell \)-argument functions f in the supported family, all inputs \((\mathsf {s}_1, \dots , \mathsf {s}_\ell )\), all \(\mathsf {pp}\) in the support of \(\mathsf {Setup}(1^\lambda , T)\), and all \(\mathsf {Z}_i\) in the support of \(\mathsf {PuzGen}(\mathsf {pp}, \mathsf {s}_i)\) the following two conditions are satisfied:
-
(1)
There exists a negligible function
 such that
such that 
-
(2)
The runtime of \(\mathsf {Solve}(\mathsf {pp}, \mathsf {Z})\), where \(\mathsf {Z}\leftarrow \mathsf {Eval}(\mathsf {pp}, f, (\mathsf {Z}_1, \dots , \mathsf {Z}_\ell ))\), is bounded by
 , for some fixed polynomial
, for some fixed polynomial  .
.
In this work we consider the stronger notion of security where time is counted starting from the moment the puzzle is generated (as opposed to the moment where the public parameters of the scheme are generated). This is termed security with reusable setup in [22] and we henceforth refer to it simply as security.
Definition 13 (Security)
A homomorphic time-lock puzzle \((\mathsf {Setup},\mathsf {PuzGen},\) \(\mathsf {Eval}, \mathsf {Solve})\) is secure if for all  , all
, all  , all PPT adversaries
, all PPT adversaries  such that the depth of
such that the depth of  is bounded by T, there exists a negligible function
is bounded by T, there exists a negligible function  such that
such that

3 Shrinking Linearly Homomorphic Encryption
In the following section we introduce the useful abstraction of linearly homomorphic encryption with compressing ciphertexts and we discuss several concrete instantiations.
3.1 Definitions
We start by providing relaxed correctness definitions for linearly homomorphic encryption. As discussed before, for Regev-like encryption schemes decryption is a linear operation which, unavoidably, introduces noise. This noise is dealt with by encoding the message accordingly and decoding the result of linear decryption, usually by applying a rounding function. In this section we provide definitions for linearly homomorphic encryption which account for noise, and allow to treat encoding and decoding of the message separately. We assume that a linearly homomorphic encryption scheme is described by four algorithms \((\mathsf {KeyGen},\mathsf {Enc},\mathsf {Dec},\mathsf {Eval})\) with the usual syntax. We further assume that each public key \(\mathsf {pk}\) specifies a message space of the form  .
.
Definition 14 (Relaxed Correctness)
Let \(\mathsf {HE}= (\mathsf {KeyGen},\mathsf {Enc},\mathsf {Dec},\mathsf {Eval})\) be a linearly homomorphic encryption scheme. Let \(B = B(\lambda )\) and  . We say that \(\mathsf {HE}\) is correct with B-noise, if it holds for every \((\mathsf {pk},\mathsf {sk})\) in the support of \(\mathsf {KeyGen}(1^\lambda )\), where \(\mathsf {pk}\) specifies a message space
. We say that \(\mathsf {HE}\) is correct with B-noise, if it holds for every \((\mathsf {pk},\mathsf {sk})\) in the support of \(\mathsf {KeyGen}(1^\lambda )\), where \(\mathsf {pk}\) specifies a message space  , every linear function
, every linear function  , all messages
, all messages  that
that
where  is a noise term with \(\Vert \mathbf {e} \Vert _\infty \le \ell B\).
is a noise term with \(\Vert \mathbf {e} \Vert _\infty \le \ell B\).
Notice that we allow the amount of noise to depend linearly on the parameter \(\ell \). We also consider linearly homomorphic encryption schemes which allow for shrinking post-evaluation ciphertexts. Such schemes will have two additional algorithms \(\mathsf {Shrink}\) and \(\mathsf {ShrinkDec}\) defined below.
-
\(\mathsf {Shrink}(\mathsf {pk},\mathsf {c}):\) Takes as input a public key \(\mathsf {pk}\) and an evaluated ciphertext \(\mathsf {c}\) and outputs a shrunk ciphertext \(\tilde{\mathsf {c}}\).
-
\(\mathsf {ShrinkDec}(\mathsf {sk},\tilde{\mathsf {c}}):\) Takes as input a secret key \(\mathsf {sk}\) and a shrunk ciphertext \(\tilde{\mathsf {c}}\) and outputs a message \(\mathsf {m}\).
Furthermore, for such schemes we assume that the public key \(\mathsf {pk}\) contains an encoding matrix  . The encoding matrix \(\mathbf {T}\) will specifies how binary messages are supposed to be encoded in the message space
. The encoding matrix \(\mathbf {T}\) will specifies how binary messages are supposed to be encoded in the message space  . We can now define the notion of shrinking correctness for a homomorphic encryption scheme \(\mathsf {HE}\).
. We can now define the notion of shrinking correctness for a homomorphic encryption scheme \(\mathsf {HE}\).
Definition 15 (Shrinking Correctness)
Let \(\mathsf {HE}= (\mathsf {KeyGen},\mathsf {Enc},\mathsf {Dec},\mathsf {Eval})\) be a linearly homomorphic encryption scheme with additional algorithms \((\mathsf {Shrink}, \mathsf {ShrinkDec})\). Let \(K = K(\lambda )\). We say that \(\mathsf {HE}\) is correct up to K-noise, if the following holds. For every \((\mathsf {pk},\mathsf {sk})\) in the support of \(\mathsf {KeyGen}(1^\lambda )\), where \(\mathsf {pk}\) specifies a message space  and an encoding matrix
and an encoding matrix  , and every \(\mathsf {c}\) with
, and every \(\mathsf {c}\) with
where \(\mathbf {\mathsf {m}} \in \{0,1\}^\ell \) and \(\Vert \mathbf {e} \Vert \le K\), it holds that
In our main construction, we will set the bounds B (in the Definition 14) and K (in Definition 15) in such a way that the amount of noise K tolerated by shrinking correctness is substantially higher than the noise B introduced by decryption. Finally, we remark that the notion of shrinking correctness also applies to non-homomorphic encryption, albeit it seems not very useful in this context, as optimal rate can be achieved via hybrid encryption.
3.2 A Ciphertext Shrinking Algorithm
We discuss a ciphertext shrinking technique which applies to a broad class of encryption schemes. Let \((\mathsf {KeyGen},\mathsf {Enc},\mathsf {Dec},\mathsf {Eval})\) be an encryption scheme where the public key specifies a message space  , the secret key \(\mathbf {S}\) is a matrix in
, the secret key \(\mathbf {S}\) is a matrix in  , (evaluated) ciphertexts are of the form \((\mathsf {c}_1,\mathsf {c}_2)\), and (noisy) decryption computes
, (evaluated) ciphertexts are of the form \((\mathsf {c}_1,\mathsf {c}_2)\), and (noisy) decryption computes
where  ,
,  . Here the two functions F and H are part of the description of the scheme and publicly known. Assume in the following that q is even. We describe a general method to shrink ciphertexts of schemes that satisfy these conditions. Consider the following algorithms \(\mathsf {Shrink}\) and \(\mathsf {ShrinkDec}\).
. Here the two functions F and H are part of the description of the scheme and publicly known. Assume in the following that q is even. We describe a general method to shrink ciphertexts of schemes that satisfy these conditions. Consider the following algorithms \(\mathsf {Shrink}\) and \(\mathsf {ShrinkDec}\).
-
\(\mathsf {Shrink}(\mathsf {pk},(\mathsf {c}_1,\mathsf {c}_2)):\) Compute \(F(\mathsf {c}_2)\) and parse it as
 . Compute the union of intervals
. Compute the union of intervals 
Pick any
 . For \(i = 1,\dots ,\ell \) compute \(w_i = \lceil y_i + r \rfloor _2\). Output \(\tilde{c} = (r,\mathsf {c}_1,w_1,\dots ,w_\ell )\).
. For \(i = 1,\dots ,\ell \) compute \(w_i = \lceil y_i + r \rfloor _2\). Output \(\tilde{c} = (r,\mathsf {c}_1,w_1,\dots ,w_\ell )\). -
\(\mathsf {ShrinkDec}(\mathbf {S},\tilde{c} = (r,\mathsf {c}_1,w_1,\dots ,w_\ell )):\) Compute \(\mathbf {v} = \mathbf {S} \cdot H(\mathsf {c}_1)\) and parse \(\mathbf {v} = (v_1,\dots ,v_\ell )\). For \(i = 1,\dots ,\ell \) set \(m_i' = (w_i - \lceil v_i + r \rfloor _2) \mod 2\). Output \(\mathbf {\mathsf {m}}' = (\mathsf {m}'_1,\dots ,\mathsf {m}'_\ell )\).
The encoding matrix \(\mathbf {T}\) for this scheme is defined to be \(\mathbf {T} = \frac{q}{2} \cdot \mathbf {I}\), where  is the identity matrix. We now state the conditions under which the modified scheme has shrinking correctness.
is the identity matrix. We now state the conditions under which the modified scheme has shrinking correctness.
Lemma 1
Let \(\mathsf {HE}= (\mathsf {KeyGen},\mathsf {Enc},\mathsf {Dec},\mathsf {Eval})\) be an encryption scheme as above, let \((\mathsf {Shrink},\mathsf {ShrinkDec})\) be as above and let \(K = K(\lambda )\). Let \(\mathsf {pk}\) be a public key for \(\mathsf {HE}\) specifying a message space  with a corresponding secret key
with a corresponding secret key  . Then given that \(q > 4 \ell \cdot K\) the scheme has shrinking correctness up to noise K.
. Then given that \(q > 4 \ell \cdot K\) the scheme has shrinking correctness up to noise K.
Proof
Let \((\mathsf {c}_1,\mathsf {c}_2)\) be a ciphertext under \(\mathsf {pk}\) for which it holds that \(F(\mathsf {c}_2) - \mathbf {S} \cdot H(\mathsf {c}_1) = \frac{q}{2} \cdot \mathbf {\mathsf {m}} + \mathbf {z}\) for a \(\mathbf {z}\) with \(\Vert \mathbf {z} \Vert \le K\). Let \(\mathbf {y} = F(\mathsf {c}_2)\), \(\mathbf {v} = \mathbf {S} \cdot H(\mathsf {c}_1)\) and parse \(\mathbf {y} = (y_1,\dots ,y_\ell )\) and \(\mathbf {v} = (v_1,\dots ,v_\ell )\). I.e., it holds that \(\mathbf {y} - \mathbf {v} = \frac{q}{2} \cdot \mathbf {\mathsf {m}} + \mathbf {z}\). Fix an index \(i \in [\ell ]\) and write \(y_i - v_i = \frac{q}{2} \cdot \mathsf {m}_i + z_i\), for a \(z_i \in [-K,K]\). This implies that \(y_i = v_i + z_i + \frac{q}{2} \cdot \mathsf {m}_i\). Note that given that \(y_i + r \notin [q/4 - B,q/4 + B]\), \(y_i + r \notin [-q/4 - B,-q/4 + B]\) and \(z_i \in [-B,B]\), it holds that
Consequently, it holds that \((\lceil y_i + r \rfloor _2 - \lceil v_i + r \rfloor _2) \mod 2 = \mathsf {m}_i\).
Thus, given that it holds for all \(i \in [\ell ]\) that \(y_i + r \notin [q/4 - B,q/4 + B]\) and \(y_i + r \notin [-q/4 - B,-q/4 + B]\) then decryption of all \(\mathsf {m}_i\) will succeed. We will now argue that under the given parameter choice such an r always exists. For every index \(i \in [\ell ]\) it holds that \(y_i + r \notin [q/4 - B,q/4 + B]\) and \(y_i + r \notin [-q/4 - B,-q/4 + B]\), if and only if \(r \notin [q/4 - y_i - B,q/4 - y_i + B]\) and \(r \notin [-q/4 - y_i - B,-q/4 - y_i + B]\). I.e., for every index i there are two intervals \([q/4 - y_i - B,q/4 - y_i + B]\) and \([-q/4 - y_i - B,-q/4 - y_i + B]\) of forbidden choices of r. Given that the set of all forbidden choices
has less than q elements, we can find an  which satisfies all constraints. By a union bound it holds that \(|U| \le \ell \cdot 4B\). Consequently, since \(q > 4 \ell B\), it holds that
which satisfies all constraints. By a union bound it holds that \(|U| \le \ell \cdot 4B\). Consequently, since \(q > 4 \ell B\), it holds that  , and the compression algorithm will find an r such that decryption will recover every \(m_i\) correctly.
, and the compression algorithm will find an r such that decryption will recover every \(m_i\) correctly.
3.3 Packed Regev Encryption
We briefly recall the linearly homomorphic packed Regev encryption and augment it with the shrinking procedures provided in the last section. This will give use a linearly homomorphic scheme with rate \(1 - O(1/\lambda )\). Let \(q = 2q'\) be a k-bit modulus, let \((n,m,\ell )\) be positive integers and let \(\chi \) be a B-bounded error distribution defined on  . Let
. Let  be a matrix which is zero everywhere, but its i-th row is \(\mathbf {g}^\top = (1,2,\dots ,2^i,\dots ,2^k)\). For a
be a matrix which is zero everywhere, but its i-th row is \(\mathbf {g}^\top = (1,2,\dots ,2^i,\dots ,2^k)\). For a  let \(\mathbf {g}^{-1}(y) \in \{0,1\}^k\) be the binary expansion of y, i.e., it holds that \(\mathbf {g}^\top \cdot \mathbf {g}^{-1}(y) = y\).
let \(\mathbf {g}^{-1}(y) \in \{0,1\}^k\) be the binary expansion of y, i.e., it holds that \(\mathbf {g}^\top \cdot \mathbf {g}^{-1}(y) = y\).
-
\(\mathsf {KeyGen}(1^\lambda ):\) Choose
 uniformly at random. Choose
uniformly at random. Choose  uniformly at random and sample
uniformly at random and sample  . Set \(\mathbf {B} = \mathbf {S} \cdot \mathbf {A} + \mathbf {E}\). Set \(\mathsf {pk}= (\mathbf {A},\mathbf {B})\) and \(\mathsf {sk}= \mathbf {S}\).
. Set \(\mathbf {B} = \mathbf {S} \cdot \mathbf {A} + \mathbf {E}\). Set \(\mathsf {pk}= (\mathbf {A},\mathbf {B})\) and \(\mathsf {sk}= \mathbf {S}\). -
\(\mathsf {Enc}(\mathsf {pk}= (\mathbf {A},\mathbf {B}),(m_1,\dots ,m_\ell )):\) Choose a random matrix
 and set \(\mathbf {C}_1 = \mathbf {A}\cdot \mathbf {R}\) and. \(\mathbf {C}_2 = \mathbf {B} \cdot \mathbf {R} + \cdot \sum _{i = 1}^\ell m_i \cdot \mathbf {G}_i\). Output \(c = (\mathbf {C}_1,\mathbf {C}_2)\).
and set \(\mathbf {C}_1 = \mathbf {A}\cdot \mathbf {R}\) and. \(\mathbf {C}_2 = \mathbf {B} \cdot \mathbf {R} + \cdot \sum _{i = 1}^\ell m_i \cdot \mathbf {G}_i\). Output \(c = (\mathbf {C}_1,\mathbf {C}_2)\). -
\(\mathsf {Eval}((f_1,\dots ,f_t),(c_1,\dots ,c_t)):\) Parse \(c_i = (\mathbf {C}_{1,i},\mathbf {C}_{2,i})\). Compute \(\mathbf {c}_1 = \sum _{i = 1}^t \mathbf {C}_{1,i} \cdot \mathbf {g}^{-1}(f_i)\) and \(\mathbf {c}_2 = \sum _{i = 1}^t \mathbf {C}_{2,i} \cdot \mathbf {g}^{-1}(f_i)\). Output \(c = (\mathbf {c}_1,\mathbf {c}_2)\).
-
\(\mathsf {Dec}(\mathsf {sk}= \mathbf {S},c = (\mathbf {c}_1,\mathbf {c}_2)\): Compute and output \(\mathbf {\mathsf {c}_2} - \mathbf {S} \cdot \mathsf {c}_1\).
First notice that under the LWE assumption, the matrix \(\mathbf {B}\) in the public key is pseudorandom. Consequently, given that \(m > (n + \ell )\cdot \log (q) + \omega (\log (\lambda ))\), we can call the leftover-hash lemma [21] to argue that ciphertexts \((\mathbf {C}_1,\mathbf {C}_2)\) are statistically close to uniform [30] and we obtain semantic security.
We now consider the homomorphic correctness of the scheme. Let  define a linear function and let
define a linear function and let  . For \(i \in [t]\) let \(\mathsf {c}_i = (\mathbf {C}_{1,i},\mathbf {C}_{2,i}) = \mathsf {Enc}(\mathsf {pk},\mathsf {m}_i)\), i.e., it holds that \(\mathsf {c}_{1,i} = \mathbf {A} \cdot \mathbf {R}_i\) and \(\mathsf {c}_{2,i} = \mathbf {B} \cdot \mathbf {R}_i + \sum _{j = 1}^\ell x_{i,j} \cdot \mathbf {G}_j\). A routine calculation shows that
. For \(i \in [t]\) let \(\mathsf {c}_i = (\mathbf {C}_{1,i},\mathbf {C}_{2,i}) = \mathsf {Enc}(\mathsf {pk},\mathsf {m}_i)\), i.e., it holds that \(\mathsf {c}_{1,i} = \mathbf {A} \cdot \mathbf {R}_i\) and \(\mathsf {c}_{2,i} = \mathbf {B} \cdot \mathbf {R}_i + \sum _{j = 1}^\ell x_{i,j} \cdot \mathbf {G}_j\). A routine calculation shows that
where \(\mathbf {z} = \mathbf {E} \cdot \sum _{j = 1}^t \mathbf {R}_j \cdot \mathbf {g}^{-1}(f_j)\). We can bound \(\Vert \mathbf {z} \Vert _\infty \) by
Consequently, the scheme \(\mathsf {HE}\) is correct with \(t \cdot k \cdot m \cdot B\)-noise. Since \(\mathsf {HE}\) fulfills the structural criteria of Lemma 1 we can augment the scheme with algorithms \(\mathsf {Shrink}\) and \(\mathsf {ShrinkDec}\) and the resulting scheme has shrinking correctness up to K-noise, given that \(q > 4\ell \cdot K\).
Rate. We finally analyze the rate of the scheme for some  and \(q \approx 4 \ell K\). Shrunk ciphertexts generated by \(\mathsf {Shrink}\) have the form \((\mathsf {c}_1,r,w_1,\dots ,w_\ell )\), where
and \(q \approx 4 \ell K\). Shrunk ciphertexts generated by \(\mathsf {Shrink}\) have the form \((\mathsf {c}_1,r,w_1,\dots ,w_\ell )\), where  ,
,  and \(w_i \in \{0,1\}\) for \(i \in [\ell ]\). Consequently, the ciphertext length is \((n+1)\log (q) + \ell \). Given that
and \(w_i \in \{0,1\}\) for \(i \in [\ell ]\). Consequently, the ciphertext length is \((n+1)\log (q) + \ell \). Given that  , we can conservatively bound \(\log (q) \le (\log (\lambda ))^2\) and observe that indeed the ciphertext is only additively longer than the plaintext. In terms of ratio, we achieve
, we can conservatively bound \(\log (q) \le (\log (\lambda ))^2\) and observe that indeed the ciphertext is only additively longer than the plaintext. In terms of ratio, we achieve
which translates to \(1 - 1/\lambda \) for \(\ell \ge n \cdot \lambda \cdot (\log (\lambda ))^2\).
4 Rate-1 Fully-Homomorphic Encryption
The following section is devoted to the presentation of our main result, an FHE scheme with optimal rate.
4.1 Definitions
Before presenting the construction of our rate 1 FHE scheme, we will augment the syntax of an FHE scheme by adding a compression algorithm and an additional decryption procedure for compressed ciphertexts. This will facilitate the exposition of our scheme.
Definition 16 (Compressible FHE)
Let \(\mathsf {FHE}= (\mathsf {KeyGen},\mathsf {Enc},\mathsf {Dec},\mathsf {Eval})\) be an FHE scheme and let  . We say that \(\mathsf {FHE}\) supports \(\ell \)-ciphertext compression if there exist two algorithms \(\mathsf {Compress}\) and \(\mathsf {CompDec}\) with the following syntax.
. We say that \(\mathsf {FHE}\) supports \(\ell \)-ciphertext compression if there exist two algorithms \(\mathsf {Compress}\) and \(\mathsf {CompDec}\) with the following syntax.
-
\(\mathsf {Compress}(\mathsf {pk},\mathsf {c}_1,\dots ,\mathsf {c}_\ell ):\) Takes as input a public key \(\mathsf {pk}\) and \(\ell \) ciphertexts \((\mathsf {c}_1,\dots ,\mathsf {c}_\ell )\) and outputs a compressed ciphertext \(\mathsf {c}^*\)
-
\(\mathsf {CompDec}(\mathsf {sk},\mathsf {c}^*):\) Takes as input a secret key \(\mathsf {sk}\) and a compressed ciphertext \(\mathsf {c}^*\) and outputs \(\ell \) messages \((\mathsf {m}_1,\dots ,\mathsf {m}_\ell )\).
In terms of correctness we require the following: Let \((\mathsf {pk},\mathsf {sk})\) be a key pair in the support of \(\mathsf {KeyGen}(1^\lambda )\) and let \(\mathsf {c}_1,\dots ,\mathsf {c}_\ell \) be valid ciphertexts (i.e., freshly encrypted ciphertext or ciphertexts that are the result of a homomorphic evaluation) such that for all \(i \in [\ell ]\) it holds \(\mathsf {m}_i = \mathsf {Dec}(\mathsf {sk},\mathsf {c}_i)\). Then it holds that
For compressible FHE schemes, we say a scheme has rate \(\rho = \rho (\lambda )\) if it holds for all \((\mathsf {pk},\mathsf {sk})\) in the support of \(\mathsf {KeyGen}(1^\lambda )\), all messages \(\mathsf {m}_1,\dots ,\mathsf {m}_\ell \) and all ciphertexts \(\mathsf {c}_1,\dots ,\mathsf {c}_\ell \) with \(\mathsf {Dec}(\mathsf {sk},\mathsf {c}_i) = \mathsf {m}_i\) (for \(i \in [\ell ]\)) that
Note that this rate definition is compatible with Definition 5 when we consider functions f which produce \(\ell \) (bits of) outputs.
4.2 Construction
In the following we describe a compressible FHE scheme which can be instantiated such that compressed ciphertexts achieve rate 1. We assume the existence of an FHE with linear decrypt-and-multiply (and any rate) and a rate-1 linearly-homomorphic encryption scheme. In this scheme, compressed ciphertexts no longer support homomorphic operations, i.e., the scheme is single-hop homormorphic. Later, we briefly discuss how this scheme can be converted into a multi-hop levelled or fully homomorphic scheme.
Notation. Since the linearly homomorphic scheme \(\mathsf {HE}\) may work with k parallel slots, we need some notation on how to address specific slots. If f is a linear function taking as input a row vector \(\mathbf {x}\) we can canonically extend f to take as input matrices \(\mathbf {X}\), where the function f is applied to each row individually. In fact, if the function f is represented by a column vector \(\mathbf {f}\), we can evaluate f on \(\mathbf {X}\) by computing \(\mathbf {X} \cdot \mathbf {f}\). Moreover, for a column vector \(\mathbf {a}\) and a row vector \(\mathbf {b}\) we let \(\mathbf {a} \cdot \mathbf {b}\) denote the outer product of \(\mathbf {a}\) and \(\mathbf {b}\). This allows us to put a row vector \(\mathbf {x}\) into a certain slot i by computing \(\mathbf {b}_i \cdot \mathbf {x}\), where \(\mathbf {b}_i\) is the i-th unit vector. Consequently, this lets us conveniently write \(f(\mathbf {b}_i \cdot \mathbf {x}) = \mathbf {b}_i \cdot f(\mathbf {x})\), where f is a linear function taking row vectors as inputs as above. For a linearly homomorphic scheme \(\mathsf {HE}\) with message space  , we denote inputs as column vectors. We can encrypt a message \(\mathsf {m}\) into the i-th slot by computing \(\mathsf {HE}.\mathsf {Enc}(\mathsf {pk}_2,\mathsf {m}\cdot \mathbf {b}_i)\), where
, we denote inputs as column vectors. We can encrypt a message \(\mathsf {m}\) into the i-th slot by computing \(\mathsf {HE}.\mathsf {Enc}(\mathsf {pk}_2,\mathsf {m}\cdot \mathbf {b}_i)\), where  is the i-th unit column vector.
is the i-th unit column vector.

4.3 Analysis
The security of our scheme is shown in the following. Recall that for LWE-based FHE schemes, e.g., [1, 19, 24], the LWE modulus is a system parameter which can be provided as an input to the \(\mathsf {KeyGen}\) algorithm. By [27] that worst-case hardness of the underlying LWE problem is not affected.
Theorem 1 (Semantic Security)
Assume that \(\mathsf {FHE}\) and \(\mathsf {HE}\) are semantically secure encryption schemes, then the scheme \(\overline{\mathsf {FHE}}\) as described above is also semantically secure.
Proof (Sketch)
Let \(\mathcal {A}\) be a PPT adversary against the semantic security of \(\overline{\mathsf {FHE}}\). Consider a hybrid experiment where we compute the compression key by
for all \(i \in [k]\). By the semantic security of \(\mathsf {HE}\) the adversary \(\mathcal {A}\) will not detect this change. In a second hybrid modification, we replace the challenge ciphertext by an encryption of 0. It follows from the semantic security of \(\mathsf {FHE}\) that the advantage of \(\mathcal {A}\) in this hybrid is at most a negligible amount smaller than in the last hybrid. Since the advantage of \(\mathcal {A}\) in this final experiment is 0, it follows that \(\mathcal {A}\)’s advantage is negligible.
The more interesting aspects of this construction is its correctness.
Theorem 2 (Correctness)
Assume the FHE scheme \(\mathsf {FHE}\) has decryption noise at most \(B_{\mathsf {FHE}}\), the HE scheme has decryption noise at most \(B_{\mathsf {HE}}\) and that \(\mathsf {HE}\) has shrinking correctness for noise up to \(K \ge \ell \cdot B_{\mathsf {FHE}} + k \cdot n \cdot B_{\mathsf {HE}}\). Then the scheme \(\overline{\mathsf {FHE}}\) has compression correctness.
Proof
Fix a public key \(\mathsf {pk}= (\mathsf {pk}_1,\mathsf {pk}_2,\mathsf {ck})\) where \(\mathsf {pk}_2\) defines a message space  and a secret key \(\mathsf {sk}= (\mathsf {sk}_1,\mathsf {sk}_2)\). Further fix ciphertexts \((\mathsf {c}_1,\dots ,\mathsf {c}_\ell )\) such that \(\mathsf {c}_i\) is a valid encryption of \(\mathsf {m}_i\). Let \(\mathbf {\mathsf {m}} = (\mathsf {m}_1,\dots ,\mathsf {m}_\ell )\). Let the linear function f be defined by
and a secret key \(\mathsf {sk}= (\mathsf {sk}_1,\mathsf {sk}_2)\). Further fix ciphertexts \((\mathsf {c}_1,\dots ,\mathsf {c}_\ell )\) such that \(\mathsf {c}_i\) is a valid encryption of \(\mathsf {m}_i\). Let \(\mathbf {\mathsf {m}} = (\mathsf {m}_1,\dots ,\mathsf {m}_\ell )\). Let the linear function f be defined by
Consider the ciphertext \(\mathsf {c}' = \mathsf {HE}.\mathsf {Eval}(\mathsf {pk}_2,f,(\mathsf {ck}_1,\dots ,\mathsf {ck}_k))\). As \(\mathsf {ck}_i = \mathsf {HE}.\mathsf {Enc}(\mathsf {pk}_2,\mathbf {b}_i \cdot \mathsf {sk}_1)\), it holds by the relaxed homomorphic correctness of \(\mathsf {HE}\) that
where \(\Vert \mathbf {z} \Vert _{\infty } \le k \cdot n \cdot B_{\mathsf {HE}}\). Moreover, it holds that
where \(\mathbf {e} = \sum _{i = 1}^k \mathbf {b}_i \cdot (\sum _{j=1}^\ell e_{ij})\) and \(\mathbf {T} = (t_{ij})\) is the encoding matrix. Since it holds that \(|e_{ij}| \le B_{\mathsf {FHE}}\), we get that \(\Vert \mathbf {e}\Vert _\infty \le \ell \cdot B_{\mathsf {FHE}}\). Consequently, it holds that
Since \(\Vert \mathbf {z} + \mathbf {e} \Vert _\infty \le \Vert \mathbf {z} \Vert _\infty + \Vert \mathbf {e} \Vert _\infty \le k \cdot n \cdot B_{\mathsf {HE}} + \ell \cdot B_{\mathsf {FHE}} \le K\), by the shrinking correctness of \(\mathsf {HE}\) we have that
This shows that \(\overline{\mathsf {FHE}}\) has compression correctness.
4.4 Instantiating with Rate 1
A suitable FHE scheme which readily supports linear decrypt-and-multiply is the GSW scheme [19] and its variants [1, 8, 24]. For the Brakerski-Vaikuntanathan variant of this scheme [8], we can set things up such that the decryption noise-bound \(B_{\mathsf {FHE}}\) is polynomial in \(\lambda \) (see Sect. 2.4). Correctness is achieved by choosing a sufficiently large polynomial modulus q.
When instantiating the linearly homomorphic scheme \(\mathsf {HE}\) with our packed Regev encryption that supports ciphertext shrinking (see Sects. 3.2 and 3.3), we obtain the following. Assume that the decryption noise of the FHE scheme \(\mathsf {FHE}\) is some polynomial \(B_{\mathsf {FHE}}\). Moreover, let  be the decryption noise of \(\mathsf {HE}\) for some fixed B-bounded error distribution \(\chi \) over
be the decryption noise of \(\mathsf {HE}\) for some fixed B-bounded error distribution \(\chi \) over  . By Theorem 2 we need to setup \(\mathsf {HE}\) (via the choice of the modulus q) such that we have shrinking correctness for noise up to \(K \ge \ell \cdot B_{\mathsf {FHE}} + k \cdot n \cdot B_{\mathsf {HE}}\). In turn, by Lemma 1 we can achieve this if \(q > 4 \ell K\). Consequently, since \(B_{\mathsf {FHE}}\), \(B_{\mathsf {HE}}\), and therefore K are of size
. By Theorem 2 we need to setup \(\mathsf {HE}\) (via the choice of the modulus q) such that we have shrinking correctness for noise up to \(K \ge \ell \cdot B_{\mathsf {FHE}} + k \cdot n \cdot B_{\mathsf {HE}}\). In turn, by Lemma 1 we can achieve this if \(q > 4 \ell K\). Consequently, since \(B_{\mathsf {FHE}}\), \(B_{\mathsf {HE}}\), and therefore K are of size  , we can choose q of size
, we can choose q of size  and achieve a polynomial modulus-to-noise ratio
and achieve a polynomial modulus-to-noise ratio  for the underlying LWE problem. For this scheme the encoding matrix \(\mathbf {T}\) is given by \(\mathbf {T} = \frac{q}{2} \cdot \mathbf {I}\), where
for the underlying LWE problem. For this scheme the encoding matrix \(\mathbf {T}\) is given by \(\mathbf {T} = \frac{q}{2} \cdot \mathbf {I}\), where  is the identity matrix (see Sect. 3.3). The overall rate of this scheme is exactly the same as that of \(\mathsf {HE}\), which, as we’ve analyzed in Sect. 3.3. That is, for length \(\ell \) messages we have
is the identity matrix (see Sect. 3.3). The overall rate of this scheme is exactly the same as that of \(\mathsf {HE}\), which, as we’ve analyzed in Sect. 3.3. That is, for length \(\ell \) messages we have  length ciphertexts, and thus for a sufficiently large
length ciphertexts, and thus for a sufficiently large  the rate is \((1-1/\lambda )\).
the rate is \((1-1/\lambda )\).
5 Fully-Homomorphic Time-Lock Puzzles
We propose a construction for a fully-homomorphic time-lock puzzle \(\mathsf {FHTLP}\). The scheme builds on the similar ideas as our rate-1 FHE construction, except that we have to explicitly use a multi-key fully-homomorphic encryption scheme with linear decrypt-and-multiply, due to the distributed nature of homomorphic time-lock puzzles. Below we describe a simplified construction that encapsulates only binary secrets, however we can easily turn it into a rate-1 scheme by using a high-rate LH-TLP and packing vectors of binary messages into a single puzzle via standard techniques.

5.1 Analysis
In the following we analyze the security and the correctness of our scheme.
Theorem 3 (Security)
Let \(\mathsf {MK}\text {-}\mathsf {FHE}\) be a semantically secure multi-key encryption scheme and let \(\mathsf {TLP}\) be a secure time-lock puzzle, then the scheme \(\mathsf {FHTLP}\) as described above is secure.
Proof
We analyze only fresh (non-evaluated) puzzles without loss of generality. The distribution ensemble induced by the view of the adversary corresponds to
over the random choices of the public parameters and the random coins of the algorithms. By the security of \(\mathsf {TLP}\) it holds that, for all PPT adversaries of depth at most T, the latter distribution is computationally indistinguishable from
We are now in the position of invoking the semantic security of the \(\mathsf {MK}\text {-}\mathsf {FHE}\) scheme. By a standard reduction, the following distribution
is computationally indistinguishable from the previous one. Although this holds for any PPT adversary, we remark in our case even computational indistinguishability against depth-bounded attackers would suffice. The proof is concluded by observing that the last distribution hides the secret information-theoretically.
What is left to be shown is that the scheme is correct.
Theorem 4 (Correctness)
Assume the MK-FHE scheme \(\mathsf {MK}\text {-}\mathsf {FHE}\) has decryption noise at most \(B_{\mathsf {MK}\text {-}\mathsf {FHE}}\) and that \(q > 4\cdot B_{\mathsf {MK}\text {-}\mathsf {FHE}}\). Then the scheme \(\mathsf {FHTLP}\) as described above is (single-hop) correct.
Proof
We unfold the computation of the solving algorithm of the underlying time-lock puzzle.
by the correctness of the \(\mathsf {TLP}\) scheme and of the \(\mathsf {MK}\text {-}\mathsf {FHE}\) decrypt-and-multiply, respectively. By our choice of parameters \(|e| \le B_{\mathsf {MK}\text {-}\mathsf {FHE}}\) (with all but negligible probability) and therefore the decryption algorithm returns the correct bit with overwhelming probability.
5.2 Instantiation
A linearly-homomorphic time-lock puzzle has been recently proposed in [22]. In this construction, all users in the system share the public parameters
where T is the parameter that dictates the hardness of the puzzle and g is the generator of  (with Jacobi symbol \(+1\)). For a secret
(with Jacobi symbol \(+1\)). For a secret  , each user can locally generate a puzzle computing
, each user can locally generate a puzzle computing
where  . The puzzle can be solved by raising the first element to the power of \(2^T\) and removing the blinding factor from the second term. Once \((N+1)^\mathsf {s}\) is known, \(\mathsf {s}\) can be recovered efficiently using the polynomial-time discrete logarithm algorithm from [26]. The puzzle hides the message up to time T assuming the inherent sequentiality of squaring in groups of unknown order. The scheme is linearly-homomorphic over the ring
. The puzzle can be solved by raising the first element to the power of \(2^T\) and removing the blinding factor from the second term. Once \((N+1)^\mathsf {s}\) is known, \(\mathsf {s}\) can be recovered efficiently using the polynomial-time discrete logarithm algorithm from [26]. The puzzle hides the message up to time T assuming the inherent sequentiality of squaring in groups of unknown order. The scheme is linearly-homomorphic over the ring  and can be generalized in the same spirit as the Damgård-Jurik approach to achieve rate 1 (see [22] for more details). As discussed in Sect. 2.4, we can use the LWE-based MK-FHE scheme of [24] (which supports linear decrypt-and-multiply) with an externally provided modulus \(q = N\). Hardness of the underlying LWE problem for arbitrary (worst-case) moduli follows by [27].
and can be generalized in the same spirit as the Damgård-Jurik approach to achieve rate 1 (see [22] for more details). As discussed in Sect. 2.4, we can use the LWE-based MK-FHE scheme of [24] (which supports linear decrypt-and-multiply) with an externally provided modulus \(q = N\). Hardness of the underlying LWE problem for arbitrary (worst-case) moduli follows by [27].
Notes
- 1.
We note that the modulus-to-noise ratio does depend (linearly) on \(\ell \).
References
Alperin-Sheriff, J., Peikert, C.: Faster bootstrapping with polynomial error. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 297–314. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_17
Boyle, E., Gilboa, N., Ishai, Y.: Breaking the circuit size barrier for secure computation under DDH. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9814, pp. 509–539. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53018-4_19
Boyle, E., Kohl, L., Scholl, P.: Homomorphic secret sharing from lattices without FHE. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019. LNCS, vol. 11477, pp. 3–33. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17656-3_1
Brakerski, Z., Döttling, N.: Two-message statistically sender-private OT from LWE. In: Beimel, A., Dziembowski, S. (eds.) TCC 2018. LNCS, vol. 11240, pp. 370–390. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03810-6_14
Brakerski, Z., Gentry, C., Halevi, S.: Packed ciphertexts in LWE-based homomorphic encryption. In: Kurosawa, K., Hanaoka, G. (eds.) PKC 2013. LNCS, vol. 7778, pp. 1–13. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36362-7_1
Brakerski, Z., Gentry, C., Vaikuntanathan, V.: (Leveled) fully homomorphic encryption without bootstrapping. In: Goldwasser, S. (eds.) ITCS 2012, pp. 309–325. ACM, January 2012
Brakerski, Z., Vaikuntanathan, V.: Efficient fully homomorphic encryption from (standard) LWE. In: Ostrovsky, R. (eds.) 52nd FOCS, pp. 97–106. IEEE Computer Society Press, October 2011
Brakerski, Z., Vaikuntanathan, V.: Lattice-based FHE as secure as PKE. In: Naor, M. (eds.) ITCS 2014, pp. 1–12. ACM, January 2014
Canetti, R., Lin, H., Tessaro, S., Vaikuntanathan, V.: Obfuscation of probabilistic circuits and applications. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 468–497. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_19
Chor, B., Goldreich, O., Kushilevitz, E., Sudan, M.: Private information retrieval. In: 36th FOCS, pp. 41–50. IEEE Computer Society Press, October 1995
Clear, M., McGoldrick, C.: Multi-identity and multi-key leveled FHE from learning with errors. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 630–656. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_31
Damgård, I., Jurik, M.: A generalisation, a simplification and some applications of Paillier’s probabilistic public-key system. In: Kim, K. (ed.) PKC 2001. LNCS, vol. 1992, pp. 119–136. Springer, Heidelberg (2001)
Dodis, Y., Halevi, S., Rothblum, R.D., Wichs, D.: Spooky encryption and its applications. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9816, pp. 93–122. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53015-3_4
Döttling, N., Garg, S., Ishai, Y., Malavolta, G., Mour, T., Ostrovsky, R.: Trapdoor hash functions and their applications. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11694, pp. 3–32. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26954-8_1
Gentry, C.: Fully homomorphic encryption using ideal lattices. In: Mitzenmacher, M. (eds.) 41st ACM STOC, pp. 169–178. ACM Press, May/June 2009
Gentry, C., Halevi, S.: Fully homomorphic encryption without squashing using depth-3 arithmetic circuits. In: Ostrovsky, R. (eds.) 52nd FOCS, pp. 107–109. IEEE Computer Society Press, October 2011
Gentry, C., Halevi, S.: Compressible FHE with applications to PIR. Technical report (personal communication) (2019)
Gentry, C., Halevi, S., Vaikuntanathan, V.: i-hop homomorphic encryption and rerandomizable Yao circuits. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 155–172. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_9
Gentry, C., Sahai, A., Waters, B.: Homomorphic encryption from learning with errors: conceptually-simpler, asymptotically-faster, attribute-based. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 75–92. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_5
Goldwasser, S., Micali, S.: Probabilistic encryption and how to play mental poker keeping secret all partial information. In: 14th ACM STOC, pp. 365–377. ACM Press, May 1982
Impagliazzo, R., Levin, L.A., Luby, M.: Pseudo-random generation from one-way functions (extended abstracts). In: 21st ACM STOC, pp. 12–24. ACM Press, May 1989
Malavolta, G., Thyagarajan, S.A.K.: Homomorphic time-lock puzzles and applications. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11692, pp. 620–649. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26948-7_22
Micciancio, D.: From linear functions to fully homomorphic encryption. Technical report (2019). https://bacrypto.github.io/presentations/2018.11.30-Micciancio-FHE.pdf
Mukherjee, P., Wichs, D.: Two round multiparty computation via multi-key FHE. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 735–763. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_26
Ostrovsky, R., Paskin-Cherniavsky, A., Paskin-Cherniavsky, B.: Maliciously circuit-private FHE. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 536–553. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_30
Paillier, P.: Public-key cryptosystems based on composite degree residuosity classes. In: Stern, J. (ed.) EUROCRYPT 1999. LNCS, vol. 1592, pp. 223–238. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48910-X_16
Peikert, C., Regev, O., Stephens-Davidowitz, N.: Pseudorandomness of ring-LWE for any ring and modulus. In: Hatami, H., McKenzie, P., King, V. (eds.) 49th ACM STOC, pp. 461–473. ACM Press, June 2017
Peikert, C., Vaikuntanathan, V., Waters, B.: A framework for efficient and composable oblivious transfer. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 554–571. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_31
Quach, W., Wee, H., Wichs, D.: Laconic function evaluation and applications. In: Thorup, M. (eds.) 59th FOCS, pp. 859–870. IEEE Computer Society Press, October 2018
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. In: Gabow, H.N., Fagin, R. (eds.) 37th ACM STOC, pp. 84–93. ACM Press, May 2005
Rivest, R.L., Shamir, A., Wagner, D.A.: Time-lock puzzles and timed-release crypto. Technical report, Cambridge, MA, USA (1996)
van Dijk, M., Gentry, C., Halevi, S., Vaikuntanathan, V.: Fully homomorphic encryption over the integers. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 24–43. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_2
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 International Association for Cryptologic Research
About this paper
Cite this paper
Brakerski, Z., Döttling, N., Garg, S., Malavolta, G. (2019). Leveraging Linear Decryption: Rate-1 Fully-Homomorphic Encryption and Time-Lock Puzzles. In: Hofheinz, D., Rosen, A. (eds) Theory of Cryptography. TCC 2019. Lecture Notes in Computer Science(), vol 11892. Springer, Cham. https://doi.org/10.1007/978-3-030-36033-7_16
Download citation
DOI: https://doi.org/10.1007/978-3-030-36033-7_16
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-36032-0
Online ISBN: 978-3-030-36033-7
eBook Packages: Computer ScienceComputer Science (R0)





 , we can construct a scheme where the ciphertext length is at most
, we can construct a scheme where the ciphertext length is at most  .
. , while secret keys are vectors
, while secret keys are vectors  , regardless of the depth parameter. More concretely, there exists an efficient algorithm
, regardless of the depth parameter. More concretely, there exists an efficient algorithm 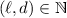 , where
, where  such that
such that 
 , for some fixed polynomial
, for some fixed polynomial  .
. . Compute the union of intervals
. Compute the union of intervals 
 . For
. For  uniformly at random. Choose
uniformly at random. Choose  uniformly at random and sample
uniformly at random and sample  . Set
. Set  and set
and set 